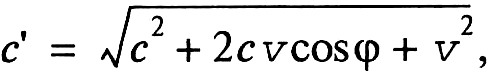[вернуться к содержанию сайта]

    Показано, что баллистическая гипотеза Ритца, основанная на предположении о векторном сложении скорости света со скоростью источника излучения, находится в противоречии с фактом существования эффекта Саньяка. На частном примере трёхзеркального кольцевого интерферометра показано, что применение баллистической гипотезы Ритца приводит к явной расчётной ошибке – возникновению разности времён распространения встречных волн при отсутствии вращения. Проведён обзор экспериментов, а также результатов обработки астрономических наблюдений и дискуссий, посвящённых проверке баллистической гипотезы Ритца. Рассмотрен ряд других физических явлений, опровергающих баллистическую гипотезу Ритца.

    Постоянство скорости света является вторым постулатом специальной теории относительности (СТО) [1]. Вот как сформулировал второй постулат СТО А. Эйнштейн в свой основополагающей работе [1] "...свет в пустоте всегда распространяется с определённой скоростью V, не зависящей от состояния движения излучающего тела". Таким образом, второй постулат СТО фактически содержит два утверждения,

    1) скорость света постоянна для произвольного направления распространения;

    2) скорость света не зависит от скорости источника излучения.

    Здесь и далее речь идёт о физической скорости света в вакууме, которая может быть измерена ¹.

    Первое утверждение второго постулата СТО и возможности его экспериментальной проверки были подробно рассмотрены нами в [4–10]. Ниже рассмотрим вопросы, связанные со вторым утверждением второго постулата СТО. Это, в первую очередь, критический анализ так называемой баллистической гипотезы Ритца [11, 12], утверждающей, что скорость света складывается со скоростью источника излучения. Несмотря на то, что в последние 70–80 лет подавляющее большинство исследователей не сомневается в справедливости СТО, у баллистической гипотезы Ритца имеются сторонники. Так было и в первой половине прошлого века [13], так есть и в настоящее время [14–17], вследствие чего баллистическая гипотеза нуждается в серьёзном критическом рассмотрении.

    Цель настоящей работы – показать, что факт существования эффекта Саньяка [18–20] (см. также [3, 21–25]) опровергает баллистическую гипотезу Ритца [11, 12], в рамках которой этот эффект не должен иметь места. Напомним, что эффект Саньяка [18–20] заключается в том, что на выходе вращающегося кольцевого интерферометра возникает разность фаз встречных волн, которая пропорциональна угловой скорости вращения и площади интерферометра [3, 18–25]. Как показано в [3, 22–25], эффект Саньяка является эффектом СТО. Эффект Саньяка уже давно нашёл практическое применение. На его основе функционируют датчики угловой скорости вращения: лазерные [26] и волоконно-оптические [27] гироскопы.

    Данная работа преследует ещё одну цель – рассмотреть различные эксперименты и результаты обработки астрономических наблюдений, посвящённых проверке баллистической гипотезы Ритца и других, близких к ней эмиссионных теорий, а также кратко осветить дискуссию по данному вопросу, которая началась сто лет назад и продолжается по сей день. Будет также рассмотрен ряд других физических явлений, опровергающих баллистическую гипотезу Ритца.

    Первые эмиссионные теории света, к числу которых относится и баллистическая гипотеза Ритца, возникли ещё в XVII веке [28, 29] и стали общепринятыми после создания в XVIII веке И. Ньютоном (1643–1727) корпускулярной теории света [30, 31]. Волновая теория света, которой придерживались Р. Гук (1635–1703) [32, 33] и X. Гюйгенс (1629–1695) [34], не получила в то время широкого признания в связи с высоким авторитетом Ньютона. Однако в самом конце XVIII–начале XIX веков в связи с разработкой Т. Юнгом (1773-1829) и О. Френелем (1788-1827) волновой теории света [28, 29] эмиссионная теория, которая с большими натяжками объясняла явления дифракции и интерференции света, испытала глубокий кризис. Тем не менее у неё имелось ещё немало сторонников. Эксперименты Ф.Д. Араго (1786–1853) [35, 36] (проведённые и доложенные в Академии наук Франции в 1810 г., но опубликованные им только спустя сорок три года), показавшие, что коэффициент преломления призмы не зависит от скорости источника излучения (различных звёзд и планет – Арктура, Альдебарана, Антареса, Ригель, α Змеи, α Кита, β и δ Льва, α Ориона, Сириуса, Луны и др.) убедили далеко не всех ².

    Вскоре после создания СТО в 1908 г. В. Ритц (1879–1909, о нём [39]) разработал довольно совершенную эмиссионную теорию света – так называемую баллистическую гипотезу Ритца [11, 12] ³, которая была направлена не только против СТО, но и главным образом против электродинамики Максвелла. В частности, работы [11, 12] объясняли результаты экспериментов Майкельсона–Морли [41–43], поскольку в ходе этих экспериментов источник излучения всегда находился в одной инерциальной системе отсчёта (ИСО) с интерферометром Майкельсона и, следовательно, скорость света в интерферометре независимо от того, в какой ИСО он находился, всегда составляла с – скорость света в вакууме. В общем случае в соответствии с гипотезой Ритца [11, 12] с'= с + v, где с – вектор скорости света в вакууме относительно источника, v – вектор скорости источника излучения и с' – вектор результирующей скорости света. Иными словами, абсолютная величина с' составляет

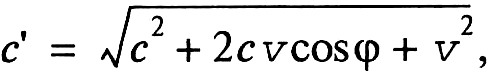                       (1)

где φ – угол между направлением скорости источника излучения и направлением распространения света, испущенного источником, относительно самого источника. Отметим, что баллистическая гипотеза Ритца [11, 12] предполагает отсутствие так называемого "светоносного эфира".

    В период 1910–1913 гг. был опубликован ряд работ [44–58], в которых также обсуждалась возможность зависимости скорости света от скорости источника излучения и возможности экспериментальной проверки этих предположений. В частности, рассматривались различные варианты эмиссионных теорий света [44, 49–51]. Как показано в [54, 59–63], все эти варианты совпадают с баллистической гипотезой Ритца в утверждении о векторном сложении скорости света со скоростью источника излучения (т.е. в направлении движения источника свет должен иметь скорость с'= с + v), но существенно различаются в вопросе о скорости света, отражённого от зеркала, и соответственно в вопросе о величине эффекта Допплера для отражённого луча.

    В частности, в соответствии с баллистической гипотезой Ритца [11, 12] если источник света движется, то скорость отражённого (при нормальном падении) луча света равна скорости света, испущенного фиктивным источником, расположенным за зеркалом и движущимся в том же направлении и с той же скоростью, что и первичный источник, т.е. с'= с – v. Движение зеркала в соответствии с [11, 12] никоим образом не влияет на скорость отражённого луча света ⁴. Следовательно, согласно [11, 12], релятивистский эффект Допплера должен совпадать с классическим эффектом Допплера.

    В соответствии с эмиссионной теорией Дж.Дж. Томсона (1856-1940) [44] и О.М. Стюарта (1869-1944, о нём [64, 65]) [51], если источник света движется, а зеркало неподвижно, скорость отражённого луча света должна составлять с'= с + v, а если источник неподвижен, а зеркало движется навстречу источнику, то с'= с + 2v (где в данном случае v – скорость зеркала). Таким образом, в рамках [44, 51] фотон ведёт себя подобно мячику, отскочившему от движущейся стенки.

    В соответствии с эмиссионной теорией Р.Ч. Толмена (1881–1948) [49, 50] если источник света движется, а зеркало неподвижно, скорость отражённого луча света должна составлять с'= с, а если источник неподвижен, а зеркало движется навстречу источнику, то с'= с + v (где в данном случае v – скорость зеркала).

    Таким образом, согласно В. Ритцу [11, 12] релятивистский эффект Допплера должен совпадать с классическим эффектом Допплера, согласно Дж.Дж. Томсону и О.М. Стюарту [44, 51], эффект Допплера должен отсутствовать, а согласно Р. Толмену [49, 60] – составлять половину от классического. Эти вопросы подробно рассмотрены в [54, 59-63].

    Измерение эффекта Допплера от вращающегося зеркала. Эксперименты Белопольского. Голицына–Вилипа. Майкельсона. Фабри–Бьюссона и Майораны. Поскольку в 10-е годы прошлого века были уже широко известны эксперименты с вращающимся зеркалами А.А. Белопольского (1854-1934, о нём [66, 67]) [68-72], а также князя Б.Б. Голицына (1862-1916) и И. Вилипа (1870-1942) [73–76], продемонстрировавшие существование классического эффекта Допплера в оптике (см. также монографию У.И. Франкфурта (1908-1982) и А.М. Френка (1928-1979) [61]), то было очевидно, что эмиссионные теории Томсона–Стюарта [44, 51] и Толмена [49, 50] не соответствуют действительности. Тем не менее Р.Ч. Толмен [50] и М.Ла Роза (1880–1933, профессор университета в Палермо, о нём [77]) [56–58] предложили провести проверку баллистических теорий света с помощью интерферометра Майкельсона с движущимся источником излучения. В 1913–1918 гг. А.А. Майкельсон (1852-1931) [78], Ш. Фабри (1867-1945) и Г. Бьюссон [79, 80] и К. Майорана (1871–1956, в то время профессор Политехнического института в Турине, в дальнейшем контр-адмирал военно-морского флота Италии, действительный член академии деи Линчей, президент итальянского физического общества, о нём [81]) [82–85] провели новые эксперименты по измерению эффекта Допплера в интерферометре Майкельсона со светом от вращающихся зеркал ⁵, также показавших полную несостоятельность теорий Томсона–Стюарта [44, 51] и Толмена [49, 50]. Оставалось лишь опровергнуть баллистическую гипотезу Ритца [11, 12], для чего был необходим непосредственно движущийся источник излучения, а не движущиеся зеркала, отражающие свет от неподвижного источника.

    Измерение сдвига интерференционных полос в интерферометре Майкельсона с движущимся источником излучения. Эксперименты Майораны. Томашека и Миллера. К. Майорана осуществил эксперименты по измерению эффекта Допплера с интерферометром Майкельсона и вращающимся на штанге источником излучения [87], показавшие отсутствие влияния скорости источника на сдвиг интерференционных полос. Однако доказательная сила этих экспериментов была оспорена в работе Ф. Мишо [88] (см. также [55, 59]), где было показано, что поскольку в [86] при изменении скорости источника излучения одновременно меняется и расстояние от него до входного делительного зеркала интерферометра, то в первом порядке по величине v/c искомый эффект должен отсутствовать вне зависимости от того, справедлива или нет баллистическая гипотеза Ритца. А эффекты более высоких порядков по v/c в таких измерениях в то время зарегистрировать было ещё невозможно.

    Как ранее указали Р.Ч. Толмен [54] и М. Ла Роза [56–58] (см. также [55, 59]), для наблюдения эффектов первого порядка по v/c необходимо использовать интерферометр Майкельсона и движущийся внеземной источник излучения, например, Солнце. Такие эксперименты в 1923–1924 гг. провёл аспирант Ф. Ленарда (1862–1947) – астроном, астролог [89, 90], химик [91] и геофизик [91] Р. Томашек (1895-1966, о нём [91]) [92, 93]. В качестве движущегося источника излучения использовались различные звёзды и планеты: Солнце, Луна, Юпитер, Сириус, Арктур, Вега. Результаты измерений [92, 93], которые проводились в течение нескольких месяцев, показали, что баллистическая гипотеза Ритца [11, 12] неверна. Однако сторонников этой гипотезы эксперименты Р. Томашека [91, 92] не убедили, поскольку свет от внеземных источников излучения проходил атмосферу Земли и оптические среды в интерферометре и вследствие этого по их мнению мог изменить величину первоначальной скорости.

    Следует отметить, что эксперименты с интерферометром Майкельсона и Солнцем в качестве движущегося источника излучения в первой половине 20-х гг. прошлого века осуществил также Д.К. Миллер (1866-1941) [94-96]. Д. К. Миллер не занимался проверкой баллистической гипотезы Ритца [11, 12], а повторял на более высоком уровне точности эксперименты Майкельсона–Морли [41–43] с целью обнаружения так называемого "эфирного ветра", т.е., иными словами, проверял первое утверждение второго постулата СТО. В ходе измерений [94–96] наблюдалась некоторая систематическая зависимость сдвига интерференционных полос от угловой ориентации интерферометра, которая, как полагал Д.К. Миллер, была связана с движением Земли относительно "светоносного эфира". Это позволило впоследствии некоторым сторонникам баллистической гипотезы Ритца утверждать, что эксперименты Д.К. Миллера подтверждают её справедливость. Однако следует особо отметить, что в ходе экспериментов [94–96] не было обнаружено различия в случаях, когда использовались неподвижный относительно интерферометра источник излучения или Солнце. Следовательно, результаты [94–96] также демонстрируют ошибочность баллистической гипотезы Ритца [11, 12]. Результаты экспериментов Май-кельсона–Морли [41–43] и их повторений обсуждались на специально проведённой 4–5 февраля 1927 г. в обсерватории на Маунт-Вильсон (Пасадена, Калифорния) конференции, на которой присутствовало большое число известных физиков и астрономов, в том числе А.А. Майкельсон и Г.А. Лоренц (1853–1928) [97]. Большая часть дискуссии была посвящена результатам экспериментов Д.К. Миллера [94, 95], однако участники конференции не пришли к определённым выводам. Проведённый в 1955 г. детальный анализ условий проведения экспериментов Миллера [94–96] показал, что в них имела место систематическая ошибка, связанная с температурным дрейфом длин плеч интерферометра Майкельсона [98]. Отметим, что как вскоре после проведения экспериментов Д.К. Миллера [94, 95], так и позднее проводилось большое число повторений экспериментов типа Майкельсона–Морли [41–43], но на всё возрастающем уровне точности (они рассмотрены в обзорах [6, 28, 61, 99, 100], перевод некоторых из этих работ на русский язык приводится в сборнике [101]), показавших отсутствие влияния гипотетического "светоносного эфира" на результаты измерений.

    Эксперименты Бонч-Бруевича. После окончания Второй мировой войны президент АН СССР СИ. Вавилов (1891–1951) поручил своему докторанту, демобилизированному офицеру А.М. Бонч-Бруевичу (1916–2006) провести данные измерения в лабораторных условиях на высоком уровне точности. Замысел С.И. Вавилова состоял в том, чтобы измерять не саму скорость света от движущегося источника излучения, а зависимость времени прохождения света, испущенного быстрыми атомами водорода, дейтерия или трития, возникшими в процессе диссоциации ускоренных электрическим полем протонов или ионов дейтерия или трития (так называемые каналовые лучи), от скорости атомов. Уже после смерти С.И. Вавилова выяснилось, что в то время в земных условиях невозможно было добиться необходимой точности измерений. По совету Г.С. Ландсберга (1890–1957) Бонч-Бруевич в качестве источника излучения использовал Солнце, поскольку вследствие его вращения один из его краёв приближается к Земле со скоростью ≈1.95 км/с, а другой удаляется с такой же скоростью. Эксперименты [102, 103] заключались в сопоставлении времён, затрачиваемых на прохождение пути 2000 м светом, испущенным двумя движущимися с различной скоростью источниками – краями Солнца. Специально для этого была разработана измерительная аппаратура [104–106]. Результаты соответствующих измерений [102, 103] подтвердили справедливость СТО. Если предположить, что скорость света лишь частично складывается со скоростью источника излучения, т.е. с'= с + kv, где k – некоторый коэффициент (k= 1 для баллистической гипотезы Ритца и k= 0 для СТО)⁶, то эксперименты [102, 103] показали, что k= 0.02 ± 0.07. Тем не менее проведённые A.M. Бонч-Бруевичем повторные оценки точности измерений показали, что вероятность зависимости скорости света от скорости источника не превышает 10^-45 [109]. Однако к экспериментам [102, 103] противниками СТО могут быть предъявлены те же претензии, что и к экспериментам Р. Томашека [92, 93] – свет от краёв Солнца проходил через атмосферу Земли, оптические среды в акустооптическом модуляторе и других элементах измерительного устройства, а также отражался от зеркал. Как отмечено в работе А.М. Бонч-Бруевича и В.А. Молчанова [103]: "...очевидно, что с точки зрения взглядов Томсона и Стюарта применение зеркал в нашем опыте допустимо, но в рамках представлений как Толмена, так и Ритца опыт недоказателен и его результат тривиален вследствие использования зеркал соответственно в целостате и на базе. В связи с этим описанный опыт должен быть дополнен достаточно убедительными экспериментальными данными, показывающими допустимость применения зеркал". Впоследствии А.М. Бонч-Бруевич высказал некоторые дополнительные сомнения в доказательной силе этих экспериментов [110].

    Эксперименты Кантора и их опровержения. В 1962 г. У. Кантор (лаборатория электроники ВМС США, Сан-Диего, Калифорния) провёл эксперименты с кольцевым интерферометром, внутри которого вращались две тонкие стеклянные пластинки толщиной 25 мкм, которые в соответствии с баллистической гипотезой Ритца [11, 12] рассматривались автором в качестве вторичных источников излучения [111]. В ходе измерений для встречных волн был обнаружен сдвиг интерференционных полос, который был проинтерпретирован У. Кантором как подтверждение справедливости баллистической гипотезы Ритца ⁷. Однако вскоре были проведены контрольные эксперименты [117–123] (они подробно рассмотрены в [61]), показавшие ошибочность результатов [111]. Так, в [117] для опровержения результатов [111] использовался тот факт, что различные участки вращающихся стеклянных пластинок имеют различную линейную скорость, однако соответствующих баллистической гипотезе Ритца изменений в интерференционной картине в [111] в пределах точности измерений (по оценке [117] k≤ 0.025) не наблюдалось. В [118] использовалась равномерно движущаяся стеклянная пластинка в интерферометре Цернике, однако в отличие от [111] сдвиг интерференционных полос не наблюдался. В [119] измерения проводились по схеме [111], но на существенно более высоком уровне точности (по оценке [119] k≤0.006), но никакого эффекта, обнаруженного в [111], также не наблюдалось. В [120, 121] измерения [111] были повторены с лазером в качестве источника излучения, в [123] – в вакууме, но вновь результаты [111] не подтвердились – вероятно, в процессе измерений [111] проявилось влияние потоков воздуха. Эксперименты [122] показали, что на результаты [111], по-видимому, повлияли тепловые эффекты. Но эксперименты [117–123] не могли служить опровержением баллистической гипотезы Ритца [11, 12], поскольку в них, как и в рассмотренных выше экспериментах, свет проходил через оптические среды, отражался от зеркал и т.п. Так, эксперименты [123] практически полностью повторяют эксперименты К. Майораны, проведённые в 1934 г. [86], за исключением того, что в качестве источника излучения в [123] использовался Не–Ne-лазер. Поскольку, как следует из баллистической гипотезы Ритца [11, 12], скорость света не зависит от скорости зеркала, то результаты измерений [121], равно как и [86], не могут свидетельствовать ни за, ни против теории Ритца [11, 12], а только лишний раз демонстрируют ошибочность теорий Томсона-Стюарта [44, 51] и Толмена [49, 50] ⁸.

    Более того, ещё раньше вышла работа Дж. Г. Фокса (1908–1985) [125], в которой было показано, что теорема затухания в теории дисперсии [63] требует, чтобы падающая световая волна гасилась на поверхности диэлектрика (оптической среды), и при этом вся информация о скорости света от движущегося источника теряется. Затем световая волна переизлучается в диэлектрике [125]. Следовательно, как эксперименты У. Кантора [111], так и контрольные эксперименты [117–123] заведомо не обладали доказательной силой для подтверждения или опровержения баллистической гипотезы Ритца [11, 12].

    В этом плане существенно большей доказательной силой обладали аналогичные измерения с гамма-лучами от движущихся источников [126–130], поскольку в отличие от света они не поглощаются и соответственно не переизлучаются оптическими средами и, следовательно, в рамках баллистической гипотезы Ритца [11, 12] должны нести информацию о скорости источника излучения, а не оптической среды, находящейся между источником и наблюдателем (приёмником). В работе [131], инициированной публикацией [132], было предложено измерять энергию γ-квантов, возникших в результате распада быстрых π⁰-мезонов. Эксперименты [129, 130] показали, что энергия γ-квантов практически не зависит от скорости π⁰-мезонов и, следовательно, скорость γ-квантов не зависит от скорости источника излучения (измерения [129] показали, что k< (3 ± 13)×10^–5). Эксперименты с измерением скорости γ-квантов, испущенных движущимися и покоящимися ядрами атомов [126, 127], также показали отсутствие зависимости этой скорости от скорости источника излучения (предельная точность таких измерений может быть доведена до k~10^–4). Такой же результат был получен при измерении времени пролета γ-квантов, возникших в результате аннигиляции летящего позитрона с электроном [127]. Работы [126, 128–131] подробно рассмотрены в [61]. Эксперименты с гамма-лучами убедили Дж.Г. Фокса в ошибочности баллистической гипотезы Ритца [133], однако позднее у него вновь возникли некоторые сомнения [134].

    Метод де Ситтера. Можно вообще не ставить сложные и дорогостоящие эксперименты, а провести тщательный анализ результатов уже известных астрофизических наблюдений. На это обстоятельство впервые указал Д.Ф. Комсток (1883–1970), инструктор по теорической физике Массачузетского технологического института [45, 46], а затем Г. Кастелнуово (1865–1952, профессор Римского университета, впоследствии пожизненный сенатор Италии, президент академии деи Линчеи) [52] и М. Ла Роза [57], предложившие проанализировать видимое в телескопе изображение так называемых двойных звёзд. Этот анализ в 1913 г. осуществил голландский астроном и физик В. де Ситтер (1872–1934, о нём [135]), который указал на то обстоятельство, что если бы скорость света зависела от скорости источника излучения, то вращающиеся вокруг общего центра масс двойные звёзды выглядели бы на большом расстоянии весьма искажёнными и в некоторых случаях наблюдалось бы изображение трёх звёзд [136–138], что в реальности не имеет места. Однако сразу же после публикации [136–138] появились работы [107, 108, 139], в которых обсуждались выводы де Ситтера [136–138]. Как отмечено выше, в [107, 108] было высказано предположение, что скорость света лишь частично складывается со скоростью источника излучения, т.е. с'= с + kv, где k – некоторый коэффициент. В. де Ситтер провёл оценку сверху величины k и показал, что k< 0.002 [140, 141]. Однако в постскриптуме к [141] отмечено, что по мнению Кортевега (Korteweg) k<0.12. П. Гутник (1871-1947) полагал, что k= 0.5 [108], а В. Цурхеллен пришёл к выводу, что k≤10^–6 [139].

    Эта дискуссия возобновилась спустя десять лет. На этот раз в качестве непримиримого оппонента В. де Ситтера выступил М. Ла Роза, который утверждал [142–149], что наличие звёзд переменной яркости (цефеид) якобы является прямым доказательством баллистической гипотезы Ритца. По мнению М. Ла Розы цефеиды – это не звёзды переменной яркости, а двойные звёзды, из которых одна тёмная или имеет малую яркость, а вторая – яркая (наблюдаемая звезда). Когда эта звезда движется к наблюдателю, то в соответствии с баллистической гипотезой Ритца скорость испущенного ею света увеличивается и вследствие этого, а также из-за эффекта Допплера она становится ярче. Когда эта звезда движется в обратном направлении, то её яркость соответственно уменьшается. Таким образом, эта звезда кажется переменной [142, 143, 146–149]. В рамках гипотезы М. Ла Розы в случае, если яркость цефеиды меняется по гармоническому закону, то наблюдаемая звезда движется по круговой орбите, если же яркость цефеиды меняется по более сложному закону, то наблюдаемая звезда движется по вытянутой эллиптической орбите, причём большая ось эллипса направлена под некоторым утлом по направлению к Земле, т.е. к наблюдателю.

    В настоящее время такое предположение может показаться абсурдным, но в то время оно ещё могло обсуждаться [150]. Ещё в 1783 г. английский астроном Дж. Гудрайк (1764–1786, о нём [151]) обнаружил [152], что некоторые из переменных звезд – это двойные звёзды, у которых одна периодически перекрывает другую, что и обеспечивает изменение их блеска. Такие звёзды именуются затменными. А.А. Белопольский допускал, что цефеиды – это двойные звёзды, которые меняют свой блеск вследствие эффекта Допплера [153, 154]. Это предположение было сделано им на основании синхронности изменения лучевых скоростей и блеска цефеид.

    Однако ещё в 1896 г. на защите докторской диссертации А.А. Белопольского [153] один из его официальных оппонентов – известный русский физик Н.А. Умов (1846–1915) – указал, что изменение блеска цефеид можно объяснить не движением двойных звёзд, а пульсацией одиночной звезды [66, 67]. Ранее А. Риттер [155] высказал такое же предположение. Отметим, что в период публикации работ Ла Розы [142, 143, 146-148] уже была известна теория пульсирующих цефеид А. Эддингтона (1882-1944) [156, 157]. Окончательную теорию цефеид в 50-е годы прошлого века разработал профессор Горьковского государственного университета С.А. Жевакин (1916–2001, о нём [150, 158]) [159–164]. Уже в его первой работе [159] было показано, что механизмом, поддерживающим автоколебания яркости и в меньшей степени размеров звезды, является отрицательная диссипация во внешней оболочке цефеид, состоящей из дважды ионизированного гелия. Отметим здесь, что в настоящее время теория С.А. Жевакина считается классической [165, 166].

    Различные возражения против баллистической гипотезы переменных звёзд М. Ла Розы [142, 143, 146-149] высказал В. де Ситтер [167-169]⁹, Ч. Нордманн и С. Ле Морван [170], П. Сале [171], Г. Грамацкий (1882-1957, о нём [172, 173]) [174, 175], Г. Тирринг (1888-1976) [176] и В. Бернхаймер [177]. В свою очередь, М. Ла Роза возражал Нордманну и Ле Морвану [178, 179], Тиррингу [180], Сале [180-182] и Бернхаймеру [182]. П. Сале, в свою очередь, опровергал новые аргументы М. Ла Розы [183]. В конце 1932 г. итальянский астроном М. Чеччини (1896-1978, в 1941-1966 гг. директор Туринской обсерватории) провёл обстоятельный анализ астрономических наблюдений различных цефеид [184] и продемонстрировал полную несостоятельность гипотезы М. Ла Розы [142, 143, 146-149]. В заключение [184] М. Чеччини отметил, что баллистическая гипотеза переменных звёзд М. Ла Розы, предполагающая двойную структуру цефеид и, следовательно, баллистическая гипотеза распространения света находятся в противоречии с астрономическими наблюдениями. Ответить на это М. Ла Роза уже не успел – вскоре он умер [77].

    В дальнейшем результаты В. де Ситтера [136–138, 140, 141] ещё не раз оспаривались. Так, в 1953 г. в работе П. Муна (1898-1988) и Д. Спенсер (р. 1920) [185] было указано, что, поскольку метрика Вселенной не является декартовой, то те двойные звёзды, которые ранее наблюдались, находятся недостаточно далеко для того, чтобы с полной уверенностью утверждать об отсутствии указанных В. де Ситтером [136–138, 140, 141] оптических явлений при наблюдении изображений двойных звёзд, которые должны иметь место в случае справедливости баллистической гипотезы Ритца [11, 12]¹⁰. В 1962 г. в работе Дж.Г. Фокса [125] было высказано предположение о том, что двойные звёзды должны иметь общую атмосферу, совершающую вращательное, но не поступательное движение. Следовательно, до Земли доходит свет, испущенный верхним слоем общей атмосферы, а не самими двойными звёздами, и указанные В. де Ситтером [136–138, 140, 141] оптические явления и не должны иметь места. Таким образом, согласно Дж.Г. Фоксу [125], то, что до сих пор никто не наблюдал искажений в изображении двойных звёзд, не является опровержением баллистической гипотезы Ритца [11, 12].

    Точку в затянувшейся дискуссии о видимом изображении двойных звёзд поставила опубликованная в 1977 г. работа сотрудника Массачузеттского технологического института К. Бречера [187], в которой приводились результаты наблюдений двойных звёзд, одна из которых являлась источником гамма-лучей. Как было указано выше, гамма-лучи не поглощаются и соответственно не переизлучаются атмосферой, в том числе и атмосферой двойных звёзд. Тогда в выражении с'= с + kv, как показывают результаты [187], k<2×10^–9.

    Метод Штрёмберга. Существует ещё один способ проверки справедливости баллистической гипотезы Ритца по результатам астрономических наблюдений. Для этого можно использовать сравнение значений звёздной аберрации света, испущенного сравнительно близкими звёздами и отдалёнными галактиками (туманностями), которые в силу расширения Вселенной удаляются от Земли с лучевой скоростью v, определяемой по допплеровскому красному смещению, и в то же время имеющие известную радиальную скорость. Если баллистическая гипотеза Ритца [11, 12] верна, то скорость света от близкой звезды составит ≈с, а от отдалённой галактики с–v, и, следовательно, значения звёздной аберрации от этих источников должна существенно различаться. Точность оценки пропорциональна величине с/(с–v)–1, вследствие чего желательно, чтобы лучевая скорость v по порядку величины была сравнима со скоростью света с. Первым эту идею высказал в 1931 г. американский астроном Дж. Штремберг (1882-1962) [188]. Он обнаружил зависимость красного смещения от расстояния до галактики раньше Е. Хаббла, принимал активное участие в дискуссии на конференции в Пасадене в 1927 г. [97] и оказывал помощь Д.К. Миллеру в обработке его результатов повторения экспериментов Майкельсона–Морли [95, 96]. Обработка результатов астрономических наблюдений группы галактик, наблюдаемых в области созвездия Большой Медведицы, позволила Дж. Штрёмбергу показать, что с'= (0.9997± 0.0024)с. Вскоре Дж. ван Бисбрук (1880–1974) пришёл к аналогичным выводам [189]. В работе [190] результаты работ [188, 189] были подвергнуты критике, однако немецкий астроном О. Хекманн (1901–1983) [191] обнаружил ошибку в работе [190].

    14 ноября 1958 г. на конференции Британского Королевского астрономического общества [192] выступил Г. Дингл (1890–1978, английский астрофизик, президент Королевского астрономического общества, о нём [193]¹¹) с предложением вновь вернуться к рассмотрению баллистической гипотезы Ритца, которая по его мнению имела преимущества перед СТО. В дискуссии приняли участие Г. Бонди, Д. Скиама, Дж. Хитроу и др. В июне 1959 г. на страницах журнала "The Observatory" имела место дискуссия между О. Хекманном [201] и Г. Динглом [202] о зависимости постоянной звёздной аберрации от скорости движения звезды или галактики. Вскоре Г. Дингл вновь предложил провести экспериментальную проверку справедливости СТО [203]. В 1960 г. О. Хекманн, используя известные данные астрономических наблюдений звёздной аберрации, показал ошибочность баллистической гипотезы Ритца [204, 205]. В 1965 г. Р. Диккенс и С. Мэйлин обработали новые результаты астрономических наблюдений и показали отсутствие различия звёздной аберрации для близких звёзд и удалённых галактик [206], что лишний раз опровергает баллистическую гипотезу Ритца (скорость разбегания наблюдаемых галактик в [206], которая определялась по допплеровскому красному смещению, составляла уже (1/15)с). Результаты [206] подробно рассмотрены в [61]). Отметим, что в настоящее время наблюдаются галактики, красное смещение от разбегания которых понижает частоту света в несколько раз и соответственно точность измерений типа [188, 189, 204–206] может быть многократно увеличена. Г. Дингл настаивал на проведении прямой экспериментальной проверки баллистической гипотезы Ритца [132], но A.M. Бонч-Бруевич в своей работе [207] указал на то, что такие измерения осуществлены им ранее [102, 103].

    Метод Александрова. Можно с ещё более существенной точностью показать ошибочность предсказаний баллистической гипотезы Ритца [11, 12]. В 1962 г. Е.Б. Александров (р. 1936 г., действительный член РАН) показал [208]¹², что если бы скорость света зависела от скорости источника, то цефеиды с коротким периодом (1.2–30 ч) на Земле наблюдались бы как звёзды с постоянной яркостью, поскольку тепловой разброс скоростей излучающих частиц плазмы звезды привёл бы к тому, что свет от различных частиц имел бы различную скорость, и на расстояниях, превышающих ~1000 световых лет, происходило бы практически полное усреднение яркости – демодуляция интенсивности излучения. В частности, как показано в [208], для цефеиды RR Лиры коэффициент демодуляции в соответствии с баллистической гипотезой Ритца [11, 12] должен был бы составить e^–3600, или, иными словами, k≤10^–1600.

    Поскольку достаточно удалённые цефеиды прекрасно наблюдаются, то этот факт с весьма высокой точностью подтверждает независимость скорости света от скорости источника. Метод Е.Б. Александрова [208] в настоящее время с наибольшей точностью опровергает баллистическую гипотезу Ритца.

    Противники СТО подвергли критике и это доказательство ошибочности баллистической гипотезы Ритца [16, 17] на основании того, что цефеиды – это не звёзды переменной яркости, а двойные звёзды. То есть в [16, 17] была реанимирована старая гипотеза М. Ла Розы о том, что цефеиды являются двойными звёздами [142, 143, 146–149], уже давно опровергнутая М. Чеччини [184]. Укажем также на возражение Дж.Г. Фокса [134], которое сводилось к тому, что цефеиды имеют внешнюю атмосферу, в которой, так же как и в атмосфере двойных звёзд, происходит поглощение и переизлучение света. Однако возражение [134] является ошибочным, поскольку атомы атмосферы цефеид также имеют разброс по скоростям.

    Эффект Саньяка заключается в том, что во вращающемся кольцевом интерферометре одна встречная волна приобретает временнýю задержку (и соответственно фазовый сдвиг) относительно другой встречной волны, которая прямо пропорциональна угловой скорости вращения и площади, охватываемой интерферометром [23–25]. Это кинематический эффект СТО, являющейся следствием релятивистского закона сложения скоростей – скорости светового импульса (или фазовой скорости волны, если измеряется разность фаз встречных волн) и линейной скорости вращения интерферометра.

    В нашей работе [5] были рассмотрены классические оптические эксперименты, подтверждающие справедливость СТО, а также проведён критический анализ предложенных в разное время преобразований для пространственных координат и времени при переходе из одной ИСО в другую, отличающихся от классических преобразований Лоренца (ПЛ). В [5] было показано, что хотя некоторые из этих преобразований могут объяснить результаты отдельных классических оптических экспериментов и, в частности, экспериментов Майкельсона–Морли [41–43], ни одно из них, за исключением преобразований Тангерлини [4, 9, 210–212] (которые являются корректными и отличаются от ПЛ процедурой синхронизации разнесённых часов в неподвижной – связанной с наблюдателем ИСО, и движущейся ИСО), не может объяснить результаты всей совокупности этих экспериментов. Этот подход можно применить и для проверки корректности баллистической гипотезы Ритца [11, 12]. В случае если предложенное В. Ритцем выражение для суммирования скорости света со скоростью источника не сможет объяснить результаты хотя бы одного из классических оптических экспериментов, то баллистическая гипотеза является ошибочной ¹³.

    Проще всего отсутствие эффекта Саньяка в рамках баллистической гипотезы Ритца может быть продемонстрировано во вращающейся системе отсчёта, сопровождающей вращение кольцевого интерферометра. В этой системе отсчёта источник-приёмник излучения неподвижен и, следовательно, скорости встречных световых волн равны между собой и составляют с. Но и пути встречных световых волн равны между собой и, следовательно, времена, затрачиваемые встречными волнами на обход кольца, также равны. Следовательно, во вращающейся системе отсчёта эффект Саньяка в рамках баллистической гипотезы Ритца не имеет места и, таким образом, баллистическая гипотеза Ритца [11, 12] является ошибочной.

    Отметим, что сходную ошибку допустили авторы работы [213] при рассмотрении эффекта Саньяка для поверхностных акустических и магнитостатических волн (так называемых "медленных" волн [214]. Авторы [213] сложили скорость медленной волны с линейной скоростью вращения среды, в которой эти волны распространяются, и также получили нулевой результат. Ошибка, допущенная авторами [213], подробно рассмотрена в [23, 24].

    Укажем здесь, что в рамках теории относительности вычисление величины эффекта Саньяка в сопровождающей вращение кольцевого интерферометра системе отсчёта осуществляется с использованием нерелятивистского гравитационного потенциала [24, 25]. В этой системе отсчёта фазовые скорости встречных волн равны по абсолютной величине, но помимо центробежного ускорения для движущихся тел и, в частности, для часов, сопровождающих точки фиксированной фазы встречных волн, имеет место ускорение Кориолиса, направление которого зависит от того, происходит ли движение в направлении вращения – в этом случае направление ускорения Кориолиса совпадает с направлением центробежного ускорения, или в направлении, противоположном вращению, – в этом случае направление ускорения Кориолиса противоположно направлению центробежного ускорения. Вследствие этого величина нерелятивистского гравитационного потенциала для встречных волн различна и это приводит к соответствующей разности времён распространения встречных волн в кольцевом интерферометре [24, 25].

    Однако поскольку вращающаяся система отсчёта является неинерциальной, то сторонники баллистической гипотезы Ритца могут возразить, что выражение (1) не может применяться в этой системе отсчёта. Кроме того, как указал Л. Зилбергштейн (1872–1948) [215], во вращающейся системе отсчёта под воздействием сил Кориолиса лучи света движутся не по прямым, а по криволинейным траекториям, причём их кривизна для встречных волн имеет различный знак. Это усложняет расчёты, однако вскоре А.К. Ланн (1877–1949) показал, что это практически не влияет на величину эффекта Саньяка [216]. Для волоконных кольцевых интерферометров обусловленная эффектом Саньяка разность времён распространения встречных волн почти на 7 порядков больше, чем та же величина, обусловленная силами Кориолиса [217–219].

    Рассмотрим эффект Саньяка [3, 21–25] в интерферометре, выполненном в виде вращающегося с угловой скоростью Ω замкнутого кольца радиуса R в лабораторной ИСО, с точки зрения баллистической гипотезы Ритца. Такое рассмотрение принято проводить и в случае рассмотрения эффекта Саньяка в рамках СТО, оно применялось в работах [3, 22–25, 220–223]. Удобство такого рассмотрения заключается в простоте расчётов – в каждой точке интерферометра линейная скорость вращения составляет RΩ и её направление совпадает с направлением распространения одной из встречных волн и противоположно для другой волны. Отметим здесь, что в нашем обзоре [24], где обсуждалось большое число некорректных объяснений эффекта Саньяка, вопрос о баллистической гипотезе Ритца не рассматривался. Следуя [24], рассмотрим кольцевой интерферометр радиуса R, на кольце которого находится светоделительное зеркало, разделяющее свет от источника излучения на две встречные волны. Для упрощения расчётов положим, что вместо светоделительного зеркала на кольце находится источник излучения (он же фотоприёмник). Линейная скорость источника v= RΩ. В общем случае в кольцевом интерферометре имеется оптическая среда с показателем преломления n. В частности, это имеет место в волоконном кольцевом интерферометре, на базе которых создаются волоконно-оптические гироскопы [27]. Тогда в рамках баллистической гипотезы Ритца (см. выражение (1)) скорости встречных световых волн в лабораторной (неподвижной) системе отсчета составят соответственно с'^± = с/n ± RΩ. (знак "+" соответствует волне, направление распространения которой совпадает с направлением вращения, знак "–" – волне, распространяющейся в противоположном направлении). Запишем выражения для длины путей встречных волн l^±:

l^±= 2πR ± RΩt^±.                            (2)

    Тогда, согласно (1), (2), времена распространения встречных волн t^± от вращающегося источника излучения до него же самого составят

t^±=l^±/с'^±= (2πR ± RΩt^±)/(с/n ± RΩ)=n2πR/c.                (3)

    Таким образом, поскольку времена распространения встречных волн равны между собой, приходим к выводу о том, что эффект Саньяка в рамках баллистической гипотезы Ритца не должен существовать. Это абсолютно неверный результат. Как отмечено во Введении, эффект Саньяка не только надёжно зарегистрирован, но уже давно нашёл практическое применение – на его основе функционируют датчики угловой скорости вращения: лазерные [26] и волоконно-оптические [27] гироскопы. Более того, эффект Саньяка надёжно зарегистрирован в диапазоне радиоволн [224], а также для волн де Бройля различных эле-ментарных частиц и ионов атомов [225].

    Сторонники баллистической гипотезы Ритца иногда утверждают, что следует рассматривать эффект Саньяка не в интерферометре, имеющем форму кольца, а в кольцевом интерферометре, образованным конечным числом зеркал. По их мнению поскольку, согласно утверждению данной теории, при отражении от зеркал при нормальном падении на зеркало и условии, что свет распространяется параллельно направлению v, скорость света должна меняться от с'=с + v до с'=с – v, то это, якобы, должно обеспечить адекватный результат.

    Рассмотрим простейший кольцевой интерферометр, образованный тремя зеркалами – светоделительным и двумя отражающими, не заполненный оптической средой и имеющий форму равностороннего треугольника со сторонами l. Как и ранее, для простоты положим, что вместо светоделительного зеркала установлен источник излучения (он же фотоприёмник) S (рисунок). Углы при вершинах треугольника составляют 60°. Для проверки справедливости баллистической гипотезы Ритца рассмотрим случай, когда кольцевой интерферометр не вращается, а совершает равномерное поступательное движение относительно неподвижного наблюдателя, причём источник S движется со скоростью v, которая параллельна противоположной стороне треугольника.

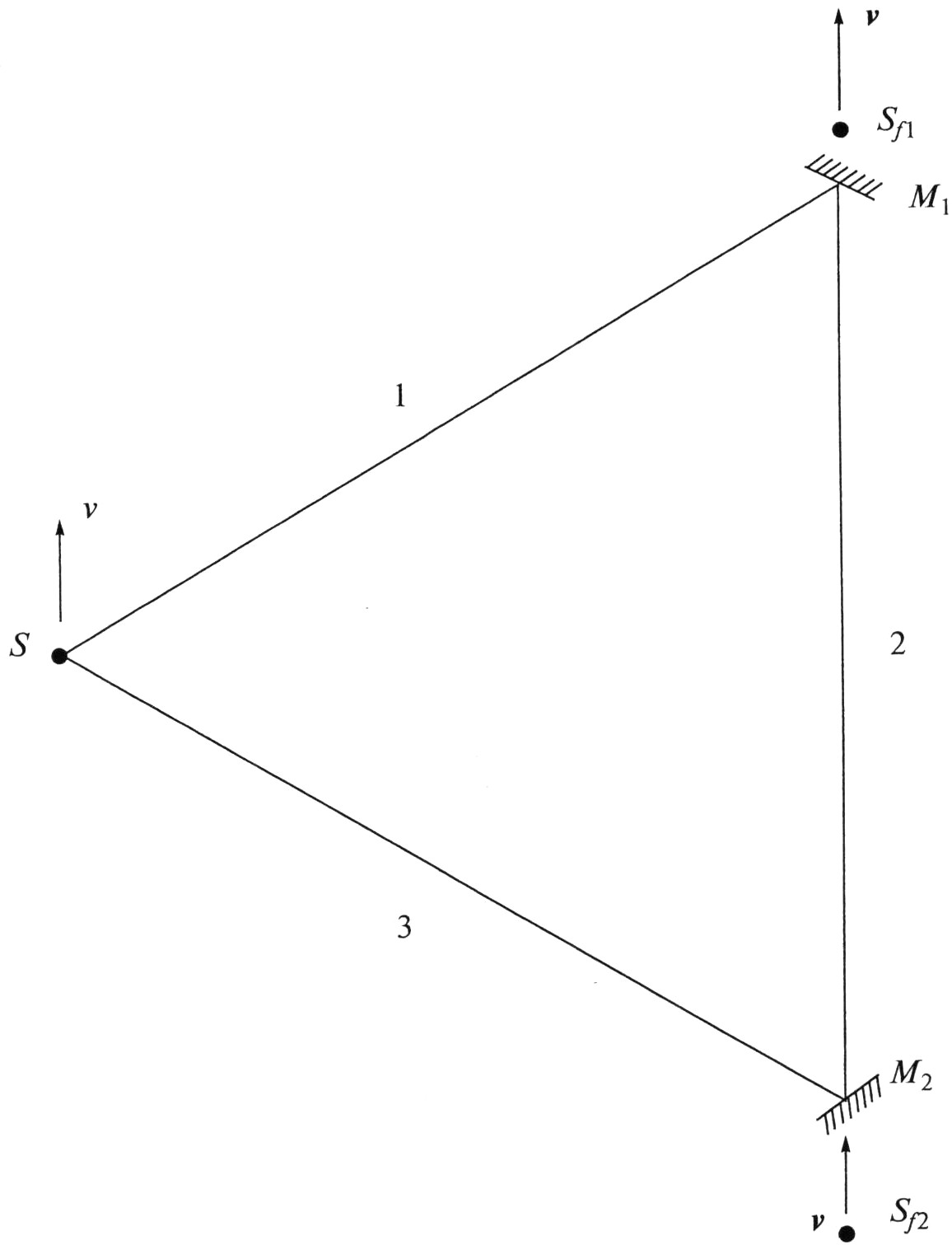
Схема кольцевого интерферометра, совершающего поступательное движение со скоростью v. S – источник излучения (и фотоприёмник), S_f1 и S_f2 – фиктивные источники излучения, M₁ и M₂ – зеркала, цифрами 1, 2 и 3 обозначены плечи интерферометра, стрелки указывают направление скоростей v источников излучения.

    В рассматриваемом случае свет не всегда движется параллельно направлению скорости v и не всегда падает на зеркала нормально. Однако если применить выражение (1), а также рассмотренное выше утверждение баллистической гипотезы Ритца о том, что скорость отражённого луча равна скорости света, испущенного фиктивными источниками излучения S_f1 и S_f2, расположенными соответственно за зеркалами М₁ и М₂ и движущимся в том же направлении и с той же скоростью v, что и первичный источник S, то можно рассчитать скорости распространения встречных волн на каждом из трёх плечей интерферометра. Знаком "+" обозначим волну, распространяющуюся по часовой стрелке, знаком "–" против. Как нетрудно показать, в соответствии с баллистической гипотезой Ритца скорости света в плечах интерферометра 1, 2 и 3 составят

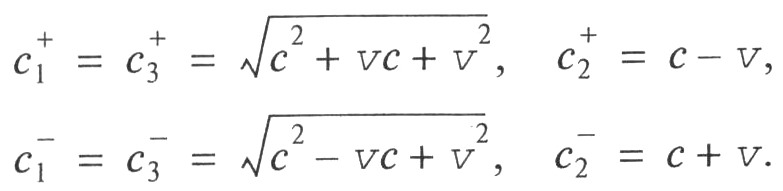
    После несложных, но громоздких вычислений получим, что возникает разность времён распространения встречных волн

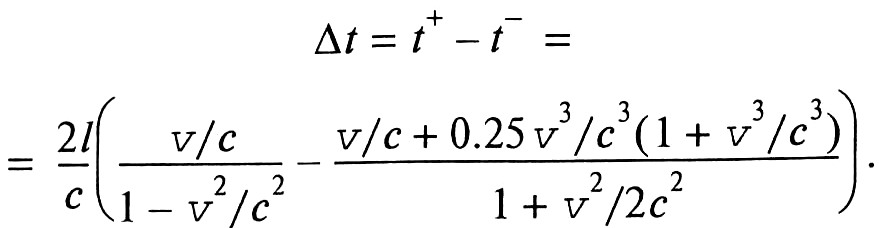                (4)

    В случае, если v<<с, Δt≈2.5lv³/c⁴. Поскольку при отсутствии вращения времена распространения встречных волн равны, то исходя из баллистической гипотезы Ритца мы вновь получили ошибочный результат. Этот парадоксальный результат можно сравнить разве что с описанной Ч.Л. Доджсоном (1832–1898, английский математик, литературный псевдоним Л. Кэрролл) фантастической ситуацией, когда чеширского кота уже нет, а его улыбка осталась [226]. В данном случае нет вращения, а эффект Саньяка есть. Следовательно, дальнейшее рассмотрение эффекта Саньяка в рамках баллистической гипотезы Ритца лишено всякого смысла.

    Как было отмечено в разд. 2.1, в соответствии с баллистической гипотезой Ритца [11, 12] движение зеркала никоим образом не влияет на скорость отражённого светового луча.

    Последнее утверждение [11, 12] свидетельствует против самой же баллистической гипотезы Ритца: поскольку при отражении света в зеркале текут токи, то оно само является источником излучения [63]. На влияние движения зеркала на результаты интерференционных измерений ещё в 1902 г. указал В.М. Хикс (1850-1934) [227]. Отметим, что если в задаче о поступательном движении трёхзеркального интерферометра (разд. 3) положить, что каждое из его зеркал является источником излучения, то получим нулевой результат, что соответствует результатам эксперимента. Однако если положить, что зеркало является источником изучения и, следовательно, движение зеркала влияет на скорость света, то вместо теории Ритца [11, 12] придём к эмиссионной теории Дж.Дж. Томсона [44] и О.М. Стюарта [51], которая давно опровергнута вследствие неправильного предсказания в [44, 51] величины эффекта Допплера (разд. 2.2). Таким образом, баллистическая гипотеза Ритца [11, 12] находится в противоречии с тем фактом, что при отражении света в зеркале текут токи: с одной стороны, движение зеркала не влияет на скорость света, а с другой стороны, должно влиять, поскольку оно является источником излучения.

    В рамках баллистической гипотезы Ритца не имеет места такое надёжно зарегистрированное в настоящее время релятивистское явление, как поперечный эффект Допплера (ПЭД) [228–235]. Это прекрасно понимал сам В. Ритц, который 14 июня 1908 г. в письме к Ф. Пашену (1865-1947) предлагал осуществить эксперимент по измерению ПЭД [61, 236]: "... Я хочу предложить Вам задачу, имеющую большое значение для принципа относительности, а следовательно, для всей электродинамики. По теории относительности Лоренца-Эйнштейна длина волны, излучаемая движущимся атомом, должна меняться по принципу Допплера не только в направлении движения; и при наблюдении перпендикулярно направлению скорости v должно существовать смещение к красному в отношении (v/c)²λ/2... Нельзя ли сделать так, чтобы дать точный ответ на вопрос о существовании эффекта? Если эффект существует, то покончено с нашим универсальным временем, с параллелограммом скоростей и всей кинематикой." Дело в том, что баллистическая гипотеза Ритца предполагает использование классических преобразований Галилея, из которых следует только классический эффект Допплера.

    Следует отметить, что из литературы известно большое число попыток получить выражение для ПЭД из чисто классических соображений, не прибегая к преобразованиям Лоренца ¹⁴. Так, например, авторы работ [16, 17, 237–241] для доказательства этого утверждения используют следующий "приём", основанный на подмене понятий: вместо излучения, испущенного источником под углом 90° к направлению скорости источника, рассматривается излучение, испущенное под углом, большим, чем 90°. По мнению указанных авторов излучение, испущенное источником в тот момент, когда он находится на минимальном расстоянии от неподвижного приёмника, должно быть направлено под углом, большим, чем 90°, к направлению его скорости, иначе оно не попадает на приёмник. Но в этом случае вследствие обычного эффекта Допплера возникает увеличение длины света порядка 0.5v²/c², численно равное ПЭД. При этом понижение частоты света составляет порядка v²/c², что не соответствует увеличению длины его волны. Однако в действительности ПЭД чисто релятивистский эффект. Он понижает частоту излучения, испущенного источником под углом 90° к направлению его скорости. Это излучение достигает приёмника потому, что оно испущено ранее того момента, когда он находится на минимальном расстоянии от приёмника. Отметим, что вследствие конечной скорости света это излучение воспринимается наблюдателем, находящимся на приёмнике, как излучение, испущенное источником, когда он находится на минимальном расстоянии от приёмника. Эти вопросы подробно рассмотрены в [242].

    Укажем здесь также на ошибочную попытку доказательства справедливости баллистической гипотезы Ритца с помощью данных по радиолокации Венеры [243–245].

    Более 50 лет после создания СТО было принято считать, что при наблюдении быстро движущегося объекта он представляется неподвижному наблюдателя сжатым в направлении движения в γ=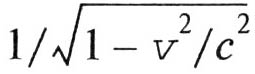 раз. Однако в 1957-1959 гг. Дж. Террел [246, 247] и Р. Пенроуз [248] обратили внимание на то, что световые кванты, пришедшие одновременно к наблюдателю, были испущены различными точками объекта в различные моменты времени – точки, расположенные дальше от наблюдателя, испустили кванты раньше, чем более близкие точки. По этой причине возникает эффект компенсации лоренцева сокращения и в случае, когда размеры объекта много меньше расстояния до него, объект, а точнее говоря его изображение – на сетчатке глаза наблюдателя или на плёнке фотоаппарата – выглядит не искажённым, а только повёрнутым на некоторый угол. В настоящее время данному вопросу посвящено большое число работ, наиболее подробно он рассмотрен в работах [249–257]. Данное явление наблюдалось в работе [258], в которой фотографировалось движение так называемой "световой гантели" – распространение двух коротких лазерных импульсов в жидкости с известным показателем преломления. Изображение "световой гантели" поворачивалось, сохраняя при этом свою форму.

    Как показано в [249–253, 256], если бы не было релятивистского сокращения длины движущегося объекта, то для неподвижного наблюдателя он выглядел бы не только повёрнутым на угол релятивистской аберрации, но и вытянутым в γ раз. Поскольку в рамках баллистической гипотезы Ритца [11, 12] сокращение длины движущихся объектов не имеет места, то очевидно, что результаты измерений [258], согласно которым "световая гантель" не растягивалась в длину, также опровергают теорию Ритца.

    Основной результат данной работы заключается в том, что баллистическая гипотеза Ритца [11, 12] находится в противоречии с фактом существования эффекта Саньяка и, следовательно, является ошибочной. Более того, утверждение баллистической гипотезы Ритца [11, 12] о том, что движение зеркала не влияет на скорость отражённого света, приводит к явно ошибочному результату, когда в не вращающемся кольцевом интерферометре времена распространения встречных волн оказываются различными.

    Ошибочность баллистической гипотезы Ритца демонстрируют как рассмотренные в разд. 2.2 данной работы многочисленные эксперименты, так и указанное В. Де Ситтером [136–138, 140, 141, 167–169] отсутствие искажений в изображении достаточно удалённых двойных звёзд, указанное Дж. Штрёмбергом [188] отсутствие различия звездной аберрации близких звёзд и удалённых разбегающихся галактик, а также указанное Е.Б. Александровым [208] отсутствие демодуляции интенсивности излучения достаточно удалённых цефеид.

    Кроме того, в рамках баллистической гипотезы Ритца не имеют места такое надёжно зарегистрированное в настоящее время релятивистское явление, как ПЭД [228–235], а также явление релятивистской аберрации.

    Многочисленные эксперименты на ускорителях демонстрируют отсутствие каких-либо нарушений предсказаний СТО (разумеется, в пределах существующей точности) [259] и, следовательно, не существует никаких оснований сомневаться в справедливости постулатов СТО. И тем не менее любой новый эксперимент, подтверждающий справедливость СТО, будет иметь большую ценность. Как сказал С.И. Вавилов A.M. Бонч-Бруевичу, когда предлагал ему поставить релятивистский опыт первого порядка по v/c, в котором можно было бы в лабораторных условиях экспериментально прямо наблюдать независимость скорости света от скорости движения источника излучения [110]: "...каждое серьёзное положение, а уж тем более фундаментальное положение в физике, должно быть подтверждено прямым экспериментом. Отсутствие такого эксперимента, а вместо этого опора на следствия, сколько бы их ни было, может порождать у не шибко грамотных людей сомнения. Эти сомнения задерживают развитие науки, с ними приходится бороться и тратить на это силы и время. В этом важность любого надёжного эксперимента, поставленного с целью прямого подтверждения второго постулата."

    Как было показано выше, один из релятивистских опытов первого порядка по v/c – это эффект Саньяка [3, 18–25], который демонстрирует ошибочность баллистической гипотезы Ритца. Более того, нынешний уровень развития экспериментальной техники позволяет осуществить эти опыты в том виде, в каком их задумал СИ. Вавилов – с измерением времени распространения каналовых лучей. Такие эксперименты послужили бы дополнительным доказательством справедливости второго утверждения второго постулата СТО.

    Что касается первого утверждения второго постулата СТО то, как отмечено в обзоре [5], результаты измерений характеристик гамма-излучения, возникающего в результате комптоновского рассеяния лазерного света на ультрарелятивистских электронах [260, 261], осуществленных Гренобльской группой исследователей, демонстрируют, что возможная анизотропия скорости света, если она и существует, не превышает 900 мкм/с.

    Автор выражает благодарность В.М. Геликонову за поддержку работы, Е.Б. Александрову, Вл.В. Кочаровскому, М.И. Петелину, С.А. Семикову и Ф.Р. Тангерлини за полезные обсуждения, Е.В. Колесниковой, Ю.Ю. Куликову, Дж. Филду, Ф. Хассельбаху и Е.Ю. Шныровой за помощь в изыскании ряда работ, Э.Е Малыкину, Я.В. Малыкиной и особо В.И. Поздняковой за помощь в работе, Н.В. Вдовиченко за полезную информацию. Работа частично поддержана грантом совета при Президенте РФ по поддержке ведущих научных школ № НШ3800.2010.2.

1. Einstein A. // Ann. Phys. (Liepzig) 1905. Ser. 4. V. 17. № 10. P. 891–921. Перевод: Эйнштейн А. // Собр. соч. М.: Наука. 1965. Т. 1. С. 7–35.
2. Тяпкин А.А. // УФН. 1972. Т. 106. В. 4. С. 617–659.
3. Логунов А.А., Чугреев Ю.В. // УФН. 1988. Т. 156. В. 1. С. 137–143.
4. Малыкин Г.Б. // УФН. 2009. Т. 179. № 3. С. 285–288; № 4. С. 442.
5. Малыкин Г.Б. // Опт. и спектр. 2009. Т. 107. № 4. С. 624–641.
6. Малыкин Г.Б. // УФН. 2004. Т. 174. № 7. С. 801–804.
7. Малыкин Г.Б. // ЖТФ. 2005. Т. 75. В. 10. С. 135–138.
8. Малыкин Г.Б., Позднякова В.И. // ЖТФ. 2007. Т. 77. В. 1. С. 138–140.
9. Малыкин Г.Б., Малыкин Э.Г. // Исследование по истории физики и механики (Сб. трудов). 2009. С. 260–294.
10. Malykin G.B., Malykin E.G. // The Abraham Zelmanov Journal. 2009. V. 2. P. 121–147.
11. Ritz W. // Ann. Chim. Phys. 1908. Ser. 8. V. 13. P. 145–275.
12. Ritz W. // Arch. Sci. Phys. Nat. de Geneva. 1908. V. 26. P. 209–236.
13. Benedicks C. Space and Time. London: Methuen & co. LTD, 1924. 122 p.
14. Смульский И.И. Электромагнитное и гравитационное взаимодействие. Новосибирск: Наука, 1994. 224 c.
15. Цивинский С.В. Физика XXI века. М.: Компания Спутник⁺, 2007. 408 с.
16. Секерин В.И. Теория относительности – мистификация века. Новосибирск: ИПП Арт-Авеню, 2007. 128 с.
17. Семиков С.А. Баллистическая теория Ритца и картина мироздания. Н. Новгород: Прессконтур, 2009. 612 с.
18. Sagnac M.G. // Compt. Rend. 1913. V. 157. № 17. P. 708–710.
19. Sagnac M.G. // Compt. Rend. 1913. V. 157. № 25. P. 1410–1413.
20. Sagnac M.G. // J. Phys. (Paris). 1914. Ser. 5. V. 4. № 3. P. 177–195.
21. Post E.J. // Rev. Mod. Phys. 1967. V. 39. № 2. P. 475–493.
22. Малыкин Г.Б. // УФН. 1997. Т. 167. № 3. С. 337–342.
23. Вугальтер Г.А., Малыкин Г.Б. // Изв. вузов. Радиофизика. 1999. Т. 42. № 4. С. 373–382.
24. Малыкин Г.Б. // УФН. 2000. Т. 170. № 12. С. 1325–1349.
25. Малыкин Г.Б. // УФН. 2002. Т. 172. № 8. С. 969–970.
26. Бычков С.И., Лукьянов Д.П., Бакаляр А.И. Лазерный гироскоп. М.: Советское радио, 1975. 424 с.
27. Андронова И.А., Малыкин Г.Б. // УФН. 2002. Т. 172. № 8. С. 849–873.
28. Whittaker E.A. History of the Theories of Aether and Electricity. London: Nelson and Sons. V. 1. 1951. 434 p.; V. 2. 1953. 319 p. Перевод: Уитекер Э. История теории эфира и электричества. М.–Ижевск: РХД. Т. 1. 2001. 512 с.; Т. 2. 2004. 464 с.
29. Кудрявцев П.С. Курс истории физики. М.: Просвещение, 1982. 448 с.
30. Newton I. Optics. The Third Edition, Corrected. London: William and John Innys, 1721. Перевод: Ньютон И. Оптика. Перевод и примечания С.И. Вавилова. М.: Гостехиздат, 1954. 448 с.
31. Вавилов С.И. Исаак Ньютон. М.-Л.: Изд. АН СССР, 1945. 230 с.
32. Hooke R. Microgaphia. London: Martyn and Allestry, 1665. 296 p.
33. Боголюбов А.Н. Роберт Гук. М.: Наука, 1984. 239 с.
34. Huygens Ch. Traité de la limierè. Leyden, 1690. Перевод: Гюйгенс Х. Трактат о свете. М.-Л.: Объед. н.-т. изд-во. НКТП СССР, 1935. 172 с.
35. Arago F.D. // Comp. Rend. 1853. V. 36. № 2. P. 38–49.
36. Arago F.D. // Ann. Chim. Phys. 1853. Ser. 3. V. 37. P. 180–196.
37. Рагульский В.В. // Письма в ЖЭТФ. 1997. Т. 65. В. 7. С. 497–501.
38. Рагульский В.В. // УФН. 1997. Т. 167. № 9. С. 1022–1024.
39. Martinez A.A. // Physics in Perspective. 2004. V. 6. № 1. P. 4–28.
40. Ritz W. // Revista di Scienza. Scientia. 1908. V. 3. № 6. P. 260–274.
41. Michelson A.A. // Am. J. Sci. 1881. Ser. III. V. 22. № 128. P. 120–129. Перевод: Майкельсон А.А. // В кн. “Творцы физической оптики” / Сост. Франкфурт У.И. М.: Наука, 1973. С. 223–235; Майкельсон А.А. // В кн. “Эфирный ветер” / Сост. Ацюковский В.А. М.: Энергоатомиздат, 1993. С. 6–17.
42. Michelson A.A., Morley E.W. // Am. J. Sci. 1887. Ser. III. V. 34. № 203. P. 333–345. Перевод: Майкельсон А.А., Морли Э.В. // Эфирный ветер / Сост. Ацюковский В.А. М.: Энергоатомиздат, 1993. С. 17–31.
43. Michelson A.A., Morley E.W. // Phil. Mag. 1887. Ser. 5. V. 24. № 151. P. 449–463.
44. Thomson J.J. // Phil. Mag. 1910. Ser. 6. V. 19. № 110. P. 301–313.
45. Comstock D.F. // Phys. Rev. 1910. V. 30. № 2. P. 267.
46. Comstock D.F. // Science. 1910. V. 31. № 803. P. 767–772.
47. Comstock D.F. // Astrophys. J. 1910. V. 31. P. 364–370.
48. Kunz J. // Am. J. Sci. 1910. Ser. 4. V. 30. № 179. P. 313–322.
49. Tolman R.C. // Phys. Rev. 1910. V. 30. № 2. P. 291.
50. Tolman R.C. // Phys. Rev. 1910. V. 31. № 1. P. 26–40.
51. Stewart O.M. // Phys. Rev. 1911. V. 32. № 4. P. 418–428.
52. Castelnuovo G. // Scientia. 1911. V. 9. № 17 (2). P. 64–86.
53. Carmichael R.D. // Phys. Rev. 1912. V. 35. № 3. P. 153–176.
54. Tolman R.C. // Phys. Rev. 1912. V. 35. № 2. P. 136–143.
55. Ehrenfest P. // Phys. Zeit. 1912. V. 13. P. 317–319.
56. La Rosa M. // Phys. Zeit. 1912. V. 13. P. 1129–1131.
57. La Rosa M. // Nuovo Cimento. 1912. Ser. 6. V. 3. № 1. P. 345–365.
58. La Rosa M. // Nuovo Cimento. 1913. Ser. 6. V. 5. № 1. P. 47–49.
59. Pauli W. Relativitätstheorie. Encyklopädie der Mathematischen Wissenschaften. Bd. 5. Heft 4. Art. 19. 1921. Перевод: Паули В. Теория относительности. М.: Наука, 1983. 336 с.
60. Tolman R.C. Relativity, Thermodynamics and Cosmology. Oxford: Clarendon Press, 1969. Перевод: Толмен Р. Относительность, термодинамика и космология. М.: Наука, 1974. 520 с.
61. Франкфурт У.И., Френк А.М. Оптика движущихся тел. М.: Наука, 1972. 212 с.
62. Smoot G.F. Test of the First Postulate. Berkeley: Univ. Calif., 1999; http://aether/lbl.gov/www/classes/homework/homework.html.
63. Born M., Wolf E. Principles of Optics. Oxford: Pergamon Press, 1968. Перевод: Борн М., Вольф Э. Основы оптики. М.: Наука, 1973. 720 с.
64. Reese H.M. //Am. J. Phys. 1944. V. 12. № 5. P. 305–306.
65. Reese H.M. // Science. 1944. V. 99. № 2583. P. 526–527.
66. Мельников О.А. // В кн. Белопольский А.А. Астрономические труды. М.: ГИТТЛ, 1954. С. 7–58.
67. Еремеева А.И. // Вестник РАН. 2004. Т. 74. № 6. Р. 524–543.
68. Belopolsky A. // Astr. Nach. 1895. Ser. 4. V. 137. № 3267 (3). P. 33–27.
69. Белопольский А.А. // Изв. Рус. астрон. общ. 1898. Т. 6. № 8–9. С. 413–421.
70. Белопольский А.А. // Изв. Импер. АН. 1900. V сер. Т. 13. № 3. С. 28–29.
71. Белопольский А.А. // Изв. Импер. АН. 1900. V сер. Т. 13. № 5. С. 461–472.
72. Belopolsky A. // Astrophys. J. 1901. V. 13. № 1. P. 15–24.
73. Prince Golitzin B., Wilip J. // Записки АН по физ.-мат. отд. 1906. Т. 17. № 6. С. 1–112.
74. Prince Golitzin B., Wilip J. // Записки АН по физ.-мат. отд. 1907. Т. 19. № 9. С. 1–38.
75. Prince Golitzin B.,Wilip J. // Astrophys. J. 1907. V. 13. P. 15.
76. Prince Golitzin B., Wilip J. // Записки АН по физ.-мат. отд. 1909. Т. 22. № 1. С. 1–106.
77. Sellerio A. // Nuovo Cimento. 1933. Ser. 7. V. 10. № 8. P. 316–328.
78. Michelson A.A. // Astrоphys. J. 1913. V. 37. № 3. P. 190–193.
79. Fabry Ch., Buisson H. // Compt. Rend. 1914. V. 158. № 21. P. 1498–1499.
80. Fabry Ch., Buisson H. // J. Phys. (Paris) 1919. V. 8. P. 234.
81. Dragoni G., Maltese G., Atti L. // Physics in Perspective. 2007. V. 9. № 3. P. 281–304.
82. Majorana Q. // Compt. Rend. 1917. V. 165. № 14. P. 424–426.
83. Majorana Q. //Compt. Rend. 1918. V. 167. № 2. P. 71–73.
84. Majorana Q. // Phil. Mag. 1918. Ser. 6. V. 35. № 206. P. 163–174.
85. Majorana Q. // Phys. Rev. 1918. V. 11. № 5. P. 411–420.
86. Majorana Q. // Nuovo Cimento. 1934. Ser. 7. V. 11. № 8. P. 518–530; № 9. P. 648.
87. Majorana Q. // Phil. Mag. 1919. Ser. 6. V. 37. № 217. P. 145–150.
88. Micheaux F. // Compt. Rend. 1919. V. 168. № 10. C. 507–509.
89. Tomaschek R. // Nature. 1959. V. 184. № 4681. P. 177–178.
90. Astrology Continued // Life. 22 February 1960. P. 106.
91. Melchior P. // Bull. Géodesique. 1966. V. 82. № 1. P. 301–302.
92. Tomaschek R. // Astr. Nach. 1923. Ser. 4. V. 219. № 5251 (19). P. 301–306.
93. Tomaschek R. // Ann. Phys. (Liepzig) 1924. Ser. 4. V. 73. № 1–2. P. 105–126.
94. Miller D.C. // Phys. Rev. 1922. V. 19. № 4. P. 407.
95. Miller D. // Proc. Nat. Acad. Sci. U.S. 1925. V. 11. P. 306–314. Перевод: Миллер Д.К. // УФН. 1925. Т. 5. В. 3. С. 177–185. Эфирный ветер / сост. Ацюковский В.А. // М.: Энергоатомиздат, 1993. С. 62–71.
96. Miller D.C. // Rev. Mod. Phys. 1933. V. 5. № 3. P. 203–242. Перевод, Миллер Д.К. В кн.: Эфирный ветер / сост. Ацюковский В.А. // М.: Энергоатомиздат, 1993. С. 185–259.
97. Conference on the Michelson–Morley Experiment // Astrophysical J. 1927. V. 68. № 5. P. 341–402. Перевод: В кн. “Эфирный ветер” / Сост. Ацюковский В.А. М.: Энергоатомиздат, 1993. С. 112–173.
98. Shankland R.S., McCuskey S.W., Leone F.C., Kuerti G. // Rev. Mod. Phys. 1955. V. 27. № 2. P. 167–178.
99. Вавилов С.И. Экспериментальные основания теории относительности. Собр. соч. М.: Изд. АН СССР, 1956. Т. 4. С. 9–109.
100. Мандельштам Л.И. Лекции по физическим основам теории относительности. Полное собрание трудов. М.: Изд. АН СССР, 1950. Т. 5. С. 90–305. Мандельштам Л.И. Лекции по оптике, теории относительности и квантовой механике. М.: Наука, 1972. С. 83–285.
101. Ацюковский В.А. (сост.) Эфирный ветер. М.: Энергоатомиздат, 1993. 289 с.
102. Бонч-Бруевич А.М. // ДАН СССР. 1956. Т. 109. № 3. С. 481–484.
103. Бонч-Бруевич А.М., Молчанов В.А. // Опт. и спектр. 1956. Т. 1. В. 2. С. 113–124.
104. Бонч-Бруевич А.М. // Изв. АН СССР. Сер. физ. 1956. Т. 20. № 5. С. 591–595.
105. Бонч-Бруевич А.М., Молчанов В.А., Широков В.И. // Изв. АН СССР. Сер. физ. 1956. Т. 20. № 5. С. 596–600.
106. Бонч-Бруевич А.М., Широков В.И. // ЖТФ. 1956. Т. 25. В. 10. С. 1825–1842.
107. Freundlich E. // Phys. Zeit. 1913. V. 14. P. 835–838.
108. Gutnick P. // Astr. Nach. 1913. Ser. 4. V. 195. № 4670 (14). P. 265–270.
109. Бонч-Бруевич А.М. // Опт. и спектр. 1957. Т. 2. В. 1. С. 141–142.
110. Бонч-Бруевич А.М. // УФН. 2001. Т. 171. № 10. С. 1087–1090.
111. Kantor W. // JOSA. 1962. V. 52. № 9. P. 978–984.
112. Kantor W. // Spectr. Lett. 1970. V. 3. № 11–12. P. 335–343.
113. Bierman A., von Kenschitski C.H., Panders D. // JOSA. 1963. V. 53. № 8. P. 1008.
114. Burcev P. // Phys. Lett. 1963. V. 5. № 1. P. 44.
115. White D.R., Alpher R.A. // JOSA. 1963. V. 53. № 6. P. 760.
116. Vyšysn V. // Phуs. Lett. 1964. V. 8. № 1. P. 36–37.
117. James J.F., Sternberg R.S. // Nature. 1963. V. 197. № 4873. P. 1192.
118. Rotz F.B. // Phys. Lett. 1963. V. 5. № 4. P. 252–254.
119. Babcock G.C., Bergman T.G. // JOSA. 1964. V. 54. № 2. P. 147–151.
120. Beckmann P., Mandis P. // Radio Sci. J. Res. NBS. 1964. V. 68. № 12. P. 1265–1268.
121. Waddoups G.C., Edwards W.F., Merrill J.J. // JOSA. 1965. V. 55. № 2. P. 142–143.
122. Záhejský J., Kolesnikov V. // Nature. 1966. V. 212. № 5067. P. 1227.
123. Beckmann P., Mandis P. // Radio Sci. J. Res. NBS. 1965. V. 69. № 4. P. 623–628.
124. Nieuwenhuijzen H. // Bull. Astr. Inst. Netherl. 1969. V. 20. № 4. P. 300–308.
125. Fox J.G. // Am. J. Phys. 1962. V. 30. № 4. P. 297–300.
126. Alväger T., Nilson A., Kjellman J. // Nature. 1963. V. 197. № 4873. P. 1191.
127. Alväger T., Nilsson A., Kjellman J. // Ark. Fys. 1963. V. 26. № 16. P. 209–221.
128. Sadeh D. // Phys. Rev. Lett. 1963. V. 10. № 7. P. 271–273.
129. Alväger T., Farley F.J., Kjellman J., Wallin I. // Phys. Lett. 1964. V. 12. № 3. P. 260–262.
130. Filippas T.A., Fox J.G. // Phys. Rev. 1964. V. 35. № 4. P. B1071–B1075.
131. Rosser W.G. // Nature. 1961. V. 190. № 4772. P. 249.
132. Dingle H. // Nature. 1959. V. 183. № 4677. P. 1761.
133. Fox J.G. // Am. J. Phys. 1965. V. 33. № 1. P. 1–17.
134. Fox J.G. // JOSA. 1965. V. 57. № 7. P. 967–968.
135. Röhle S. Dissertation. Johannes Gutenberg-Universität in Mainz. Mainz, 2007.
136. de Sitter W. // Phys. Zeit. 1913. V. 14. № 9. P. 429.
137. де Ситтер В. // ЖРФХО. Часть физ-я. 1913. Т. 45. В. 4. С. 147–148.
138. de Sitter W. // Konicl. Acad. Wettenschappen Amsterdam. 1913. V. 15. P. 1297–1298.
139. Zurhellen W. // Astr. Nach. 1914. Ser. 4. V. 198. № 4729 (1). P. 1–10.
140. de Sitter W. // Phys. Zeit. 1913. V. 14. № 25. P. 1267.
141. de Sitter W. // Konicl. Acad. Wettenschappen Amsterdam. 1913. V. 16. P. 395–396.
142. La Rosa M. // Rend. Accad. Lincei. 1923. V. 32. Parte 2.
143. La Rosa M. // Astr. Nach. 1924. Ser. 4. V. 222. № 5319 (5). P. 249–254.
144. La Rosa M. // Astr. Nach. 1924. Ser. 4. V. 223. № 5346 (18). P. 293–296.
145. La Rosa M. // Astr. Nach. 1924. Ser. 4. V. 223. № 5350 (21). P. 359–368.
146. La Rosa M. // Z. Phys. 1924. V. 21. № 6. P. 333–347.
147. La Rosa M. // Nature. 1924. V. 114. № 2878. P. 933–934.
148. La Rosa M. // Nuovo Cimento. 1924. Ser. 7. V. 1. № 1. P. 49–98.
149. La Rosa M. // Ann. Phys. (Leipzig) 1924. Ser. 4. V. 75. P. 195–200.
150. Gautschy A. // Vist. Astron. 1997. V. 41. № 1. P. 95–115.
151. Personalia // The Observatory. 1912. V. 35. № 455. P. 435–436.
152. Goodricke J. // Thil. Trans. 1786. V. 76. P. 48–61.
153. Белопольский А.А. Исследование спектра переменной звезды δ Cephei (3.7–4.9 з. вел.) при помощи 30-ти дюймового рефрактора обсерватории в Пулково. СПб.: тип. АН. 1895. докт. дисс.
154. Белопольский А.А. // Изв. АН СССР. Сер. физ. 1928. Т. 7. № 1. С. 1–8 (B кн. А.А. Белопольский. Астрономические труды. М.: ГИТТЛВ. 1954. С. 226–233.)
155. Ritter A. // Ann. Phys. Chim. (Wiedemann Annalen.) 1879. Ser. 2. V. 8. P. 157–183.
156. Eddington A.S. // Month. Not. Roy. Astron. Soc. 1918. V. 79. P. 2.
157. Eddington A.S. // Month. Not. Roy. Astron. Soc. 1919. V. 79. P. 177.
158. Куликов Ю.Ю. Препринт НИРФИ № 504. ФНГУ НИРФИ, 2006. 68 с.
159. Жевакин С.А. // Астрон. журнал. 1953. Т. 30. № 2. С. 161–179.
160. Жевакин С.А. // ДАН СССР. 1954. Т. 99. № 2. С. 217–220.
161. Жевакин С.А. // ДАН СССР. 1954. Т. 99. № 3. С. 353–356.
162. Жевакин С.А. //ДАН СССР. 1958. Т. 119. № 5. С. 907–910.
163. Жевакин С.А. //ДАН СССР. 1958. Т. 123. № 2. С. 252–255.
164. Zhevakin S.A. // Ann. Rev. Astron. Astrophys. 1963. V. 1. P. 367–400.
165. Самусь Н.Р. // Звёзды. М.: Физматлит, 2009. С. 203–247.
166. Фадеев В.К. // Звёзды. М.: Физматлит, 2009. С. 248–261.
167. de Sitter W. // Bull. Astr. Inst. Netherl. 1924. V. 2. № 57. P. 121–122.
168. de Sitter W. // Bull. Astr. Inst. Netherl. 1924. V. 2. № 64. P. 163–164.
169. de Sitter W. // Konicl. Acad. Wettenschappen Amsterdam. 1924. V. 33. P. 607–608.
170. Nordmann Ch., Le Morvann C. // Compt. Rend. 1924. V. 179. № 21. P. 1139–1141.
171. Salet P. // Compt. Rend. 1925. V. 180. № 9. P. 646–648.
172. Kienle H. // Astr. Nach. 1947. Ser. 5. V. 275. № 69. P. 268–269.
173. Wattenberg H. // Die Sterne. 1958. V. 34. № 1–2. P. 57–58.
174. Gramatzki H.J. // Astr. Nach. 1924. Ser. 4. V. 223. № 5336 (8). P. 135–136.
175. Gramatzki H.J. // Astr. Nach. 1925. Ser. 4. V. 224. № 5367 (15). P. 247–252.
176. Thirring H. // Z. Phys. 1925. V. 31. № 1. P. 133–138.
177. Bernheimer W.E. // Z. Phys. 1926. V. 36. № 4. P. 302–310.
178. La Rosa M. // Nuovo Cimento. 1925. Ser. 7. V. 2. № 2. P. 159–169.
179. La Rosa M. // Compt. Rend. 1925. V. 180. № 12. P. 912–914.
180. La Rosa M. // Z. Phys. 1925. V. 34. № 1. P. 698–704.
181. La Rosa M. // Compt. Rend. 1925. V. 180. № 23. P. 1738–1740.
182. La Rosa M. // Astr. Nach. 1928. Ser. 4. V. 234. № 5604 (12). P. 236–244.
183. Salet P. // Compt. Rend. 1926. V. 183. № 25. P. 1263–1264.
184. Cecchini M. // Sem. Mat. Fis. di Milano (Milan J. Math.). 1932. V. 6. № 1. P. 109–126.
185. Moon P., Spencer D.E. // JOSA. 1953. V. 43. № 8. P. 635–640.
186. Moon P., Spencer D.E., Moon E.E. // Phys. Essays. 1989. V. 2. № 3. P. 275.
187. Brecher K. // Phys. Rev. Lett. 1977. V. 39. № 17. P. 1051–1054; № 19. P. 1236.
188. Strömberg G. // Publ. Astr. Soc. Pacific. 1931. V. 43. № 254. P. 266–267.
189. van Biesbroeck G. // Astrophys. J. 1932. V. 75. № 1. P. 64–65.
190. Thüring M. // Astr. Nach. 1941. Ser. 4. V. 271. № 6. P. 241–264.
191. Heckmann O. // Astr. Nach. 1942. Ser. 4. V. 272. № 5. P. 215–219.
192. Meeting of the Roy. Astron. Soc. // The Observatory. 1958. V. 78. № 907. P. 232–241.
193. Whitrow G.J. // Roy. Astron. Soc. Ouart. J. 1980. V. 21. P. 333–338.
194. Dingle H. Relativity for All. London, 1922.
195. Dingle H. // Nature. 1962. V. 195. № 4845. P. 985–986.
196. Dingle H. // Nature. 1963. V. 197. № 4874. P. 1248–1249.
197. Dingle H. // Nature. 1963. V. 197. № 4874. P. 1287–1288.
198. Born M. // Nature. 1963. V. 197. № 4874. P. 1287.
199. Möller C. // Proc. Roy. Soc. (London). Ser. A. 1962. V. 270. № 1342. P. 306–314.
200. Dingle H. Science at the Crossroads. 1972.
201. Heckmann O. // The Observatory. 1959. V. 79. № 910. P. 105–106.
202. Dingle H. // The Observatory. 1959. V. 79. № 910. P. 106–107.
203. Dingle H. // Month. Not. Roy. Astron. Soc. 1959. V. 119. № 1. P. 67–69.
204. Heckmann O. // Mitt. Hamburg Sternw. 1960. V. 10. № 110.
205. Heckmann O. // Ann. D'Astrophys. 1960. V. 23. № 3. P. 410–415.
206. Dickens R.J., Malin S.R. // The Observatory. 1965. V. 85. № 949. P. 260–269.
207. Бонч-Бруевич А.М. // Опт. и спектр. 1960. Т. 9. В. 1. С. 134–135.
208. Александров Е.Б. // Астрон. журнал. 1965. Т. 62. В. 3. С. 676–678.
209. Александров Е.Б. // Частное сообщение. Апрель. 2009.
210. Tangherlini F.R. Dissertation. Stanford Univ., 1958. 135 p. Tangherlini F.A. // The Abraham Zelmanov Journal. 2009. V. 2. P. 44–120.
211. Tangherlini F.R. // Suppl. Nuovo Cimento. 1961. V. 20. № 1. P. 1–86.
212. Tangherlini F.R. // Nuovo Cimento. B. 1994. V. 109. № 9. P. 929–951.
213. Newburgh R.G., Blacksmith P., Budreau A.J., Sethares J.C. // Proc. IEEE. 1974. V. 62. № 12. P. 1621–1628.
214. Вугальтер Г.А., Гилинский И.А. // Изв. вузов. Радиофизика. 1989. Т. 32. № 10. С. 1187–1220.
215. Silberstein L. // JOSA. 1921. V. 5. № 4. P. 291–307.
216. Lunn A.C. // JOSA. 1922. V. 6. № 2. P. 112–120.
217. Arditty H.J., Lefevre H.C. // Opt. Lett. 1981. V. 6. № 8. P. 401–403.
218. Lefevre H.C., Arditty H.J. // Appl. Opt. 1982. V. 21. № 8. P. 1400–1409.
219. Arditty H.J., Lefevre H.C. // Fiber-Optic Rotation Sensors / Ed. by Ezekiel S., Arditty H.J. Berlin: Springer-Verlag, 1982. P. 44–51.
220. Witte H. // Verhandl. deut. Physik. Ges. 1914. V. 16. № 3. P. 142–150.
221. Witte H. // Verhandl. deut. Physik. Ges. 1914. V. 16. № 15. P. 754–755.
222. Langevin P. // Compt. Rend. 1937. V. 205. № 5. P. 304–306.
223. Trocheris M.G. // Phil. Mag. 1949. Ser. 7. V. 40. № 310. P. 1143–1154.
224. Берштейн И.Л. // ДАН СССР. 1950. Т. 75. № 5. С. 635–638.
225. Hasselbach F. // Rep. Prog. Phys. 2010. V. 73. № 1. P. 016101.
226. Кэрpол Л. Алиса в стране чудес. СПб.: Азбука классики, 1998. 192 с.
227. Hicks W.M. // Phil. Mag. 1902. Ser. 6. V. 3. № 13. P. 9–44.
228. Ives H.E., Stilwell G.R. // JOSA. 1938. V. 28. № 7. P. 215–226.
229. Otting G. // Phys. Zeit. 1939. V. 40. № 14. P. 681–687.
230. Ives H.E., Stilwell G.R. // JOSA. 1941. V. 31. № 5. P. 369–374.
231. Madelberg H.I., Witten L. // JOSA. 1962. V. 52. № 5. P. 529–536.
232. Летохов В.С., Чеботаев В.П. Нелинейная лазерная спектроскопия сверхвысокого разрешения. М.: Наука, 1990. 512 с.
233. Bagaev S.N., Chebotaev V.P., Dmitriev A.K., Om A.E., Nekrasov Yu.V., Skvortsov B.N. // Appl. Phys. B. 1991. V. 52. P. 63–66.
234. Bagaev S.N., Dmitriev A.K., Ohm A.E., Okhapkin M.V., Nikulin V.A., Skvortsov B.N. // Laser Phys. 1994. V. 4. № 2. P. 373–375.
235. Bagaev S.N., Dmitriev A.K., Okhapkin M.V., Shalnev E.V., Skvortsov B.N., Nikulin V.A. // Laser. Phys. 1996. V. 6. № 2. P. 226–230.
236. Ritz W. // Gesammelte Werke. Paris, 1910. P. 523–524.
237. Лаврова Т.М. // II н.-т. конф. учёных и специалистов вузов, НИИ и предприятий. Калинин, 1969. С. 127–128.
238. Демиденко В.Н. // Сер. Проблемы исследования Вселенной. В. 11. Физические аспекты современной астрономии. Л., 1985. С. 131–135.
239. Колоколов Е.П. // Сер. Проблемы исследования Вселеной. В. 15. Проблемы пространства и времени в современном естествознании. СПб., 1991. С. 121–124.
240. Демиденко В.Н. // Сер. Проблемы исследования Вселенной. В. 16. Проблемы пространства и времени в современном естествознании. Часть II. СПб., 1993. С. 233–240.
241. Акимов О.Е. Естествознание. Курс лекций. М.: ЮНИТИ-ДАНА, 2001. 639 с.
242. Купряев Н.В. // УФН. 2005. Т. 175. № 9. С. 1013–1015.
243. Wallace B.G. // Spectr. Lett. 1969. V. 2. № 12. P. 361–367.
244. Wallace B.G. // Found. Phys. 1973. V. 3. № 3. P. 381–388.
245. Уоллес Б.Дж. // Сер. Проблемы исследования Вселенной. В. 15. Проблемы пространства и времени в современном естествознании. СПб., 1991. С. 258–267.
246. Terrell J. The Clock Paradox // Los Alamos Document Ladc-2842. April 1957.
247. Terrel J. // Phys. Rev. 1959. V. 118. № 4. P. 1041–1045.
248. Penrose R. // Proc. Cambridge Phil. Soc. 1959. V. 55. Pt. 1. P. 137–139.
249. Weisskopf V.F. // Phys. Today. 1960. V. 13. № 9. P. 24–27; Weisskopf V.F. Physics in Twentieth Century. Massachusetts: MIT Press, 1972. Перевод: Вайскопф В. Физика в двадцатом столетии. М.: Атомиздат, 1977. С. 179–186.
250. Угаров В.А. // Эйнштейновский сборник 1973 / Под ред. Гинзбурга В.Л. М.: Наука, 1974. С. 201–206.
251. Болотовский Б.М. // Эйнштейновский сборник 1980–1981 / Под ред. Кобзарева И.Ю. М.: Наука, 1985. С. 142–160.
252. Болотовский Б.М. // Эйнштейновский сборник 1986–1990 / Под ред. Кобзарева И.Ю. М.: Наука, 1990. С. 279–328.
253. Field J.H. // Proc. XX Workshop on High Energy Physics and Field Theory. Protvino. 24–26 June 1997 / Ed. by Filimonova I.V., Petrov V.A. 1997. P. 214–248.
254. Малыкин Г.Б. // УФН. 1999. Т. 169. № 5. С. 585–590.
255. Малыкин Г.Б. // ПММ. 1999. Т. 63. В. 5. С. 775–780.
256. Field J.H. // Am. J. Phys. 2000. V. 68. № 4. P. 367–374.
257. Малыкин Г.Б. // УФН. 2006. Т. 176. № 8. С. 865–882.
258. Duguay M.A. // Am. Scientist. 1971. V. 59. P. 551. Перевод: Дюге М. // УФН. 1973. Т. 109. В. 1. С. 157–166.
259. Plettner T., Byer R.L., Siemann R.H. // J. Phys. B. 2005. V. 38. № 9. P. S741–S752.
260. Gurzadyan V.G. et al. // Mod. Phys. Lett. A. 2005. V. 20. № 1. P. 19–28.
261. Gurzadyan V.G. et al. http://arxiv.org/abs/astro-ph/070127.

Примечания:

1 Отметим, что существует понятие координатной скорости света, зависящей от выбора системы координат, т.е. от метрики пространства-времени, а при переходе от одной системы координат к другой – также и от вида используемых пространственно-временных преобразований (см., например, [2-5]).

2 Эксперимент Араго был повторен на более высоком уровне точности В.В. Рагульским [37, 38].

3 В работе [40] В. Ритц рассмотрел теорию гравитации.

4 Последнее утверждение [11, 12] свидетельствует против самой баллистической гипотезы Ритца: поскольку в зеркале при отражении текут токи, то оно является источником излучения. Этот вопрос будет рассмотрен ниже в разд. 4.1.

5 К. Майорана повторил эти измерения в 1934 г. на более высоком уровне точности [86] – вся экспериментальная установка находилась в вакуумированной камере.

6 Такое предположение ранее высказали Э. Фрейндлих и П. Гутник [107, 108].

7 Позднее У. Кантор предпринял попытку доказать это теоретически [112]. Отметим, что предпринимались также бесплодные попытки как использования результатов [111] для доказательства несамосогласованности СТО [113], так и для доказательства совместимости результатов [111] с СТО [114, 115] и даже ОТО [116] (см. также [61]).

8 В дальнейшем измерение эффекта Допплера от вращающихся зеркал с лазерным источником излучения неоднократно повторялись, но в отличие от рассмотренных выше экспериментов [78–80, 82–86, 123] они уже не преследовали целей проверки справедливости СТО, а имели чисто практическое назначение, в частности, для создания сдвига частоты лазерного излучения [124].

9 Дискуссия между В. де Ситтером и М. Ла Розой, равно как и вся первая и вторая дискуссии, весьма подробно рассмотрена в [135].

10 Спустя 36 лет авторы [185] в соавторстве со своим сыном продолжили рассмотрение данного вопроса [186].

11 В молодые годы Г. Дингл был последовательным сторонником и пропагандистом СТО (см., например, его монографию [194]), но с возрастом стал непримиримым противником СТО – укажем на дискуссию Р. Дингла [195–197] с М. Борном [198] и с К. Мёллером, Г. Бонди, П. Виго и Л. Эссеном [199], а также монографию Г. Дингла [200].

12 Работа [208] была написана в 1962 г., но в силу ряда обстоятельств опубликована только в 1965 г. [209].

13 Ещё 45 лет назад Дж.Г. Фокс указал на имеющиеся проблемы с объяснением эффекта Саньяка в рамках баллистической гипотезы Ритца [133], однако в этой работе не было проведено никаких расчётов.

14 Как показано в [5], применение преобразований Тангерлини [210–212] так же, как и преобразований Лоренца, позволяет получить выражение для ПЭД.

Дата установки: 03.02.2011
Последнее обновление: 10.02.2011
[вернуться к содержанию сайта]

W