Баллистическая (эмиссионная) теория. Результаты опыта Майкельсона и его аналогов чаще всего трактовались как свидетельство отсутствия неподвижной системы отсчёта (эфира), другими словами, как подтверждение принципа относительности, т.е. первого постулата специальной теории относительности. Не входя здесь в обсуждение споров вокруг правомерности такой интерпретации, вспомним, что результаты опытов типа майкельсоновского легко объяснялись и так называемой баллистической (эмиссионной) теорией. В основе этой теории, первый вариант которой был предложен швейцарским физиком Ритцем [1], лежало предположение о том, что движение источника оказывает влияние на скорость света, испущенного этим источником. Баллистическая теория была выдвинута, чтобы избежать такой ломки представлений, к которой с необходимостью приводило одновременное принятие обоих постулатов специальной теории относительности, т. е. принципа относительности и независимости скорости света от скорости источника. Если в теории Лоренца отказывались от первого, сохраняя второй, то в баллистической теории сохранялся принцип относительности, но отвергался постулат постоянства скорости света в любой инерциальной системе отсчёта. Отрицание этого положения приводило не только к необходимости отказа от эфира как неподвижной среды, в которой распространяется свет, но и к вынужденному пересмотру уравнений Максвелла в пустоте. Баллистическая теория встретилась с трудностями при объяснении ряда явлений: опытов типа Физо, эффекта Допплера, спектроскопически-двойных звёзд и др. В поисках ответа на эти вопросы было разработано даже несколько вариантов баллистических теорий, отличающихся своими выводами относительно скорости света после отражения от движущегося зеркала. По Ритцу, свет после отражения распространяется так, будто он исходит из некоторого центра, движущегося со скоростью источника и в том же направлении; по Томсону и Стюарту [2], скорость света складывается со скоростью изображения реального источника, а по Толмэну [3] – со скоростью самого зеркала.
В беседе с Шенклендом Эйнштейн говорил, что он ещё до 1905 г. размышлял о возможности баллистической теории, но отказался от этой мысли, так как не мог придумать дифференциальное уравнение, решение которого давало бы волны со скоростью, зависящей от движения источника.
И всё же довольно длительное время баллистическая теория противопоставлялась теории относительности, ибо не требовала коренного пересмотра основных представлений о пространстве и времени (даже в наши дни иногда появляются отголоски прежних споров, о чём речь впереди). Баллистическая теория не сыграла особой роли в развитии современной физики, но дискуссии, развернувшиеся вокруг неё, выявили необходимость постановки прямых экспериментов по доказательству независимости скорости света от скорости источника – второго постулата специальной теории относительности.
Но осуществить их было нелегко, ибо в опытах с замкнутыми путями света теории Лоренца, Ритца и Эйнштейна дают одинаковые результаты, если измерения проводить с точностью до величии первого порядка относительно v/с [4]. Значит, и в этом случае необходимо было достигнуть точности порядка (v/с)2≈10-8. Ещё в 1912 г. итальянский физик Ла Роза обратил внимание, что этому требованию удовлетворяет опыт, проведённый по схеме Майкельсона — Морли, но с источником света, движущимся относительно остальных частей установки с достаточно большой скоростью. Такими источниками могли быть Солнце, звёзды и другие светящиеся небесные тела.
Опыт был осуществлён в 1923 г. Томашеком [5]. В его опыте поочерёдно наблюдалась интерференционная картина, полученная с помощью земного и внеземного (Солнце, Луна, Юпитер, Сириус, Арктур) источников. Никакой разницы при этом не наблюдалось. Наблюдавшиеся смещения полос составляли не более 1/8 теоретически ожидаемых.
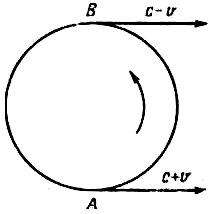
Другая возможность выбора между рассматриваемыми теориями основана на опытах первого порядка, но с разомкнутым путём света. Такой вариант можно было осуществить при астрономических наблюдениях двойных звёзд. Этот вопрос был детально рассмотрен голландским астрономом де Ситтером в 1913 г. [6]. Основная идея заключается в следующем (рис. 26). Если верна теория Ритца, то свет, идущий от звезды, находящейся в положении А (т. е. приближающейся к Земле), приходит на Землю через время L/c+v после излучения, а из положения В (т. е. удаляющейся от Земли) – через время L/c–v (L – расстояние до Земли). Если обозначить Т период полуобращения, то на Земле интервал между двумя наблюдениями будет Т+2Lv/c2 при движении звезды от В к А и Т–2Lv/c2 – при движении звезды от А к В. При больших скоростях движения звезды оба слагаемых одного порядка, так что в видимом с Земли движении звёзд должны были бы наблюдаться отклонения от законов Кеплера. Отсутствие таких наблюдаемых отклонений свидетельствовало против гипотезы о сложении скорости звезды со скоростью испускаемого ею света. Учитывая фактическую точность имевшихся астрономических наблюдений, де Ситтер показал, что если скорость света с' в системе наблюдателя представить суммой c'=c+kv, то можно утверждать, что k< 0,02 (по теориям Лоренца и Эйнштейна k=0, по Ритцу k=1). Все эти данные “позволяют почти с достоверностью считать правильным положение о постоянстве скорости, а теории истечения Ритца и других признать ведущими к непреодолимым затруднениям”.

рис. 26
Прямые экспериментальные подтверждения второго постулата теории относительности. И всё же вопрос о прямой экспериментальной проверке независимости скорости света от скорости источника не был снят. Исторически первой попыткой в этом направлении был опыт Майораны [7]. С помощью интерферометра Майкельсона с неравными плечами измерялись смещения интерференционных полос при замене неподвижного источника движущимся. Если скорость света не зависит от скорости источника, то длина волны меняется согласно обычной формуле для эффекта Допплера и сдвиг Δ полос составит
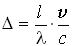 ,
,
где l – разность хода обоих лучей, v – скорость источника. В качестве движущихся источников применялись ртутные дуговые лампы, прикреплённые к концу стержня длиной 2 м, вращавшегося вокруг оси, проходящей через его центр. В опыте v=79,77 м/сек, l=232 мм, λ=0,546 мкм, что даёт Δ=1,113 полосы. При изменении направления вращения смещение удвоится и Δ=2,226 полосы. Опыт дал Δ=0,238, что с точностью порядка 5% (по оценке Майораны) согласуется с расчётными данными. Недостатком схемы Майораны было использование на пути луча разделительной пластинки; это позволяло утверждать, что измеряется скорость света, испускаемого не источником, а пластинкой, которая не двигалась относительно трубы интерферометра.
В опыте М. А. Бонч-Бруевича измерялась разница времён прохождения определённого расстояния световыми лучами, исходящими от противоположных краёв солнечного диска. Вследствие вращения Солнца разница скоростей обоих лучей согласно баллистической гипотезе должна была бы составлять 3,5 км/сек, что в условиях опыта соответствовало разности времён 75·10-12 сек. Измерения после статистической обработки дали величину примерно в восемь раз меньшую. Окончательный результат сводился к тому, что вероятность справедливости постулата независимости скорости света в 1045 больше, чем баллистической гипотезы [8]. Но, как и в случае опыта Майораны, против доказательной силы опыта можно было высказать то возражение, что на пути лучей в установке использовались неподвижные зеркала, отражаясь от которых свет мог изменить свою скорость.
Новая волна опытов началась в 1962 г., после того как американский физик Кантор [9] опубликовал результаты опытов, якобы противоречащих теории относительности. Суть опыта заключается в следующем (рис. 27).
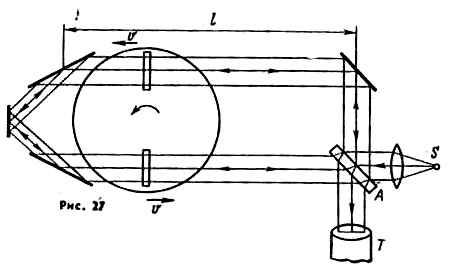
Рис. 27
Свет от источника S расщепляется в полупрозрачной пластинке А на два пучка, проходящих через интерферометр в противоположных направлениях (с помощью соответствующим образом расположенных зеркал). На пути лучей размещаются две очень тонкие прозрачные пластинки, укреплённые на одном диаметре диска, причём часть светового пучка проходит через пластинки, а часть – над пластинками. При неподвижном диске в трубе Т обе интерференционные картины соответствуют неподвижному источнику. При вращении диска (для скорости 61 об/сек линейная скорость центра пластинок равнялась 4690 см/сек) лучи, проходящие сквозь пластинки, дают интерференционную картину, соответствующую движущимся пластинкам, рассматриваемым, по замыслу Кантора, в качестве вторичных источников. Наблюдение велось в свете лампы, вспышки которой синхронизированы с моментами, когда окошки движутся вдоль и против луча. Пренебрегая ввиду малой толщины пластинок (тысячные доли дюйма) эффектом увлечения света движущимися телами, можно было ожидать следующие результаты: если скорость источника не оказывает влияния на скорость света, то никакого смещения между обеими картинами не должно быть; если же c'=c±kv (v – линейная скорость пластинки), то возникнет смещение интерференционных полос, которое при справедливости гипотезы Ритца (k=1) должно равняться 0,74. Кантор получил значение 0,5, что соответствовало k=2/3. По мнению Кантора, этот результат опровергает теорию относительности, во всяком случае качественно.
Естественно, что этот результат вызвал сразу же множество откликов. Дальнейший ход событий напомнил ситуацию 20-х годов, наступившую после опубликования результатов Миллера. Противники теории относительности (не удивительно ли, что они сохранились после 50 лет блестящей истории этой теории?!) поспешили прямо или косвенно объявить о ниспровержении “кумира” [10], другие авторы пытались исправить расчёты Кантора так, чтобы согласовать его результаты со специальной [11] или общей теорией относительности [12]. А наиболее трезвые мыслители предложили повторить опыты и лишь затем делать какие-то выводы. И такие опыты были проделаны как со светом видимого спектра, так и с γ-излучением.
Оригинальна идея, лежащая в основе опытов Джемса и Стернберга [13]. Если, как полагал Кантор, c'=c+kv, т. е. вторичные источники передают часть своей скорости проходящему через них свету, то, поскольку при вращении различные точки пластинки имеют различную линейную скорость и свет вследствие этого становится неоднородным по скорости, фронт волны должен повернуться на некоторый угол θ=kωx/c (ω – угловая скорость диска, х – расстояние от диска до места наблюдения). В условиях опыта при k=1 θ=20", а при k= 2/3 (число, полученное Кантором) θ=13,3". Хотя применявшийся телескоп позволял измерить углы порядка 0",5, никакого изгиба не было обнаружено, в полном соответствии с теорией относительности (k= 0). С учётом ошибок измерения k во всяком случае меньше 0,025.
Ротц [14] вводил движущуюся равномерно стеклянную пластинку на пути одного из трёх лучей в интерферометре Цернике. Хотя точность установки позволяла определить смещение полос порядка 0,005, никакого влияния движения стекла на скорость света не было обнаружено.
Весьма точными были опыты Бабкока и Бергмана [15], использовавших схему Кантора (рис. 28). Они ввели ряд усовершенствований: увеличили длину плеч интерферометра, меняли направление вращения диска, улучшили синхронизацию вспышек лампы с положением пластинок, уточнили способ измерения скорости пластинок.
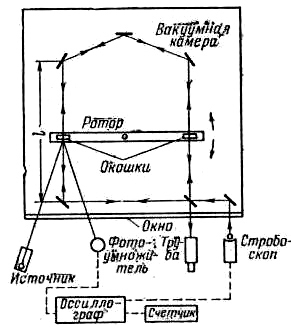
Рис. 28
Было учтено ещё одно обстоятельство. Фокс [16] высказал предположение, что на результаты опыта может оказать влияние среда, через которую проходят световые лучи (обычно воздух). По его мнению, фотоны поглощаются молекулами воздуха и вновь излучаются, но уже со скоростью с относительно воздуха, так что влияние скорости первичного источника исчезает. Во избежание подобных возражений вся оптическая часть установки была помещена в вакуумную камеру. При k=1 смещение должно было равняться 2,9; при k= 2/3 Δ=1,9. Опыт дал Δ=0,0120±0,006; это означало, что k<0,006. Подобные опыты проводились также с использованием лазеров [17], причём скорость пластинки доводилась до 63 м/сек, но результат оставался прежний: коэффициент k мало отличался от нуля. Для устранения возможности переизлучения света атомами среды был поставлен опыт [18] с отражением света от движущегося зеркала в условиях высокого вакуума (10-6 мм рт. ст.). Наконец, в специально поставленном опыте было показано, что положительные результаты Кантора могли быть обусловлены температурными эффектами [19].
К оптическим опытам нужно отнести и наблюдения Диккенса и Мейлина [20], пытавшихся найти зависимость скорости света от скорости источника по методу, предложенному Динглером. Он состоит в сравнении аберрации света, идущего от быстро разбегающихся внегалактических туманностей и от близких звёзд, радиальная скорость которых относительно Солнца ничтожна. Наблюдения проводились одновременно 26-дюймовым рефрактором обсерватории Херстмонсо и 74-дюймовым рефлектором в Претории (Южная Африка). В обоих случаях разница в аберрации не превышала ошибок измерений; отсюда авторы пришли к выводу, что если красное смещение действительно обусловлено эффектом Допплера, а значит скорость разбегания туманностей порядка 20 000 км/сек, то их наблюдения отрицают зависимость скорости света от скорости источника.
Опыты с γ-квантами. Другой способ избежать возможное вмешательство молекул воздуха состоит в использовании вместо видимого света слабо поглощаемых жёстких γ-квантов. Существующие экспериментальные методы ядерной физики позволяют провести подобные опыты с достаточной точностью. Источниками фотонов большой энергии могут быть: γ-излучение возбуждённых ядер, аннигиляция электронно-позитронной пары, распад π-мезонов и др. Все эти опыты проводились в 1963–1964 гг.
В эксперименте группы шведских физиков [21], проведённом в Нобелевском физическом институте, измерялось различие в скорости γ-квантов, испускаемых движущимися и покоящимися атомными ядрами. С этой целью мишень из углерода С12 и мишень из кислорода О16 бомбардировались α-частицами с энергией 14 МэВ, выходящими из циклотрона. В результате получались возбуждённые ядра С12* и О16* с некоторой скоростью отдачи. Различие между ними заключается в том, что возбуждённые ядра С12* на уровне 4,43 МэВ обладают малым временем жизни (период полураспада 6,5·10-14 сек.) и успевают излучить γ-квант до своей остановки, тогда как ядра О16* на уровне 6,13 МэВ живут значительно дольше (период полураспада 1,2·10-11 сек.) и излучают γ-квант уже после остановки. Измерения допплеровского смещения показали, что ядра С12* в момент излучения обладали средней скоростью v= (1,8±0,2) 10-2c, а ядра О16* действительно покоились. Мишени располагались одна за другой на расстоянии 30 см друг от друга и их можно было менять местами. Первый, контрольный, приёмник регистрировал разницу моментов пролёта γ-квантов от обеих мишеней на расстоянии 1 м (примерно вдоль линии полёта α-частиц), второй, основной, – на расстоянии 5 м. В первом положении α-частицы попадали сначала на углеродную мишень, во втором – на кислородную. Если скорость γ-квантов не зависит от скорости источника, то разница между моментами прибывания γ-квантов во второй приёмник при двух положениях мишеней (τ1– τ2) будет такой же, как на контрольном (Δ1 – Δ2), т. е. δ=(τ1– τ2) – (Δ1 – Δ2)=0. Если же скорости источника v и γ-кванта складываются, то кванты, испускаемые ядрами углерода, пройдут путь S между приёмниками быстрее, и разница при первом положении уменьшится:
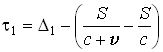 ,
,
а при втором увеличится:
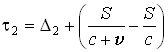 .
.
Тогда
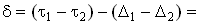
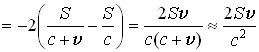 .
.
В условиях данного опыта
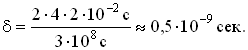
Среднее значение, полученное при измерениях, было
δ=(–0,2±0,2)·10
–9 сек.,что подтверждало справедливость второго постулата теории относительности.
Саде [22] измерял время пролёта двух γ-квантов, получаемых в процессе аннигиляции летящего позитрона с электроном (+е+–е→2γ). Когда позитрон попадает в вещество, он тормозится и сталкивается с покоящимся электроном, образуя два γ-кванта. Этот процесс называется аннигиляцией. Если до аннигиляции позитрон успел остановиться, то полученные γ-кванты разлетаются в противоположные стороны, т. е. под углом 180°. Но часть позитронов успевает аннигилировать до торможения, тогда кванты разлетаются под определённым углом, зависящим от импульса позитрона. (Это можно выразить иначе: в системе центра масс позитрона и электрона кванты разлетаются под углом 180°, а в лабораторной системе отсчёта – под меньшим углом, измеряемым импульсом позитрона.) В опыте Саде источником позитронов служил радиоактивный Cu64. Пучок позитронов направлялся на мишень из органического стекла, где происходила аннигиляция. Приёмники располагались на одинаковых расстояниях (60 см) от мишени по направлениям, составлявшим угол в 20 и 135° с направлением полёта позитронов, чем выделялись γ-кванты, возникшие при аннигиляции позитронов с определённой скоростью (0,89 с). При таких условиях скорость центра масс, т. е. источника γ-квантов, составляла примерно 0,6 с. Специальная электронная схема позволяла измерить разницу во времени регистрации γ-квантов приёмниками с точностью 0,2·10-9 сек. Если второй постулат верен, то γ-кванты достигнут приёмников одновременно; в противном случае к скорости с нужно прибавить проекцию скорости источника в направлении наблюдения, и тогда разность времён будет порядка 2·10–9 сек. В пределах ошибок измерения никакой разницы не было зарегистрировано. Точность была порядка 10%.
Ещё в 1961 г. Россер [23] предложил использовать γ-кваиты, получаемые при распаде нейтральных π0-мезонов. Опыт был осуществлён на Женевском ускорителе протонов [24]. π-Мезоны высокой энергии получались бомбардировкой бериллиевой мишени ускоренными протонами с импульсом около 19 ГэВ/с. Получаемые при распаде π0→2γ фотоны обладали энергией порядка 6 ГэВ. Несмотря на большую скорость π0-мезонов – источника γ-квантов – было установлено, что коэффициент k в выражении c'=c+kv не может быть больше (–3±13)·10–5, другими словами, скорость источника не отражается на скорости испускаемых им фотонов. Несколько меньшая точность была получена в опыте Филиппаса и Фокса [25],
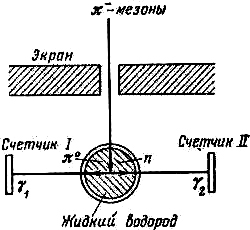
Рис. 29
где π0-мезоны получались бомбардировкой жидкого водорода пучком выходящих из циклотрона π–-мезонов (рис. 29). При этом происходила реакция
π–+р → π0+ п + 3,3 МэВ
(р – протон, п—нейтрон). Выделяемая в реакции энергия уносится мезоном и нейтроном, причём скорость мезона достигает 0,2 с. Регистрировались распады, в которых один квант летит в направлении движения π0-мезона, а второй – в противоположном. Максимальная разность времени полёта γ-квантов до счётчиков наблюдалась бы при направлении разлёта, указанном на рис. 29. В пределах точности, допускаемой использованными приборами (8 %), не была обнаружена зависимость скорости γ-квантов от скорости источника.
Проведённый обзор позволяет утверждать, что второй постулат специальной теории относительности достаточно надёжно обоснован экспериментально.
Эффект Допплера в каналовых лучах.
Как уже было показано (стр. 44), релятивистское рассмотрение эффекта Допплера даёт для частоты при наблюдении перпендикулярно направлению распространения луча величину![]() (1)
(1)
Отмечаемое наблюдателем уменьшение частоты, излучаемой источником, движущимся перпендикулярно оси спектрального прибора, является непосредственным следствием релятивистского замедления часов. Если рассматривать движущийся атом, колеблющийся с собственной частотой ν
0, как часы, то, поскольку в системе наблюдателя период колебания![]()
частота
![]() (1')
(1')
Таким образом, экспериментальное подтверждение существования отличного от нуля поперечного допплер-эффекта II порядка было бы одновременно подтверждением эйнштейновской формулы для замедления часов. На реальную возможность проведения подобных опытов со светом, излучаемым каналовыми лучами, указал Эйнштейн [
1] после ознакомления с результатами исследований Штарка по допплер-эффекту в каналовых лучах. Он обратил внимание на то обстоятельство, что в принципе точность, достигаемая при измерениях в опытах с каналовыми лучами, вполне достаточна для обнаруженияΔν
=ν0β2/2,но установка Штарка и его сотрудников, не будучи специально приспособленной для этой цели, не обладала точностью, необходимой для получения надёжных результатов. Кроме того, трудность возникала при определении собственной частоты излучения ν
0, но здесь на помощь могло прийти то обстоятельство, что в спектре излучения можно было достаточно явно выделить частоты, принадлежащие покоящимся излучателям (неподвижным часам), от частот, излучаемых движущимися ионами (т. е. движущимися часами).В связи с этим заслуживает упоминания следующий исторический факт. В 1906 г. на 78-м собрании немецких естествоиспытателей в Штутгарте с докладом “Применение телеобъектива к эффекту Допплера в каналовых лучах” [
2] выступили Б. Штрассер и М. Вин. Целью их работы было определение скорости каналовых частиц на отдельных участках разрядной трубки, что существенно для суждений о механизме явлений, происходящих в трубке. Используя идею, высказанную ещё раньше Pay [3], они внесли в установку зеркало, позволившее обратить эффект. Выступая в дискуссии по этому докладу, тюбингенский физик Ганс обратил внимание, что, судя по фотографиям, представленным докладчиками, смещение линий, полученных при движении каналовых частиц к спектрографу и от него, по величине одинаково. Но это не вытекает из теории a priori. Строгая теория (имелась в виду нерелятивистская), развитая с учетом членов второго порядка, дает зависимость смещения не только от относительной скорости источника и наблюдателя, но и от абсолютной скорости каждого из них в эфире (см. стр. 42). Но эти скорости неизвестны, если неизвестна скорость установки (т. е. Земли) в эфире. Точные замеры спектрограмм могли бы выявить член второго порядка, и по разнице смещений можно было бы определить величину этой неизвестной скорости. Тут же Ганс говорил, что если теория относительности (которую он называет принципом относительности Лоренца, Эйнштейна и Планка) верна, то подобная постановка вопроса лишена смысла. Докладчики резонно ответили Гансу, что точность их опытов была недостаточна для обнаружения членов второго порядка относительно v/c.Действительно, установка Штрассера и Вина не могла выявить квадратичный эффект, но, хотя теория относительности оказалась верной, постановка вопроса не была лишена смысла, поскольку именно из этой теории строго вытекает некоторая асимметрия в смещении частот, причём именно второго порядка. Запишем релятивистскую формулу эффекта Допплера для длины волны
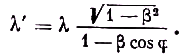
При движении источника под углами φ=0 и φ
=π (οротивоположные направления) имеем соответственно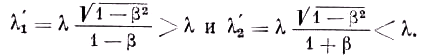
Если бы смещения λ
1' и λ2' от λ были симметричны, т. е. λ1'–λ=λ–λ2', то среднее положение для двух смещённых линий совпадало бы с положением несмещённой линии λ. Но простой расчёт даёт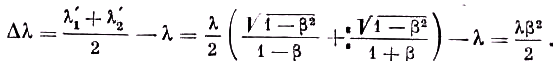 (2)
(2)
Отсюда видно, что теория относительности предсказывает несколько большее смещение в красную сторону, чем в фиолетовую, в отличие от классической теории, где
![]()
Дело обстоит таким образом, что на симметричные красное и фиолетовое смещения, обусловленные продольным эффектом Допплера, накладывается независимое от направления движения красное смещение второго порядка, обусловленное поперечным эффектом. Последний и вызывает асимметрию, которую необходимо было экспериментально обнаружить. Уже в начале века не представляло особых трудностей получение каналовых частиц со скоростями порядка 10
7–108 см/сек, причём сложность измерения этих скоростей не могла быть серьёзной помехой для осуществления опытов. Существенно было другое. Наряду со смещением спектральной линии наблюдается её расширение, вызванное распределением скорости частиц в значительном интервале. К тому же было практически очень трудно установить с достаточной точностью направление наблюдения под прямым углом к скорости движения каналовых частиц, а малейшее отклонение даёт продольную компоненту, покрывающую искомый поперечный эффект. Таким образом, хотя исторически проблема оказалась связанной с допплеровским смещением, наблюдаемым на быстро движущихся каналовых частицах, работы Штарка и его последователей не наталкивали на идею решающего опыта для проверки формулы (1).Хотя соответствующий эксперимент не удавалось поставить, возможность его осуществления живо обсуждалась. Так, Шульц в 1923 г. [4] предлагал найти тот угол φ
0, при котором релятивистская теория предсказывала нулевой эффект вследствие компенсации продольного эффекта, благодаря которому при φ=0 происходит смещение в фиолетовую сторону, поперечным, для которого при φ=π/2 смещение происходит в красную сторону. Значит, в этом случае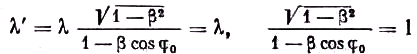
и
![]()
При
v=2·108 см/сек φ0=89°48'33'',14. Но практического пути к осуществлению опыта Шульц не указал. Существенно было его замечание, что расчёты, проведённые на основании баллистической теории Ритца, приводят к другим результатам, а значит, опыт мог бы дать критерий для выбора между баллистической теорией и теорией относительности. В связи с этим интересно привести выдержку из письма 1908 г. самого Ритца известному немецкому физику-экспериментатору Пашену: “Я хочу предложить Вам задачу, имеющую большое значение для вопроса о принципе относительности, а следовательно, и для всей электродинамики. По теории относительности Лоренца–Эйнштейна длина волны, излучаемая движущимся атомом, должна меняться по принципу Допплера не только в направлении движения; и при наблюдении перпендикулярно направлению скорости должно существовать смещение к красному в отношении (v/с)2λ/2 ... Νельзя бы сделать так, чтобы дать точный ответ на вопрос о существовании эффекта? Если эффект существует, то покончено с нашим универсальным временем, с параллелограммом скоростей и всей кинематикой” [5].Но даже такой искусный мастер эксперимента, как Пашен, не смог бы ответить на поставленный вопрос. В дальнейшем дель Лунго и Шерцер [
6] своими расчётами вновь подтвердили принципиальную возможность обнаружить поперечный эффект с помощью каналовых лучей, а позже, после появления ускорителей элементарных частиц, Гюйе [7] предлагал использовать для этой цели свечение пучка положительных ионов, ускоренных в циклотроне.Опыты Айвса–Стилуэлла. В 1937 г. с серией работ выступил Айве [
8]. С точки зрения электронной теории Лоренца он рассмотрел изменения, которые должны наблюдаться в излучении движущихся атомов по сравнению со спектром, полученным от покоящихся атомов, и наметил установку, с помощью которой можно было бы наблюдать эффекты второго порядка. Уже в следующем году им были опубликованы результаты первых опытов, выполненных совместно с Стилуэллом [9].В основе установки Айвса лежала конструктивная идея Pay [
10]. Последний ставил себе задачу обнаружить продольное допплеровское смещение в полосатом спектре, обусловленном излучением молекул. Трудность заключалась в том, что в полосе линии расположены столь тесно, что нельзя было с уверенностью распознать смещение. Требовалось либо значительно увеличить разрешающую способность спектрографа, либо найти новый метод выделения смещённых линий. Максимально достигнутая в это время разрешающая способность не решала задачу; тогда Pay предложил следующий способ выделения смещённых линий. Коллиматор спектрографа устанавливался перпендикулярно направлению движения каналовых частиц (рис. 30), так, чтобы ось трубки и щель были параллельны. Внутрь разрядной трубки вносился цилиндрический стеклянный стержень А перпендикулярно световому лучу. В отсутствие стержня в спектрограф попадает свет, идущий перпендикулярно оси трубки, а потому не дающий смещения. При наличии стержня окажутся несмещенными те линии, которые образует свет, проходящий через центр стержня. Но в этом случае благодаря преломлению в стержне до спектрографа доходят и такие лучи, которые излучаются каналовыми частицами не перпендикулярно направлению их движения. Чем меньше угол между осью трубки и испускаемым световым лучом, тем больше компонента скорости частиц вдоль луча, а значит, тем больше продольное допплеровское смещение. Верхние лучи дают смешение в красную сторону (направление излучения совпадает с направлением движения каналовых лучей), нижние — в фиолетовую сторону (направления противоположны). Поэтому в спектре смещённые линии окажутся наклонными по отношению к прямым несмещённым. По наклону смещённые линии теперь легко отличить от несмещённых.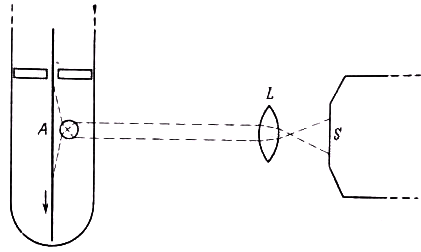
Рис. 30
Используя идею Pay и внеся дополнительное вогнутое зеркало, позволившее выделить эффект второго порядка при прохождении света в противоположные стороны, Айвс смог впервые установить правильность предсказания Эйнштейна о существовании эффекта второго порядка.
Приведём основные детали расположения аппаратуры. В наполненной водородом трубке (рис. 31) между оксидной нитью А и алюминиевым электродом В происходит дуговой разряд при не очень высокой разности потенциалов (порядка 100 в). Ионизированные вылетающими из нити электронами молекулы водорода Н2 и Н3 через отверстия в электроде В попадают в ускоряющее поле между первым и вторым (С) электродами, разность потенциалов которых составляла несколько тысяч вольт. Давление поддерживалось низким, чтобы при прохождении ускоряющего поля ионы водорода не сталкивались между собой. Благодаря такому устройству удавалось получить весьма однородный по скорости поток каналовых частиц. При диссоциации ионов получались нейтральные атомы, излучение которых (линии серии Бальмера) и наблюдалось. Для измерений использовался спектрограф, изготовленный “чародеем физического эксперимента” знаменитым Робертом Вудом. Через систему отверстий во втором электроде, в точности повторяющей отверстия в первом, свет попадал на вогнутое зеркало М и, отразившись, на щель спектрографа, расположенную в центре кривизны зеркала. Направление наблюдения составляло с направлением движения частиц угол порядка 7° и совпадало с осью зеркала. Таким образом, на спектрограф попадало излучение, идущее как по направлению движения излучателей, так и против него, и появлялась возможность проверки формулы (2).
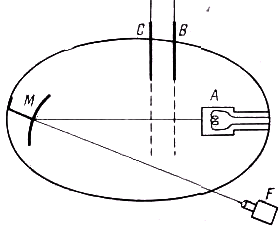
Рис. 31
Промер полученных спектрограмм производился очень тщательно на компараторе Аббе, и авторы оценивали достигнутую ими точность в определении длины волны в 0,0025 Å. Скорость частиц определялась как по приложенному напряжению, так и по продольному допплеровскому смещению. Поскольку оптический спектр каналовых лучей помимо линий, соответствующих атомам водорода, даёт и множество линий молекулярного спектра, ускоряющий потенциал необходимо было подобрать так, чтобы смещенные линии попадали между полосами молекулярного спектра.
При напряжении 6788 в значение λβ2/2, вычисленное по напряжению, должно было равняться 0,0116 Å, вычисленное по продольному смещению — 0,0109 Å; опыт дал 0,011 А. При напряжении 11566 в соответственно получалось 0,0198; 0,0203; 0,0205. Таким образом, в пределах ошибок наблюдения опыт подтвердил релятивистскую формулу (2). Как это ни парадоксально, Айвс рассматривал теорию своего опыта в рамках классической электронной теории Лоренца (что для 1938 г., по выражению В. Л. Гинзбурга, было “полнейшим анахронизмом” [11]); последовательно релятивистскую трактовку этих опытов дал Джонс [12].
Анализируя достоинства и недостатки установки Айвса, Джонс отметил ряд возможных источников погрешностей. Положение основной линии, от которой измерялись смещения, предполагалось совершенно неизменным. Эта линия должна принадлежать атомам газа, возбуждённым в трубке при столкновении с каналовыми частицами. Но при этом сами атомы могут иметь компоненту скорости вдоль направления распространения света, что вызовет допплеровское смещение. Поэтому Джонс
считал, что для получения несмещённой линии необходимо использовать автономный источник.На некоторые недостатки установки Айвса указал Оттинг [
13]. Использование широкого недостаточно светосильного пучка каналовых частиц требовало продолжительного времени освещения, поскольку применялся дифракционный спектрограф, полученные спектрограммы не фотометрировались, и, наконец, применение вогнутого зеркала приводило к нелинейной зависимости от cosφ, так как пучок имел конечную ширину.Чтобы избежать этих ошибок, Оттинг воспользовался установкой, созданной Биллингом по идее Эйнштейна [
14]. Светящийся каналовый луч находится в фокальной плоскости линзы L, которая направляет свет в интерферометр Фабри–Перо S1S2, из которого свет идёт в зрительную трубу F, установленную на бесконечность. Пусть светящаяся частица пробегает вдоль оси трубки К со скоростью v, испуская свет частоты ω. Зеркала интерферометра в начале параллельны и при однократном отражении удлиняют путь света на Δ. Длина пути света от атома, находящегося в точке Р2, до наблюдателя будет s, а длина пути света, испускаемого в точке Р1, после прохождения интерферометра будет s+Δ. Βследствие конечности скорости света наблюдатель в определённый момент t видит атом не в точке О, где он в этот момент находится, а в точках Р1 и Р2, где он находился в моменты t1=t–(s+Δ)/c и t2=t–s/c. В фокальной плоскости объектива возникают два изображения, V1 и V2. Расстояние D между Р1 и Р2 равно D= vΔ/c видимое из линзы L под углом β=vΔ/cf, где f — фокусное расстояние линзы. Разность фаз между колебаниями светового вектора в V1 и V2 φ=ωΔ/c. Если теперь наклонить зеркало S2 на угол β/2, то точка P1 также отобразится в V2 и изображения совпадут. Когда атом пробегает вдоль К, угол α, под которым плоские волны проходят интерферометр, меняется; поэтому меняется и разность хода Δ=Δ0cosα θ разность фаз φ=ωΔ0cosα/c. При интерференции обоих лучей вдоль прямой Z появятся тёмные и светлые места. Если одну частицу заменить однородным по скорости пучком частиц, то максимумы и минимумы интерференционных картин для всех частиц совпадут и общее изображение каналового луча будет изборождено интерференционными полосами. Поскольку интерференционные методы позволяют очень точно измерить длину волны, Оттинг внёс в установку Биллинга дополнительное зеркало, позволившее вести наблюдения и при распространении света в обратном направлении, а значит, обнаружить асимметрию смещений, определяемую формулой (2). Кроме того, Оттинг воспользовался более интенсивной бальмеровской линией Нα, тогда как у Айвса промеривалось смещение линии Н. При напряжении в трубке 11680 в вычисленное по формуле (2) смещение равнялось 0,027 Å, измеренное — 0,026 Å; при напряжении 13890 в соответственно 0,033 Å и 0,035 Å.Вторая серия опытов, проведённых с более однородным по скорости пучком частиц, дала такие же результаты [
15].В 1941 г. Айвс и Стилуэлл [
16] видоизменили свою установку, чтобы получить большие скорости частиц без опасности разрушения трубки. Для этого они ввели в трубку несколько последовательных электродов, причём при общем напряжении более 40 000 в напряжение между соседними электродами было меньше критического для пробоя. Кроме того, специально исследовалось влияние тех факторов, на которые указывали Джонс и Оттинг. В 1962 г. Мандельберг и Уиттен [17] повторили опыт Айвса и Стилуэлла с более современными средствами и использовали лучшую методику отработки данных измерений, но никаких принципиально новых решений не внесли. Использовался пучок атомов водорода, движущихся со скоростью 2,8·108 см/сек. Обработка результатов дала для показателя степени в релятивистском выражении (1–β2)–1/2 величину – (0,498±0,025). Если в опытах Айвса и Оттинга погрешность достигала 10–15%, то здесь она была значительно меньше.Измерение поперечного допплер-эффекта с помощью эффекта Мёссбауэра. Совершенно новые возможности проверки формулы поперечного допплеровского смещения, т. е. релятивистского замедления времени, появились после открытия эффекта Мёссбауэра (см. стр. 109). Частота, испускаемая без отдачи ядрами Fe
57 в металлическом железе, может быть определена столь точно, что возникла возможность провести измерения влияния гравитационного поля на частоту излучения. Однако в первых опытах, предпринятых Паундом и Ребкой, получались довольно значительные флуктуации результатов. Оказалось, что главный источник погрешностей был обусловлен неучтенной разностью температур между источником и поглотителем. На эффект температурной зависимости красного смещения частоты γ-излучения впервые указал Джозефсон [18]. При столь прецизионных измерениях даже весьма малая разность температур может оказать влияние. Действительно, благодаря тепловому движению атомов в твёрдом теле происходит допплеровское смещение частоты (учитывая члены первого и второго порядков):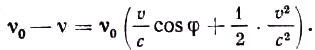 (3)
(3)
Поскольку при тепловом движении атомов частота изменения направления скорости порядка 10
17–1018, то за время жизни ядерного уровня в изотопах, используемых при опытах с эффектом Мёссбауэра, это изменение происходит столь много раз, что среднее значение vcosφ αудет равно нулю и линейный эффект Допплера скажется лишь в небольшом уширении линии. Тогда из (3) останется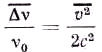 , (4)
, (4)
где
v2 — средняя квадратичная скорость ядер-излучателей. Наличие определяемого формулой (4) поперечного допплер-эффекта в прецизионных опытах должно учитываться. Обозначая U энергию решётки на единицу массы, имеем![]() и
и 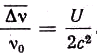
Изменение относительного смещения с температурой
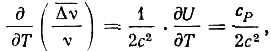 (5)
(5)
где ср
— теплоёмкость при постоянном давлении. Значит, увеличение или уменьшение температуры меняет величину квадратичного допплеровского смещения. При высоте башни, где проводились опыты, в 22 м разница температур между верхней и нижней частью в 1° С приводит к смещению частоты γ-квантов примерно такого же порядка, как и гравитационное смещение.Для проверки формулы (5) Паунд и Ребка [
19] измеряли температурную зависимость энергии γ-квантов по поглощению излучения, испускаемого ядрами Со57, поглотителем, обогащённым Fe57. Небольшое смещение частоты, обусловленное различием температур излучателя и поглотителя, измерялось с помощью преобразователя, двигающего источник вперёд и назад по отношению к поглотителю. Они писали: “Поскольку экспериментальные данные согласуются с расчётной кривой, то наш результат может рассматриваться как экспериментальное доказательство квадратичного эффекта Допплера с использованием теплового движения атомов, а не движения по кругу”1. Подобные опыты, но с ядрами Sn119, находящимися на метастабильном уровне, провели Бойл и др. [20] с тем же результатом.Вторая группа опытов, также связанная с измерением гравитационного смещения с помощью эффекта Мёссбауэра, основана на другом круге идей. Если источник и поглотитель разместить на диске, вращающемся с угловой скоростью ω, на расстояниях соответственно
R1 и R2, то гравитационное смещение вызывается уже не гравитационным полем, а эквивалентной ему ускоренно-движущейся системой. По Эйнштейну, в поле тяготения с потенциалом Ф относительное смещение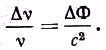
Эквивалентный потенциал для ускоренной системы будет
Rω/2, ηначит,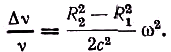
Если этот опыт рассматривать в системе отсчёта, связанной с ускоренно-движущимся поглотителем, то имеем дело с “псевдогравитационным” смещением, т. е. с принципом эквивалентности и общей теорией относительности. Если же его рассматривать в инерциальной системе источника, то дело сводится просто к квадратичному допплер-эффекту. Действительно, если в формулу (1
') подставить v=ωR, получим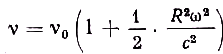 и
и 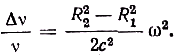
В опытах Хея и др. [
21] измерялось смещение энергии γ-квантов, испускаемых ядрами Fe57 в ускоренной системе. Источник Со57 был нанесён на поверхность железного цилиндра с радиусом 0,8 см. К внутренней поверхности второго цилиндра радиусом 13,28 см, концентричного первому, приклеивалась железная фольга, обогащенная Fe57. Оба цилиндра жестко скреплялись, и вся система вращалась со скоростью 500 об/сек. Определялась зависимость числа квантов, испускаемых Fe57 после резонансного поглощения, от угловой скорости. Подтверждена с уверенностью порядка 95% формула (6).В линейно ускоренной системе подобный опыт осуществил Бёммель [
22]. Источник и поглотитель, расположенные на расстоянии d друг от друга, одновременно движутся с ускорением а вдоль оси, проходящей через их центры. Роль разности потенциалов играет величина ad, поэтому![]() (7)
(7)
Для достижения необходимого ускорения источник и поглотитель закреплялись на синхронно-колеблющихся пьезоэлектрических вибраторах с частотой 10 Мгц. Обнаруженный сдвиг частот соответствовал теоретически ожидаемому.
Наиболее точные опыты этого типа принадлежат Кюндигу [23]. Источник Со57, внедренный в железо, располагался в центре ротора, а поглотитель — железо, обогащённое изотопом Fe57, — на расстоянии 9,8 см от него. Скорость вращения достигала 600 об/сек. Для каждого значения скорости снималась полная линия резонансного поглощения, что позволило повысить точность измерений. Результаты подтверждают формулу (6) с точностью до 1,1%.
1. W. Ritz. Recherches critiques sur l'électrodynamique générale. Ann. de Physique, 1908, 13, p. 145–175; Recherches critiques sur les théories électrodynamiques de Cl. Maxwell et de H.A. Lorentz. Arch. sci. phys. nat., 1908. 24, p. 209–236.
2. J. J. Thomson. On a theory of the structure of the electric field and its applications to Röntgen radiation and to light. Phil. Mag., 1910, 19, p. 301–313: O. M. Stewart. The second postulate of relativity and the electromagnetic emission theory of light. Phys. Rev., 1911. 32, p. 418–428.
3. R. С. Tolman. The second postulate of relativity. Phys. Rev., 1910, 30, p. 291; 31, p. 26–40.
4. P. Ehrenfest. Über die Entberlichkeit des Lichtäthers. Phys. Z., 1912, 13, S. 317–319.
5. R. Tomaschek. Über den Michelsonverscuh mit Fixsternlicht. Astr. Nach., 1923, 219, S. 301–306; Über das Verhalten des Lichtes Außerirdischer Lichtquellen. Ann. Phys., 1924, 73, S. 125–126.
6. W. de Sitter. Ein astronomischer Beweis für die Konstanz der Lichtgeschwindigkeit; Proc. Acad. Amster., 1913, 15, p. 1297–1312; Phys. Z. 1913, 14, S. 429; Über die Genauigkeit, innerhalb welcher die Unabhängigkeit der Lichtgeschwindgkeit von der Bewegung der Quelle behauptet werden kann. Phys. Z., 1913, 14, S. 1267–1268.
7. Q. Majorana. Experimental demonstration of the constancy of velocity of light emitted by a moving source. Lincei Rend., 1918, 27, p. 402–406; Phys. Rev., 1918, 11, p. 411–420; Phil. Mag., 1919, 37, р. 145–150.
8. А. М. Бонч-Бруевич. Экспериментальная проверка независимости скорости света от скорости движения источника излучения относительно наблюдателя. ДАН, 1956, 109, стр. 481–484; А. М. Бонч-Бруевич, В. А. Молчанов. Новый оптический релятивистский опыт. Оптика и спектроскопия, 1956, 1, стр. 113–124.
9. W. Kantor. Direct first-order experiment on the propagation of light from a moving source. JOSA, 1962, 52, p. 978–984.
10. J. Palacios. Optica de los cuerpes en movimento. Comentarios al experimento de Kantor. Rev. Real. acad. cienc. exact. Madrid, 1963, 57, p. 237–291; E. Herrera. La vitesse de la lumière par rapport aux corps en mouvement. Genié civil, 1963, 140, p. 262–264:
11. D. Burcev. On Kantor's experiment. Phys. Lett., 1962, 5, р. 44; D. R. White, R. A. Alpher. Comments on an experiment concerning Einstein's light velocity postulate. JOSA, 1963, 53, p. 760.
12. V. Vysin. The possibility of an interpretation of Kantor's direct first order experiment on the propagation of light from a moving source. Phys. Lett., 1964, 8, p. 36–37.
13. J. F. James, R. S. Sternberg. Change in velocity of light emitted by a moving source. Nature, 1963, 197, p. 1192.
14. F. Rots. New test of the velocity of light postulate. Phys. Lett., 1963, 7, p. 252–254.
15. G. С. Babcock, Т. G. Bergmann. Determination of the constancy of the speed of light. JOSA, 1964, 54, p. 147–151.
16. J. G. Fox. Experimental evidence for the second postulate of special relativity, Amer. J. Phys., 1962, 30, p. 297–300.
17. P. Beckmann, P. Mandics. Experiment of the constancy of the velocity of electromagnetic radiation. J. Res. Nat. Bur. Standarts. 1964, D68, p. 1265–1268; R. O. Waddoups, W. E. Edwards, J. J. Merrill. Experimental investigation of the second postulate of special relativity. JOSA, 1965, 55, p. 142–143.
18. P. Beckmann, P. Mandics. Test of the constancy of velocity of electromagnetic radiation of high vacuum. J. Res. Nat. Bur. Standarts, 1965, D69, p. 623–628.
19. J. Zaheysky, V. Kolesnikov. Optical experiments, to verify the second postulate of the special theory of relativity. Nature, 1966, 212, p. 1227.
20. R. J. Dickens, S. R. Malin. A test of the Ritz theory of light propagation. Observatory, 1965, 85, p. 260–262.
21. T. Alväger, A. Nilsson, J. Kjellman. A direct terestrial test of the second postulate of special relativity. Nature, 1963, 197, p. 1191.
22. D. Sadeh. Experimental evidence for the constancy of the velocity of gamma rays, using annihilation in flight. Phys. Rev., Letters, 1963, 10, p. 271–273.
23. W. G. Rosser. Velocity of light by a moving source. Nature, 1961, 190, p. 249.
24. T. Alväger, F. Parley, J. Kjellman, J. Wallin. Test of the second postulate of special relativity. Phys., Letters, 1964, 12, p. 260–262.
25. T. A. Filippas, J. G. Fox. Velocity of gamma rays from a moving source. Phys. Rev., 1964, 135, p. 1071–1075.
1. А. Эйнштейн. О возможности нового доказательства принципа относительности. Собрание научных трудов, т. I, стр. 49–50.
2. В. Strasser, M. Wien. Anwendung der Teleobjective auf den Doppler-effekt von Kanalstrahlen. Phys. Z., 1906, 7, S. 744–748.
3. H. Rau. Beobachtungen an Kanalstrahlen. Phys. Z., 1906, 7, S. 421–423.
4. P. A. Schultz. Ueber die Größe des Dopplereffekts. Z. Phys., 1923, 15, S. 121–125.
5. W. Ritz. Gesammelte Werke Paris, 1910, p. 523–524.
6. O. Scherzer. Die Meßbarkeit des quadratischen Dopplereffekts. Ann. Phys., 1938, 32, S. 242–244; С. del Lungo. Sopra l'effeto Doppler e il movimento assoluto. Cim., 1927, 4, p. 29–30.
7. Ch. E. Guye. Sur la possibilité de verifier experimentallment la relation ![]() C.R., 1938, 206, p. 29–31.
C.R., 1938, 206, p. 29–31.
8. H Ives. Light signals on moving bodies as measured by transported rods and clocks. JOSA, 1937, 27, p. 263–273; Apparent lengths and times in system experiencing the Fitzgerald–Larmor–Lorentz contractions. JOSA, 1937, 27, p. 310–313; The Doppler effect considered in relation to the Michelson–Morley experiment. JOSA, 1937, 27, p. 389–392.
9. H. E. Ives, G. R. Stilwell. Experimental study of the rate of moving atomic clock. JOSA, 1938, 28, p. 215–226.
10. H. Rau. Beobachtungen liber den Doppler-effekt an Linien- und Bandspektren der Kanalstrahlen. Ann. Phys., 1924, 73, S. 266–271.
11. В. Л. Гинзбург. В кн.: В. Паули. Теория относительности. M.–Л., 1947, стр. 38. Примечание.
12. R. С. Jones. On the relativistic Doppler-effect. JOSA, 1939, 29, p. 337–339.
13. G. Otting. Der quadratische Doppler-effekt. Phys. Z., 1939, 40, S. 681–687.
14. H. Billing. Ein Interferenzversuch mit dem Lichte eines Kanahlstrahlen Ann. Phys., 1938, 32, S. 577–592; А. Эйнштейн. Об интерференционных свойствах света, испускаемого каналовымн лучами. Собрание научных трудов, т. III, стр. 517–524.
15. E. Rilchardf, G. Offing. Uber die Messung des quadratischen Doppler-effektes mit Kanalstrahlen. Verb. D. Phys. Ges„ 1939, 20, S. 147.
16. H. Ives. G. Stilwell. An experimental study ul the rate of a moving atomic clock. JOSA, 1941, 31, p. 369–374, 459.
17. H. I. Mandelberg. L. Wiften. Experimental verification of the relativistic Doppler effect. JOSA, 1962, 52, p. 529–536.
18. В. D. Josephson. Temperature-dependent shift of γ-rays emitted by a solid. Phys. Rev. Lett., 1960, 4, p. 341–342. (Русский перевод в сб.: “Эффект Мёссбауэра”. М„ 1962, стр. 310–312).
19. R. V. Pound, С. Р. Rebka. Variation with temperature of the energy of recoil-free γ-rays from solids. Phys. Rev. Lett., 1960, 4, p. 274–276. (“Эффект Мёссбауэра”, стр. 305–309).
20. A. J. Boyle, D. S. Bumbury, C. Edwards. H. E. Hall. A thermal red shift of the recoilless γ-emission of Sn119m. Proc. Phys. Soc., 1960, 76, p. 165–166. (“Эффект Мёссбауэра”, стр. 313–316).
21. H. S. Hay, I. P. Schiffer, T. E. Cranshaw, P. A. Egelsfaff. Measurement of the red shift in a accelerated system using the Mössbauer effect in Fe57. Phys. Rev., Lett., 1960, 4, p. 165–166. (“Эффект Мёссбауэра”, стр. 415–417).
22. H. E. Bömmel. Measurement of the frequency shift of gamma rays in accelerated systems using the Mässbauer effect. “Mossbauer effect”, Ld. 1962, p. 229–232.
23. W. Kündig. Measurement of the transverse Doppler-effect in an accelerated system. Phys. Rev., 1963, 129, p. 2371–2375.
Приведём несколько обзоров по экспериментальным основам специальной теории относительности, опубликованные на русском языке в последние годы.
1. H. Г. Басов, О. H. Крохин, А. H. Ораевский, Г. M. Страховский, Б. M. Чикачев. О возможности исследования релятивистских эффектов с помощью молекулярных и атомных часов. УФН, 1961, 75, стр. 3–60.
2. А. Г. Молчанов. Опытная проверка постулатов специальной теории относительности. УФН, 1964, 83, стр. 753–755.
3. Г. M. Страховский, А. В. Успенский. Экспериментальная проверка теории относительности. УФН, 1965, 86, стр. 421–432.
4. А. Г. Баранов. О некоторых экспериментах по проверке постулатов специальной теории относительности. Эйнштейновский сборник 1966 г. M., “Наука”, 1966, стр. 284–297.
5. Д. И. Блохинцев. Обоснованность специальной теории относительности опытами в области физики высоких энергий. УФН, 1966, 89, стр. 185–199.
6. M. С. Козодаев. Экспериментальные аспекты специальной теории относительности. Вестник Академии Наук СССР, 1966, № 2, стр. 177–182.
7. А. M. Френк. Некоторые вопросы экспериментальных основ теории относительности. В кн.: У. И. Франкфурт. Специальная и общая теории относительности. M. “Наука”, 1968, стр. 241–262.
8. В. Д. Шмидт-Отт. Некоторые новые измерения в связи с доказательством справедливости специальной теории относительности. УФН, 1968, 96, стр. 519–527.
1. Сборник "Эффект Мёссбауэра". М., 1962, стр. 307.
Дата установки: 16.08.2006
Последнее обновление: 28.04.2009
[вернуться к содержанию сайта]