[вернуться к содержанию сайта]

C.А. Семиков
Нижегородский госуниверситет им. Н.И. Лобачевского
ОБ ЭКСПЕРИМЕНТАЛЬНОЙ ПРОВЕРКЕ БАЛЛИСТИЧЕСКОЙ ТЕОРИИ СВЕТА
(напечатано в журнале “Вестник ННГУ”, №4, 2013 г.)

Исследованы эксперименты по проверке баллистической теории Ритца. Показана неоднозначность их результатов и предложены способы её разрешения. Рассмотрен предсказанный Ритцем эффект трансформации частоты света, а его следствия сопоставлены с данными астрономических наблюдений и лабораторных экспериментов. Предложена схема установки для проверки эффекта Ритца и плавного преобразования длины волны и длительности лазерных импульсов.

Ключевые слова: скорость света, баллистическая теория, преобразование частоты света.

    В 1908 г. швейцарский физик Вальтер Ритц выдвинул баллистическую (эмиссионную) теорию света [1] в качестве классической альтернативы специальной теории относительности (СТО). В 1909–1911 гг. баллистические гипотезы независимо выдвинули Д.Ф. Комсток, Дж. Кунц, Р. Толмен, О.М. Стюарт и Дж.Дж. Томсон [2]. Согласно баллистическим теориям, свет распространяется, как в теории Ньютона,– аналогично потоку частиц, испущенных относительно источника со стандартной скоростью света c. При движении источника со скоростью v, скорость света c' определяется в системе наблюдателя по классической кинематике как векторная сумма c' = c + v,– аналогично скорости снарядов из движущегося орудия (отсюда название теории). Баллистическая теория, приняв принцип относительности Галилея, автоматически объясняла аберрацию звёздного света, результаты опытов Майкельсона-Морли, Троутона-Нобла и других попыток выявить инерциальное движение Земли [2, 3].

    Распространив баллистический принцип на электромагнетизм с гравитацией, Ритц классически объяснил в 1908 г. все электродинамические и релятивистские эффекты, включая рост массы быстрых электронов и вековое смещение перигелиев Меркурия, Венеры и Земли [1, 4]. Однако век назад, в 1913 г., теорию Ритца отклонили, как отмечено [5, 6], без достаточных экспериментальных оснований. Эти основания, современные опыты и эффекты баллистической теории, доступные для проверки, и рассмотрим. В частности исследуем предсказанный теорией эффект плавной трансформации длительности импульсов и перестройки частоты оптического излучения в любые другие диапазоны электромагнитных волн.

    В 1910 г. Д.Ф. Комсток [7], и в 1913 г. Де Ситтер [8] показали, что при добавлении орбитальной скорости v звёзд в двойных системах к скорости света, их свет видели бы то раньше (при скорости c + v), то позднее (при скорости c – v), чем при постоянстве скорости света. В итоге видимое движение звёзд исказилось бы, отличаясь от кеплеровского. Равномерное движение звёзд по круговой орбите показалось бы неравномерным от ускорения их видимого движения за картинной плоскостью и замедления – перед ней. Де Ситтер показал, что у спектрально-двойных звёзд подобные искажения отсутствуют, вопреки теории Ритца.

    Однако уже в 1913 г. немецкий астроном П. Гутник [9] показал, что искажённое движение звезды не будет заметно отклоняться от законов Кеплера, но появится мнимый избыточный эксцентриситет. Так, звезда с круговой орбитой покажется летящей по вытянутой к Земле эллиптической орбите. Изучив статистику спектрально-двойных звёзд, Гутник отметил, что у большинства их расчётные орбиты вытянуты именно в сторону Земли (долготы периастров группируются возле значения 90°). Эта аномалия открыта в 1908 г. Дж.М. Барром [4] и подтверждена астрономами [10, 11], но не объяснена однозначно. Выдвинутые гипотезы, объясняющие эффект Барра наблюдательной селекцией или галактической ориентацией орбит, противоречат наблюдениям. Как показал Бэттен [11], эффект обусловлен именно искажениями, создающими иллюзию вытянутых к Земле орбит. Для современной астрономии эффект Барра интересен тем, что может объяснить аномально высокие эксцентриситеты орбит экзопланет. Тогда их истинные орбиты, как у планет Солнечной системы,– почти круговые, а искажения создают иллюзию избыточных эксцентриситетов.

    Как показал Э. Фрейндлих [12], видимые искажения малы и в том случае, если зависимость скорости света от скорости источника по каким-то причинам ослаблена, то есть

c' = c + kv,                            (1)

где k << 1 и по оценкам Де Ситтера составляет k < 0.002 [2, 8].

    Снижение влияния скорости источника на скорость света объяснил в 1965 г. Дж.Г. Фокс [5]. Поскольку тесные пары двойных звёзд окружены общими атмосферами межзвёздного газа [11], присутствующего и на всём пути света к Земле, то по теореме погашения (экстинкции) Эвальда-Озеена исходный свет звезды постепенно гасится облаками газа и переизлучается ими со скоростью c относительно облаков. Тогда выражение (1) имеет смысл средней скорости света на пути r от звезды к Земле, а коэффициент k приобретёт смысл относительной доли k = l /r пути l, на котором свет звезды, ещё не будучи переизлучён, движется со скоростью c + v. На этом пути l лучи и набирают разность хода. Для концентрации атомов N ~ 1 см^–3 и показателя преломления n межзвёздного газа, у света с длиной волны λ, Фокс оценил характерную длину l = λ/2π(n – 1) в один световой год [5]. Поскольку расстояния r до спектрально-двойных звёзд составляют сотни световых лет, отношение k = l /r – как раз порядка сотых или тысячных долей. Так что аргумент де Ситтера не имеет силы.

    Так и в других астрономических проверках теории Ритца, включая опыт Р. Томашека, опыт А.М. Бонч-Бруевича, анализ К. Брэчера [13], исследовали не первичное излучение звёзд, а свет, прошедший сквозь звёздные атмосферы, межзвёздный газ и земную атмосферу, линзы оптических приборов, т.е. “утративший память” о скорости источника в ходе переизлучений. Как отмечено [5, 6], теорема погашения ставит под сомнение все астрономические проверки теории Ритца. То же относится и к земным лабораторным опытам, в которых пытались сравнивать скорости света от движущихся источников [13, 14].

    Если в отношении групповой скорости света среда ведёт себя как вторичный источник, испускающий свет со скоростью c, то на фазовую скорость среда влияет сложнее, ввиду интерференции исходного и вторичного излучения. Рассмотрим для примера опыт Физо с движущейся водой [14]. Вычислим скорость света от источника, движущегося к границе среды со скоростью v, по аналогии с расчётом в молекулярной оптике для неподвижного источника [3, с. 425]. Если в вакууме источник испускает свет со скоростью c + v, то поле единичной падающей волны опишется уравнением E₀ = exp [i(ωt – k'x)], где ω – циклическая частота падающей волны, k' = ω/(c + v) – её волновое число. Волна возбуждает в среде вторичные волны интенсивности E₁ = − ikxb exp [i(ωt – kx)], где k = ω/c – их волновое число, x – толщина пройденного слоя среды, излучающей со скоростью c новую волну, b – безразмерный коэффициент, характеризующий оптическую плотность среды. Результирующее поле E = E₀ + E₁ = (exp [ix(k – k')] – ikxb) exp [i(ωt – kx)], что, с учётом разложения exp (x) ≈ 1 + x при малых x и (k – k') ≈ ωv/c² = kv/c, даёт E ≈ (1 + ikxv/c – ikxb) exp [i(ωt – kx)] ≈ exp [i(ωt – kx(1 + b – v/c))]. Здесь kx(b – v/c) – сдвиг фазы, пропорциональный пути x и меняющий фазовую скорость c*. По сути, в среде волновое число k = ω/c заменяется новым k* = ω/c* = k(1 + b – v/c). Отсюда c* = ck/k* = c/(1 + b – v/c). При v = 0 получим номинальную скорость света в среде c* = c/(1 + b), где (1 + b) – коэффициент преломления n. Для 0 < v << c получим

,                        (2)

а для околосветовых скоростей v ~ c точный расчёт по выше описанному методу даёт

.                            (3)

    В системе отсчёта источника, где со скоростью v движется среда, найдём из (2), по принципу относительности, что скорость света в среде c' = c* – v = c/n – v(1 – 1/n²). Тем самым баллистическая теория объясняет опыт Физо, где открыта эта зависимость [14]. В других опытах с движущимися источниками и средами проверять теорию Ритца тоже следует на базе молекулярной оптики, дающей однозначные выводы. Это устранит неоднозначность в трактовке опытов, выполненных У. Кантором, Т. Бергманом и др. [14]. Итак, переизлучение ставит под сомнение результаты всех лабораторных опытов по проверке теории Ритца.

    В этом плане выгодно отличается опыт группы Александрова [6, 15], где измерялась скорость синхротронного излучения от электронов, движущихся с околосветовыми скоростями v ~ c в вакуумной камере накопителя, где скорость света по баллистической теории на всём пути сохраняла значение c + v. В первом варианте измерялось время пролёта синхротронного излучения – по моменту его регистрации фотодетектором относительно момента прибытия электронов к резонатору. Во втором варианте сравнивалось время регистрации излучения фотодетектором в случаях, когда канал вывода свободен, и когда перекрыт стеклянной пластинкой, которая по теории Ритца, переизлучив свет, снизила бы его скорость от c + v до номинального значения c и сдвинула бы момент регистрации импульсов излучения.

    В первом варианте измеренная скорость излучения оказалась равна c, а во втором – не произошло сдвига импульсов на 9 нс. Однако и этот опыт в его нынешней постановке нельзя считать прямым, а вывод – однозначным. Во-первых, напрямую не измерена скорость электронов v. Она рассчитана косвенно на основе формул СТО, дающих v ≈ c [6]. А в классической физике скорость электронов ищут иначе, и их скорость может превышать световую, как отмечал Ритц [1]. Поэтому сдвиг, следующий из теории Ритца, отличен от ожидаемого в [6], и нужны прямые замеры скорости электронов пролётно-импульсным методом: по времени пролёта дистанции, измеренному установленными вдоль неё детекторами частиц. В ускорителе скорость электронов нельзя определить однозначно, деля длину их орбиты на период ускоряющего поля или импульсов излучения, т.к. эти периоды отличаются, если в ускорителе крутится несколько сгустков электронов. А число сгустков тоже не измерено напрямую.

    Во-вторых, раз импульсы излучения образуют периодичную последовательность, нельзя сказать однозначно, произошёл их сдвиг или нет, раз сдвиг по теории Ритца не равен 9 нс. Так, сдвиг, кратный периоду повторения импульсов, не проявится (стробоскопический эффект). Эффект можно исключить, варьируя смещение в ходе отдаления фотодетектора.

    В-третьих, нет оценок эффективности переизлучения стеклянной пластинкой. Среда переизлучает лишь часть света, и, чем среда толще и плотнее, тем выше доля вторичного излучения среды со скоростью c, и ниже доля первичного, посланного источником со скоростью c + v. Как показал Фокс [5], оценка длины переизлучения l применима лишь для скоростей v << c. А для v ~ c длина l может быть много меньше или больше. В первом случае остаточный газ в вакуумной камере сразу переизлучит свет со скоростью c, лишив опыт смысла. А в случае ослабленного переизлучения стеклянная пластинка замедлит лишь малую долю света, и основная его часть сохранит скорость c + v, не изменив осциллограмму.

    Действительно, согласно (3), c* = c/n* = c/[n – v/(c + v)], и для излучения электронов, имеющих скорость v ≈ c, показатель преломления стекла n = 1.5 становится равен n* = n – v/(c + v) ≈ 1. Это на порядки увеличивает l = λ/2π(n* – 1), отчего на толщине пластинки свет почти не переизлучается: он проходит сквозь пластинку, сохранив скорость c + v, и лишь малая часть света переизлучится со скоростью c. На осциллограмме из [15] видно, что после ввода пластинки высота импульсов снизилась: первичное излучение со скоростью c + v ослабло, и возникли слабые импульсы, запаздывающие на Δt = 17 нс (рис. 1). Они не могут быть результатом переотражений (т.к. для них Δt = 36 нс), но могут соответствовать вторичному излучению, идущему от пластинки со скоростью c, на что указывает величина задержки Δt, согласующаяся с теорией Ритца при классической оценке скорости электронов. Вторичные импульсы малы ввиду слабого переизлучения и, возможно, от LC-фильтра, сгладившего сигнал фотодетектора и “звон”, заметный на других осциллограммах [6].

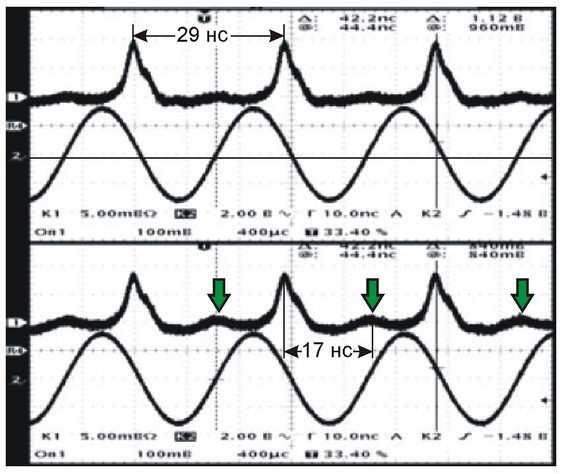
    Итак, в опыте следует, во-первых, напрямую измерять скорость электронов; во-вторых, исключить строб-эффект, меняя пролётные дистанции; в-третьих, оценить вклад переизлучения, применяя всё более толстые и плотные пластинки и оценивая сопутствующие изменения осциллограмм. В таком виде опыт сможет стать решающим и войти в учебники. А в нынешнем виде он неоднозначен и, как отмечено [15], не нов, повторяя схему опыта А.С. Мазманишвили и её недочёты. Таким образом, в физике высоких энергий тоже нет однозначных свидетельств против баллистической теории. Поэтому рассмотрим новые эффекты, которые можно положить в основу современной проверки теории Ритца.

    Выше был рассмотрен эффект, искажающий видимое движение звёзд за счёт изменения их лучевой скорости, вызывающего вариации скорости света. Рассмотрим эффект количественно на примере источника, излучающего световые сигналы через малый интервал времени dt и находящегося от приёмника на расстоянии r. Свет, испущенный источником в момент t, достигнет приёмника в момент t' = t + r/c', где c' – скорость света в вакууме. Время dt' между приёмом двух световых сигналов найдётся дифференцированием t' по t:

.                        (4)

    Здесь рассмотрен общий случай, когда скорость света c' играет роль не константы c (как постулирует СТО), а переменной, как в общей теории относительности (ОТО) и в баллистической теории. Так, вариации скорости света в вакууме выявлены при космической радиолокации [16]. Если второе слагаемое в (4) характеризует эффект Доплера dt' = (1 + v_r/c')dt, т.к. ∂r/∂t = v_r – лучевая скорость источника относительно приёмника, то третье слагаемое характеризует изменение периода сигналов за счёт вариации скорости света. Данный эффект

,                          (5)

следует из баллистического принципа c' = с + v, меняющего скорость света при ускорении источника. В направлении приёмника скорость света c' = с – v_r, где v_r – лучевая скорость источника (проекция v на луч зрения – на радиус-вектор r источника). Дифференцируя ∂c'/∂t = – ∂v_r /∂t = – a_r (где a_r – лучевое ускорение источника) и подставляя в (5), при v_r << c получим

.                            (6)

    Природа эффекта прозрачна: по баллистическому принципу ускоряемый источник в каждый последующий момент сообщает свету немного иную скорость, и последовательные сигналы (или фронты световых волн), испущенные с разными скоростями, догоняют друг друга (сокращая длину волны), либо расходятся (наращивая длину волны), приходя к приёмнику чаще или реже. Из преобразования периода dt (6) можно найти для изменения исходной длины волны λ = cdt, частоты света f = 1/dt и длительности импульса Δt, соответственно,

, , .                    (7)

    Этот эффект, дополняющий эффект Доплера, будем далее называть эффектом Ритца: Ритц вывел (6) ещё в 1908 г. [1]. При v_r << c формула (4) даёт общее преобразование периода

,                           (8)

    Если доплер-эффект dt' = (1 + v_r /c)dt в оптике хорошо известен, то на Земле выявить эффект Ритца (6) – сложнее, ввиду его малости. Однако на дистанциях r порядка светового года умеренные ускорения a_r ~ c²/r ≈ 9.5 м/с² могут менять видимую длительность в разы.

    Так, уже в 1910 г. Комсток [7] показал как этот эффект исказил бы равномерное движение двойных звёзд по круговой орбите, которое, регулярно меняя проекцию a_r центростремительного ускорения a звезды, покажется неравномерным, идущим по вытянутой к Земле орбите эксцентриситета ε = ra/c². Затем Ла Роза [17] показал, что эффект Ритца проявится и в вариациях яркости и спектра двойных звёзд [18]. По закону сохранения энергии света, испущенного звездой в интервале Δt и воспринятого в интервале Δt' (7), звезда, которая излучала в апертуру телескопа мощность P, воспримется как обладающая мощностью излучения

.                            (9)

    Подобные вариации яркости (9) и длины волны λ_max (7) спектрального максимума открыты у цефеид и других переменных звёзд, но трактуются по закону смещения Вина Т_cλ_max = const как колебания их температур Т_c и размеров [18]. Если параметр ε = ra/c² ≈ 1 и выше, то частота и яркость двойной звезды меняется на порядки, согласно (7) и (9), создавая короткие мощные импульсы рентгеновского, гамма- или радиоизлучения. Поскольку в двойных системах новых, сверхновых, барстеров, пульсаров и других переменных звёзд наблюдают именно такие вспышки, то эффект Ритца наиболее просто объясняет их свойства.

    В Галактике при концентрации N ~ 1 см^–3, переизлучение идёт на длине l ~ 1 св. год < r [5], и в формулах (6–9) следует заменить r на l, и эффект Ритца снизится. Для межгалактических дистанций N ≤ 6×10^–11 см^–3 [19], а пропорциональная 1/N длина l ≥ 2×10¹⁰ св. лет >> r. То есть у большинства галактик нет переизлучения, и по эффекту Ритца (7) длина волны λ света, испущенного видимыми участками галактических ядер-балджей (где спектральные линии наиболее интенсивны, а ускорения направлены от нас, a_r > 0), растёт пропорционально расстоянию r галактик: λ' = λ(1 + ra_r/c²). Эффект напоминает хабблов закон красного смещения у галактик λ' = λ(1 + rH/c), причём постоянная Хаббла H = 74 (км/с)/Мпк близка к коэффициенту a_r/c, рассчитанному по ускорениям a_r = V_b²/R_b в галактиках. Так, взяв за образец нашу Галактику, характеристики которой типичны для спиральных галактик, а балдж имеет радиус R_b = 0.002 Мпк и окружную скорость V_b = 205 км/с [20], получим расчётное значение постоянной Хаббла H_с = a_r/c ≈ 70 (км/с)/Мпк, близкое к измеренному H.

    Эффект Ритца объясняет красное смещение и его аномалии без гипотез о расширении Вселенной, о тёмной материи и энергии. Так, избыток красных смещений у квазаров по сравнению с галактиками и отличия красных смещений у связанных, равноудалённых галактик объяснимы по эффекту Ритца разницей их ускорений a_r, дающих разные H_с = a_r/c. А дефицит красного смещения у самых далёких галактик [21] может быть вызван переизлучением межгалактическим газом, существенным для дистанций r > l ~ 2×10¹⁰ св. лет, на которых эффект Ритца и красное смещение снижены. Начиная с таких дистанций r ~ l (r ~ 10¹⁰ св. лет, где красное смещение z ~ 0.8) как раз и выявлены отклонения от закона Хаббла в виде дефицита красного смещения, истолкованные как ускоренное расширение Вселенной [21].

    На лабораторных дистанциях r ~ 1 м, при доступных ускорениях a_r источников, сдвиг частоты по эффекту Ритца столь мал, что выявляется лишь по эффекту Мёссбауэра. Так, в опыте Бёммеля при ускорении источника γ-лучей открыт сдвиг частоты Δf/f = (f ' – f)/f = ra_r/c² пропорциональный дистанции r и ускорению источника a_r [14]. При размещении γ-источников на крутящихся дисках тоже открыт сдвиг частоты, совпадающий с найденным по эффекту Ритца [22]. Итак, астрономические наблюдения и лабораторные эксперименты не противоречат эффекту Ритца, хотя обычно трактуются по общей теории относительности.

    Для однозначной проверки эффекта Ритца (7) и трансформации частоты света в разы следует обеспечить ra_r/c² ~ ±1, что для лабораторных дистанций r ~ 1 м требует a_r ~ ±c²/r ~ ±10¹⁷ м/с². Это ускорение недостижимо для источников света, но его легко сообщить электронам и ионам, способным излучать или переизлучать свет. В электрическом поле E ускорение a = Ee/m электрона (где e/m = 1.76×10¹¹ Кл/кг – его удельный заряд) достигает 10¹⁷ м/с² при E ~ 10⁶ В/м. Для ионов E ~ 10⁹ В/м. Такие напряжённости легко достижимы.

    Установкой для проверки эффекта может служить вакуумная камера, где пучок электронов или ионов в поле E получает ускорение a_r ~ 10¹⁷ м/с² (рис. 2). Лазерное импульсное излучение с несущей частотой f и длительностью импульсов Δt ~ 1 пс фокусируется на пучке, испытывая томсоновское рассеяние на электронах (или ионах) – вторичных источниках излучения частоты f, которое проходит в вакууме путь r ~ 1 м до светофильтра (отсекающего свет частоты f) и попадает в спектрометр или детектор. При справедливости эффекта Ритца они зафиксируют сигнал изменённой длительности и частоты (7) – это первый критерий.

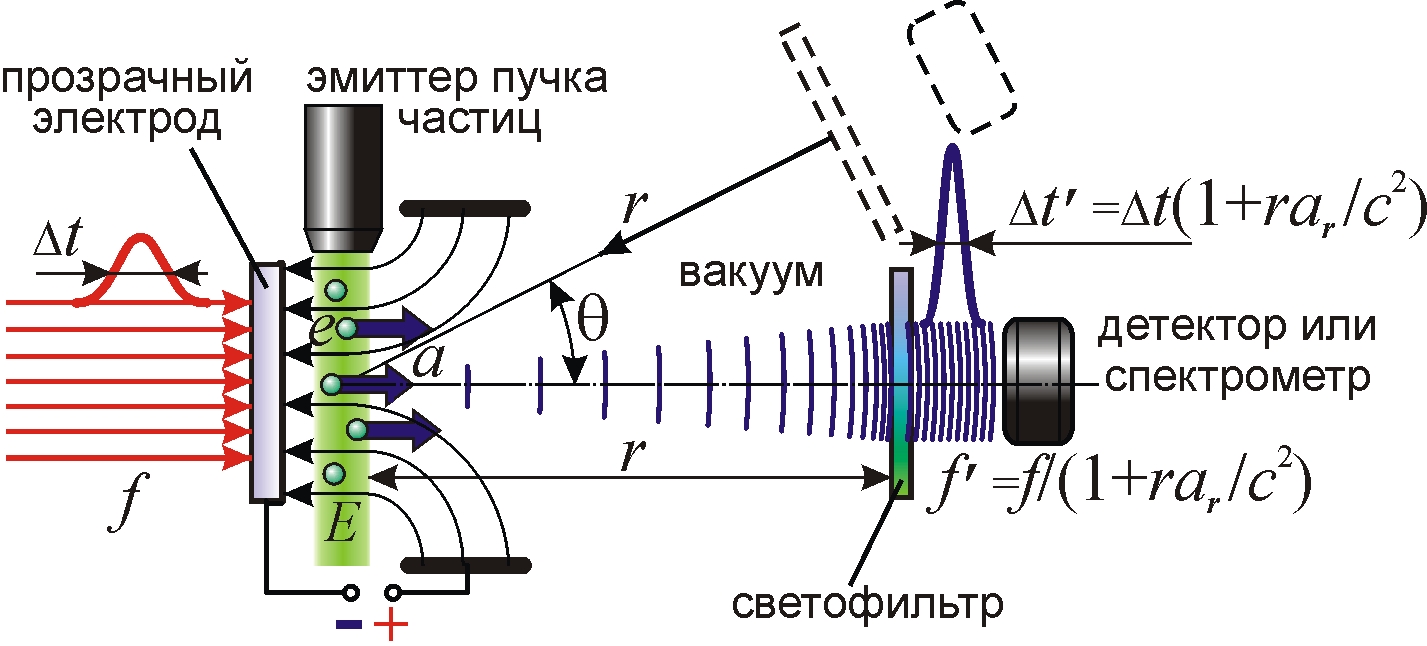
    Из зависимости преобразованной частоты f ' и коэффициента трансформации k = f '/f от a_r и E (рис. 3) видно, что при a_r = -c²/r частота f ' стремится к бесконечности, и малая вариация a_r (от изменения E или r) вызывает изменение частоты на порядки. Это открывает простой способ перестройки частоты света из оптического в УФ-, рентгеновский и гамма-диапазон. При обратном знаке поля и ускорения частота снижается, что позволит трансформировать оптическое излучение в инфракрасное и терагерцовое. ОТО не предсказывает подобных сдвигов частоты, поскольку приёмник излучения не ускоряется вместе с источником.

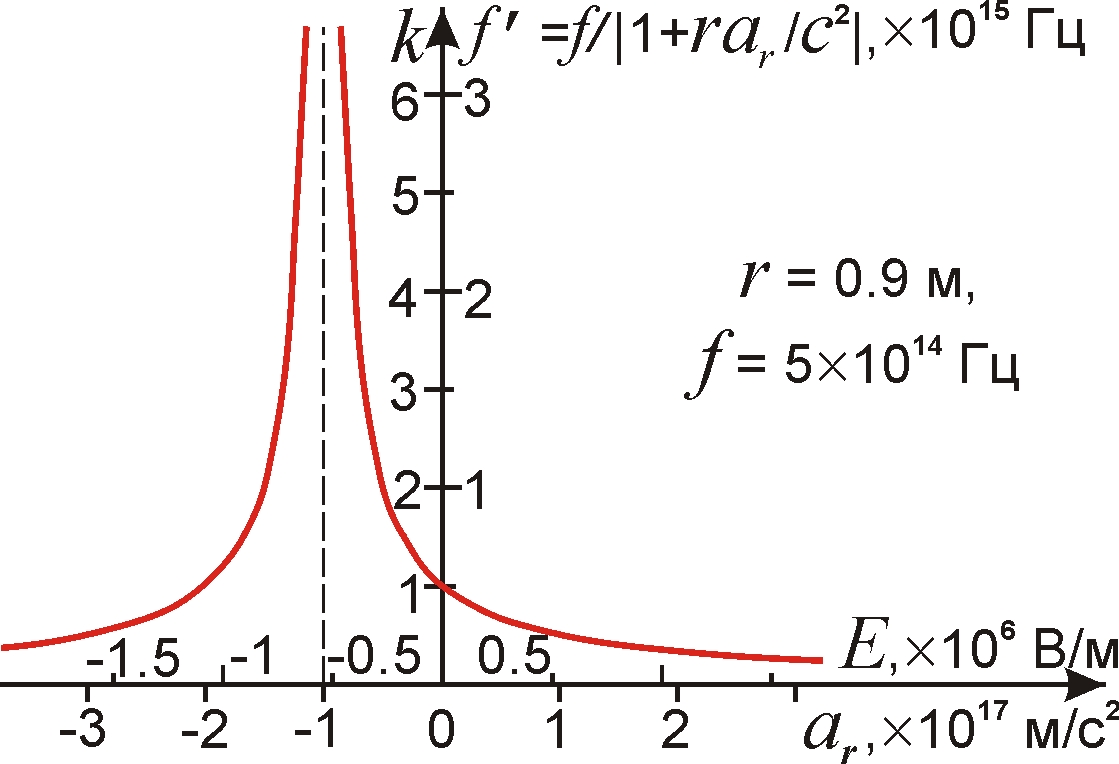
    Эффект Ритца отличен и от эффекта Доплера, не меняющего частоту в ходе переизлучения в прямом направлении. А генерация пучка частиц и электрического поля короткими импульсами, синхронными с лазерными импульсами, не только снизит затраты энергии на эмиссию и разгон частиц, но и сделает скорости V = a_rΔt ~ 10⁵ м/с, полученные частицами за время пикосекундного лазерного импульса Δt ~ 10^–12 c, недостаточными для доплеровского преобразования частоты в разы и для генерации высокоэнергичного тормозного излучения.

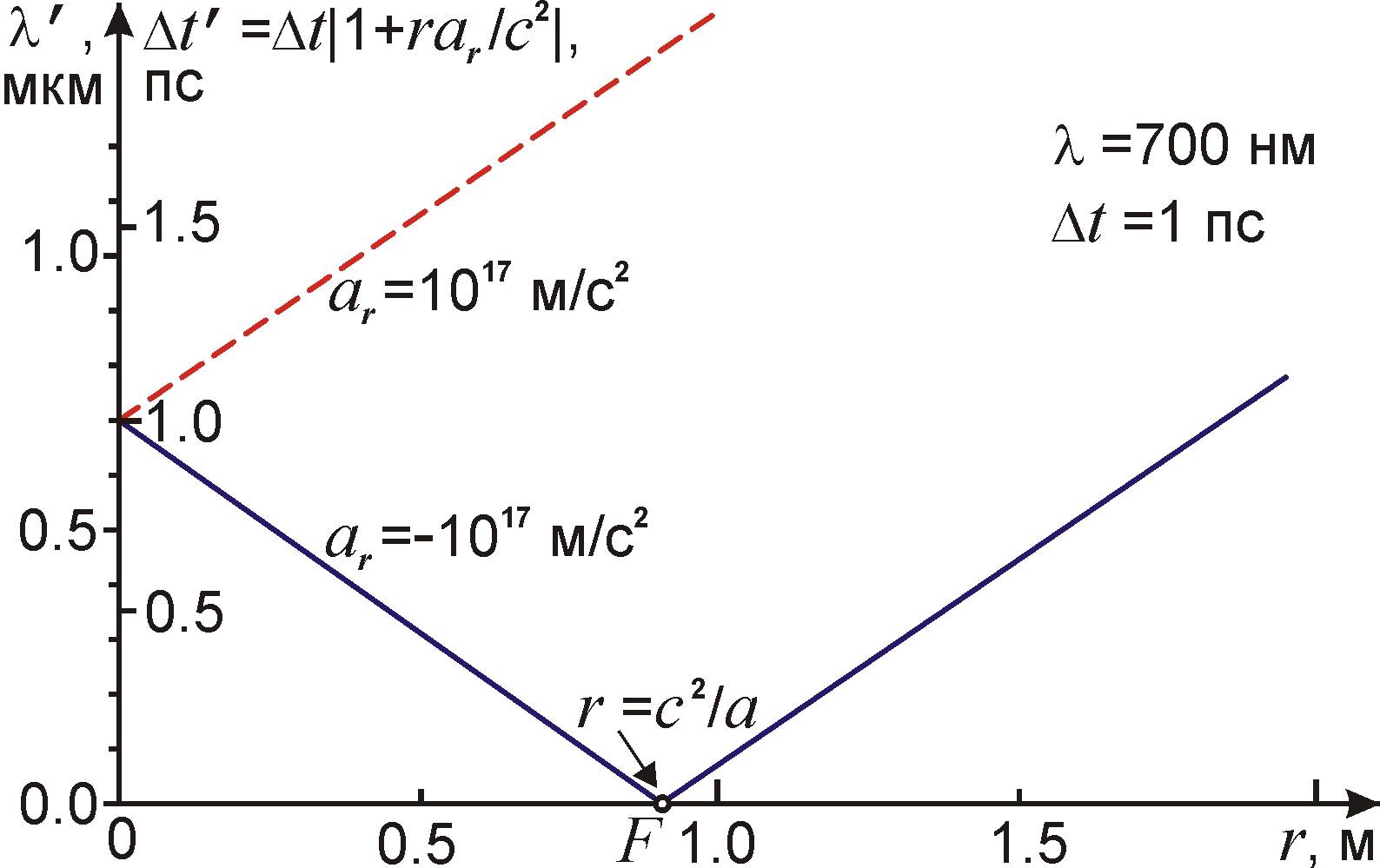
    Вторым критерием проверки эффекта Ритца служит соответствие опыту зависимости (7) длины волны и длительности преобразованных импульсов от пройденного светом пути r (рис. 4). Третий критерий даёт анализ зависимости f ' от угла θ, под которым спектрометр регистрирует излучение (рис. 2). Поскольку эффект Ритца (7) зависит не от абсолютной величины ускорения a, а от его проекции a_r = -acosθ на r, то должна выполняться зависимость

.                            (10)

    В полярных координатах угловая зависимость (10) соответствует эллипсу (рис. 5) с фокусом в полюсе, а параметр ε = ra/c² < 1 – эксцентриситету этого эллипса. При критическом значении ε = 1 эллипс превращается в параболу, а максимальная частота f ' стремится к бесконечности. При ε > 1 угловая зависимость – это ветвь гиперболы, и частота обращается в бесконечность в направлении θ₀ = arccos(c²/ra) асимптот гиперболы. В пределах угла |θ| < θ₀, где знаменатель отрицателен (задние фронты обгоняют передние), следует брать модуль частоты: зависимость изобразится второй, зеркально обращённой ветвью гиперболы.

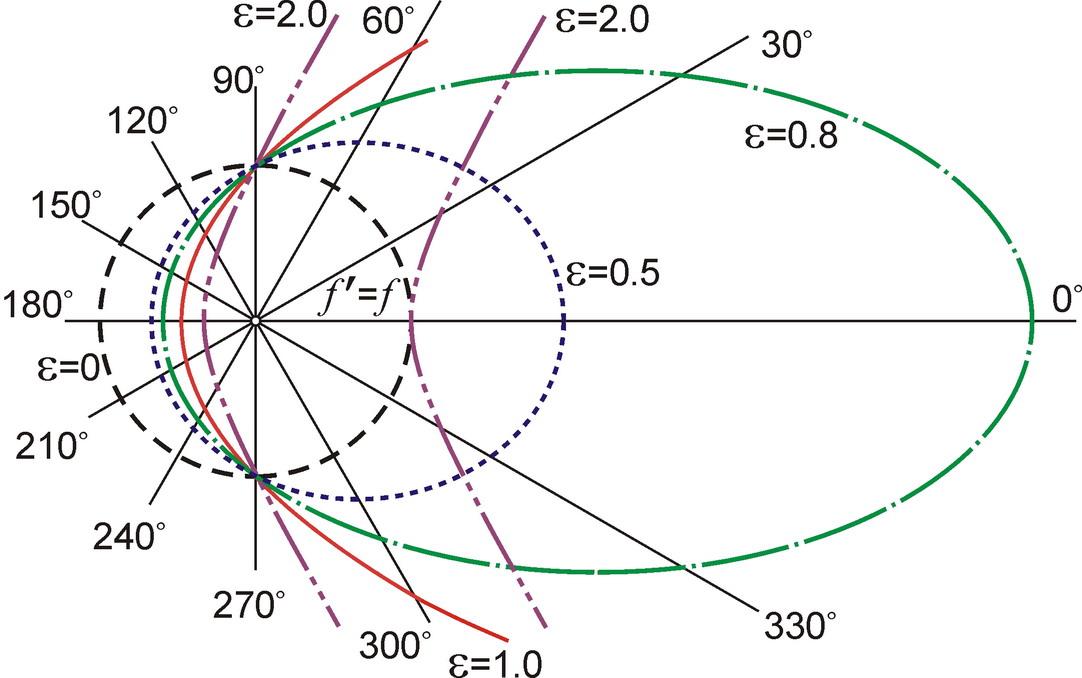
    Эффект Ритца позволяет неограниченно сжимать длительность импульсов Δt' (7) и наращивать их пиковую мощность P' (9), за счёт одновременного сокращения длительности импульсов и длины волны, периода световых колебаний (рис. 4), с пропорциональным уширением частотного спектра (7). Тогда длительность импульса, ограниченная снизу шириной спектра и периодом световых колебаний [23], может стать сколь угодно малой, а интенсивность – сколь угодно высокой. По сути, в точке F, где r = c²/a (ε = 1) реализуется абсолютная фазовая фокусировка: все волновые фронты достигают приёмника одновременно.

    Оценим мощность трансформированных импульсов. При мощности P₀ лазерного излучения, мощность рассеянного электронами излучения P = P₀(1 – e^–τ) ≈ P₀τ = P₀Nσ_Tx, где τ = Nσ_Tx << 1 – оптическая толща слоя электронного пучка, N – концентрация в нём электронов, x ≈ 0.001 м – толщина пучка, σ_T = (8π/3)r_e² ≈ 6.65×10^–29 м² – эффективное сечение томсоновского рассеяния, а r_e – классический радиус электрона. При концентрации электронов N = 10²⁶ м^–3, достижимой при взрывной электронной эмиссии [24], получим P ~ P₀×10^–5. А из условия (9), при сжатии Δt ~ 10^–12 c в 10⁵ раз, генерируются импульсы гамма-излучения с мощностью P', равной исходной (P' ~ P×10⁵ ~ P₀) и длительностью Δt' ~ 10^–17 c. Также возможна генерация пучков когерентного рентгеновского и гамма-излучения, если высока однородность электронного пучка и поля E: лазерный пучок, проходя сквозь сгусток электронов, когерентно рассеивается ими в параллельный пучок, преобразуемый далее по эффекту Ритца.

    При ненаправленном рассеянии мощность сигнала, поступающая в телесный угол Ω = πR²/L² (в апертуру детектора радиуса R), составит P_Ω = P₀NxΩdσ/dΩ, где dσ/dΩ = σ_T(3/16π)(1 + cos²θ) – дифференциальное сечение томсоновского рассеяния. Тогда, при θ = 0° и R/L ~ 0.05, получим P_Ω ~ P₀×10^–8. А мощность P_Ω' сигнала на детекторе, с учётом (9), будет

.                        (11)

    При ε < 1, как видно из диаграмм направленности (рис. 6) по энергии (пропорциональной P_Ω), и пиковой мощности P_Ω' (11) они максимальны в прямом направлении (θ = 0°).

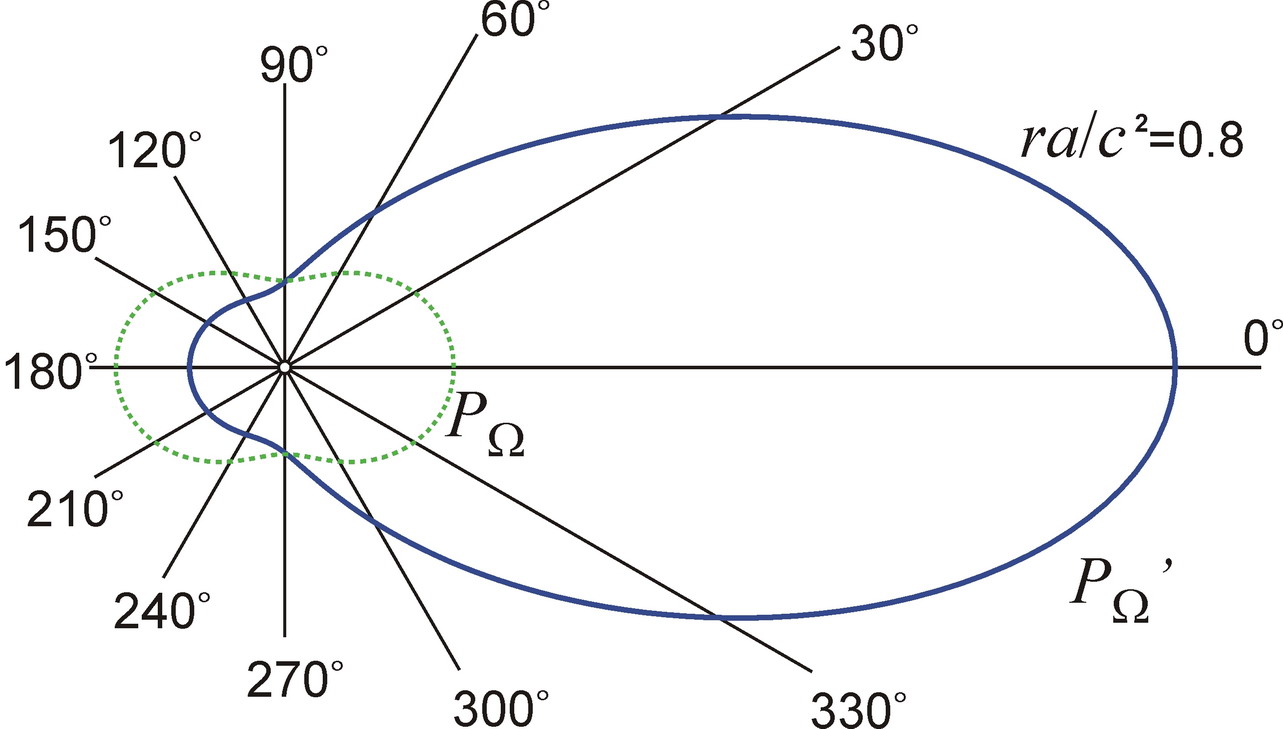
    Электроны и ионы можно ускорять и световым давлением сфокусированного лазерного пучка, который одновременно бы ускорял частицы и, после переизлучения ими, трансформировался по эффекту Ритца. Подобный эффект реально открыт в генераторах аттосекундных импульсов, где в луче фемтосекундного лазера атомы инертных газов приобретают гигантские ускорения, вплоть до 10²³ м/с² [23]. Тогда регистрируемые импульсы рентгеновского излучения аттосекундной длительности могут быть фемтосекундными оптическими импульсами, преобразованными по эффекту Ритца (7). Проверить это можно при анализе критериев (7–11), т.е. угловой зависимости спектра и мощности, а также зависимости частоты f ' от расстояния и от ускорения (пропорционального интенсивности в фокусе пучка).

    Показано, что баллистическая теория и эффект Ритца до сих пор не проверены однозначно. В пользу их справедливости косвенно свидетельствует ряд астрономических и лабораторных данных. Предложена схема установки, которая в случае подтверждения эффекта Ритца позволит плавно преобразовывать частоту, длительность и мощность импульсов света во всём диапазоне частот, времён и мощностей, без фундаментальных ограничений.

    Выражаю благодарность за дискуссии профессору ННГУ М.И. Бакунову.

Дата установки: 05.02.2014
[вернуться к содержанию сайта]

W