[
вернуться к содержанию сайта]Если источник света имеет скорость u, указывающую в положительном направлении оси X, то, согласно теории Ритца, скорость света, испускаемого в том же самом направлении, есть c + u, где c - это скорость света, испускаемого неподвижным источником. В других теориях (Lorentz, Einstein) скорость света - это константа, всегда равная c и не зависящая от движения источника. Далее будет показано, что принятая Ритцем зависимость скорости света от движения источника абсолютно недопустима.
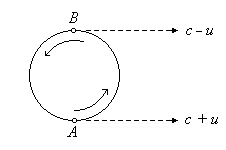
Вообразим двойную звезду и наблюдателя, расположенного на огромном расстоянии Δ в её плоскости. Свет, испускаемый звездой от точек, лежащих возле A (см. рис.) становится виден, в соответствии с теорией Роскоши, спустя время Δ/(c+u),

тогда как свет, испускаемый от точки B, - через время Δ/(c-u). Обозначим через половину орбитального периода звезды (её путь, как считаем ради простоты, является кругом), так что интервал времени между этими двумя наблюдениями есть T+2uΔ/c2 [*]. Если звезда входит во вторую половину её периода от B до A, то наблюдаемый интервал времени есть T-2uΔ/c2. В общепринятой теории оба интервала равны T. Теперь, если 2u
Δ/c2 имеет тот же порядок величины, что и T, то, если бы теория Ритца была справедлива, то было бы невозможно привести наблюдения в согласие с законами Кеплера. Для всех спектрально двойных звёзд 2uΔ/c2 действительно оказывается в настоящее время не только того же порядка величины, что и T, но, вероятно, в большинстве случаев даже много больше. Возьмём, например, u=100 км/с, T = 8 дней, Δ/c=33 световых года (то есть параллакс 0,1''), тогда получим приближённо T-2uΔ/c2=0. Все эти измерения того же порядка, что и у наиболее известных спектрально двойных звёзд. (Большинство параллаксов будет, вероятно, меньшее 0,1'').Существование спектрально двойных звёзд и то обстоятельство, что ... в большинстве случаев видимая лучевая скорость оказывается исчерпывающе представимой кеплеровым движением, является, таким образом, сильным доказательством постоянства скорости света. Можно ещё напомнить, что во многих случаях лучевые скорости найденных орбит подтверждаются визуальными измерениями (как с δ Equulei [дельта Малого Коня], ζ Herculis [дзета Геркулеса], и т.д.) или наблюдением затмения одного из компонентов двойной звезды другим (как у переменных типа Алголя).
Лейден, февраль 1913 г.
(Поступило 14 февраля 1913 г.)
[*] Это по сути T+2uΔ/(c2-u2), где u<<c.
В теории Ритца свет, испущенный источником, движущимся со скоростью u, распространяется через пространство в направлении движения источника со скоростью c + u, c - скорость света, испускаемого неподвижным источником. В других теориях (Лоренц, Эйнштейн) скорость света всегда равна c, независимо от движения источника. Теперь легко видеть, что гипотеза Ритца ведёт к следствиям, которые являются абсолютно недопустимыми.
Рассмотрим один из компонентов двойной звезды. Наблюдатель расположен на большом расстоянии Δ. Пусть в момент t проекция скорости звезды в направлении к наблюдателю равна u. Тогда из закона движения звезды мы можем вывести уравнение:
u = f (t - t0) (1)
Свет, испущенный звездой в момент времени t, достигает наблюдателя в момент τ = t + Δ/c - au. В теории Ритца мы имеем, пренебрегая второй и более высокими степенями u/c, a= Δ/c2. В других теориях мы имеем a= 0. Если теперь мы положим τ0 = t0 + Δ/c, то получим
u = f (τ - τ0 + au) или u = φ(τ - τ0) (2)
Функция φ не будет отличаться от f, только если au будет неизмеримо малой величиной. Поэтому, если одно из этих двух уравнений (1) и (2) находится в согласии с законами механики, то другое - нет. В настоящее время a далеко от малой величины. В случае спектрально двойных u не является малой величиной, и, следовательно, au может достигать больших значений. Возьмём, например, u = 100 км/с и примем параллакс в 0'',1, откуда Δ/c = 33 года, мы находим приближённо u = 4 дня, то есть совершенно того же порядка величины, что и периоды обращения наиболее известных спектрально двойных.
В настоящее время видимые скорости спектрально двойных, т. е. уравнение (2), фактически удовлетворительно представляются кеплеровым движением. Кроме того, во многих случаях орбита, полученная на основе лучевых скоростей, подтверждается визуальными измерениями (как для дельты Малого Коня, дзеты Геркулеса, и т.д.) или наблюдениями затмений (как у переменных типа Алголя). Таким образом, мы не можем избежать вывода о том, что a= 0, то есть скорость света не зависит от движения источника. Теория Ритца вынудила бы нас предположить, что движение двойных звёзд подчиняется не закону Ньютона, а намного более сложному закону, в зависимости от расстояния звезды от Земли, который является, очевидно, абсурдным.
В Proc. Amst. Acad. февраль 1913 г. (том 15, с. 1297) и в данном журнале 14, 429, 1913 г. я показал, что существование спектрально двойных звёзд, движения которых подчиняются законам Кеплера, в выборе между теориями света Ритца (эмиссионная теория) и Лоренца (постоянная скорость света) решают спор в пользу последней.
Если оставить точку зрения, согласно которой надо выбирать только между этими двумя теориями, то вопрос перерастает в иной. Закон для скорости света в направлении источника тогда становится, например,
v = c + ku.
Если допускаем лишь k = 0 (Лоренц) или k = 1 (Ритц), то выбор однозначен. Даже если кто-то допускает промежуточные значения k, то должен быть поставлен вопрос о верхнем пределе для значения k. Невозможно экспериментально подтвердить существование константы какой-либо [неопределённой] величины, но только константу в пределах некоторых границ.
Как подчеркивают мр. П. Гутник (Astr. Nachr. 195, p. 265
) и мр. Э. Фрейндлих (этот журнал 14, 835), в движении весьма точно возникает видимый эксцентриситет, который пропорционален ku0Δ, где u0 - это максимальное значение u.В отношении нахождения верхнего предела для k мы берём, например, известную звезду подобную β Aurigae [бета Возничего]. Её наблюдательные данные следующие:
π=0
'',014, e=0,005, u0=110 км/с, T=3,96 сут.Мы устанавливаем в качестве верхних пределов те, которые ещё допустимы за счёт неточности наблюдений, таким образом можно найти:
π
<0'',05, или Δ>65 световых лет, e<0,015,таким образом, можно найти:
k < 0,002.
Возможно, другие звёзды дадут ещё меньшие величины. Естественно, наименьшие величины предоставят звёзды с наименьшими параллаксами. К сожалению, параллаксы для большинства звёзд всё ещё неизвестны. Имеется, однако, большое количество спектрально двойных звёзд с большими скоростями и малым или бесконечно малым эксцентриситетом, и не может быть подвергнут сомнению тот факт, что большинство этих звёзд имеет малые параллаксы и потому даёт ещё много меньшие величины k, чем β Aurigae. Была отобрана только эта звезда, поскольку её параллакс известен и потому относительно велик.
Мр. Фрейндлих подчёркивает, что статистика спектрально двойных звёзд показывает некоторое предпочтение линий апсид в направлении к солнцу. Это говорило бы за гипотезу измеримой величины k. Имеется, однако, другой статистический факт, который является, по моему мнению, намного более достоверным и который говорит против этого. Это уже было подчёркнуто мр. Гутником. Спектрально двойные звёзды с коротким периодом, а значит большим u, имеют малые или бесконечно малые эксцентриситеты, в то время как звёзды с большими периодами и визуально двойные звёзды имеют обычно большие эксцентриситеты. Если бы k имело довольно большую величину, то всё было бы совсем наоборот.
Впрочем, малая величина верхнего предела для k, найденная выше, делает все дальнейшие представления этого типа излишними.
Лейден, октябрь 1913 г.
(Поступило 28 октября 1913 г.)
В моём докладе на собрании в февраля этого года (см. эти Труды, том 15, страница 1297) я указал, что существование спектрально двойных, движение которых удовлетворяет законам Кеплера, несовместимо с теорией Ритца, находясь в то же время в согласии с теорией Лоренца.
С тех пор мр. П. Гутник1 и Э. Фрейндлих2 выдвинули гипотезу, по которой скорость света могла бы зависеть от скорости источника в форме, отличной от простого сложения, постулированного в соответствии с теорией Ритца. Наиболее простой была бы гипотеза, по которой
v = c + xu,
где v - скорость света, испущенного источником, имеющим скорость u. Задача тогда уже не в том чтобы решить, будет ли x = 0 или x = 1, исключив промежуточные величины, но в том, чтобы назначить верхнюю границу для x.
Тогда мы имеем, используя обозначения моей прежней работы,
a=x
Δ/c2. [*]Если истинная орбита является кругом, то уравнение (1) приобретает вид:
u=u0
cos[2π(t-t0)/T] (1)Если x очень мало, мы находим для уравнения (2) следующее приближённое выражение
u=u0 cos[2π(τ- τ0)/T+x (2πu0Δ/Tc2)cos(2π(τ- τ0)/T)] (2)
где, естественно, u, u0, c, Δ, τ и T должны быть выраженными в тех же единицах (км и сек). Видимые скорости, таким образом, покажут фальшивый эксцентриситет величины
e= xπu0Δ/Tc2
Это значение складывается с истинным эксцентриситетом и не может быть отделено от него наблюдениями.
Теперь легко рассчитать верхнюю границу для x. Берём хорошо известную звезду типа β Aurigae. Наблюдения дают
π=0
'',014, e=0,005, u0=110 км/с, T=3,96 сут.В качестве наибольших величин, которые ещё совместимы с наблюдениями, мы можем взять
π < 0
'',05 или Δ > 65 световых лет,e < 0,015,
Тогда мы находим x < 0,002.
Вполне возможно, другие звёзды дадут ещё меньшие величины x. Наименьшие величины, конечно, найдены у звёзд, имеющих наименьшие параллаксы. К сожалению, параллаксы большинства спектрально двойных всё ещё неизвестны, и таким образом невозможно дать численные значения. Мы можем, однако, с уверенностью предположить, что для большинства этих звёзд величина, которая была бы найдена, оказалась ещё меньше, чем приведённая выше.
Постскриптум. В процессе дискуссий на заседании было сделано замечание (профессором Кортевегом), что звезда β Aurigae могла бы иметь истинный эксцентриситет такой величины, которая бы в точности скомпенсировала фальшивый эксцентриситет, вызванный движением. Это, конечно, вполне справедливо. Если бы этот истинный эксцентриситет3 был e = 0,90, мы нашли бы x = 0,12, [беря снова π= 0'',05 и пользуясь той же самой приближённой формулой, что и выше, хотя это и не верно для столь больших эксцентриситетов]. Таким образом, если бы нам была известна только эта звезда, нам пришлось бы принять в качестве верхнего предела для x это значение в 0,12. Имеется, однако, значительное число звёзд с большими величинами u0, у которых видимый эксцентриситет очень мал или равен нулю. Некоторые из них имеют, несомненно, очень малые параллаксы. Очевидно, было бы абсурдом предположить, что все они обладают именно теми истинными эксцентриситетами и положениями периастров, которые в точности уничтожают видимый эксцентриситет для наблюдателя на нашей Земле.
Примечания:
Astronomische Kriterien für die Unabhängigkeit der Fortplanzungsgeschwindigkeit des Lichtes von der Bewegung der Lichtquelle, Astr. Nachr. 4670 (195, 265). Zur Frage der Konstanz der Lichtgeschwindigkeit, Physik. Zeitschr. (14, 835). Для β Aurigae большой эксцентриситет особенно невероятен из-за предположительно больших размеров обоих компонентов по сравнению с их взаимным расстоянием.[*] Δ п
редставляет собой расстояние от двойной звезды до наблюдателя.Дата установки: 26.08.2007
Последнее обновление: 18.12.2012
[
вернуться к содержанию сайта]