[вернуться к содержанию сайта]

УДК: 535.015

ЭФФЕКТ ТРАНСФОРМАЦИИ ЧАСТОТЫ СВЕТА ПРИ УСКОРЕНИИ ИСТОЧНИКА И КРИТЕРИИ ЕГО ЭКСПЕРИМЕНТАЛЬНОЙ ПРОВЕРКИ
С.А. Семиков
Нижегородский Госуниверситет
Дата поступления: 14.02.2014
(напечатано в журнале “Нелинейный мир”, №6, 2014, с. 3–15)

    Одна из актуальных задач физики состоит в открытии новых способов преобразования оптического излучения в другие частотные диапазоны электромагнитных волн, с возможностью плавной перестройки частоты излучения. Как правило, такую трансформацию осуществляют посредством нелинейных эффектов в среде (генерация гармоник, фазовая самомодуляция, эффект Рамана и т.д.) [1], что налагает существенные ограничения на степень и КПД преобразования частоты света, на предельную мощность и длительность выходного сигнала (ввиду поглощения и оптического пробоя среды).

    Ниже будет предложен новый способ плавной трансформации длительности лазерных импульсов и перестройки частоты оптического излучения в любые другие диапазоны электромагнитных волн, за счёт ускоренного движения источника. Данный способ выгодно отличается тем, что трансформация несущей частоты и длительности импульсов осуществляется в вакууме и, таким образом, не имеет указанных ограничений.

    Эффект преобразования длительности электромагнитных воздействий от ускоренно движущегося источника был предсказан век назад (в 1908 г.) швейцарским физиком Вальтером Ритцем на основе разработанной им баллистической теории света [2], поддержанной также Дж.Дж. Томсоном, Д.Ф. Комстоком, Р. Толменом и др. [3]. Согласно этой теории, электромагнитные воздействия и свет распространяются, как в корпускулярной теории Ньютона, аналогично потоку частиц, причём источник дополнительно сообщает свою скорость v испущенному свету, движущемуся относительно источника со стандартной скоростью c (скорость света), а относительно приёмника – со скоростью c + v, подобно тому как движущееся орудие придаёт добавочную скорость выстреленным снарядам [4]. Эта механическая модель электромагнитных воздействий удовлетворяла принципу относительности Галилея, объясняя результат опытов Майкельсона, Троутона-Нобла и других попыток выявить инерциальное движение Земли [2, 3]. В рамках теории Ритц объяснил и волновые свойства света [2]. А Дж.Дж. Томсон, применяя к излучению баллистический принцип, вывел верные выражения для полей E и H колеблющегося заряда [5]. Этот изящный вывод до сих пор применяют в курсах физики [6, с. 131].

    Основное содержание баллистической теории Ритца, как отметил академик М.А. Ельяшевич [7], составляет бесполевой домаксвеллов подход в электродинамике, восходящий к работам Вебера, Гаусса и Римана. В рамках этого подхода электрические воздействия рассматривались лишь как функции относительных положений, скоростей и ускорений зарядов, а не пустого пространства меж ними. Магнитные, индукционные и даже гравитационные силы в теории Ритца получались в качестве малых поправок к электрической силе от взаимного движения зарядов. Также Ритц описал все электродинамические эффекты и классически объяснил релятивистские эффекты, включая рост массы быстрых электронов и смещение перигелия Меркурия, ещё в 1908 г. верно предсказав величины смещений перигелиев других планет [2] и получив для них формулу, совпавшую с найденной спустя 7 лет Эйнштейном в рамках общей теории относительности [4].

    Отметим, что в пользу баллистической теории свидетельствует и ряд космических наблюдений, например космическая радиолокация и лазерная локация [8, 9], а также рассмотренные ниже наблюдения двойных звёзд, экзопланет и красное смещение галактик. Не противоречат баллистической теории и эксперименты по измерению скорости излучения быстро летящих частиц, например,– синхротронного и аннигиляционного излучения [3, 10]. Как показано в работах [11–17], результаты таких экспериментов вполне согласуются с теорией Ритца, если учесть переизлучение средой и верно определить величину и направление скорости излучающих частиц, исходя из теории или прямых измерений. Таким образом, на данный момент у баллистической теории и у закона механического добавления скорости источника к скорости света нет ни одного известного противоречия с экспериментами, но есть ряд подтверждений.

    Для однозначной проверки влияния относительной скорости источника на скорость света предлагалось применить и фемтосекундные лазеры (В. Подгорный, В. Соколов), длительность импульсов которых Δt ~ 10^–14 с – позволяет измерять соответствующие разности времён хода двух лучей, у одного из которых скорость равна c, а у другого – (c+v), ввиду движения источника со скоростью v. На пути L ~ 10 м эта разность времён Δt = L/c – L/(c + v) = Lv/c² наберётся уже при разнице скоростей источников v ~ 100 м/с, достижимой в лаборатории. Такой опыт можно поставить в вакууме (для движущегося лазерного источника, или соединённого с ним подвижного конца оптического волокна) или в воздушной среде, если применить неподвижный импульсный лазер, навстречу которому со скоростью v движутся два световода-приёмника, отделённых дистанцией L, скажем, на ободах ультрацентрифуг. По измеренной автокоррелятором задержке импульсов Δt, дающей их скорость в системе приёмников, легко оценить влияние на неё скорости источника относительно приёмников. В этом случае переизлучение воздухом не будет менять скорость света, поскольку источник неподвижен относительно воздуха.

    В случае влияния скорости источника на скорость света, если источник ускоренно движется к приёмнику, то волновые фронты, приобретая в моменты испускания всё более высокие скорости, будут догонять друг друга, сокращая длину волны и регистрируемый приёмником период световых колебаний. Если a – ускорение источника, то первый световой сигнал (или фронт), испущенный неподвижным источником со скоростью света с, достигнет приёмника, расположенного на расстоянии L, через время t₁ = L/с. Второй сигнал (или фронт), испущенный через малый период dt, когда источник наберёт скорость dv = adt и станет испускать свет со скоростью с' = с + dv, достигнет приёмника через время t₂ = dt + L/с' после испускания первого. В итоге сигналы прибудут к приёмнику с меньшим временным разрывом

                            (1)

    Если ускорение a источника направлено от приёмника, то гребни световых волн будут расходиться, наращивая регистрируемые приёмником период световых колебаний dt' ≈ dt(1 + La/c²) и длину волны λ' = сdt' = λ(1 + La/c²), по сравнению с длиной волны неподвижного источника λ = сdt. Из классической кинематики легко вывести общий закон изменения длительности, длины волны и частоты света [12], соответственно:

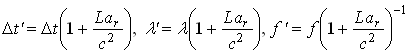,                    (2)

где a_r – лучевое ускорение источника (проекция ускорения на луч зрения r), f – частота неподвижного источника. Этот эффект (2) далее будем называть эффектом Ритца [12, 18, 19]. Отчасти он напоминает нелинейный эффект фазовой самомодуляции [1], который тоже меняет частоту и длину волны пропорционально пройденному светом пути L за счёт неравенства скоростей света в среде.

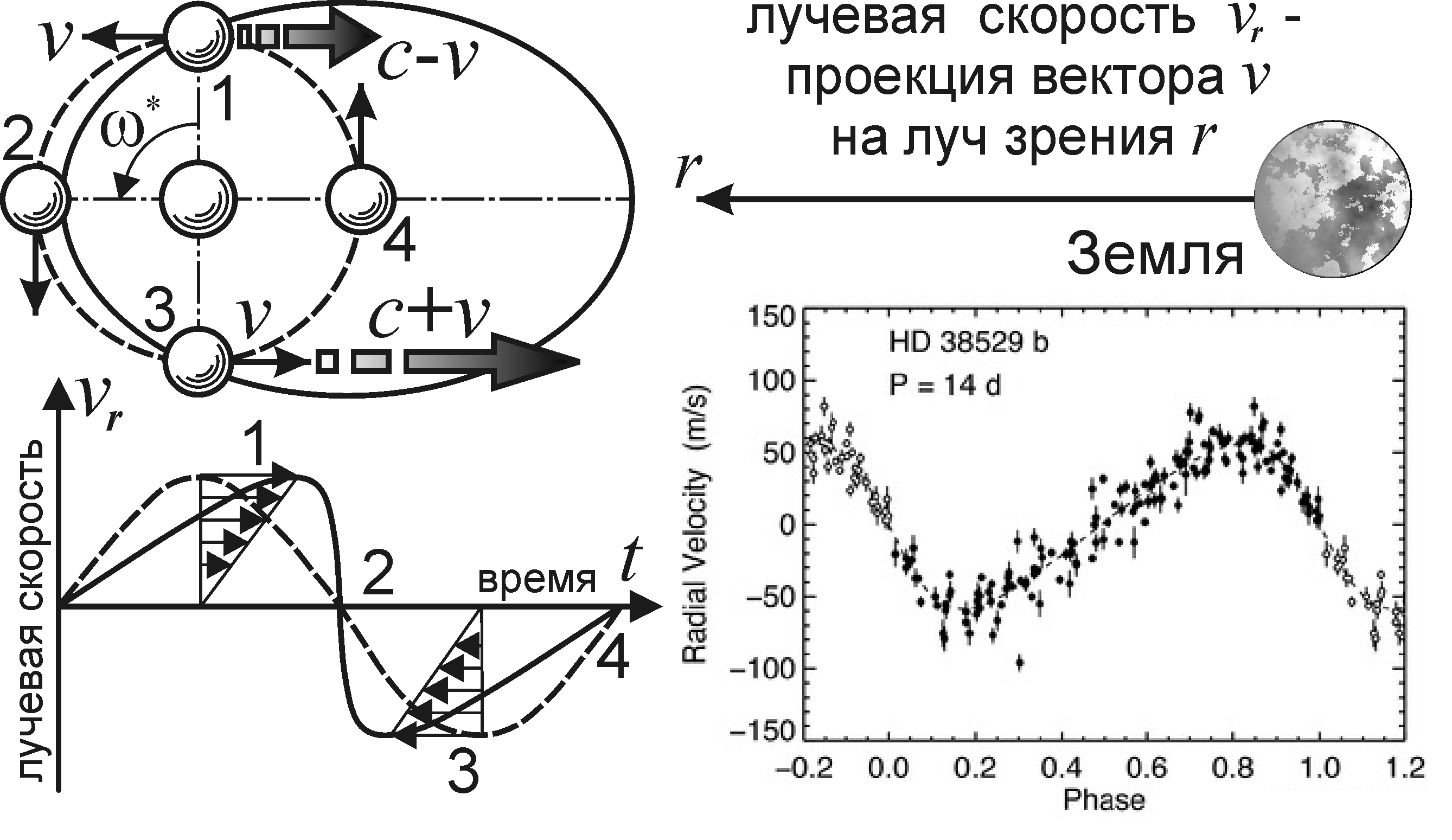
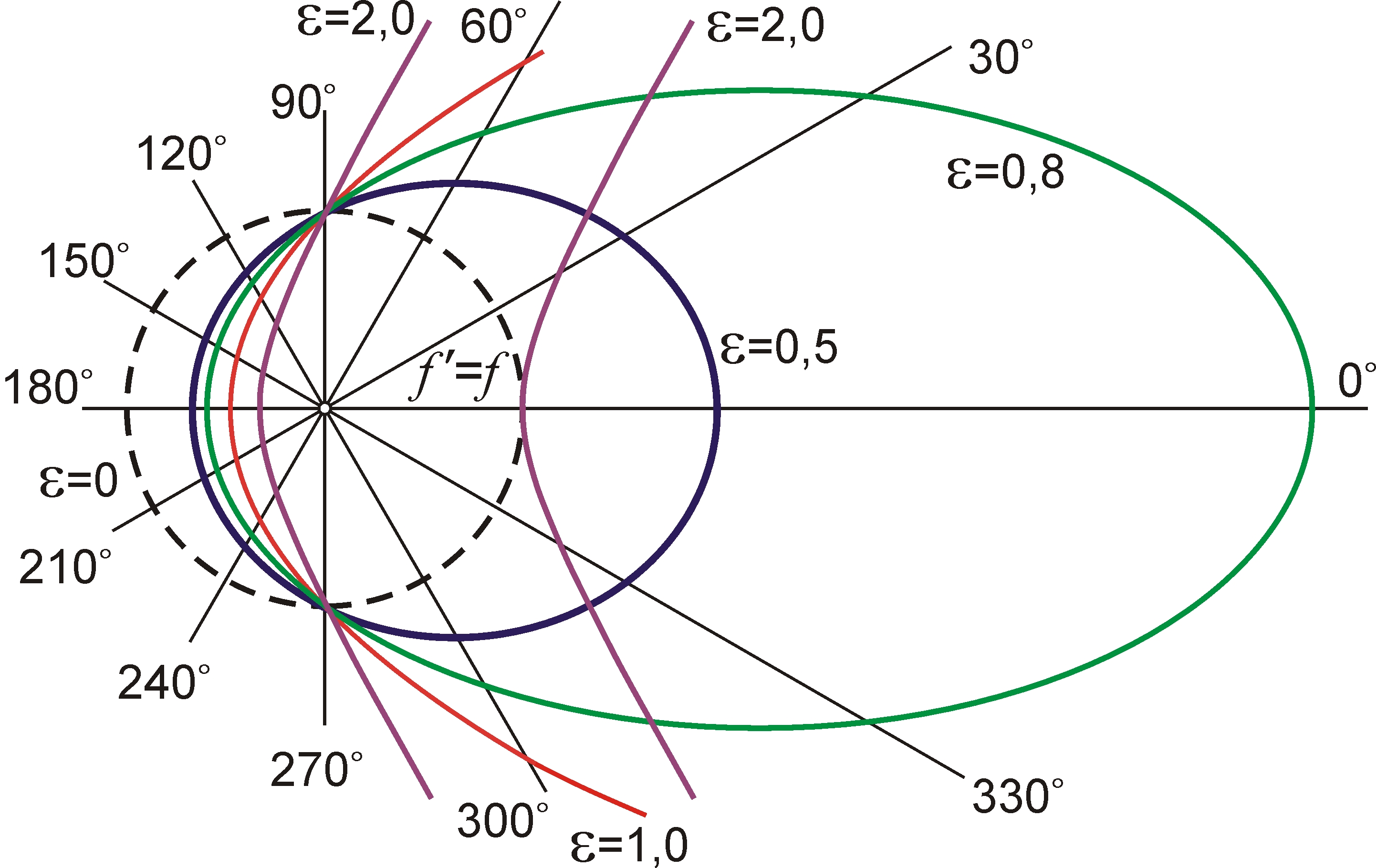
    При этом эффект Ритца выгодно отличается тем, что меняет частоту света в вакууме. Однако до сих пор эффект оставался, по сути, незамеченным, ввиду его малости, поскольку в знаменателе (2) стоит квадрат скорости света. Тем не менее, эффект проявился бы на дистанциях L порядка нескольких световых лет. На это в 1910 г. обратил внимание Д.Ф. Комсток [20], рассмотрев возможные искажения в движении двойных звёзд от периодичного сжатия-растяжения интервалов времени (2) видимого движения звёзд по орбите, в ходе которого периодично меняется проекция a_r центростремительного ускорения a звезды (рис. 1). Равномерное движение звёзд по круговой орбите покажется неравномерным, словно звезда движется по вытянутой к Земле эллиптической орбите (возникает мнимый эксцентриситет орбиты ε = La/c²). А наблюдаемая кривая лучевых скоростей v_r(t), за счёт запаздывания света звезды из точки 1 и опережения из точки 3, примет вместо синусоидальной – пилообразную форму, тоже соответствующую эллиптической орбите. Подобные искажения, как отметили в 1913 г. астрономы Гутник [21] и Фрейндлих [22], реально открыты у спектрально-двойных звёзд в виде эффекта Барра [4, 23], то есть в виде преобладания звёзд с орбитами, вытянутыми в сторону Земли (с долготой периастра ω* возле значения 90°, рис. 1). Этот эффект до сих пор не получил однозначного объяснения. Затем Ла Роза [24] показал, что эффект Ритца проявился бы и в регулярных вариациях яркости и спектра двойных звёзд, что позднее было отмечено и В.И. Секериным [18, 19]. По закону сохранения энергии света, испущенного звездой в интервале Δt и воспринятого в интервале Δt' (2), звезда, которая в отсутствие ускорения излучала бы в апертуру телескопа мощность P, воспримется наблюдателем как обладающая мощностью излучения

.                            (3)

    Кроме того, как отметил Цурхеллен [25, 26], в этом случае эффект (2) должен приводить к изменению частоты и длины волны света, излучённого звездой. Подобные периодичные вариации яркости (3) и длины волны λ_max (2) спектрального максимума были реально открыты у цефеид и других физически переменных звёзд, но трактовались по закону смещения Вина Т_cλ_max = b = const как колебания их температуры Т_c и размеров [18, 19]. Когда параметр эксцентриситета ε = La/c² достигает величины ε ≈ 1 и выше, видимая частота и яркость света от двойной звезды изменяется на порядки, создавая, согласно (1–3), короткие мощные импульсы рентгеновского, гамма-излучения или радиоизлучения, аналогичные реально регистрируемым вспышкам сверхновых, барстеров, пульсаров и других переменных звёзд, у которых открыта двойственность и вращение.

    Таким образом, баллистическая теория и эффект Ритца не противоречат наблюдениям двойных звёзд, вопреки известному аргументу Де Ситтера [27], и позволяют объяснить ряд аномалий звёздных систем, включая эффект Барра и избыточные эксцентриситеты орбит экзопланет. Действительно, эффект Барра отчётливо наблюдается у экзопланет, орбиты которых не могут иметь высоких эксцентриситетов ε и неоднородного распределения по ω*. Например, экзопланеты WASP-18b и WASP-33b столь близки к своим звёздам, что должны обладать ε = 0. Поэтому кривые v_r(t) этих систем, соответствующие эксцентриситетам ε = 0,01 и 0,174, считают искажёнными, вероятно, приливными эффектами [28]. Проще объясняет искажения теория Ритца, предсказавшая эффекты [22], открытые у WASP-18b и WASP-33b, где ω* ≈ 90° [28], а орбитальные скорости v достаточны для искажений. Другие аномалии экзопланет тоже нашли простое объяснение в баллистической теории [29–31].

    Искажённая кривая лучевых скоростей соответствует эллиптической орбите лишь в первом приближении, а отклонения, как отметил Э. Фрейндлих [22], имеют вид гармоник орбитального периода, реально выявленных у двойных звёзд и экзопланетных систем. У последних гармоники интерпретируют как реальное существование экзопланет с периодами, относящимися к основному как 1:2, 1:3, 1:4 и т.д. В итоге, согласно [32], уже половине открытых экзопланет начинают приписывать орбитальный резонанс 1:2. Теоретически он возможен, но редок, и форму графиков v_r(t) проще объяснить модуляцией скорости света, исказившей синусоиду графика лучевых скоростей и породившей гармоники, примерно так же, как это происходит в клистроне, модулирующем скорость электронов.

    Как отметил Дж. Фокс [11], проверяя баллистическую теорию в космосе, следует также учесть переизлучение света межзвёздным газом, так что основную часть пути лучи света движутся с одинаковой скоростью c, утратив избыточную скорость, сообщённую звездой. В итоге, эффективная длина L_ef ~ λ/(n – 1) (где n – показатель преломления среды), на которой свет, ещё не утратив избыточную скорость, преобразуется по эффекту Ритца (2), и которую Фокс на основании известной концентрации атомов водорода в Галактике (N ~ 1 см^–3) оценил в один световой год, оказывается меньше дистанций L звёзд (в сотни и тысячи световых лет). То есть искажения снижаются пропорционально L_ef/L,– в сотни раз. Таким образом, малая величина наблюдаемых искажений [3, 27] не противоречит эффекту Ритца.

    Эффект Ритца окажется более значим на огромных межгалактических дистанциях L, где к тому же существенно ниже концентрация атомов нейтрального водорода N ≤ 6·10^–11 см^–3 [33]. При таком условии, поскольку L_ef растёт пропорционально 1/N, получим L_ef ≥ 2·10¹⁰ св. лет >> L. То есть переизлучение практически отсутствует для большинства наблюдаемых галактик. В частности, по эффекту Ритца λ' = λ(1 + La_r/c²) длина волны λ света, испущенного видимыми участками ярких галактических ядер-балджей, дающими наиболее интенсивные спектральные линии и обладающими ускорениями, направленными от нас (a_r > 0) к центрам галактик, должна расти пропорционально расстоянию L до галактик (рис. 2). Такой эффект напоминает красное смещение в спектрах галактик λ' = λ(1 + LH/c), открытое Э. Хабблом. Коэффициент пропорциональности H = 74 (км/с)/Мпк (постоянная Хаббла) близок к коэффициенту a_r/c, рассчитанному по известным ускорениям a_r = V_b²/R_b в галактиках. Взяв за образец нашу Галактику, характеристики которой типичны для спиральных галактик, а балдж имеет радиус R_b = 0,002 Мпк и окружную скорость V_b = 205 км/с [34], получим расчётное значение постоянной Хаббла H_с = a_r/c ≈ 70 (км/с)/Мпк, близкое к измеренной величине H.

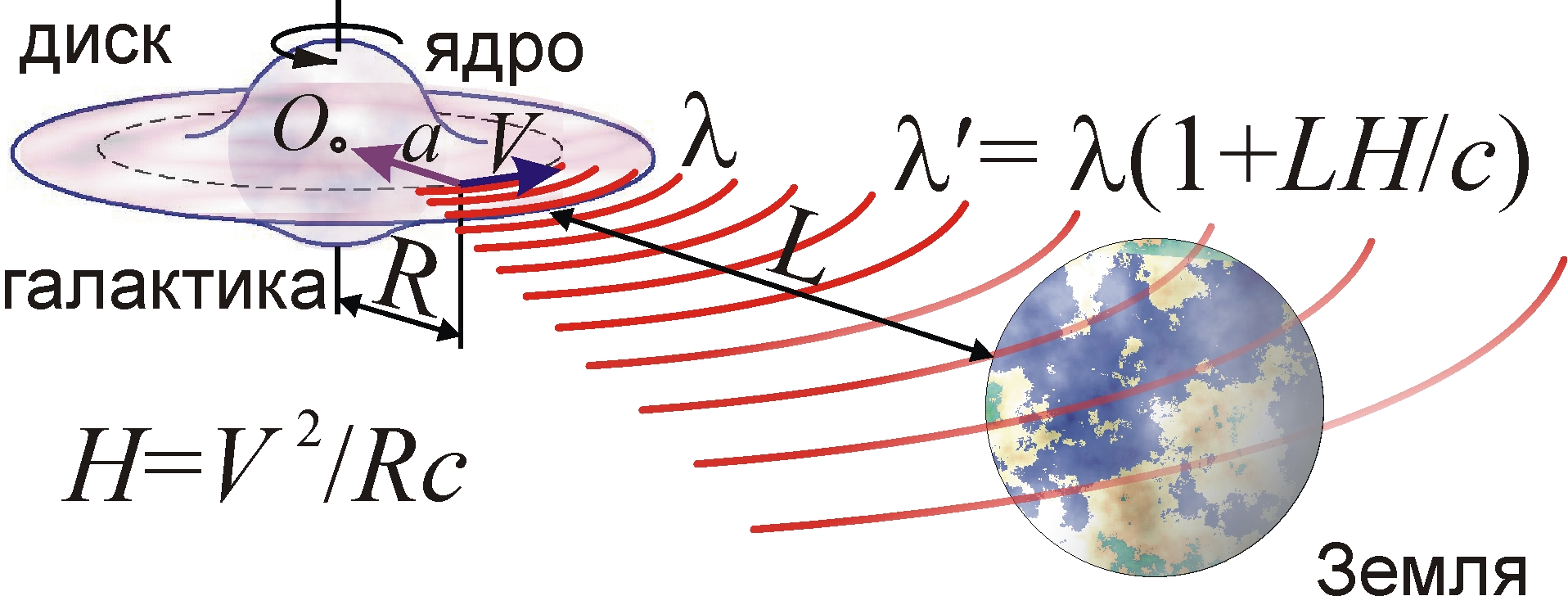
    Сам Хаббл доказывал, что красное смещение обусловлено не доплер-эффектом от удаления галактик [35], но неким эффектом постепенного падения частоты света, по мере его движения к нам, а галактики имеют сравнительно небольшие пекулярные скорости. Эту гипотезу выдвинули в 1929 г. астрофизики А. Белопольский [36] и Ф. Цвикки [37]. Её поддержал ряд астрономов и физиков [41], включая К.Э. Циолковского [38] и С.И. Вавилова [39]. Да и позднее многие астрофизики, включая академика В.А. Амбарцумяна, отрицали теорию Большого взрыва и расширения Вселенной, призванную объяснить красное смещение, и отмечали, что можно говорить лишь о локальных движениях галактик, но не о расширении Вселенной в целом. Интересно, что американский физик Д. Джоунс, рассматривая красное смещение галактик как результат эффекта нарастания длины волны света пропорционально пройденному им пути, предположил, что подобный эффект будет наблюдаться при пропускании лазерного излучения по протяжённым световодам [40, с. 150]. Как оказалось, подобный эффект в световодах реально имеет место в виде рамановского смещения частоты, хотя в этом случае он связан исключительно с нелинейными свойствами среды [1].

    Гипотезу о недоплеровской природе красного смещения подтвердил и фотометрический критерий, предложенный Э. Хабблом и Р. Толменом для выяснения природы красного смещения [35]. Однако сам механизм такого эффекта красного смещения оставался неопределённым. Пионер нелинейной оптики С.И. Вавилов так характеризовал эту неопределённость [39, с. 133]: “Можно ли считать это смещение также доплеровским, вызванным трудно постижимой рецессией туманностей, или же причина кроется в новых, неизвестных нам доселе свойствах света,– это вопрос открытый... Хаббл, установивший самый факт и закон красного смещения, считает, что фотометрические данные не благоприятствуют интерпретации красного смещения как доплерова”.

    Как отметил С.И. Вавилов [39, с. 133], “изучая свет спиральных туманностей, мы имеем дело с лучами, не испытавшими никаких воздействий со стороны вещества в течение десятков и сотен миллионов лет и существовавшими без всяких воздействий в течение этих громадных периодов”, поэтому данный эффект должен отличаться от известных эффектов преобразования частоты при взаимодействии света со средой [1, 6]. Эффект Ритца (2) идеально подходит на роль эффекта преобразования частоты света в космическом вакууме, поскольку не только естественно переходит в хаббловский закон красного смещения, но и снимает все прежние возражения против трактовки красного смещения по гипотезе Белопольского и Цвикки. Красное смещение по эффекту Ритца проявляется аналогично доплер-эффекту: одинаково на всех частотах, ведя к пропорциональному замедлению видимых процессов, согласно формуле (2), что объяснит растяжение длительности вспышек сверхновых Ia в галактиках, пропорционально их красному смещению z = (λ' – λ)/λ [19]. К сходным выводам пришёл и С. Девасиа [42]. По-видимому, впервые эффект красного смещения проассоциировали с эффектом Ритца в 2000 г. А.Н. Тропников – в электронной публикации [43] и А. Сайреника – в электронной публикации [44], упомянутой, например, во втором издании журнала “Advances in Chemical Physics” [45]. Однако в ряде поисковиков эти публикации или их обновлённые версии проиндексированы 2006 и 2009 гг. К тому же, в указанных работах [43, 44] нет объяснения механизма появления именно красного, а не синего смещения, не получено значение постоянной Хаббла, совпадающее с известным и не объяснены парадоксы красного смещения, что однако сделано в независимом анализе [18, 19, 46].

    Недоплеровская трактовка красного смещения галактик по эффекту Ритца объясняет и отрицательный результат опыта, предложенного Г. Динглом [47]. Дингл предложил сравнить угол аберрации α звёзд нашей Галактики, испускающих свет со скоростью близкой к c, и угол аберрации α' далёких галактик (удаляющихся, если судить по красному смещению, с огромной скоростью v, т.е. испускающих свет со скоростью c – v). Угол аберрации равен отношению орбитальной скорости Земли V к скорости света от источника, и по баллистической теории углы α' = V/(c – v) и α = V/c различались бы, а по СТО совпадали бы. Наблюдения показали, что углы аберрации звёзд и далёких галактик равны [48], что сочли аргументом против теории Ритца [3, 49]. Но, как отмечал сам Дингл [47] и авторы наблюдений [48], этот вывод справедлив лишь в случае, если красное смещение галактик вызвано их удалением. А эффект Ритца объясняет красное смещение без гипотезы о гигантских скоростях галактик, противоречащих и ряду других наблюдений [50, с. 9].

    То есть, баллистическая теория и эффект Ритца не противоречат данным внегалактической астрономии, объясняя красное смещение и его аномалии без гипотез о расширении Вселенной, о тёмной материи и тёмной энергии. Например, аномально высокие красные смещения квазаров и отличающиеся в разы красные смещения у связанных, равноудалённых галактик можно объяснить по эффекту Ритца разницей их ускорений a_r, дающих разные H_с = a_r/c и разные красные сдвиги [19]. А дефицит красного смещения у наиболее далёких галактик [51] может быть следствием переизлучения межгалактическим газом, становящегося заметным, когда дистанции L сопоставимы с L_ef ~ 2·10¹⁰ св. лет, по превышении которой вызванное эффектом Ритца красное смещение стало бы расти всё медленней. Примерно на таких дистанциях (L ~ 10¹⁰ св. лет, что соответствует красному смещению z ~ 0,8), когда L ~ L_ef, и выявлены отклонения от закона Хаббла в виде дефицита красного смещения, интерпретированные как ускоренное расширение Вселенной [51].

    На лабораторных дистанциях L ~ 1 м и при технически доступных ускорениях a_r источников света сдвиг частоты по эффекту Ритца столь мал, что мог бы регистрироваться лишь при помощи эффекта Мёссбауэра. В опыте Бёммеля (1962 г.) при поступательном ускоренном движении источника γ-лучей, действительно, наблюдался сдвиг частоты излучения на поглотителе Δf/f = (f' – f)/f = La_r/c² пропорциональный дистанции L и ускорению источника a_r [3]. Сдвиг частоты регистрировался и при размещении излучателя с поглотителем на быстро вращающемся диске, придающем γ-источнику центростремительное ускорение. Сдвиг частоты по эффекту Ритца, рассчитанный с учётом переизлучения в материале диска, совпадает с результатом этих опытов [16].

    Таким образом, астрономические наблюдения и лабораторные эксперименты не противоречат существованию эффекта Ритца, хотя обычно трактуются по общей теории относительности. Также на данный момент нет опытов, однозначно доказывающих отсутствие зависимости скорости света от скорости источника, поскольку во всех проведённых опытах либо не учтён эффект переизлучения, либо не измерена напрямую скорость источника излучения [11, 12, 15].

    Для однозначной проверки эффекта Ритца и трансформации частоты света в разы (или даже на порядки), следует обеспечить в формуле (2) La_r/c² ~ ±1. Поэтому для лабораторных дистанций L ~ 1 м требуется a_r = ±c²/L ~ ±10¹⁷ м/с². Это ускорение недостижимо для светоизлучающих приборов, но его легко сообщить электронам или ионам, которые могут либо сами излучать свет (при возбуждении ионов), либо служить переизлучающими центрами.

    Такое ускорение типично для элементарных частиц, летящих с околосветовыми скоростями V ~ с в магнитном поле циклических ускорителей (синхротронов) с радиусом орбит R ~ 1 м (рис. 3). При этом центростремительное ускорение a = V²/R ~ 10¹⁷ м/с². Поэтому в синхротроне эффект Ритца позволит преобразовывать внешнее лазерное излучение при рассеянии на движущихся электронах. Обычно лазерные импульсы, рассеянные электронами, преобразуют эффектом Доплера при достижении лоренц-фактором значений γ >> 1 [1, с. 171], что требует мощных ускорителей с большим расходом энергии, а значит с низким КПД преобразования света. Напротив, эффект Ритца позволит трансформировать излучение даже при γ ~ 1 в компактных циклотронах, синхротронах и накопителях малой мощности с низкими синхротронными потерями, поскольку уже при V ~ с центростремительное ускорение электронов a ~ a₀ ~ 10¹⁷ м/с² (при L ~ R ~ 1 м). При γ ~ 1 рассеянное излучение электрона ещё не обладает острой направленностью синхротронного излучения, и максимальная эффективность преобразования ритц-эффектом будет достигнута для излучения, вылетающего вдоль ускорения a электрона, то есть поперёк его скорости,– вдоль радиуса орбиты.

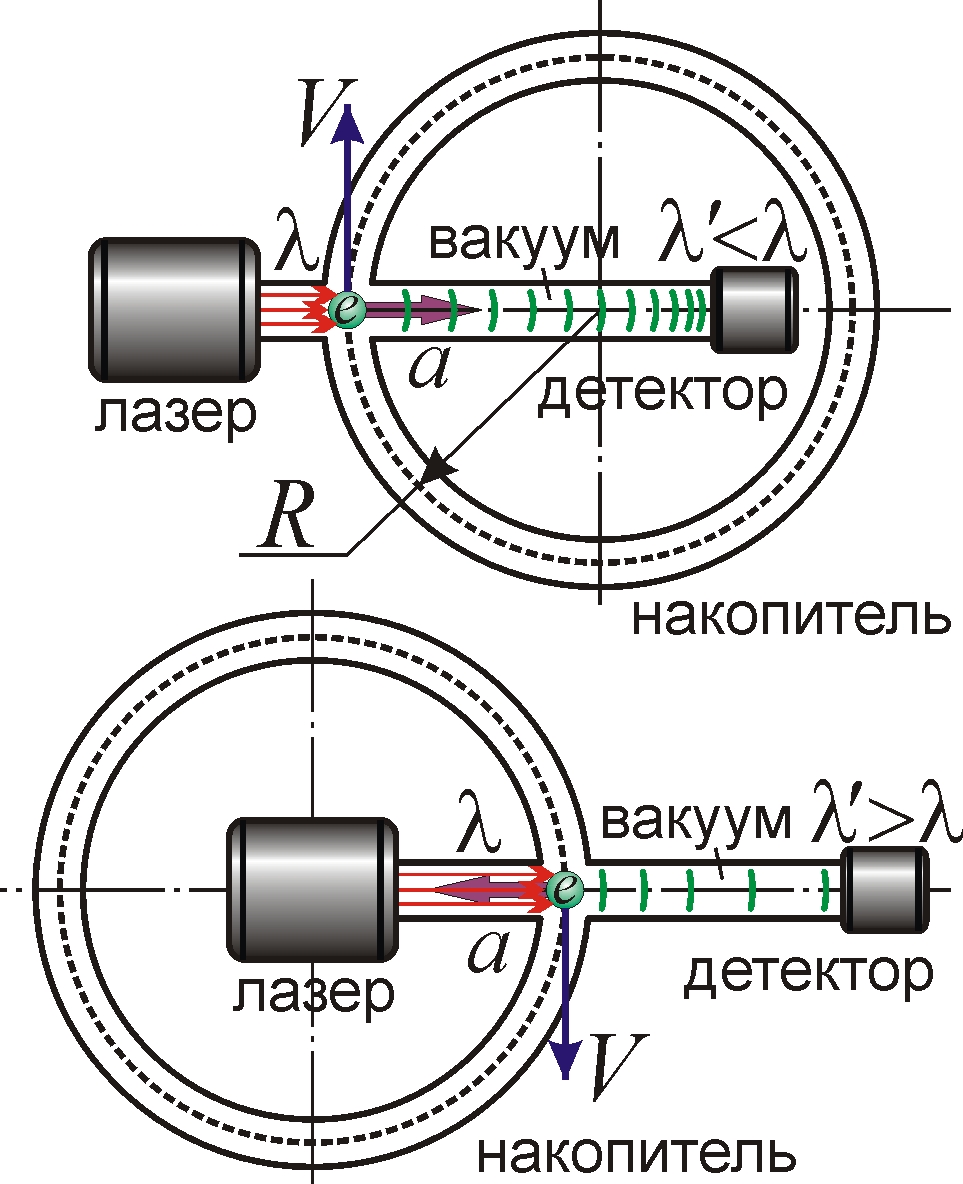
Рис. 3. Схемы трансформаторов частоты лазерного излучения на банчах электронов, циркулирующих в накопителе: для сокращения длины волны λ (вверху) и для растяжения длины волны (внизу).

    Поскольку при V ~ с время τ ~ R/V пролёта банча электронов через область облучения – порядка наносекунды, то длительность преобразуемых лазерных импульсов должна быть того же порядка: Δt ≤ τ. Удобно применить генераторы наносекундных или пикосекундных лазерных импульсов, частота повторения которых совпадает с частотой обращения электронных сгустков – с частотой ускоряющего поля в синхротроне или накопителе электронов. Габариты установки по трансформации света можно сократить в разы при пропорциональном сокращении L и R до нескольких см. А уменьшив радиус орбиты электрона R до 100 мкм, без изменения базы L ~ 1 м, скорость электронов можно снизить до V ~ с(R/L)^1/2 ~ 0,01с (достижимой даже в электронной пушке), существенно сократив энергозатраты на разгон электронов, генерацию магнитного поля и сократив габариты установки.

    Также для придания электронам критического ускорения a_r ~ ±10¹⁷ м/с² можно применить электрическое поле. В электрическом поле E ускорение a = Ee/m электрона (где e/m = 1,76·10¹¹ Кл/кг – его удельный заряд) достигает 10¹⁷ м/с² при напряжённости поля E ~ 10⁶ В/м. Для ионов поле должно быть в тысячи раз выше: E ~ 10⁹ В/м. Такие напряжённости поля легко достижимы в существующих установках. А в фокусе лазерного пучка достигнуты даже значения E = 10¹² В/м [1].

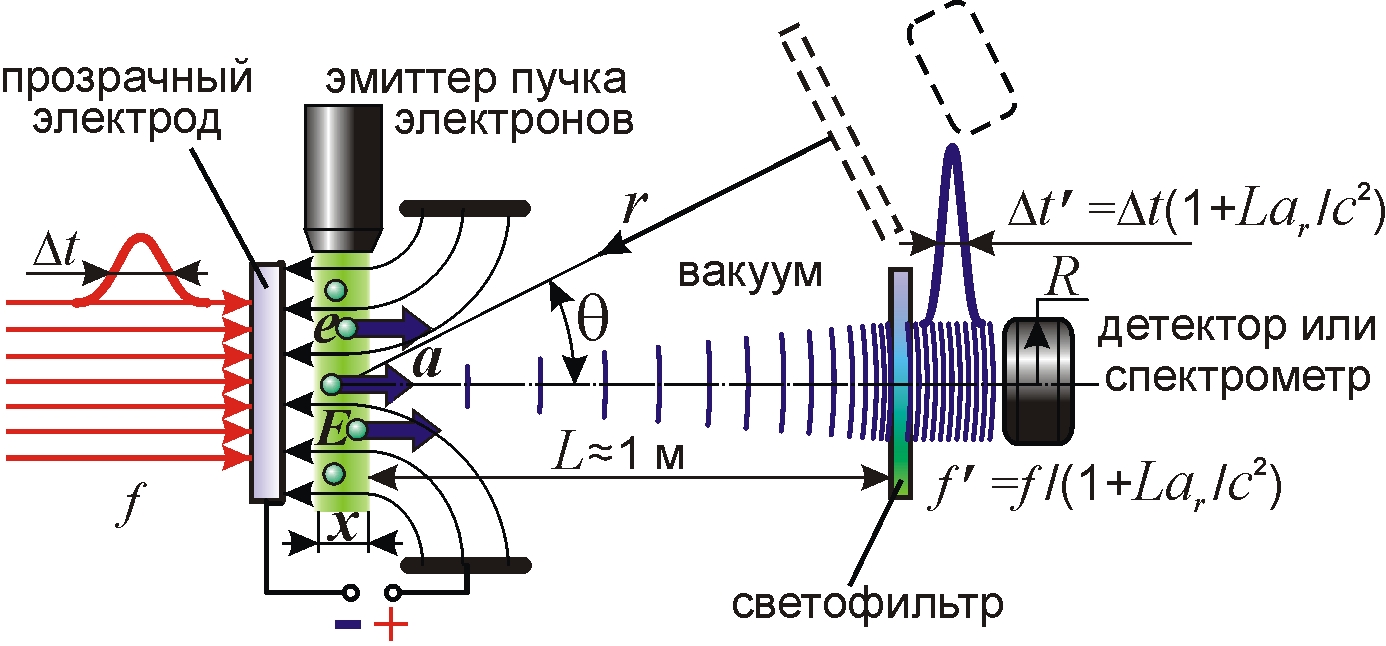
    На основе этого можно предложить схему установки по проверке эффекта Ритца и трансформации частоты света (рис. 4). Установка представляет собой вакуумную камеру, где пучок электронов или ионов приобретает в электрическом поле ускорение ~ 10¹⁷ м/с². Лазерное импульсное излучение с несущей частотой f и длительностью импульса Δt ~ 1 пс фокусируется на пучке и претерпевает томсоновское рассеяние на электронах (или ионах), играющих роль вторичных источников излучения частоты f. Переизлучённый ими свет свободно пролетает в вакууме дистанцию L ~ 1 м до светофильтра (отсекающего излучение частоты f), после чего попадает в спектрометр или детектор, которые в случае справедливости эффекта Ритца зафиксируют сигнал изменённой длительности и частоты (2).

    Трансформированная частота f', как видно из (2), зависит от лучевого ускорения электронов a_r, а значит, от ускоряющего поля E. Видно, что при a_r = -c²/L частота f' стремится к бесконечности, и малая вариация a_r, вызванная изменением E или L, вызывает огромное изменение частоты f'. Это открывает простой способ перестройки частоты света из оптического в УФ-, рентгеновский и гамма-диапазон. При обратном знаке поля и ускорения частота будет снижаться, что позволит трансформировать оптическое излучение в инфракрасное и терагерцовое. Отметим, что общая теория относительности не предсказывает подобных сдвигов частоты (2), поскольку для их создания приёмник излучения должен ускоряться вместе с источником, тогда как в установке он покоится.

    Эффект Ритца отличен и от эффекта Доплера, который не меняет частоту в ходе переизлучения в прямом направлении. К тому же скорости, приобретаемые частицами за время пикосекундного лазерного импульса Δt ~ 10^–12 c, составят V = a_rΔt ~ 10⁵ м/с, то есть они недостаточны для доплеровского преобразования частоты света в разы или для генерации квантов высокоэнергичного тормозного излучения. Генерация электронного пучка и электрического поля короткими импульсами, синхронными с лазерными импульсами, также позволит снизить затраты энергии на эмиссию, разгон частиц и упростить схему генератора высокого напряжения.

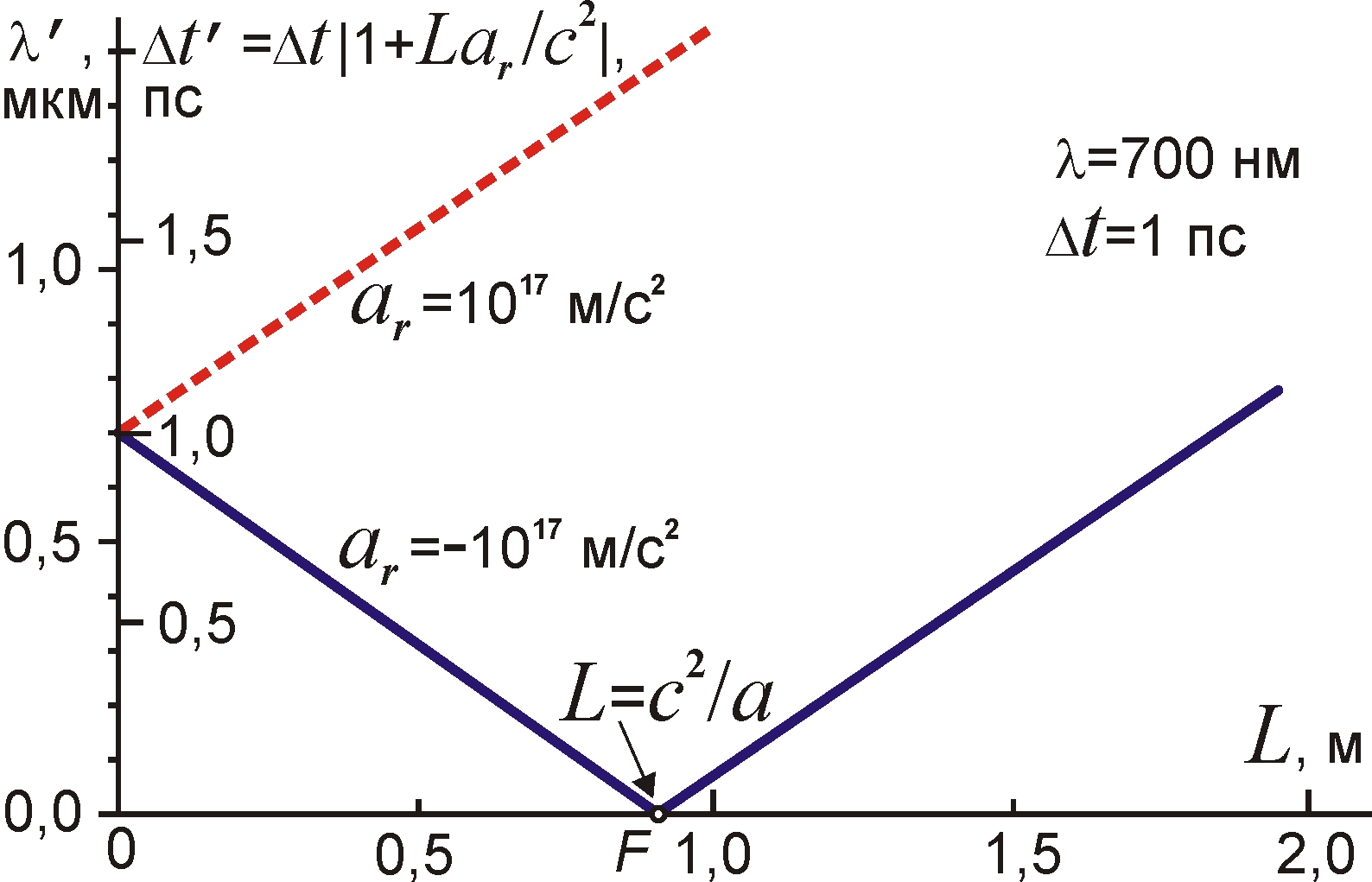
    Важная особенность эффекта Ритца состоит в том, что частота, длина волны и длительность преобразованного импульса света зависят от дистанции L, пройденной светом (рис. 5). Анализ этой зависимости при вариации расстояния L до детектора должен стать основным критерием проверки эффекта Ритца.

    Ещё один критерий даёт исследование зависимости f ' от угла θ (рис. 4), под которым регистрируют излучение. Поскольку эффект Ритца (2) зависит не от абсолютной величины ускорения a, но от его проекции a_r = -acosθ на луч зрения r, то для него должна выполняться зависимость

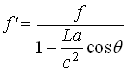.                            (4)

    В полярных координатах угловая зависимость (4) соответствует эллипсу (рис. 6) с фокусом в полюсе (источнике), а параметр ε = La/c² < 1 соответствует эксцентриситету этого эллипса. При критическом значении параметра эксцентриситета ε = 1 эллипс превращается в параболу, а максимальная частота f ' становится бесконечной. При ε > 1 угловая зависимость имеет вид ветви гиперболы (ε > 1) и частота обращается в бесконечность в направлении θ₀ = arccos(c²/La) асимптот гиперболы с эксцентриситетом ε. В пределах угла |θ| < θ₀, где знаменатель отрицателен (т.к. задние фронты обгоняют передние), следует брать модуль частоты: зависимость изобразится второй, но зеркально обращённой (относительно полюса) ветвью гиперболы. Поскольку томсоновское рассеянное излучение линейно поляризовано, то полученное при его трансформации по эффекту Ритца излучение также должно быть линейно поляризованным, особенно при наблюдении под большими углами θ. Это открывает путь генерации поляризованных рентгеновских и гамма-пучков.

    Главное достоинство эффекта Ритца состоит в возможности неограниченного сжатия длительности импульсов Δt' (2) и неограниченного повышения их пиковой мощности P' (3). Такую возможность открывает одновременное сокращение длительности импульса и длины волны, периода световых колебаний (рис. 5), с пропорциональным уширением спектра. Поэтому длительность импульса, которая ограничена снизу только шириной спектра и периодом световых колебаний [1], может стать сколь угодно малой, а интенсивность – сколь угодно высокой. По сути, в точке F, где L = c²/a (т.е. ε = 1) реализуется абсолютная фазовая фокусировка, когда волновые фронты, испущенные в разные моменты, приходят к приёмнику одновременно.

    Оценим мощность трансформированных импульсов. Если исходное лазерное излучение имеет мощность P₀, то мощность рассеянного электронами излучения составит P = P₀(1 – e^–τ) ≈ P₀τ = P₀Nσ_Tx, где τ = Nσ_Tx << 1 – оптическая толща слоя электронного пучка, N – концентрация электронов в нём, x ≈ 0,001 м – толщина пучка, σ_T = (8π/3)r_e² ≈ 6,65·10^–29 м² – эффективное сечение томсоновского рассеяния, а r_e – классический радиус электрона. При концентрации электронов N = 10²⁶ м^–3 [52] (достижимой при фотоэмиссии из фольги под действием лазерных импульсов или в пучках взрывной электронной эмиссии, дающей импульсы длительностью ~ 100 пс), получим P ~ P₀·10^–5. Но при условии сжатия импульсов в 10⁵ раз и выше, из формулы (3) вытекает возможность генерации импульсов гамма-излучения с мощностью равной, или выше исходной: P' ~ P·10⁵ ~ P₀.

    Таким образом, появляется возможность генерации монохроматического рентгеновского или гамма-излучения плавно перестраиваемой частоты с пиковой мощностью до 10¹⁵ Вт (пиковая мощность петаваттного лазера), однако крайне малой длительности Δt' ~ 10^–17 c. Также открывается возможность создания пучков когерентного рентгеновского и гамма-излучения со свойствами лазерного излучения, если удастся обеспечить высокую однородность электронного пучка и ускоряющего электрического поля. При таком условии параллельный лазерный пучок, проходя сквозь электронный пучок, будет когерентно рассеиваться электронами в прямом направлении в такой же параллельный световой пучок, преобразуемый далее по эффекту Ритца.

    Впрочем, достаточно однородное поле (как в плоском конденсаторе) создать трудно не только потому, что в одном из электродов должно быть отверстие для свободного выхода излучения, но и потому, что сам электронный пучок (особенно при высоких концентрациях электронов) создаёт собственное неоднородное электрическое поле, наложенное на внешнее. Это создаёт и неоднородности концентрации электронов в пучке. Поэтому, для того чтобы все переизлучающие электроны находились в одном и том же поле E и приобретали одинаковые ускорения, электронный пучок следует фокусировать, в той же точке фокусируя и лазерный пучок. Это обеспечит одинаковое преобразование частоты излучения всеми электронами, однако рассеяние в этом случае будет некогерентным и ненаправленным. В этом случае мощность рассеянного сигнала, поступающая в телесный угол Ω = πR²/L² (в апертуру детектора радиуса R), составит P_Ω = P₀NxΩdσ/dΩ, где dσ/dΩ = σ_T(3/16π)(1 + cos²θ) – дифференциальное сечение томсоновского рассеяния. Тогда, при θ = 0° и R/L ~ 0,05, при тех же параметрах получим P_Ω ~ P₀·10^–8. А мощность сигнала, регистрируемая детектором после преобразования по эффекту Ритца, согласно формуле (3), будет

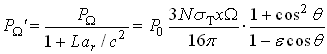.                        (5)

    На рис. 7 представлены диаграммы направленности рассеянного излучения по энергии импульса (пропорциональной P_Ω), и по пиковой мощности импульса P_Ω' (5). Видно, что при ε < 1 максимум пиковой мощности достигается в прямом направлении (θ = 0°), где также максимизируется частота (рис. 6).

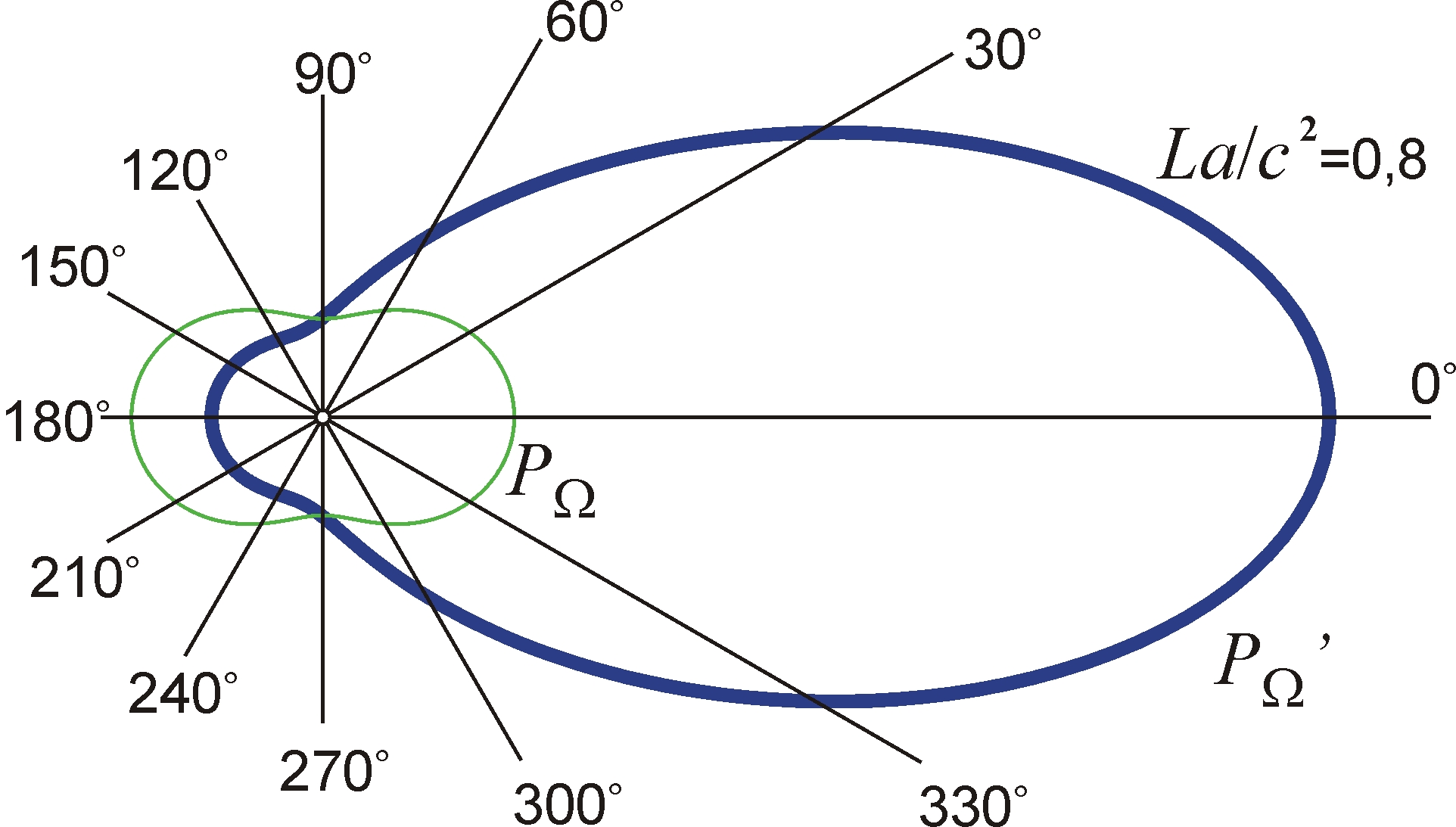
Рис. 7. Диаграмма направленности рассеянного излучения по энергии импульсов (или пиковой мощности P_Ω в момент рассеяния) и по пиковой мощности P_Ω', изменённой по эффекту Ритца.

    Эксперимент, отчасти напоминающий указанный, ещё в 1950 г. планировал академик С.И. Вавилов, как раз имея в виду проверку баллистической теории. Будучи пионером нелинейной оптики, в 1942 г. он заинтересовался трансформацией оптического спектра в вакууме [39], типа красного смещения в спектрах галактик. Вавилов отметил, что “Экспериментальные попытки (без каких-либо серьёзных опытных или теоретических оснований) влиять силовыми полями на частоту светового потока, начинающиеся с Фарадея и продолжающиеся до последнего времени [53], никакого положительного результата не дали” [39, с. 133]. В баллистической теории эти основания появились: Вавилов предложил модулировать скорость пучка ионов, меняя величину ускоряющего поля и проверить предсказанное теорией Ритца изменение фазы и, следовательно, частоты модулированного светового сигнала [54]. Однако смерть Вавилова в 1951 г. помешала ему построить установку и осуществить эксперимент. Его ученику А.М. Бонч-Бруевичу пришлось так видоизменить схему эксперимента, применив в качестве источника движущиеся края Солнца, что не только не могли наблюдаться предсказанные Вавиловым эффекты, но и баллистическая теория не могла быть проверена [55].

    Электроны, атомы и наночастицы может ускорять и давление света p = 2I/c (рис. 8). Оно сообщает частице радиуса r ~ 10^–9 м, плотности ρ ~ 10³ кг/м³ и массы M = 4πr³ρ/3, ускорение a = pπr²/M ~ I/ρcr ~ 10¹⁷ м/с² уже при интенсивности света I ~ 10¹⁶ Вт/см², достижимой в фемтосекундных импульсах [1]. Фемтосекундные импульсы способны также ускорять и электроны посредством пондеромоторной силы (возникающей при релятивистских скоростях электрона), полем кильватерной волны в плазме и т.д. [1]. В таком случае лазерный свет, ускоряя частицы, переизлучался бы ими, далее преобразуясь ритц-эффектом.

    Действительно, в опытах наблюдается преобразование фемтосекундных лазерных импульсов оптического диапазона в аттосекундные импульсы рентгеновского диапазона, после рассеяния фемтосекундных импульсов на электронах, ускоренных лазерным импульсом [56]. Эффект трактуют как результат доплеровского увеличения частоты при отражении импульсов “электронным зеркалом”. Однако такое преобразование может быть также результатом преобразования частоты по эффекту Ритца, что легко проверить, исследовав зависимости (2–5), которые не будут выполняться в случае доплеровского преобразования частоты.

    Обычно давление света постоянной интенсивности на частицу считают постоянным, ввиду его усреднения по времени и поверхности макрообъектов. Но для частиц размером менее длины волны λ сила давления света осциллирует на удвоенной частоте f колебаний светового поля. Переменное давление, модулируя ускорение источника и величину эффекта Ритца (2), исказит профиль излучаемой волны, формируя нечётные гармоники f [17]. Гармоники с номерами H > 1 возникают уже при I << I₀, а при I ~ I₀ мощности, заключённые в гармониках Hf и исходном излучении частоты f,– сравнимы. Гармоники реально регистрируют в генераторах аттосекундных импульсов, где в фокусе фемтосекундного лазера атомы и наночастицы под действием светового давления получают гигантские ускорения, вплоть до 10²³ м/с² [1]. Выходит, регистрируемые при этом импульсы рентгеновского излучения аттосекундной длительности могут быть и преобразованными по эффекту Ритца (2) фемтосекундными оптическими импульсами.

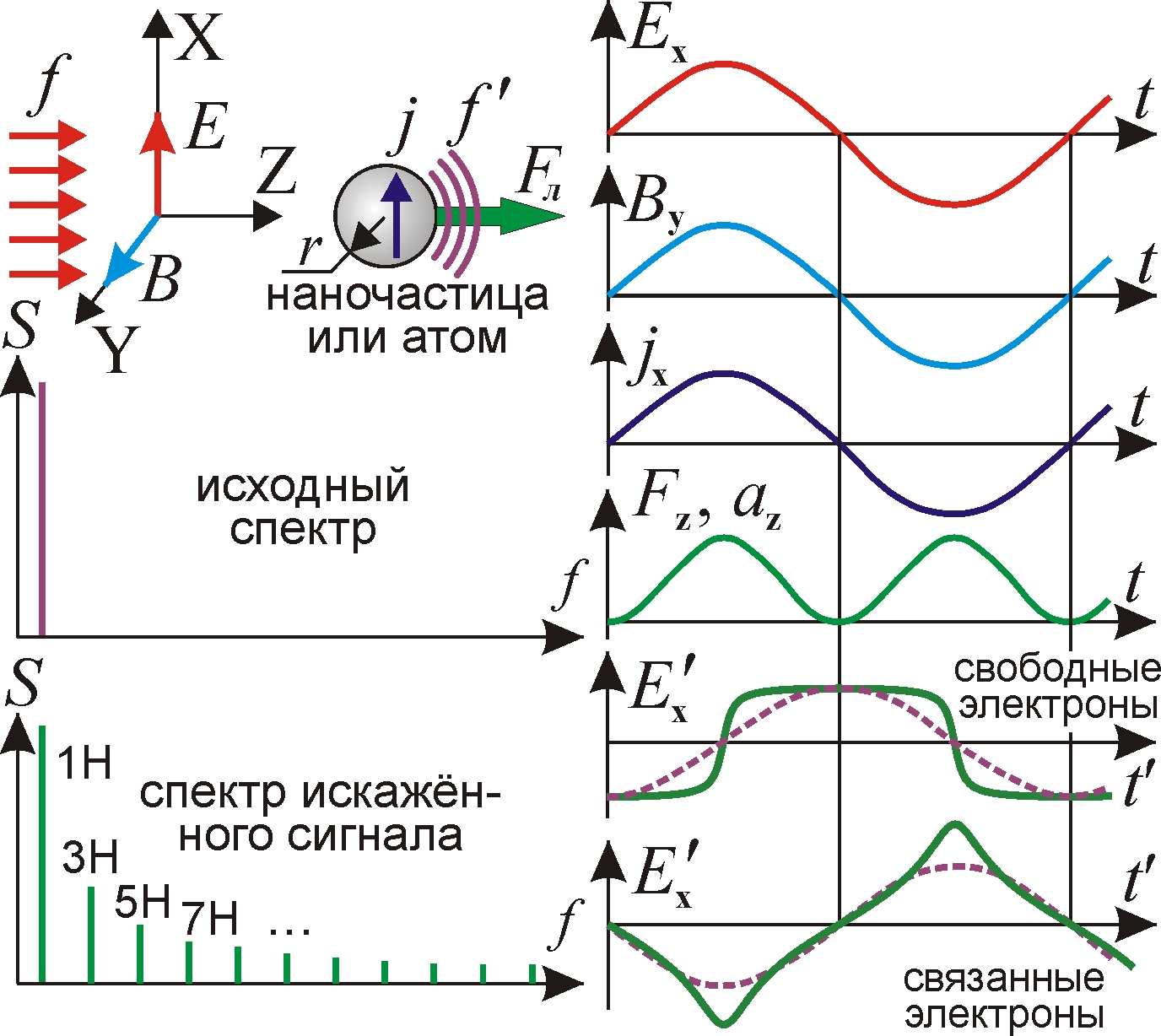
    Рассмотрим генерацию гармоник в поле E(t) = E₀sin(w t) и B(t) = B₀sin(w t) линейно поляризованной волны. Сила Лоренца,– давления света на частицу радиуса r и проводимости s ,

F_л(t) ~ r³j(t)B(t) = r³s E₀B₀[1 – cos(2w t)]/2,                    (6)

быстро меняется от осцилляций поля B(t) и плотности тока j(t) = s E(t) в частице, модулируя с частотой 2w её ускорение a = F_л(t)/M. Тогда профиль волны, переизлучённой электронами проводимости, исказится, приняв форму типа “меандра”: E'(t) = E₀[cos(w t) – cos(3w t)/3 + cos(5w t)/5 – …]; а у волны, переизлучённой связанными электронами,– форму типа “треугольника”: E'(t) = E₀[cos(w t) + cos(3w t)/9 + cos(5w t)/25 + …]. Спектр образуют нечётные гармоники частоты f, вплоть до предельной частоты f_max, синтезирующей самый острый или самый крутой участок профиля.

    В опытах спектр аттосекундных импульсов, формируемых фемтосекундными импульсами в струе газа или при абляции поверхности, образован как раз нечётными гармониками [1]. За резким спадом мощности первых гармоник идёт медленное убывание – “плато”, подобное асимптотическому убыванию 1/H гармоник “меандра” с обрывом на частоте f_max. Реализацию данного механизма можно проверить, изучив зависимость спектра импульсов от дистанции L, наращивающей искажения E'(t). А сжатие импульса, повышая интенсивность I, вызовет рост частот выше значений Hf за счёт постоянной составляющей ускорения a и силы давления (6), усреднённой по времени: F_л ~ r³s E₀B₀/2 [12, 17]. Подобный рост частот Hf при сжатии импульсов реально наблюдается [57]. При падении лазерного луча на поверхность, отражённый свет рассеивается на испаряемых ионах, которые колеблются также и под действием электрического поля E(t) световой волны в плоскости падения. Поскольку кулоновская сила eE много больше силы светового давления F_л, то даже при I << I₀ эффективность генерации гармоник должна быть выше и зависеть от угла падения и поляризации падающего света. Проверка этой зависимости служит ещё одним критерием проверки эффекта Ритца.

    Расчёт выполнен для линейно поляризованного света. У циркулярно поляризованного света давление не осциллирует, создавая постоянное ускорение частиц. То есть, циркулярно поляризованный свет не создаёт гармоник частоты f, а может лишь наращивать её по эффекту Ритца (2). Действительно, как показали опыты [57], гармоники генерирует только линейно, а не циркулярно поляризованный свет. Но циркулярно поляризованное излучение позволит наблюдать преобразование частоты по эффекту Ритца в чистом виде при I ~ I₀ ~ 10¹⁶ Вт/см².

    Для частиц размером менее микрона оценку I₀ следует уточнить, поскольку металл такой толщины прозрачен для света, передающего частице лишь малую часть своего импульса, пропорциональную числу электронов в частице. То есть, сила давления света F_л меняется как r³, и ускорение a уже не зависит от r: a = F_л/M ~ r³s E₀B₀/r r³ ~ 2s m ₀I/r , откуда I₀ ~ 10¹⁴ Вт/см² (для a ~ a₀). При увеличении радиуса r частицы ускорение может даже расти, ввиду изменения свойств вещества при переходе от микро- к макромасштабам. Это объяснит более эффективную генерацию гармоник при облучении наночастиц, а не атомов, например, серебра [57]. Для частиц размером в нанометры и эта оценка I₀ неточна: при поперечнике порядка десяти атомов начинает сказываться дискретная структура вещества, оказываются велики краевые эффекты и ЭДС зарядов, наведённых полем E(t), а давление Лапласа, сжимая частицу, сильно меняет её проводимость s и другие свойства.

    Выяснить основной механизм генерации аттосекундных импульсов можно, изучив зависимость спектра и мощности от расстояния L и ускорения a_r (зависящего от I) [12, 17]. Подтверждение эффекта Ритца, при анализе зависимостей (2–5), позволит повысить эффективность трансформации излучения.

    Показано, что баллистическая теория Ритца и вытекающий из неё эффект трансформации длины волны и длительности световых импульсов до сих пор не проверены однозначно. Приведённые в качестве примеров астрономические и лабораторные данные косвенно свидетельствуют в пользу справедливости эффекта Ритца. Показано, что современная лазерная физика открывает ряд новых возможностей в плане проверки баллистической теории и эффекта Ритца. Предложена схема экспериментальной установки, которая в случае подтверждения эффекта позволит плавно трансформировать частоту света, длительность и интенсивность лазерных импульсов во всём диапазоне частот, времён и интенсивностей, без каких-либо фундаментальных ограничений. По крайней мере, ограничения здесь будут носить уже чисто технический, а не принципиальный характер.

    Выражаю благодарность профессорам Нижегородского госуниверситета М.И. Бакунову и Н.С. Степанову за обсуждение эффекта Ритца, ценные замечания, дополнения и советы по анализу эффекта и схеме его экспериментальной проверки. Работа выполнена в рамках программы развития "ННГУ – НИУ".

Баллистическая теория света,– классическая теория, выдвинутая в 1908 г. швейцарским физиком Вальтером Ритцем,– утверждает, что скорость света зависит от скорости источника, которая векторно добавляется к скорости испущенного им света. Большинство экспериментов и астрономических наблюдений, включая наблюдения двойных звёзд, опыты с синхротронным и аннигиляционным излучением, не противоречат баллистической теории. Приводимые в литературе возражения против теории Ритца, как показал ряд авторов, несостоятельны, поскольку в подобных опытах не учитывался эффект переизлучения света средой и не измерялись напрямую величины и направления скоростей источников света. Учёт переизлучения и правильное определение скорости источников приводит к подтверждению баллистической теории.

Показано, что из баллистической теории следует эффект изменения частоты света, мощности и длительности световых импульсов пропорционально ускорению источника и пройденному светом пути (эффект Ритца). Эффект связан с тем, что при ускоренном движении источника к приёмнику волновые фронты, приобретая в моменты испускания всё более высокие скорости, догоняют друг друга, сокращая длину волны и регистрируемый приёмником период световых колебаний. Если ускорение a источника направлено от приёмника, то гребни световых волн расходятся, наращивая регистрируемые приёмником период световых колебаний и длину волны.

Данный эффект изменения длины волны и длительности световых сигналов позволяет объяснить искажения наблюдаемых движений и графиков лучевых скоростей двойных звёзд (эффект Барра), а также вариации яркости и цвета переменных звёзд, входящих в двойные системы, в ходе вариаций их лучевого ускорения при орбитальном движении. Также эффект Ритца способен качественно и количественно объяснить хаббловский закон красного смещения – нарастания длины волны света галактик пропорционально их расстоянию, ввиду наличия у звёзд (в видимой части галактических ядер) ускорения характерной величины, направленного от нас к центрам галактик. Эффект объясняет и ряд парадоксов красного смещения.

Предложены схемы установок для проверки эффекта Ритца и преобразования частоты света в земных условиях. Поскольку для лабораторных дистанций L ~ 1 м преобразование частоты света существенно лишь при ускорении источника a ~ 10¹⁷ м/с², то единственная возможность наблюдать эффект – это применить в качестве источников – заряженные частицы – электроны и ионы, ускоряемые электрическим или магнитным полем, поскольку характерные ускорения частиц в мощных ускорителях составляют величину именно такого порядка. Короткие лазерные импульсы при рассеянии на ускоряемых частицах должны далее преобразовываться по эффекту Ритца в импульсы с длительностью и несущей частотой, изменённой пропорционально пройденной светом дистанции. Предложены критерии проверки эффекта Ритца – влияние величины ускорения, дистанции и угла наблюдения на степень преобразования несущей частоты и мощности лазерных импульсов.

Другая возможность проверки эффекта Ритца открывается при воздействии лазерного излучения на атомы и наночастицы металлов. В этом случае лазерное излучение ускоряло бы частицы давлением света и одновременно рассеивалось бы ими, преобразуясь далее по эффекту Ритца. С одной стороны, это позволило бы наблюдать плавное преобразование длины волны, пропорционально пройденному светом пути. С другой стороны, колебания давления света и ускорения частиц на удвоенной частоте осцилляций светового поля привели бы по эффекту Ритца, за счёт искажения профиля световой волны,– к генерации нечётных гармоник основной частоты. Поскольку подобный эффект реально наблюдается, то, изучив зависимость номеров и интенсивностей гармоник от давления света и дистанции, легко установить, связана ли отчасти их генерация с эффектом Ритца, или нет.

Предложенные схемы установок и критерии позволят проверить баллистическую теорию и эффект Ритца, а в случае их подтверждения,– построить простые и эффективные трансформаторы частоты лазерного оптического излучения в другие частотные диапазоны.

Ballistic theory of light is a classical theory proposed in 1908 by a Swiss physicist Walter Ritz which claims that light velocity depends on velocity of the source which is added vectorially to velocity of the light emitted by it. The majority of experiments and observations, including observations of binary stars, experiments with synchrotron and annihilation radiation, do not contradict to ballistic theory. Objections against Ritz theory which can be found in literature are untenable, as has been shown by a number of authors, because in this kind of experiments effect of light re-emission by the medium was not taken into account and the values and directions of light source velocities were not measured directly. Consideration of re-emission and the right measurement of source velocity could lead to confirmation of ballistic theory.

We show that a certain effect follows from ballistic theory – Ritz effect – that is an effect of change of light frequency, power and duration of light pulses proportionally to source acceleration and distance covered by the light. The effect is caused by the fact that at accelerated motion of the source towards the receiver wave fronts gaining larger and larger velocities at the moments of emission, approach one another shortening the wavelength and the period of light oscillations registered by the receiver. If acceleration of the source a is directed from the receiver than wave fronts drift apart, increasing the wavelength and the period of light oscillations registered by the receiver.

The above-mentioned effect which changes wavelength and duration of light signals allows to explain distortion of observed motions and curves of radial velocities of binary stars (the Barr effect) as well as variations of brightness and color of variable stars belonging to binary systems in the course of variations of their radial acceleration at orbital motion. Apart from that, Ritz effect allows to qualitatively and quantitatively explain the Hubble law of redshift, that is the increase of wavelength of galactic light proportionally to their distance due to the presence of stars acceleration of characteristic value in the visible part of galactic nuclei directed from us towards the centers of galaxies. The effect also explains a number of paradoxes of redshift.

We propose the schemes for devices for testing Ritz effect and transformation of light frequency under Earth conditions. Due to the fact that for laboratory distances L ~ 1 m transformation of light frequency is relevant only at source acceleration a ~ 10¹⁷ m/s², the only possibility to observe the effect is to use as sources charged particles – electrons and ions – accelerated by electric or magnetic field because characteristic particles accelerations in powerful accelerators have the value of that order. Short laser pulses when scattered on accelerated particles further must transform according to Ritz effect into pulses with duration and carrier frequency changed proportionally to the distance covered by the light. We put forward criteria for testing Ritz effect – the dependence of value of acceleration, distance, observation angle on the degree of transformation of carrier frequency and the power of laser pulses.

Another possibility for testing Ritz effect is impact of laser emission on atoms and nano-particles of metals. In this case laser emission would accelerate the particles by light pressure and simultaneously would be scattered by these particles, further transforming according to Ritz effect. On the one hand, this would allow to observe smooth transformation of wavelength proportional to the distance covered by light. On the other hand, oscillations of light pressure and accelerations of particles at doubled frequency of oscillations of light field would, according to Ritz effect, result in generation of odd harmonics of the main frequency. Due to the fact that such an effect is really observed, studying of dependence of numbers and intensity of harmonics on light pressure and distance would allow to ascertain if their generation is partially caused by Ritz effect or not.

The proposed schemes for devices and criteria will allow to check ballistic theory and Ritz effect and in the case of their confirmation to create simple and effective transformers of laser optical emission frequency into other frequency ranges.

Дата установки: 14.06.2014
[вернуться к содержанию сайта]

W