[вернуться к содержанию сайта]

Дж. Дж. Томсон.
ЭЛЕКТРИЧЕСТВО И МАТЕРИЯ
(М.-Л.: ОГИЗ, 1928 – фрагменты из книги,
см. оригинал на сайте www.ivanik3.narod.ru)

ПРЕДИСЛОВИЕ.

    Книга Дж. Дж. Томсона "Электричество и материя", появившаяся в 1903 году, сохраняет всё своё значение и в настоящее время. Она представляет собой доступное изложение взглядов автора на строение электромагнитного поля. Максвелловская теория электромагнитного поля обыкновенно изображается как перевод великих идей Фарадея на современный математический язык. Теория Томсона представляет собой также перевод, но гораздо более близкий к подлиннику.

    Оригинальные работы Дж. Дж. Томсона были напечатаны в промежуток времени от 1880 года до наших дней: они представляют собой одно стройное целое, поэтому появившиеся в 1924 и 1925 году замечательные работы Томсона, дающие синтез волновой и квантовой теории света, остались незамеченными, так как, будучи оторваны от всех предшествующих работ, они кажутся изобилующими всякими произвольными допущениями. На самом же деле они находятся в стройной логической связи с тем, что было найдено Томсоном раньше и что, по-видимому, основательно забыто.

    Книга "Электричество и материя" даёт, как мы уже сказали, в сжатой и доступной форме основные взгляды Томсона на электромагнитное поле, которые сохранили всё своё значение в наши дни, устарели лишь некоторые части V и VI глав, где речь идёт о строении атома; к этим главам сделаны соответствующие примечания редакции. В качестве приложения к этой части дан перевод речи Дж. Дж. Томсона "Материя и эфир". Вторая часть книги посвящена опубликованной в 1924 году замечательной работе Томсона "Структура света" и связанным с этой работой вопросам. По Томсону квант света представляет замкнутую кольцеобразную фарадеевскую силовую линию или, как предпочитает выражаться Томсон, “”световой квант есть замкнутая фарадеева трубка”. Свойства этих световых квант поразительно сходны со свойствами вихревых колец, поэтому в качестве приложения к этой части книги даны статьи покойного проф. Н. Е. Жуковского "Основы уче-ния о вихрях", Вильяма Томсона (Лорда Кельвина) "О вихревом атоме" и статьи З. А. Цейтлина, посвящённые истории и методологии вихревой теории материи. В конце книги приложен перевод первой главы из сочинений Томсона "Новейшие исследования в области электричества и магнетизма'', где даётся изложение взглядов Томсона, но уже в математической форме. Читатель, владеющий элементами математики, сейчас же увидит из этой статьи, насколько прочно обоснованы взгляды Томсона и насколько близка его теория электромагнитного поля к той картине, которую представлял себе Фарадей.

    В заключение необходимо напомнить, что Томсон, работая изложенным в настоящей книге методом, первый пришёл к понятию электромагнитной массы в 1881 году, первый установил изменение этой массы со скоростью, и притом данное им этим явлениям объяснение было обосновано на строго материалистической почве. Работы Томсона в то время остались незамеченными. Через 20–25 лет после работ Томсона понятие об электромагнитной массе стало выдвигаться на первый план, но, вследствие формального подхода тогдашних теоретиков, те же самые взгляды, которые были высказаны Томсоном, были изложены на идеалистический лад и привели к выводам о дематериализации материи. Блестящая материалистическая критика этого идеалистического учения дана у Ленина в 5 главе "Материализма и эмпириокритицизма". Весьма характерно, что в последние годы трудности, на которые натолкнулась так называемая теория квант, привели к новой вспышке идеализма в физике, и в этой области мы видим опять, как Томсон пришёл к синтезу основного противоречия теории квант и опять на строго материалистической почве. Уже по этой одной причине изложенные в настоящей книге взгляды Томсона заслуживают самого серьёзного внимания тех, кто интересуется методологическими проблемами современного естествознания.

    27 V 1927 г.

    В этих лекциях, читанных в Yale University в мае 1903 г., я сделал попытку рассмотреть значение последних успехов в области учения об электричестве для наших понятий о строении материи и природе электричества; последние вопросы, вероятно, настолько тесно связаны друг с другом, что решение одного из них дало бы решение другого. Характерной особенностью новейших изысканий в области электричества, как изучение и открытие катодных и рентгеновых лучей, радиоактивных веществ является то обстоятельство, что они указывают на тесную связь между материей и электричеством.

    Избирая эту связь предметом "Лекций памяти Silliman'а", мне казалось, что размышления о значении для этой связи последних работ в области электричества имеют тем большее значение, что такого рода рассмотрение возбуждает множество вопросов, которые могли бы служить некоторым из моих слушателей замечательными объектами для новых изысканий.

    Кембридж. Август. 1903 г.

стр. 40
ГЛАВА III.
РЕЗУЛЬТАТЫ УСКОРЕНИЯ ФАРАДЕЕВСКИХ ТРУБОК.
Лучи Рентгена и свет.

    Мы рассмотрели, как ведут себя силовые линии, когда они находятся в покое или в равномерном движении; в этой главе мы рассмотрим те явления, которые получаются в результате неравномерного движения.

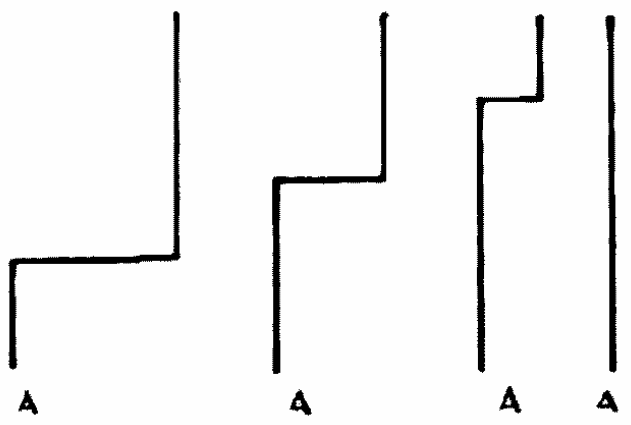
    Начнём со случая движущейся заряженной точки, движущейся так медленно, что силовые линии вокруг неё распределены равномерно, и посмотрим, что должно случиться, если мы внезапно остановим точку. Фарадеевские трубки, соединённые со сферой, обладают инерцией; они находятся также в состоянии натяжения, причём натяжение в какой-либо точке пропорционально массе единицы длины. Поэтому любое возмущение, сообщённое одному концу трубки, пройдёт вдоль неё с постоянной и конечной скоростью; действительно, фарадеевская трубка представляет замечательную аналогию с натянутой струной. Положим, что имеем туго натянутую вертикальную струну, движущуюся равномерно справа налево; когда мы внезапно остановим этот конец, например, А, что случится со струной? Конец А сразу придёт в состояние покоя, но силы, при этом обнаруживающиеся, распространяются с конечной скоростью, и каждая часть струны будет по инерции двигаться, как будто ничего не случилось с концом А, до тех пор, пока возмущение, выходящее из точки А, не достигнет её. Итак, если V есть скорость, с которой возмущение перемещается вдоль струны, а t есть время, которое протекло после остановки А, то части струны, находящиеся от А на расстояниях больших, чем Vt, не почувствуют остановки и будут иметь те же скорости и положения, какие они имели бы, если бы струна продолжала равномерно двигаться вперёд. Форма струны через последовательные промежутки времени показана на рис. 12; длина горизонтальный части убывает по мере увеличения расстояния от неподвижного конца.

Рис. 12

    Возвратимся теперь к тому случаю, когда движущаяся заряженная частица внезапно останавливается, причём на остановку тратится время τ. Чтобы найти конфигурацию фарадеевских трубок после того, как от начала процесса остановки заряженной частицы прошло время t, опишем из заряженной частицы, как из центра, две сферы, одну радиусом Vt, другую – радиусом V(t–τ); так как возмущение ещё не достигло тех частей фарадеевских трубок, которые расположены вне нашей внешней сферы, то эти трубки будут в том же положении, в каком они находились бы, если бы продолжали двигаться вперёд с тою скоростью, какой они обладали в момент остановки частицы, между тем как трубки, находящиеся внутри внутренней сферы, займут своё конечное положение, так как возмущение уже прошло через них. Так, рассмотрим трубку, которая была расположена вдоль линии OPQ (рис. 13), когда частица остановилась. Это будет конечным положением трубки, так как в момент t часть трубки в пространстве внутренней сферы займёт положение ОР, между тем как часть P'Q' вне внешней сферы будет в том положении, какое она занимала бы, если бы частица не остановилась, т. е. если О' есть положение, которое занимала бы частица, если бы она не становилась. P'Q' будет прямой линией, проводящей через О'. Чтобы сохранить свою непрерывность, трубка должна изогнуться в промежутке между обеими сферами и примет поэтому форму OPP'Q'.

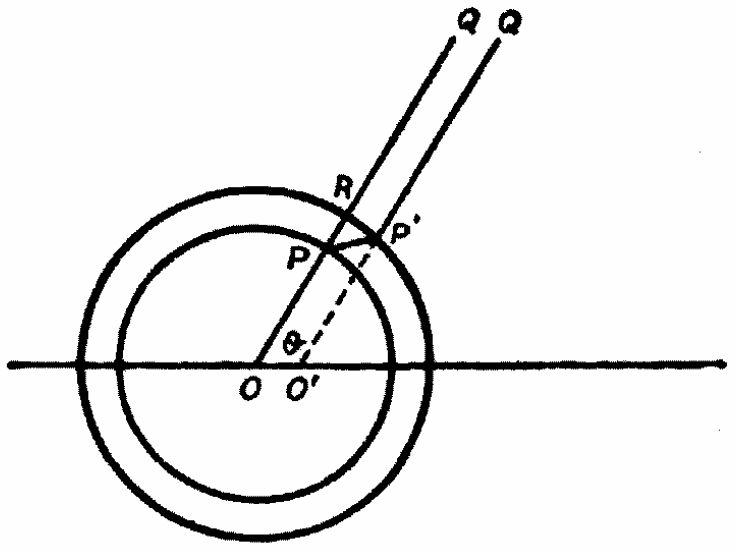
Рис. 13

    Таким образом, трубка, которая до остановки частицы была радиальной, имеет теперь в промежутке между сферами тангенциальную составляющую, обусловливающую тангенциальную электрическую силу. Остановка частицы вызывает радикальное изменение в электрическом поле, созданном частицей и, как показывает нижеследующее вычисление, вызывает электрические и магнитные силы более значительные, чем те, которые существуют в поле, когда частица движется равномерно.

    Если мы предположим, что толщина δ промежутка так мала, что часть фарадеевской трубки внутри его может быть рассматриваема, как прямая, тогда, если T есть тангенциальная электрическая сила внутри волнового импульса, R – радиальная сила, будем иметь:

T/R=P'R/PR=OO'sinθ/δ=vtsinθ/δ.                        (1)

    Здесь v есть скорость, с которой частица движется до остановки, θ – угол, который ОР образует с направлением движения частицы, t – время, протекшее после остановки частицы; так как R=e/OP² и OP=Vt, где V – скорость света, получим, если r=OP,

T=evsinθ/Vrδ.                            (2)*

    Тангенциальная фарадеевская трубка, движущаяся вперёд со скоростью V, вызывает в Р магнитную силу Н, равную VT; эта сила будет перпендикулярна к плоскости чертежа и будет по направлению противоположна магнитной силе, существовавшей в Р до остановки частицы; так как её величина определяется уравнением

Н=evsinθ/rδ,

то она превосходит магнитную силу eVsinθ/r², ранее существовавшую, в отношении r к δ. Таким образом, волновой импульс, вызванный остановкою частицы, есть место действия интенсивных электрических и магнитных сил, которые изменяются обратно пропорционально расстоянию от заряженной частицы, тогда как силы, имевшие место до остановки частицы, изменялись обратно пропорционально квадрату расстояния; этот волновой импульс распространяется вовне со скоростью света и составляет, по моему мнению, рентгеновские лучи, которые появляются, когда отрицательно заряженные частицы из которых состоят катодные лучи, внезапно останавливаются, ударяясь о твёрдое препятствие.

    Легко показать, что энергия, заключённая в волновом импульсе, равна

2e²v²/δ;

эта энергия излучается в пространство. Количество излучающейся энергии зависит от δ, толщины волнового импульса, т. е. от быстроты, с которой остановилась частица; если частица остановилась мгновенно, вся энергия в поле поглотится волновым импульсом, будет излучена и во вне; если же она постепенно останавливалась, только часть энергии излучится в пространство, а остальная часть обратится в тепло в том месте, где катодные лучи остановились.

    Легко показать, что количество движения в волне в какой-нибудь момент равно и противоположно количеству движения в поле вне волны; так как в пространстве, сквозь которое прошла волна, нет никакого количества движения, то полное количество движения в поле после остановки частицы равно нулю.

    Предыдущие рассуждения приложимы только к тому случаю, когда частица движется так медленно, что фарадеевские трубки до остановки частицы равномерно распределены; однако, эти же принципы позволят нам определить результаты остановки заряженной частицы во всех тех случаях, когда задано распределение фарадеевских трубок при равномерном движении.

    Предыдущий метод может быть приложен и к тому случаю, когда заряженная частица, вместо того, чтобы остановиться, изменила каким-либо образом свою скорость; так, если скорость частицы, вместо того, чтобы дойти до нуля, уменьшается на Δv, то можно показать, как на стр. 42, что это вызовет волну, в которой магнитная сила H определяется уравнением

Н=eΔvsinθ/rδ,

а тангенциальная электрическая сила T определяется уравнением

T=eΔvsinθ/Vrδ,

    Теперь, толщина волны δ есть пространство, пройденное светом в продолжение того промежутка времени, в течение которого скорость частицы менялась; поэтому, если Δt есть время, нужное для того, чтобы вызвать изменение скорости Δv, то δ=V·Δt и потому имеем:

Н=(esinθ/Vr)·Δv/Δt, T=(esinθ/V²r)·Δv/Δt;

но Δv/Δt равно –f, где f есть ускорение частицы, поэтому имеем:

Н=-efsinθ/Vr, T=-efsinθ/V²r.

    Эти уравнения показывают, что заряженная частица с ускоренным движением вызывает волну электрических и магнитных сил, причём силы изменяются обратно пропорционально расстоянию от частицы.

    Отсюда следует, что если заставить заряженное тело вибрировать таким образом, чтобы его ускорение периодически изменялось, то от заряженного тела будут исходить периодические волны электрических и магнитных сил. Согласно электромагнитной теории света, эти волны должны быть световыми волнами, если только периодические изменения в ускорении заряженного тела происходят с достаточной быстротой.

    Вернёмся, однако, к случаю заряженной частицы с ускоренным движением; мы уже видели, что из частицы выходят электрическая и магнитная силы и распространяются по радиусам со скоростью света и что силы и радиальные и магнитные перпендикулярны к тому направлению, в котором они распространяются; но, так как каждая единица объёма электромагнитного поля имеет (см. стр. 23) количество движения, равное произведению из плотности фарадеевских трубок и магнитной силы, причём направление количества движения перпендикулярно к обеим этим величинам, то должно существовать в той волне, которая вызвана ускорением заряженной частицы, как и вообще во всякой электрической или световой волне, определённое количество движения в направлении распространения волны. Таким образом, если какая-нибудь волна, например, световая, поглощается тем веществом, сквозь которое проходит, то количество движения волны сообщится поглощающему веществу, которое будет поэтому испытывать силу, которая стремится его толкать по направлению распространения света. Так, когда свет падает нормально на поглощающее чёрное вещество, он отталкивает это вещество. Максвелл показал, что это отталкивание, вызываемое излучением, есть следствие электромагнитной теории света; оно было недавно открыто и измерено Лебедевым при помощи очень красивых опытов, которые были подтверждены и разработаны Никольсом и Гуллем (Nichols, Hull).

стр. 60
ГЛАВА V.
СТРОЕНИЕ АТОМА. ¹)

    Мы видели, что безразлично, получаем ли мы корпускулы посредством катодных лучей, ультрафиолетового излучения или раскалённых металлов, и каковы бы ни были присутствующие металлы или газы, — мы получаем всегда один и тот же род корпускул. Так как корпускулы, сходные во всех отношениях, могут быть получены от весьма различных агентов и материалов, и масса корпускул меньше массы всякого известного атома, то мы видим, что корпускула должна быть составной частью атома весьма различных субстанций. Таким образом, атомы этих субстанций имеют нечто общее.

    Перед нами возникает идея, что атомы химических элементов построены из более простых систем; эта мысль в разных видах высказывалась более, чем одним химиком. Так, Проут (Prout) в 1815 г. высказал гипотезу, что атомы всех химических элементов построены из атомов водорода. В таком случае, предполагая, что при соединении водородных атомов для образования атома другого элемента нет потери веса, атомные веса всех элементов должны бы быть целыми числами; это, однако, не согласуется с опытом. Чтобы избегнуть этого несогласия, Дюма (Dumas) предположил, что первоначальный атом не водородный, но меньший атом, имеющий лишь половину или четверть массы водородного атома. Идея о сложной природе атома получила дальнейшее подтверждение, благодаря открытию Ньюландса (Newlands) и Менделеева, известному под именем периодического закона, который показывает, что в свойствах элементов заметна периодичность, если элементы расположены в порядке возрастающих атомных весов. Простые отношения между атомными весами некоторых элементов, имеющих подобные химические свойства, например, тот факт, что атомный вес натрия есть среднее арифметическое между атомными весами лития и калия, — все указывают на то, что атомы различных элементов имеют нечто общее. Это подтверждается также сходством в строении спектров элементов той же группы в периодическом ряду; это сходство с большой очевидностью установлено новейшими работами над рядами линий в спектрах, частота которых подчиняется определённым численным отношениям. Сэр Норман Локиер (Lockyer), основываясь на спектроскопических наблюдениях, уже давно высказал мысль, что элементы в действительности это —соединения, которые при подходящих условиях могут быть разложены. В пользу этого взгляда говорят далее явления радиоактивности, о которых я буду говорить ниже, так как имеются достаточные основания для допущения, что радиоактивность зависит от изменений, происходящих в атомах радиоактивных веществ. Если это так, то мы должны обратиться к проблеме строения атома и посмотреть, не можем ли мы представить себе модель, которая могла бы объяснить замечательное свойство радиоактивных веществ. Поэтому не мешает рассмотреть, какое значение имеет существование корпускул для проблемы строения атома; и, если даже модель атома, к которой нас приведут эти соображения, будет груба и несовершенна, то, может быть, она покажет нам пути исследований, которые могут дать нам новые сведения о строении атома.

    Исходя из гипотезы, что атом есть агрегат известного числа более простых систем, рассмотрим, какова природа одной из этих систем. Мы видели, что корпускула, масса которой гораздо меньше массы атома, образует составную часть атома, и на корпускулу естественно смотреть, как на составную часть первоначальной системы. Но корпускула обладает определённым зарядом отрицательного электричества, а, так как со всяким зарядом электричества мы всегда ассоциируем равный заряд противоположного рода, то мы должны ожидать, что отрицательный заряд корпускулы соединён с равным зарядом положительного электричества. Поэтому представим себе нашу первоначальную систему электрической парой (дублетом) с отрицательной корпускулой на одном конце и равным положительным зарядом на другом; при этом оба конца соединены электрическими силовыми линиями, которым мы приписываем материальное существование. По причинам, которые выяснятся позже, мы должны предположить, что объём, в котором распределено положительное электричество, гораздо больше объёма корпускулы. ²) Поэтому силовые линии близ корпускулы более сжаты, чем в других местах системы, и, следовательно, количество эфира, связанного силовыми линиями, массу которого мы рассматриваем, как массу системы, будет гораздо больше вблизи корпускулы, чем где-либо. Если, как мы предположили, объём корпускулы очень мал сравнительно с объёмом, занятым положительным электричеством, то масса системы практически будет зависеть от массы эфира, связанного вблизи корпускулы. Таким образом, масса системы будет практически независима от положения её положительного конца и приблизительно равна массе корпускул, если бы они одни находились в поле. Эта масса (см. стр. 38) для каждой корпускулы равна 2e²/3a, где e — заряд корпускулы, a — её радиус, который, как мы видели, приблизительно равен 10^-13 см.

    Теперь представим себе, что мир состоит из неизмеримого числа таких электрических пар, и мы рассматриваем его, как нашу первоначальную систему. Если бы они были в покое, то их взаимное притяжение сблизило бы их точно так, как притяжение сближает ряд маленьких магнитов, если они могут свободно двигаться, так что они образуют агрегаты более, чем одной системы.

    Однако, если бы отдельные системы двигались первоначально со значительными скоростями, то относительная скорость двух систем, когда они сближаются так, что оказывают друг на друга заметное притяжение, было бы достаточна, чтобы удалить системы друг от друга, несмотря на их взаимное притяжение. В этом случае образование агрегатов последовало бы лишь, когда кинетическая энергия единиц уменьшилась бы до такой степени, что при столкновении их стремление к разделению, зависящее от их относительного движения, было бы не достаточно, чтобы помешать им оставаться вместе под действием взаимного притяжения.

    Рассмотрим, каким образом кинетическая энергия такого агрегата должна уменьшаться. Мы видели (стр. 48), что, когда скорость заряженного тела изменяется, то тело теряет энергию, так как тело порождает электрические волны, которые излучаются в пространство и несут с собой энергию. Поэтому, когда единицы сталкиваются, т. е. сближаются так тесно, что они взаимно ускоряют или замедляют заметным образом своё движение, то излучается энергия, которая не вполне поглощается соседними единицами. Поэтому энергия постоянно теряется и через известное, хотя, может быть, и очень долгое время, кинетическая энергия уменьшится до величины, при которой агрегат единиц начинает распадаться на группы по две единицы. Потом образуются агрегаты, содержащие большее число единиц.

    Рассматривая вопрос о дальнейшем соединении этих сложных групп, мы должны помнить, что возможность соединения зависит не только от скорости агрегата, как целого, т. е. от скорости центра тяжести, но и от относительных скоростей корпускул внутри агрегата.

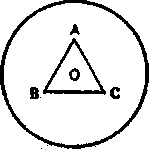
Рис. 15

    Представим себе агрегат, состоящий подобно атому Эпинуса у лорда Кельвина из сферы равномерно положительного заряда, обладающего радиальной электрической силой, которая у всякой внутренней точки пропорциональна расстоянию от центра. Допустим также, что внутри этой сферы вращаются гораздо меньшие отрицательно заряженные корпускулы. Число корпускул есть число единиц, образовавших агрегат, и общий отрицательный заряд корпускул равен положительному заряду сферы. Чтобы быть определённее, возьмём пример, показанный на рис. 15, из трёх корпускул А, В, С, расположенных внутри сферы по углам равностороннего треугольника, центр которого совпадает с центром сферы. Сначала предположим, что корпускулы находятся в покое; они будут в равновесии, когда они на таком расстоянии от центра сферы, что отталкивание между корпускулами, которое, очевидно, будет радиально, как раз уравновесит радиальное притяжение, производимое на корпускулы положительным зарядом сферы. Простое вычисление показывает, что это произойдёт, когда расстояние корпускулы от центра будет равно 0,57 радиуса сферы. Теперь предположим, что корпускулы вместо того, чтобы быть в покое, описывают круговые орбиты вокруг центра сферы. Их центробежная сила увлечёт их дальше от центра на расстояние, зависящее от скорости их вращения по орбитам. При возрастании этой скорости расстояние от центра сферы до корпускул будет возрастать до тех пор, пока при известной скорости корпускулы достигнут поверхности сферы. Дальнейшее возрастание скорости заставит их сначала вращаться вне сферы и, наконец, совсем покинуть сферу, когда атом уже распадётся.

    Таким образом, мы видим, что состав агрегата не постоянен, когда кинетическая энергия, зависящая от скорости корпускул внутри сферы относительно её центра, превосходит известную величину. Ради краткости мы назовём эту кинетическую энергию корпускул внутри атома корпускулярной температурой атома. Предыдущий результат можно выразить иначе, сказав, что атом устойчив лишь до тех пор, пока его корпускулярная температура не превышает известной величины.

    Мы должны тщательно различать корпускулярную температуру, которая представляет среднюю кинетическую энергию корпускул внутри атома, и молекулярную температуру, которая является средней кинетической энергией, зависящей от движения центра тяжести атома. Вероятно, эти температуры не находятся в тесной связи друг с другом. Они были бы пропорциональны друг другу, если бы здесь был приложим известный закон равного распределения энергии между различными степенями свободы атома. Но этот закон несовместим с физическими свойствами газов, и в кинетической теории газов доказательство его не принимает в расчёт времени, необходимого для установления состояния, предполагаемого законом. Возможно, что это время так долго, что газы никогда не могут прийти в это состояние.

    Возьмём теперь случай двух агрегатов А и В, корпускулярные температуры которых высоки, хотя не так, чтобы сделать А и В в отдельности неустойчивыми. Чтобы дать им наибольшую возможность соединения, предположим, что центры тяжести А и В, когда они сближены между собою, находятся в покое. Соединяются ли тогда А и В так, чтобы образовать более сложный агрегат, как это было бы, если бы корпускулы их были в покое? Я думаю, легко видеть, что это вовсе не необходимо. Ибо, когда А и В сближаются под влиянием взаимного притяжения, то потенциальная энергия, вызываемая расхождением А и В, уменьшится, а кинетическая энергия возрастет. Это увеличение кинетической энергии корпускул А и В увеличит стремление корпускул покинуть свои атомы, и, если приращение кинетической энергии значительно, то как А, так и В могут потерять одну или несколько корпускул. Отделение одной корпускулы оставит А и В положительно заряженными, и они будут стремиться к расхождению, благодаря отталкиванию их зарядов. Когда они разойдутся, то они будут оба положительно заряжены. Но, так как теперь в области, где расположены А и В, движутся свободные корпускулы с отрицательными зарядами, то эти положительные заряды наконец нейтрализуются корпускулами, которые сталкиваются с А и В и остаются в соединении с ними.

    Итак, мы приходим к заключению, что соединение может быть устойчиво лишь тогда, когда корпускулярная температура после соединения меньше известной предельной величины; иначе образуемый комплекс будет неустойчив и неспособен к продолжительному существованию. но корпускулярная температура агрегата, образуемого из А и В, зависит от корпускулярных температур А и В до соединения, а также от уменьшения потенциальной энергии системы, вызванного соединением А и В. Если корпускулярные температуры А и В до соединения были очень высоки, то корпускулярная температура после соединения будет также высока. Если они превосходят известный предел, то корпускулярная температура после соединения будет слишком высока для сохранения устойчивости агрегата АВ, и он не образуется. Таким образом, одним из условий для образования сложных агрегатов является требование, чтобы корпускулярная температура их составляющих до соединения была достаточна низка.

    Если молекулярная температура газа, в котором А и В — молекулы, очень высока, то соединение их может быть задержано большой относительной скоростью А и В, которая, несмотря на их взаимное притяжение удаляет их друг от друга. Но следует иметь в виду, что мы не можем вызвать соединение простым понижением молекулярной температуры, т. е. охлаждением газа. Соединение возможно лишь тогда, когда корпускулярная температура, т. е. кинетическая энергия, вызываемая движением корпускул внутри атома, уменьшена ниже известной величины. Мы можем предупредить соединение, повышая молекулярную температуру газа, но не можем вызвать соединение понижением её.

    Приведём определённый пример: причина, по которой с этой точки зрения атомы водорода, находящиеся на земле, не соединяются для образования другого элемента даже при крайне низкой температуре, когда водород становится жидким, — состоит в том, что даже при этой температуре кинетическая энергия корпускул внутри атома, т. е. корпускулярная температура, слишком высока. Здесь будет полезно повторить то, что мы установили ранее, именно, что между корпускулярной и молекулярной температурами нет тесной связи, и что последнюю можно понизить почти до абсолютного нуля, не изменяя существенно первой.

    Теперь мы должны перейти к обсуждению того значения, какое эти выводы имеют для теории, что различные химические элементы постепенно развились путём соединения первоначальных единиц.

    Предположим, что достигнута первая ступень, и мы имеем известное число систем, образованных соединением двух единиц. Когда эти двойные системы, как мы можем их назвать, впервые образовались, то корпускулы в системе должны были иметь значительный запас кинетической энергии. Это должно быть так, потому что при соединении двух единиц должен был возникнуть запас кинетической энергии, равный уменьшению потенциальной энергии, благодаря соединению двух единиц. Так как эти двойные системы имеют первоначально высокую корпускулярную температуру, то они не легко будут соединяться друг с другом или с другой единицей. Прежде чем произойдёт такое соединение, кинетическая энергия корпускул должна уменьшиться.

    Сейчас мы должны перейти к обсуждению способа, каким происходит это уменьшение; но мы выскажем заранее вывод из этого обсуждения, сказав, что скорость убывания корпускулярной температуры, вероятно, сильно колеблется среди отдельных двойных систем.

    Поэтому некоторые системы, вероятно, достигли состояния, когда они способны соединяться между собою или с отдельной единицей задолго раньше других. Системы первого рода будут соединяться, и мы будем иметь системы, из коих одни содержат три, другие — четыре единицы, тогда как в то же время остаётся много двойных систем. Таким образом, появление более сложных систем вовсе не вызывает одновременно исчезновения всех более простых.

    Тот же принцип применяется к образованию дальнейших агрегатов из систем, содержащих три или четыре единицы. Одни из этих систем будут готовы к соединению ранее других, и возникнут системы, содержащие восемь единиц прежде, чем более устойчивые, содержащие четыре, три, две или одну только единицу, исчезнут. С дальнейшим ходом агрегации число наличных систем с различным числом единиц будет возрастать.

    Таким образом, если мы допустим, что системы, содержащие различное число единиц соответствуют разным химическим элементам, то можно ожидать появления элементов всё более высоких атомных весов по мере того, как мир будет старше. Однако появление их не предполагает уничтожения элементов более низкого атомного веса. Во всяком случае число атомов последних будет уменьшаться, так как по нашей гипотезе более тяжёлые элементы строятся из материала, доставляемого более лёгкими. Но не все атомы последних будут потреблены сразу, так что возможно одновременное существование большого числа элементов.

    Однако, если корпускулярная температура атомов, благодаря излучению, постоянно падает, то более лёгкие элементы со временем исчезнут, и, если более тяжёлые атомы не распадутся, то атомный вес самого лёгкого оставшегося элемента будет постоянно возрастать. По этой теории, так как водород — самый лёгкий известный элемент, и атом водорода содержит около тысячи корпускул, ³) то все агрегаты из менее, чем тысячи единиц, вступили в соединение и не существуют более в свободном состоянии.

Как корпускулы в атоме теряют или приобретают кинетическую энергию.

    Если бы кинетическая энергия, возникающая из движения корпускул относительно центра тяжести атома, могла превращаться благодаря столкновениям в кинетическую энергию, зависящую от движения атома, как целого, т. е. в молекулярную температуру, то так как число корпускул в атоме чрезвычайно велико, из кинетической теории газов следовало бы, что удельная теплота газа при постоянном давлении приблизительно равна удельной теплоте при постоянном объёме; но на самом деле этого нет ни в одном газе. Отсюда мы заключаем, что кинетическая энергия корпускул уменьшается не от столкновений.

    Но мы видели (стр. 48), что движущаяся электрическая частица излучает энергию всякий раз, когда её скорость изменяется по величине или направлению. Таким образом, корпускулы в атоме вызывают электрические волны, испускают лучистую энергию, теряя кинетическую.

    Количество энергии, которую корпускулы теряют таким образом, сильно изменяется в зависимости от числа корпускул и способа их движения. Таким образом, если одна корпускула описывает круговую орбиту радиуса a со скоростью v, то потеря энергии от радиации в секунду равна 2e²v⁴/3Va², где e есть заряд корпускулы, a V — скорость света. Если вместо одной корпускулы на противоположных концах диаметра движутся все корпускулы по той же орбите с тою же скоростью, как одна корпускула, то потеря энергии в секунду двумя корпускулами гораздо меньше потери энергии одной корпускулой, и, чем меньше скорость корпускулы, тем больше уменьшение потери энергии, вызываемой возрастанием числа корпускул. Влияние увеличения числа корпускул показано в следующей таблице, которая представляет размер излучения каждой корпускулы для разных чисел корпускул, расположенных на равных угловых расстояниях на круговой орбите.

    Таблица относится к двум случаям: в одном — скорость корпускул равна десятой доле скорости света, в другом — одной сотой. В обоих случаях излучение одной корпускулы принято за единицу.

Число корпускул	Излучение каждой корпускулы
	v=V/10	v=V/100
1	1	1
2	9,6×10–2	9,6×10–4
3	4,6×10–3	4,6×10–7
4	1,7×10–4	1,7×10–10
5	5,6×10–5	5,6×10–13
6	1,6×10–7	1,6×10–17

    Таким образом, мы видим, что излучение от каждой из группы шести корпускул, движущихся с десятой долей скорости света, менее пятимиллионной части излучения одной корпускулы, описывающей ту же орбиту с тою же скоростью. Если же скорость корпускул составляет лишь сотую часть скорости света, то уменьшение радиации гораздо больше.

    Если корпускулы выведены из симметрического положения, в которых они находились на равных расстояниях вокруг центра, находящегося в покое, то излучение сильно увеличится. В атоме, содержащем большое число корпускул, количество излучаемой энергии изменяется очень быстро, смотря по роду движения корпускул в атоме. Так, например, если бы большое число корпускул двигалось близко друг от друга по круговой орбите, то излучение было бы крайне мало. Оно исчезло бы совершенно, если бы корпускулы были расположены так тесно, что образовали бы непрерывное кольцо отрицательного электричества. Если бы то же число частиц двигалось вокруг в беспорядке, то излучение, т. е. корпускулярное охлаждение, было бы значительно больше, хотя бы кинетическая энергия корпускул в последнем случае была не больше, чем в первом.

    Таким образом излучение энергии корпускул, скорость которых не одинакова, представляет процесс, который постепенно понижает корпускулярную температуру атома и, если наш взгляд правилен, позволяет атому образовать новые соединения, вызывая образование новых химических элементов.

    Этот процесс охлаждения должен быть крайне медленным: хотя корпускулярная температура при образовании нового элемента, вероятно, также очень высока и должна значительно убывать прежде, чем атом может войти в новые соединения, однако, мы должны допустить, что некоторые элементы существовали без изменения много тысяч или даже миллионов лет. В самом деле мы не можем непосредственно доказать, что в атоме происходят изменения. Однако я думаю, что некоторые явления радиоактивности, которых я коснусь ниже, если не доказывают, то допускают вполне обоснованную гипотезу, что подобные вековые изменения происходят в атоме.

    Мы должны также помнить, что корпускулы всякого атома получают и поглощают излучение других атомов. Это вызывает повышение корпускулярной температуры атома и таким образом способствует удлинению времени, необходимого для понижения температуры до того уровня, когда возможны новые соединения атома.

    Тот факт, что сила излучения зависит в такой степени от пути и способа движений корпускул в атоме, показывает, что продолжительность жизни различных атомов отдельного элемента не одинакова. Некоторые из них готовы к новым изменениям гораздо раньше других. Важно выяснить, как велико количество энергии, необходимое для образования сложного атома или для перераспределения корпускул внутри его. Если атом содержит n корпускул, каждая c зарядом e, измеренным в электростатических единицах, то общее количество отрицательного электричества в атоме будет ne, и равное количество положительного электричества, распределено по сфере, заряженной положительно. Поэтому работа, необходимая для разложения атома на его составные единицы, может выразиться через (ne)²/a, где a радиус шара, содержащего корпускулы. А так как атом возник из соединения этих единиц, то (ne)²/a будет того же порядка величины, как кинетическая энергия, сообщённая этим составным частям в течение всей их жизни со времени их возникновения, как отдельных данных, до момента их вступления в число членов нашего атома. В течение этого периода они должны были излучить большое количество энергии, но следующее вычисление покажет, какое огромное количество кинетической энергии должны содержать корпускулы в атоме даже, если они удержали лишь чрезвычайно малую долю сообщённой им энергии. Вычислим величину (ne)²/a для всех атомов, находящихся в одном грамме вещества. Пусть N будет число этих атомов в грамме, тогда N(ne)²/a есть величина энергии, полученной этими атомами. Если М есть масса атома, то NM=l, так что

N(ne)²/a=(ne)²/Ma

если m есть масса одной корпускулы, то

nm=М,

а потому

N(ne)²/a=(e/m)(ne/a);

если же e измеряется в электростатических единицах, то

e/m=3×10¹⁷ и e=3,4×10^–10;

а потому

N(ne)²/a=10,2×10⁷×n/a.                        (1)

    В случае атома водорода n=1000, ⁴) и, если мы за радиус этого атома a примем величину, обычно принимаемую в кинетической теории газов, т. е. 10^–8, то

N(ne)²/a=1,02×10¹⁹ эргов.

    Эта величина энергии была бы достаточна, чтобы поднять миллион тонн на высоту, значительно превосходящую 90 метров. Далее из уравнения (1) мы видим, что эта энергия пропорциональна числу корпускул, так что, чем больше молекулярный вес элемента, тем больше будет количество энергии, содержащейся в атомах каждого грамма.

    Мы возвратимся к природе внутренних изменений в атоме при рассмотрении некоторых явлений радиоактивности; но прежде желательно рассмотреть ближе способ, которым корпускулы располагаются в атоме. Мы начнём со случая, когда корпускулы находятся в покое. Корпускулы предполагаются в сфере однородного положительного заряда, который оказывает радиальную притягательную силу на каждую корпускулу, пропорциональную её расстоянию от центра сферы; и задача состоит в том, чтобы расположить корпускулы в сфере так, чтобы они были в равновесии под действием этого притяжения и их взаимных отталкиваний. Две корпускулы А и В, как легко видеть, находятся в равновесии, если они лежат на прямой линии с центром сферы (рис. 16), и ОА=ОВ= 1/2 радиуса сферы.

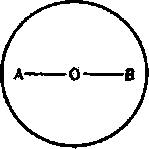
Рис. 16.

    Три корпускулы А, В, С находятся в равновесии, если ABC представляет равносторонний треугольник с центром в О (рис. 17), и ОА=ОВ=ОС=(1/5)^1/3 или 0,57 радиуса сферы.

Рис. 17.

    Четыре корпускулы находятся в равновесии, если они расположены на вершинах углов правильного тетраэдра с центром, совпадающим с центром сферы. В этих случаях все корпускулы находятся на поверхности сферы, концентрической со сферой положительного заряда, и можно думать, что для всякого числа корпускул положение равновесия будет состоять в симметрическом расположении на поверхности сферы. Во всяком случае такое расположение технически должно представлять равновесие, но математическое вычисление показывает, что это расположение не устойчиво и не может сохраняться, кроме случая, когда число корпускул очень мало, около семи или по большей мере восьми. Когда число корпускул больше этого предельного числа, то корпускулы распадаются на две группы. Одна группа, содержащая меньшее число корпускул, находится на поверхности маленького тела, концентрического со сферой, другая — на поверхности большего концентрического тела. Когда число корпускул ещё более возрастает, то наступает стадия, в которой равновесие не может быть устойчиво даже при двух группах, и корпускулы делятся на три группы, расположенные на поверхностях концентрических шаров. Чем более возрастает число корпускул, тем более групп необходимо для равновесия. Для значительного числа корпускул задача нахождения равновесия становится слишком сложной для вычисления. Мы должны обратиться к опыту и попытаться устроить модель, в которой силы, вызывающие равновесие, подобны тем, которые мы предположили действующими в корпускуле. Такую модель представляет простой и изящный опыт, впервые произведённый, насколько мне известно, профессором Майером. В этом опыте несколько маленьких магнитов плавают в сосуде с водой. Магниты состоят из стальных иголок, намагниченных до равной силы, и плавают, воткнутые на маленьких кружках пробки. Магниты расположены так, что все полюсы находятся выше или ниже поверхности. Эти положительные полюсы подобно корпускулам отталкиваются друг от друга с силами, изменяющимися обратно пропорционально расстоянию между ними. Притягательная сила действует со стороны отрицательного полюса (если магниты имеют положительные полюсы над водой), подвешенного на некотором расстоянии над поверхностью воды. Этот полюс производит на положительные полюсы маленьких плавающих магнитов притягательную силу, составляющая которой, параллельная поверхности воды, будет направлена радиально к О, проекции отрицательного полюса на поверхности воды. Если отрицательный полюс находится на некотором расстоянии над поверхностью воды, то эта составляющая приблизительно пропорциональна расстоянию от О. Таким образом, силы на полюсах плавающих магнитов имеют большое сходство с силами, действующими на корпускулу в нашем гипотетическом атоме. Главное различие состоят в том, что корпускулы могут свободно двигаться по всем направлениям в пространстве, тогда как полюсы плавающих магнитов принуждены двигаться в плоскости, параллельной поверхности воды.

    Расположения, принимаемые плавающими магнитами по мере возрастания числа магнитов от двух до девятнадцати, представлены на чертеже 18, который дан Майером.

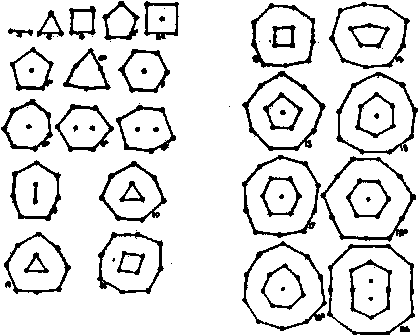
Рис. 18

    Конфигурации, принимаемые магнитами при ещё большем числе их, могут быть получены из следующей таблицы, также данной Майером. Из этой таблицы можно видеть, что когда число плавающих магнитов не превосходит пяти, то магниты располагаются на углах правильного многоугольника, пять магнитов по углам пятиугольника, четыре по углам квадрата и т. д. Когда число больше пяти, то расположение становится иным. Так, шесть магнитов не располагаются на углах шестиугольника, но делятся на две системы, так что один находится в центре, а пять вне его по углам правильного пятиугольника. Это расположение в двух группах продолжается до тех пор пока число их не достигнет пятнадцати, когда получатся три группы; при двадцати семи магнитах получатся четыре группы и т. д.

РАСПОЛОЖЕНИЕ МАГНИТОВ (МАЙЕР).

    Здесь, например, формула 3·7·12·13 обозначает, что тридцать пять магнитов располагаются так, что внутри образуется кольцо из трёх магнитов, затем кольцо из семи, потом из двенадцати и одно из тринадцати — снаружи.

    Я думаю, что эта таблица даёт некоторые указания для объяснения некоторых свойств атомов. Возьмём, например, химический закон, называемый периодическим законом; согласно этому закону, если мы расположим элементы в порядке возрастания их атомных весов, то, взяв элемент низкого атомного веса, положим, литий, мы найдём известные свойства, связанные с ним. Этих свойств не обнаруживают элементы, непосредственно следующие за ним в ряду возрастающих атомных весов; но свойства появляются снова, когда мы достигнем натрия, затем они снова исчезают на время, но появляются опять, когда мы дойдём до калия, и т. д. Рассмотрим теперь расположения плавающих магнитов и допустим, что число их пропорционально атомному весу элемента. Тогда, если какое-либо свойство связано с треугольным расположением магнитов, то оно обнаруживалось бы элементами, коих атомный вес по этой шкале, равен трём; но оно не появлялось бы, пока мы не достигли бы атомного веса десять, когда свойство снова показывается, так как здесь мы имеем снова треугольное расположение в средине и кольцо из семи магнитов снаружи. Когда число магнитов возрастает, то треугольное расположение исчезает на время, но появляется, снова при двадцати магнитах и снова при тридцати пяти. Треугольное расположение появляется и исчезает таким же образом, как и свойства элементов в периодическом законе. Как пример свойства, которое может быть связано с особенной группировкой корпускул, возьмём числа колебаний системы, как они обнаруживаются положением линий в спектре элемента. Сначала возьмём случай 3 корпускул, когда они сами по себе находятся в положительно заряженном шаре. Три корпускулы имеют девять степеней свободы, так что здесь возможны девять периодов. Некоторые из этих периодов в данном случае бесконечно велики, а многие, из возможных периодов равны между собою, так что здесь нет девяти различных периодов.

    Допустим, что спектральные линии трёх корпускул представлены на чер. 19, где цифры под линиями представляют число периодов, совпадающих на этой линии, т. е., если периоды даны “уравнением с девятью корнями; допустим, что только один корень представляем период, соответствующий линии А, тогда как линии В соответствуют два равные корня, линии С — три, линии D — один, линии Е – два равные корня. Эти периоды имеют между собою известные численные отношения, независимые от заряда корпускул, от размера сферы, в которой они находятся или от их расстояния от центра сферы. Каждое из этих количеств, хотя не влияет на отношение периодов, имеет большое влияние на абсолютную величину каждого из них. Теперь предположим, что эти три корпускулы находятся в сфере не одни, но образуют лишь одну из многих групп в ней точно так, как треугольник из магнитов представляет составную часть групп, состоящих из 3, 10, 20 и 35 магнитов. Рассмотрим, как присутствие других групп влияет на периоды колебаний трёх корпускул. Абсолютные величины периодов вообще были бы различны, но отношение между различными периодами было бы гораздо устойчивее, могло бы быть изменено, но не нарушено. Пользуясь терминологией теории планетных движений, мы можем считать движение трёх корпускул "возмущённым" ⁵) другими группами.

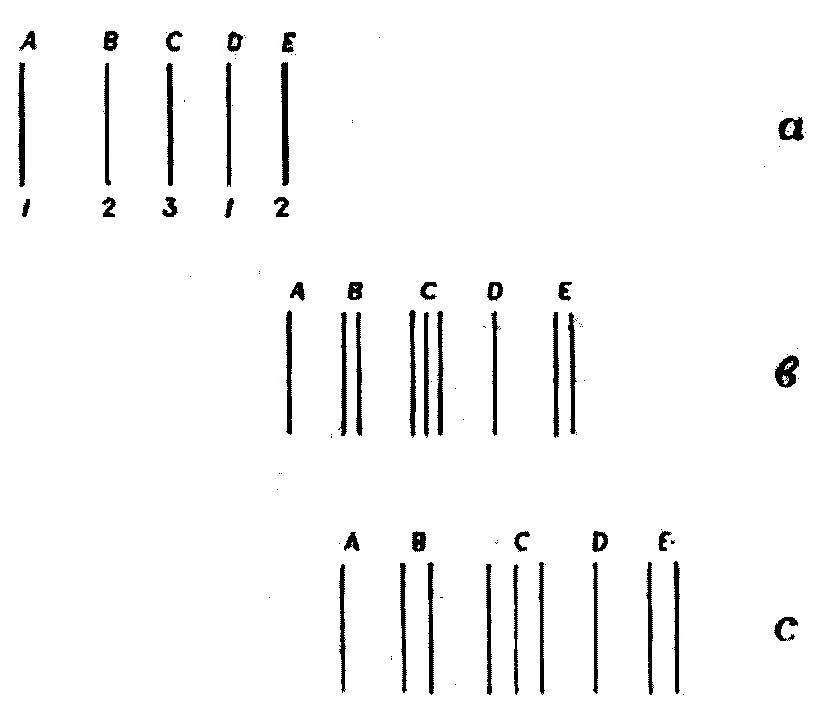
Рис. 19.

    Когда группа трёх корпускул была одна, здесь были различные смещения, которые имели тот же период колебаний; например для линии С здесь были три смещения одинакового периода. Когда же здесь есть другие группы, то эти различные смещения уже не симметричны относительно этих групп, так что три периода уже не вполне равны между собою. Но они были бы приблизительно равны, если бы влияние других групп не было очень велико. Так, в спектре C вместо одной линии представило бы триплет, тогда как В и E дали бы; дуплеты, А и D остались бы простыми линиями.

    Таким образом, спектр теперь имел бы вид черт. 19 а; чем больше число групп, окружающих группу трёх корпускул, тем более движение последней будет возмущено, и тем больше будет расхождение составных частей триплетов и дублетов. Изображение по мере возрастания числа групп представлено на черт. 19 в, с. Поэтому, если мы допустим, что элемент, содержащий эту особенную группировку корпускул, принадлежит к той же группе в классификации элементов согласно периодическому закону, то получим в спектрах этих элементов гомологичные ряды линий, в которых расстояния между составляющими дублетов и триплетов возрастают с атомным весом элементов. Исследования Ридберга (Rydberg), Рунге (Runge) и Пашена (Paschen) и Кейзера (Keyser) показали присутствие в спектрах элементов той же группы рядов линий, имеющих во многих отношениях сходные свойства, как в описанных нами.

    Другой интересный пункт в опытах Майера состоит в том, что для одного и того же числа магнитов существует более одной устойчивой конфигурации. Эти конфигурации соответствуют разным количествам потенциальной энергии, так что переход от конфигурации и большей потенциальной энергии к меньшей сообщит корпускуле кинетическую энергию. Из количеств потенциальной энергии, заключённых в атоме, которые мы определили на стр. 70, мы заключаем, что даже ничтожная перемена потенциальной энергии разовьёт количество кинетической энергии, которое, будучи превращено в теплоту, далеко превзойдёт количество теплоты, развиваемой при каком-либо известном химическом соединении атомов.

    Рассмотрение таблицы показывает, что в ней есть известные места, где природа конфигурации меняется очень быстро с числом магнитов. Так, пять магнитов образуют одну группу, а шесть магнитов – две; четырнадцать магнитов образуют две группы, пятнадцать — три; двадцать семь магнитов образуют три группы, двадцать восемь — четыре и т. д. Если мы расположим химические элементы в порядке их атомных весов, то найдём, что в известных местах различие свойств последовательных элементов чрезвычайно велико; так, например, мы видим крайнее различие в свойствах между фтором и натрием. Затем наблюдается большая или меньшая непрерывность свойств, пока мы не дойдём до хлора, за которым следует калий; следующий перерыв лежит между бромом и рубидием и т. д. Это явление кажется аналогичным перегруппировке магнитов.

    До сих пор мы предполагали, что корпускулы находятся в покое; если же они находятся в состоянии устойчивого движения и описывают круговые орбиты около центра сферы, то центробежная сила, возникающая из этого движения, будет удалять корпускулы от центра сферы, не нарушая во многих случаях конфигурации. Так, например, если в сфере находятся три корпускулы, то в состоянии равномерного движения они расположатся по углам равностороннего треугольника, как если бы они были в покое, но этот треугольник будет вращаться около центра сферы, и расстояние корпускул от центра будет больше, чем когда они в покое, и будет возрастать со скоростью корпускул.

    Но во многих случаях вращение существенно для устойчивости конфигурации. Так, возьмем случай четырёх корпускул. При быстром вращении они находятся в устойчивом равномерном движении, располагаясь по углам квадрата, плоскость которого перпендикулярна к оси вращения. Когда же скорость вращения корпускул падает ниже известной величины, то расположение четырёх корпускул в одной плоскости становится неустойчивым, и корпускулы стремятся поместиться по углам правильного тетраэдра, который представляет устойчивое расположение, когда корпускулы находятся в покое. Систему четырёх корпускул по углам квадрата можно сравнить с волчком, который подобно корпускулам устойчив лишь, когда его скорость вращения превосходит известную критическую величину. Предположим, что вначале скорость корпускул превосходит эту величину, но тем или иным способом корпускулы постепенно теряют свою кинетическую энергию; квадратное расположение сохранится, пока скорость корпускул не уменьшится до критической величины. Тогда расположение станет неустойчиво, и в системе произойдёт сотрясение, сопровождаемое развитием большой кинетической энергии.

    Подобные же рассуждения применяются ко многим группировкам корпускул. В таких случаях, когда корпускулы вращаются с большой скоростью (как в случае четырёх корпускул), конфигурация будет существенно отлична от конфигурации того же числа корпускул, когда они в покое. Таким образом, должна быть критическая скорость корпускул, так что для скоростей больших, чем критическая, конфигурация устойчива; она неустойчива, когда скорость падает ниже критической величины. Когда наступает неустойчивость, то происходит известное содрогание или взрыв, сопровождаемый сильным уменьшением потенциальной энергии и соответственным увеличением кинетической энергии корпускул. Это возрастание кинетической энергии корпускул может быть достаточно для того, чтобы оторвать значительное число их от первоначальной системы.

    Эти рассуждения имеют непосредственную связь с теорией строения атомов, принятой нами в этой главе. Именно они показывают, что в атомах особого рода, т. е. определённого атомного веса, корпускулярное охлаждение, вызываемое принятым нами медленным излучением движущихся корпускул, может по достижении известного предела вызвать внутри атома неустойчивость и такое увеличение кинетической энергии корпускул, что излучение сильно возрастёт, и возможно отделение части атома. Атом станет выделять энергию, источник которой в потенциальной энергии, зависящей от расположения корпускул в атоме. При рассмотрении явлений радиоактивности мы увидим, что есть группа тел, которые обнаруживают явления аналогичные только что описанным.

    Допустим, что сначала образуются более лёгкие элементы соединением пары единиц, отрицательный элемент которой образует корпускулы, а из соединения атомов более лёгких элементов происходят атомы более тяжёлых элементов. Тогда мы должны ожидать, что корпускулы тяжелых атомов располагаются как бы в пучки, причём расположение корпускул в каждом пучке подобно расположению в атоме более лёгкого элемента. В более тяжёлом атоме эти пучки будут играть роль вторичных единиц, так что каждый пучок соответствует одному из магнитов в модели, состоящей из плавающих магнитов, тогда как в самых пучках корпускулы аналогичны магнитам.

    Теперь мы должны перейти к рассмотрению того, может ли атом, построенный предположенным нами способом, обладать некоторыми свойствами реального атома. Даст ли, например, эта модель атома объяснение электрохимических свойств реального атома, свойств вроде того, что химические элементы делятся на два класса, электроположительные и электроотрицательные. Почему, например, при таком составе атома, атом калия или натрия стремится приобрести положительное электричество, а атом хлора отрицательный заряд? Затем указывает ли что-нибудь в модели атома на присутствие такого свойства, как так называемая у химиков валентность, т.е. свойство, позволяющее нам делить элементы на группы и называть элементы одноатомными, двухатомными, трёхатомными, так что молекула соединения двух элементов первой группы содержит то же число атомов каждого элемента, тогда как молекула соединения элемента А первой группы с элементом В второй содержит вдвое более атомов А, чем В, и т. д.

    Вернёмся к свойствам модели атома. Она содержит очень большое число корпускул в быстром движении. Из явлений, связанных с проводимостью электричества через газы, мы знаем, что одна или несколько таких корпускул может быть отделена от атома. Они могут оторваться, благодаря их большой скорости, позволяющей им выйти из сферы притяжения атома. Они могут также оторваться, благодаря столкновению атома с другими быстро движущимися атомами или свободными корпускулами. Когда же корпускула оторвалась от атома, то последний будет заряжен положительно. Этим будет затруднено выделение второй отрицательно заряженной корпускулы, Ибо, вследствие положительного заряда атома, он будет сильнее прежнего притягивать вторую корпускулу. Теперь нетрудно понять, что лёгкость, с которою частица может оторваться или быть выброшена из атома, может сильно изменяться в атомах разных элементов. В некоторых атомах скорости корпускул могут быть так велики, что корпускула сразу отрывается от атома. Может даже случиться, что после отделения одной притяжение оставшегося в атоме положительного электричества будет недостаточно, чтобы удержать вторую или даже третью корпускулу. Такие атомы получат положительные заряды одной, двух или трёх единиц, смотря по тому, потеряли ли они одну, две или три корпускулы. С другой стороны, есть атомы, в которых скорости корпускул так малы, что лишь немногие или даже ни одна корпускула не отрывается сама собою. Атомы могут даже быть способны присоединять одну или даже более одной корпускулы прежде чем отталкивание, производимое отрицательным электричеством на эти чуждые корпускулы, заставит некоторые из первоначальных корпускул оторваться. Когда такие атомы вступают в область, где находятся корпускулы, то, благодаря соединению с этими корпускулами, атомы получают отрицательный заряд. Величина отрицательного заряда будет зависеть от силы, с которой атом удерживал свои корпускулы. Если бы отрицательный заряд одной корпускулы был недостаточен для вытеснения корпускулы, отрицательный заряд двух корпускул был способен к этому, то максимальный отрицательный заряд атома был бы равен единице. Если бы две корпускулы были недостаточны для вытеснения корпускулы, а необходимы три, то максимальный отрицательный заряд был бы равен двум единицам и т. д.

    Таким образом, атомы этого класса стремятся получить заряд отрицательного электричества и соответствуют электроотрицательным химическим элементам, тогда как атомы класса, рассмотренного нами раньше и легко теряющие корпускулы, приобретают положительный заряд и соответствуют атомам электроположительных элементов. Мы можем представить себе атомы, в которых корпускулы так точно уравновешены, что, хотя они сами по себе не теряют корпускул и потому не получают положительного заряда, но отталкивание, вызываемое приближающейся к атому чуждой корпускулой, достаточно для того, чтобы вытеснить корпускулу. Такой атом не мог бы получить ни положительного ни отрицательного заряда.

    Предположим, что известное число атомов, легко теряющих свои корпускулы, смешаны с известным числом атомов, не могущих удержать чуждую корпускулу. Назовем атом первого класса А, атом второго класса В и предположим, что атомы А такого рода, что теряют одну корпускулу, тогда как атомы В такого рода, что могут удержать одну, но не более одной корпускулы. Тогда корпускулы, выделяемые атомами А, пристанут, наконец, к атомам В, и, если число обоего рода атомов у нас равно, то наконец все атомы А будут заряжены единицей положительного электричества, а все атомы В единицей отрицательного электричества. Противоположно заряженные атомы будут притягивать друг друга, и возникнет соединение АВ. Если бы атомы А были такого рода, что теряли бы две корпускулы, а атомы В те же, что и прежде, то атомы А получили бы заряд двух положительных единиц, атомы В — заряд одной отрицательной единицы. Таким образом, для образования нейтральной системы два атома должны соединиться с одним атомом А, и возникло бы соединение АВ₂.

    Таким образом, с этой точки зрения одновалентный положительный атом имеет свойство при условиях, когда он соединяется с другим атомом, терять одну только корпускулу, прежде чем достигнет устойчивости. Одновалентный электроотрицательный атом может присоединять одну только корпускулу, не вытесняя других корпускул из атома. Двувалентный электроположительный атом теряет две корпускулы, но не более и т. д. Таким образом, валентность атома зависит от лёгкости, с которой корпускулы могут отрываться или приставать к атому. На неё могут влиять обстоятельства, при которых происходит соединение атомов. Так, для корпускулы, оторвавшейся от атома, легче противостоять притяжению положительного заряда, если атом окружён хорошими проводниками, чем, если он изолирован в пространстве. Поэтому понятно, каким образом на валентность атома в некоторой степени могут влиять физические условия, при которых происходит соединение.

    Допуская, что притяжение между атомами в химическом соединении электрического происхождения, мы можем сказать, что способность элемента вступать в химическое соединение зависит от того, способен ли ею атом получать электрический заряд. С изложенной точки зрения это предполагает, что или незаряженный атом неустойчив и должен потерять одну или более корпускул прежде, чем он достигнет устойчивости, или же он так устойчив, что может удержать одну или более добавочных корпускул, не вытесняя ни одной первоначальной корпускулы. Если степень устойчивости такова, что атом, хотя устойчивый в незаряженном состоянии, становится неустойчив, присоединяя добавочную корпускулу, то атом не способен получить ни положительного ни отрицательного заряда и потому не может войти в химическое соединение. Такой атом будет иметь свойства таких элементов, как аргон или гелий.

    Взгляд, что силы, связывающие атомы в молекулы химических соединений, электрического происхождения, был впервые высказан Берцелиусом; это было также мнением Дэви и Фарадея. Гельмгольц также признавал, что химические силы электрического происхождения. Вообще же, химики, по-видимому, мало пользовались этой идеей, находя представление о "единицах сродства" более плодотворным. Но учение о единицах сродства в известном отношении почти тождественно с электрической теорией. Теория единиц, представленная графически, предполагает, что от каждого одновалентного атома выходит прямая линия (символ сродства); двухвалентный атом находится на конце двух таких линий, трёхвалентный — на конце трёх и т. д. Если представить химическое соединение такой графической формулой, то каждый атом должен быть на конце соответственного числа линий, представляющих сродство. Но по электрической теории химических соединений одновалентный атом имеет одну единицу заряда, если мы примем за единицу заряд корпускулы. Таким образом, атом есть начало или конец одной фарадеевой трубки: начало, если заряд атома положителен, конец, если заряд отрицателен. Двухвалентный атом имеет две единицы заряда и потому представляет начало или конец двух фарадеевых трубок. Итак, если мы определим "сродство" химиков, как признак наличности единичной фарадеевой трубки, связывающей заряженные атомы в молекулу, то структурные формулы химиков могут без труда быть переведены на электрическую теорию. Но здесь есть некоторое различие, которое заслуживает более близкого рассмотрения: символ, обозначающий сродство в химической теории, не предполагает направления. По этой теории не делается различия между концами линии сродства. По электрической же теории есть разница между концами, так как один конец соответствует положительному заряду, а другой — отрицательному. Один или два примера лучше всего объяснят результат этого различия. Возьмем газ этан, структурная формула которого пишется так:

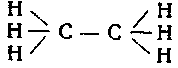
    По химической теории нет разницы между двумя атомами угля в этом соединении; но по электрической теории здесь есть различие. Ибо допустим, что все атомы водорода заряжены отрицательно; тогда три фарадеевы трубки, идущие от атомов водорода к каждому атому углерода, дают положительный заряд в три единицы на каждом атоме углерода. Но в дополнение к фарадеевым трубкам, идущим от атомов водорода, здесь имеется трубка, идущая от одного атома углерода к другому. Это обозначает добавочный положительный заряд на одном атоме угля и отрицательный заряд на другом. Таким образом, один из атомов углерода будет иметь заряд в четыре положительные единицы, а другой будет иметь заряд в три положительные и одну отрицательную единицы, т. е. в две положительные единицы, так что с этой точки зрения два атома углерода находятся не в одинаковом положении. Ещё большее различие должно быть между атомами, когда мы имеем то, что называется двойной связью, т. е. когда атомы углерода связаны двумя единицами сродства, как в соединении

    Здесь, если бы один атом углерода имел заряд в четыре положительные единицы, то другой имел бы заряд в две положительные и две отрицательные единицы.

    Мы могли бы ожидать, что откроем такие различия при исследовании того, что известно под именем аддитивных свойств, т. е. свойств, которые могут быть вычислены, когда известен химический состав молекулы. Пусть, например, А, В, С будут атомы трёх химических элементов; тогда, если p есть величина некоторой физической постоянной для молекулы А₂, q — величина для В₂ и r для С₂, и эта постоянная подчиняется аддитивному закону, — величина эта для молекулы вещества, химический состав которого выражается формулой A_xB_yC_z, будет

px/2+ qy/2 + rz/2.

    Существование таких отношений можно ожидать лишь, когда атомы, которые встречаются в различных соединениях, соответствующих разным величинам х, у, z, те же самые. Если атом А встречается в различных состояниях в разных соединениях, то для этих соединений надо пользоваться различными величинами р.

    Хорошо известный пример аддитивных свойств представляет преломляющая способность разных веществ по отношению к свету, и в этом случае химики находят нужным пользоваться различными величинами преломления через атом углерода, смотря по тому, имеет ли атом одну или две связи. Но они пользуются той же величиной для преломления атома углерода, когда он имеет одну связь с другим атомом или, как в соединении СН₄, он вовсе не связан с другим атомом углерода.

    Можно, правда, представить себе, что в соединении один атом заряжен положительно, а другой отрицательно, когда атомы разного рода. Но этого трудно достигнуть, когда атомы одного рода, как в молекулах элементарных газов Н₂, O₂, N₂ и т. д. В этом отношении надо заметить, что электрическое состояние атома, зависящее от его способности выделять или присоединять корпускулы, может в широких размерах обусловливаться обстоятельствами, внешними для атома. Так, например, атом газа, окружённый быстро движущимися атомами или корпускулами, которые постоянно сталкиваются с ним, будет, благодаря этим столкновениям, терять корпускулы и таким образом приобретёт положительный заряд. С другой стороны, можно ожидать, что при равенстве прочих условий атом, находящийся в газе, будет менее способен терять корпускулу, чем если он находится в твёрдом или жидком теле. Ибо, когда корпускула в газе покинула атом, то она не может противопоставить притяжению положительно заряженного атома ничего, кроме собственной скорости, так как другие атомы слишком удалены для того, чтобы оказывать какое-либо действие на неё. Когда же атом находится в жидком или твёрдом теле, то притяжения других атомов, окружающих этот атом, могут удержать корпускулу, покинувшую свой атом, от падения обратно в атом. Как пример такого действия, можно взять ртуть в жидком или газообразном состоянии. В жидком состоянии ртуть — хороший проводник электричества. Один способ представления этой проводимости состоит в предположении, что корпускулы оставляют атомы ртути и странствуют по промежуткам между атомами. Если на эти заряженные корпускулы действует электрическая сила, то они приходят в движение и образуют электрический ток, причём проводимость жидкой ртути указывает на присутствие большого числа корпускул. Когда же ртуть в газообразном состоянии, то её электропроводность, как доказал Стрётт, представляет чрезвычайно малую долю проводимости, свойственной тому же числу жидких молекул. Это указывает на то, что даже атомы электроположительного вещества, подобно ртути в газообразном состоянии, могут терять сравнительно мало корпускул. Теперь предположим, что у нас большое число атомов одного рода в газообразном состоянии, движущихся по всем направлениям и приходящих во взаимное столкновение. Те, которые движутся быстрее и потому сталкиваются сильнее, будут легче терять корпускулы, чем движущиеся медленнее. Первые, благодаря потере своих корпускул, становятся положительно заряжены, и, если атомы не слишком электроположительны, чтобы удерживать отрицательный заряд даже в газообразном состоянии, то выделенные корпускулы стремятся пристать к атомам, движущимся медленнее.

    Таким образом, некоторые из атомов, будут заряжены положительно, другие отрицательно, и атомы с противоположными зарядами соединятся в двухатомные молекулы. Это не применимо к весьма электроположительным газам. Они не образуют молекул; но, так как в газе много свободных корпускул, то можно ожидать, что он обладает значительной электропроводностью.

стр. 85
ГЛАВА VI.
РАДИОАКТИВНОСТЬ И РАДИОАКТИВНЫЕ ВЕЩЕСТВА. ⁶)

    В 1896 году Беккерель (Becquerel) открыл, что уран и его соли обладают способностью выделять лучи, которые, подобно лучам Рентгена и катодным лучам, действуют на фотографическую пластинку и делают газ, через который они проходят, проводником электричества.

    В 1898 г. Шмидт (Schmidt) открыл, что торий обладает подобными же свойствами. Эта способность выделять лучи называется радиоактивностью, а вещества, обладающие этой способностью, называются радиоактивными.

    Это свойство урана подало повод к тщательному исследованию большого числа минералов, содержащих это вещество, и г. и г-жа Кюри (Curie) нашли, что некоторые из них и особенно некоторые виды смоляной обманки более радиоактивны, чем равные объёмы чистого урана, хотя только часть этих минералов состояла из урана. Это указывало на то, что эти минералы содержат вещество или вещества гораздо более радиоактивные, чем самый уран, и начато было систематическое исследование с целью изолирования этих веществ. После долгих исследований, которые г. и г-жа Кюри вели с удивительным искусством и настойчивостью в сотрудничестве гг. Бэмона (Bemont) и Дебиерна (Debiern), им удалось установить существование трёх новых радиоактивных веществ в смоляной обманке: радий, связанный в минерале с барием и весьма похожий на него по своим химическим свойствам полоний, связанный с висмутом, и актиний, с торием. Им удалось изолировать первый из них и определить атомный вес, оказавшийся равным 225. Спектр его был открыт и исследован Демарсе (Demarcay). Полоний и актиний до сих пор ещё не изолированы, и спектры их не исследованы. Активность полония оказалась преходящей: она исчезает через несколько месяцев после его получения.

    Эти радиоактивные вещества встречаются не только в редких минералах. Недавно я нашёл, что многие виды воды из глубоких колодцев содержат радиоактивный газ, а Эльстер и Гейтель (Elster a. Geitel) нашли, что подобный газ содержится в почве.

    Эти радиоактивные вещества должны оказать величайшие услуги при исследовании вопросов, касающихся природы атома и изменений, происходящих в атоме от времени до времени. Ибо свойства этих веществ так резко выражены, что сравнительно легко открыть чрезвычайно малые количества их. Количество этих веществ, могущих быть открытыми, относится к соответствующему количеству других веществ, которые можно открыть обыкновенными способами химического анализа, как одна секунда к тысячам лет. Поэтому перемены, которые в нерадиоактивных веществах должны бы происходить в течение почти геологических эпох, пока они станут достаточно заметны, могут в радиоактивных веществах вызывать заметные действия в течение немногих часов.

    Резерфорд нашёл, что излучение урана состоит из трёх различных типов, которые он называет лучами α, β и γ, а затем найдено то же самое для тория и радия.

    Излучение α весьма легко поглощается и не способно проникать более, чем на несколько миллиметров, в воздух при атмосферном давлении. Излучение β проникает гораздо сильнее, а излучение γ обладает наибольшей из всех способностью проникновения. Исследования над действием магнитных и электрических сил на эти три типа излучений показали, что они имеют совершенно различный характер. Беккерель показал, что лучи β отклоняются электрическими и магнитными силами, и направление отклонения показывает, что лучи несут заряд отрицательного электричества. Пользуясь методом, описанным в главе IV, он определил величину e/m, отношение заряда к массе носителей отрицательного электричества; он нашёл, что оно составляет около 10⁷ и что скорость для некоторых лучей больше двух третей скорости света. Таким образом, он доказал, что лучи β состоят из корпускул, движущихся с поразительной скоростью.

    Лучи α далеко не так легко отклоняются, как лучи β, но Резерфорд недавно показал, что они могут отклоняться в направлении, показывающем, что они несут положительный заряд. Он находит, и его измерения были подтверждены Декудром (Des Coudres), что отношение e/m равно 6×10³, ⁷) и скорость этих частиц составляет 2×10⁹ в секунду. Величина e/m показывает, что носители положительного заряда имеют массы, сравнимые с массами обыкновенных атомов: так, для водорода e/m равно 10⁴, а для гелия – 2,5×10³. Необыкновенная скорость, с которою выбрасываются эти частицы, предполагает громадное потребление энергии, к чему мы ниже возвратимся. Один из наиболее интересных выводов из этого факта состоит в том, что величина e/m показывает, что выделяемые атомы не атомы радия, так что радий должен быть соединением, содержащим более лёгкие элементы, или же атом радия распадается на такие элементы. Величина e/m для лучей α, полученная Резерфордом и Декудром, указывает на существование газа, который тяжелее водорода, но легче гелия. Лучи γ, насколько нам известно, не отклоняются ни магнитными ни электрическими силами.

    Радиоактивные вещества имеют большое сходство с веществом, выделяющим вторичные лучи под влиянием лучей Рентгена. Как известно, вторичные лучи содержат лучи типов β и γ, и часть лучей чрезвычайно легко поглощается и проникает в воздух при атмосферном давлении не далее одного миллиметра. Поэтому возможно, что более близкое исследование покажет, что лучи α, т. е. частицы, заряженные положительно, здесь также присутствуют. Эта аналогия поднимает вопрос, не освобождается ли энергия, когда лучи Рентгена попадают на тело. Это, как мы увидим, бывает в радиоактивных веществах, когда энергия, выделяемая излучающими веществами, больше энергии рентгеновых лучей, падающих на них. Этот избыток энергии происходит от изменений, имеющих место в атомах тела, подверженного действию рентгеновых лучей. Этот вопрос заслуживает исследования, так как оно может указать способ действием внешних сил освобождать энергию, заключённую в атоме, что радиоактивные тела делают самопроизвольно.

    Резерфорд открыл, что торий выделяет нечто радиоактивное, увлекаемое воздушными течениями, как будто это газ. Чтобы не предрешать вопроса о физическом состоянии вещества, выделяемого радием, Резерфорд назвал его "эманацией". Эманация может проходить через воду или сильнейшую кислоту и нагреваться до температуры раскалённой платины, не теряя нимало своей радиоактивности. Этой косностью она похожа на газы аргон и гелий, из коих последний почти всегда находится в соединении с торием. Радиоактивность эманации тория весьма непостоянна и падает до половины своей величины почти в одну минуту.

    Супруги Кюри нашли, что радий также выделяет радиоактивную эманацию, которая гораздо устойчивее выделяемой торием, так как она теряет половину своей активности почти в четыре дня.

    По-видимому, с полным основанием можно думать, что эти эманации представляют радиоактивное вещество в газообразном состоянии. Они могут увлекаться воздушными течениями с одного места на другое. Подобно газам они проникают через пористую пробку со скоростью, показывающей, что их плотность очень велика. Они диффундируют постепенно через воздух и другие газы. Коэффициент диффузии эманации радия через воздух был измерен Резерфордом и мисс Брукс (Brooks), которые пришли к заключению, что плотность эманации – около 80. Эманация радия превращена в жидкость Резерфордом и Содди, и я, благодаря любезности проф. Дьюара (Dewar), имел возможность обратить в жидкость радиоактивный газ, полученный из воды глубоких колодцев, очень похожий на эманацию и, вероятно, тождественный с нею. Одним словом, эманации выдерживают всякое испытание, которым можно доказать их газообразное состояние. Правда, они не могут быть открыты ни иными химическими методами ни спектральным анализом, но это лишь потому, что они получаются в крайне малых количествах даже для того, чтобы их можно было открыть спектральным анализом. Этот метод оказывается слишком грубым в сравнении с электрическими методами, которые мы можем применить к радиоактивным веществам. Я думаю, что не будет преувеличением сказать, что электрическим методом с достоверностью можно открыть количество радиоактивного вещества, меньшее одной стотысячной доли наименьшего количества, которое можно открыть спектральным анализом.

    Всякая часть соли радия или тория даст эманацию всё равно, находится ли эта часть на внутренней или внешней стороне соли, но эманация, идущая изнутри соли, не выделяется в воздух, но остаётся заключённой в соли и скопляется там. Когда такая радиоактивная соль разлагается в воде, то сначала развивается большее количество эманации, которая была скрыта в твёрдой соли. Эманацию можно извлечь из воды кипячением или пропусканием воздуха через неё. Скрытую эманацию можно также извлечь из солей в твёрдом виде, нагревая их до высокой температуры.

ИНДУЦИРОВАННАЯ РАДИОАКТИВНОСТЬ. ⁸)

    Резерфорд открыл, что вещества, подверженные действию эманации тория, становятся радиоактивны, а супруги Кюри почти одновременно открыли, что тем же свойством обладает эманация радия. Это явление называется индуцированной радиоактивностью. Количество её не зависит от природы вещества, в котором она индуктируется. Так, бумага становится так же радиоактивна, как металл, в соприкосновении с эманациями тория или радия.

    Индуцированная радиоактивность развивается именно на веществах, заряженных отрицательно. Так, если эманация содержится в замкнутом сосуде, в котором находится отрицательно заряженная проволока, то индуцированная радиоактивность сосредоточивается на этой проволоке и может быть обнаружена на отрицательно заряженных телах, когда она слишком слаба, чтобы быть замеченной на незаряженных поверхностях. Тот факт, что природа индуцированной радиоактивности не зависит от вещества, в котором она индуктируется, указывает на то, что она происходит от радиоактивной материи, которая выделяется из эманации на веществах, к которым она прикасается.

    Дальнейшее подтверждение этого представляет опыт мисс Гэтс (Gates), состоявший в том, что индуктированная на тонкой проволоке радиоактивность выделялась путём накаливания проволоки и осаждалась на поверхности заряженных предметов. Радиоактивность, индуктированная эманацией тория, существенно отличается от индуктированной активности эманации радия. Активность эманации тория в одну минуту падает до половины своей величины, тогда как индуктированная ею радиоактивность требует около одиннадцати часов, чтобы уменьшиться в той же пропорции. Эманация радия, которая гораздо постояннее эманации тория, требуя около четырёх дней для уменьшения на половину, даёт начало гораздо менее постоянной индуктированной радиоактивности: она падает до половины своей величины приблизительно в сорок минут вместо одиннадцати часов, как эманация тория. Эманация актиния сохраняет свою активность лишь несколько секунд, а зависящая от неё индуктированная радиоактивность почти так же постоянна, как активность радия.

    Резерфорд и Содди весьма интересным и важным исследованием показали, что радиоактивность тория вызывается переходом тория в форму, называемую ими ThX, которая может отделяться от остального тория химическим способом. После этого отделения оставшийся торий на некоторое время лишается большей части своей радиоактивности, которая теперь находится в ThX. Радиоактивность тория X медленно убывает, тогда как активность остального тория возрастает, пока не достигнет своей первоначальной величины. В это время радиоактивность ThX исчезает. Время, необходимое для падения радиоактивности ThX до половины первоначальной величины, по определению Резерфорда и Содди, равно времени, необходимому для тория, от которого ThX отделился, чтобы восстановить половину его первоначальной активности. Все эти факты поддерживают взгляд, что радиоактивная часть тория ThX постоянно порождается самым торием; так что, если бы активность ThX была постоянна, то радиоактивность тория должна бы была постоянно возрастать. Но активность ThX постоянно убывает. Это исключает неограниченное возрастание активности смеси. Она достигает постоянной величины, когда возрастание активности, благодаря возникновению нового ThX, уравновесится падением активности наличного количества. Здесь возникает вопрос о том, что делается с ThX и эманацией, когда они потеряют свою радиоактивность. Этот отмирающий ThX, как мы можем его назвать, постоянно собирается в торий. Но так как он потерял свою радиоактивность, то мы располагаем только обыкновенными методами химического анализа. А так как последние почти бесконечно менее чувствительны, чем средства, применяемые нами к радиоактивным веществам, то необходимы почти геологические периоды, чтобы отмирающий ThX скопился в количестве, достаточном для его обнаружения химическим анализом. Возможно, что тщательное исследование минералов, в которых встречаются торий и радий, может дать важные указания. Замечательно, что гелий почти неизменно входит в состав этих минералов.

    Вы, вероятно, заметили, что радиоактивность, обнаруженная Резерфордом и Содди, тесно связана с изменениями, происходящими в радиоактивном веществе. Так, в тории, который известен нам лучше всех, сначала происходит превращение его в торий X, затем превращение последнего в эманацию и вещество, образующее лучи α. Радиоактивность эманации сопровождается дальнейшим превращением, к продуктам которого относится вещество, вызывающее индуктированную радиоактивность.

    По этому воззрению, вещество в радиоактивном состоянии постоянно превращается из одного состояния в другое. Эти превращения могут сопровождаться освобождением энергии, достаточной для пополнения унесённой лучами, выделяемыми радиоактивным веществом. Как велико количество энергии, выделяемой радиоактивными веществами, с очевидностью показывают недавние опыты супругов Кюри с солями радия. Они нашли, что эти соли выделяют столько энергии, что поглощение её самой солью достаточно для поддержания постоянной температуры соли выше температуры воздуха на весьма заметную величину – в одном из их опытов на 1,5°С. Из их измерений следует, что грамм радия выделяет в час энергии, достаточной для того, чтобы нагреть такое же количество воды от точки замерзания до точки кипения. Это развитие теплоты идёт непрерывно и, видимо, не уменьшаясь. Если же только что изложенные нами взгляды верны, то эта энергия возникает от превращения радия в другие формы материи, и её развитие должно прекратиться, когда запас радия истощится; если только этот запас не пополняется постоянным превращением в радий других элементов.

    Мы можем определить приблизительно вероятную долговечность образца радия, соединяя наши результаты, а именно, что грамм радия выделяет 100 калорий в час и что лучи α по Резерфорду представляют частицы, массы которых сравнимы с массой атома водорода, выбрасываемой со скоростью около 2×10⁹ сантиметров в секунду. Ибо допустим, что теплота, измеренная супругами Кюри, происходит от бомбардировки соли радия этими частицами; чтобы получить высший предел долговечности радия, допустим далее, что вся масса радия превращается в частицы а (на самом деле, как мы знаем, кроме частиц α возникает также эманация). Пусть будет x долговечность грамма радия в часах; так как грамм выделяет в час 100 калорий или 4,2×10⁹ эргов, то количество энергии, выделяемой радием в течение его жизни, равно x×4,2×10⁹ эргов. Если N есть число частиц α, выделенных в это время, m – масса одной из них в граммах, v – скорость, то энергия частиц α равна Nmv²/2, но она равна также x×4,2×10⁹ эргам, поэтому Nmv²/2= x×4,2×10⁹. Но, если грамм радия обращается в частицы α, то Nm=1, а по опытам Резерфорда v=2×10⁹. Поэтому x=4×10¹⁸/2×4,2×10⁹=10⁹/2,1 часов или почти 50 000 лет.

    По этому определению следует ожидать, что долговечность известного количества радия измеряется 50000 лет. Этот результат показывает, что мы не можем ожидать, что в течение нескольких месяцев откроем заметные перемены. Грамм радия в течение всей своей жизни выделит около 5×10¹⁰ калорий. Этот результат показывает, что, если эта энергия происходит от превращений в состоянии радия, то энергия, развиваемая при этих превращениях, должна быть гораздо больше энергии, развиваемой при какой-либо известной химической реакции. По принятой нами теории различие между процессами в радии и обыкновенными химическими реакциями состоит в том, что в последних изменения молекулярные, а в радии – атомистические и проявляются в разложении элементов. Пример, данный на стр. 70 показывает, как велико количество энергии, заключенное в атоме, если считать его построенным из корпускул.

    Я думаю, что нам удастся лучше осветить процессы, происходящие в радии, если мы рассмотрим модель атома, описанную на стр. 77 и представляющую случай, когда корпускулы, вращаясь с большой скоростью, устойчивы при известном расположении, которое становится неустойчиво, когда энергия падает ниже известной величины, и заменяется иным расположением. Волчок, вращающийся около вертикальной оси, представляет другую модель того же типа. Он устойчив в вертикальном положении, если кинетическая энергия, зависящая от его вращения, превосходит известную величину. Если эта энергия постепенно убывает и достигает критической величины, то волчок становится неустойчивым и опрокидывается, вызывая значительное количество кинетической энергии.

    Проследим повеление атома этого типа, т. е. атома, который в одной конфигурации равномерного движения устойчив, когда кинетическая энергия корпускул превышает известную величину, но становится неустойчивым и переходит к отличной конфигурации, когда кинетическая энергия падает ниже этой величины. Предположим теперь, что атом сначала обладает запасом кинетической энергии много выше критической величины. Благодаря излучению быстро движущихся корпускул, кинетическая энергия будет убывать; но, пока движение остаётся равномерным, убывание будет чрезвычайно медленно и может длиться тысячи лет, пока энергия приблизится к критической величине. С приближением к этой величине движение будет легко нарушено, и, вероятно, произойдут значительные отклонения от расположения равномерного движения, сопровождаемые возрастающей потерей кинетической энергии через излучение. Теперь атом выделяет гораздо большее число лучей, и кинетическая энергия быстро приближается к критической величине. По достижении этой величины наступает переворот, первоначальное расположение нарушается, потенциальная энергия системы сильно уменьшается, сопровождаясь равным возрастанием кинетической энергии корпускул. Увеличение скорости корпускул может вызвать разрыв атома на две или более систем, соответствующих выделению лучей α и эманации.

    Мы предполагали, что энергия, излучаемая радием и другими радиоактивными веществами, происходит из внутреннего источника, т. е. вследствие изменений в составе атома. Так как изменения этого рода до сих пор не были известны, то желательно исследовать вопрос, из каких других источников может происходить эта энергия. Один источник, который представляется сам собою, лежит вне радия. Можно допустить, что радий получает свою энергию, поглощая известную форму излучения, которая проникает чрез все тела на поверхности земли, но поглощается до известной степени лишь радиоактивными телами. Это излучение должно быть очень пронизывающего характера, так как радий сохраняет свою активность, даже окружённый толстым слоем свинца или помещённый в глубоком погребе. Мы знакомы с лучами Рентгена и лучами самого радия, которые могут вызывать заметные действия после прохождения через несколько дюймов свинца, так что идея о существовании весьма пронизывающей радиации не кажется столь невероятной, как это было несколько лет тому назад. Интересно припомнить, что более ста лет тому назад Лесаж (Le Sage) предполагал весьма пронизывающее излучение, чтобы объяснить тяготение. Лесаж принимал, что вселенная наполнена чрезвычайно малыми частицами, которые движутся с очень большими скоростями. Он назвал их ультрамировыми корпускулами и допускал, что они обладают способностью проникать через такие массы, как солнце или планеты, испытывая лишь небольшое поглощение. Однако, они поглощаются до известной степени и отдают небольшую долю своего движения телам, через которые они проходят. Если бы направление ультрамировых корпускул, проходящих через тело, было распределено равномерно, то движение, сообщённое ими телу, не стремилось бы двигать его в одном направлении более, чем в другом, так что тело А, будучи одиноко в мире и подвержено бомбардировке корпускул Лесажа, оставалось бы в покое. Если же по соседству от А находится другое тело В, то В задержит от А некоторые корпускулы, движущиеся в направлении ВА, так что А не получит столько движения в этом направлении, как оно получило бы, будучи одно в поле; но лишь в последнем случае оно получило бы в этом направлении достаточное количество движения, чтобы уравновесить его. Таким образом, в присутствии B количество движения в противоположной направлении получит перевес, так что А будет двигаться в направлении АВ, т. е. будет притягиваться к В. Максвелл обратил внимание на то, что передача движения корпускулами Лесажа телу, через которое они проходят, должна вызывать потерю кинетической энергии корпускулами; и если бы потеря движения была достаточна для объяснения тяготения, то кинетическая энергия, потерянная ультрамировыми корпускулами, была бы достаточна, чтобы, превращаясь в теплоту, довести тяготеющее тело до белого каления. То обстоятельство, что все тела не находятся в состоянии белого каления, послужило для Максвелла аргументом против теории Лесажа. Однако, нет необходимости предполагать, что энергия корпускул превращается в теплоту; мы можем представить себе, что она превращается в сильно пронизывающее излучение, которое может выделяться из тяготеющего тела. Простое вычисление может показать, что количество кинетической энергии, превращаемой в секунду в одном грамме тяготеющего тела, должно быть неизмеримо больше энергии, выделяемой в то же время одним граммом радия.

    Мы видели в первой главе, что волны электрической и магнитной силы обладают количеством движения в направлении их распространения. Поэтому корпускулы Лесажа можно заменить сильно пронизывающими лучами Рентгена. Последние, будучи поглощены, сообщили бы движение телам, через которые они проходят, и соображения, подобные данным Лесажа, показали бы, что два тела взаимно притягиваются обратно пропорционально квадрату расстояния между ними. Если бы поглощение этих волн на единицу объёма зависело только от плотности и было пропорционально ей, то притяжение между телами было бы прямо пропорционально произведению их масс. Следует заметить, что по этой теории всякие изменения в тяготении распространялись бы со скоростью света, тогда как астрономы, по их мнению, установили, что оно распространяется с гораздо большей скоростью.

    Как в корпускулах Лесажа, так и в лучах Рентгена потеря движения должна сопровождаться потерей энергии; на каждую единицу потерянного движения пришлось бы v единиц потерянной энергии, если v есть скорость света. Если бы эта энергия превратилась в энергию лучей того же типа, как падающие лучи, то небольшое размышление покажет, что поглощение лучей не вызвало бы гравитационного притяжения. Чтобы вызвать такое притяжение, превращённые лучи должны бы были быть более пронизывающего типа, чем первоначальные лучи. Затем, как и в корпускулах Лесажа, поглощение энергии от этих лучей, если они служат причиной тяготения, должно быть огромно, – так велико, что энергия, выделяемая радием, была бы лишь чрезвычайно малой долей энергии, превращённой в радии. По этим соображениям, я думаю, что количество энергии, излучаемой радием, не может быть серьёзным аргументом против допущения, что энергия происходит от внешнего излучения. Основание, заставляющее меня думать, что источник энергии находится в самом атоме радия, а не вне его, состоит в том, что радиоактивность веществ во всех случаях, когда мы могли её локализировать, была преходящим свойством. Ни одно вещество не бывает радиоактивно долгое время. Но можно спросить, как согласовать это утверждение с тем обстоятельством, что торий и радий сохраняют свою активность без заметного уменьшения с течением времени. На это можно ответить, что, как это доказали для тория Резерфорд и Содди, лишь чрезвычайно малая часть массы радиоактивна в данное время, и эта часть теряет свою активность в несколько часов и должна быть заменена новым запасом из нерадиоактивного тория. Все радиоактивные вещества, описанные нами, ThX, эманации тория и радия, вещество, вызывающее индуцированную радиоактивность, активны по большей мере в течение нескольких дней и затем теряют это свойство. Но этого следовало ожидать по теории, принимающей, что источником радиоактивности служит превращение в атоме; но этого нельзя ожидать, если источником является внешнее излучение.

ПРИМЕЧАНИЯ:

*) Уравнение (2) получается, если один из множителей r мы заменим величиной Vt, так как, по определению, r есть путь, пройденный светом за время t. (Прим. ред.)

1) Эта глава в значительной степени устарела: в ней не учтены позднейшие работы как самого Томсона и его учеников, так и Резерфорда. Но несмотря на это, высказанные в ней замечательные мысли ни в коем случае не утратили своего значения. (Прим. ред.).

2) Теперь доказано, что объём положительного ядра значительно меньше объёма корпускулы; таким образом, этот вывод Томсона опровергнут. (Прим. ред.)

3) Это вытекает из предположения, что ядро обладает малой массой и большим объёмом. Теперь нам известно, что ядро атома водорода имеет размер меньший, чем электрон, и массу, в 1800 раз большую. В атоме водорода, как мы теперь предполагаем, только один электрон. Таким образом, в этой части мы далеко ушли вперёд. Необходимо однако отметить, что изложенные в этой главе соображения были первой попыткой подойти к вопросу о строении атома. (Прим. ред.)

4) Мы уже указывали, что для водорода n=1. (Прим. ред.)

5) Хотя происхождение спектральных линий теперь объясняется перескакиванием электрона с одной устойчивой орбиты на другую, согласно теории Бора, однако, вопрос о "возмущении" играет и теперь большую роль в теории спектров. (Прим. ред.)

6) Эта глава была написана в то время, когда учение о радиоактивных процессах только начинало развиваться, так что она имеет теперь только исторический интерес.

7) Теперь доказано, что α-частицы представляют собой атомы гелия, лишённые двух электронов. (Прим. ред.)

8) Индуцированная радиоактивность представляет собой радиоактивные продукты распада эманации. (Прим. ред.).

Дата установки: 14.03.2010
Последнее обновление: 26.11.2012
[вернуться к содержанию сайта]

W