[вернуться к содержанию сайта]

СВЕРХСВЕТ – ЛЕГКО!
(напечатано в журнале "Инженер" №11-12, 2011)

    Ещё со школьной скамьи нас приучают к печальной мысли о невозможности превысить скорость света c=3·10⁸ м/с и достичь далёких звёзд, расположенных за десятки и сотни световых лет от Земли. Такой световой барьер возвела на пути Человека специальная теория относительности (СТО), догмы которой релятивисты охраняют не хуже инквизиторов, спаливших Джордано Бруно за слова о достижимости далёких звёздных миров, отгороженных от Земли, по воззрениям церкви, мнимым барьером "хрустальной сферы". Так и световой барьер релятивистов является скорее мысленным, психологическим, чем физическим. Людям издавна внушали, что они не смогут подняться в небо, обогнать ветер, превысить скорость звука (3·10² м/с), выйти в космос, прорвав гравитационный барьер. Но ещё в прошлом веке были построены аэропланы и дальнобойные баллистические орудия, стреляющие сверхзвуковыми снарядами [1]. Затем появились реактивные самолёты, преодолевшие звуковой барьер и превысившие скорость звука в разы. А в космос вырвались ракеты, летящие со скоростями в десятки километров в секунду. Нет сомнений, что люди однажды преодолеют и световой барьер на звездолётах, летящих в сотни раз быстрее света. Более того, физики уже давно регистрируют сверхсветовые частицы и сами разгоняют электроны до гиперсветовых скоростей, и лишь навязанные теорией относительности мысленные оковы мешают это осознать. Последовательное применение классической физики, развитой в Баллистической Теории Ритца (БТР), позволит сбросить эти оковы и освоить галактические просторы.

    Со сверхзвуковым движением люди впервые столкнулись на примере метеоритов, падающих на Землю из космоса с огромной скоростью. Ударную волну от сверхзвуковых метеоров мы порой слышим как гром, напоминающий выстрел мощного орудия или "взрыв" от сверхзвукового самолёта [1]. Такие небесные звуки-"бронтиды" люди слышали задолго до создания мощной артиллерии и сверхзвуковой авиации. Эти звуки и породили выражение "как гром средь ясного неба". Именно так и прозвучало в середине XX в. сообщение английских физиков об открытии частиц космических лучей, летящих со сверхсветовой скоростью и несущих подтверждение классической физике и баллистической теории [2]. Эти частицы покрывали путь до земных детекторов за время, много меньшее тратимого светом, как предвидели античные атомисты (см. эпиграф), эти предтечи Галилея и Ритца. Некоторые физики сочли открытые частицы мнимыми "тахионами", которые якобы и не пересекали световой барьер, если всегда имели сверхсветовую скорость. А большинство вообще списало всё на ошибки эксперимента, поскольку он противоречил догме СТО. Такое самодурство академиков XX века, не признающих баллистической теории и падения из космоса сверхсветовых частиц, очень напоминает отрицание французскими академиками XVIII века болидов и засвидетельствованного падения с неба камней-метеоритов, противоречивших догме.

    Конечно, наблюдения сверхсветовых частиц редки, и могли б оказаться ошибкой, не будь других фактов, подтвердивших побитие светового рекорда. Так, огромная кинетическая энергия W=mV²/2>>mс² частиц космических лучей свидетельствует, что многие из них летят со сверхсветовой скоростью V>c [3]. Не замечают этого исследователи, поскольку вместо классической применяют нелепую релятивистскую формулу W=(γ–1)mс², где даже беспредельный рост энергии частицы W от увеличения гамма-фактора γ=1/(1–v²/c²)^1/2 сохраняет скорость на уровне v≈c. Итак, сверхсветовые частицы давно обнаружены, но математическая обработка по формулам СТО мешает осознанию этого факта. Все эффекты сверхсветовой скорости V релятивисты показывают в кривом зеркале своих формул как релятивистские эффекты от приближения v к скорости света c. Такие "ультрарелятивистские" частицы с энергией W>>mс² правильней называть сверхсветовыми (V>c) и даже гиперсветовыми (V>>c).

    Вывести релятивистов на чистую воду можно лишь прямым замером скорости частиц пролётным методом, по школьной формуле V=L/T, где L – это путь, пройденный частицей за время T (рис. 1). Именно так открыли сверхсветовые частицы англичане. Также в физике космических лучей давно известно, что быстрые частицы, например мюоны, за время своего распада T проходят в атмосфере Земли путь L раз в 10 больший пути, проходимого за это время светом V=L/T>c. Ещё А.А. Денисов верно истолковал это как регистрацию сверхсветовых частиц. Но и здесь релятивисты перевернули всё с ног на голову: увеличение пробега L=VT энергичных частиц они объяснили не ростом скорости до V>c, а ростом времени жизни T по релятивистской формуле T'=γT, отчего путь рос как L=vγT, при их скорости v≈c. Всё представили так, словно открытие длиннопробежных частиц подтвердило релятивистский эффект растяжения времени (у мюонов в 10 раз), хотя реально открыли обычное удлинение пути L=VT быстрых частиц, имеющих скорость V в γ≈10 раз выше скорости света c.

    Эффект растяжения времени подтверждался якобы и количественно: находя по измеренным энергиям частиц W их скорости v и гамма-фактор γ, получали именно то удлинение пути L=vγT, какое наблюдалось. Но и здесь релятивисты обманули, ибо все детекторы, якобы меряющие энергию частиц W=mV²/2, реально работают на измерении импульса частиц p=mV. Так сделали, чтобы согласовать релятивистские формулы для энергии W=(γ–1)mс² и импульса p=mγv, который при высоких скоростях v≈c пропорционален W≈mγс²≈pс, вопреки классической механике, где W=p²/2m. Поэтому прямые и независимые замеры W и p у сверхэнергичных частиц выявят ошибочность СТО. Выражая в формуле L=vγT величину vγ не через истинную энергию, а через замеренную величину W=pс=mvγс, получают L=Tp/m. Лишь при таком ложном значении энергии релятивисты получают согласное с опытом и с классической теорией удлинение пути L=Tp/m=VT, где V>c. То есть и здесь релятивисты приходят к верному результату лишь потому, что одна ошибка у них компенсирует другую.

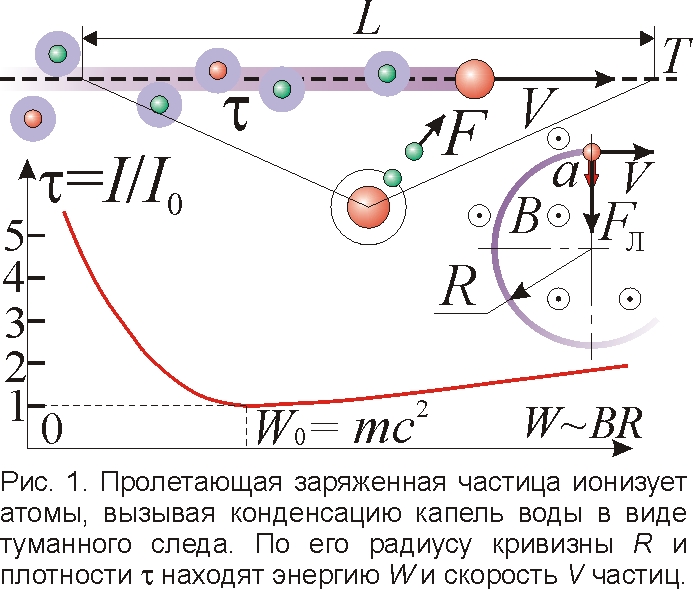
    Итак, именно релятивистский анализ мешает физикам верно оценить скорость и энергию частиц. Так, энергию частиц космических лучей ищут с помощью камеры Вильсона. Заряженная частица, пролетая через камеру, оставляет в ней видимый трек – след из капелек воды (рис. 1), подобно реактивному самолёту, за которым тянется инверсионный след из атмосферной влаги. Если этот шлейф загибается дугой радиуса R, то, даже не видя самолёта, можно найти силу F=ma, заставляющую его лететь по кругу с ускорением a=V²/R. Аналогично, измерив радиус R трека частицы с зарядом e и массой m, находят действующую на неё в магнитном поле B силу Лоренца F_Л=eVB=mV²/R. Отсюда, по классической механике скорость частицы V=eBR/m, её импульс p=mV=eBR, а энергия W=mV²/2=(eBR)²/2m. Такой анализ сразу выявляет у многих частиц космических лучей сверхсветовые скорости V=eBR/m>c. Но по СТО те же значения e, B, R, m говорят якобы о куда меньших скоростях и энергиях, ибо измеренный в камере Вильсона огромный импульс p=mV=eBR обусловлен будто бы не ростом скорости V выше светового барьера, а релятивистским нарастанием массы m в γ раз, так что p=mγv. Отсюда релятивисты находят заниженную в γ раз скорость v≈c и энергию W=pс=eBRc≈(eBR)²/γm, вместо классического W=p²/2m=(eBR)²/2m.

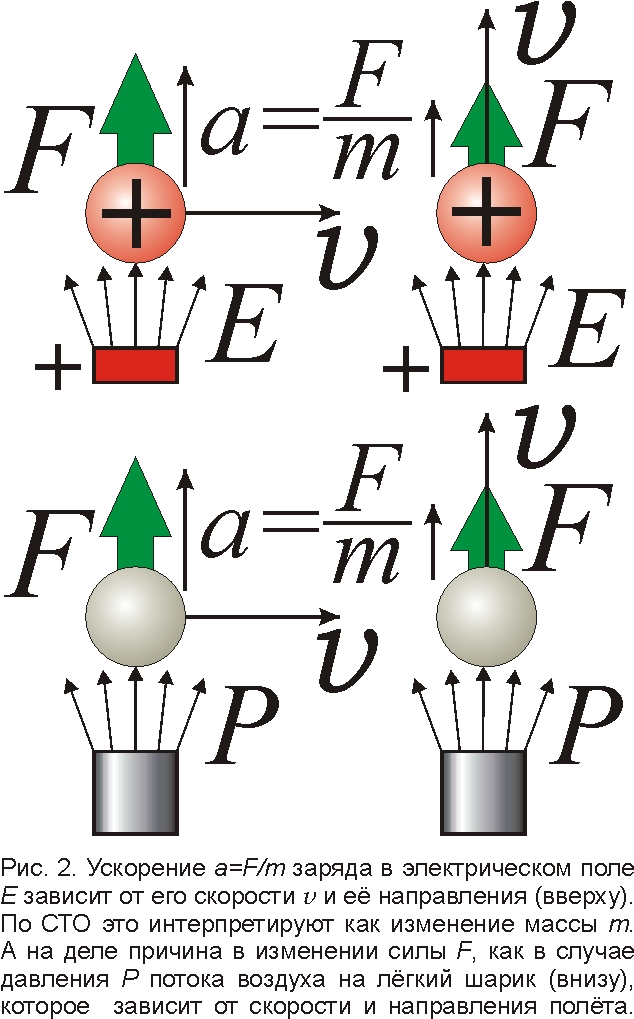
    Сами физики-ядерщики видят несуразность растущей массы [4]. Если масса m – это коэффициент между силой F и вызванным ею ускорением a=F/m, то по СТО масса зависела бы не только от величины, но и от направления скорости по отношению к силе F, словно масса тел неоднозначна (рис. 2)! Это доказывает, что реально зависимость ускорения a=F/m от скорости заряда вызвана изменением не массы, а силы, как следует из теории Ритца [5, 6]. В электродинамике Ритца воздействие на заряд вызвано ударами потока частиц-реонов, поэтому сила давления этого потока и ускорение a=F/m зависят и от скорости, и от направления полёта заряда. Аналогично в аэродинамике сила F давления потока (атомов воздуха) на крыло самолёта и его ускорение a=F/m зависят от скорости и направления движения самолёта (от угла атаки). Не появись законы аэродинамики до Эйнштейна, пожалуй, он и там бы выдумал переменную массу самолёта при постоянной силе давления. А релятивисты утверждали бы (как делают в отношении ускорителей и атомных станций), что самолёты работают только по формулам СТО, что масса самолёта бесконечно нарастает с приближением его скорости к звуковой (к скорости атомов воздуха). Они бы ввели запрет на превышение скорости звука, и люди, не зная сверхзвуковых самолётов, летали б на уродливых горбовидных "этажерках" конструкции Эйнштейна (оказавшейся малоэффективной и неустойчивой [7]). Подобная ситуация ныне в электродинамике и физике ускорителей. И даже специалисты по физике высоких энергий, например Л.Б. Окунь, пишут, что неверно говорить о нарастании массы частиц, разгоняемых ускорителем: растёт лишь импульс частиц [4]. Но раз масса m не меняется, то рост импульса p=mV вызван ростом скорости, вплоть до значений V>>c!

    В камере Вильсона можно определить скорость частицы и по плотности τ её следа, пропорциональной количеству капель, то есть концентрации I ионов, на которых оседает влага (рис. 1). Заряженная частица, проносясь мимо нейтральных атомов, ионизует их, отрывая электроны, словно несущийся автомобиль, взметающий брызги воды, шлейф пыли, оторвав её от земли. Количество возникших ионов пропорционально квадрату импульса p=FT, сообщённого электрону пролетевшей частицей, где F – кулонова сила, T=L/V – время её эффективного воздействия на отрезке пути L возле атома [8]. Ионизация I и плотность следа τ=I/I₀ должны снижаться при увеличении скорости V частицы, ввиду снижения T~1/V. Казалось бы, неограниченный рост скорости V снижал бы плотность следа τ~p²~F²/V² до нуля. А на деле ионизация I падает до фиксированного значения I₀, после чего τ=I/I₀ почти не меняется. Это якобы доказывает, что скорость V перестаёт расти, достигнув скорости света c [9]. При этом забывают, что с приближением V к c уже заметно меняется сила F, растущая пропорционально (1+V²/2с²) [5, 6, 8], отчего плотность следа τ~F²/V² при V>c перестаёт убывать и даже слегка нарастает (так и машина при разгоне поднимает всё больше брызг, пыли). Если в камере Вильсона скорость нельзя узнать напрямую, по формуле V=L/T, то в искровой камере [10], где ионизационный след от пролетевшей частицы вызывает искровые пробои между рядами электродов, скорость можно измерить по времени запаздывания T импульсов от электродов, разнесённых на расстояние L. Отметим, что на графиках зависимости ионизации от энергии частицы часто вместо энергии W ставят магнитную жёсткость BR трековой камеры [9], прямо пропорциональную не энергии W=(eBR)²/2m, а импульсу p=eBR и скорости.

    То есть во всех случаях меряют не энергию, а импульс p частицы, а по нему, на основе формул СТО, определяют энергию ультрарелятивистских частиц как W=pс, вопреки классической формуле W=p²/2m. Если теория относительности ложна, то почему физики не заметили этого, измерив энергию напрямую? Оказывается, заметили, хотя бы при замерах энергий частиц от радиоактивного распада калориметрическим методом, то есть по температуре нагрева тела, поглощающего все излучения и частицы. Давно открыто, что энергия, выделяемая при β-распаде, ниже теоретической [11], но сочли, что недостающую энергию уносит гипотетическое нейтрино (в чём многие сомневаются). Да и другие замеры энергий ядерных реакций выявляли нестыковки (достигающие десятков процентов) разных методов и теоретических оценок. А причина ошибок – в формулах СТО и ложных оценках энергий по ним.

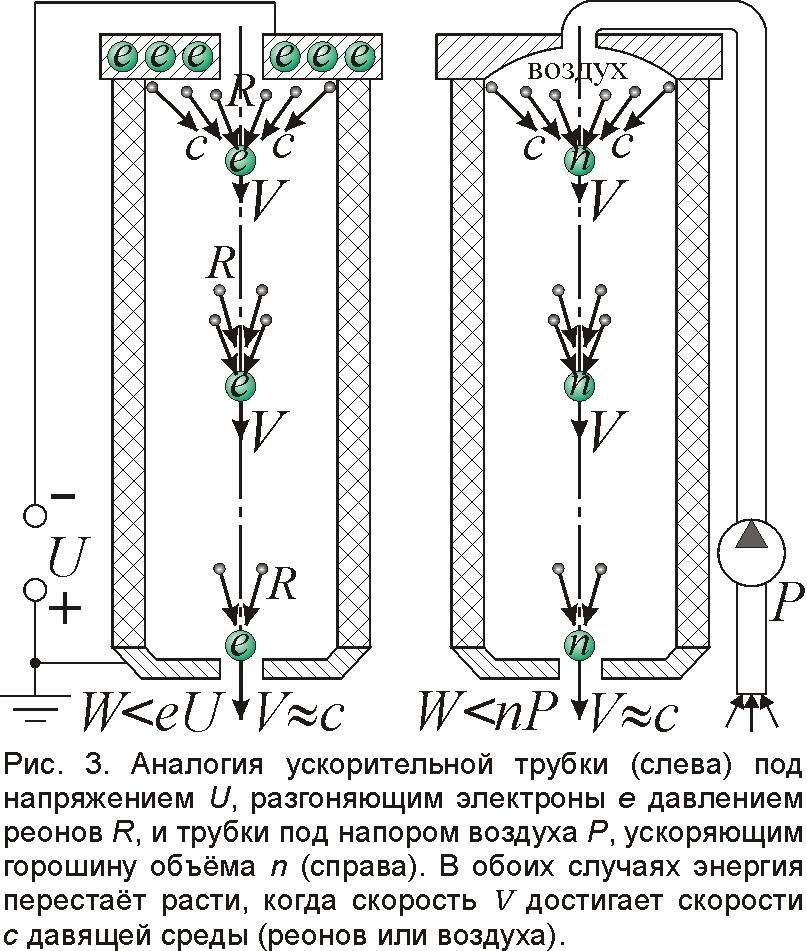
    Казалось бы, в ускорителях прямого действия, устроенных наподобие электронной пушки телевизора (рис. 3), энергию электронов можно найти напрямую как W=eU, по известной разности потенциалов U между электродами ускорительной трубки [12]. Когда электрон с зарядом e=1,6·10^–19 Кл проходит разность потенциалов U=1 вольт (1 В), он набирает энергию W=eU=1 электронвольт (1 эВ=1,6·10^–19 Дж), а при U=1 мегавольт (МВ), он накопит энергию W=eU=1 мегаэлектронвольт (1 МэВ). Но так однозначно энергия частицы и потенциал связаны лишь в электродинамике Максвелла, где электрическая сила не зависит от взаимного движения зарядов (пренебрежение этой зависимостью и привело в начале XX века к нестыковкам, породив теорию относительности [5, 6]). А по теории Ритца величина силы зависит от скорости электрона, раз его ускоряют толкающие сзади реоны R, вылетающие из электрода со скоростью света (то есть ускорительная трубка, электронная пушка аналогичны трубке для стрельбы горохом и артиллерийской пушке, где снаряды разгоняет давление газа – удары атомов). По мере роста скорости электрона разгоняющая сила давления реонов падает: реонам приходится догонять электрон, ударяя с меньшей скоростью и частотой. А при разгоне электрона до скорости света c воздействие падает до нуля. Так и сила давления ветра (ударов атомов воздуха), толкающая воздушный шар, падает до нуля при разгоне шара до скорости ветра: быстрее шар уже не летит. Выходит, энергию электрона можно искать как W=eU лишь на малых скоростях V<<c (так и энергия, набранная шариком в трубе с перепадом давлений P, пропорциональна ему, лишь пока скорость шарика много меньше скорости ветра от этого напора P). Если же скорость электрона в ускорительной трубке приблизится к скорости света (W порядка W₀=mc²=0,5 МэВ), то W<eU, раз W зависит от скорости электрона, а не только от U. Не потому ли ускорительные трубки разгоняют электроны лишь до энергий W порядка 1 МэВ, тогда как протоны, имея при той же энергии скорость V<<c, разгоняются уже до десятков МэВ? А если энергия электронов, измеренная релятивистами по методу импульса, и совпадает с расчётной величиной W=eU, то лишь потому, что оба значения отличаются от истинного: одна ошибка компенсирует другую.

    Упомянув об ускорителях, отметим, что увеличение длин пробега L=VT энергичных частиц до значений L>cT (т.е. V>c) было открыто не только у космических лучей, но и у частиц, разогнанных ускорителями [13]. То есть физики, сами того не ведая, давно создают сверхсветовые частицы, преодолевая световой барьер. Это подтверждают и энергии частиц. Так, на резонансных ускорителях, в отличие от ускорительных трубок, уже давно получены электроны с энергией W порядка нескольких ГэВ. Если учесть, что энергия W=mV²/2, при которой электрон обладает световой скоростью V≈c, составляет порядка W₀=mc²=0,5 МэВ (её называют "энергией покоя"), то электроны с энергией в ГэВ=1000 МэВ обладают гиперсветовыми скоростями. Давно получены и сверхсветовые протоны. Не замечают физики этих гигантских скоростей опять же лишь от применения формулы СТО для энергии W. Если б кто-то измерил скорость частиц V=L/T напрямую, то результат ошеломил бы всех.

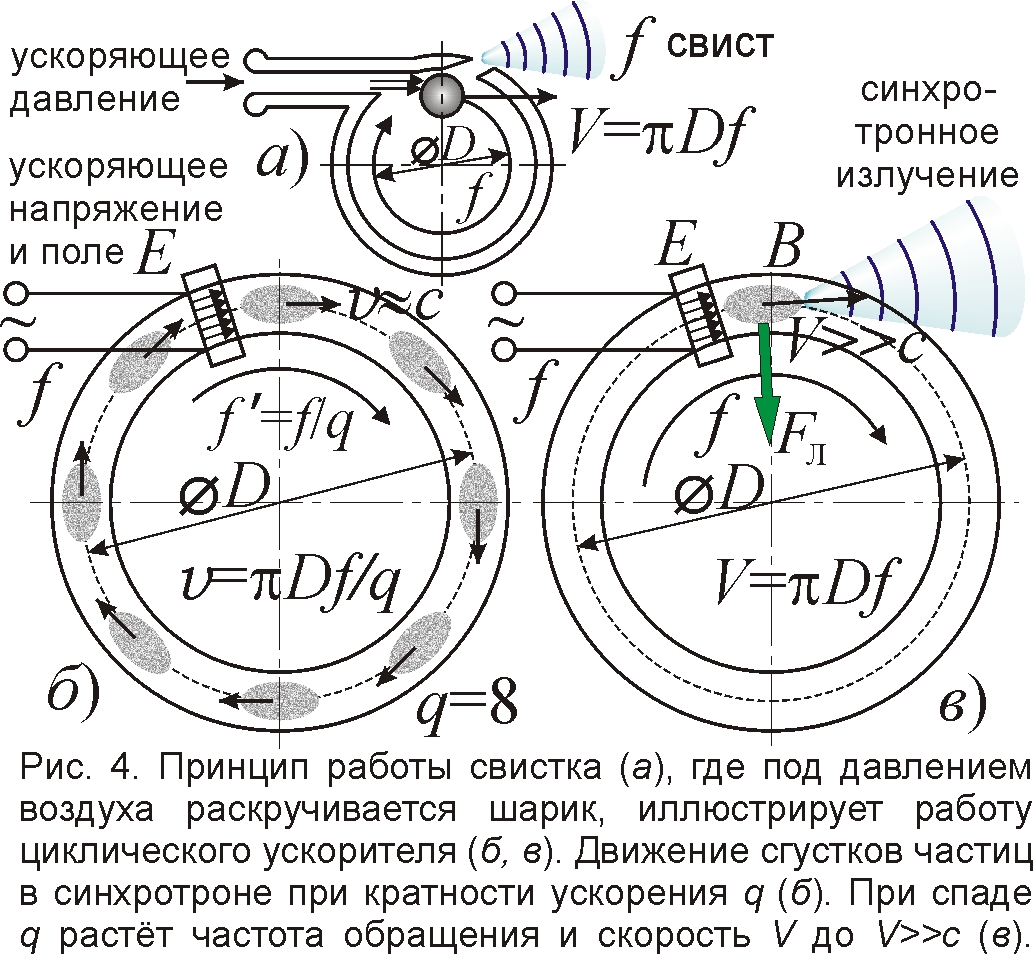
    Такую оценку легко сделать для циклических ускорителей, устроенных наподобие милицейского свистка, где шарик закручивается под давлением струи воздуха, и с каждым оборотом всё больше ускоряется, когда в неё попадает (рис. 4). Так и в циклическом ускорителе летящие по кругу частицы разгоняются "давлением" электрического поля E в ускоряющем промежутке, куда частицы попадают каждый оборот и получают новую порцию энергии. Поле E циклично меняется, и частицы ускоряются лишь в случае резонанса, когда частота колебаний ускоряющего поля совпадает с частотой обращения частиц по кольцу ускорителя. Аналогично, для разгона качелей, к ним надо периодично прикладывать силу с частотой равной частоте качаний, иначе разгон неэффективен. Так и ускоритель разгоняет лишь резонансные частицы, облетающие кольцо ускорителя диаметром D за один период T колебаний ускоряющего поля. Отсюда скорость частиц V=L/T=πD/T=πDf, где f – частота колебаний ускоряющего поля (так и скорость шарика в свистке V=πDf, где D – диаметр свистка, а f – частота издаваемого им свиста, то есть колебаний ускоряющего давления, равная частоте обращения шарика, рис. 4). Раз для ускорения применяют высокочастотные поля f=3–30 МГц, а диаметры D синхротронов достигают сотен метров, то ускоренные ими электроны получают скорости V=πDf=10¹⁰ м/с, что в десятки раз больше скорости света c=3·10⁸ м/с [3]. Это согласуется со значением скорости, найденным по энергии электронов W=mV²/2. Сверхсветовые рекорды ускорителей подтверждает и А.В. Мамаев (см. www.acmephysics.narod.ru).

    Однако релятивисты, применяя формулы СТО, продолжают считать скорость электронов v≈c. А чтобы примирить с этой скоростью гигантские значения V=πDf, предполагают, что частицы крутятся в ускорителе не с частотой ускоряющего поля f, а с частотой f'=f/q, в целое число q раз меньшей, где q назвали "кратностью ускорения". Тогда в q раз меньше и скорость частиц v=πDf'≈c. Измеренная частота прихода сгустков (банчей) частиц равна частоте ускоряющего поля f, но, полагая, что по кольцу циркулирует не один, а q сгустков, с частотой f регистрируют приход якобы не одного, а разных сгустков, пролетающих мимо детектора. Формирование вдоль кольца ускорителя многих сгустков, крутящихся с меньшей частотой, в принципе, возможно, однако энергии частиц в таких сгустках будут пропорционально ниже. Ясно, что гипотеза о кратности ускорения – это лишь уловка, ведь никто не доказал, что в случае высокоэнергичных частиц детектор регистрирует разные сгустки.

    Спорность гипотезы многих сгустков следует из того, что до высоких энергий частицы разгоняют лишь на высоких q. Это доказывает, что q – это "кратность ускорения" в ином смысле, говорящем во сколько раз скорость частицы V=πDf=πDf'q=cq превышает световую (может, поэтому так и назвали q?). И впрямь, почему никто не может ускорить электроны до энергий заметно выше 1 МэВ, а протоны – выше 1 ГэВ (когда W>W₀) при q=1, дабы частота обращения частиц совпала с частотой f ускоряющего поля, сниженной до f'=c/πD? Просто на таких частотах разгон до высоких энергий невозможен! Ведь при энергиях W>W₀ частицы сверхсветовые, V=πDf>c, и для разгона нужны частоты f в q=V/c раз большие, чем f'=c/πD.

    Итак, при высоких скоростях частиц в синхротроне остаётся обычно один сгусток, циркулирующий с частотой f колебаний ускоряющего поля. Но при меньших энергиях в ускорителе и впрямь может крутиться много сгустков, число которых q сокращается при разгоне частиц, поскольку всё меньше сгустков попадает в фазу с ускоряющим полем. Это объясняет, почему в синхротронах, где диаметр D орбиты электронов и частота f ускоряющего поля постоянны, скорость электронов V=πDf/q всё же нарастает, по мере снижения q от начального значения до единицы. А релятивисты ошибочно считают, что q не меняется при ускорении электрона, отчего он всегда движется с примерно одинаковой скоростью v=πDf/q≈c. То, что реально скорость электрона растёт, многократно превосходя c, доказывает и величина магнитного поля B, которое по мере разгона наращивают, чтобы удержать электрон на круговой орбите радиуса R=D/2 силой Лоренца F_Л=eVB=ma=mV²/R (рис. 4). Именно многократный рост скорости V заставляет пропорционально наращивать магнитное поле B=mV/eR.

    А по СТО скорость электронов в синхротроне почти не меняется: V≈c. То есть, вроде бы и поле B=mV/eR увеличивать незачем. И всё же релятивисты заявляют, что поле надо наращивать, поскольку якобы растёт масса m частицы. Лишь поэтому они получают из теоретических расчётов то же верное значение B, как в классическом случае, а утверждение релятивистов, будто ускорители работают лишь по формулам теории относительности,– это миф. Ведь классическая физика предсказывает те же самые значения поля B=mV/eR=p/eR для разгона электронов до "энергий" W=pс=mVс и импульсов p=mV. Если теория относительности рост энергий и импульсов электронов объясняет нелепым увеличением их массы m, то классическая теория – увеличением скорости V, естественным для разгоняемых частиц. А в СТО термин "ускоритель" теряет смысл, раз в ней скорость частиц V≈c перестаёт расти, приблизившись к скорости света. Так, в синхротроне скорости электронов за всё время разгона по СТО "почти не меняются", несмотря на рост их энергий и импульсов в сотни раз.

    Релятивисты обычно "доказывают" увеличение массы на примере первого циклического ускорителя – циклотрона, разгоняющего протоны при постоянной частоте ускоряющего поля (рис. 5). Считали, что по классической теории циклотрон может разогнать протоны до огромных энергий, ведь частицы в однородном поле B, летя по спирали и наращивая радиус орбиты R, должны всегда обращаться с одной частотой f=V/2πR, где V/R=eB/m. То есть протон, крутясь с постоянной частотой f=eB/2πm, всегда пребывал бы в резонансе с ускоряющим полем частоты f, а его энергия и скорость V=2πRf неуклонно бы росли при расширении витков орбиты R. Реально же при разгоне протон выходит из резонанса, отчего его энергия в циклотроне ограничена на уровне 10–20 МэВ. Релятивисты объясняют это ростом массы m разгоняемого протона, ведущим к спаду частоты обращения f=eB/2πm: протон выходит из резонанса с ускоряющим полем и перестаёт разгоняться. Но это – ещё один нелепый миф релятивистов, ведь главная причина снижения частоты f=eB/2πm и выхода из резонанса – это спад магнитного поля к краям магнита по закону B=B₀(1–hR²) [14]. Поле B циклотрона делают неоднородным, дабы обеспечить устойчивость орбит протонных сгустков, а константу h так и называют: "относительный спад поля". Именно спад поля на несколько процентов, а не мифический рост массы m, нарушает условие резонанса, ограничивая энергию протонов [12].

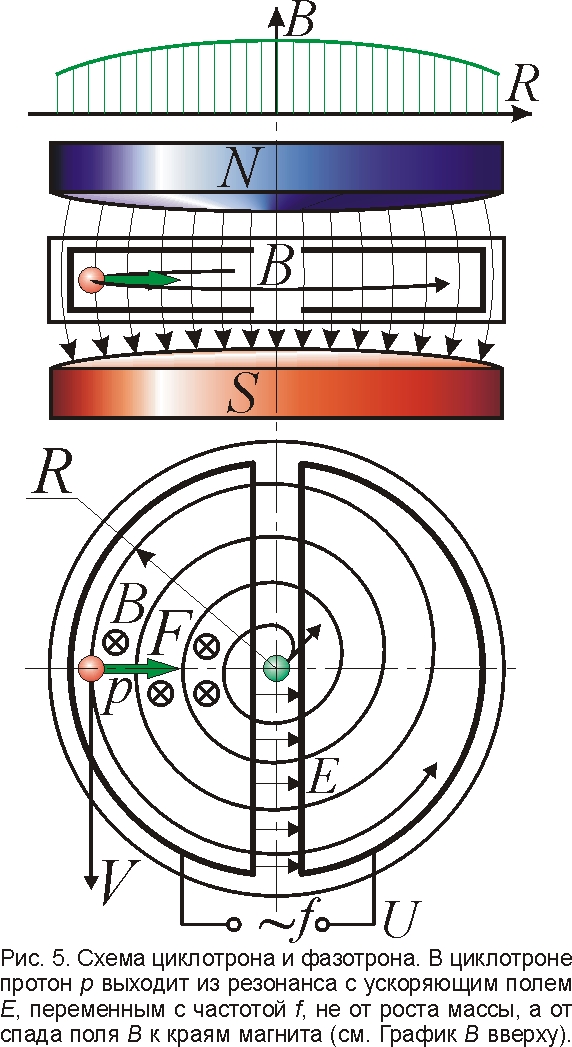
    В фазотронах – ускорителях типа циклотронов, но с убывающей во времени частотой f ускоряющего поля, этим компенсируют в первую очередь спад магнитного поля B при увеличении радиуса R орбиты протона, а не "релятивистский рост его массы". При увеличении R в десятки раз поле в фазотроне уменьшается на проценты по закону B=B₀(R₀/R)ⁿ (n~0,1 – показатель спада магнитного поля [14]). И, дабы протоны двигались в фазе с ускоряющим полем, его частоту снижают на те же проценты по закону f=eB/2πm [12]. В итоге протоны не выпадают из резонанса с ускоряющим полем и разгоняются уже до энергий, достигающих 1 ГэВ. Конечно, при расчёте фазотронов учитывают и релятивистские поправки к частоте, но, во-первых, их роль слабее, а во-вторых, не исключено, что эти ложные поправки к частоте f как раз и ограничивают энергии протонов в фазотронах на характерном уровне в 1 ГэВ. Ведь именно при такой энергии W≈mc² скорость протонов достигает световой, то есть релятивистские поправки к частоте становятся велики, и вместо того, чтобы поддерживать резонанс, на деле выводят из него. Эти ложные поправки сказываются и при меньших энергиях. Но, пока они малы, их компенсирует открытый Векслером принцип автофазировки, автоматически удерживающий сгусток в фазе с ускоряющим полем [12]. К тому же в резонанс с частотой f, заниженной по вине релятивистов, просто попадают и ускоряются частицы, летящие по орбитам большего радиуса, где поле B и частота обращения протонов eB/2πm пропорционально ниже. Без этого фазотроны не разогнали бы протоны даже до энергий в 1 ГэВ. В любом случае, расчёт частоты ускоряющего поля по классическим формулам повысил бы эффективность фазотронов, которые стали б выдавать протоны более высоких энергий и токов. Итак, если отклонения частоты от классической f=eB/2πm и возникают, то вызваны они не ростом массы m, а неучтённым спадом магнитной силы и поля B при разгоне частицы [5, 6].

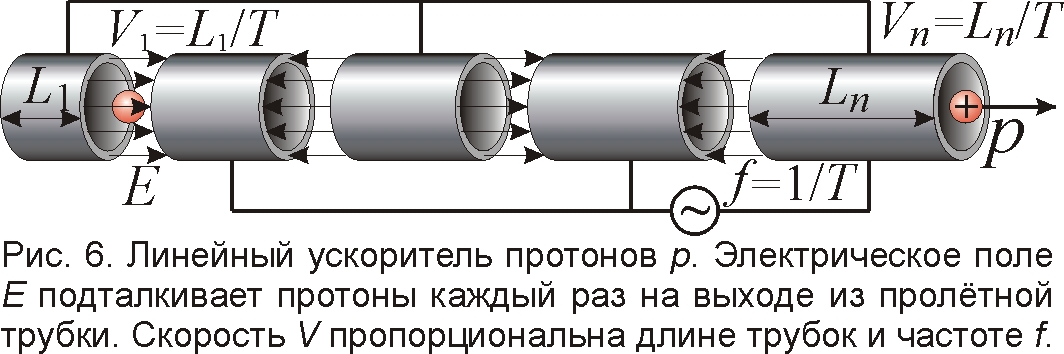
    Кроме циклических ускорителей есть линейные. Казалось бы, в них скорость V частиц должны знать точно, раз по значению V подбирают длины выстроенных в линию дрейфовых трубок, дабы частица пролетала каждую трубку за полупериод T/2 колебаний приложенного к ним напряжения (рис. 6). Тогда частица всякий раз попадает в зазор меж трубками, когда их электрическое поле E ускоряет частицы [11, 12]. Поэтому скорость частиц на выходе из ускорителя задана отношением V=2L/T удвоенной длины L крайних трубок ускорителя к периоду T напряжения и поля. А эта, найденная пролётным методом скорость, всегда ниже скорости света. Впрочем, линейные ускорители этого типа применяют лишь для разгона тяжёлых частиц – протонов, ядер, ионов, не превышающих скорость света, судя по их энергии.

    Так, протон обретает сверхсветовую скорость лишь при кинетической энергии W=mV²/2 порядка его "энергии покоя" W_0p=mc²=938 МэВ≈1 ГэВ. А мощнейшие линейные ускорители разгоняют протоны максимум до энергий в сотни МэВ, то есть в доли ГэВ. Значит, протоны летят там с досветовой скоростью. Поэтому здесь нет сильных расхождений с классической механикой, и ускоритель работает. Зато с позиций СТО непонятно, почему протоны не удаётся разогнать до более высоких энергий, хотя по идее здесь нет ограничений: достаточно удлинить ускоритель, добавив новые трубки, и протоны можно будет разгонять неограниченно [12]. А проблема как раз в том, что ускоритель становится уже не эффективен, раз длины L последних трубок подбирают по СТО из условия 2L/T≈с, хотя для сверхсветовых частиц нужно 2L/T=V>с. То есть из-за оценок скорости по формулам СТО получают заниженные значения длин трубок, из-за чего летящие частицы выходят из резонанса с ускоряющим полем и далее не разгоняются. На малых скоростях ложное определение скорости по СТО (выводы которой в пределах процентов совпадают с классической механикой) слабо сказывается, и лишь снижает эффективность ускорителя. А для более высоких скоростей и энергий протонов линейные ускорители, рассчитанные по СТО, уже непригодны, и нужно вести расчёт по классическим формулам, применяя удлинённые трубки. Вот почему для разгона протонов до энергий больше 1 ГэВ применяют уже не линейные, а циклические ускорители, где обманным путём занижают истинную скорость протонов в q раз.

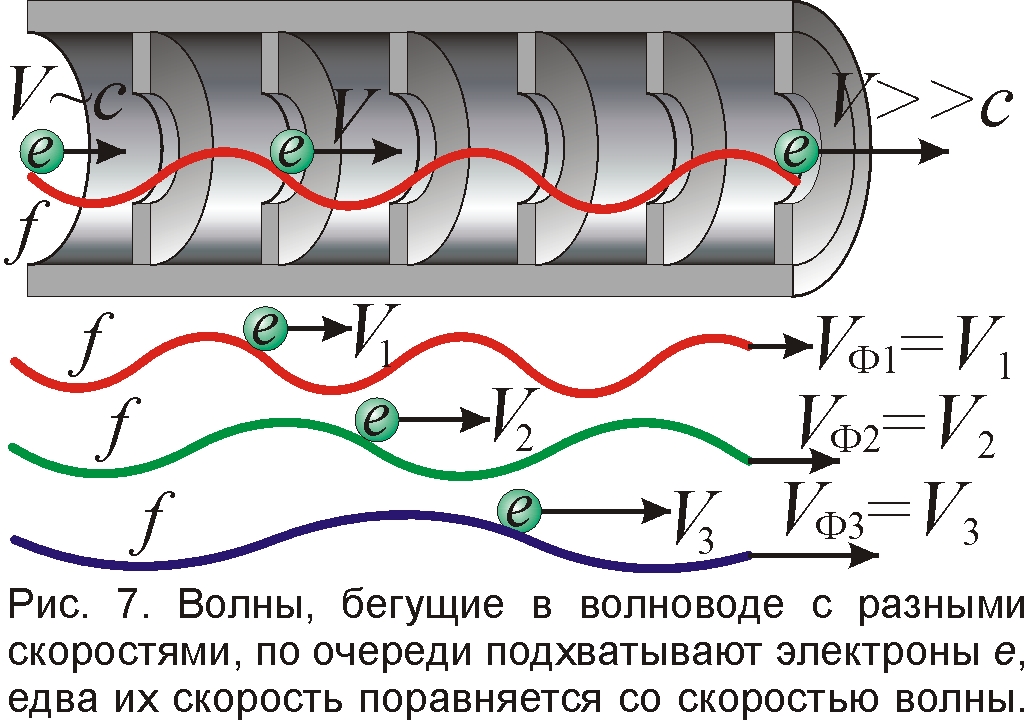
    Вот и для разгона электронов до энергий в сотни МэВ (то есть до сверхсветовых скоростей), эти трубчатые ускорители оказались непригодны. Поэтому используют линейные ускорители иного типа, где электроны разгоняет продольное поле электромагнитной волны, бегущей в волноводе: она несёт электроны, словно морская волна, выносящая на своём гребне сёрфингистов (рис. 7). Чтобы разгон был эффективен, скорость электронов должна совпадать с фазовой скоростью волны, бегущей в волноводе. Но ведь скорость волн в полых волноводах выше скорости света [15]. Значит, и скорость электронов сверхсветовая! Это противоречие с теорией относительности пытались обойти, делая внутри волновода рёбра, диафрагмы для снижения фазовой скорости V_Ф основной волны до скорости света [12]. Но где гарантия, что снижение V_Ф столь значительно? Ведь напрямую скорость электронов и несущей их волны никто не измерял. К тому же в волноводах на заданной частоте f=1/T возбуждается не только основная волна, но и высшие типы волн (высшие моды), имеющие более высокие фазовые скорости, вплоть до бесконечных [15]. И никто не доказал, что в волноводе разгон электронов производит основная волна, а не высшие типы волн, сообщающие свою сверхсветовую скорость электронам. По мере разгона электронов, эти высшие волны, независимо бегущие по волноводу, подхватывают по эстафете электронный сгусток, едва его скорость сравнивается с фазовой скоростью более быстрой волны. Банч электронов, словно бочка, скачет с волны на волну, обретая всё более высокую сверхсветовую скорость.

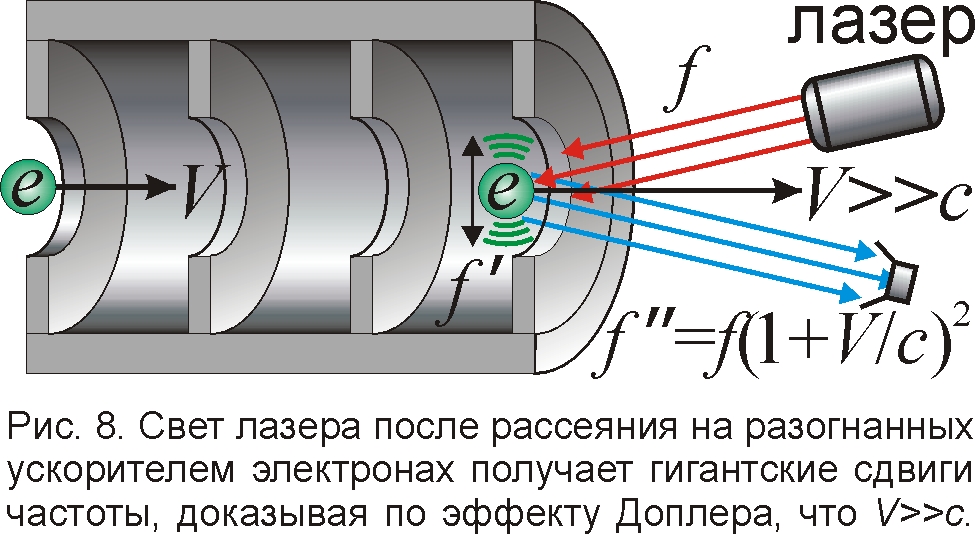
    Скорость частиц в линейном ускорителе легко измерить по эффекту Доплера, направив на пучок ускоренных электронов луч лазера и замерив сдвиг частоты отражённого электронами света (рис. 8). Именно так автоинспекторы определяют скорость движущегося автомобиля посредством "радара". Если луч лазера частоты f направить навстречу пучку, то электроны, летящие со скоростью V, воспримут его по эффекту Доплера как свет частоты f'=f(1+V/c). То есть лазерный луч будет вызывать колебания электронов на большей частоте f', на ней электроны и станут переизлучать свет, отражая его, словно электронное зеркало. Но поскольку электроны-излучатели движутся, то неподвижный наблюдатель опять от эффекта Доплера воспримет их свет как излучение частоты f''=f'(1+V/c)=f(1+V/c)². И точно, в экспериментах по отражению лазерного света частоты f≈10¹⁵ Гц от электронов, разогнанных линейным ускорителем SLAC, возникает гамма-излучение с частотой f''≈10²⁵ Гц [16]. Отсюда (1+V/c)²=f''/f≈10¹⁰. Выходит, найденная по Доплеру скорость электронов достигает величины V≈10⁵c, превышая световую в 100 тысяч раз! Это вполне согласуется с измеренной по импульсу "энергией" электронов W=pс=mVc=50 ГэВ. Если учесть, что энергия электронов на световой скорости W₀≈mc²=0,5 МэВ, то при W=mVc=50 ГэВ их скорость V≈с(W/W₀)=10⁵c. Итак, снова независимые оценки скорости разными методами привели к одному результату, подтвердившему классическую механику, а также реальность сверхсветовых частиц.

    Однако релятивисты и здесь не замечают промахов СТО, условившись считать доплеровское изменение частоты по релятивистской формуле, где всё перевёрнуто с ног на голову: f'=f/(1–v/c), и гигантский рост частоты происходит даже при скорости v≈c. Хотя по Доплеру V>>c, ибо рост частоты света обусловлен уменьшением дистанции (где не должны скапливаться волны), а потому пропорционален скорости сближения источника или зеркала. То есть релятивисты закрывают глаза на выявленное радарным методом превышение частицами дозволенной скорости света и нарушение правил движения СТО, совсем как иные недобросовестные автоинспекторы "не замечают" превышения скорости за условленную мзду. Кроме того, при больших скоростях в формуле эффекта Доплера релятивисты учитывают упомянутый эффект растяжения времени T'=γT, и пишут формулу в виде f'=f/γ(1–v/c)=f(1–v²/c²)^1/2/(1–v/c). Если источник излучает под углом φ к направлению движения, то изменение частоты f'=f(1–v²/c²)^1/2/(1–cosφ v/c) [17]. Но объяснение сильного роста частоты по этой релятивистской формуле ничего не стоит, пока она не доказана строго.

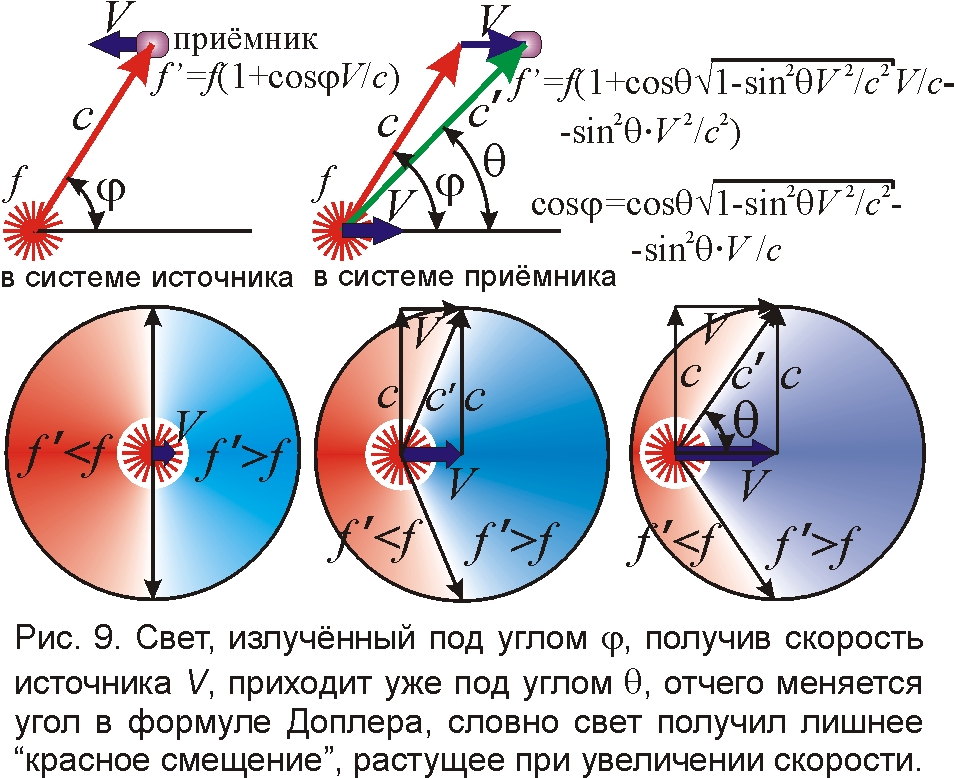
    Релятивисты уверяют, что её доказывает поперечный эффект Доплера, где излучение испытывает красное смещение (снижение частоты f'<f), когда идёт от источника под углом 90º (поперёк его движения). А классическая формула Доплера f'=f(1+cosφV/c) будто бы не даёт сдвига частоты: f'=f. Но, применяя классическую формулу, надо помнить, что в ней угол φ – это не угол θ, под которым принимают излучение, а угол, под которым источник его испускает (рис. 9). Ведь источник по баллистическому принципу сообщает свою скорость свету, и эти углы разнятся на угол аберрации [17]. Чтобы излучение пришло под углом θ=90º, оно должно вылететь под углом φ>90º, так что cosφ=-V/c и f'=f(1–V²/c²), то есть частота снижается [6]. Именно такое покраснение света было зафиксировано в опыте Айвса, а по релятивистской формуле изменение частоты в два раза меньше f'=f(1–v²/2c²) [17]. То есть подтвердилась именно классическая формула. Да и сам Айвс трактовал опыт классически.

    Итак, лишнее красное смещение света у быстро летящих частиц вызвано не замедлением процессов, а восприятием излучения, испущенного частицей чуть назад, что по Доплеру снижает частоту. Источник, сообщая лучам света свою скорость, меняет их направления тем сильнее, чем выше его скорость. За счёт этого даже у света, идущего вперёд под углом θ<90º, можно обнаружить красное смещение, вместо синего. Если релятивисты объясняют это растяжением времени, то в классической теории это вызвано тем, что свет, испущенный источником назад, может полететь вперёд, получив скорость источника. Угол θ, под которым излучение источника регистрируют на прежней частоте (f'=f, на границе красного и синего смещений), найдётся из условия, что под таким углом идёт луч, испущенный источником под углом φ=90º, когда f'=f(1+cosφV/c)=f. Этот луч, отклоняясь на угол аберрации, приходит под углом θ=arctg(c/V). То есть рост скорости V снижает этот угол от 90º до нуля, как подтверждают эксперименты. Свет, испытавший синее смещение, сосредоточен внутри конуса с углом раствора 2θ. Причём конус сужается при увеличении скорости V (рис. 9).

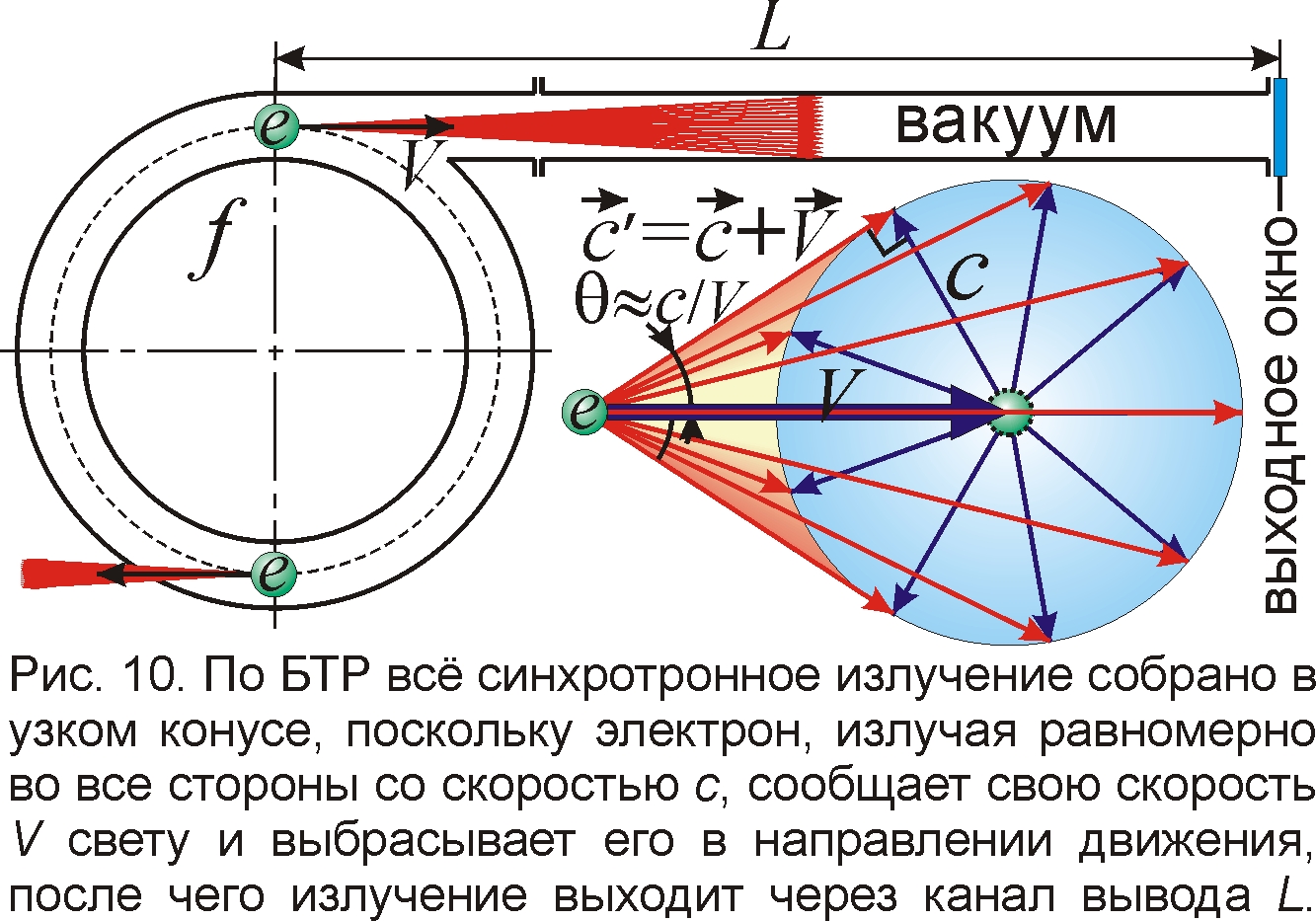
    Всё это очень напоминает характер синхротронного излучения от быстро летящих электронов: ускоренно двигаясь в магнитном поле синхротрона, они испускают излучение, сконцентрированное в конусе, расходящемся вдоль оси движения частицы (рис. 10), подобно пучку света фар от автомобиля, или ливню капель, отлетающих по касательной от мокрого велосипедного колеса, получив его окружную скорость. Так и свет отрывается от электронов, крутящихся в вакуумной камере синхротрона (напоминающей велосипедную), вылетая по касательной узким конусом синхротронного излучения. Легко понять, что причина этого тоже в передаче электроном своей скорости свету, отчего лучи света, разлетавшиеся радиально, улетают в основном вперёд от движущегося электрона, обретя его скорость, подобно авиабомбе или осколкам крылатой ракеты, продолжающим лететь вперёд после отделения [1]. А если скорость частицы V>c, то назад её свет вообще не доходит: все лучи, получив скорость источника, идут вперёд в пределах конуса с углом образующей к оси θ= arcsin(c/V)≈ c/V. Именно эти свойства были обнаружены у синхротронного излучения: оно собрано в пределах узкого конуса с углом раствора θ≈mc²/W, который сужается при увеличении скорости и энергии W электрона [18]. Здесь в качестве W берут "энергию", найденную релятивистски W=pс=mVc, откуда получают согласный с БТР и с опытом результат θ≈mc²/W=c/V.

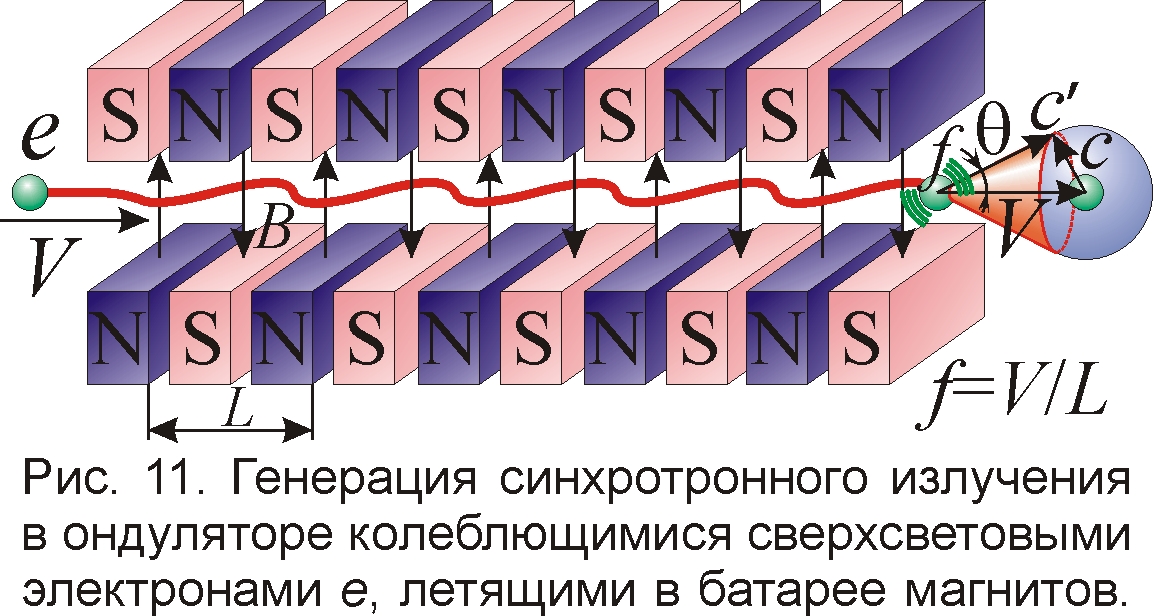
    Много общего у синхротронного излучения с ондуляторным, которое получают в ондуляторах – приборах в виде батареи магнитов, полюса которых чередуются с периодом L (рис. 11). Если электрон, покинув синхротрон на большой скорости V, полетит через ондулятор, то в периодично меняющемся поле начнёт колебаться с частотой пересечения f=V/L периодов L. При этом электрон излучает на той же частоте f, но неподвижный наблюдатель по эффекту Доплера воспримет его излучение на частоте f'=f(1+V/c)= V/L(1+V/c)≈V²/Lc (при V>>c). И точно, частота ондуляторного излучения сильно растёт при увеличении импульса p и скорости V электрона по закону f'≈f₀γ² [18], где f₀=c/L, а γ=p/mc=V/c, откуда в полном согласии с БТР f'≈V²/Lc. Поскольку электрон излучает на строго фиксированной и очень высокой частоте f', то на основе ондуляторов даже строят источники рентгеновского излучения и рентгеновские лазеры на свободных электронах. И снова огромная частота f'= V/L(1+V/c) говорит о том, что скорость V электронов в ондуляторах во много раз превышает скорость света. И только ложная релятивистская формула эффекта Доплера заставляет всех думать, будто v<c. Кроме того, раз электроны движутся с огромной скоростью, их ондуляторное излучение, подобно синхротронному, сосредоточено в конусе с углом θ≈mc²/W=c/V.

    Итак, острая направленность синхротронного и ондуляторного излучений подтверждает баллистический принцип, по которому источник сообщает свою скорость свету. Зато этот факт в корне противоречит догмам теории относительности, по которой, как бы быстро ни перемещался источник, свет от него идёт во все стороны со скоростью c, раз источник по СТО не может двигаться быстрее света и не может сообщить свою скорость свету. Выходит, тот факт, что синхротронное излучение сверхэнергичных электронов идёт лишь вперёд по их движению, и никогда – назад, доказывает справедливость БТР и ложность СТО.

    О том же говорит и спектр синхротронного излучения. Электрон, облетая кольцо синхротрона по кругу с частотой f, должен генерировать излучение на частоте f своего вращения (так и частота звука милицейского свистка совпадает с частотой вращения в нём шарика, рис. 4). Обычно электроны, крутясь в магнитном поле B, и впрямь излучают на своей гирочастоте f=eB/2πm. Но электрон при наращивании скорости, вопреки электродинамике Максвелла, начинает излучать и на более высоких частотах-гармониках 2f, 3f, 4f, … . И в синхротроне, где электроны крутятся с огромной скоростью, они излучают не только на ВЧ-частоте f своего вращения, но и на высших её гармониках, отчего излучение становится видимым. Этот "чудо-свет" и назвали синхротронным. Поскольку в рамках теории Максвелла и СТО не могли верно предсказать свойств синхротронного излучения, его долго не могли обнаружить, и лишь случайно открыли в 1947 г., а уже потом подогнали теоретическую базу [18].

    А в баллистической теории такое излучение было предсказано Ритцем ещё 1908 г. Летящий по кругу электрон, сообщая свою скорость электромагнитным воздействиям (переносимым реонами), в одних точках орбиты ускоряет их, и они приходят к наблюдателю раньше, а в других – тормозит, и они запаздывают (рис. 12). В итоге исходный синусоидальный профиль электромагнитной волны искажается, как в случае излучения звёзд, летящих по круговой орбите [19]. Такой негармонический, но периодичный сигнал при разложении в ряд Фурье, то есть в спектр, как раз даёт, кроме основной частоты колебаний f, ещё и ряд её гармоник на частотах 2f, 3f, 4f, … . Их интенсивность должна расти с увеличением искажений, пропорциональных скорости V электрона и расстоянию L, пройденному светом в вакууме [19]. Причём спектр должен быть задан через Фурье-интеграл от бесселевых функций, подобно спектру клистрона (он тоже работает на искажении синусоидального сигнала от модуляции скорости несущих его электронов [20]). Но именно таков спектр синхротронного излучения: он тоже задан через бесселевы функции, причём интенсивность высших гармоник быстро нарастает с увеличением скорости электронов и приближением её к скорости света. Ведь тогда искажения станут хорошо заметны и спектр обогатится гармониками уже на расстоянии порядка радиуса орбиты. И лишь у обычных антенн, как показал Ритц, где электроны движутся с ничтожной скоростью дрейфа V, излучение идёт лишь на частоте колебаний f.

    Итак, синхротронное излучение, вопреки заверениям релятивистов, подтверждает не СТО, а классическую физику и БТР. Поэтому все приборы, генерирующие синхротронное излучение, работают по теории Ритца, а применение ошибочной теории относительности может сильно снижать их эффективность, исправляемую лишь путём эмпирической доводки. Если бы физики сразу применяли в расчётах баллистическую теорию, приборы сходу б заработали эффективно. Раз по БТР спектр синхротронного излучения зависит не только от скорости электронов (как в СТО), но и от дистанции L, пройденной излучением в вакууме, то при малом L спектр беден гармониками. Вот почему в синхротронах стремятся увеличить расстояние от излучающих электронов до окон вывода синхротронного излучения. А для получения высокочастотных рентгеновских лучей делают даже специальные вакуумированные каналы вывода синхротронного излучения [18], где оно успевает преобразоваться по Ритцу. Эти каналы имеют вид многометровых труб, напрямую пристыкованных к вакуумной камере ускорителя, откачанных до высокого вакуума и не содержащих перегородок (лишь тогда нет переизлучений, и трансформация спектра идёт по всей длине канала, вплоть до выходного окна, рис. 10). С позиций баллистической теории установка таких длинных вакуумных каналов вполне оправдана, раз спектр уширяется и частотный максимум смещается пропорционально пути L. А вот с позиций СТО и электродинамики Максвелла протяжённые вакуумные каналы – это лишняя роскошь, хотя без каналов не обходятся, причём, в согласии с БТР, их длину подбирают тем большей, чем сильнее сдвиг спектра.

    Вот и выходит, что вся "релятивистская электроника", которую правильней назвать высокоэнергичной, подтверждает не теорию относительности, а теорию Ритца. И всё же излучение электронов, крутящихся в накопительных кольцах и синхротронах, порой пытаются привлечь в качестве аргумента против БТР. Так, в опыте, инициированном энтузиастом баллистической теории, полковником артиллерии П.И. Филипповым [21], физики сравнивали скорость синхротронного излучения от быстрых электронов и его же скорость после переизлучения выходным окном, где свет тормозился. Оказалось, что импульсы этих излучений приходят почти синхронно, хотя по БТР излучение, испущенное напрямик электронами, должно, обретя их скорость, двигаться гораздо быстрее, а его импульс на экране должен опережать заторможенный на пару наносекунд. Но в опыте не учли сверхсветовую скорость V>>c электронов с энергией 70 МэВ, и считали по СТО V≈c, отчего, сделав неверные оценки времени опережения импульса, его и не обнаружили. Быстрый импульс либо вовсе не замечали от сильного опережения (тогда одиночный заторможенный импульс принимали за сумму двух синхронных), либо его фиксировали от сгустка электронов, сделавшего лишний оборот, или от следующего сгустка, и внесённое этим запаздывание (при V>>c составлявшее как раз порядка наносекунд), компенсировало опережение. Кроме того, детекторы могли регистрировать свет, переизлучённый металлическими стенками камеры ускорителя и диафрагмами на пути луча, которые, будучи неподвижны, уже не сообщали свету добавочной скорости. То же можно сказать о сообщении Е.Б. Александрова, заявившего, что синхротронное излучение от электронов, разогнанных мощным ускорителем, всегда летит со скоростью света c. Проблема этих и других экспериментов по проверке БТР состоит в том, что их проводят физики, не знающие этой теории и того, что реально она предсказывает. В итоге, продолжая отчасти пользоваться СТО, они опровергают опытом не БТР, а свой ошибочный расчёт, своё ложное представление о выводах теории Ритца. На Земле вообще трудно выявить влияние скорости источника на скорость света, ввиду переизлучения промежуточными средами – воздухом, линзами, зеркалами и т.д. И лишь в вакууме космоса эффекты БТР ярко проявились, подтвердив эту теорию и реальность сверхсветовых скоростей [3, 19, 22].

    Сам Эйнштейн так обосновал невозможность превысить скорость света: если б наблюдатель мог угнаться за световой волной, летящей со скоростью света, он бы обнаружил неизменные значения электрического и магнитного поля этой волны в отсутствие поблизости зарядов и токов, что невозможно по Максвеллу [7]. Отсюда Эйнштейн заключил, что тела не могут лететь со скоростью равной или большей c, вопреки классической механике. Но проблема не в механике, а в теории Максвелла, ошибочно дающей одни и те же значения поля вне зависимости от движения наблюдателя. А в теории Ритца поля меняются, и наблюдатель, летящий со скоростью световой волны, просто её не увидит (все поля занулятся), поскольку реоны, несущие волну, не догоняют и не обгоняют его, то есть не оказывают воздействия. Так и на воздушном шаре в потоке ветра наблюдатель не ощущает дуновений, если шар летит со скоростью ветра, а слушатель не слышит звука, если удаляется от источника со скоростью звука, то есть атомов воздуха [1]. Уже из эффекта Доплера видно: чем быстрее наблюдатель удаляется от источника, тем меньше энергия и частота принимаемых им сигналов f'=f(1–V/c). Когда наблюдатель улетает вместе со световой волной на скорости V=c, энергия и частота света обнуляется f'=0: сигнал исчезает, и рассуждение Эйнштейна теряет смысл.

    Отметим, что сами физики в исследованиях электромагнитных процессов часто пользуются преобразованиями Галилея, а не Лоренца, причём не только из удобства, но и потому, что формулы СТО порой вообще отказывают. Так, при анализе лазерных световых импульсов и солитонов часто описывают процессы в бегущей системе координат, движущейся со световой или околосветовой скоростью, в том числе для анализа изменений формы импульса и того, как один импульс догоняет другой, взаимодействует с ним, обмениваясь энергией за счёт нелинейных эффектов. При этом, пользуясь преобразованиями Галилея, получают согласные с опытом результаты! Так же и при анализе волн в плазме физики спокойно переходят в бегущую систему отсчёта, пользуясь для удобства механикой Галилея. А эта бегущая система зачастую перемещается со сверхсветовой скоростью (в плазме возможно сверхсветовое распространение волн и фронтов концентрации ионов [23]), на которой преобразования Лоренца вообще неприменимы: релятивистские формулы дают абсурдные результаты. А преобразования Галилея не только продолжают работать, но и легко приводят к верным выводам! Понимая, что это противоречит букве законов СТО, физики называют такой переход в бегущую систему координат осторожным термином "сопоставление электродинамических систем" [23]. Это напоминает осторожное предисловие к книге Коперника, где новая гелиоцентрическая система не противопоставлялась, а сопоставлялась геоцентрической системе Птолемея (опекаемой церковной цензурой) лишь в качестве удобной для расчётов системы.

    Складывается впечатление, что физики разных направлений давно осознали реальность сверхсветовых скоростей, ошибочность теории относительности и спокойно пользуются классическими преобразованиями Галилея там, где отказывают формулы СТО. Но из-за жёсткой цензуры (обтекаемо названной "рецензированием научных работ"), стоящей глухим барьером на пути работ, критикующих теорию относительности, эти данные не могут попасть в печать. И сами учёные, получив новые революционные результаты, вынуждены представлять их как подтверждение СТО, хотя всё наоборот. Это ещё раз доказывает, что световой барьер поставила не Природа, а научная цензура и так называемая "научная мафия", изживающая "еретиков" и управляющая потоками информации, подобно инквизиции и церковной цензуре, запрещавшей новаторские работы Коперника, Бруно и Галилея. Более всего от этого страдают честные физики (которых всё же большинство), поскольку одни не могут открыто сообщить важные результаты, противоречащие СТО, а другие не могут ими воспользоваться, дабы улучшить свои теории и установки. А ведь учёт сверхсветовой скорости частиц и расчёт по формулам БТР позволит повысить эффективность ускорителей и других приборов, где частицы движутся с околосветовой и сверхсветовой скоростью. Поскольку стоимость и энергопотребление мощных ускорителей сопоставимы с расходами на крупный город [12], выигрыш от экономии материалов и энергии может оказаться колоссальным.

    Но суть даже не в этом нецелевом расходе бюджетных средств, на котором паразитирует научная мафия, а в том, что наложенные ей ограничения мешают научно-техническому прогрессу, созданию ещё более важных и грандиозных устройств, чем ускорители. В том числе это космолучевые ракетные двигатели и передатчики, способные посредством сверхсветовых частиц придать кораблям и сигналам скорости, в сотни раз большие скорости света [3, 24]. Не зря К.Э. Циолковский, открывший путь в космос вопреки запретам научной цензуры и гравитационному барьеру, отрицал и световой барьер, и теорию относительности. И ныне спутники, ракеты приносят колоссальную пользу, не сравнимую с расходами на них. А если и впредь следовать курсом Циолковского, Бруно и античных атомистов, легко построим сверхсветовую технику для быстрого пересечения бескрайних космических пустынь и достижения звёзд, преодолев мнимый барьер, о котором Бруно ещё полтысячелетия назад писал: "Кристалл небес мне не преграда боле, рассекши их, подъемлюсь в бесконечность".

Источники:

1. Перельман Я.И. Занимательная физика. М.: Наука, 1991.
2. Барашенков В.С. Вселенная в электроне. М., 1988.
3. Семиков С. Космические лучи – путь к звёздам // Инженер №4, 2008.
4. Окунь Л.Б. Понятие массы // Успехи физических наук, Т. 158, вып. 3, 1989.
5. Семиков С. О природе электричества и магнетизма // Инженер №1, 2006.
6. Семиков С. О природе массы и времени // Инженер №5, 2006.
7. Зелиг К. Альберт Эйнштейн. М.: Атомиздат, 1966.
8. Ракобольская И.В. Ядерная физика. М.: МГУ, 1971.
9. Росси Б. Космические лучи. М.: Атомиздат, 1966.
10. Мякишев Г.Я. Элементарные частицы. М.: Наука, 1979.
11. Сивухин Д.В. Атомная и ядерная физика. Ч.2. М.: Наука, 1989.
12. Гольдин Л.Л. Физика ускорителей. М.: Наука, 1983.
13. Чернин А.Д. Физика времени. М.: Наука, 1987.
14. Краткий справочник инженера-физика. Ядерная физика. М.: Госатомиздат, 1961.
15. Никольский В.В. Электродинамика и распространение радиоволн. М.: Наука, 1989.
16. Крюков П.Г. Фемтосекундные импульсы. М.: Физматлит, 2008.
17. Ландсберг Г.С. Оптика. М.: Наука, 1976.
18. Михайлин В.В., Тернов И.М. Синхротронное излучение. М.: Знание, 1988.
19. Семиков С. Ключ к загадкам космоса // Инженер №3, 2006.
20. Гапонов В.И. Электроника. М.: Физматгиз, 1960.
21. Мазманишвили А.С. 25 лет баллистическому эксперименту // Электромагнитные явления, т. 2, №1 (5), 2001.
22. Семиков С. Трансформаторы спектра в космосе и на Земле // Инженер №3, 2011.
23. Степанов Н.С. Волны в нестационарных и неоднородных средах. Горький, 1986; Миллер М.А., Сорокин Ю.М., Степанов Н.С. Ковариантность уравнений Максвелла и сопоставление электродинамических систем // Успехи физических наук, Т. 121, вып. 3, 1977.
24. Дёмин В.Н., Селезнёв В.П. К звёздам быстрее света. М., 1993.

Дата установки: 04.11.2011
Последнее обновление: 27.11.2011
[вернуться к содержанию сайта]

W