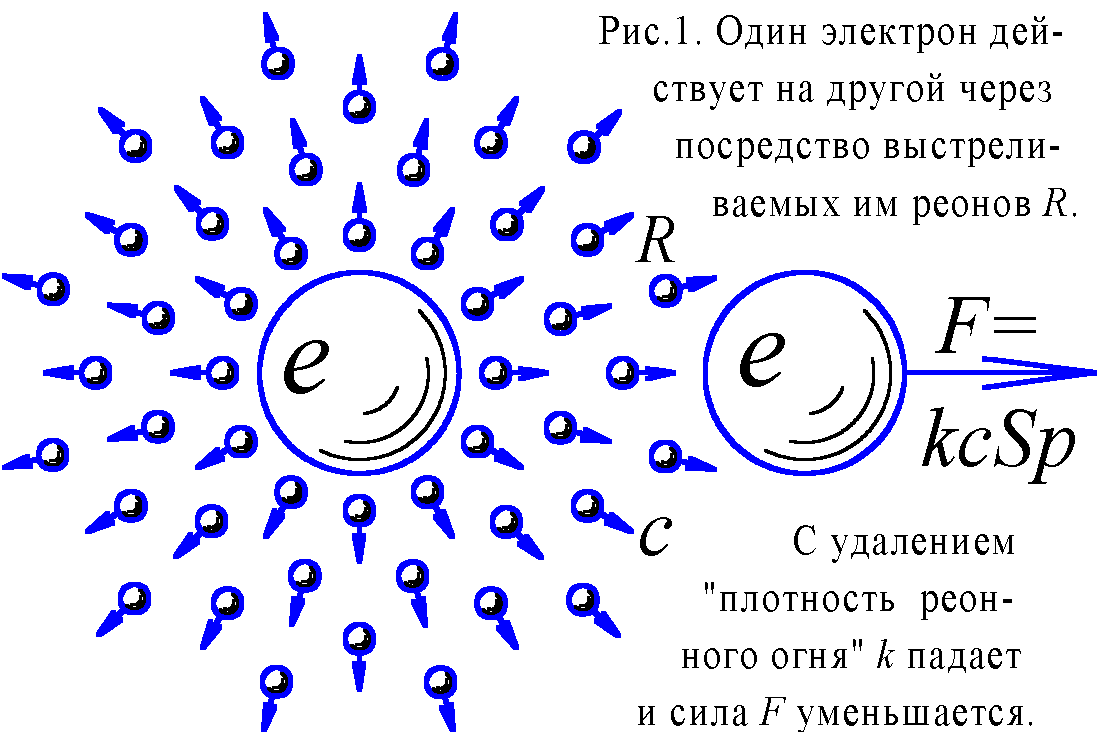
Электрические заряды постоянно испускают во всех направлениях частицы, разлетающиеся с постоянной скоростью вдоль прямых линий. Воздействие на заряд зависит лишь от расположения и скорости этих частиц возле него… Можно сказать, что это будет своего рода механическая теория электричества.
В. Ритц
Что собой представляют электрические и магнитные воздействия? Современная физика, к сожалению, не может ответить на этот вопрос, оправдывая свою беспомощность ньютоновой отговоркой: “Довольно и того, что эти силы существуют и действуют согласно изложенным законам”. Впрочем, со времён Ньютона наметились и некоторые подвижки. Так, в квантовой электродинамике (КЭД) предполагают, что притяжение и отталкивание передают от одного заряда к другому особые частицы – виртуальные фотоны, испускаемые зарядами.
Но авторы КЭД ни словом не обмолвились о Вальтере Ритце, уже в 1908 г. построившем теорию взаимодействия зарядов через посредство излучаемых ими частиц. И не удивительно, ведь тогда учёным пришлось бы признать, что их концепции основаны на Баллистической Теории Ритца (БТР), противоречащей теории относительности. Поэтому КЭД украла у теории Ритца лишь её рабочую идею (см. эпиграф), оставив без внимания основные выводы БТР. Здесь мы ещё отодвинем завесу над теорией Ритца, лишь слегка приоткрытую в [1].
Напомним, как по Ритцу протекает взаимодействие двух электронов. Первый электрон излучает, “расстреливает” по всем направлениям со скоростью света c особые микрочастицы, условно названные в [1] реонами. Спустя время часть их долетает до второго электрона и поглощается им, причём каждый реон передаёт электрону элементарную порцию (квант) воздействия – стандартный импульс p. Полная сила отталкивания электронов F = np, где n – частота попаданий реонов в электрон, а p – импульс, передаваемый каждым реоном. Частота попаданий в площадку S перпендикулярную потоку частиц находится как n=kvS, где k – концентрация частиц в потоке, а v – его скорость. Для электрона в потоке реонов скорость частиц v = c, а S – площадь экваториального сечения электрона, откуда F = kcSp. С удалением от электрона концентрация k выстрелянных им реонов убывает пропорционально квадрату расстояния (рис. 1). Отсюда сразу следует закон Кулона: сила F отталкивания электронов обратно пропорциональна квадрату расстояния между ними.
Так электрическое воздействие передаётся, но как создают его реоны, попавшие в электрон? Каковы смысл и величина элементарного импульса p? Скорая смерть Ритца не дала ему ответить на эти вопросы, но ответы сами собой вытекают из его баллистической модели. Скажем, если автоматные пули, попавшие в консервную банку, заставляют её отлетать в направлении удара, передавая ей свой импульс mv, то не могут ли и реоны, попав в электрон, создать отталкивание, отдавая электрону свой импульс? Огромная скорость c реонов, даже при ничтожной их массе mR, делает этот импульс p= mRc ощутимым. Обмен “выстрелами” и создаст отталкивание зарядов с силой F = kc2SmR, действующей вдоль “линии огня”.
Конечно, эта модель грубо механистична. В дальнейшем она может быть уточнена и даже изменена. Но как первое приближение, дающее наглядную механическую трактовку, она весьма удобна. Судя по некоторым замечаниям Ритца из его “Критических исследований по общей электродинамике” (их полный перевод на русский недавно вышел в Интернете [2]), он и сам пришёл к этой механической модели, но отложил её рассмотрение ввиду серьёзных противоречий. Действительно, реонная перестрелка легко объясняет взаимодействие двух одноимённых зарядов – отталкивание двух электронов или протонов. Но как же с её помощью объяснить притяжение зарядов разного знака?
Рассмотрим взаимодействие электрона e–, имеющего отрицательный заряд, и его античастицы – позитрона e+ с положительным зарядом. Реоны, излучённые электроном, ударяя в позитрон, не отталкивают, а притягивают его: позитрон в корне отличается от электрона характером взаимодействия с реонами. Так же и частицы, испускаемые позитроном, радикально отличаются от реонов, поскольку уже не отталкивают, а притягивают электрон (рис. 2).
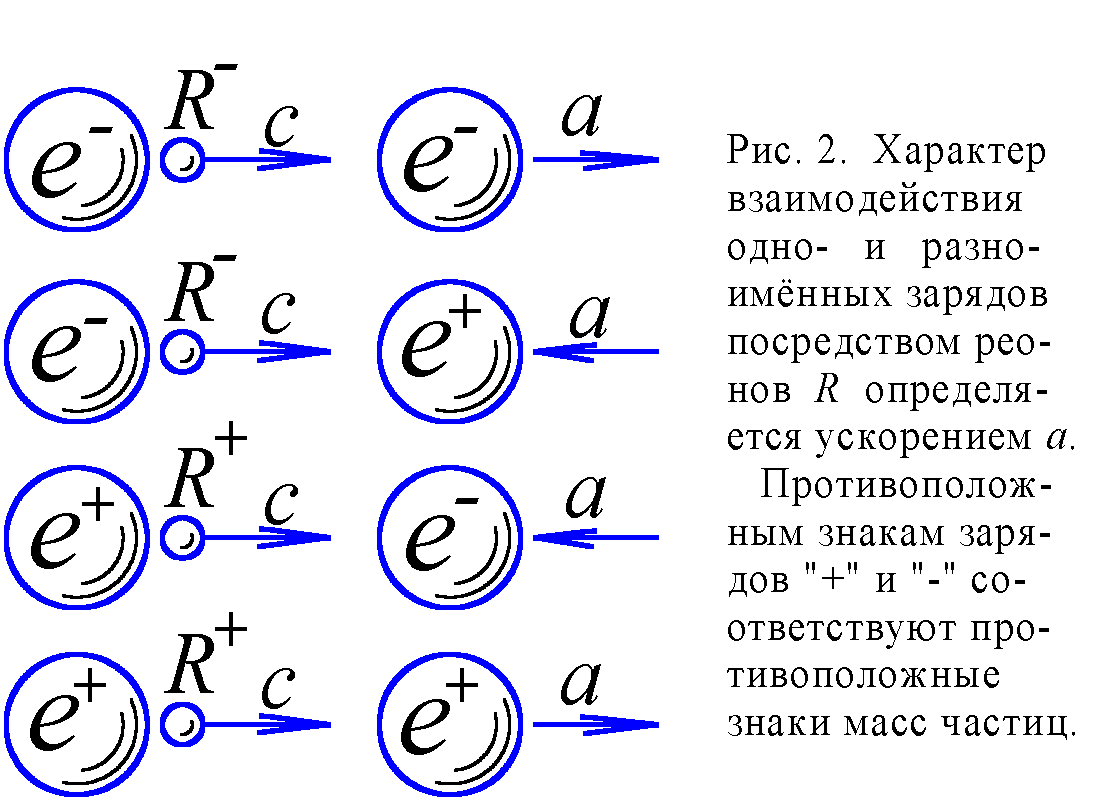
Эту несообразность легко устраняет один, на первый взгляд, парадоксальный вывод: у электрона и позитрона разные знаки имеют не заряды, но массы. Так, если у электрона масса положительна (+me), то у антиэлектрона-позитрона она отрицательна (–me). В таком случае, сила F, создаваемая ударами реонов по позитрону, придаёт ему по второму закону Ньютона ускорение a = F/-me, направленное против силы ударов: позитрон будет притягиваться к электрону. Сам же позитрон, имея минусовую массу, и реоны испускает с антимассой (–mR) – антиреоны, создающие при соударениях с электроном силу F = –kc2S mR, направленную против ударов и, следовательно, подталкивающую электрон к позитрону. Итак, воздействие заряда на заряд определяется величиной ускорения a = kc2S mR/me (рис. 2). Когда заряды одноимённые, то mR и me одного знака и ускорение a положительно (отталкивание), когда же разноимённые, то величина mR/me, как и a отрицательна (притяжение).
Вывод дикий, но парадоксальный в гораздо меньшей степени, чем многие выводы теории относительности. Надо к тому же добавить, что Дирак, собственно и предсказавший существование антиэлектрона-позитрона, считал, что у того должен быть отнюдь не антизаряд, но именно антимасса. Сама Природа требует существования отрицательной массы. Так, при аннигиляции электрона с позитроном обе частицы уничтожаются. Но куда же при этом исчезает их масса? По теории относительности она переходит в энергию. Классическая механика не признаёт такого перехода, а потому надо признать, что массы электрона и позитрона равны и противоположны по знаку, а потому взаимно уничтожаются, давая в сумме ноль.
Далее, известно, что нейтрон распадается на электрон и протон, а тот в свою очередь можно заставить распасться на… позитрон и нейтрон! Но нейтрон тяжелее протона, причём на величину того же порядка, что и масса позитрона. Отсюда может следовать лишь один вывод: позитрон имеет отрицательную массу. Становится ясным и устройство этих частиц: нейтрон состоит из тяжёлой нейтральной частицы и равного числа электронов и позитронов, тогда как у протона позитронов на один больше, чем электронов, отсюда его положительный заряд (рис. 3). Это отменяет некоторые законы превращения элементарных частиц, но зато снимает так и не разрешённый современной физикой вопрос о том, почему в природе частиц много больше, чем античастиц. По крайней мере, электронов и позитронов в атомах будет поровну: электроны атомной оболочки компенсируются позитронами ядра. Надо думать, что и у других элементарных частиц заряженность связана только с присутствием в них электронов и позитронов: лишь они способны испускать и поглощать реоны и антиреоны. Все же прочие частицы прозрачны для реонов, проходящих сквозь них, словно пуля “навылет”.
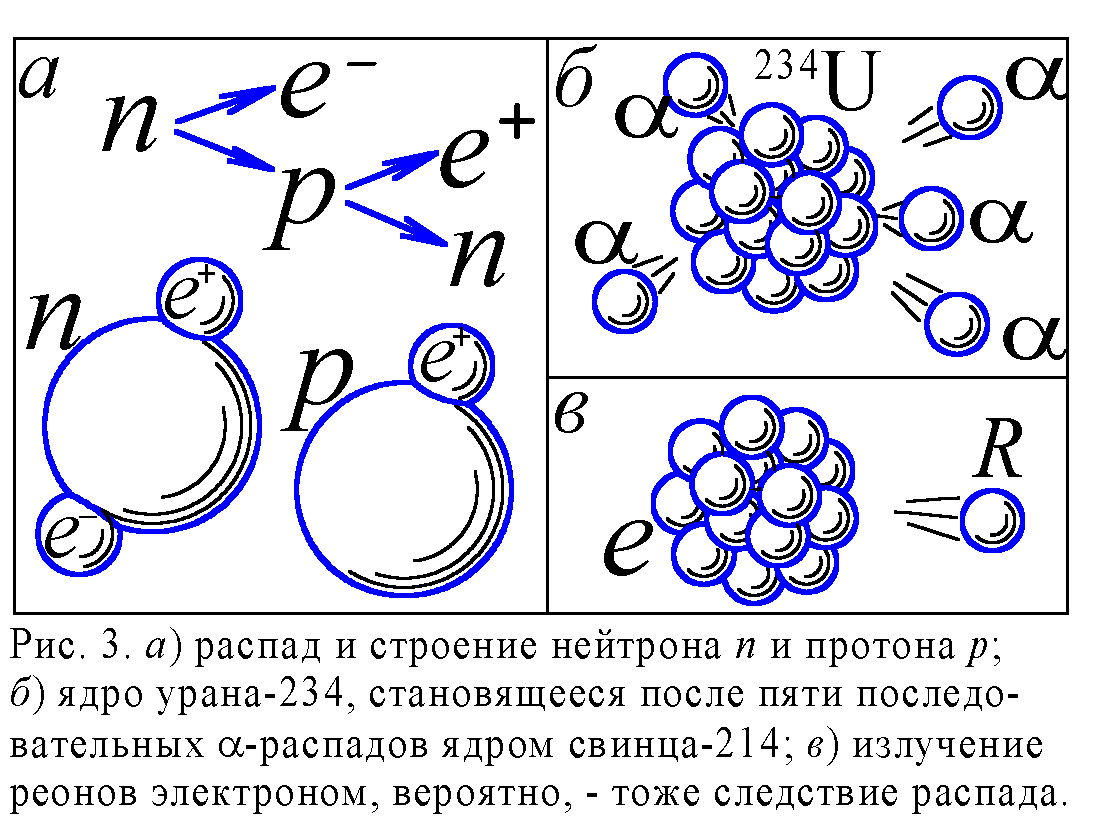
Но что же вызывает испускание реонов и антиреонов зарядами? Возможно, электрон и позитрон просто распадаются, подобно тяжёлым ядрам [1], постепенно теряя вместе с испускаемыми частицами свою массу. Думается, и сам Ритц, говоря об эмиссии, излучении частиц зарядами (он называл БТР эмиссионной теорией), сравнивал потоки реонов, идущие от электронов, с α- и β-лучами тяжёлых ядер. Утечка реонов с электрона должна приводить к постепенному, пусть и крайне медленному, убыванию его массы. Такое уменьшение массы электрона, предсказанное всё тем же Дираком, иногда и впрямь подтверждается экспериментами.
Итак, мы объяснили, как возникает сила электростатического взаимодействия. Но что же собой представляет сила магнитная? Известно, что магнитное поле создаётся движением электрических зарядов. Физики говорят, что в зависимости от движения зарядов часть их электрического поля переходит в магнитное и наоборот (поэтому говорят об электромагнитном поле, считая электричество и магнетизм лишь различными проявлениями его). Но как происходит этот переход, почему его вызывает движение зарядов, и что вообще такое магнетизм, современная физика объяснить не может. Теория же Ритца даёт на это простой ответ.
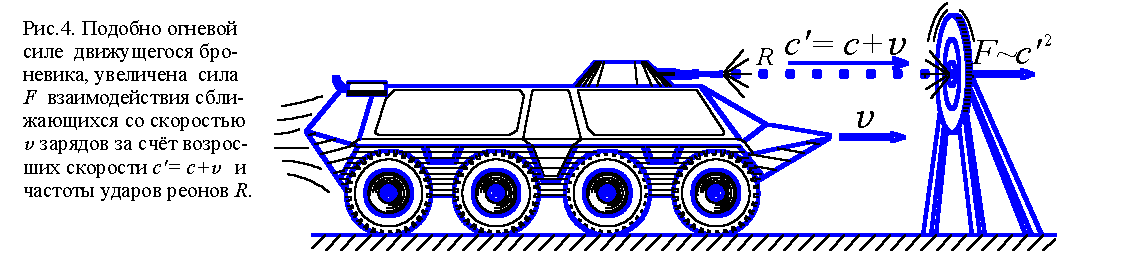
Рассмотрим два неподвижных заряда, взаимодействующих с силой F = kc2SmR. Изменится ли эта сила при сближении зарядов со скоростью v? Видимо, да. Ведь увеличится скорость c встречного потока реонов: вместо c следует писать c΄= c + v, откуда F = k(c+v)2SmR. Сила вырастет по сравнению с той, что испытывали бы покоящиеся заряды на том же удалении. Напротив, расхождение зарядов уменьшит эту силу. Причину этих изменений поясняет баллистическая модель (рис. 4). Если стоящий броневик, расстреливающий цель, поедет к ней, то увеличится частота и скорость ударов пуль, а значит и сила ударов по мишени.
А теперь рассмотрим заряженную нить и возле неё в т. O заряд q. Сила отталкивания заряда от нити F = qτ/2πε0r, где τ – линейная плотность заряда нити, r – расстояние от неё до заряда, а ε0 – электрическая постоянная. Сила же взаимодействия заряда с малым участком нити M длиной dl, имеющим заряд τdl, даётся законом Кулона F = qτdl/4πε0OM2. Перпендикулярная нити составляющая этой силы выразится через углы φ и dφ κак Fу = qτcos(φ)dφ/4πε0r (рис. 5). Найдём, как изменится сила при движении заряда параллельно нити со скоростью v. По отношению к движущемуся заряду встречные реоны будут иметь скорость c΄ отличную от c: из c векторно вычтется скорость v заряда, и направлена скорость c΄ реонов будет уже не вдоль MO, а вдоль M΄O (вспомним звёздную аберрацию – отклонение лучей света от звёзд, вызываемое движением Земли [1]).
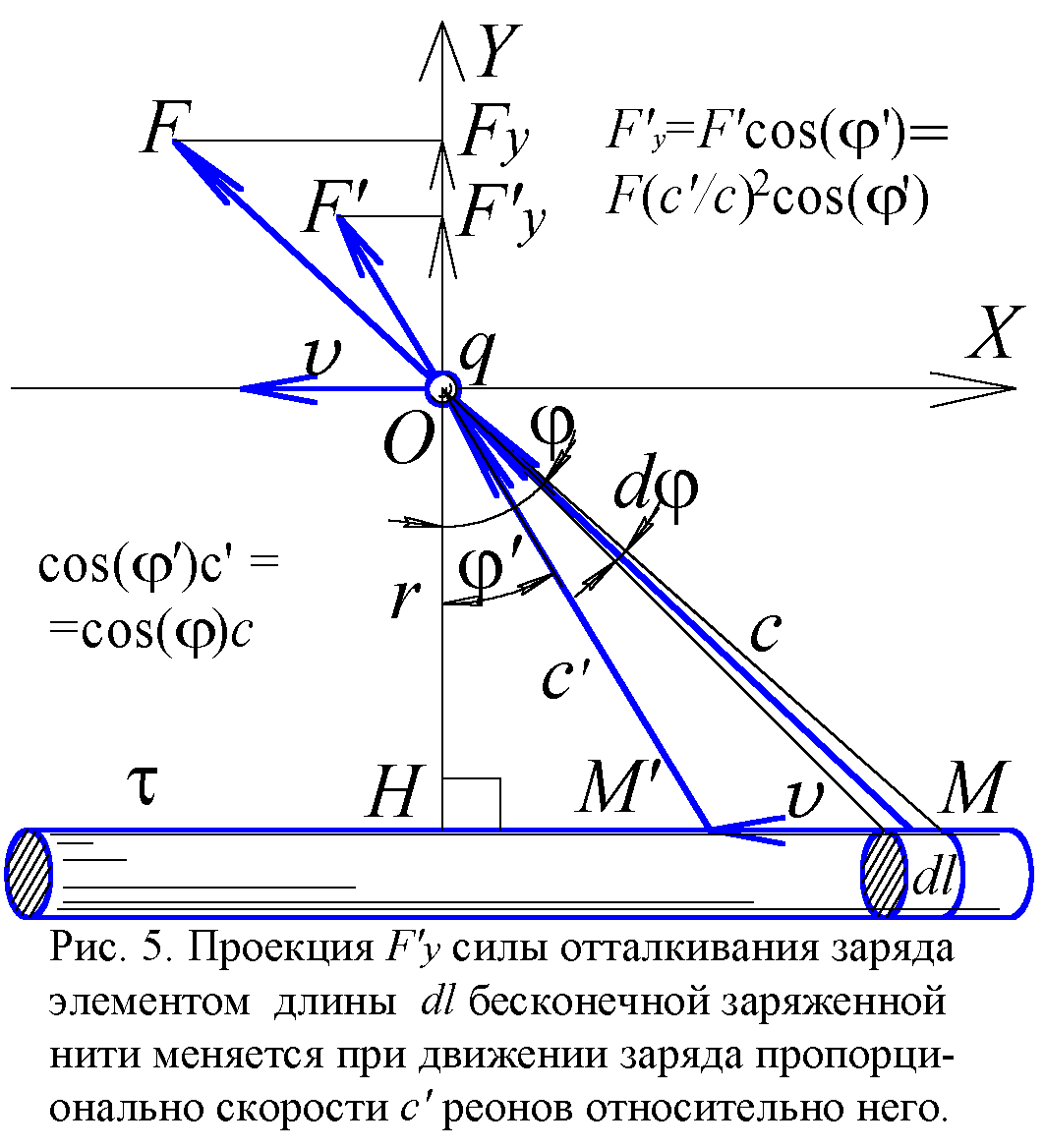
Из треугольника скоростей OMM΄: c΄=
или, считая v/c малым, c΄ ≈ c(1– sin(φ)v/c + (v/c)2cos2(φ)/2). Соответственно меняется и сила: F΄ = F (c΄/ c)2. Но поскольку сила меняет и направление (F΄ действует вдоль c΄ ), то интересующая нас составляющая Fу изменится в несколько меньшей степени: Fу΄ = Fу (c΄/ c) = (1– sin(φ)v/c+ (v/c)2cos2(φ)/2)cos(φ)dφ·qτ/4πε0r. Остаётся найти суммарную силу воздействия на заряд со стороны всех элементов нити, проинтегрировав Fу΄ в пределах φ от –π/2 до +π/2. В итоге, полная сила Fу΄ = (1 + v2/3c2)qτ/2πε0r = qτ/2πε0r + v2qτ/6πε0rc2. Первое слагаемое – это сила взаимодействия нити с покоящимся зарядом, а второе – это прибавка к ней, возникшая за счёт движения. Итак, движение заряда со скоростью v вдоль нити вызывает рост силы отталкивания (или притяжения) на величину v2qτ/6πε0rc2.
Этот результат имеет весьма важные последствия. Рассмотрим два параллельных проводника с сонаправленными токами. Поскольку ток в металле создаётся движением электронов, заменим каждый проводник движущейся отрицательно заряженной нитью (рис. 6). У первой нити линейная плотность заряда – τ1 и скорость v1, а у второй – соответственно –τ2 и v2. В целом проводники нейтральны, поэтому добавим неподвижные положительно заряженные нити +τ1 и +τ2 (они соответствуют положительным и неподвижным ионам металла). Найдём, с какой электрической силой Fэл первый проводник (нити +τ1 и –τ1) действует на элемент длины l второго проводника (нити +τ2 и –τ2). Fэл складывается из четырёх сил:
а) F1, действующей со стороны неподвижной нити +τ1 на неподвижный заряд +τ2l;
б) F2, действующей со стороны неподвижной нити +τ1 на движущийся заряд –τ2l;
в) F3, действующей со стороны движущейся нити –τ1 на неподвижный заряд +τ2l;
г) F4, действующей со стороны движущейся нити –τ1 на движущийся заряд –τ2l.
Скорость заряда q = τ2l относительно соответствующей нити равна для случая
а) нулю, и потому сила отталкивания F1 = τ1τ2l/2πε0r (по формуле Fу΄);
б) v2 , и сила притяжения F2 = τ1τ2l/2πε0r + v22τ1τ2l /6πε0rc2;
в) v1 , и сила притяжения F3 = τ1τ2l/2πε0r + v12τ1τ2l /6πε0rc2;
г) (v1– v2) , и сила отталкивания F4 = τ1τ2l/2πε0r + (v1– v2)2τ1τ2l /6πε0rc2.
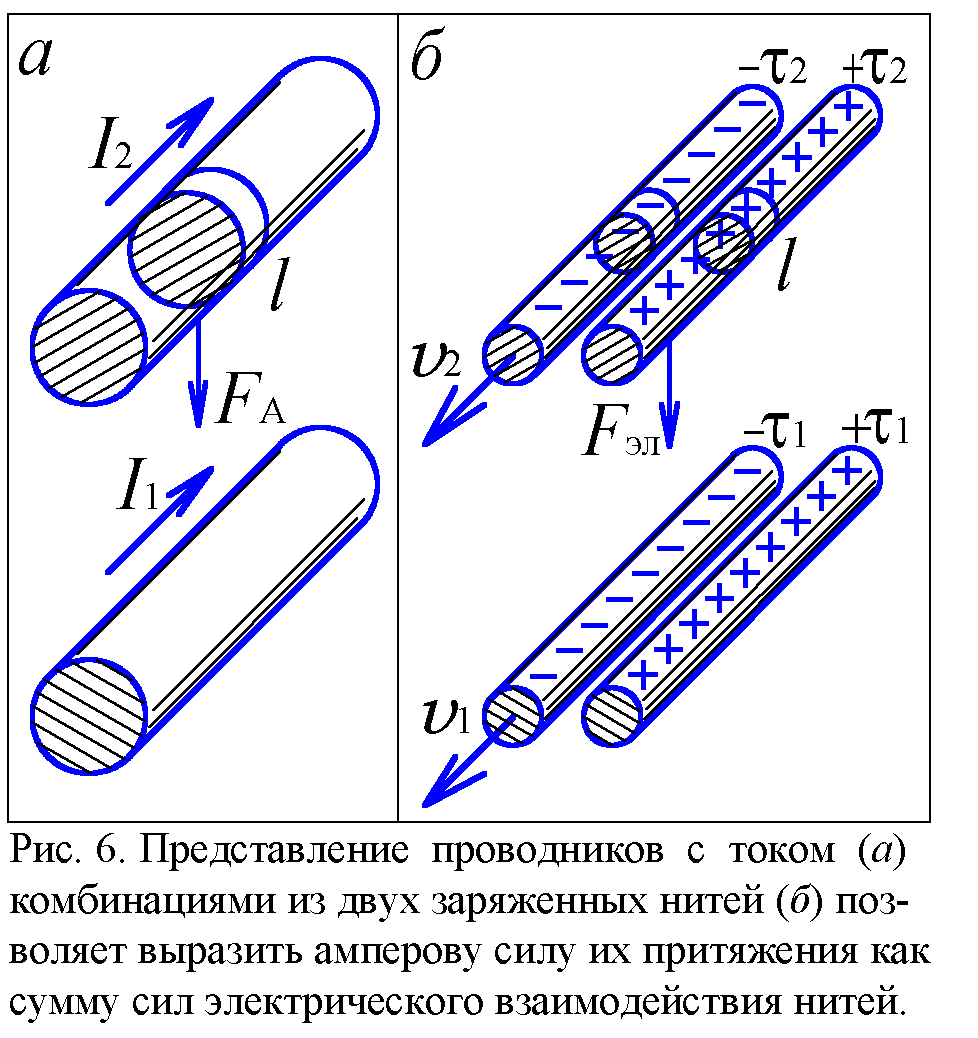
Результирующая сила притяжения Fэл= F2+F3 –F1–F4 = v1v2τ1τ2l /3πε0rc2. Таким образом, движение зарядов в проводниках нарушает баланс сил взаимодействия, силы перестают компенсировать друг друга. В результате проводники с током притягиваются, или же отталкиваются, если токи направлены в разные стороны (v1v2 отрицательно). Величина v1τ1 есть не что иное, как сила тока I1 в первом проводнике, а v2τ2 – сила тока I2 во втором. Учитывая это и применяя известную формулу 1/c2 = ε0μ0, получим Fэл= μ0I1I2l/3πr. Но ведь похоже описывает взаимодействие параллельных токов и закон Ампера: FА= μ0I1I2l/2πr, дающий, правда, величину силы в полтора раза большую. Это небольшое несоответствие в принципе можно устранить, уточнив формулы реонного воздействия или же формулы Кулона и Ампера (изменение их коэффициентов в полтора-два раза вполне допускается точностью экспериментов по измерению отношения электрической и магнитной единиц заряда [3]).
Итак, надобность в магнитном поле отпадает, ибо то, что принято считать магнитной силой, возможно, всего лишь не скомпенсированная прибавка силы электрической, возникающая от движения зарядов. В свою очередь, эта прибавка – естественное следствие баллистической модели взаимодействия зарядов и сложения скорости распространения света или электрического поля со скоростью источника. Другими словами, по Ритцу магнитных сил и полей не существует, а за их проявления мы ошибочно принимаем результат изменения сил электрических. Именно поэтому не найдены магнитные “заряды” – предсказанные Дираком монополи, существование которых должно проистекать из равноправия, обратимости полей. А свет, вопреки Максвеллу, вполне может распространяться и без помощи магнитного поля. Наоборот, именно конечная скорость света, реонов и порождает магнитные эффекты.
Влияние движения заряда на величину электрической силы, как показал Ритц, позволяет объяснить и релятивистские эффекты, скажем, результат экспериментов Кауфмана [4], где впервые обнаружился странный факт увеличения массы электронов с ростом их скорости. Ритц предположил, что для объяснения эксперимента ни к чему считать массу переменной. В опытах Кауфмана о массе электрона судили по тому, насколько он отклонялся электрическим и магнитным полем. Эти отклонения измеряли по следу, оставляемому электронным лучом на люминесцентном экране. Отклонения дают величину ускорения a, связанную по второму закону Ньютона a = F/m с массой электрона. Так вот, когда обнаружилось, что при нарастании скорости электрона его ускорение оказывается меньше расчётного, то посчитали, что это вызвано увеличением его массы. Но ведь куда естественней предположить, что масса постоянна, а изменяется сила. Такой вывод тем более естественен, что, как было показано, скорость заряда действительно может влиять на величину электрической и магнитной силы.
Теоретически след электронного луча на экране должен был иметь форму параболы с уравнением y = kx2Em/H2, где k – некоторая постоянная, E и H – напряжённости электрического и магнитного полей, а m – масса электрона. Наблюдаемая же кривая отличалась от этой параболы так, будто с ростом скорости масса m увеличивалась пропорционально (1 + v2/2c2). Но ведь, как выяснено, почти так же, пропорционально (1 + v2/3c2) нарастает со скоростью заряда электрическая сила и поле E. Учёт переменности E при постоянной массе внесёт в уравнение параболы почти те же изменения, что и учёт переменности m при постоянном E. Разница же коэффициентов в полтора раза устраняется более точным расчётом, см. [2].
Итак, баллистическая модель и теория Ритца не только согласуются со всеми электрическими и магнитными эффектами, включая релятивистские, но и позволяют в рамках классической картины мира наглядно описать их природу. Но самое удивительное состоит в том, что идея влияния движения заряда на величину электрической силы возникла уже очень давно. Задолго до Ритца (как он сам же замечает) её высказал Вебер, ещё в середине 19-го века построивший на её основе электродинамику, рассматривающую магнитные и индукционные силы как следствие изменения (при движении и ускорении зарядов) сил электрических [3, 5].
Но эта замечательная концепция была отвергнута, причём по иронии судьбы тем самым фактом, из которого должна бы была проистекать. Дело в том, что Вебер был сторонником теории дальнодействия, то есть мгновенного распространения воздействий. А формулы свои, описывающие влияние движения на величину электрической силы, он не вывел, а просто подобрал [5]. А между тем, как было показано, их можно вывести строго, придерживаясь прямо противоположного принципа, – считая, что воздействие передаётся не мгновенно, а с задержкой, через некий промежуточный агент (реоны). Предположение же о мгновенной передаче воздействия с бесконечной скоростью реонов (c=∞), как легко проверить, привело бы, напротив, к постоянной, не зависящей от движения зарядов величине силы.
Следует заметить, что теории Вебера и Ритца приводят к закону взаимодействия токов отличному от общепринятого. Так, считается, что магнитные силы всегда перпендикулярны токам (рис. 7). Но это нарушает принцип действия и противодействия, особенно если один ток идёт вдоль, а другой поперёк соединяющей их линии MN – здесь одна из сил вообще нулевая. В теории же Вебера силы магнитного взаимодействия всегда равны и противоположно направлены. Да и сам Ампер, открывший взаимодействие токов, утверждал, что магнитные силы действуют вдоль линии, соединяющей элементы, а экспериментально найденный им и подтверждённый Вебером закон взаимодействия токов [3], как и закон, вытекающий из теории Ритца, не совпадает с общепринятым, следующим из закона Био-Савара-Лапласа.
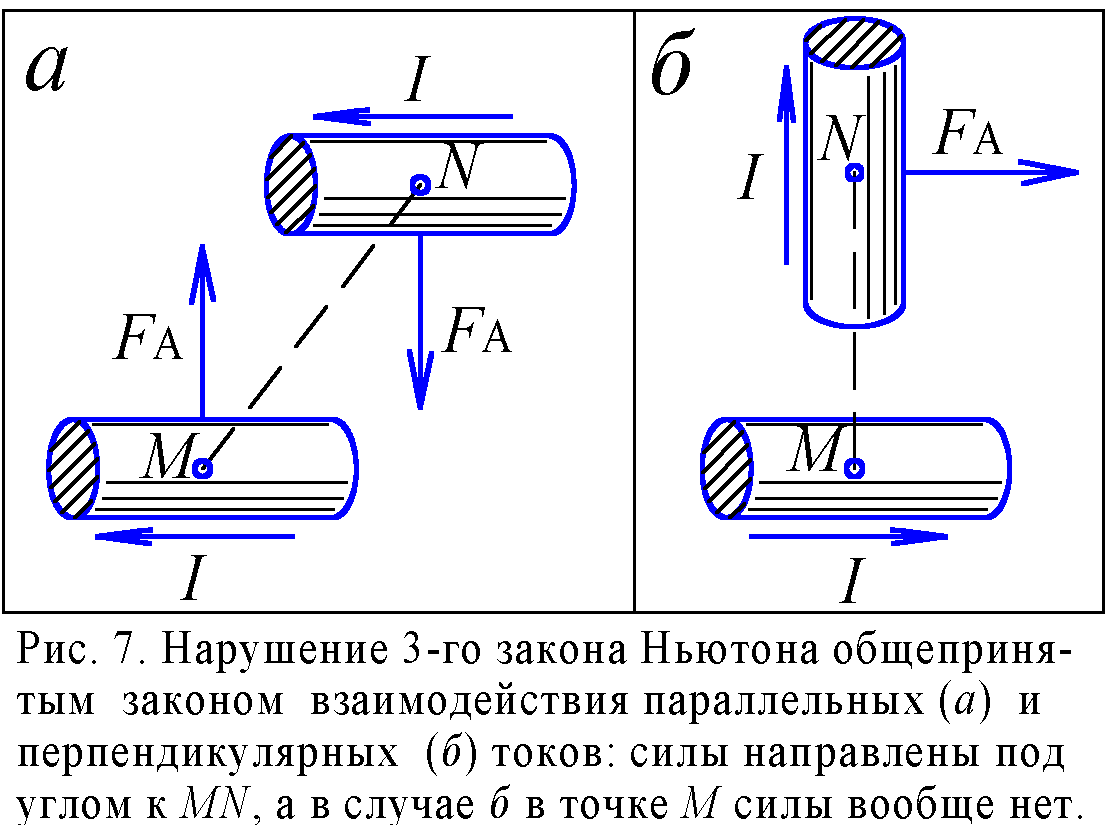
Экспериментально же выявить ошибочность общепринятого закона до сих пор не удалось потому, что такой задачи никто не ставил, хотя расхождение с законом Ампера-Вебера должно было к этому давно побудить. Конечно, опыты Ампера и Вебера трудоёмки, но зато оборудование для них нужно самое простое. Точное установление в эксперименте действительного закона взаимодействия токов явилось бы самым простым и действенным доказательством Баллистической Теории Ритца. Возможно, именно ошибочные представления о природе электричества и магнетизма, об управляющих ими законах тормозят прогресс науки, не позволяя создать высокотемпературные сверхпроводники и другие кажущиеся пока фантастичными устройства, вроде антигравитора и генератора силового поля.
Сергей Семиков
Дата установки: 28.07.2006
Последнее обновление: 27.01.2012
