[вернуться к содержанию сайта]

ТЕМПЕРАТУРНЫЕ АНОМАЛИИ И КРИСТАЛЛИЧЕСКИЕ КРИОТЕХНОЛОГИИ
(напечатано в журнале "Инженер" №5, 2016)

    В наше время температурными аномалиями никого не удивишь – температура скачет, бьёт вековые рекорды, времена года меняются местами. А в физике температурные аномалии, открытые век назад при анализе поведения веществ возле абсолютного нуля, вызвали ещё большую неразбериху: газы, жидкости и твёрдые тела вблизи T = 0 K обнаружили необычные свойства, которые не могли объяснить по классической физике [2, 3]. Но и в квантовой физике их зачастую трудно понять. Неожиданно выход нашёлся – снова в классике.

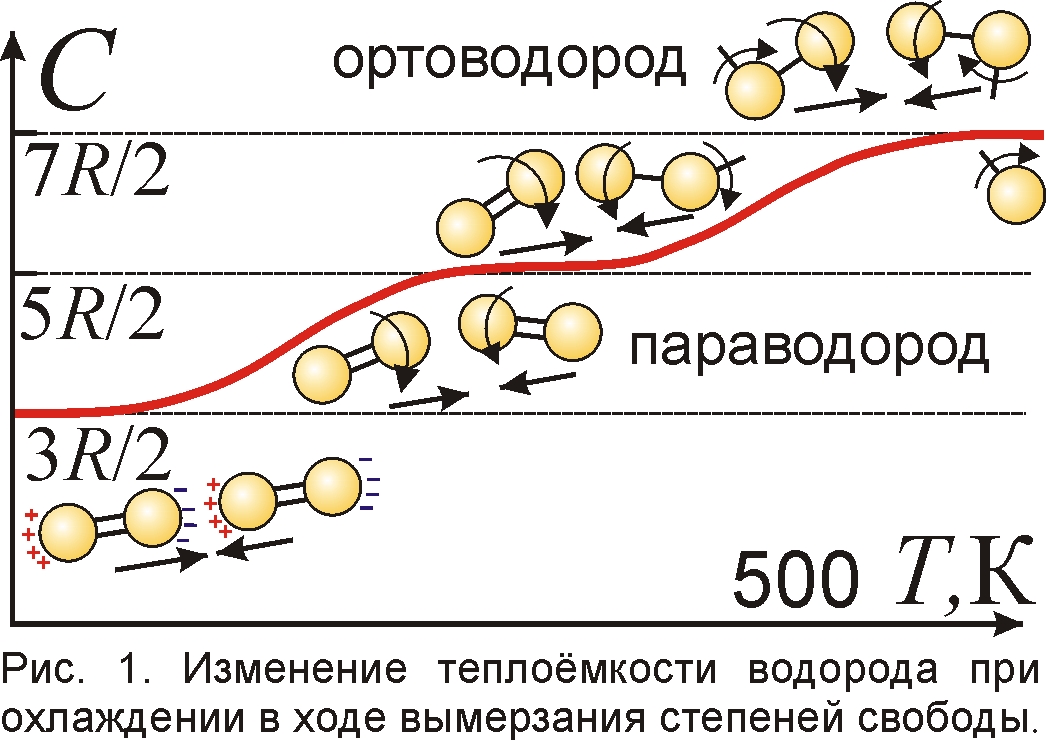
    Ряд аномалий обнаружен у газов. Их теплоёмкость C_V снижалась при охлаждении, вопреки классической термодинамике. Причина – в остановке вращения молекул при охлаждении, что вполне объяснимо классически [4, 5]. При низких температурах молекулы, за счёт малой скорости, успевают до столкновения сориентироваться силами Ван-дер-Ваальса (ВДВ) вдоль соединяющей их линии и получают лишь лобовые, а не косые удары (рис. 1). В итоге молекулы перестают вращаться, исчезает часть теплоёмкости, связанная с вращением, о чём прозорливо догадался ещё Ломоносов [1]. Эту гипотезу подтверждает температурный ход теплоёмкости для газов больших молекулярных масс и моментов инерции. Если у водорода спад C_V заметен при 200 K, то у газов с более крупными молекулами,– при T~50 K [6].

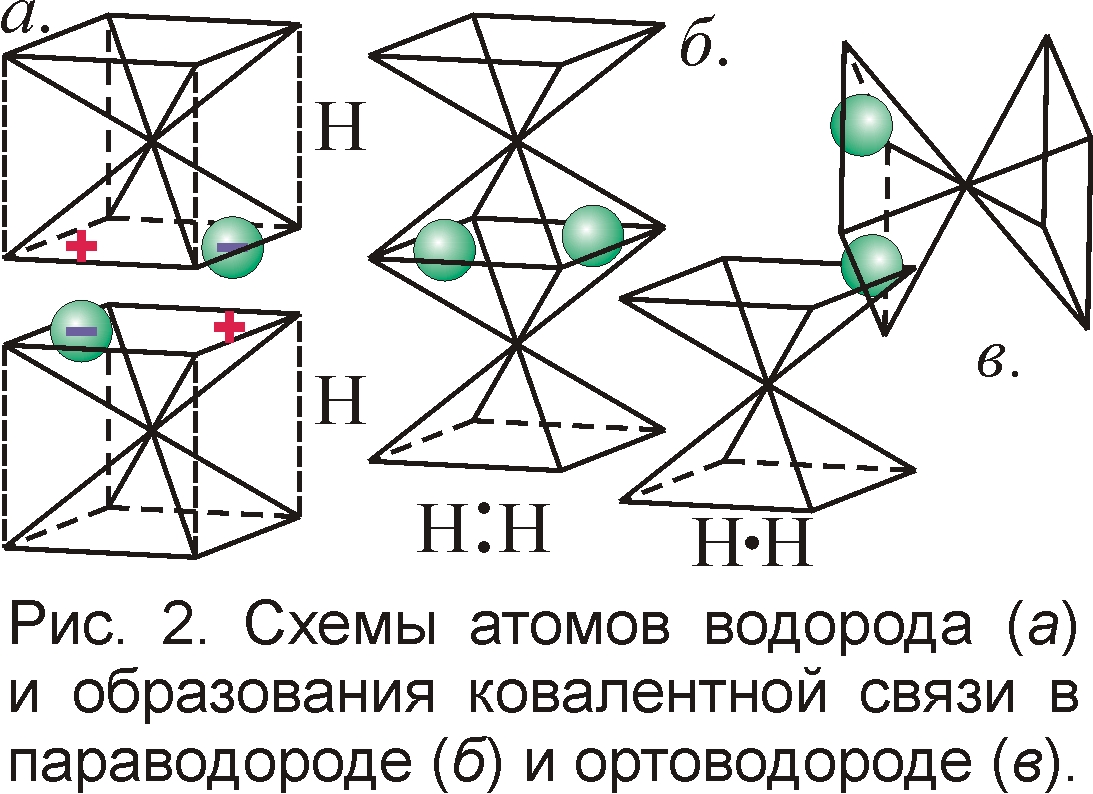
    У двухатомных молекул могут вымерзать и колебательные степени свободы. При охлаждении атомы в молекулах сковываются всё большим числом связей и прекращают колебания, образуя жёсткие молекулы, отчего исчезает связанная с колебаниями теплоёмкость. Так, спад теплоёмкости обнаружен у молекулярного водорода H₂. Атомы водорода скованы ковалентной связью из двух электронов. При нагреве рвётся сначала одна связь, затем – другая, и двухатомный газ постепенно становится одноатомным. И наоборот – при охлаждении, что проявляется в спаде теплоёмкости газа (рис. 1). При высоких температурах атомы в полужёстких молекулах колеблются, у них 7 степеней свободы, и C_V=7R/2. У атома водорода в электронном слое всего два места, и лишь одно занято электроном (рис. 2). Электрон второго атома водорода попадает в вакантное место, образуя химическую связь. А пустое место в слое второго атома заполняет электрон первого. Так возникает молекула водорода H:H, где атомы H связаны ковалентной связью из пары электронов, обозначаемых точками. Т.е. ковалентная связь объяснима классическим кулоновским притяжением электрона к положительному потенциалу вакансии в остове атома, без квантовых заморочек. Радиус действия и длина такой связи определяется размером атома, поскольку поле мультиполя спадает на расстоянии порядка размера системы зарядов. При высоких температурах T у большинства молекул H₂ одна связь порвана, и молекула H·H – полужёсткая: её атомы могут вращаться, колебаться вокруг точки связи – электрона. При малых T энергии не хватает для разрыва связей, и атомы образуют жёсткие молекулы H:H, а теплоёмкость снижена до C_V=5R/2 (рис. 2).

    В водороде одновременно есть молекулы типа H·H и H:H. При охлаждении теплоёмкость убывает от C_V=7R/2 до 5R/2 ввиду плавного изменения доли молекул H·H и H:H. В лаборатории даже удалось разделить водород на два компонента – ортоводород и параводород, с разными свойствами и теплоёмкостями [5, 6]. При низких T, когда число связей максимально, водород почти целиком состоит из параводорода [7], очевидно, образованного частицами H:H. А ортоводород, возникающий при нагреве, состоит из частиц H·H. Поскольку ортоводород можно перевести в параводород и обратно химическими методами (нагрев-охлаждение, катализаторы [7, Ч.1, с. 333]), то они отличаются лишь структурой связей. Не зря параводород H:H удаётся перевести в ортоводород H·H электрическим разрядом, применяемым для ионизации молекул, разрыва атомных связей. В чистом виде параводород и ортоводород получить сложно: всегда образуются их смеси. За счёт столкновений связи постоянно рвутся и восстанавливаются: обеспечивая баланс между молекулами орто- и параводорода, поочерёдно обращающихся друг в друга. При нагреве падение доли параводорода H:H (C_V=5R/2) и рост доли ортоводорода H·H (C_V=7R/2) наращивает теплоёмкость их смеси.

    Спад теплоёмкости твёрдых тел при охлаждении тоже объясним в рамках классической физики [4, 5]. В зависимости от числа связей между молекулами, они связаны жёстко или подвижно. При охлаждении число связей растёт, и кристалл становится более жёстким. А при T=0 K кристалл по сути – одна жёсткая молекула. Объединение молекул в сверхкристалл подтвердил и эффект Мёссбауэра: есть кристаллы, где атомы объединены в сверхрешётку и движутся как одно целое, а воздействие на один атом воспринимает сразу весь кристалл [7].

    Второй температурной аномалией является сверхпроводимость – потеря сопротивления при низких температурах. Несмотря на развитую квантовую теорию сверхпроводимости, до сих пор не удалось создать высокотемпературные сверхпроводники, у которых сопротивление исчезает уже при комнатных температурах. А новые сверхпроводники ищут больше наугад [8]. Поэтому много надежд возлагают на классические теории сверхпроводимости [9–11].

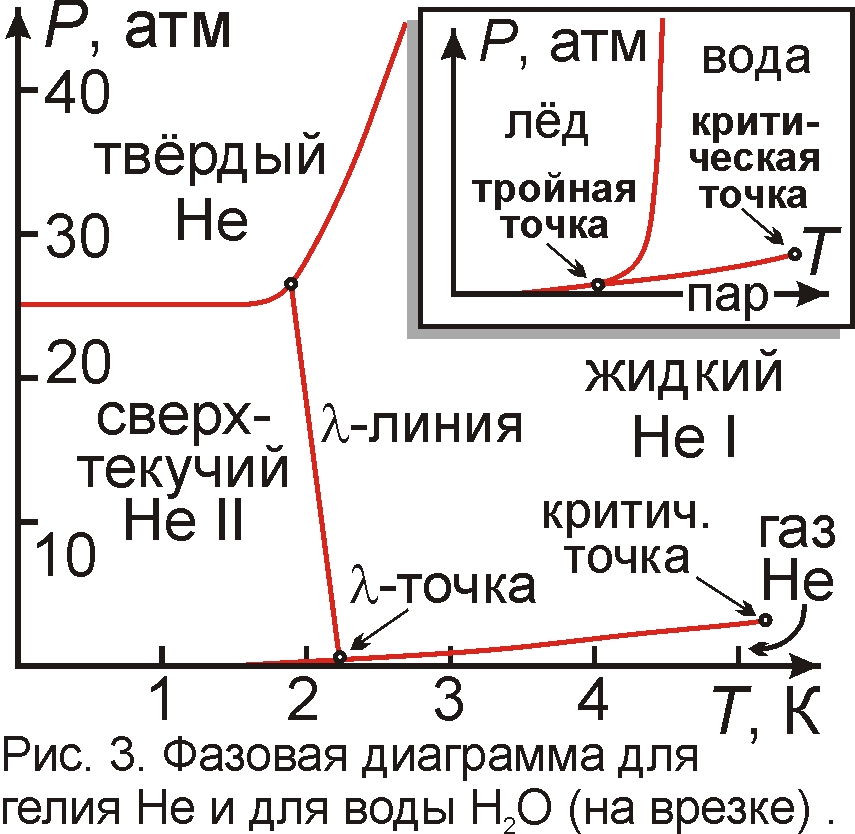
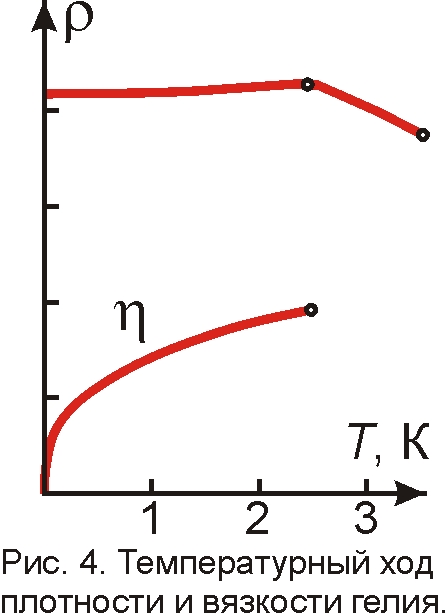
    Ещё одна температурная аномалия – сверхтекучий гелий (рис. 3). Его способность течь без вязкости по каналам можно объяснить тем, что на деле это не жидкость, а газ [12]. А у газов вязкость при спаде T снижается по закону η=a(T)^1/2, где a – константа. Примерно так и меняется вязкость η у сверхтекучего гелия (рис. 4). Кроме того, сверхтекучесть проявляется лишь при протекании гелия через тонкие капилляры (10^–4 мм) и пористые тела. Это означает, что происходит сепарация гелия: по капиллярам легче всего проходят наименее энергичные атомы гелия, движущиеся с минимальными скоростями, образующие гелий ничтожной вязкости η. Поэтому в капилляры просачивается только гелий со сверхнизкой температурой и наименьшей вязкостью, а более вязкие и высокотемпературные фракции – отфильтровываются. Принцип как в хроматографии: идёт сепарация молекул за счёт разницы их подвижностей. Пористые фильтры с капиллярным эффектом делают и из пучка свитых металлических проволочек, образующих фитиль, по которому гелий быстро перетекает из верхней колбы в нижнюю [3]. На деле такой фитиль ускоряет ток гелия за счёт теплообмена между сосудами: он охлаждает колбу, нагретую при оттоке из неё сверхтекучего гелия [4], снова делая его текучим. Это напоминает историю М. Задорнова про северного умельца, выделявшего спирт из тормозной жидкости: на морозе жидкость стекала по стальному лому, и вязкие фракции вымерзали, а легкотекучие, спиртовые стекали в бутылку. То же происходит и с гелием.

    Газообразность сверхтекучего гелия подтверждает и кипение при его образовании из обычного жидкого гелия [12], и его огромная сжимаемость [2] характерная для газов, а жидкости почти несжимаемы. Обычно газы занимают весь предоставленный объём, а сверхтекучий гелий собирается на дне сосуда, подобно жидкости. На деле тяжёлые газы обычно тоже собираются на дне колбы. Поэтому можно переливать, словно воду, из стакана в стакан и другие тяжёлые газы, например хлор, собирающийся на дне стакана. А сверхтекучий гелий, судя по всему, образован даже не одноатомными или двухатомными молекулами, а огромными конгломератами из сотен, тысяч атомов (z~10³) – это уже нанокристаллы, хотя и неразличимые глазом (размером ~0,01 мкм), поэтому гелий выглядит прозрачным [12]. В итоге высота h, на которую в среднем взлетают молекулы гелия, определится из условия kT=Mgh – равенства их кинетической тепловой энергии и потенциальной энергии подъёма на высоту h. Отсюда h=kT/Mg~4 см, где k – постоянная Больцмана, T~1 К – температура гелия, M=mz – средняя масса молекулы (кристалла) гелия из z атомов массы m, g – ускорение свободного падения. Тогда гелий и впрямь не может подняться выше стенок стакана и собирается на его дне, растекаясь подобно жидкости или атмосфере Юпитера, Сатурна. При этом плотность гелия фиксирована, поскольку при увеличении концентрации кристаллов гелия, они чаще сталкиваются и разбиваются на части меньшей массы M, отчего высота подъёма h растёт. Т.е. добавление гелия в сосуд приводит не к росту его концентрации, а к увеличению уровня. Даже при абсолютном нуле гелий остаётся сверхтекучим, нанокристаллы не останавливаются, не смерзаются, т.к. испытывают, кроме тепловых, и нулевые колебания, имеющие не квантовую, а чисто классическую природу, связанную с постоянными ударами реонов по атомам [10]. Из-за встряски атомов гелия среда из кристаллов становится текучей как в опыте с песком, который при встряхивании ведёт себя словно жидкость, как показали Гук и Брэгг [13, с. 72]. Не зря на рынке сахарный песок насыпают слегка встряхивая совок и кристаллы песка “текут” как жидкость, а у гелия атомы и кристаллы встряхивают удары реонов. Наличие в сверхтекучем гелии нанокристаллов-снежков обосновывают и сами физики, например Р. Аткинс [14]. В опытах даже наблюдали эти тонущие в гелии кристаллы и взвесили нанокристаллы весом в сотни атомов гелия [2]. Можно их обнаружить и рентгенографией.

    Скорость звука в сверхтекучем гелии c=240 м/с и мало зависит от температуры. Но для идеальных газов скорость звука c порядка средней тепловой скорости молекул V, которую легко определить по средней кинетической энергии атомов MV²/2~3kT/2. При T=1 К получим c~80 м/с. Поскольку газ не идеален, т.к. расстояния между частицами гелия сопоставимы с их размерами, то истинная скорость выше. Ведь атомы передают звуковой импульс частично в газовой среде, а частично в твёрдой – в нанокристаллах гелия, по которым звук распространяется на порядки быстрее: c~1000 м/с. В итоге скорость звука промежуточная с~240 м/с, и почти не зависит от T, так как при охлаждении спад скорости атомов гелия компенсируется ростом размеров кристаллов и доли пути, проходимой звуком в твёрдой среде: атом при ударе в кристалл с одной стороны, ведёт к отделению атома с другой стороны кристалла с той же скоростью, как в маятнике Ньютона. Есть и так называемый “второй звук”, который чуть меньше и задан скоростью передачи тепловых колебаний. Если в однокомпонентных газах скорости 1-го и 2-го звука совпадают, то в экзотических газах, где размер частиц варьирует, эти скорости отличаются. Кроме того, твёрдая среда подразумевает наличие двух типов волн – продольных и поперечных, с разной скоростью. Кристаллы сверхтекучего гелия при временном слипании могут образовывать и твёрдую среду, сеть, при малом изменении давления, встряске становящейся текучей, подобно железным опилкам в когерере Попова.

    Кстати, и сами физики сомневаются, жидкость ли сверхтекучий гелий, т.к. при λ-переходе пузырьки в гелии исчезают [2, с. 46]. Но считают гелий жидким, поскольку видна свободная поверхность и мениск. На деле их можно наблюдать и в газе, если его показатель преломления велик (у гелия ~1,01) и быстро меняется с высотой: именно так мы видим струи воздуха над костром и “водную поверхность” над нагретым от асфальта или песка воздухом, образующим миражи [15]. При этом на стенках сосуда, имеющих чуть иную температуру, чем основная масса гелия, его температура меняется, отчего мнимая граница гелия изгибается, образуя “мениск”. Так же и “капли”, “струи” сверхтекучего гелия удаётся увидеть за счёт его заметного показателя преломления и большого градиента. Примерно так можно видеть и струи морозного воздуха, втекающего в тёплое помещение и наоборот – струю пара, выходящего на мороз, за счёт конденсации пара при спаде температуры, образовании капель и кристаллов, формирующих туман, стелющийся по земле. Образует гелий и капли – это сгущения тумана из кристаллов, типа “снега”, хлопьев, выпадающих на некоторых планетах при вымерзании атмосферы, например хлопьев сухого льда на Марсе.

    Жидкостью сверхтекучий гелий считают и потому, что он якобы образует плёнку на стенках, с которой гелий вытекает из пробирки. На деле течь может и газ, если он проходит сквозь стенки, так как в стекле всегда есть микротрещины, непроницаемые для обычных жидкостей и газов, но не для сверхтекучего гелия [12]. Вот почему скорость вытекания гелия не зависит от длины пути по стенкам, но растёт при увеличении шероховатости стекла, числа его дефектов, царапин, трещин, по которым и сочится гелий [16, с. 127]. Просачивание гелия сквозь стенки подтверждает и то, что сужение в пробирке влияет на скорость утечки гелия лишь если расположено ниже внешней границы жидкости [3]. Оттого не влияет на скорость гелия и намотанная на пробирку нагретая проволока. При течении через фильтры гелий может даже перетекать в сосуд, где уровень выше, если в этом сосуде выше температура [12]. Это напоминает явление осмоса и подтверждает отличие молекул “холодного” и “тёплого” гелия, ведущих себя как разные газы: первый легко проходит через фильтр, а второй – нет. Т.е. фильтр аналогичен полупроницаемой мембране, обеспечивающей выравнивание давлений, концентраций по обе стороны только для одного сорта молекул – “холодного” гелия.

    Необычно происходит и переход сверхтекучего гелия в твёрдое состояние. Прежде всего, граница перехода из одного состояния в другое в осях PT горизонтальна (рис. 3). Это означает, что переход в твёрдое состояние происходит без выделения и поглощения тепла, с нулевой теплотой кристаллизации [2, 3, 17], хотя по термодинамике кристаллизацию должен сопровождать нагрев. Его отсутствие означает оседание на поверхность кристалла не отдельных атомов, а нанокристаллов. Идёт чисто механическое слипание кристаллов при их сближении под давлением. Примерно так не выделяется тепла при образовании сугроба из снежинок. Да и выглядит твёрдый гелий как сугроб: он лёгок, а граница между твёрдым и сверхтекучим гелием очень нечёткая, волнистая [14, 17] и колеблется при встряхивании, как у снежного холма, заноса, на который гелиевый ветер то наносит, то сдувает снежинки. Так и горка сухого цемента при встряхивании образует волны, буруны из парящих цементных частиц в виде аэрозоля, которые затем плавно оседают, образуя плавный переход от твёрдой к аэрозольной фазе. У гелия давление P=25 атм перехода из аэрозоля в твёрдое состояние соответствует условию постоянного контакта частиц. Поскольку давление растёт с концентрацией частиц, то при давлениях порядка атмосферного концентрация должна быть в q~25 раз выше, т.е. размеры частиц лишь в q^1/3~3 раза меньше расстояний меж ними. Оттого кинетику такого газа, далёкого от идеального, следует рассчитывать с учётом тройных столкновений и взаимодействий меж атомами, переходя к модели газа ВДВ и более сложным.

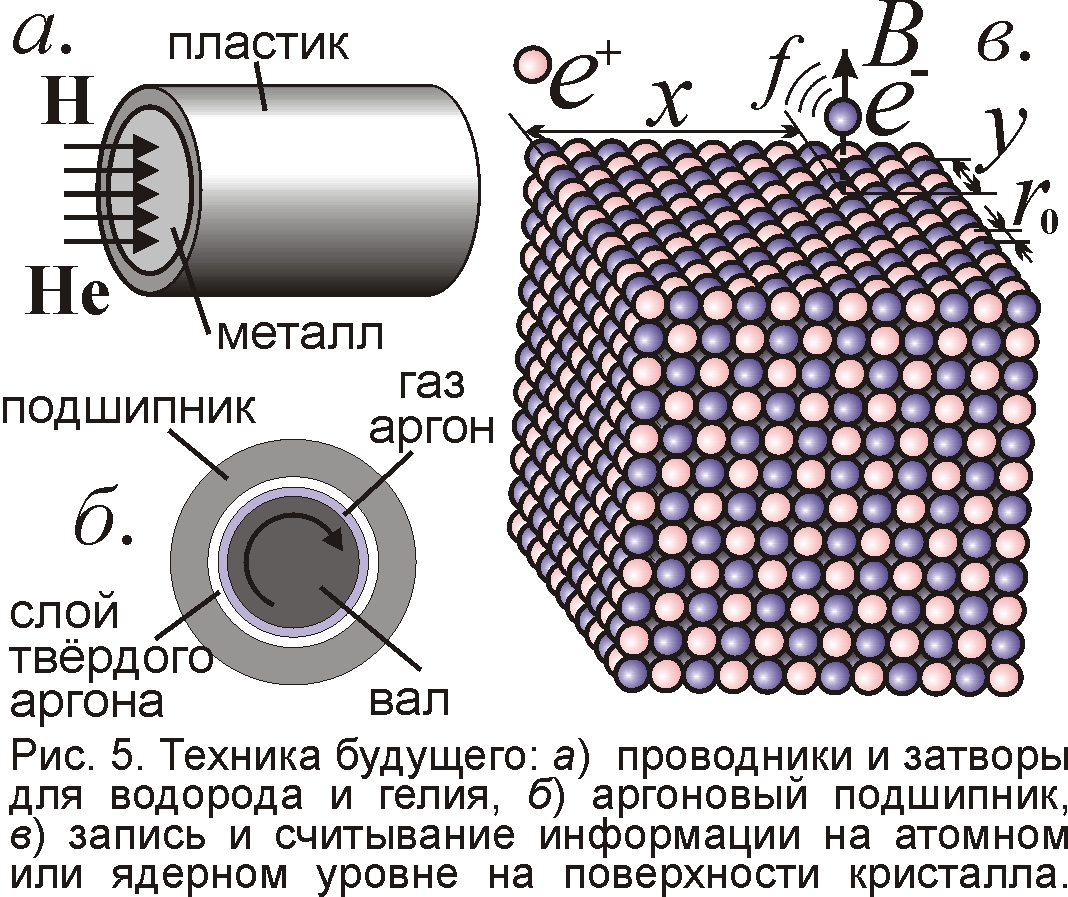
    Пористость твёрдого гелия подтверждает и аномально высокая диффузия в нём, растущая при снижении температуры, вопреки обычной диффузии. Поэтому такую диффузию назвали квантовой, хотя на деле наблюдается классический ток больших групп атомов, образующих в порах гелия газ с очень низкой вязкостью η, убывающей при охлаждении (рис. 4). Аналогично объясняется аномально высокая диффузия водорода в металлах при T≈0 K, поскольку в металле атомы водорода разобщены и ведут себя как газ, а вязкость газов мала при T≈0 K. Даже при обычной температуре герметичные металлические баллоны пропускают водород, который тоже можно назвать сверхтекучим, не зря с ним связывают надежды на создание новых типов сверхтекучести и сверхпроводимости [12, 18]. Той же природы сверхтекучесть у спин-поляризованного водорода и у газа из атомов рубидия, которым слипнуться и образовать жидкость или кристалл мешает магнитное поле. Недавно выяснилось, что сверхтекучестью обладает и твёрдый гелий – он может легко проникать через тончайшие поры, поэтому его называют квантовым кристаллом. На деле это следствие пористой молекулярной структуры твёрдого гелия, где атомы легко отрываются и текут по порам, образуя сверхтекучий гелий. Нечто подобное наблюдается для водорода в металлах [18]. По идее любой объект может быть переведён в сверхтекучее состояние, так что его атомы будут легко проходить сквозь стены (рис. 5), как в фантастических устройствах-плоскоходах и диффузоходах.

    Аналог сверхтекучести обнаружен и у обычных тонкодисперсных сыпучих тел, типа цемента, мелкого песка [19]. Они тоже напоминают жидкость со свободной поверхностью, текут, кипят, фонтанируют, представляя собой мириады кристаллов, которые при пересыпании движутся в воздушной среде, играющей роль смазки, с очень низкой вязкостью [20]. А сами микрочастицы, перекатываясь при контакте, играют ту же роль, что шарики в подшипниках, на порядки снижая трение. Не зря спортсмены-штангисты, гимнасты, игроки в бильярд снижают трение с помощью талька и мела. Таков же механизм образования “сверхтекучих” зыбучих песков – ещё одного примера текучей среды из твёрдых частиц. Сходно с потоком воды сходят с гор и потоки снега – снежные лавины. Аналогия сыпучих тел и гелия ещё раз доказывает, что сверхтекучий гелий может быть аэрозолем из нанокристаллов [21].

    То что сверхтекучий гелий образован нанокристаллами, подтверждается ростом его плотности ρ (рис. 4) при нагреве [3], а у жидкостей и газов плотность при нагреве падает. Единственное исключение – вода, рост температуры которой от 0 до 4 °C тоже наращивает плотность, видимо, за счёт плавления микрокристаллов льда [22], своей шестиугольной формой напоминающих кристаллы гелия [17]. У гелия рост плотности при нагреве связан с плавлением, измельчанием кристаллов, ростом их концентрации, т.е. вызван спадом расстояний и ростом силы притяжения меж кристаллами. В лямбда-точке эта сила и соединяет атомы гелия в жидкий гелий. То что плотность и ряд других свойств гелия не меняются при переходе на лямбда-линии из нормального в сверхтекучее состояние, не доказывает, что это фазовый переход 2-го рода, а означает, что на лямбда-линии гелий проходит через критическое состояние, в котором плотность и ряд других параметров жидкости и её паров совпадают. Действительно, у гелия критическая точка, в которой получают жидкий гелий (5,2 K), близка к λ-точке (2,2 K), которая может быть критической точкой для многоатомного гелия. λ-точка служит и тройной точкой [12], как видно из сходств диаграмм воды и гелия (рис. 3).

    Ещё один необычный эффект, открытый недавно,– аномально быстрый рост кристаллов гелия со скоростью в 10 раз выше теоретической [17]. Столь быстрый рост можно объяснить тем, что к кристаллическим плоскостям присоединяются уже готовые нанокристаллы, а не отдельные атомы, и происходит взрывообразный рост граней. При этом рост граней кристалла ускоряется и за счёт меньшей скорости нанокристаллов при той же температуре. Поэтому столкновение кристаллов происходит с меньшей скоростью (чем у атомов), и силы Ван-дер-Ваальса успевают сориентировать нанокристаллы до их присоединения. По той же причине грани кристаллов гелия получаются не плоскими, а скруглёнными (из-за поверхностного натяжения), поскольку происходит обрастание кристалла не отдельными атомами, а кристаллами, наподобие снежного кома, у которого грани лишь обозначены, так как некоторые кристаллы всё же успевают при контакте сориентироваться. Да и сами физики отмечают, что такой эффект возможен, если к кристаллу гелия присоединяются не отдельные атомы, а группы атомов [2]. При образовании совершенной грани гелия скорость нарастания, напротив, снижена [17], поскольку кристаллы должны соединяться так, чтобы не получалось полостей, как в игре “Тетрис”, а на это требуется время – пока найдётся кристалл соответствующей формы, или пока полость не заполнится доверху отдельными атомами.

    Сверхтекучесть гелия найдёт и важное практическое применение – для создания подшипников, где трение снижено до ничтожной величины. Можно применить не только гелий, но и другие инертные газы, у которых коэффициент вязкости мал в газообразном и в жидком состоянии. Так, могут найти применение неоновые, аргоновые, криптоновые и ксеноновые подшипники-антифрикционы (рис. 5). Как показали опыты, атомы инертных газов, адсорбированные поверхностью, снижают коэффициент трения, так что говорят о сверхскольжении [23]. Для этого не обязательно подавать газ под давлением в зазор между поверхностями, можно просто покрыть поверхности затвердевшими инертными газами. В этом случае при трении образуется жидкость или газ, т.е. жидкая или газовая смазка, снижающая трение [20]. Примерно так снижается коэффициент трения при движении санок, лыж, коньков по снегу, льду. Самыми дешёвыми будут аргоновые подшипники, ведь аргона много в земной атмосфере ~1%. Для подшипников подойдут и другие отвердевшие газы, например углекислый (сухой лёд), аммиак и т.д. Со временем для подшипников подберут газы, твердеющие, как вода, уже при температуре ~0 °C, например газы высокой молекулярной массы.

    Сверхтекучесть прокладывает мостик и на уровень микромира ядра, ибо одна из моделей ядра представляет его сверхтекучим [7, Ч. 2]. Как у сверхтекучего гелия, свойства ядер удаётся объяснить, считая их микрокристаллами (рис. 5) из элементарных частиц [24, 25]. А медленное сближение ядер повысит эффективность ядерных сил, успевающих, как в случае газов (рис. 1), ориентировать ядра, обеспечив холодный ядерный синтез. Из-за кристаллической структуры ядро имеет правильную форму. Поэтому протоны p и нейтроны n образуют сверхстабильные ядра, когда их количество равно магическим числам – 2, 8, 14, 20 и т.д. При росте массы ядра протонные и нейтронные слои растущей ёмкости чередуются, образуя ядро в виде пирамиды или бипирамиды (рис. 6). Если слои целиком заполнены, стабильность ядра выше. Так алхимия, “магия” чисел, превращений элементов нашли рациональное объяснение.

    Интересно, что в последнее время пирамидальное, тетраэдральное строение ядра подтвердил и опыт [26]. Давно выявлены в опытах и гантелеобразные ядра из двух симметричных половинок, наподобие бипирамиды [7, Ч. 2]. Магические числа складываются из так называемых удвоенных треугольных чисел вида i(i+1). Есть два способа образовать такие числа. Первый – при периодичном размещении частиц в виде квадратных или прямоугольных слоёв [24, 25]. Второй – при размещении частиц, как в бильярде, в виде треугольных слоёв (рис. 6) [27]. Первый способ проще, поскольку и сами протоны с нейтронами, предположительно имеют форму кубических кристаллов. В пользу второго способа свидетельствуют экспериментальные данные [26]. Если в ядре и нейтроны n, и протоны p соединяются попарно, тогда частицы при плотной упаковке, вплотную примыкая одна к другой, как раз образуют треугольные слои, гексагональную кристаллическую решётку. Если такие слои наложить один на другой, то при энергетически выгодной минимальной поверхности образуется ядро в виде тетраэдра. Интересно, что именно пирамидкой прежде складывали пушечные ядра.

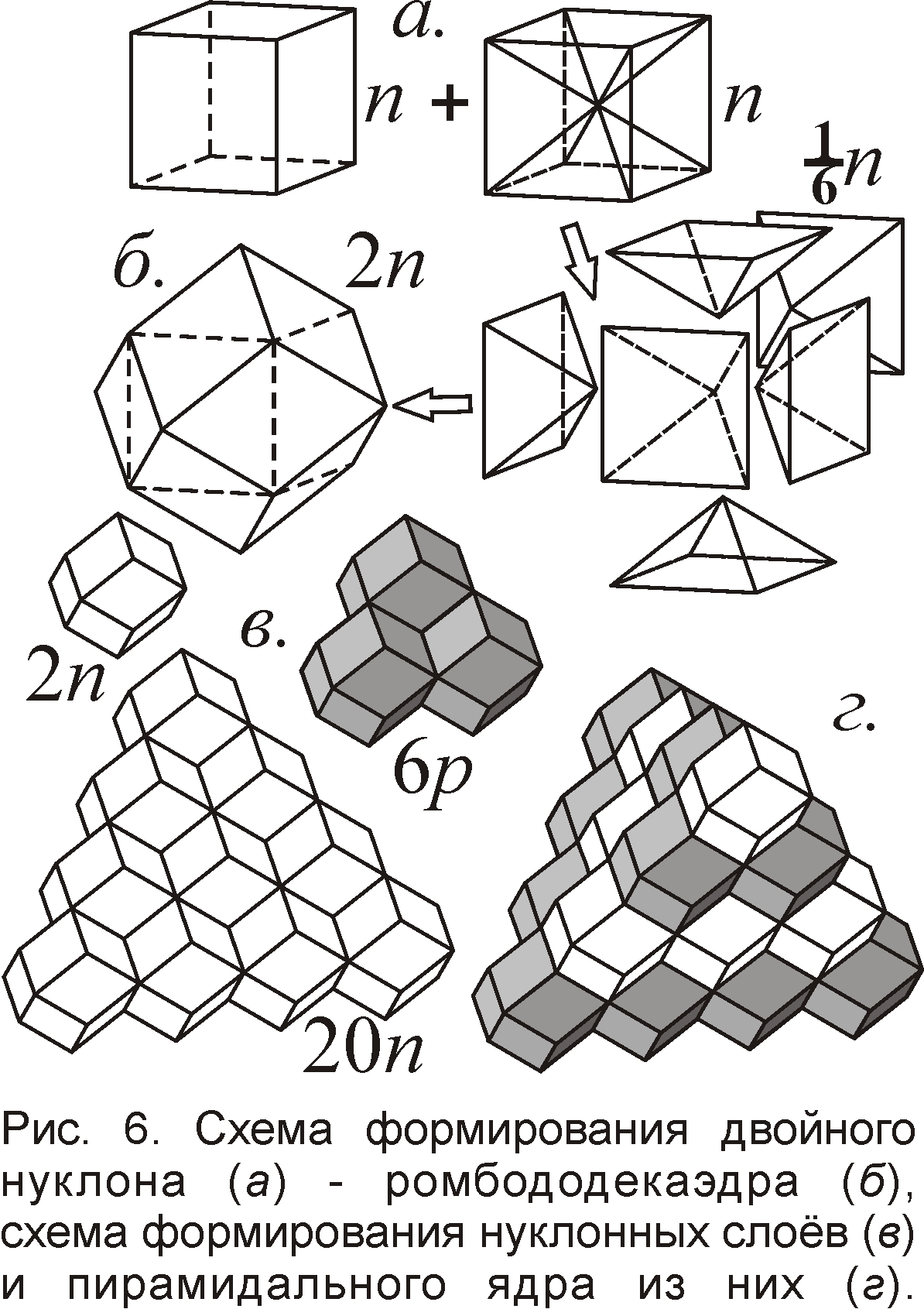
    Чтобы нуклоны в пирамиде были прочно связаны гранями, они должны иметь форму ромбододекаэдра (рис. 6), типичную для пчелиных сот, кристаллов граната [28]. Тогда соседние нуклоны плотно контактируют гранями, обеспечивая высокую интенсивность и насыщенность ядерных сил. Ромбододекаэдр легко образуется из двух нуклонов, имеющих форму куба (рис. 5), если один кубический кристалл рассечь по диагональным плоскостям спайности на шесть частей – пирамидок, соединённых вершинами в центре куба, а затем присоединить их квадратными основаниями к квадратным сторонам другого кубического нуклона. Такая метаморфоза идёт спонтанно, поскольку при этом минимизируется удельная поверхность частиц и максимальна энергия связи, не зря и в мире атомов широко распространены подобные сотовые, коробчатые, многогранные формы – ароматические соединения, графен, фуллерены. И точно, по современным теориям и экспериментам, нуклоны в ядре связаны попарно, образуя пары нейтрон-нейтрон и протон-протон. По этой причине более стабильны ядра с чётным числом протонов и нейтронов, а нуклоны часто вылетают из ядра парами – нейтрон-нейтрон, протон-протон или обе пары, собранные в альфа-частицу [7, Ч.2].

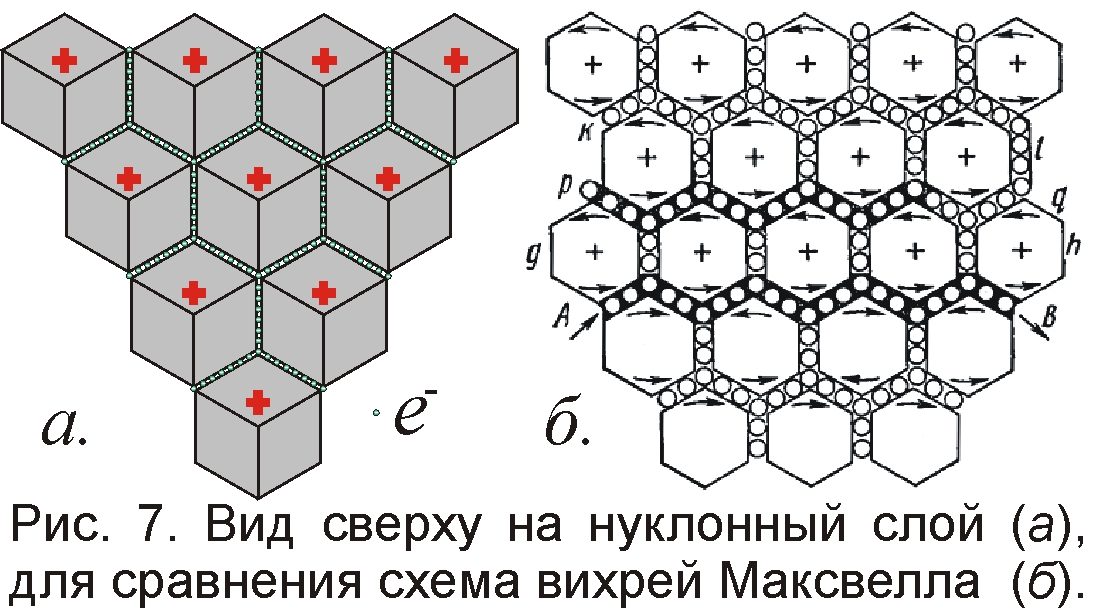
    Такие кристаллические структуры с трёхлучевой и шестилучевой симметрией естественно образуются, кристаллизуясь подобно снежинкам, дендритам. Так и многоярусный атом нарастает подобно дендриту морозного узора на стекле, на котором тоже ярус за ярусом кристаллизуются “ветви”. Выходит, прав был Кеплер – атомы и их ядра и впрямь напоминают шестиугольные снежинки [27, 28]. Уже сам Кеплер упоминал о форме ромбододекаэдров у микрочастиц. А ведь во времена Кеплера не то что о ядрах и протонах, даже об атомах ещё не знали. Интересен в этом ключе известный рисунок Максвелла с изображением эфирных вихрей в виде шестиугольных положительно заряженных ячеек, типа пчелиных сот, контактирующих через отрицательно заряженные частицы – электроны (рис. 7) – совсем как модель ядра. Выходит, и прежде физики интуитивно догадывались о структуре микромира.

    Похоже, и в глубокой древности люди знали или догадывались об устройстве микромира, атомов, поскольку на многих древних символах встречаются изображения многоярусных пирамид со встречными вершинами – мандалы и т.д. Да и в современных символах, гармонизаторах энергии двойная пирамида – типичный элемент. Яркий пример – лечебная энергетическая пирамида А.Ф. Панова, гранёные бипирамиды культуры Ньюэйдж и т.д. Возможно, эти символы в культуре возникли не случайно, а отражали структуру микромира.

    Однако возможности для внедрения этих знаний в практику, в криотехнику появились лишь недавно. Так, представления о кристаллическом строении атома и ядра позволят построить новые элементы памяти и микропроцессоры атомных размеров [27]. Атомы охлаждённого вещества, не испытывая соударений и внешних воздействий, смогут долго сохранять электроны в узлах (рис. 5). Это позволит записывать и хранить информацию на атомарном уровне, использовать атом как триггер, переводя электроны в заданные узлы решётки pump-импульсом лазера. Считывание информации производят probe-импульсом с частотой f, соответствующей данному узлу. Координаты электрона в узле установят по резонансному отклику электрона. Рабочим веществом таких устройств могут быть атомы переходных элементов, включая атомы редкоземельных элементов, с богатым спектром частот, т.е. вариантов размещения электронов в атоме. Не зря в лазерной технике в качестве активных центров применяют именно элементы переходных групп – хром, эрбий, иттербий, тулий, неодим и т.д.

    На некоторых типах атомов, где электроны с трудом занимают отдельные узлы, но легко их покидают (генерируя запрещённые линии), можно построить аналоги диодов и транзисторов. Тогда атом с набором узлов будет работать как микросхема, ячейка памяти. Более надёжны элементы на электронах внутренних оболочек, с резонансными частотами в рентгеновской области (их частоты f выше, ввиду меньшего шага решётки a), т.к. на них не влияют соседние атомы и температура. Из ансамбля атомов можно собрать кристалл-микросхему рекордно высокого быстродействия, малого размера и энергопотребления. Переключение элементов, считывание и запись информации осуществит луч лазера, послойно сканирующий кристалл. Более удобен ВУФ- или рентгеновский лазер, облучающий область размером 10^–9 м [29]. Т.к. рентген-микроскопия достигла разрешения в один атом, то X-лучи особенно удобны для записи и считывания информации с атомов. В кристалле с рёбром ~1 см число элементов ~10²³, т.е. в миллиарды раз больше, чем в любой из ЭВМ и в крупнейших ПЗУ.

    Описание таких устройств возможно и на языке квантовой физики, где узлам и излучению электронов в них соответствуют энергетические уровни и переходы. А квантовые компьютеры аналогичны рассмотренным атомарным компьютерам. Другое применение магнитной модели – создание трёхмерных изображений-голограмм в воздухе. Для этого можно переводить молекулы воздуха в возбуждённое метастабильное состояние, пропуская воздух через область облучения УФ-лучами или лазерными pump-импульсами, а затем облучая воздух в заданных точках probe-импульсом, высвобождающим запасённую энергию. Обновление воздуха в области экспонирования позволит формировать динамичные картины – объёмные фильмы, для реализации 3D-телевидения. Подобные устройства уже существуют.

    Поскольку шаг r₀ электрон-позитронной решётки в 10⁵ раз меньше шага a атомного остова (рис. 5), ядерные частоты колебаний f в 10⁸–10¹⁰ раз больше частот оптических атомных спектров, т.е. лежат в гамма-диапазоне, в согласии с опытом. Размещение электронов или протонов в узлах электрон-позитронного “кристалла” открывает ещё один способ записи и обработки информации – уже на ядерном уровне. Информация записана в виде координат x, y электронов или протонов в ядре. Т.к. энергии связи в ядрах много выше, чем в атомах, то для хранения информации не обязательно охлаждать вещество до температур близких к T=0 К, и можно построить сверхъёмкие носители информации и ядерные компьютеры, работающие при комнатной температуре. Таким образом, если современникам Максвелла атомные, эфирные вихри и шестерни в его теории напоминали станки и заводы, то в магнитной модели атом и атомное ядро напоминают электронные приборы (циклотрон, рупорную антенну) и полупроводниковые кристаллы, где по узлам решётки смещаются заряды. Сам атомный кристалл может выступать в качестве микросхемы. Это ещё одна иллюстрация фрактальной парадигмы, по которой мир на всех уровнях самоподобен, как пирамида Серпинского [30].

    Гипотезу о строении атомов и ядер легко проверить методом Лауэ: облучая атомы гамма-лучами с длиной волны ~10^–15 м, по дифракционной картине можно установить шаг и тип кристаллической решётки. Также кристаллическую структуру ядер можно установить по рассеянию высокоэнергичных частиц на ядрах [31]. Действительно, картина рассеяния имеет трёхлучевую симметрию и обнаруживает заряженные точечные центры рассеяния – партоны, представленные, очевидно, электронами и позитронами в ядре [24]. Кроме того, опыты показали, что при очень высоких энергиях сечение рассеяния аномально нарастает, т.е. силы отталкивания растут при увеличении энергии, скорости рассеиваемых частиц. Именно такую зависимость сил от скорости предсказывает баллистическая теория Ритца. Мощное электрическое поле и лазерное излучение может вести к распаду таких ядер, при достижении порога E ~ e/4πε₀r₀² ~ 10¹⁹ В/см, при котором поле E разделяет электроны и позитроны, ведя к дезинтеграции частиц, распаду ядер, нарушая баланс сил притяжения и отталкивания (рис. 8). Для нестабильных ядер лазерное облучение и сильные поля E будут менять скорость распада. Такие эффекты, подтверждающие электрическую природу ядерных сил, обнаружены в экспериментах [32, 33]. Повысить КПД таких процессов можно, ориентируя ядра электрическим или магнитным полем и действуя лазерным полем в направлении наименьшей интенсивности сил связи между зарядами ядер [34]. Также можно рассекать “лазерным скальпелем” ядерный “кристалл” по “плоскостям спайности”, поочерёдно разрывая связи, создавая дислокации и другие дефекты, как в реальных кристаллах облегчающие деформацию и разрыв.

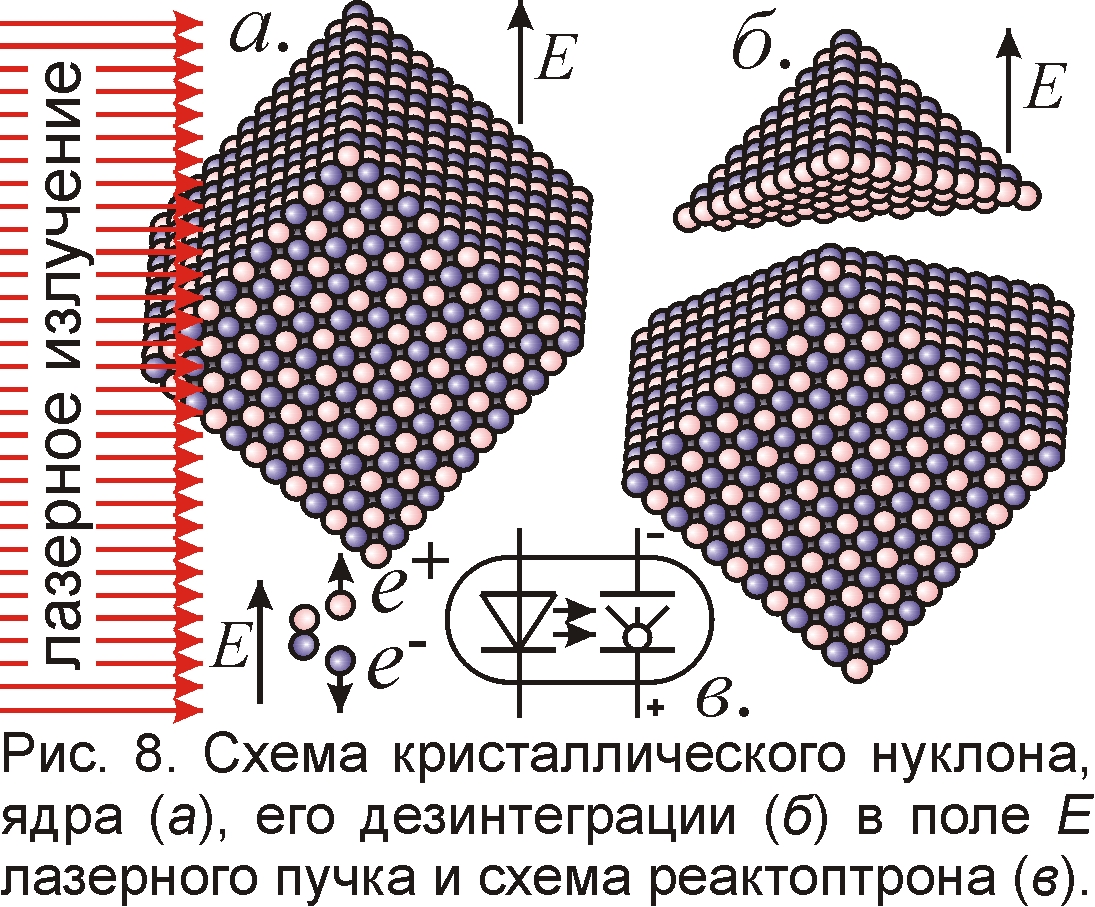
    Модель позволяет осуществить и реакции ядерного синтеза, если ориентировать ядра магнитным полем для максимизации ядерных сил и плавно сближать пондеромоторной силой в лазерном поле. Применение для этих целей полупроводниковых лазеров и KLM-лазерных микрочипов позволит реализовать компактные неисчерпаемые источники энергии (реактоптроны, рис. 8), встроенные в микросхемы для автономного питания. Усиливая α- или β-распад [33], дабы излучённые одним электродом α-частицы или электроны осаждались на другом, можно создать напряжение, ЭДС, регулируемые яркостью света. Микропроцессор не потребует особой защиты от излучений, т.к. проникающая способность α- и β-лучей мала.

    Хотя открытие сверхтекучести сделано русским физиком П.Л. Капицей, и криотехнологии наиболее интенсивно развивались в СССР (в лаборатории Л.В. Шубникова), развитие криотехнологий в основном идёт на западе. Одна из причин – сверхтекучесть мозгов в 1990-е годы, когда государство совершенно охладело к науке, а сопротивление границ страны потеряло контроль и стало нулевым. Теорией сверхпроводимости и теорией Ритца до 1990 гг. активно занимался В.С. Околотин [35], а после лихих 90-х все исследования заморозили. Также теорией сверхтекучести занимались физики Л.Б. Болдырева и Н.Б. Сотина, ныне развивающая эти исследования в США [36]. О результатах поиска новых сверхпроводников отечественные учёные тоже докладывают из-за рубежа [8]. Впрочем Россия быстро восстановила лидерство и в этой области. Так, аномалии кристаллизации гелия были открыты в 1996 г. именно в России и Финляндии [17] – странах, славящихся своими холодами. Также в России классическую теорию кристаллизации сверхтекучего гелия и строения ядер автор докладывал на 50-м научно-техническом семинаре-миниконференции в ННГУ (22 октября 2015 г.) и на 2-й Российско-Белорусской конференции им. Лосева (17 ноября 2015 г.) [27]. Кстати, именно со сверхпроводимостью связывают освоение левитации и летающего транспорта. Поэтому в России исследование экстремальных температур и освоение криотехнологий, начатое северным помором М.В. Ломоносовым, должно стать приоритетным направлением.

Источники:

Дата установки: 28.03.2016
Последнее обновление: 5.05.2016
[вернуться к содержанию сайта]

W