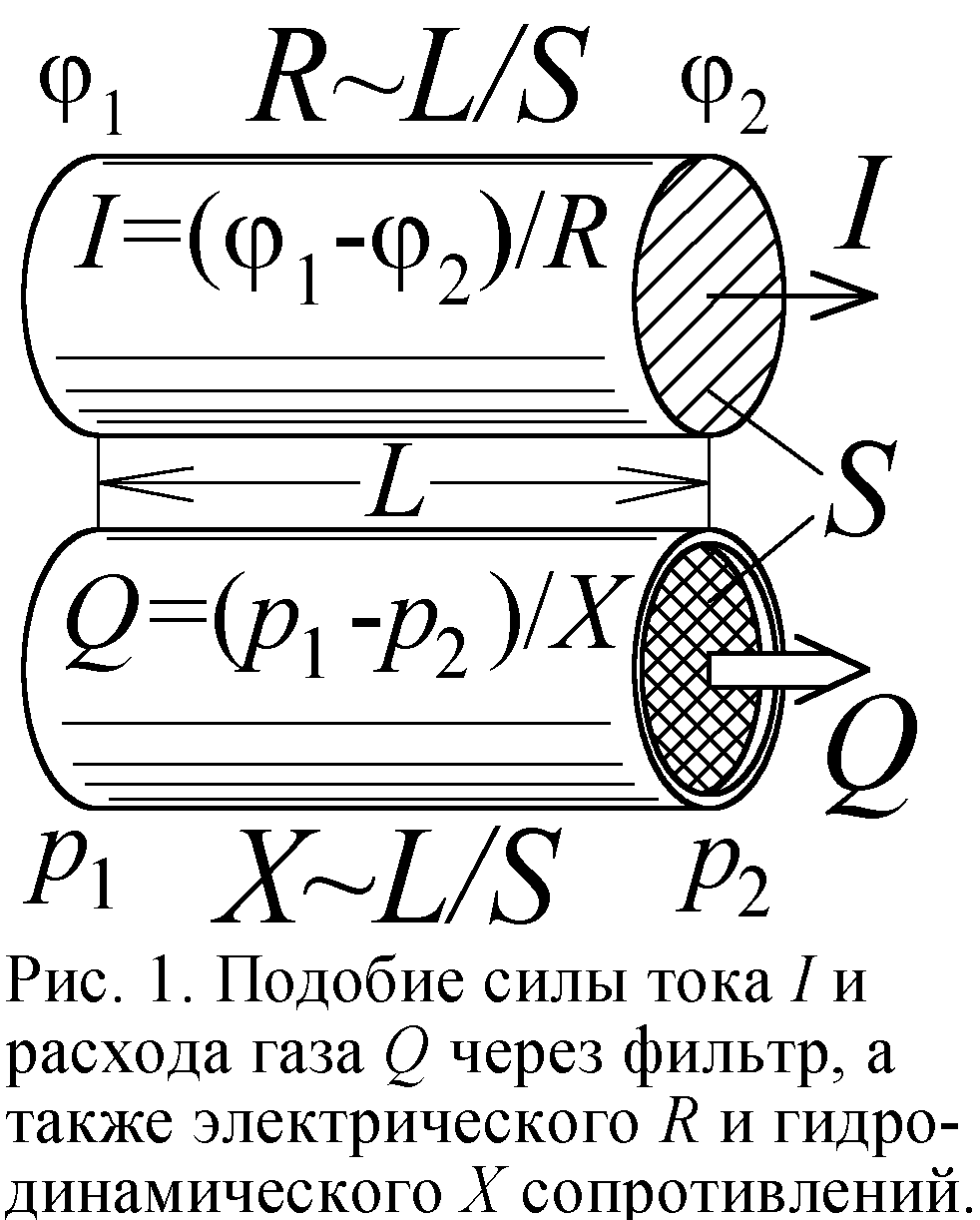
[вернуться к содержанию сайта]
Казалось бы, что уж проще и наглядней электрического сопротивления? Закон Ома, резисторы, электрические потери в проводах и выделение тепла нагревательными приборами, – со всем этим мы знакомы с детства. Однако теоретики нагнали столько тумана в интуитивно всем ясное явление сопротивления, что его природа стала тайной за семью печатями. Случилось это, когда сопротивление отнесли к квантовым явлениям, которые уже нельзя представить наглядно, а можно лишь описать формулами, отрёкшись от здравого смысла и приняв на веру догматы квантовой механики. Но наглядный классический подход и здесь отнюдь не исчерпал себя, а зачастую даже лучше объясняет загадки сопротивления, чем квантмех.
Электрический ток в металлах представляет собой направленное движение электронов – течение своего рода электронного газа, в котором роль атомов играют электроны. И подобно тому, как обычные газы испытывают сопротивление от движения по трубопроводу, так и электронный газ, протекая по проводнику, тормозится им. То есть возникает электросопротивление, микроскопическая картина которого подобна той, что существует в газе. Атомы газа, сталкиваясь друг с другом и с атомами стенок трубопровода, усиливают их колебания, расходуя на это часть своей кинетической энергии. Это и вызывает сопротивление току газа и соответствующий нагрев трубопровода, ибо рост колебаний атомов означает рост температуры. Вполне естественно, что долгое время так же объясняли и электросопротивление.
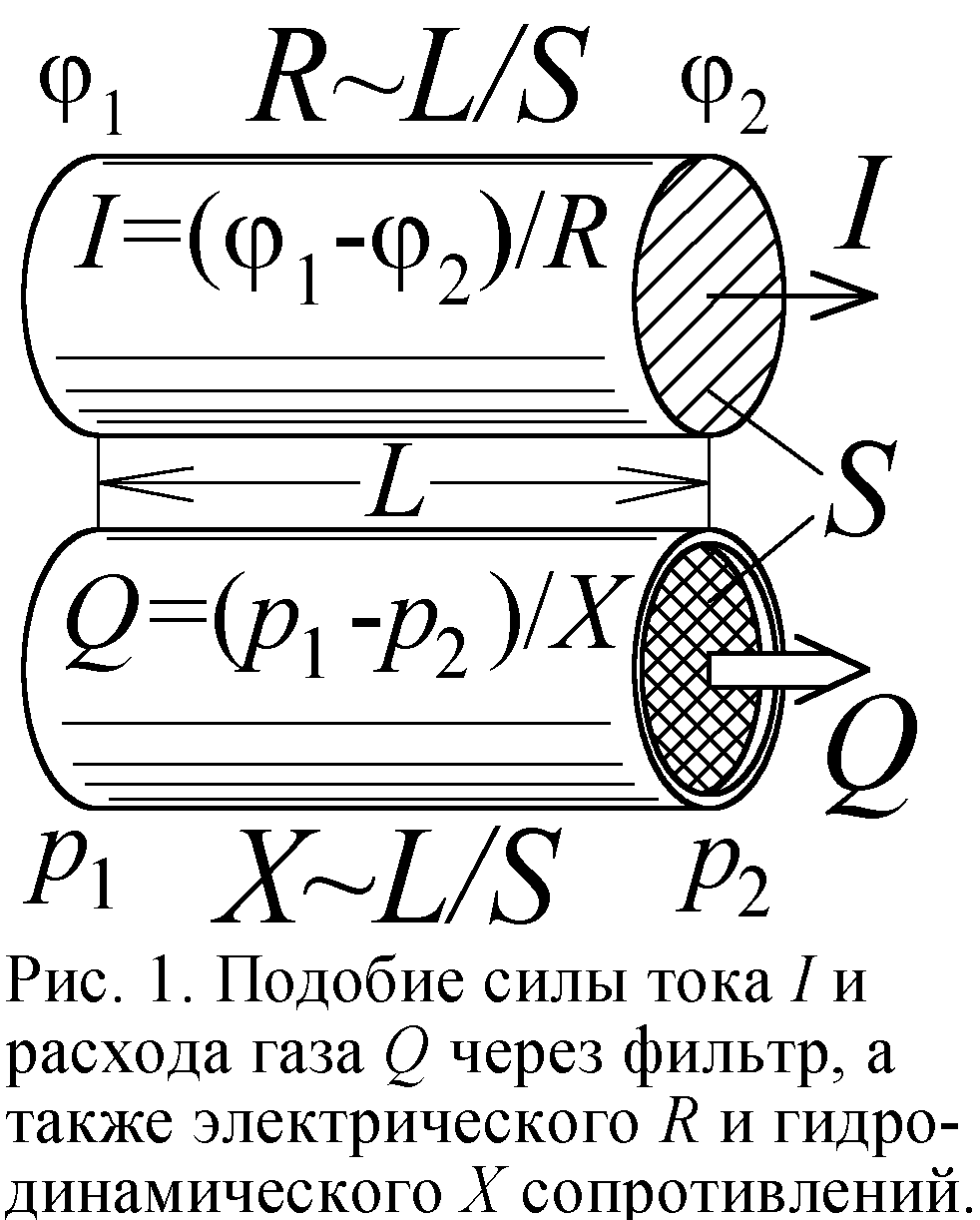
Электроны, набрав в электрическом поле скорость, то и дело теряют часть её в столкновениях с ионами металла, усиливая их колебания. Так создаётся электросопротивление и выделяется джоулево тепло от идущего тока. Не зря электроток в проводнике легко моделировать с помощью газа, текущего через трубку-фильтр (рис. 1). Расход газа через эту трубу подчиняется точно тем же законам, что и ток в проводнике – он пропорционален разности давлений (напряжению), площади сечения
S трубы и обратно пропорционален её длине L [1]. Удельное же сопротивление такой трубы, как у металла, растёт с повышением температуры (рис. 2). Соединяя трубы, можно моделировать и разветвлённые электросети (рис. 3).
Но современные учёные отвергают это простое и наглядное объяснение сопротивления проводников. По их мнению, сопротивление связано с рассеянием электронов на фононах – возбуждениях кристаллической решётки металла [
2]. После абсурдных фотонов – квантов света, выдумали фононы – кванты звука, квазичастицы упругих колебаний. Учёные сочли, что упорядоченная кристаллическая решётка металлов в идеале вообще не оказывает сопротивления движению электронов. Однако атомы примесей, дефекты и тепловые колебания кристаллической решётки нарушают её идеальность. И чем сильней искажена решётка металла, тем хуже он проводит ток. Именно этим в квантовой физике объясняют температурный рост сопротивления металлов и его заметную прибавку при введении даже ничтожной примеси. Полагали, что такое объяснение сопротивления много лучше классического. На самом же деле как раз квантовое объяснение не выдерживает критики.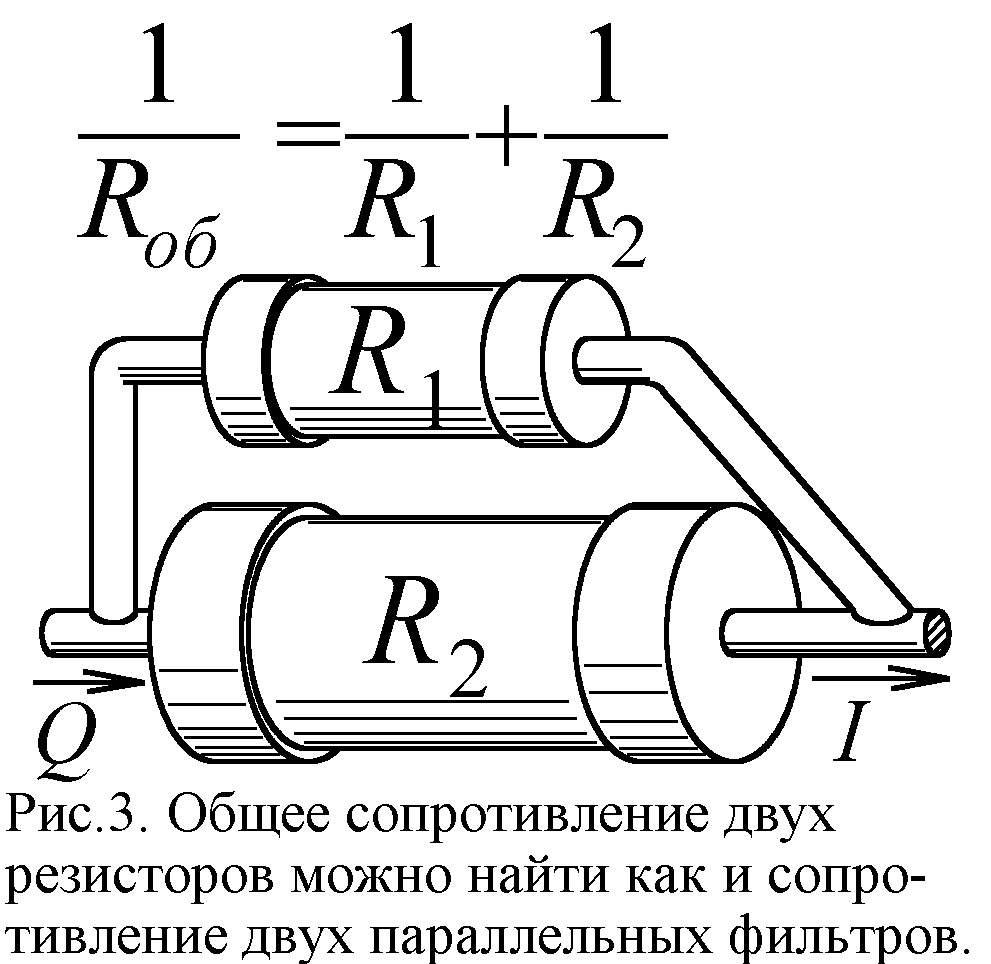
Ведь по квантовой теории расплавленные металлы, у которых полностью разрушена кристаллическая решётка, вообще не могут проводить ток. А меж тем они проводят ток почти так же хорошо, как твёрдые, кристаллические. Скажем, жидкая ртуть, которую мы обычно наблюдаем при температуре на 60 градусов выше точки её плавления, была бы по квантовой теории диэлектриком. Однако удельной электропроводностью она не слишком уступает другим металлам (например, свинцу лишь в 5 раз), а такие металлы как висмут даже превосходит. Да и меняется при нагреве сопротивление жидкой ртути совсем как у твёрдых металлов.
Вообще металлы в момент плавления увеличивают сопротивление всего в полтора-два раза [
3]. Уже одного этого достаточно, чтоб отвергнуть как ошибочную квантовую трактовку сопротивления. Ведь, если по квантовой теории даже ничтожные искажения кристаллической решётки, вносимые фононами и примесными атомами, заметно наращивают сопротивление, то в расплаве, где порядок кристаллической решётки предельно нарушен, сопротивление росло б неограниченно. Но самое смешное, что некоторые проводники при плавлении не только не увеличивают сопротивления, но даже, напротив, уменьшают его тоже в полтора-два раза. Таковы металлы висмут, сурьма, галлий и полупроводник германий [3, с. 126].Столь странное поведение проводников с точки зрения квантовой теории совершенно загадочно. Но мы легко решим эту проблему, если заметим, что все эти материалы – висмут, сурьму, галлий и германий – объединяет другое аномальное свойство. Если все прочие металлы и полупроводники при плавлении расширяются, то эти четверо сжимаются, уменьшая свой объём на несколько процентов. Это убедительно доказывает, что кристаллическая решётка и её дефекты сами по себе не влияют на сопротивление: основную роль играет плотность размещения атомов вещества. И рост сопротивления металлов при плавлении связан лишь с их расширением – отдалением атомов. Зато металлы, уменьшающие объём при расплавке, уменьшают и удельное сопротивление. По той же причине взаимосвязаны скорость звука в металле и его проводимость – и то и другое растёт вместе с плотностью вещества.
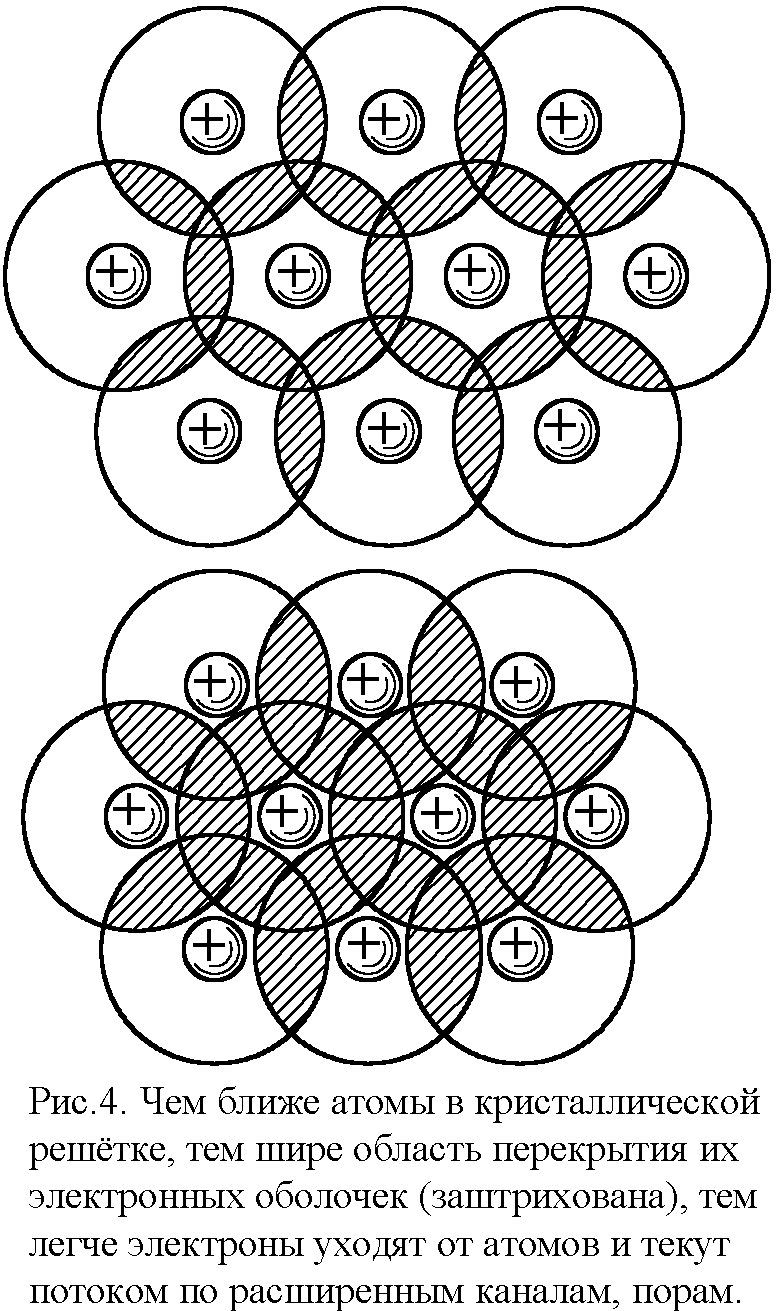
Классически это легко объяснить. Известно, что проводимость пропорциональна числу носителей заряда – свободных электронов. Вот почему при нагревании, освещении (внутренний фотоэффект) сопротивление диэлектриков и полупроводников падает: их обычно связанные электроны обретают скорости, достаточные для отрыва от атомов, и начинают участвовать в переносе заряда. К тому же ведёт и рост плотности металла: его атомы сближаются, их электрические поля всё больше перекрываются, и электронам требуется всё меньше энергии для отрыва от атомов и участия в переносе заряда (рис. 4). Электроны всё меньше взаимодействуют с атомами, что как бы наращивает ширину "пор" металла, сквозь которые сочится электронный газ. Потому-то рост плотности и снижает сопротивление.
И точно, давно замечено, что металлы, наращивая под давлением плотность, уменьшают сопротивление. Так, сопротивление хрома под давлением p уменьшается на 6·10–7p своей начальной величины. Более того, при сжатии под огромным давлением становятся проводниками даже диэлектрики, к примеру, водород, сера. А некоторые материалы, скажем, кремний, германий, переходят под большим давлением в сверхпроводящее состояние. Не исключено поэтому, что температурный рост сопротивления вызван отчасти температурным расширением тел. А у металлов с отрицательным термическим коэффициентом расширения можно ожидать и минусовой термический коэффициент сопротивления. Поэтому, интересно было б узнать, как меняется сопротивление веществ, сжимающихся при нагреве, – магнитных сплавов, германия возле -243 °С, плутония выше 400 °С, а также хрома в районе 37 °С – температуры, возле которой хром вдруг перестаёт менять объём. Впрочем, сопротивление должно меняться и в зависимости от состояния электронного газа. Ведь скорость течения газа через фильтр зависит как от размеров и формы пор фильтра, так и от свойств газа.
Прежде считали, что классическая теория проводимости Друде не может объяснить, почему введение даже малой примеси в чистый металл заметно меняет его сопротивление. Так, введение в медь всего 1 % марганца увеличивает её сопротивление в три раза. Ясно, что столь сильное влияние связано с нарушением примесными атомами правильной кристаллической решётки меди. Поэтому в квантовой теории проводимости сочли, что именно строгая периодичность решётки обеспечивает проводимость. Но на деле дефекты решётки просто меняют плотность металла и связывают электроны. Все знают, что уложенные правильными рядами предметы занимают меньший объём, чем беспорядочно сваленные. Вот и дефекты, примесные атомы, нарушая порядок, распирают металл и увеличивают его сопротивление. Так что и здесь важна не сама кристаллическая решётка, а лишь её межатомные расстояния.
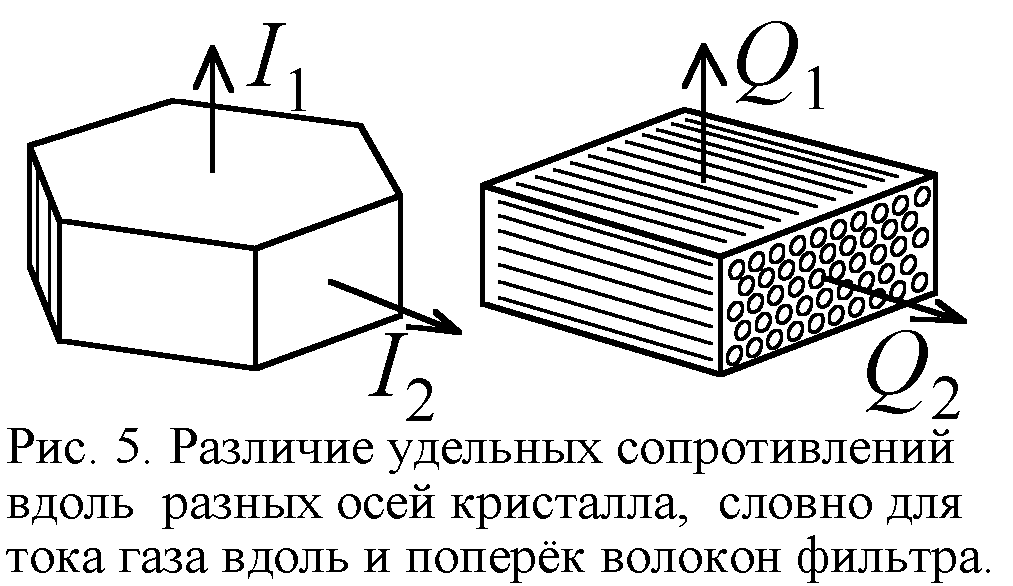
По той же причине заметно разнятся удельные сопротивления разных кристаллических модификаций одного и того же металла. Каждой упаковке атомов отвечает своя плотность и свои межатомные расстояния. Важную роль играет и пространственное их расположение. Недаром сопротивление металлического кристалла зависит от направления, в котором идёт ток (рис. 5). Также сопротивление металла во многом зависит от его механической и термической обработки, меняющей структуру и плотность металла, за счёт изменения величины зёрен, кристаллической модификации, числа дефектов. В классической теории проводимости учитывалось лишь состояние электронного газа и почти не уделялось внимания материалу (фильтру), по которому он тёк. Но вместо того чтоб учесть влияние материала, физики совсем отказавшись от наглядной картины проводимости, заменив классическую теорию квантовой. И хоть классический подход пока не везде достаточно развит количественно, зато квантовая теория даже качественно не способна правильно описать многие явления.
Далее рассмотрим тайны сверхпроводимости [
4]. Как многие отмечали, квантовая её теория в корне ошибочна, с чем и связано крайне ограниченное применение сверхпроводников, которые по идее должны бы уже давно произвести революцию в технике. Поэтому большие надежды в последнее время возлагают на классическую теорию сверхпроводимости. Любой газ, в том числе электронный, постепенно теряет вязкость с падением температуры (рис. 2). Поэтому, согласно классической теории, при абсолютном нуле сопротивление должно стать нулевым: металл перейдёт в сверхпроводящее состояние. Но реально сверхпроводящее состояние наступает даже до того. Электроны, образующие электронный газ, как и атомы обычных газов, имеют разные скорости, подчиняющиеся максвелловскому распределению (рис. 6). Поэтому в металле всегда есть электроны с почти нулевой скоростью. При комнатной температуре их ничтожно мало. Однако возле абсолютного нуля процент таких электронов уже заметен, и они способны создавать токи достаточной величины.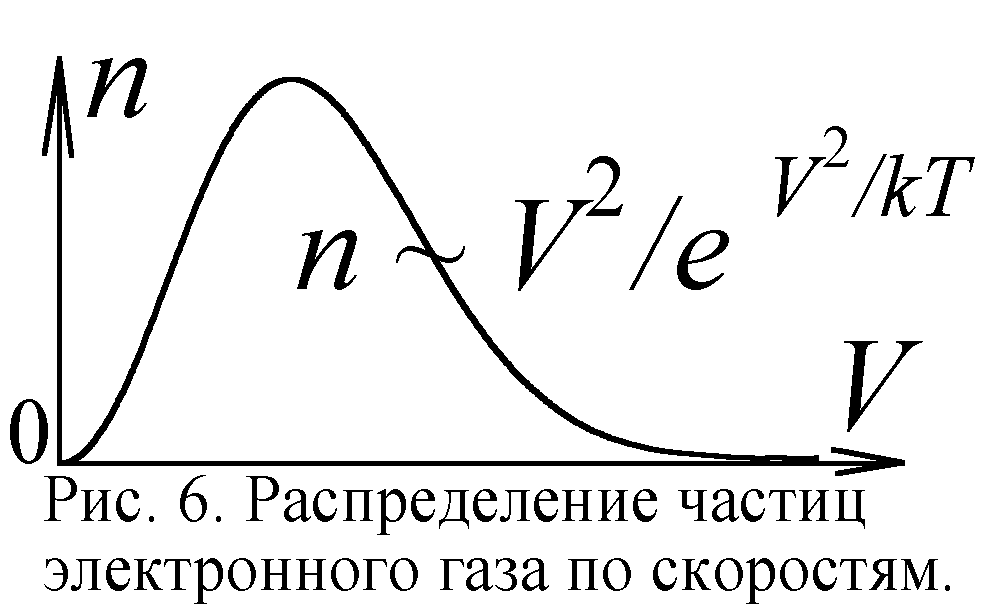
Конечно, быстрых электронов больше, но, образуя электронный газ высокой вязкости, они создают лишь ничтожные токи в сравнении с токами медленных электронов (так же идёт разделение в порах быстрых и медленных молекул сверхтекучего гелия [
1]). А потому вносимое ими сопротивление ничтожно. Наличие токов медленных и быстрых электронов аналогично протеканию тока через два параллельных резистора, первый с малым сопротивлением, второй – с большим: почти весь ток идёт по резистору R1, а сопротивление второго не заметно (рис. 3). С другой стороны, именно быстрые электроны могут вызывать ничтожно малое, но всё ж ощутимое сопротивление сверхпроводника. Не исключено, что их ток и задаёт величину критических токов и магнитных полей, разрушающих сверхпроводимость.Настоящей загвоздкой для квантовой теории проводимости стало открытие сверхпроводников, которые при высоких температурах становятся диэлектриками. Зато по классической теории при низких температурах диэлектрики вполне могут быть сверхпроводниками. Диэлектрик лишь потому не проводит ток, что в нём почти нет свободных электронов: все электроны связаны с атомами. Думали, что по классической теории диэлектрики вообще не проводят ток [
2, с. 22]. На деле же из-за разброса скоростей (рис. 6) в диэлектрике всегда есть электроны со скоростью достаточной для отрыва. С ростом температуры и скорости электронов всё большая их часть отделяется от атомов и переносит заряд, с чем и связан рост проводимости диэлектриков при нагреве. Но у диэлектриков с высокой степенью теплового расширения возможен заметный рост проводимости и при охлаждении. Ведь охлаждаемый диэлектрик, уменьшаясь в объёме, сближает атомы, их поля всё больше перекрываются, высвобождая много электронов. Для этих диэлектриков сжатие охлаждением аналогично сжатию давлением, превращающим их в проводники. Поэтому у диэлектриков при низких температурах вполне могут открыться металлические и сверхпроводящие свойства.Итак, поведение электронов в веществе вполне соответствует законам классической механики и термодинамики. Квантовая же механика, мало того, что "безумна", так ещё и даёт предельно ошибочные предсказания, хоть теоретики и привыкли твердить, что квантовый подход лучше классического. Чтобы ещё раз доказать адекватность классического описания движения электронов, рассмотрим для них напоследок туннельный эффект.
Известно, что электрон может покинуть металл, лишь затратив энергию равную работе выхода
A. Вот почему для интенсивного вылета электронов из металла нужен нагрев. Только так возникают электроны со скоростями и энергиями достаточными для ухода с поверхности (термоэлектронная эмиссия). В холодных же металлах энергия электронов мала. Но, как оказалось, электроны всё же покидают металл, если приложить снаружи достаточно сильное электрическое поле. Считали, что по классической теории такое невозможно. Ведь для того чтоб электрон набрал в электрическом поле энергию выхода, ему надо пройти там некоторый путь, отойдя от поверхности. А чтоб выйти из металла, нужна энергия выхода. Получается порочный круг: электрон мог бы набрать требуемую энергию, если б перепрыгнул через энергетический барьер, но для этого ему и нужна энергия [5]. Но электроны как-то выходят, словно беря энергию взаймы и следуя не поверх барьера, а сквозь него, как сквозь туннель. Вот почему данный туннельный эффект считают возможным лишь по квантовой механике.И всё же туннельный эффект не доказывает квантовых фантазий о размытом в виде волны электроне, но допускает чисто классическую трактовку, если правильно истолковать работу выхода. Прежде всего, подвижные электроны, даже в холодном металле, то и дело покидают его поверхность, придавая ей положительный заряд, который тянет электроны обратно (рис.7). В итоге над поверхностью любого металла реет облако взмывающих и падающих электронов – своего рода электронная атмосфера, окружающая металл тонким слоем. Эта прослойка и задаёт работу выхода. Каждый электрон, вырвавшись с поверхности металла, влетает в облако, электрическое отталкивание которого создаёт силу
FT, тянущую электрон назад. Электрон между отрицательно заряженной вершиной облака и положительно заряженной поверхностью оказывается как меж пластин конденсатора с запирающим полем.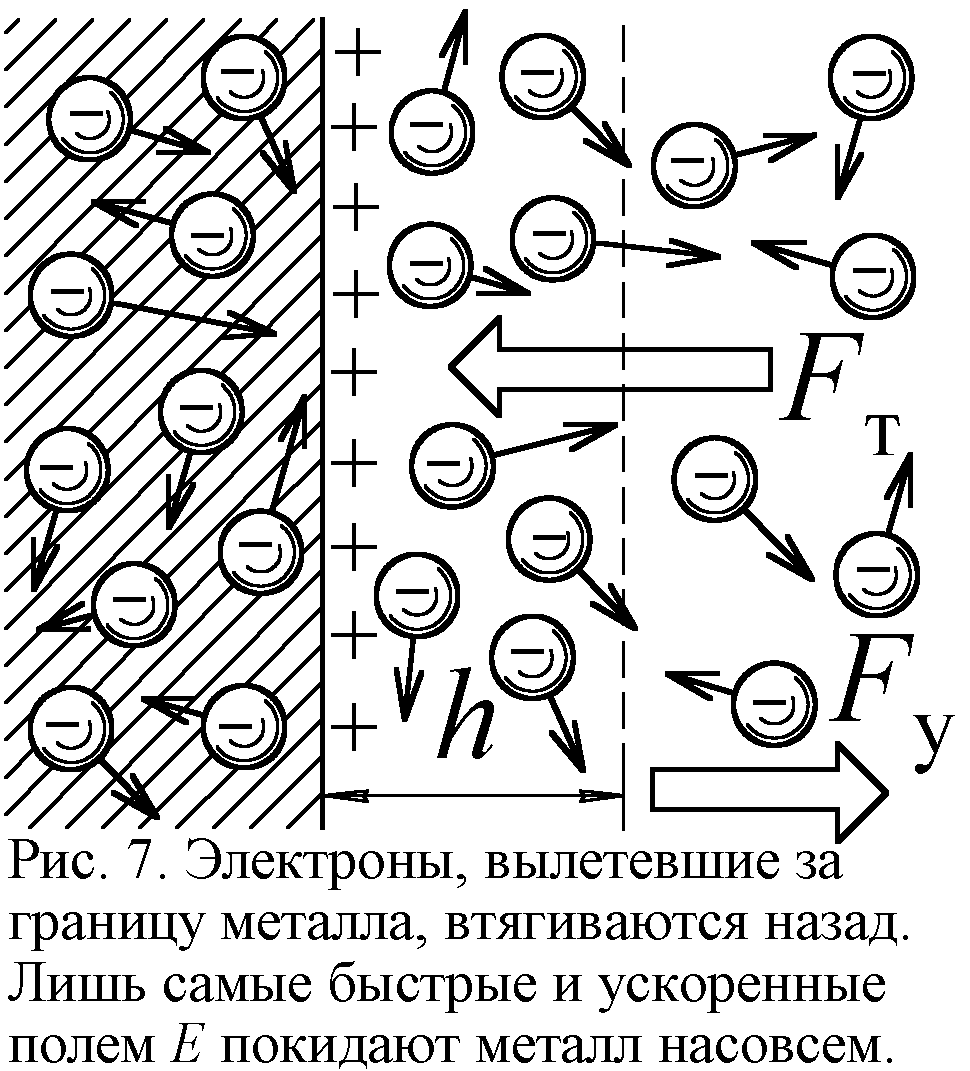
По сути, тонкий слой электронного газа, обволакивающий поверхность металла, аналогичен атмосфере Земли, атомы которой тоже не могут уйти в космическое пространство, поскольку для этого необходимо преодолеть земное притяжение, совершив своего рода работу выхода. Но скорости атомов меньше первой космической, и, взлетев до некоторой высоты, они возвращаются к поверхности. Лишь у планет с горячей атмосферой или малыми размерами атомы непрестанно утекают в пространство. Подобно концентрации атомов в атмосфере, концентрация электронов падает с удалением от поверхности по экспоненциальному закону. И лишь редкие высокоскоростные электроны доходят до верхних слоёв облака.
Нагрев металла ускоряет движение электронов, и всё большему их числу удаётся покинуть металл. Так возникает термоэлектронная эмиссия, аналогичная утечке атомов газа из нагретой атмосферы. В случае холодной эмиссии реализуется иной вид утечки – не от роста скорости частиц электронного газа, а от падения запирающей силы и работы выхода (это соответствует утечке газов с малых планет, не способных удержать атомы своим полем). Ведь при холодной эмиссии электрон находится не только в запирающем поле электронной атмосферы, но и во внешнем ускоряющем поле
E, которое снижает возвратную силу FT и позволяет электронам, преодолев притяжение металла, покинуть его насовсем.Прежде считали, что внешнее поле не способно придать достаточную энергию электрону, поскольку внутри металла электрическое поле отсутствует, а выйти из металла электрон по прежним представлениям не мог. Реально же электроны вылетают из металла и на пути
L набирают в поле E энергию EL. Так внешнее поле успевает сообщить электрону энергию A достаточную для полного вылета из металла. Здесь и впрямь наблюдается своего рода туннельный эффект: электронный газ выходит на некоторую высоту из металла, не будучи скован его границам, словно он и впрямь размыт. Но размытость эта не имеет ничего общего с квантомеханической неопределённостью положения и энергии электрона, с его представлением в виде волны. Явление имеет чисто классическую природу, ибо газы и атмосферы, в том числе электронные, не могут иметь чётких границ. Их граница всегда условна, размыта.И численно ток электронов при холодной эмиссии вполне соответствует классической теории. Как было сказано, концентрация электронов в приповерхностном слое металла спадает с расстоянием
h от границы по экспоненциальному закону, подобно плотности земной атмосферы с высотой: n~e–h/kT. Набрать энергию A, достаточную для полного улёта от металла, способны только электроны, прошедшие в ускоряющем поле путь L=A/E. Иначе говоря, покинуть металл смогут электроны, взлетающие на высоту h>L. Число их легко найти интегрированием их концентрации n~e–h/kT в пределах h от высоты L до бесконечности. Отсюда найдём, что процент электронов от всех вылетевших и способных покинуть металл, пропорционален e–L/kT= e–A/kTE. Эта зависимость тока холодной эмиссии и была найдена в опытах [5]. Кстати, зависимость e–A/kT от температуры T верно описывает и ток термоэлектронной эмиссии.Похоже объясняется туннельный эффект для двух металлических пластин, отделённых тонким слоем диэлектрика. Электроны одной пластины влетают внутрь диэлектрика и при малой его толщине могут пройти в другую пластину. В отсутствие напряжения этот поток уравновешивается обратным. Но под напряжением через такой контакт пойдёт небольшой ток, величина которого экспоненциально растёт с температурой и с уменьшением толщины диэлектрика. Такое же тонкое электронное облако создаётся на спае двух металлов, имеющих разную концентрацию электронов, чем и обусловлена контактная разность потенциалов.
Итак, движение электронов в веществе подчиняется законам классической механики, а поведение электронного газа – классической аэрогидродинамике и термодинамике (разве что с мелкими поправками). Классическая теория металлов Друде была неточной не по вине классического подхода, а от недоучёта роли проводящей среды и межэлектронного взаимодействия. Перспективы применения классической механики в материаловедении и физике твёрдого тела грандиозны, но малоизученны. Слишком долго наука шла по тупиковому пути квантовой механики, с чем и связаны её нынешние проблемы и застой. Мало того, что оказались ненадёжны опытные основы квантовой физики (фотоэлектрический, комптоновский и туннельный эффекты), квантовая механика вообще не смогла объяснить ряд явлений. Поэтому только классическая физика позволит, наконец, решить проблему высокотемпературной сверхпроводимости и создать новые материалы с уникальными свойствами, не говоря уж о том, чтобы сделать в проблеме сопротивления всё тайное явным и наглядным.
С.Семиков
Источники:
1. Сверхтекучий гелий – газ? // "Инженер" №2, 2007.
2. Волькенштейн Ф.Ф. Электроны и кристаллы. М., 1983.
3. Уманский Я.С., Скаков Ю.А. Физика металлов. М.: Атомиздат, 1978.
4. Кресин В.З. Сверхпроводимость и сверхтекучесть. М.: Наука, 1978.
5. Сивухин Д.В. Атомная и ядерная физика. Ч.1. М.: Наука, 1986.
Дата установки:
10.11.2007