
[вернуться к содержанию сайта]
Перед вами четыре различных по жанру произведения. Изящная миниатюра-шутка “Новогодний подарок, или О шестиугольных снежинках” поражает безудержной игрой воображения, отточенностью формы и глубиной идеи, позволяющих автору предугадывать правильные ответы на многие вопросы геометрии формообразования природных объектов; “Разговор с звёздным вестником, недавно ниспосланным смертным Галилео Галилеем, падуанским математиком” — написанный за рекордно короткий срок отзыв на сочинение собрата по едва зарождающемуся точному естествознанию, необычайно содержательный, блещущий новизной мысли и исполненный редкой благожелательности; “Сон, или Посмертное сочинение о лунной астрономии” — одно из первых произведений ныне столь популярной научно-фантастической литературы, изобилующее достоверными астрономическими деталями. Четвёртое произведение, гороскоп, представляет собой автопортрет, достойный кисти великого мастера, написанный рукой, беспощадно бичующей пороки оригинала как действительные, так и мнимые, надуманные или по крайней мере явно преувеличенные. Все четыре произведения принадлежат перу великого астронома и естествоиспытателя Иоганна Кеплера.
Мы надеемся, что наш читатель, знавший Кеплера лишь как учёного, откроет для себя Кеплера-писателя. Желая облегчить знакомство с произведениями, написанными более трёх веков назад, мы поместили в конце книги примечания переводчика. В них содержатся сведения о первоизданиях всех четырёх произведений Кеплера, помещённых в данном сборнике, переводах их на новые языки и объяснения наиболее важных слов и реалий.
Пользуясь случаем, мы хотели бы поблагодарить кандидата философских наук В. П. Визгина, члена-корреспондента АН СССР И. И. Гуревича, доктора физико-математических паук М. Л. Левина за ценные замечания. Мы искренне признательны профессору К. А. Куликову и профессору И. И. Шафрановскому, любезно предоставившим в наше распоряжение редкие и труднодоступные издания, необходимые в работе над переводом.
Ю. Данилов, Я. Смородинский
Поскольку мне доподлинно известно, сколь сильно ты любишь Ничто не по причине его незначительной ценности, а скорее как прелестную забаву шаловливо щебечущего воробья, то нетрудно догадаться, что любой дар будет для тебя тем приятнее и желаннее, чем сильнее он будет походить на Ничто.
Ведь в любом случае для того, чтобы размышления о ничтожном доставили тебе удовольствие, оно должно быть и малым, и почти неощутимым, и малоценным, и наименее протяжённым, то есть быть почти Ничем. В природе встречается великое множество таких вещей, но между ними имеются различия. Вспомни хотя бы об одном из атомов Эпикура: такой атом и есть Ничто. Разумеется, тебе и прежде случалось получать от меня Ничто. Итак, нас будут интересовать элементы, то есть самое малое из того, что есть в каждом предмете 2
.Прежде всего обратимся к Земле. Не будем грезить о сокровищах Архимеда, разложившего Землю на мельчайшие песчинки, 10 000 которых умещается в одном маковом зёрнышке 3
. Стоит изъять лишь одну-единственную песчинку из великого множества их, как собьётся весь его счёт мириадов песчинок. Кроме того, форму песчинок нельзя увидеть глазом, и Архимед также умалчивает о ней. Поэтому его песчинки ничего не говорят разуму и не рождают страсть к неизвестным вещам. К тому же мелкие песчинки обладают протяжённостью, поскольку пыль и труха заполняют старые, насквозь прогнившие балки. Я подарил бы тебе слишком много, если бы вздумал подарить тебе такую песчинку.Искры огня, хотя они малы и быстро гаснут, всё же меньше осколков пирита, которые удаётся отбить, ударив камень о камень, и не уступают но размерам частицам копоти от горящих углей, которые я также отношу к пылинкам. “Фигурные пирамиды”, которые мне никогда не приходилось видеть, я оставляю Платону 4
, чтобы он мог создавать из них огонь.Я могу подарить тебе ветер и дым, но если они и продаются, то не в исландских кожаных мехах, а на бумаге и словах, причём так происходит по всему земному шару, Таким образом, дым — вещь ценная, а мне обходится ещё дороже. Для умозрительного рассмотрения он
не подходит, поскольку беспорядочен и бесформен.Обратимся, наконец, к воде. Приставшую к сосуду каплю священные псалмопевцы почитают весьма важной вещью. А наши германцы ничто не ценят меньше, чем капельку вина, которую, опорожнив кубок, стряхивают на ноготь, чтобы посмотреть, прилипнет ли она. Если бы я принёс такую каплю, то подарил бы тебе меньше, чем знаменитый перс, предложивший своему царю пригоршню воды из реки Хаосп. Капля вина с ногтя германца была бы более почётным подарком, чем обкусанный обрезок ногтя отрицающего такую малость итальянца. Наконец, шаровидная форма капли наводит на геометрические размышления, однако я опасаюсь, что она недостаточно мала для тебя, столь любящего Ничто.

А что если нам перейти к животным? Я боюсь их, как афинских сов. Однако недавно я видел у тебя несколько томов о вещах удивительных и редких одного из тех авторов, которые в духе учения древнего Парменида отвергают движение на том основании, что одна его часть (а именно прошлое) не совершенна. Поскольку в этом сочинении шла речь о многих диковинных животных, то не думаю, чтобы совсем крохотные твари были обойдены молчанием. Впрочем, оставим догадки. У тебя имеются замечания Скалигера5
к работе Кардано6 “О тонких материях”. В упражнении CXCIV из раздела 7 ты встретишь упоминание о крохотном существе — подкожном клеще. Но и клещ слишком велик. Ведь это существо может ползать и не лишено души. Стану ли я предлагать тебе душу, если отказываюсь дарить тебе даже неодушевлённую каплю? Вряд ли ты можешь надеяться и на то, чтобы, разрезав труп бродячего животного, обнаружить в нём нечто новое, как показал анатом доктор Иессен.Погруженный в подобного рода размышления, я перехожу мост, терзаемый стыдом за свою невежливость: ведь непрестанно играя на одной и той же струне (предлагая Ничто или находя нечто мало отличающееся от него, но не дающее пищу твоему острому разуму), я оставил тебя без новогоднего подарка! И тут мне подворачивается удобный случай: водяные пары, сгустившись от холода в снег, выпадают снежинками на мою одежду, все, как одна, шестиугольными, с пушистыми лучами7
. Клянусь Гераклом, вот вещь, которая меньше любой капли, имеет форму, может служить долгожданным новогодним подарком любителю Ничего и достойна математика, обладающего Ничем и получающего Ничто, поскольку падает с неба и таит в себе подобие шестиугольной звезды!Её необходимо поскорее передать моему покровителю, пока мой крохотный подарок ещё твёрд и не обратился в Ничто под действием тепла, исходящего от тела.
Что за вещее слово! Что за предмет, столь любезный Вакгеру, питающему слабость к Ничему! Ведь если спросить у германца, что такое Nix (лат. — снег), то он ответит: Nihil (лат. — ничто), если только сумеет сказать на латыни.
Итак, прими сей дар, который очень походит на Ничто, и сделай серьёзную мину, а если ты благоразумен, то затаи дыхание, чтобы не оказалось, что ты и впрямь получаешь Ничто. Подобно Сократу, я вынужден говорить о блошиных прыжках: о том, почему снежинки, прежде чем сбиться в крупные хлопья, падают шестиугольниками и пушистыми, как пёрышки с шестью лучами.
Прочь убирайся, достойный презрения за своё невежество мужлан и сводник Аристофан! Что мне за дело до Сократа и до содержания аристофановой комедии8
? Лучше я обращу свои помыслы к царственному псалмопевцу, который, воздавая богу хвалу, упоминает о снеге, падающем, как пух9. Если я не ошибаюсь, то здесь речь идёт о моих снежинках с пушистыми лучами. Вероятно, однажды, когда он сидел усталый или стоял, опершись на пастушеский посох, и охранял своё стадо, ему довелось увидеть, как эти маленькие звёздочки падают на овечью шерсть и пристают к ней, и это запомнилось ему.Но шутки в сторону — займёмся делом. Поскольку всякий раз, когда начинает идти снег, первые снежинки имеют форму шестиугольной звезды, то на то должна быть определённая причина. Ибо если это случайность, то почему не бывает пятиугольных или семиугольных снежинок, почему всегда падают шестиугольные, если только они от соударений не утрачивают форму, не слипаются во множестве, а падают редко и порознь?
Когда я недавно рассуждал с кем-то на эту тему, то мы сошлись прежде всего на том, что причину следует искать не в веществе, а в действующем начале. Ведь вещество снега — это пар. Выделяясь под действием какого-то своего тепла из Земли, пар становится сплошным и как бы жидким. Следовательно, ни на какие звёздочки пар не разделён.
Ты спросишь, откуда мне это известно? Ведь даже если бы пар состоял из звёздочек, то этого нельзя было бы заметить, поскольку пар прозрачен. Отвечаю: пар возникает при разложении подземной влаги, о чём свидетельствует его лёгкость и то, что он возносится вверх. Фигуры при разложении не возникают, поскольку форму имеет лишь то, что способно само себя ограничить, ибо форму придают телу его границы. Возникающий при разложении пар по своим свойствам близок к жидкости и течёт, то ость не может сам себя ограничить, не имея какой-либо определённой формы, пока не сгущается в снег или в капли.
Но коль скоро установлено, что причина свойственной снегу шестиугольной формы кроется в действующем начале, то позволительно спросить, каково это действующее начало, как оно действует, является ли форма искони присущей телу или приобретается под влиянием внешних воздействий, принимает ли материал шестиугольную форму в силу необходимости или по своей природе и что следует считать врождённым: воплощенный в шестиугольном архетип красоты или знание цели, к которой приводит эта форма? Чтобы решить эти вопросы, мы обратимся к наглядным примерам, но станем рассматривать их геометрически. Для наших вопросов такой экскурс будет чрезвычайно полезен.
Если спросить у математиков, в каком порядке построены пчелиные соты, то они ответят, что в шестиугольном. Ответ прост и следует из рассмотрения отверстий, или входов, и стенок, образующих соты. Любая ячейка в сотах окружена шестью другими ячейками, каждая из которых имеет с ней по одной общей стенке. Взглянув на основание ячейки, ты увидишь три плоскости, образующие тупой трёхгранный угол. Основание, или, лучше сказать, донышко ячейки, соединяясь с её боковыми сторонами, образует шесть других многогранных углов, из которых три угла, расположенные повыше, имеют по три ребра и подобны трёхгранному углу, лежащему в основании ячейки, а три угла расположенные пониже, имеют по четыре ребра. Кроме того, следует иметь в виду, что соты расположены в два слоя: входы в ячейки одного слоя обращены в сторону, противоположную той, куда направлены входы в ячейки другого слоя, а их плотно закрытые донышки соприкасаются. Трёхгранное донышко одной ячейки входит между трёхгранными донышками трёх ячеек другого слоя так, что каждая ячейка соприкасается не только боковыми стенками с шестью примыкающими к ней ячейками того же рода, но и тремя плоскостями, образующими её донышко, с тремя ячейками из другого ряда. Таким образом, у любой пчелы оказывается по девять соседок, от каждой из которых её отделяет общая стенка. Все три грани донышка ячейки одинаковы и имеют форму, которую геометры называют ромбом.
Вспомнив о ромбах, я приступил к геометрическим изысканиям, чтобы выяснить, какое тело, аналогичное пяти правильным и четырнадцати архимедовым телам, можно составить из одних ромбов. Я нашёл два таких тела, из которых одно родственно кубу и октаэдру, а другое — додекаэдру и икосаэдру (третье тело — сам куб — родственное двум тетраэдрам
, сложенным своими основаниями). Первое тело ограничено двенадцатью, второе — тридцатью ромбами. Первое тело объединяет с кубом следующее свойство. Подобно тому как восемь пространственных углов восьми кубов можно расположить вокруг общей вершины так, что они заполнят всё пространство, не оставив ни малейшего зазора, то же делают и правильные ромбические тела первого типа, если вокруг одной вершины расположить по четыре пространственных угла с тремя рёбрами и, аналогично, по шесть пространственных углов с четырьмя рёбрами. Следовательно, всё пространство можно заполнить правильными ромбическими телами так, что одна и та же точка будет служить вершиной четырёх пространственных углов с тремя рёбрами, а также шести пространственных углов с четырьмя рёбрами. Подведём итог: если пространство заполнено равными кубами, расположенными в правильном порядке, то одного куба 32 других куба касаются отдельными вершинами и, кроме того, шести кубов касаются его четырьмя вершинами, что составляет всего 38 кубов. Если же пространство заполнено равными ромбическими телами, то одного правильного тела шесть других касаются отдельными вершинами, из которых по четыре ребра, и, кроме того, 12 тел касаются его четырьмя вершинами. Следовательно, ромбического тела касаются всего 18 других тел.Таким образом, эта геометрическая фигура почти правильно заполняет пространство, подобно тому как правильные шестиугольники, квадраты и равносторонние треугольники сплошь заполняют плоскость. Именно такую форму, как уже говорилось, имеют ячейки пчелиных сот, если не считать того, что эти ячейки не имеют крышек, повторяющих по форме донышки.
Если бы они достроили эти крышки, то каждая пчела оказалась бы заключённой между 12 или 18 другими пчёлами, окружающими её со всех сторон так, что из ячейки не было бы выхода. Поэтому пчёлам не нужна такая крышка, однако ничто не мешает им построить на ромбических гранях крышки шести стенок, подогнав их размеры к своим крохотным тельцам, причём возводить эти стенки в различных направлениях и неодинаковыми по форме
.Разрезав большой плод граната, нетрудно заметить, что большинство зёрен имеет форму той же ромбической фигуры, если её не искажает ряд корешков, подводящих к зёрнам питательные соки.
В этих двух примерах хочется спросить: кто же виновник того, что пчелиные соты и зёрна граната имеют форму правильной ромбической фигуры? Причина не может таиться в самом материале. Ведь пчёлам негде взять готовые ромбические листочки, которые можно было бы собрать, а затем построить из них свои домики. Столь же маловероятно, чтобы лишь в плодах граната зёрна сами по себе становились ребристыми, в то время как во всех других плодах зёрна остаются круглыми, что отнюдь не мешает им вздуваться и набухать, если подводимая к ним влага проникает сквозь жесткую оболочку и переполняет её.
Следовательно, причину формы зёрен граната надлежит искать в душе растения, пекущейся о его росте. Однако сама по себе эта причина недостаточна, и действует она в плоде не по каким-то формальным свойствам, а в силу необходимости, проистекающей из свойств материала. Действительно, в начале, пока зёрнышки малы и им хватает места внутри кожуры, они круглые. Затем кожура затвердевает, а зернышки продолжают расти, тесня и сдавливая друг друга, как горошины внутри своих продолговатых стручков. Но горошины не могут двигаться:
ведь они размещены в продолговатом стручке в определённом порядке и испытывают сжатие с двух сторон. Что же касается круглых зёрен в плодах граната, то вначале у них имеется больше свободного пространства, каждое зёрнышко в отдельности легко проникает между трёх зёрнышек соседнего слоя (такое проникновение облегчается тем, что зёрна имеют круглую форму), а жидкость из тесного места заполняет освободившееся пространство. Если насыпать некоторое количество одинаковых по величине шариков из мягкого материала в какой-нибудь круглый сосуд и начать равномерно сдавливать его со всех сторон обручами, то большинство шариков примет форму ромбических тел, в особенности если, предварительно встряхнув сосуд, заставить шарики перекатиться и расположиться как можно более тесно. Если шарики выстроились вдоль прямой и их относительное расположение нельзя ничем нарушить, то после сжатия они превратятся в кубы.
В общем случае одинаковые по величине шары, собранные в каком-нибудь сосуде, располагаются в нем двумя способами – в соответствии с двумя способами их расположения на каждой плоскости.
Если собрать равные по величине шары, разбросанные по горизонтальной плоскости, так, чтобы они касались друг друга, то шары расположатся либо в вершинах равносторонних треугольников, либо в вершинах квадратов. В первом случае каждый шар окружён шестью другими, во втором — четырьмя. В обоих случаях характер касания для всех шаров, кроме наружных, одинаков. Расположение в вершинах правильного пятиугольника не позволяет шарам сохранять равновесие, расположение в вершинах правильного шестиугольника распадается на несколько треугольных. Таким образом, как я и говорил, на плоскости существуют лишь два расположения.
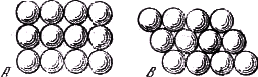
Рис. 1
Итак, если ты перейдёшь теперь к построению плотнейшей пространственной упаковки шаров и для этого станешь накладывать одно на другое плотнейшие расположения шаров на плоскости, то возникнут либо квадраты А, либо треугольники В (рис. 1). Если получились квадраты, то либо каждый шар верхнего ряда будет стоять на шаре нижнего ряда, либо, наоборот, шары верхнего ряда расположатся в углублениях между четырьмя шарами нижнего ряда. В первом случае каждый шар касается четырёх соседних шаров из того же ряда, одного шара вверху и одного шара внизу, то есть всего шести шаров. Это — кубическое расположение шаров, и при сжатии образуются кубы, но оно не является плотнейшим расположением. Во втором случае каждый шар, помимо четырёх соседних шаров, расположенных в той же плоскости, касается ещё четырёх шаров над ним и четырёх шаров под ним, то есть всего 12 шаров. При сжатии из шаров получаются ромбические тела. Это расположение очень напоминает октаэдр и пирамиды. Эта укладка шаров плотнейшая: при любом другом расположении в тот же сосуд не удаётся добавить шаров. С другой стороны, если ряды шаров на плоскости расположены в треугольном порядке, то при построении тела либо каждый шарик верхнего ряда стоит на шарике нижнего ряда, причём и в этом случае упаковка не является плотнейшей, либо каждый шарик верхнего ряда располагается в углублении между четырьмя шариками нижнего ряда. В первом случае каждый шар касается шести соседних шаров, расположенных в той же плоскости, одного шара над собой и одного шара под собой, то есть всего восьми шаров. Расположение напоминает по внешнему виду призму, и при сжатии шары превращаются в столбики с шестью четырёхугольными боковыми гранями и двумя шестиугольными основаниями. Во втором случае получается то же самое, что получалось ранее при квадратном расположении шаров. Пусть В (рис. 2) — три попарно соприкасающихся шара. Положим на них сверху ещё один шар А. Пусть С – другая группа из шести шаров, D — ещё одна группа из 10 шаров и Е — группа из 15 шаров. Меньшую группу всегда клали на большую, чтобы получилась пирамида. При таком наложении слоёв каждый из верхних слоёв располагается между тремя нижними. Но если извлекать по одному шару из перевёрнутой
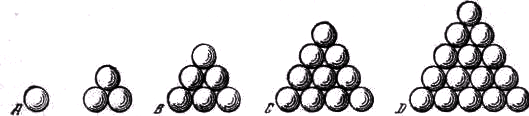
Рис. 2
пирамиды, обращённой вверх не вершиной, а целой гранью, то четыре шара под ним всякий раз будут располагаться в квадратном порядке. Кроме того, как и прежде, один шар касается 12 других: шесть соседних шаров, расположенных в той же плоскости, три шара вверху и три внизу. Таким образом, в плотнейшей пространственной упаковке треугольное расположение шаров не может встречаться без квадратного, и наоборот.
Отсюда следует, что зёрна граната сдавливаются в ромбические тела не только в силу свойств, присущих материалу, но и вследствие одновременного влияния роста зёрен. Круглые зёрна не могут без вреда для себя долго выдерживать сжатие и, смещаясь, заставляют вытесненное зерно проникать в промежутки между тремя или четырьмя зёрнами соседнего слоя.
Пчелиные соты подчиняются иной закономерности. Ведь пчёлы не скапливаются беспорядочно, как зёрна в гранате, а по своему усмотрению выстраиваются рядами так, что головы всех пчел обращены либо в одну, либо в другую, противоположную первой сторону, а задними концами своих тел пчёлы упираются друг в друга.
Для того чтобы из скопления такого рода возникла фигура, пчелиные соты должны были бы выделять какое-нибудь вещество, подобно тому, как наращивает свою закрученную раковину улитка. Однако несомненно, что пчёлы сами строят свои соты, возводя этаж за этажом всё здание от самого основания.
Таким образом, пчёлы от природы наделены инстинктом, позволяющим строить соты именно такой, а не другой формы. Этот архетип заложен в них творцом. Здесь ни при чём ни материал, ни воск, ни тельца пчёл, ни рост.
Установив это, мы вправе спросить о конечной цели, не той, которую преследует своими действиями пчела, а о конечной цели, поставленной самим богом, создателем пчелы, когда он предначертал пчеле свои законы зодчества.
И здесь, наконец, при определении конечной цели, мы приступаем к рассмотрению тел и материала. Относительно конечной цели можно высказать три утверждения. Первое утверждение общеизвестно среди физиков, рассматривающих лишь шестиугольную форму в том виде, как она (вместе с отверстиями) выглядит снаружи.
Плоскость можно покрыть без зазоров лишь следующими фигурами: равносторонними треугольниками, квадратами и правильными шестиугольниками. Среди этих фигур правильный шестиугольник покрывает наибольшую площадь. Пчёлы же стремятся строить как можно более вместительные соты, чтобы запасти побольше мёда.
Те же соображения применимы и к трёхмерному пространству, если воспользоваться ими следующим образом. Трёхмерное пространство можно заполнить, не оставляя пустых мест, лишь кубами и правильными ромбическими телами, но ромбическое тело имеет больший объём, чем куб. Однако одного этого соображения недостаточно. Действительно, если пчёл интересует лишь ёмкость сот, то почему они не строят себе круглое гнездо, что заставляет их использовать крохотные участки пространства, как будто во всём улье не остаётся свободного места? Наиболее правдоподобна следующая (вторая) причина, хотя, в силу приведённых выше соображений, её нельзя считать достаточной: нежным тельцам пчёл удобнее покоиться в ячейке, имеющей форму геометрической фигуры с большим числом затуплённых углов, которая приближается к сфере, чем в кубе с его небольшим числом сильно выступающих вершин и плоским дном, не соответствующим форме тельца пчелы.
К этому следует добавить третью причину: объём работы сократится, если две пчелы всегда будут возводить одну общую стенку. Кроме того, плоские перегородки обладают большей прочностью и позволяют сотам оставаться в целости, чем отдельные круглые ячейки, которые легко раздавить. Наконец, между круглыми телами, даже если они расположены очень близко друг от друга, остаются зазоры, а через эти зазоры может проникнуть холод. Чтобы позаботиться обо всём этом, пчёлы, как гласит стих Вергилия, “в городах обитают под крышей единой”.
Я полагаю, что приведённые соображения избавляют меня от необходимости пускаться в философствование о совершенстве, красоте и превосходстве ромбической фигуры. Не стану я беспокоиться и о том, как извлечь сущность крохотной души, заключённой в пчеле, из созерцания возводимых ею фигур (нечто подобное следовало бы предпринять, если бы назначение фигуры оставалось неясным).
То же относится и к плоду граната. Свойства, заложенные в материале, проявляются в том, что зёрна граната при последующем росте сдавливаются и принимают форму ромбического тела. Поэтому мы напрасно стали бы размышлять о сущности души, заложенной в гранатовом дереве, которая заранее предопределяет, что зёрна примут форму ромбических тел.
Наоборот, если спросят, почему у всех деревьев и кустарников или по крайней мере у большинства из них цветы, распускаясь, приобретают пятиугольную форму, то есть имеют по пяти лепестков (у яблонь и груш эта форма цветков соответствует также строению плода, основанному на числе пять или на родственном числе 10, поскольку внутри плода семена находятся в пяти камерах и заключены между 10 перегородками, что также наблюдается у огурцов н тому подобных овощей и фруктов), то я отвечу, что здесь рассуждения о красоте и свойствах фигуры, в которых проявляется душа растения, были бы вполне уместны. Свои соображения по этому поводу я изложу ниже.
Существуют два правильных тела, додекаэдр и икосаэдр, из которых первое ограничено правильными пятиугольниками, а второе – равносторонними треугольниками, но прилегающих друг к другу так, что образуются некие пятигранные пространственные углы. Построение этих тел и в особенности самого пятиугольника невозможно без той пропорции, которую современные математики называют божественной. Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности. Привести числовой пример, в котором были бы выписаны все члены, невозможно. Однако чем дальше мы будем уходить от единицы, тем более полным будет наш пример. Пусть оба младших члена будут числами 1 и 1 (ты можешь считать их неравными). Сложив их, мы получим 2. Прибавив к 2 больший из младших членов, получим 3, а прибавив к 3 число 2, получим 5. Прибавив затем к 5 число 3, получим 8, прибавив к 8 число 5, получим 13, прибавив к 13 число 8, получим 21. Отношение числа 5 к 8 приближённо равно отношению числа 8 к 13, а отношение числа 8 к 13 приближённо равно отношению числа 13 к 21.
По образцу и подобию этой продолжающей саму себя пропорции сотворена, как я полагаю, производительная сила, и этой производительной силой запечатлён в цветке подлинный символ пятиугольной фигуры. Я опускаю все остальные соображения, которые мог бы привести в подтверждение сказанного в этих приятнейших рассуждениях. Для них потребовалось бы особое место. Здесь же я привёл их лишь в качестве примера, чтобы мы были более сведущими и лучше подготовленными к исследованию шестиугольной фигуры снега.
Если бы мы вздумали исследовать, откуда у снега берётся эта фигура, и отделили бы внешние причины от внутренних, то среди внешних причин нам прежде всего встретился бы холод. Во всяком случае, сгущение водяных паров происходит под влиянием холода, а ведь именно при сгущении пар превращается в звёздообразные фигуры. Следовательно, можно считать, что возникновение звёздообразных фигур обусловлено холодом. Это, в свою очередь, наводит на новые размышления о том, не является ли холод неким природным началом, чем-то вроде тепла медиков? Ведь насколько можно судить, холод
– это не просто отсутствие тепла, поскольку недостающее качество не обладает разумом, создателем шестиугольной формы, и не способно производить какие-либо действия.Но, чтобы не смешивать вопросов, оставим сгущение паров холоду. По-видимому, пар, сгущаясь, естественнее всего принимает шарообразную форму. Впрочем, если представить, что холод охватил огромное пространство и пар соприкасается с холодом вдоль наружной поверхности последнего, то, сгустившись, пар примет совершенно плоскую форму, аналогичную форме поверхности, и границы его будут соответствовать границам холодного участка. Представь себе, что весь верхний слой пара сгустился под действием холода. Сгустившись, он стал весомым, а став весомым, начал падать и под действием различного рода случайностей рассыпался на мельчайшие осколки и листочки. Шестиугольники, в особенности шестиугольные звёзды с лучами, испещрёнными множеством полосок, получаются не из всех листочков. Из самых маленьких они заведомо не получаются, а из каких листочков получаются, мне вообще неизвестно.
Эти полоски напоминают о том, что происходит в плохом гипокаустерии, когда зимний холод проникает сквозь щели в окнах. Возле этих узких щелей холодный воздух вступает в противоборство с водяным паром. Всякий раз, когда они приходят в соприкосновение, тепло устремляется вверх, а холод опускается вниз. Ведь в тепле вещество расширяется, а на холоде становится более плотным и тяжёлым, и от этого тепло выталкивается вверх. Поэтому, когда скопившийся внутри пар устремляется наружу, скопившийся снаружи холод, чтобы избежать пустоты, устремляется внутрь, отчего края открытого окна или щели становятся особенно холодными. Достигая их, пар будет непрестанно замерзать, а его вещество — охлаждаться настолько, что, достигнув его, новая порция пара также замерзает. Подача пара не прекращается ни на миг, между тем как прямо внутрь поступает холодный воздух. Движения пара и воздуха то в одну, то в другую сторону и создают те полоски и острые лучи. На них и оседает пар.
Однако всё это не позволяет высказать какие-либо утверждения относительно формы наших снежинок. О каком движении то в одну, то в другую сторону может в этом случае идти речь, о каком отверстии, ведущем наружу, о каких узких щелях, о каком противоборстве в необъятных воздушных просторах? Предположим, что за время падения с высоты во влажном воздухе некая толика пара осаждается на лучах. Но почему именно в шести местах, почему непременно по шестеричному принципу? Кто снабдил утолщённую среднюю часть, прежде чем она начала падать, шестью замёрзшими рожками? Что за причина определяет на её поверхности, которой ещё только предстоит сгуститься, те шесть точек, к которым прикрепляются шесть лучей?
Поскольку внешняя причина
– холод – сделать этого не может, то должна быть какая-то внутренняя причина, либо сопутствующая пару, либо присущая ему в той или иной степени.Размышляя об этом, я удивился тому, что лучи распределяются не по всей поверхности шара. Ведь если их виновником следует считать внутреннее тепло, то почему оно действует лишь в тонком наружном слое, где оно равномерно распределено по всем направлениям, а не только в плоском слое пара?
Предаваясь этим мучительным размышлениям (ведь разум требовал, чтобы лучи были распределены по всей поверхности центрального ядра), я вдруг вспомнил, что мне не раз случалось с удивлением наблюдать, как звёздочки такого рода ложились плашмя не сразу же после того, как выпадали на землю. Несколько мгновений отдельные их части стояли торчком и лишь некоторое время спустя опускались на землю.
Приведённые выше соображения стали как бы отцом, а это наблюдение – как бы матерью следующего моего мнения. Шестиугольные звёздочки возникают при падении трёх опущенных диаметров, соединённых в одной точке так, что концы их равномерно распределяются по окружности, и опускаются на землю лишь тремя опушенными лучами, в то время как три других луча, служащие продолжениями первых, остаются приподнятыми до тех пор, пока лучи, на которые опирается звёздочка, не
разогнутся и другие лучи, торчащие вверх, не опустятся на ту же плоскость в промежутках между первыми тремя лучами.Сначала я рассмотрю это утверждение в целом и лишь затем проверю, правильно ли оно, чтобы его безосновательность, если
таковая обнаружится, не помешала моему намерению сказать несколько слов о таком Ничто.Я исхожу из того, что какова бы ни была причина появления у снежинок шести лучей, она должна действовать одинаково по всем направлениям. Например, если шесть лучей обусловлены холодом, то холод должен окружать все частицы пара, отстоя от них на одинаковых или почти одинаковых расстояниях. Если причину их появления надлежит искать во внутреннем тепле, то оно должно также действовать из одного и того же центра одинаково по всем направлениям на сфере.
Однако само по себе это замечание не решает вопрос, а лишь по-иному ставит его. Ведь оно не объясняет, почему из одного центра всегда возникают не пять и не
семь, а именно шесть пушистых лучей.Если ты спросишь математика, в какой фигуре три диаметра пересекаются в одной точке ортогонально, или в виде двойного креста, то математик ответит: в октаэдре, противоположные вершины которого соединены. Но октаэдр имеет именно шесть вершин. Как же случается что падающий снег, прежде чем стать плоским, тремя своими опушенными диаметрами, расположенными под прямыми углами друг к другу, образует остов октаэдра (если концы соседних лучей соединить 12 отрезками прямых, то получится октаэдр)?
По какой причине на этих трёх опушенных лучах пар сгущается раньше, чем на всей сфере?
Я могу предложить некое объяснение, согласно которому так происходит в силу необходимости, диктуемой свойствами вещества. Правда, моё объяснение исходит из некоего предположения, ещё более удивительного, чем
-то, что подлежит объяснению. Однако я не могу не заметить, что и сравнение многих ошибочных заключений способно рождать истину. Предположим, что пар, едва почувствовав проникающий в него холод, замерзает и превращается в шарики определённой величины. Такое предположение не противоречит здравому смыслу. Ведь капля – наименьшее естественное количество воды, поэтому для того, чтобы вода не растекалась под действием своего веса, её необходимо разделить на количества, которые меньше капли. Нетрудно допустить, что взятому в определённом количестве пару свойственна некая неподатливость, позволяющая ему сопротивляться холоду. Это количество пара мы условимся называть воображаемой каплей.Предположим далее, что эти воображаемые шарики соприкасаются в определённом порядке, образуя квадратное расположение на плоскости и кубическое расположение в пространстве, о которых говорилось выше. Каждый шарик касается тогда шести других. Мы можем изобразить на плоскости лишь четыре из них (рис. 3) и мысленно представить себе один шарик сверху и один шарик снизу. Коль скоро это установлено и предполагается впредь, холод проникает через промежутки между шарами, и шарики от одной точки касания до другой, ей противоположной, защищены от холода. Поэтому сгущение пара происходит лишь по направлению к центрам шариков, но так, будто оно происходит и по направлению к диаметрам, соединяющим точки касаний, которые сами защищены от холода.

Рис. 3
Однако справедливо будет спросить, какая же сила располагает шарики в прямоугольном порядке?
Если бы они не могли располагаться иначе под влиянием свойств, присущих материалу, то вопрос был бы исчерпан. Однако, как говорилось выше, свойства материала допускают два других расположения шариков. Кроме того, все три расположения могут перемешиваться, приводя к самым различным расположениям.
Может быть, причину такого расположения шариков следует видеть в том, что лишь при нём свойства расположения одинаковы по всем направлениям и точки касания распределены равномерно, в то время как при других расположениях этого не происходит? Ведь если каждый отдельный шар касается 12 других, то, как показано выше, промежутки между шарами имеют попеременно то три, то четыре вершины. Здесь же они все имеют по четыре вершины. Там некие два диаметра, соединяющие попарно точки касания, пересекаются под прямым углом, в то время как четыре остальных диаметра этим свойством не обладают. Здесь же все три диаметра пересекаются одинаковым образом и любые два из них образуют прямой угол. Там, если соединить точки касания отрезками прямых, получится кубооктаэдр, здесь же – октаэдр внутри каждого шарика.
Отсюда понятно преимущество, которым прямое расположение шариков обладает перед косым. Однако остаётся невыясненной причина, по которой шарики предпочитают располагаться именно в этом порядке. Быть может, их вынуждает к этому холод? Но каким образом?
Ведь, холод либо приводит к сгущению вещества, либо проникает в него там, где в веществе зияют поры или оно сопротивляется слабее. Чтобы предоставить более обильную пищу для размышлений, скажу иначе: холод, опускающийся отвесно к земле, мог бы служить причиной, по которой шарики располагаются в глубину вдоль прямых, но что заставляет их располагаться вдоль прямых в поперечных направлениях?
Итак, остаётся лишь предположить, что кубическое расположение капель, если только оно действительно кубическое, то есть если наше Ничто есть Нечто, обусловлено внутренней теплотой пара.
Однако на той стадии, которой мы достигли в своих рассуждениях, безразлично, сама ли теплота придаёт каждой капле форму октаэдра или она разделяет всё вещество на упорядоченные ряды звёздочек, а распределение вещества внутри отдельных шариков определяется общим внешним порядком. Однако ни в каком другом случае расположение шаров не может оставаться неизменным, поскольку различные возмущения могут легко нарушить его.
Но, как мы и предполагали ранее, имеются основания считать, что отдельные капли могут выстраиваться в определённом порядке сами, без прикосновений извне. Ведь если бы форма отдельных капель определялась бы относительным расположением и касаниями множества капель, то все звёзды по форме были бы почти одинаковыми, в то время как в действительности они значительно отличаются по величине. И даже в строении многих звёздочек можно заметить много необычного.
Итак, мы не сможем продвинуться дальше, если не выясним, каким образом внутренняя теплота закрепляет воображаемые капли пара вдоль трёх диаметров, расставляя их в октаэдрическом или по крайней мере в шестиугольном порядке так, что вещество, сгущаясь, скапливается вдоль указанных диаметров.
Может показаться, будто эти крохотные пушинки летают порознь и, лишь падая на землю, случайно соединяются накрест. В действительности такое мнение ложно. Ведь пушинки не могли бы всегда собираться по три, соединяться непременно в середине и в одной точке. Следует также добавить, что все пушинки от центра либо звёздочки, либо двойного креста направлены наружу, как иголки на еловой ветке. Это свидетельствует о том, что формообразующая сила сосредоточена в центре и действует оттуда одинаково по всем направлениям.
Но, быть может, три избранных диаметра возникают по той же причине, по которой в телах живых существ имеются три избранных направления? Разве тела животных не имеют верха и низа, передней и задней, а также правой и левой сторон? Если кто-нибудь выскажет нечто подобное, то его мнение в значительной мере совпадает с моим, но вопреки ожиданию такое допущение приведёт его к парадоксам. Ведь прежде всего ему необходимо рассмотреть природу теплоты, которая обусловливает сходство между строением тела животных и снежинками.
Затем он должен понять, для чего это нужно. Что общего у животного со снегом? Ведь снегу три выделенных направления нужны не для жизни, поскольку снег не наделён жизнью. Далее ему придётся обратить внимание на то, что различные стороны тела животного не столько сотворены по архетипу геометрических фигур, а именно куба, первого из тел, сколько предназначены в силу необходимости для достижения некоей цели. Первое различие (между верхом и низом) связано с местом пребывания животных – поверхностью Земли: ноги направлены вниз, чтобы они могли служить опорой весу животного, голова направлена вверх, чтобы удобнее было непрестанно наполнять жилы влагой и чтобы глаза и уши наиболее удалённые от поверхности Земли, позволяли животному держать под наблюдением как можно более широкий круг и избегать препятствий и чтобы, наконец, пища опускалась на место под действием своего веса, а питьё – в силу своего жидкого состояния, не требует (как это происходит у живущих на одном месте растений) постоянного подсасывания. Вторым различием (между передней и задней частью тела) животные наделены для того, чтобы они могли передвигаться по поверхности Земли от одного места к другому по прямой. Поэтому два названных мной направления всегда пересекаются под прямым углом и задают некоторую плоскость. Поскольку животные не могут быть плоскими, а непременно наделены объёмными телами, то третьего выделенного направления (между правым и левым) требует объёмность тел. Это направление как бы разделяет тела животных на две половины, чтобы при ходьбе было заметно попеременно различие между движущим и движимым. Следовательно, не то, что имеет форму куба, напоминает красотой своей фигуры человека, а человек уподобляется кубу, словно искусно собранному из различных потребностей, как из элементов.
Итак, изучив всё, что только было возможно, я пришёл к следующему заключению. Шестиугольная форма снега обусловлена той же причиной, что и правильные фигуры, а также постоянные числовые соотношения, присущие растениям. Но поскольку в растениях ничто не происходит без ведома высшего разума (не того, который проявляется в логических умозаключениях, а того, что первоначально был запечатлён в замысле создателя и сохранён до наших дней чудесными свойствами природы животных), то я считаю, что и в снеге столь упорядоченная форма проявляется отнюдь не случайно.
Следовательно, в теле Земли существует некая формообразующая сила, носителем которой является пар, подобно тому, как человеческая душа является носителем духа. Поэтому нигде не встречается пар, ставший, как принято говорить, тем, что он есть (иначе говоря, чистым паром), без участия некоей теплоты. Та же теплота поддерживает пар, позволяя ему оставаться паром. Следовательно, пар неотделим от некоего формообразующего начала, называемого также творящей теплотой.
Я доведу изложение своих взглядов до конца лишь после того, как устраню два возражения. Действительно, ты можешь возразить мне, сославшись на то, что конечная цель, преследуемая растениями, состоит в создания некоего природного тела. Отсюда следует, что в любом веществе заключено формообразующее начало. Ведь там, где есть средство для достижения определённой цели, царит порядок, нет места случаю, поскольку там всё решает чистый разум и трезвый расчёт. В образовании же снега нельзя усмотреть никакой цели, а шестиугольная форма не придаёт ему прочности и не превращает в природное тело с чёткой и незыблемой формой. На это я отвечу, что формообразующее начало не только стремится достичь цели, но и способствует украшению, не только порождает естественные тела, но и не чуждо мимолётным забавам, о чём свидетельствуют многочисленные примеры ископаемых. Из игры (поскольку мы говорим, что природа забавляется) я извлекаю всеобщее начало и переношу его в область серьёзных намерений. Я считаю, что теплоту, охранявшую до сих пор вещество, одолел холод, и она как действовала (исполненная формообразующего начала), соблюдая порядок, и как сражалась, не нарушая его, так и в бегство обратилась, сохраняя известный порядок, и отступила.
О Поликсене, принесённой в жертву на могиле Ахилла стих Еврипида гласит: “Заботы иной она перед смертью не знала, как встретить свой час достойно и с честью”.
То же сообщает в своих письмах Плиний-младший о юной весталке, которую Домициан приказал похоронить заживо.
На редких пушинках, выстроенных как бы в боевом порядке, она задержалась дольше, чем во всём остальном веществе, боясь (как гласит история об Олимпии) пасть постыдной и недостойной смертью.
Кто-нибудь другой возразит мне, сославшись на то, что в каждом растении имеются свои особые жизненные силы и к тому же тела растений обособлены друг от друга. Поэтому неудивительно, что каждому растению присуща своя особая форма. Предполагать же, что каждая снежинка обладает своей неповторимой формой, было бы просто смешно. Следовательно, нельзя выводить формы снежинок из деятельности души так же, как мы делали с растениями.
На это я отвечу, что оба предмета имеют гораздо больше сходного между собой, чем полагает тот, кто выдвинул подобное возражение. Каждому растению действительно присуща особая сила, но все эти силы являются порождениями одной и той же общей силы, сосредоточенной в Земле. К растениям она относится так же, как сила воды – к рыбам, сила человеческого тела – ко вшам, сила собачьего тела – к блохам и сила овечьего тела – ко вшам иного рода. Ведь не все растения развиваются из семян. Большинство из них зародились самопроизвольно, хотя в дальнейшем они и стали распространяться при помощи семян. Что же касается силы Земли, то она сама по себе едина и всюду одна и та же, но разделяется по телам, растёт вместе с телами и в них и в зависимости от внутренних свойств вещества строит ту или иную внешнюю форму. То же можно сказать и о паре, над которым безраздельно властвовала вся душа Земли. Не удивительно, что когда холод стремится разорвать сплошное вещество, сжимая одни части его вокруг других, душа Земли придаёт форму как отдельным частям, так и всему веществу в целом.
Поистине мертва жизнь без философии! Ведь если бы прелюбодейка из басни Эзопа знала о формообразующей силе снега, то она смогла бы убедить мужа в том, будто зачала от снега, и её хитрому супругу было бы не так легко избавиться от незаконнорожденного.
О том, что надлежит считать первопричиной шестиугольной формы снега, я уже говорил. Изучим теперь саму фигуру: выясним, состояла ли она из трёх пересекающихся диаметров, как предполагалось до сих пор, или с самого начала была шестиугольной, о чём я скажу ниже. Будем придерживаться пока того пути, по которому мы начали следовать. Итак, причина, по которой душа Земли предпочитает подражать расположению вершин октаэдра, может быть следующей.
Прежде всего весь род душ родствен геометрически правильным, или космопоэтическим, фигурам, как в том убеждают многочисленные примеры. Поскольку душа сотворена по образу и подобию бога-творца, то в разуме бога-творца заключена равновечная богу истинная сущность таких фигур. Поскольку почти достоверно установлено, что души своей глубинной сущностью воспринимают количественные величины, лишённые физического вещества (или, наоборот, наделённые им, спорить не буду), то ясно, что величины, обладающие формой, душам воспринимать легче, чем бесформенные величины.
Если же количественные величины наделены формой, то они с необходимостью являются правильными фигурами, причём пространственными, поскольку душам свойственна природа не плоских фигур, а объёмных тел. Но среди правильных тел первым по праву считается куб, первозданная фигура, отец всех остальных тел. Октаэдр, имеющий столько же вершин, сколько у куба граней, является как бы его супругой, а центры граней куба соответствуют вершинам октаэдра.
Итак, мельчайшая частица пара, отделившаяся от общей массы, прежде всего принимает форму куба, если вообще принимает, о чём мы уже договорились, какую-нибудь форму, или форму его спутника – октаэдра. Кроме того, начинает действовать необходимость, обусловленная свойствами сваленных в кучу одинаковых по своим размерам шариков. Ведь шарики перемешаны и в точках касания выглядят, как заготовки кубов и октаэдров. Почему октаэдры встречаются чаще, чем кубы? Может быть, потому, что куб возникает при расширении, а октаэдр при сжатии? Ведь и вещество, и согревающая сила при враждебном нападении холода сжимаются. Откуда же известно, что одна фигура возникает при расширении, а другая при сжатии? Это следует из того, что у куба все его восемь вершин обращены наружу, а у октаэдра вокруг центра имеется такое же число вершин, обращённых внутрь. Ведь если восемь вершин куба отсечь равными гранями и, перевернув отрезанные части, поместить их внутрь оставшейся части куба, то получится именно октаэдр. Таким образом, обе фигуры можно разделить так, что число вершин куба возрастёт до восьми, а число вершин октаэдра уменьшится до шести.
Гранильщики драгоценных камней утверждают, что в алмазах встречаются естественные октаэдры совершеннейшей и изящнейшей формы. Если это так, то свидетельство ювелиров существенно подкрепляет сказанное выше. Ведь жизненная сила, придавшая в недрах Земли алмазам форму октаэдров, почёрпнутую из сокровеннейших глубин своей природы, выйдя из Земли вместе с паром, придала образовавшемуся из пара снегу ту же самую форму.
Что же касается трёх пересекающихся накрест диаметров, то форма октаэдра свойственна им ничуть не больше, чем форма куба. Три диаметра такого рода соединяют в октаэдре вершины, в кубе – центры противоположных граней. В октаэдре вершины, совпадающие с концами трёх диаметров, обращены к центру, у куба вершины завершают его тело и обращены наружу. Следовательно, мы столько хлопочем при выборе целой фигуры там, где предостаточно элементов и одной и другой фигуры.
Далеко ли я, глупец, ушёл, если, намереваясь подарить тебе почти Ничто, почти Ничего не делая, я умудрился из этого почти Ничто сотворить почти целый мир со всем, что в нём находится? Не я ли, отправляясь затем от крохотной души самого маленького из живых существ, трижды обнаруживал душу самого большого из живых существ – земного шара – в атоме снега?
Итак, я возвращаюсь и принимаюсь ревностно доказывать, что всё подаренное и сказанное мной тебе и впрямь можно считать Ничем. Впрочем, может случиться и так, что мои хилые умозаключения, сталкиваясь с противоположными аргументами, будут рассыпаться в прах так же быстро, как тают мои снежинки.
Пока я писал эти строки, снова пошёл снег, причём ещё пуще прежнего. Я прилежно принялся разглядывать снежинки. Все они были с прямыми лучами, но двух родов. Одни снежинки были очень маленькими, с различным числом торчащих кругом лучей, голых, лишённых опушки и полосочек и очень тонких. В центре лучи сходились к шарику несколько большей величины. Таких снежинок было больше всего. Среди них были разбросаны гораздо более редкие снежинки второго рода – шестиугольные звёздочки, ни одна из них, ни пока она падала, ни после того, как опускалась на землю, не напоминала по форме другую. Пушинки у звёздочек располагались в одной плоскости с лучами. Седьмой, более короткий луч торчал вниз, как корень, на который могли опускаться падающие снежинки, и, опустившись, держались на нем некоторое время. Это обстоятельство не ускользнуло от меня во время предыдущих моих наблюдений, но было неверно истолковано мной так, будто три диаметра, образующие остов снежинки, не лежат в одной плоскости. Поэтому то, о чём я говорил прежде, ничуть не менее близко к Ничему, чем то, о чём я поведал тебе только что.
Снежинки первого рода, напоминающие по форме градины, как мне кажется, возникают из пара, почти лишённого теплоты и начавшего сгущаться в водяные капли. Поэтому они круглые, некрасивы с виду, лишены формообразующей силы, а их центральные ядра усажены со всех сторон лучами по той же причине, по которой на окне образуется иней (о чём говорилось выше).
Что касается снежинок второго рода, имеющих форму звёздочек, то в них нельзя усмотреть ни куба или октаэдра, ни соприкосновения капель, поскольку эти звёздочки падают плоскими, а не в виду пересекающихся диаметров, как я предполагал выше.
Хотя и в данном случае формообразующая сила остаётся на месте и по-прежнему предопределяет форму снежинок, снова возникает вопрос о выборе формы. Прежде всего, почему снежинки плоские? Может быть, выше я безосновательно лишил плоскость формообразующей силы? Ведь все цветы имеют форму правильных плоских пятиугольников, а не объёмного додекаэдра. Причина, порождающая плоскую фигуру, могла бы состоять в том, что холод соприкасается с тёплым паром вдоль некоторой плоскости, причём не весь пар оказывается окружённым холодом равномерно. Тогда образовались бы звёздочки, но выпадали бы градины.
Но почему возникает именно правильный шестиугольник? Не потому ли, что из всех правильных фигур шестиугольник является первой, из которой нельзя собрать объёмное тело? Ведь и равносторонний треугольник, и квадрат, и правильный пятиугольник тела образуют. Может быть, потому, что правильными шестиугольниками можно покрыть плоскость без единого зазора? Но тем же свойством обладают и равносторонний треугольник, и квадрат. Может быть потому, что из всех правильных плоских фигур, способных сплошь, без единого зазора покрывать плоскость, правильный пятиугольник ближе всего подходит к кругу? Может быть, причину следует искать в различии между силой, вызывающей бесплодие, и другой, плодотворящей силой, считая, что первая порождает правильные пятиугольники, а вторая равносторонние треугольники и правильные шестиугольники? Может быть, наконец, сама формообразующая природа в своей глубочайшей сущности сопричастна правильному шестиугольнику?
Из пяти приведённых мною причин первая, вторая и третья основаны на том, что формообразующие силы сами держат совет и, сообразуясь с местностью, выстраивают боевые порядки. Поскольку столкновение тёплого пара и холодного воздуха происходит на плоскости, а не в некотором объёме, то и формообразующие силы отдают предпочтение скорее плоским, нежели объёмным фигурам. Во второй и в третьей причинах формообразующие силы принимают во внимание необходимость, диктуемую свойствами вещества. Ведь первая причина учитывает своеобразие правильного шестиугольника, отмечая, что именно эта фигура особенно подходит для столкновения пара и холода. При столкновении на плоскости и действовать должны плоские фигуры, но отнюдь не обязательно, чтобы это были фигуры, из которых можно было бы составить объёмное тело. Следовательно, фигура должна быть лишь такой, чтобы соответствовала как фигурам физических тел, заключающих в себе часть пространства, так и фигурам на плоскости, не ограничивающих никакого объёма. Здесь учитывается лишь формальное свойство, а не необходимость, обусловленная свойствами материала.
Относительно второй и третьей причин надлежало бы сказать следующее. Формообразующая сила избирает правильный шестиугольник и по необходимости, вызываемой свойствами вещества, чтобы не оставалось зазоров и чтобы пару было удобнее сгущаться до консистенции снега.
Для этого удобнее всего было бы воспользоваться кругами, но поскольку между маленькими кружками остаются промежутки, то формообразующая сила избрала ближайшую к кругу фигуру. Правда, этой причине противоречит упоминавшаяся выше неодинаковость звёздочек, часть которых очень мала, с необычайно тонкими и гладкими лучами, без пушка. Это свидетельствует о том, что пар не превращается в снег одновременно на больших поверхностях, а выделяется постепенно на маленьких, неодинаковых по форме участках поверхности. Не относится к делу и соображение о том, что не должно быть зазоров, поскольку оно подразумевает лишь разбиение всей поверхности на равные правильные шестиугольники. Таким образом, вторая и третья причины отпадают, если только их нельзя свести к первой в такой степени, чтобы формообразующее начало избирало правильный шестиугольник не в силу необходимости, обусловленной свойствами вещества и пространства, а лишь из-за присущего ему свойства сплошь, без единого зазора покрывать плоскость и быть наиболее близкой к кругу из всех фигур, обладающих тем же свойством.
Четвёртая причина не может быть истинной в столь неприкрытом виде. Ведь белые лилии имеют по три и шесть лепестков и не бесплодны. То же самое можно сказать и о чашечках многих других цветов, в особенности лесных. Может быть, в этом и кроется различие, состоящее в том, что плоды цветов с пятью лепестками, как у яблонь и груш, сочны или содержат мягкую внутреннюю часть, как у роз и огурцов, в которой скрыты семена.
Что же касается цветов с шестью лепестками, то из них не вырастает ничего, кроме семян в сухой оболочке, и плод сидит прямо на цветке. Может быть, различие состоит в том, что цветы с шестью лепестками не встречаются у деревьев и кустарников, а лишь у трав и в особенности у луковичных растений? Может быть, кто-нибудь другой изучит соки растений, чтобы выяснить, не в них ли кроется различие между формами цветов?
Я этого не знаю и поэтому ограничусь лишь тем, что напомню другим о четвёртой причине.
В пользу пятой причины свидетельствуют другие произведения всё той же формообразующей силы, а именно кристаллы. Все они имеют шестиугольную форму, хотя весьма редко встречаются и октаэдрические алмазы. Но формообразующая сила Земли не только охватывает форму но и сведуща в геометрии, непрестанно упражняясь в ней. В бытность мою в Дрездене мне довелось видеть в королевском дворце, называемом также конюшней, столик, украшенный медью с большим содержанием серебра. В центре его крышки, до половины выступая наружу, подобно распускающемуся цветку, сиял додекаэдр величиной с небольшой орех.
В описаниях Баденских источников Болль упоминает и о передней части икосаэдра, встретившейся ему среди минералов. Вполне возможно, что формообразующая сила действует по-разному в зависимости от различного содержания влаги. В купоросе часто встречаются кристаллы куборомбической формы, в селитре форма кристаллов иная. Поэтому химики должны сказать, нет ли в снеге какой-нибудь соли, какого рода эта соль и какие фигуры она может порождать. Постучавшись в дверь химии, я вижу, сколько ещё мне осталось сказать, чтобы постичь подлинную причину данного явления, и поэтому предпочитаю услышать, что думаешь по этому поводу ты, проницательнейший из мужей, нежели утомлять тебя своими догадками.
Вот и всё.
Конец.
Небольшая, но значительная по содержанию работа Кеплера, впервые опубликованная в 1611 г. [
1]. Перевод выполнен по [2, с. 261–280] и сверен с немецким переводом [3, 4].И.И. Шафрановскпй, посвятивший подробному анализу сложного и причудливого сочинения Кеплера работу
[5] и третью главу “Иоганн Кеплер – ранний предшественник структурной кристаллографии” [6], назвал его “первым по времени собственно кристаллографическим трактатом, свидетельствующим о приоритете Кеплера в области теоретической кристаллографии”. “Изобилие глубочайших идей, широта подхода при рассмотрении причин образования снежинок, замечательные геометрические обобщения, смелость и остроумие высказанных гипотез поражают и сейчас, – продолжает Шафрановскпй. – Не всегда ясно, иронизирует автор над читателем или же преподносит ему под видом шуток результаты своих сокровеннейших размышлений. Местами кажется, что Кеплер пишет пародию, высмеивая схоластические построения и фантастические измышления своих коллег. И здесь же, рядом, нас изумляют блестящие догадки и гениальные прогнозы, приближающие его высказывания к современным воззрениям на геометрию и природу кристаллографических структур” [6, с. 50].Высокие научные достоинства кеплеровского трактата “О шестиугольных снежинках” отмечает и академик В.И. Вернадский [
7]: “Первой научной работой в кристаллографии явился небольшой труд Кеплера "О снеге". В нём впервые точно и ясно выражен закон о сохранении постоянства гранных углов, правда, для одного вещества – снега. Эта работа явилась следствием увлечения Кеплера гармонией мира, его исканий разнообразных численных и геометрических соотношений в природных явлениях. Значение работы заключается в том, что он впервые доказал, что кристаллы подчиняются законам геометрии”. Вакгер фон Вакенфельс, Иоганн Маттей (1550–1619) – советник императора Рудольфа II. По воззрениям древнегреческих атомистов, в частности Демокрита (460–370 гг. до н. э.) и Эпикура (341–270 гг. до н. э.), вещество не обладает безграничной делимостью. Мельчайшие неделимые частицы вещества, недоступные непосредственному восприятию, получили название атомов (от греч. атомос – неделимый). В работе “Псаммит” (“Исчисление песчинок”) Архимед (287–212 до н. э.) показал, что число песчинок, вмещаемых сферой неподвижных звёзд, конечно. Если диаметр сферы неподвижных звёзд не превышает 100000000 миллионов стадий (примерно 2 световых года), а в одном маковом зёрнышке умещается мириад песчинок, то число песчинок в сфере неподвижных звёзд не превышает 1063. Платон (427–347 гг. до н. э.) сопоставил каждому из четырёх элементов – земле, огню, воздуху и воде – одно из пяти правильных (платоновых) тел: земле – куб, огню – тетраэдр, воздуху – октаэдр и воде – икосаэдр. Пятое тело (додекаэдр), по мнению Платона, соответствует всему мирозданию. Скалигер, Жюль Сезар (1484–1558) – французский гуманист филолог, критик, поэт и врач. Кеплер с юношеских лет восхищался сочинениями Скалигера “Экзотерические упражнения в 15 книгах” (1557 г.). В одном из примечаний ко второму изданию (1621 г.) своей первой работы “Тайны мироздания” Кеплер дал следующий отзыв об “Упражнениях” Скалигера: “Эта книга побудила меня к размышлениям о всевозможных вопросах: о небе, о душах и духах, о стихиях, о природе огня, о происхождении источников, о морских приливах и отливах, о виде материков и морей” [8]. Кардано Джеронимо (ок. 1501–1576) – итальянский философ, математик и врач. С именем Кардано связана формула решения неполного кубического уравнения и “карданов подвес”. Первое упоминание о шестиугольной форме снежинок. Имеется в виду комедия Аристофана (445—386 гг. до н. э.) “Облака”. “Даёт снег; как волну; сыплет иней, как пепел” – псалом 147, стих 5.1. Kepleris J. Strena, seu de nive sexangula. Francofurti ad Moenum: apud Tampach, 1611, 21 p.
2. Kepler J. Gesammelte Werke / Herausgegeben von Caspar M. und Hammer F. München, 1941, Bd. 4.
3. Kepler S. Über den hexagonalen Schnee / Aus dem Lateinischen üborsetzt und bearbeitet von Stunz H. und Borm H. Acta Albertina Ratibonensia, 1956/1958. Bd. 22, S. 7—35.
4. Kepler J. Neujahrsgabe oder vom sechseckigen Schnee / Unter Mitwirkung von Caspar M. und Neuhart F. übertragen von Rossman F. Bei W. Keiper, 1943, 64 S.
5. Шафрановский И. И. Кристаллографические представлении И. Кеплера и его трактат “О шестиугольном снеге”. M., 1971, 24с.
6. Шафрановский И. И. История кристаллографии с древнейших времён до начала XIX столетия. Л.: Наука, 1978, с. 50–64.
7. Вернадский В. И. Основы кристаллографии. M., 1904, ч. 1, вып. 1, с. 15.
8. Johannis Kepleri Astronomi Opera Omnia / Ed. Frisch Ch. Prancofurti ad Moenum et Eriangae: Heyder et Zimmer, 1871, vol. 8, pt 2, p. 673.
Дата установки: 30.12.2008
[вернуться к содержанию сайта