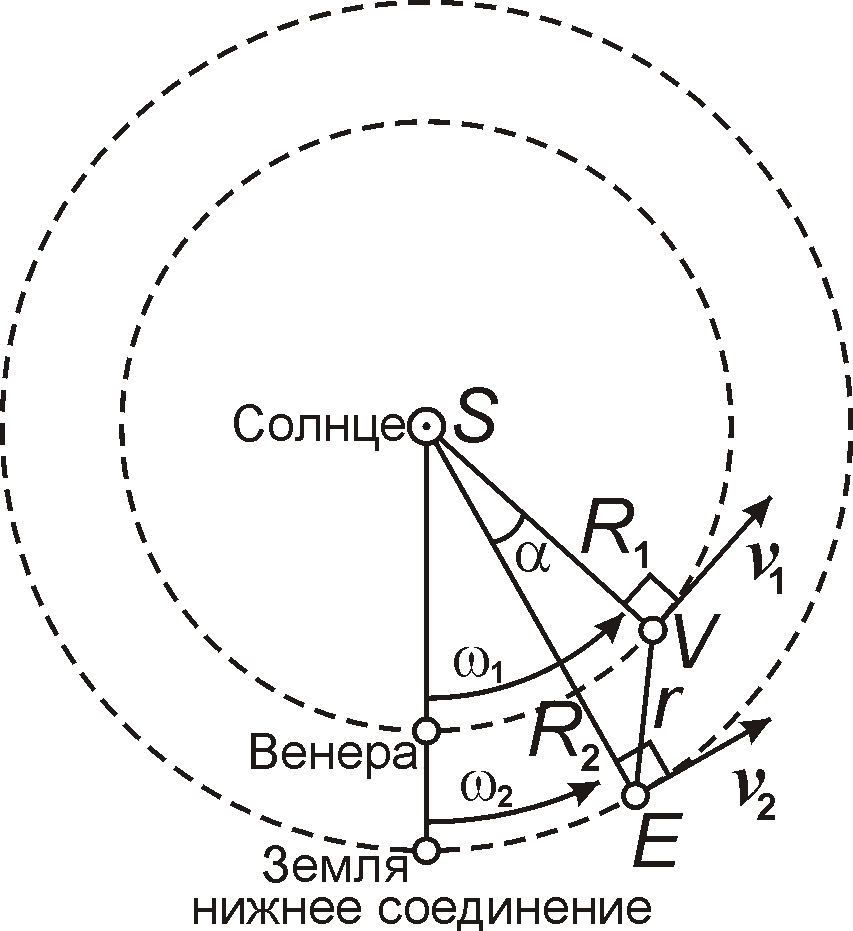
Рис. 1. Схема движения Земли и Венеры возле нижнего соединения.
[вернуться к содержанию сайта]
За прошедшие полвека сеансы космической радиолокации и лазерной локации, проведённые в СССР, России и США, выявили ряд аномалий в виде превысивших возможные ошибки систематических отклонений измеренных скоростей и расстояний космических тел и аппаратов от расчётных. Ввиду растущей точности методов и расчётов на ЭВМ, в последние годы выявляют всё больше подобных аномалий [1].
Пионер космической навигации В.П. Селезнёв [2], американский физик Б. Уоллес [3, 4] и ряд астрономов [5] назвали в качестве возможного источника таких ошибок – отклонения скорости сигналов от применяемого в расчётах номинального значения скорости света c, предписанного специальной теорией относительности (СТО). Тогда как по баллистической теории Ритца (БТР) в космическом вакууме скорость света зависит от скорости источника, которая механически добавляется к скорости сигнала, что подтверждается данными астрономии и объясняет ряд аномалий [6, 7]. Так, уже в 1960-х гг. при радиолокации Венеры выявили систематические расхождения (на сотни км превысившие возможные ошибки) между измеренными радарами положениями планеты и её предвычисленными положениями – эфемеридами, рассчитанными из данных астрономии. Как показал Б. Уоллес [3, 4], расхождения снизятся в разы, если учесть баллистическую зависимость скорости света от скорости источника – радара на Земле, движущегося со скоростью v ввиду осевого вращения Земли, вращения системы Земля-Луна и обращения вокруг Солнца. От сообщения радиолучу скорости v меняется его скорость c + v и время τ движения сигнала, по которому ищут расстояние r Земля-Венера (рис. 1). В итоге расчётное расстояние cτ (или cτ/2, с учётом времени движения отражённого луча), найденное из постоянной скорости света c, отличается от истинного расстояния (c + v)τ.

Рис. 1. Схема движения Земли и Венеры возле нижнего соединения.
Одной из целей радиолокации Венеры было уточнение астрономической единицы (а.е.) – радиуса земной орбиты R2. Измерив радаром расстояние r Земля-Венера, из углов треугольника SVE (Солнце-Венера-Земля) вычисляли расстояние R2 Земля-Солнце, пропорциональное r. Но, вопреки названию, расчётная а.е. регулярно менялась [5] с периодами, равными суткам, месяцу и году, с которыми меняется относительная скорость Земли, вносящая отклонения в расчётные дистанции Венеры и в R2 [3, 4]. Измеренное радаром значение а.е. отличалось и от значения, известного из астрономии. Причём разница превышала погрешность методов, что не нашло объяснений [5], хотя ожидалось по баллистической теории.
Венера тоже сообщает при сближении свою скорость vr отражённому сигналу, и он достигает Земли за меньшее время τ, занижая расчётное r. Предельно сблизившись с Землёй в нижнем соединении, Венера удаляется, скорость сигнала становится ниже c, и он тратит большее время τ, завышая r. Оттого до соединения расчётное значение дистанции Земля-Венера r' = cτ/2 и а.е. выходило ниже реального, а после соединения – выше [5]. Если учесть, что сигнал лишь к Венере идёт со скоростью с относительно Земли, пролетая путь r за время τ1 = r/c, а отражённый сигнал при лучевой скорости Венеры vr вернётся со скоростью c' = c – vr за время τ2 = r/c', то общая задержка τ = τ1 + τ2 = r/c + r/c'. Найденное из номинальной скорости с расстояние r' = сτ/2 ≈ r + rvr/2c превысит реальное r на Δr = rvr/2c. Из треугольника SVE (рис. 1) лучевая скорость Венеры vr = (ω1 – ω2)R1R2·sin(α)/r, где ω1, ω2 – угловые гелиоцентрические скорости Венеры и Земли, R1, R2 – радиусы их орбит, α = (ω1 – ω2)t – угол VSE между ними, а t выражено в сутках, истёкших с момента нижнего соединения. Тогда отклонение Δr = r' – r = (ω1 – ω2)R1R2·sin[(ω1 – ω2)t]/2c ≈ 3350·sin(0,011t) км, или в световых секундах (по запаздыванию) Δτ = Δr/c ≈ 0,011·sin(0,011t) с.
Фактически наблюдают именно такие вариации систематических ошибок-невязок расстояний Δr (рис. 2.а) или времён Δτ (рис. 2.б), т.е. разностей измеренных τo и вычисленных τc по таблицам Ньюкома. Внесение этих поправок снижает систематические отклонения: остаются лишь случайные ошибки, которые ещё снизятся, если учесть влияние вращения Земли на скорость сигналов [3, 4], а также переизлучение межпланетной плазмой. По мере роста r и слоя пройденной плазмы переизлучённый ею сигнал восстанавливает скорость c, отчего отклонения перестают расти с отходом от нижнего соединения (рис. 2).
Эти аномалии не удавалось объяснить, и расхождения формально устраняли коррекцией эфемерид планет, например, внося поправки Данкомба, сместившего Венеру вперёд по орбите на 290 км [5]. Поскольку даже при этом остались расхождения, Венеру сместили ещё на 270 км [8], построив численную теорию движения планеты, соответствующую данным радаров [9]. Но расхождения в сотни км радарных данных с таблицами Ньюкома-Данкомба и с визуальными данными остаются и пока не объяснены [10]. Хотя считают, что отклонения были лишь в первых сеансах радиолокации, а по мере её уточнения ошибки снизились на порядки, фактически эфемериды постепенно корректировали по данным радаров, отчего свежие радарные замеры всё меньше расходились с эфемеридами.
Эти ошибки проявились и в 2004, 2012 гг. при наблюдении прохождения Венеры по диску Солнца: моменты контакта с диском Солнца на минуту отставали от эфемеридных, содержащих радарные “поправки”, сместившие Венеру вперёд по орбите на сотни км. Это можно проверить точными замерами положений Венеры с помощью телескопов и радиотелескопов, так как радиоизлучение горячей поверхности Венеры отчётливо регистрируется.
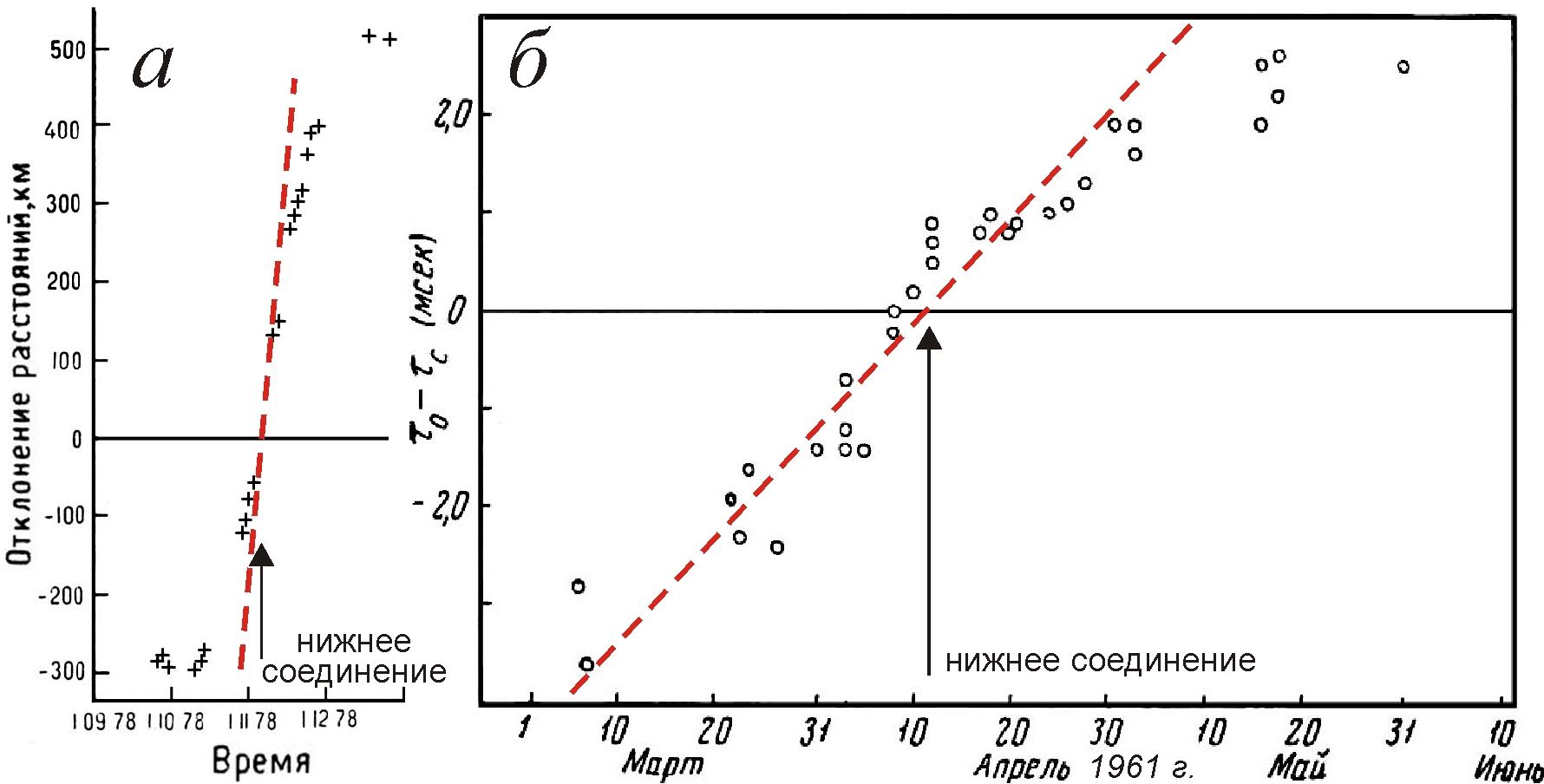
Рис. 2. Отклонения радарных расстояний Венеры от эфемеридных, измеренные в километрах (а, кресты) [9] и световых миллисекундах (б, кружки) [5, с. 242], в сравнении с прогнозом теории Ритца (пунктир).
На ложный “сдвиг” Венеры впервые обратил внимание космический навигатор, обучавший первые отряды космонавтов,– проф. В.П. Селезнёв [2], сотрудник С.П. Королёва и автор монографии “Навигационные устройства” (М.: Оборонгиз, 1961), создавший навигационные системы первых космических кораблей. Селезнёв показал, что без учёта баллистической теории "на основе научных сведений о свете астронавигация в принципе невозможна" [11, с. 308]. Он же отметил значение баллистической теории в навигации космозондов, ряд аварий которых, скажем у “Фобосов”, вызван радарными ошибками [2, 11].
Рассмотрим в этом ключе эффект “Пионеров” [12, 13]. Скорости АМС “Пионер-10” и “Пионер-11”, измеренные радаром (по доплер-сдвигу сигнала АМС), отличались от расчётных [1]. Измеренное ускорение “Пионеров” в поле тяготения солнечной массы M превысило расчётное ускорение a' = GM/r2 на величину Δao = (8,74 ± 1,33)·10−10 м/с2 (на расстоянии r Урана [13]). Если же “Пионеры”, улетая от Солнца и Земли со скоростью v ≈ 10 км/с, излучали сигнал со скоростью c – v, наращивая его запаздывание τ, то по номинальной скорости сигнала c решали, что скорости и ускорения АМС измерены на расстоянии r' = сτ ≈ r + rv/c, а не на истинном r = (c – v)τ, где тяготение Солнца и ускорение a = GM/r2 выше расчётного a' = GM/r'2 на Δac = a – a' ≈ 2av/c = 2vGM/cr2. На дистанции Урана r ≈ 3·1012 м при v ≈ 10 км/с это составит расчётную величину Δac ≈ 9,9·10–10 м/с2, близкую к измеренной Δao ≈ 9·10–10 м/с2 [13]. Сходные аномалии выявлены у АМС “Улисс” [14] и “Кассини”, у которого на расстоянии Сатурна (r ≈ 1,5·1012 м) измеренный избыток ускорения Δao ≈ 3·10−9 м/с2 [15] близок к расчётному Δac = 2vGM/cr2 ≈ 4·10–9 м/с2. Это ставит под сомнение гипотезу радиационного торможения [16], объясняющую эффект “Пионеров” спецификой их конструкции. Также радиационная сила от асимметричного нагрева корпуса создала бы, кроме ускорения Δa ≈ 10−9 м/с2, ещё и момент, уводящий главный лепесток (φа ~ 3°) антенн “Пионеров” от направления на Землю и ведущий к потере связи через год свободного полёта АМС, вопреки фактам.
Открыта и Flyby-аномалия [13, 14], т.е. невязки ожидаемых скоростей и измеренных радаром у АМС, пролетающих мимо планет по гиперболе. Так, у АМС “Галилео” и “NEAR” после пролёта мимо Земли выявлен прирост скорости на величину порядка нескольких мм/с, вопреки закону сохранения энергии. Вероятная причина ошибок – применение в замерах скорости аппаратов релятивистской формулы доплер-эффекта f ' = f(1 – v2/c2)1/2/(1 ± v/c), по которой при сближении частота f повышена до f1 ≈ f(1 + v/c + v2/2c2), а при удалении – снижена до f2 ≈ f(1 – v/c + v2/2c2). В классике f1 = f(1 + V/c) и f2 = f(1 – V/c), причём измерены как раз такие симметричные смещения частоты: f1 – f = f – f2. То есть из классических формул скорость аппаратов сохраняется. Однако, рассчитывая скорость по СТО, получают при сближении v ≈ V – V2/2c, а при отдалении v ≈ V + V2/2c, отсюда – ложный вывод о приросте скорости на величину ∆v ≈ V2/c. При скорости АМС V ~ 103 м/с это как раз создаст иллюзию прироста скорости ∆v ~ 1–10 мм/с.
Возможно, и у спутников Земли, Луны аномалии движения связаны не только с аномалиями гравитационного поля (масконами), но и с ошибками радиолокации от неучёта вариаций скорости света и применения формул СТО. Ошибки выявляют и сети спутников GPS и ГЛОНАСС [17], использующие метод радиолокации с наземных станций слежения и группы искусственных спутников. Навигационный модуль в мобильном устройстве ловит радиосигналы, посланные спутниками и содержащие информацию о положении каждого спутника (находимом станциями) и времени излучения сигнала (по атомными часам спутника). Вычитая это время из времени приёма сигнала, мобильный приёмник по времени τ движения радиоимпульса рассчитывает расстояние r = cτ до спутника. По расстояниям r1, r2, r3, r4 до трёх-четырёх спутников и по их координатам микроЭВМ рассчитывает положение приёмника на земной поверхности.
Полагают, что GPS и ГЛОНАСС подтверждают формулу r = cτ и постоянство скорости c сигналов от спутников [18]. Проверим это. Спутники выводят на орбиты радиуса R порядка 26000 км. Скорость спутников V ≈ 4 км/с снизит скорость их сигнала до c' = c – Vr, где Vr – лучевая скорость спутника для приёмника O. Тогда поправка расстояния Δ = rVr/c, где для спутника в зените Z скорость Vr = 0, но растёт при снижении высоты h спутника над горизонтом: Vr = V·sinα·cosh, где sin α = RE/R ≈ 0,25, RE ≈ 6400 км – радиус Земли (рис. 3). Тогда максимальная ошибка дистанции Δ = rVr/c = 67 м у спутника возле горизонта H. Поскольку обычно приёмник ловит спутники с h > 10º – 15º и располагается под углом θ > 0º к плоскости орбиты спутника, то Vr = V·sinα·cosh·cosθ, что при cosh ≤ 1, cosθ ≤ 1 даёт среднюю ошибку Δ = rV·sinα·cosh·cosθ/c ~ 20 м.
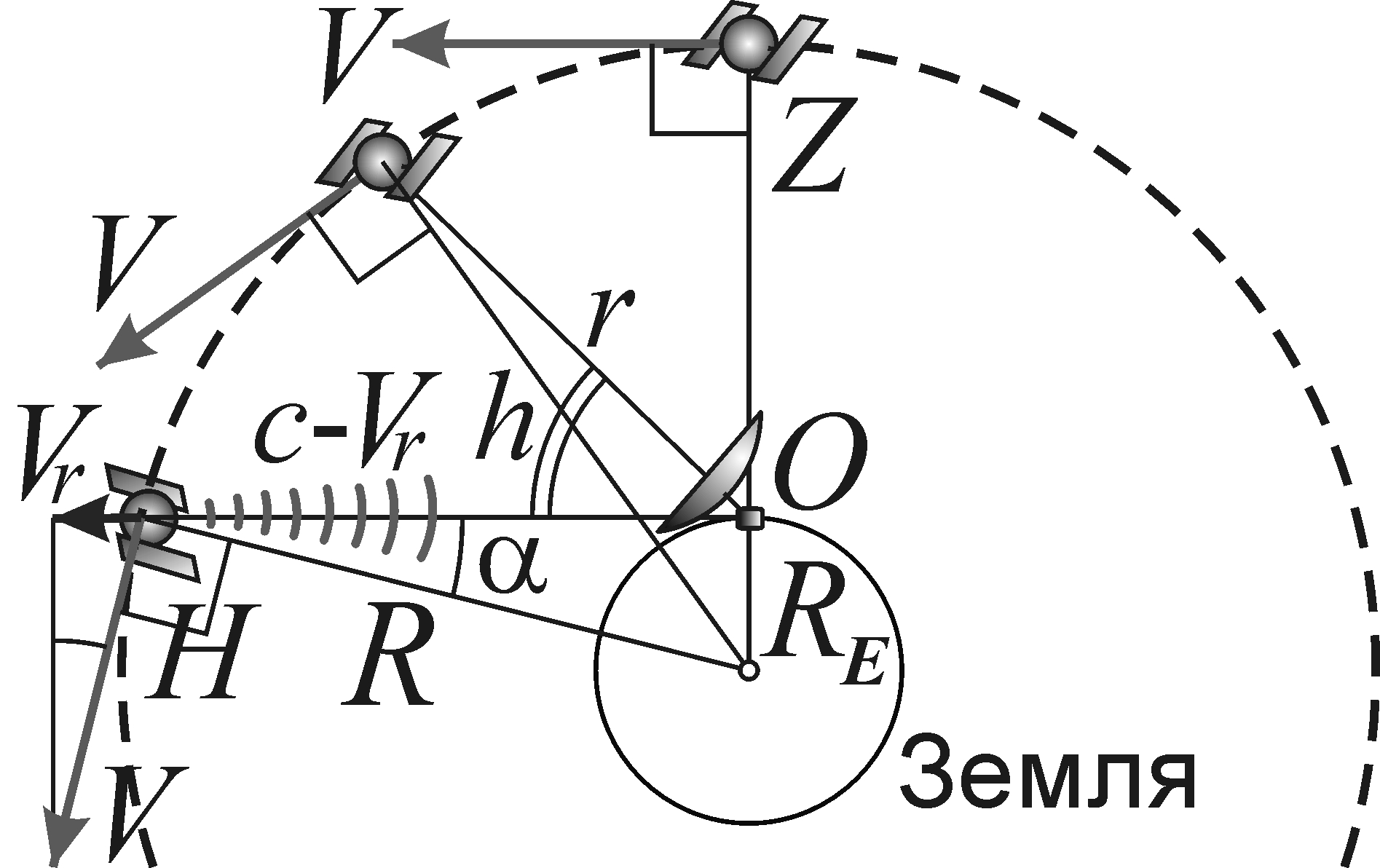
Рис. 3. Схема движения и локации навигационных спутников Земли.
Эта ошибка в расстоянии до одного спутника, а расчёт координат ведут по 6–10 спутникам. Все они дают ошибки разных знаков и величин, случайно суммируемые в разных направлениях, и их взаимная компенсация при усреднении ещё снижает ошибку. И это – общая ошибка по высоте и по горизонтали, а ошибка в измерении проекции на земной шар ещё ниже. В итоге, вносимая вариацией скорости света поправка к горизонтальным координатам приёмника – порядка 5 м, что сравнимо с наблюдаемыми ошибками. Эти ошибки снижают, применяя корректирующие процедуры, в том числе дифференциальные методы с привязкой к базовым станциям. Кроме того, одну ошибку компенсируют другой, исправляя эфемериды спутников, “сдвигая” их вперёд по орбите на сотни метров.
Так, если координаты и эфемериды спутника найдены по временам распространения его сигналов до базовых станций с известными координатами, то из постоянной скорости сигнала положение спутника получают смещённым от реального, что точно компенсирует ошибку замера расстояний до мобильных приёмников. Оттого и считают, что GPS не противоречит СТО [18]. Если же положения спутников измерить разными методами: визуально (телескопами); лазерной локацией (по времени движения света к спутнику и обратно); радиолокацией (по временам движения радиосигнала от наземной станции к спутнику или от спутника к станции), то в случае влияния скорости источника на скорость света эти методы дадут разные результаты. Об ошибках в системе GPS и противоречиях с теорией относительности неоднократно заявлял и Р. Хатч – глава компании NavCom и Института систем космической навигации (ION).
Итак, проверка баллистической теории в космосе крайне актуальна, т.к. радарные ошибки от неучёта вариаций скорости света снижают точность космических программ и ведут к авариям космических кораблей, простых судов и машин с GPS. Однако постоянство скорости света в космосе до сих пор не проверено с применением спутников, ракет и радаров, хотя вопрос о проверке поднимался. Причём, когда в 1961 г. на конференции NASA в США этот вопрос был поставлен, такую проверку даже сочли излишней [19], хотя в том же году неточности в скорости света дали о себе знать при радиолокации Венеры [3-5].
Открыты неточности и при Лазерной Локации Луны (ЛЛЛ) и искусственных спутников, с уголковыми отражателями на поверхности [20]. При скорости лазерного источника порядка vr ≈ 460 м/с (скорость вращения на экваторе Земли) свет пройдёт расстояние r ≈ 3,84·108 м до Луны быстрее на время Δt = r/c – r/(c + vr) = rvr/c2 ≈ 2·10–6 с, что соответствует разнице в 600 м, легко измеримой лазерным радаром (лидаром). С учётом отражения от Луны на скорости c, ошибка составит Δr ≈ 300 м, при точности метода ~ 1 см [21]. Тогда при синхронном измерении расстояния Земля-Луна станциями из противоположных точек Земли, когда одна движется к Луне, а другая удаляется (рис. 4.а), теория Ритца подтвердится в случае выявления разницы дистанций Δr ~ 300 м. Для станций умеренных широт разница меньше: Δr ~ 100 м.
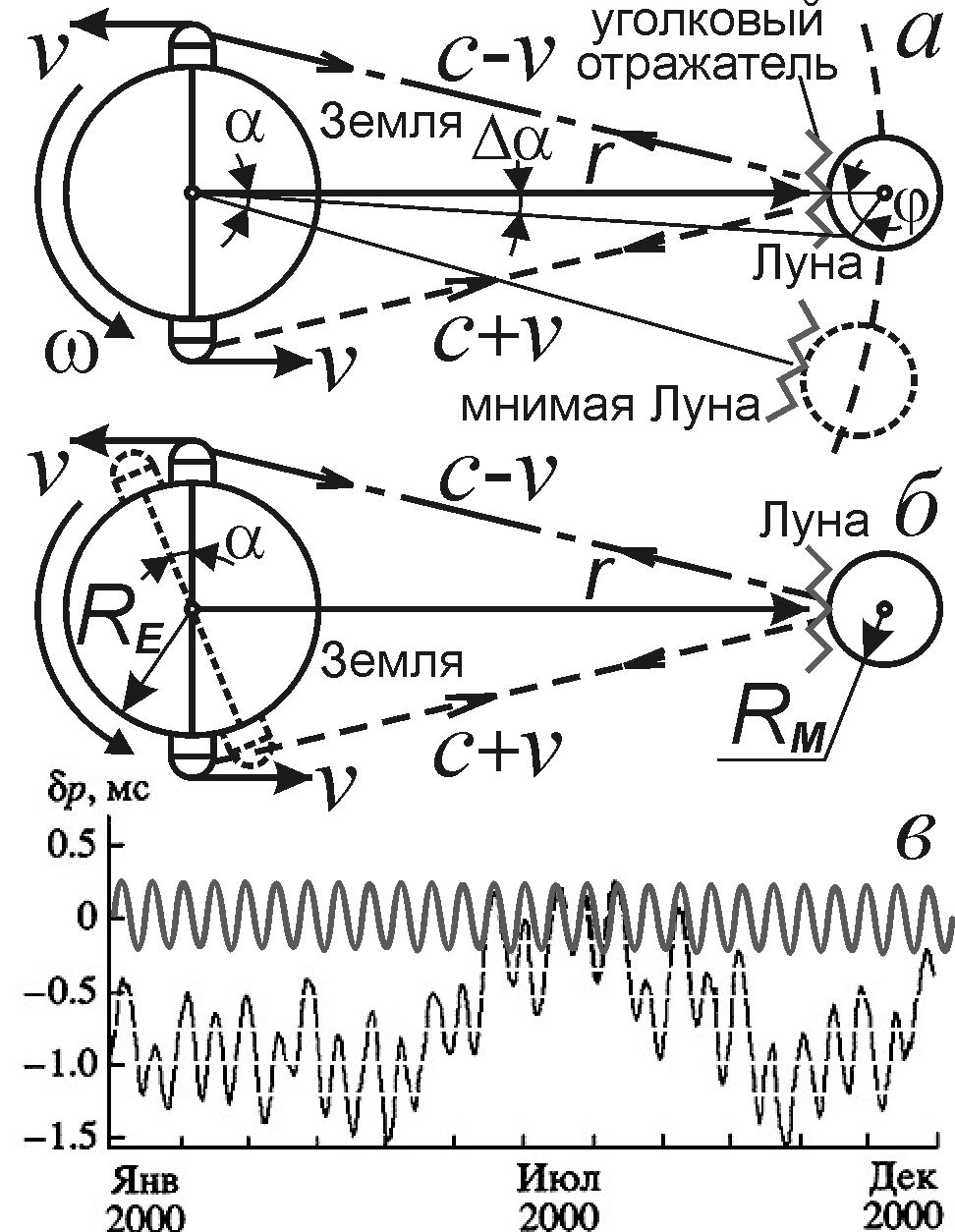
Рис. 4. Схема лазерной локации Луны. Неучтённая вариация скорости света создаёт иллюзию сдвига или поворота Луны (а), Земли (б) и вариации суток (в).
Лазерную локацию может вести и одна станция, меряющая расстояние Земля-Луна в течение ночи. Тогда невязки менялись бы с периодом в сутки со скоростью порядка 100 м/24 ч ≈ 4 м/ч, а предельное отклонение от истинного расстояния составило бы около ста метров. И точно, невязки данных ЛЛЛ и визуальных данных (на основе которых рассчитаны эфемериды Луны) достигают сотни метров и меняются на величину порядка 4 м в час [22, с. 193]. Как показал сотрудник NASA Д. Джезари, изучив данные лазерной локации Луны, вариации систематических невязок отвергают постоянство скорости света, а учёт баллистического принципа исключает вариации [20]. А в СТО расхождение данных ЛЛЛ с эфемеридами удаётся снизить лишь путём коррекции эфемерид на основе данных лазерной локации. По сути, локационные данные, как в случае Венеры, сравнивают друг с другом, а не с данными астрономии.
Считая скорость света константой, находят, что Луна на восходе ближе, чем на закате. Это неравенство расценят как поворот Земли в сторону вращения на лишний угол α = Δr/RE = 4,5·10–5 = 9'',4 (рис. 4.б) или как смещение уголкового отражателя с Луной на расстояние rα = 17 км (рис. 4.а). От наклона лунной орбиты к плоскости земного экватора расстояние r до Луны меняется на величину Δr ~ RE(1 – cos 23,5°) = 530 км с периодом в полмесяца (13,7 сут). Это меняет угол α на Δα = αΔr/r = 0'',013, что воспримут как покачивание Земли вокруг оси с амплитудой Δα/2 = 0'',0066 и периодом T ≈ 14 сут по закону δα = -0'',0066·cos(2πt/T), где t отсчитывают от пересечения Луной экваториальной плоскости Земли (от восходящего узла). Это покачивание создаёт иллюзию колебания скорости вращения Земли (ω = 2π рад/сут) на величину δω = d(δα)/dt = 1,4·10–8·sin(2π/T) рад/сут, а длительности суток p – на величину δp= -pδω/ω, словно день то удлиняется, то сжимается на 0,2 мс каждые 14 дней: δp = -0,2·sin(2πt/T) мс (рис. 4.в). Лазерная локация Луны выявила как раз такие вариации (рис. 4.в, пунктир): их период – 14 суток, а амплитуда – доли миллисекунды [23]. Выходит, вариации p отчасти иллюзорны и вызваны неучтённой вариацией скорости света.
Регулярные колебания дистанции r и скорости vr объяснят и другие “вариации” вращения Земли и Луны, выявленные лидарами и имеющие характерные периоды колебаний r и vr. Так, от полёта по эллиптической орбите расстояние Луны меняется от 350 до 400 тыс. км (Δr ~ 50 тыс. км). Соответственно колеблется угол α (направления на мнимую Луну) на Δα = αΔr/r ~ 1''. Это колебание, синхронное с орбитальным движением, воспримется как “сдвиг” Луны по орбите (как у Венеры), меняющийся в такт её приближению-отдалению. Эти смещения не вполне согласуются с законами Кеплера, т.к. форма и наклон лунной орбиты регулярно меняются [22, с. 63], внося лишнюю вариацию Δr ~ 20 тыс. км и Δα = αΔr/r ~ 0'',5. Её интерпретируют как регулярное смещение уголкового отражателя на Δαr ~ 1 км в ходе покачиваний Луны (радиуса RM) на угол φ = Δαr/RM ~ 2'. Действительно, лидары выявили у Луны регулярные повороты на 2', в отличие от видимых качаний Луны (оптической либрации), объясняемые реальным покачиванием (физической либрацией).
“Покачивания” Луны и Земли за счёт приливных сил открыты и в астрономических наблюдениях [22], но лидарные “качания” частично вызваны неучтённой вариацией скорости света. Это можно проверить, сравнив амплитуду “покачиваний” Луны или Земли, измеренную лидарами, телескопами и радиоинтерферометрами. Если теория Ритца справедлива, их данные разойдутся на величину, меняющуюся по найденным законам. Будут расходиться и данные станций разных широт: возле экватора колебания δp – синусоидальные, а вдали от него – максимумы разной высоты, что и открыто (рис. 4.в). Измеренные лидаром положения Луны ведут и к ошибкам в координатах аппаратов на ней. Возможно, поэтому лазерный луч, по мере его заострения и засветки на Луне всё меньшей области, и перестал находить отражатели “Луноходов”, ложно смещённых на rα ~ 17 км.
Итак, новый анализ всего массива данных радиолокации и лазерной локации, сопоставление их между собой, с визуальными данными и с данными расчётных положений планет или АМС позволит проверить постоянство скорости света в космосе и уточнить параметры осевого и орбитального вращения планет и Луны. А в действующих программах параллельное вычисление координат на базе баллистической теории и на базе постоянства скорости света позволит сравнить точность этих процедур расчёта и повысить надёжность космической навигации. Работа выполнена в рамках программы развития “ННГУ – НИУ”.
1. Андерсон Дж. и др. // Земля и Вселенная. 2002, №5. С. 78.
2. Селезнёв В.П. Космический навигатор // Наука и религия. 1998, №5-6. С. 26.
3. Wallace B.G. // Spectroscopy Letters. 1969. V. 2. P. 361.
4. Wallace B.G. // Spectroscopy Letters. 1971. V. 4. P. 79.
5. Фундаментальные постоянные астрономии. М.: Мир, 1967, 382 с.
6. Толчельникова-Мури С.А. // Известия ВУЗов. Геодезия и аэрофотосъёмка. 2001, №6. С. 85.
7. Мушаилов Б.Р., Теплицкая В.С. // Космические исследования. 2012, №6. С. 452.
8. Котельников В.А. и др. // ДАН. 1965. Т. 163, № 1. С. 50.
9. Петров Г.М. // Земля и Вселенная. 1982, № 1. С. 8.
10. Кислик М.Д. и др. // ДАН. 1978. Т. 241, №5. С. 1046.
11. Селезнёва Н.В. Покорение космического пространства. М.: Либроком, 2013, 360 с.
12. Семиков С.А. Баллистическая теория Ритца и картина мироздания. Н. Новгород: Стимул-СТ, 2010, 612 с.
13. Anderson J.D., Nieto M.M.; http://arxiv.org/pdf/0907.2469v2.pdf.
14. Anderson J.D. et al. // Phys. Rev. Lett. 1998. V. 81. P. 2858.
15. Anderson J.D., Lau E.L., Giampieri G.; http://arxiv.org/abs/gr-qc/0308010v1.pdf.
16. Turyshev S.G. et al. // Phys. Rev. Lett. 2012. V. 108. P. 241101.
17. Семиков С.А. // Инженер. 2010, №10. С. 6.
18. Open Questions in Relativistic Physics. Monreal: Apeiron, 1998, P. 81.
19. Франкфурт У.И. Специальная и общая теория относительности. М.: Наука, 1968, 332 с.
20. Gezari D.Y.; http://arxiv.org/abs/0912.3934.
21. Алёшкина Е.Ю. // Природа. 2002, №9. С. 57.
22. Бронштэн В.А. Как движется Луна? М.: Наука, 1990, 208 с.
23. Сидоренков Н.С. // Вестник РАН. 2004. Т. 74, № 8. С. 701.
Дата установки: 17.09.2013
[вернуться к содержанию сайта]