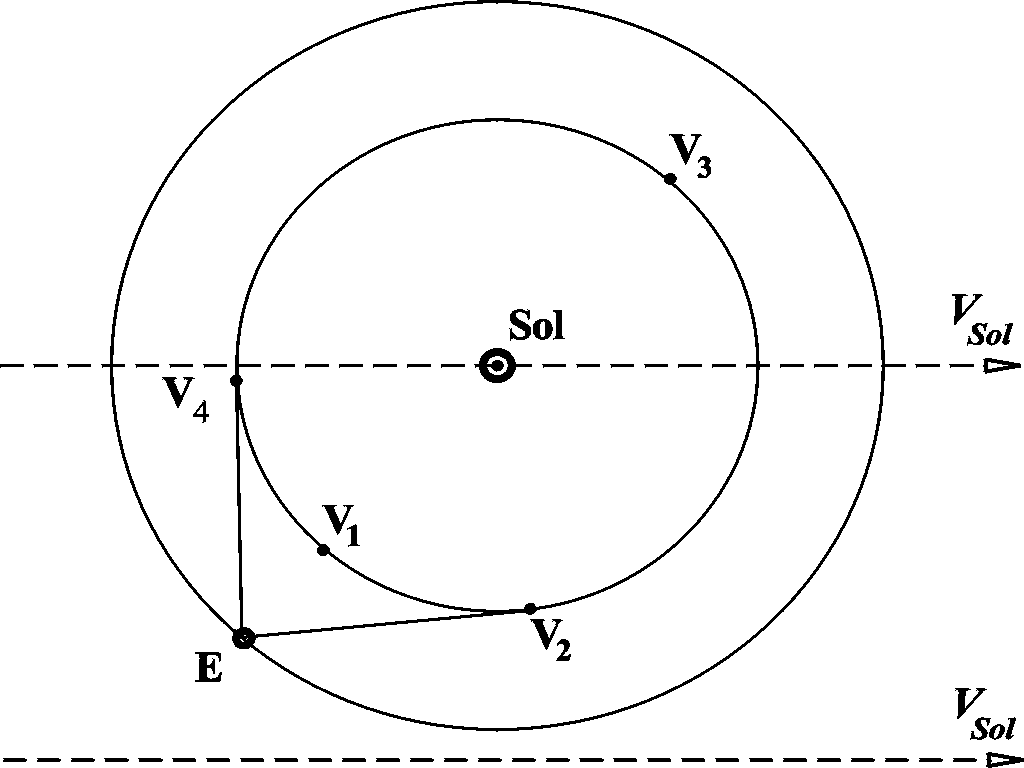
Рис. 1.
[вернуться к содержанию сайта]
В статьях [10-13] описана обработка измерений путевого времени света до Венеры и обратно, а также разностей частот сигналов: отправленного на Венеру и эха. Для обоих случаев мы выводим классические формулы, используя галилеево правило сложения скорости света и тела, а также формулы, соответствующие релятивистскому правилу.
Авторы работ [10-13] учитывали влияние скорости вращения Земли на измерения путевого времени света; проведение наблюдений вблизи нижнего соединения Венеры позволяло считать расстояние Земля-Венера постоянным в течение сеанса.
Члены второго порядка относительно V/C учитывались для разностей частот отправленного и вернувшегося сигнала по формуле Мюльмана, которая совпадает с выведенной нами классической формулой и не совпадает с релятивистской формулой. Отсутствие оснований для утверждения о подтверждении СТО радарными наблюдениями Венеры было признано на симпозиуме № 21 Международного Астрономического союза (см. ([13], с. 186). В статье показано также, почему скорость инерциального движения всей Солнечной системы не повлияла на результаты измерений.
Чтобы дискуссия вокруг СТО завершилась, физики должны отказаться от двусмысленных формулировок и небрежностей в математике, вернуться к научному языку строгих дефиниций и логики.
Радарные наблюдения Венеры проводились в 1958-1962 годах с целью уточнения астрономической единицы (а.е.) – значения большой полуоси орбиты Земли. Метод был косвенным, поскольку определялись расстояния не Земля – Солнце, а Земля – Венера. Существует возможность определения из радарных наблюдений расстояний Земля – Венера, а также относительных радиальных скоростей двух планет соответственно в км и км/c, т.е. в земных единицах. В небесной механике расстояния между телами Солнечной системы выражаются через их отношение к большой полуоси орбиты Земли, т.е. в а.е. Следовательно если найти расстояние Земля – Венера (R) в километрах, то можно получить значение а.е. в километрах.
На практике надо получить из наблюдений ряд не зависящих от эфемерид (от динамической теории) значений Robs для фиксированных моментов времени ti, затем для этих моментов вычислить эфемеридные значения Rcal. Рассматривать способ определения значения а.е. на основе сравнения значений Robs с Rcal мы не будем. Наша задача – ответить на вопрос, подтвердили ли наблюдения Венеры специальную теорию относительности. Для этого мы рассмотрим раздельно (в частях II и III) возможности двух методов: во-первых, измерений суммарного путевого времени света до Венеры и обратно, во-вторых, измерений разности частот сигналов, отправленного к Венере и вернувшегося к наблюдателю (эха).
Прежде всего мы остановимся на вопросах терминологии и тех сведениях из астрономии, которые необходимы физикам, чтобы разобраться в некоторых из тех нерешенных проблем, которые в начале века породили СТО.
I. Любая скорость, будь то скорость тела или света, равна пути, пройденному телом или световым сигналом, делённому на затраченное время. Пока наблюдения проводились на поверхности Земли, была уверенность, что расстояния между пунктами, откуда отправился и куда пришёл “путешественник” (тело или сигнал), не изменилось за время эксперимента; пункты на земной поверхности служили реперами – телами отсчёта. Если в земных условиях скорость объекта измерять не относительно неподвижных реперов, но относительно какого-либо движущегося тела N, то измеренная скорость будет характеризовать не только движение объекта, но и движение тела N. То же можно сказать и о движениях, происходящих в космическом пространстве: прежде всего необходимо позаботиться о системе отсчёта, или системе координат (СК), относительно которой будет изучаться движение. В идеале (в математике) СК должна быть столь же жёсткой, как твёрдое тело, на практике приходится довольствоваться наилучшим из найденных приближений к этому математическому идеалу ([1], с. 116-119). СК должна быть неподвижной хотя бы в течение того времени, пока производятся наблюдения за изучаемым движением.
В эпоху от Коперника до Ньютона система координат с началом в барицентре Солнечной системы, осями, направленными на “неподвижные звёзды” и единицей расстояния – большой полуосью орбиты Земли, удовлетворяла всем требованиям практики – её можно было считать невращающейся и неподвижной. Поэтому скорость объекта N, отсчитанная в этой СК, характеризовала только скорость самого объекта N, а не некоторую комбинацию скорости N со скоростями одного или нескольких тел отсчёта, как это было бы в случае подвижности последних. Хотя ещё Николай Кузанский и Джордано Бруно полагали, что движение присуще всем небесным телам, Системой Мира (см. часть III часть “Principia” Ньютона) была только Солнечная система. За её пределами располагалась неопределённо далекая сфера неподвижных звёзд. Иначе и не могло быть, ведь расстояния до звёзд, движения Солнца и звёзд в пространстве тогда были неизвестны.
Только после открытия Э. Галлеем собственных движений звёзд (1718 г.) астрономы стали изучать изменения взаимных положений звёзд на небесной сфере (медленные изменения конфигураций звёзд в созвездиях), а затем и лучевые скорости звёзд. Отсюда удалось определить сначала движение Солнца по отношению к разным группам звёзд (относительные движения), а затем из анализа последних вывести движение самогó Солнца, его движение по отношению к центру Галактики. Следуя определению Ньютона, движение Солнца по отношению к центру Галактики – неподвижной точке в изолированной системе тел, — надо назвать абсолютным. Аналогично в Солнечной системе абсолютными движениями являются орбитальные движения планет относительно барицентра Солнечной системы ([2], с. 40-41). Поскольку период обращения Солнца вокруг центра Галактики составляет примерно 210 млн. лет, в течение нескольких тысячелетий допустимо считать движение Солнечной системы равномерным и прямолинейным – инерциальным.
Не будем здесь вдаваться в детали построения СК астрономами; заметим, что и после обнаружения движений звёзд по небесной сфере астрономы “поддерживают” постоянство направлений координатных осей в барицентрической СК, для чего в качестве реперов стали использовать средние места звёзд и их изменения на определённую эпоху, далёкие звёзды с исчезающе малыми собственными движениями, внегалактические объекты и т.д. Иначе говоря, астрономы стремятся, чтобы барицентрическая СК была невращающейся, однако, теперь её нельзя считать неподвижной. Эта система координат движется вместе с Солнечной системой с постоянной скоростью VSol., поэтому её стали называть инерциальной системой.
Ещё в 1879 г. Максвелл (см. об этом [3], с. 95-96) поставил вопрос о возможности изучения движения Солнечной системы по наблюдениям спутников Юпитера. В статьях [4, 5] развивается идея Максвелла и предложены астрономические наблюдения тел Солнечной системы, которые позволили бы уточнить направление и значение VSol. Сторонники Эйнштейна отвергают такие предложения, поскольку согласно СТО, никакими наблюдениями внутри Солнечной системы это движение не может быть обнаружено. При этом они ссылаются на принцип Галилея, но не учитывают отличия данной задачи от тех, которые решал Галилей: астрономы ранее изучили, используя внешние реперы, положения и движения всех тел в Солнечной системе на любой момент времени, поэтому современным астрономам a priori известны эти движения в предположении, что Солнечная система неподвижна [6].
Поскольку установили, что Солнечная система движется, возникла задача – проверить, нет ли таких расхождений в непосредственно наблюдаемых (obs) и предвычисленных видимых (cal) положениях тел, которые зависели бы от ранее неизвестной скорости общего движения всех тел системы. Очевидно, такая проверка не обнаружила бы искомых расхождений, если бы свет распространялся мгновенно. Нельзя было бы обнаружить VSol. и в том случае, если бы эта скорость, добавленная к скорости света с, составила сумму, практически неотличимую от с. Так оно было при точности измерений прошлого века, но в последнее время появились способы, где ошибки измерений на два порядка меньше прежних. Из сказанного, разумеется, не следует, что теперь любые измерения, производимые внутри Солнечной системы, позволят обнаружить её движение. Нам необходимо понять, почему на результаты радарных наблюдений Венеры скорость VSol. не повлияла.

Рис. 1.
На рис. 1 показаны разные конфигурации Земли, Венеры и Солнца. Положение EV1 называется нижним соединением планет, положение EV3 – их верхним соединением, положения EV2 и EV4 – элонгациями Венеры. Вся Солнечная система движется как единое целое в направлении, показанном стрелками (к северной части созвездия Лебедь) со скоростью VSol.= 300 км/c ± 50 км/с.
Поскольку наблюдателя на Венере нет и время прихода сигнала на Венеру (t2) не фиксируется по часам, нет возможности по отдельности определить время t2 – t1, затраченное светом на путь в прямом, и t3 – t2 – в обратном направлениях. Бóльшая часть радарных наблюдений проводилась вблизи нижних соединений и лишь некоторые – вблизи элонгаций. Время, которое требуется свету для прохождения расстояния от наблюдателя к Венере и обратно, равно 4.6 мин. для нижнего соединения и 11.6 мин. для элонгаций. Угловое движение Земли за сутки составляет 0.9° , а Венеры – 1.6° , поэтому очевидно, что положение обеих планет по отношению к направлению инерциального движения Солнца за путевое время света практически остаётся постоянным. Следовательно, возможное влияние скорости VSol на промежутки времени t2 – t1 и t3 – t2 оказывается равным по величине и противоположным по знаку. Таким образом, на измеренную по часам сумму этих промежутков времени скорость инерциального движения VSol не повлияет. Все остальные движения, которые рассматриваются в задаче (Венеры и Земли вокруг Солнца и наблюдателя вокруг земной оси), являются вращениями, поэтому некоторые физики справедливо отрицают возможность проверки СТО с помощью радарных наблюдений Венеры. Тем не менее, распространилось мнение, будто эти наблюдения подтвердили СТО, будто классическая кинематика оказалась недостаточной и потребовался учёт “релятивистских эффектов”. Далее мы покажем необоснованность такого мнения.
II. Рассмотрим задачу, решаемую по измерениям путевого времени света. Пусть из точки Е1 на рис. 2a и b был послан сигнал в момент t1, отмеченный по часам; Венера при этом находилась в точке V1. Пока сигнал шёл, Венера переместилась в точку V2, где сигнал отразился от её поверхности, затем он вернулся на Землю, занявшую в это время положение Е3; момент t3 возвращения сигнала в точку Е3 был отмечен по часам. Сплошной линией соединены одновременные положения планет. Пунктирная линия соединяет разновременные положения, т.е. отмечает путь сигнала в принятой нами системе отсчёта (напомним, что это барицентрическая не вращающаяся СК).
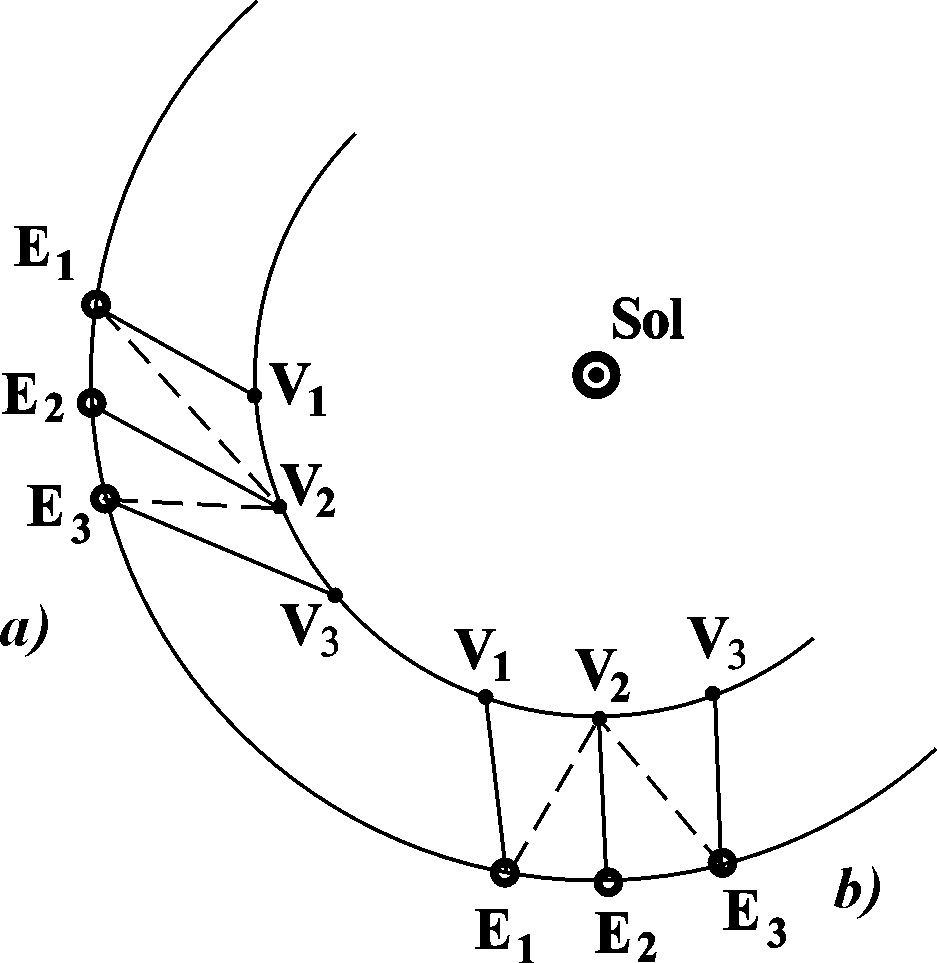
Рис. 2.
Прямые, представляющие собой расстояния между одновременными положениями тел, обозначим так: E1V1 = R1, E2V2 = R2, E3V3 = R3.
Из очевидных соотношений
Е1V2 = (t2 – t1)с (1)
и
V2E3 = (t3 – t2)с (1')
можно записать
E1V2= R1 + e ,
где e - увеличение или уменьшение светового пути за счёт движения Венеры за время t2–t1, следовательно
E1V2 = R1 ± V V ( t2 – t1), (2)
где знак перед VV — радиальной составляющей скорости Венеры на отрезке времени t2–t1, зависит от того, увеличивается или уменьшается за счёт этой скорости путь света по сравнению с расстоянием R1.
Вторая часть пути света
V2E3 = R3± V’V (t3 – t2), (3)
где V’V – радиальная составляющая скорости Венеры на отрезке времени t3 – t2, её знак определяется аналогично, из сравнения V2E3 с R3. Очевидно, учитывая (1) и (1’), можно (2) и (3) переписать в виде:
![]() (2¢
)
(2¢
)
![]() , (3¢
)
, (3¢
)
На Венере нет наблюдателя, который отметил бы по часам время прихода сигнала, и только разность t3–t1 является измеренной величиной, которая может быть использована для составления уравнений наблюдений. Величины, достаточно хорошо известные, ошибки которых не могут повлиять на выводимые из наблюдений расстояния, можно заимствовать из эфемерид, т.е. считать известными a priori.
Складывая (2’) и (3’), мы получаем возможность определить сумму расстояний R1 + R3, если известны VV и V’V и скорость света с. Определить по отдельности расстояния R1 и R3 можно в том случае, если провести замкнутый цикл перекрывающихся наблюдений, т.е. получить цепочку уравнений:
R1 +R3 = l1, R3+R5 = l2, …, R2n+1 + R1 = lm ,
но во время рассматриваемой кампании наблюдения велись лишь на части орбиты. В таком случае число неизвестных остаётся на единицу больше числа уравнений. Достаточно найти хотя бы одну из разностей R i – Ri+n, чтобы, присоединив её к измеренным суммам, найти все расстояния Ri.
Авторы обработки радарных наблюдений Венеры пошли по иному пути. Они оставили в качестве неизвестных в условных уравнениях расстояния R2, что позволяло отнести одно звено наблюдений к одной “неподвижной” точке, а именно, к положению Венеры в момент отражения от неё сигнала, t2. Тогда можно записать
R2 + VE (t2 – t1) = E1V2, R2 – V’E (t3 – t2) = V2E3, (4)
Здесь знаки перед VE, расставленные в соответствии с прежним правилом, соответствуют расположению планет на рис. 2а. Из (4), учитывая (1) и (1’), получим
![]() (4¢
)
(4¢
)
в этом случае радиальная составляющая скорости Земли заимствуется из эфемерид.
Такой способ невыгоден потому, что момент t2 прихода сигнала на Венеру не отмечен по часам. Приходится использовать эфемериды, чтобы решить вопрос, к какому моменту времени относится полученное из наблюдений расстояние R2. Между тем, для определения а.е. требуется вычислить расстояние Rcal, по моменту времени, не зависящему от эфемерид. Выгоднее определять расстояния в моменты, отмеченные по часам, тем более, что существует принципиальная возможность из доплеровских наблюдений находить изменения расстояний.
Отмеченный нами недостаток метода сохранился бы, даже если бы Солнечная система была неподвижна. Но она движется, и если постулат СТО о постоянстве скорости света, в какой бы инерциальной СК она ни была измерена (см. [7] с. 387), неверен, то при определённых конфигурациях, как это видно из рис. 1, возникает опасность внести в вычисленное значение момента t2 дополнительную ошибку.
Действительно, вычисления производятся с постоянной c, т.е. не допускается, чтобы при прочих одинаковых условиях, совпадение направления VSol с направлением от источника света к приёмнику способствовало увеличению путевого времени света, а противоположность этих направлений – его уменьшению, или, как сказали бы современные физики, не допускается, чтобы “однонаправленная скорость света” была непостоянна (далее мы покажем, что термин, взятый в кавычки, неудачен).
Эфемеридные значения вычисляются без учёта VSol, исходя из того, что барицентрическая СК неподвижна, а поэтому световой сигнал распространяется в ней с одинаковой скоростью во все стороны от той точки c постоянными координатами, где он был испущен. Поскольку барицентрическая СК в действительности движется, координаты названной точки окажутся не постоянными, но непрерывно изменяющимися в той искомой “неподвижной” СК, где свет распространяется с постоянной скоростью по всем направлениям. Скорость света, измеренная по отношению к любой движущейся точке, как уже было сказано, будет зависеть от движения последней. Поэтому не измеренное значение скорости света, но выведенное из анализа многих измерений, принимается астрономами за постоянное. В вакууме с = Const, в воздухе с′ = Const и т.д. в других средах, все эти значения выведены из анализа многих измерений.
В искомой СК, которую выше мы обозначили как “неподвижную”, Солнце движется равномерно и прямолинейно в течение всех опытов. Следовательно, таковой может быть, например, СК с центром в центре масс нашей Галактики (строго говоря, движение Солнца в Галактике тоже является вращением, но с периодом в 2.108 раз бóльшим, чем вращение Земли вокруг Солнца), либо СК с другим “аттрактором”, нам пока неизвестным [4-6]. Во всяком случае, о равноправии систем координат говорить не приходится.
Таким образом, правила классической кинематики требуют перехода к новой, неподвижной СК после определения величины и направления VSol, тогда как СТО запрещает пересмотр алгоритмов, предложенных в то время, когда о движении Солнца ничего не было известно.
Как упомянуто выше, из-за движения Солнца при некоторых положениях двух планет относительно направления скорости VSol интервалы времени t2–t1 и t3–t2 могут различаться больше, чем это допускают эфемериды, т.е. возникает дополнительная опасность отнести значения расстояний R2 к неверным моментам времени. Тем не менее, вероятность привнесения этой дополнительной ошибки в значение a.е. невелика, если последнее выводить из многих сравнений Robs с Rcal при разных конфигурациях планет и разной ориентации направления Земля-Венера по отношению к VSol.
Мы отвлеклись от темы. В нашу задачу не входит критика методики обработки наблюдений Венеры. В соответствии с нашей темой мы должны отметить, что авторы работ [8-11] не упоминают о движении Солнечной системы и о возможном влиянии VSol на измеренные или вычисленные по эфемеридам величины, т.е. они не касаются тех проблем, которые обсуждались на рубеже веков и связаны с СТО, они не пользуются ни преобразованиями Лоренца, ни релятивистскими сокращениями пространства-времени, т.е. у них нет оснований говорить о проверке или использовании СТО.
Далее мы рассмотрим все случаи упоминания СТО в указанных работах.
В работе [8] теория относительности не упоминается, и нет вывода формулы, по которой проводилась редукция наблюдений. Уделяя достаточно внимания учёту вращения Земли вокруг оси, влияющему на длину пути, авторы не пишут об учёте орбитальных движений планет. На с. 184 написано: “Допускается приближение, заключающееся в том, что весь путь принимается равным удвоенному нерелятивистскому расстоянию в тот момент, когда сигнал прибывает на Венеру. Верится, однако, что это упрощение приведёт к пренебрежимо малым ошибкам, поскольку орбитальные скорости Земли и Венеры малы по сравнению со скоростью света”. Это означает, что авторы использовали формулу
2R2 = (t3 – t1)с (5)
и что они считали её нерелятивистской.
Очевидно, формула (5) приближенная, справедливая для V< < c. В релятивистской литературе утверждается, что только формулы второго приближения различаются в классической механике и в СТО. Выше по правилам классической механики мы получили формулы, из которых следуют выражения более точные, чем (5). В качестве примера рассмотрим два случая, представленные на рис. 2.
При наблюдениях вблизи одной из элонгаций, как видно из рис. 2а,
E1V2 > R2 > V2E3.
Тогда, складывая (4), получаем
2 R2 +[ V E (t2 — t1) – V’E (t3 - t2)] = c (t3 – t1).
В [9] на с. 193 отмечается, что обычно на практике выполнялось условие VE = V’E. Несмотря на это, мы не имеем права приравнять нулю выделенную квадратными скобками разность, поскольку нет измерений, свидетельствующих, что t2— t1=t3- t2. Следует избежать вычитания неизвестных отрезков времени; это можно сделать, если сложить уравнения (4¢ ).
Тогда при VE = V’E получим формулу, более точную, чем (5):
![]() (6)
(6)
Для наблюдения в нижнем соединении, представленного на рис.2b,
E1V2 > R2, R2 < V2E3.
Тогда, вместо (4’) получаем
![]()
Сложив последние уравнения, получим
![]() , (7)
, (7)
откуда при VE = V’E следует
2 R2 = (t3 — t1) (c - VE). (7¢ )
Если бы свет распространялся медленно, рис. 2 отражал бы отношение между путями, пройденными в прямом и обратном направлениях, но в действительности цикл наблюдений короткий, и вблизи соединений расстояние между планетами практически не изменяется, т.е. относительная радиальная скорость планет V=V’ = 0, тогда t2 – t1 = t3 – t2, и справедлива формула (5). Поскольку большая часть наблюдений во все годы проводилась вблизи нижних соединений, можно предположить, что использование формулы (5) не внесло существенных ошибок в значительную часть определявшихся расстояний.
И. Шапиро, так же как и авторы [8], удовлетворился формулами первого приближения. Он пишет: “Влияние релятивистских поправок на запаздывание эха незначительно” ([9], с.237). При этом он называет релятивистскими поправками (sic!) члены второго порядка, которые, как мы видели, появляются благодаря сложению скоростей света и тел, против чего возражают сторонники СТО, так что точнее было бы назвать квадратичные члены “антирелятивистскими”.
III. В анализируемой литературе только при обработке доплеровских наблюдений была сделана заявка на использование релятивистских формул. Авторы работы [10] посвящают раздел III “Relativistic Doppler equations and propagation time” выводу формулы для разностей частот сигнала и эха ![]() , которую они называют релятивистской и которая сначала была найдена ими эмпирическим путём, как решение, приводящее к наименьшим остаточным уклонениям между наблюдаемыми и эфемеридными значениями.
, которую они называют релятивистской и которая сначала была найдена ими эмпирическим путём, как решение, приводящее к наименьшим остаточным уклонениям между наблюдаемыми и эфемеридными значениями.
Мы не будем повторять здесь анализа, проведённого нами в [12-13], где показаны, во-первых, две ошибки, допущенные авторами работы [10] при выводе формулы, следующей далее под номером (14), которую авторы хотели выдать за релятивистскую; во-вторых, несовпадение исходной формулы, которой воспользовались авторы, с релятивистским выражением.
Формула (14), которую авторы использовали для обработки наблюдений, не может быть названа релятивистской, что мы докажем, выведя её из известной классической формулы для разностей частот n и n ′:
![]() (8)
(8)
где n - частота сигнала, отправленного с источника, n ′ - частота принятая, u – скорость приёмника, w – скорость источника.
При радарных наблюдениях на первом этапе Венера являлась приёмником излучения, на втором – источником. Поэтому следует записать в соответствии с (8) для сигнала, пришедшего на Венеру
![]() , (9)
, (9)
и для сигнала, вернувшегося на Землю (эха)
![]() . (10)
. (10)
Здесь мы пользуемся теми же обозначениями, что и в предыдущем разделе.
Подставляя (9) в (10), получаем
![]() . (11)
. (11)
После деления на с2 последние члены в числителе и знаменателе (11) окажутся членами второго порядки относительно V/c, ими можно пренебречь, но при высокой точности наблюдений можно воспользоваться эфемеридами для их учёта без риска внести ошибку в искомые неизвестные. После этого уравнения (11) примут вид
![]() . (12)
. (12)
Допуская, как и прежде, что за время путешествия сигнала в одну сторону влияние радиальной скорости каждой из планет на изменение расстояния между ними постоянно, можно перейти к относительным радиальным скоростям планет для промежутков времени t2 – t1 и t3 – t2 следующим образом:
![]() (13)
(13)
где знак перед ![]() положителен при удалении планет друг от друга и отрицателен – при их сближении. Выражения (13) не позволяют упростить формулу (12), поэтому авторы работы [10] использовали эфемериды для учёта изменения радиальной скорости наблюдателя относительно момента t2, что позволило им вместо (13) перейти к величинам
положителен при удалении планет друг от друга и отрицателен – при их сближении. Выражения (13) не позволяют упростить формулу (12), поэтому авторы работы [10] использовали эфемериды для учёта изменения радиальной скорости наблюдателя относительно момента t2, что позволило им вместо (13) перейти к величинам
![]() (13¢
)
(13¢
)
Такие обозначения были приняты в работе [10]. Тогда уравнения (12) можно записать в виде
![]() , (12′)
, (12′)
откуда, видоизменяя пропорцию, получаем формулу
![]() , (14)
, (14)
которая совпадает с формулой, использованной при редукции наблюдений Венеры, записанной в [10] на с. 193 и повторенной в [11] на с. 186.
Добавим, что в [12] на основании известного релятивистского выражения
![]() , (15)
, (15)
где V – относительная скорость приёмника и источника излучения, мы, сохраняя члены второго порядка, вывели релятивистскую формулу
![]() , (16)
, (16)
которая не совпадает с формулой (14), что ещё раз свидетельствует о нерелятивистском происхождении формулы (14).
Итак, при обработке доплеровских наблюдений теория относительности также не потребовалась. Через год после опубликования статьи [10] выступая с отчётным докладом о проведённой работе на симпозиуме № 21 Международного Астрономического союза, Д.О. Мюльман – автор формулы (14) – уже не упоминал ни о теории относительности, ни о релятивистском происхождении формулы (14) (см. [11], с.186). Замечание И. Шапиро на том же симпозиуме [9] об отсутствии необходимости использовать релятивистские поправки мы цитировали выше.
В Трудах симпозиума № 21 напечатана также дискуссия по радарным наблюдениям, содержащая следующее замечание Дж. М. Клеменса – директора Морской обсерватории США – о членах второго порядка в формуле (14): “Поскольку эти члены могут быть истолкованы вне рамок теории относительности, нельзя рассматривать их как новое подтверждение теории относительности” ([9], с. 254).
IV. Остановимся на полемике между сторонниками и противниками СТО, поскольку она касается интерпретации радарных наблюдений Венеры.
Некоторые противники Эйнштейна, отстаивая гипотезу Ритца, противопоставляют второму постулату СТО тезис о зависимости скорости света от скорости источника. Это мнение обычно опровергают ссылкой на де-Ситтера и наблюдения двойных звёзд, попутно тезис о постоянстве скорости света читателю представляют как откровение СТО. Между тем, скоростью света в качестве постоянной, астрономы пользовались уже в 18 веке. Другая часть противников СТО утверждает, что скорость распространения света зависит от скорости наблюдателя – приёмника излучения.
По-видимому, и сторонники, и противники СТО не проводят чётких границ между относительной скоростью, измеряемой в конкретных опытах или наблюдениях, и выводимой на основе многих наблюдений скоростью, присущей только данному телу или только световому сигналу.
Мы писали выше о невозможности измерить скорость безотносительно к чему бы то ни было. Например, если скорость кометы измеряется относительно подвижной Земли (точнее, относительно земного наблюдателя), но записать уравнение, справедливое для собственной скорости кометы v (таковой будет её орбитальная скорость, или скорость относительно барицентра Солнечной системы), а затем подставить вместо v её измеренную скорость, тогда неизбежны ошибки – предвычисленное положение кометы окажется неверным. Аналогично, если в уравнении записана скорость света, то она не может быть относительной скоростью – f(c, V), не должна зависеть от скоростей каких-либо других тел.
Утверждение о том, что скорость света зависит от направления, противоречит классической физике – свет в вакууме распространяется во все стороны с одинаковой скоростью. Вместе с тем, если речь идет об измеренной скорости, то она может быть функцией – f (c, V). Нужно знать условия опыта, чтобы судить о том, чью скорость представляет V. Было бы нелепо приписать свету странное свойство – распространяться в однородной среде в разных направлениях с различными скоростями, и без этого на рассуждения о “загадочной природе света” физики и философы потратили слишком много времени.
Двусмысленность формулировок создаёт препятствия для конструктивной полемики. Например, утверждение Эйнштейна на с. 396 в [9], что “свет распространяется в пустоте с постоянной скоростью совершенно независимо от движения источника света”, не входит в противоречие с характеристикой собственной скорости света, наряду со скоростями источника, приёмника и других тел. Из утверждения на той же странице, что “один и тот же луч света имеет одну и ту же скорость света относительно всех наблюдателей” уже не ясно, постоянство относительной скорости “луча” и наблюдателя или собственной скорости “луча” света имеет в виду автор. Пример с вагоном на с. 539-540 (c + V = c) и формулировка постулата на с. 387 рассеивают сомнения, убеждают, что именно относительную скорость Эйнштейн принимает за постоянную величину.
При обсуждении опытов с целью измерения скорости света возникают споры о том, в какой системе координат её надо измерять: в СК, связанной с приёмником или с источником излучения. Сторонники СТО полагают, что измеренная в любой инерциальной СК скорость света будет постоянной; некоторые из сторонников считают, что скорость света будет постоянной, относительно чего бы её ни измеряли. Оба эти утверждения неверны
Поскольку все тела подвижны, возникает вопрос, можно ли указать такую систему координат и времени, чтобы отнесённая к ней скорость света была постоянной.
До открытия движений Солнца и звёзд астрономы ответили бы так: скорость света будет постоянной, если её отсчитывать от той точки, где находился источник света в момент испускания сигнала, при условии, что координаты точки выражены в общепринятой барицентрической СК, а время отсчитано в астрономической шкале.
Астрономы XX века не предлагают такой единственной универсальной “неподвижной” СК, которая удовлетворила бы специалистов всех областей. Но они могут указать наблюдения, которые помогли бы уточнить направление движения Солнца и этим внесли бы вклад в поиск СК, которая сегодня нужна уже многим специалистам [3, 4-6]. В настоящее время для решения разных задач приходится использовать разные СК; часто прибегают к методическим приёмам для достижения “неподвижности” системы отсчёта, например, усредняя результаты измерения путевого времени в прямом и обратном направлениях.
Некоторые противники СТО, не задумываясь о том, как можно отсчитать координаты тел относительно эфира, защищают эфир в качестве универсальной неподвижной системы отсчёта, в которой свет распространяется с постоянной скоростью. Реакцией на эту точку зрения является Примечание И. Шапиро в [9] на с. 238: “Классическое дифференцирование, в котором скорость света предполагается равной с по отношению к эфиру, приводит к тому же результату (имеется в виду результат СТО.- С.Т.), но без первого члена в скобках”. Шапиро ошибается, полагая, что классическая система отсчёта связана с эфиром. Такой системы координат нет в астрономии. Дифференцирование относительно несуществующей СК не может быть доведено до числа, а, следовательно, практическая проверка теории не может состояться.
Изначально отрицая существование эфира, Эйнштейн, как известно, был вынужден вернуться к его признанию – мысль релятивистов оказалась в порочном круге (см. [14], с. 258-259). Эйнштейн писал: “Давний опыт, не имеющий пока исключений, показывает, что физические явления зависят только от движений тел относительно друг друга, т.е. что с физической точки зрения абсолютного движения не существует” (разрядка Э.) (см. [7], с. 412). В рамках учений Эйнштейна нет принципиальной возможности решать задачи, связанные со скоростью света, ибо с одной стороны, скорость света всегда постоянна, а с другой – только относительное движение сохраняет право на существование. Тогда, на естественно возникающий вопрос, относительно чего постоянна скорость света, возможен один ответ – относительно любого тела.
Надо признать, что брешь между физиками и астрономами возникла ещё до появления СТО из-за невнимания физиков к задачам построения систем координат и времени. Скорость света может быть найдена по известному расстоянию и времени его преодоления, т.е. по величинам, зависящим от координат и шкалы времени. Можно находить “с” также из сравнения скорости света со скоростями небесных тел, предполагая последние известными. В этом случае возникает иллюзия независимости скорости света от координат, поскольку забывают, что скорости небесных тел были ранее определены астрономами посредством изучения их движений в конкретной системе координат и времени.
Теоретик может дать любое имя той СК, где свет распространяется с постоянной скоростью, но ни он, ни кто другой не сможет создать, “построить” систему отсчёта, опираясь на эфир, космическое пространство, мировую линию фотона и т.п. Для проверки теоретических построений и эфир, и неоэфир, и пустое пространство в равной степени остаются пустым звуком. Системы отсчёта “строятся”, или пространство “математически организуется” с помощью тел отсчёта, либо их проекций.
Поскольку явно нецелесообразно пересчитывать скорости планет на СК, связанную с иным аттрактором, нежели центр масс тел Солнечной системы, в дальнейшем в случае необходимости “поправку за движение Солнечной системы” будут вводить либо в расстояния, либо в путевое время света, либо в его скорость, т.е. будут производить вычисления со скоростью света, приведённой к подвижной барицентрической СК; величина приведённой скорости окажется изменяющейся в зависимости от угла между направлением “наблюдатель – приёмник” и направлением на апекс Солнца. Так будет лишь после того, когда из надёжных опытов и наблюдений определят точное направление движения Солнечной системы. Кроме наблюдений, рассмотренных в [4-6], можно предложить космический эксперимент для уточнения этого направления.
Анализ статей по обработке радарных наблюдений Венеры свидетельствует о том, что формулы СТО не использовались при обработке наблюдений и задача проверки СТО не ставилась. Замечание Клеменса при подведении итогов работы на 21 симпозиуме МАС о том, что нет оснований говорить о новом подтверждении СТО, ни у кого из астрономов не вызвало возражения.
На вопрос, кем распущен слух “о новом подтверждении СТО”, автор настоящей статьи не может ответить. Если в этом повинны средства массовой информации, то надо выяснить, с чьей подачи они действовали. Мнение о подтверждении СТО по наблюдениям Венеры широко распространилось также и в среде специалистов, до такой степени, что релятивистскими поправками стали называть члены второго порядка относительно V/с в любых формулах. В результате такой “терминологической диверсии” все наблюдения, для редукции которых используются ряды с указанными членами, стали подаваться как подтверждение или использование СТО на практике, даже если к проблеме инерциального движение эти наблюдения не имели никакого отношения.
На примере, приведённом в разделе II, читатель мог убедиться в абсурдности такой терминологии даже с формально-математической точки зрения, ведь сторонники Эйнштейна отвергают формулы, содержащие сложение скоростей с и V. С их точки зрения формулы (2′) – (4′) неверны. Между тем именно из них, равно как и из эквивалентных им формул (2) – (4), появляются члены второго порядка, тогда как релятивистский подход в данном случае может дать лишь формулу первого приближения (5).
В разделе III представлен случай, когда и классическая (14), и релятивистская формулы (16) содержат различные члены второго порядка, причём в релятивистской формуле эти члены появились благодаря тому, что уже в исходной формуле (15) был нарушен запрет СТО (требование c + V = c). Заметим также, что в теории звёздной аберрации релятивистский подход приводит к квадратичным членам, отличным от тех, которые получаются, исходя из классической механики [14, 15]. Так что нет ни малейшего основания называть релятивистскими все поправки, являющиеся функциями V2/с2.
1. Мурри С.А. К вопросу о месте геометрии в естествознании. В кн.: Проблемы пространства, времени, движения, т.1, 1997, С-Пб., Искусство России, с. 115-131.
2. Толчельникова-Мурри С.А. Специфика подхода к понятиям пространство и время в математике и астрометрии. В кн.: Проблемы пространства и времени в современном естествознании, 1991, Л., ТНЦ СО АН СССР, с. 25-55.
3. Толчельникова-Мурри С.А. К проблеме обнаружения движения Солнечной системы относительно эфира. В кн.: Проблемы пространства и времени в современном естествознании, 1993, С.-Пб., ТНЦ РАН, с. 95-105.
4. Tolchelnikova- Murri S.A. A New Way to Determine the Velocity of the Solar System. In: “Galilean Electrodynamics”, 1992, v.3, № 4, с. 72-75.
5. Смирнов Б.Н., Толчельникова-Мурри С.А. Задача Максвелла и хронометрические наблюдения спутников больших планет – Геодезия и картография, 1996, №10, с. 20-23.
6. Смирнов Б.Н., Толчельникова-Мурри С.А. Можно ли определить инерциальное движение Солнечной системы, опираясь на идею Максвелла. В кн.: Проблемы пространства, времени, движения, т.1, 1997, С-Пб., Искусство России, с. 191-195.
7. Эйнштейн А. Собрание научных трудов в 4-х томах, том 1, 1965, М., “Наука”.
8. Pettengill G.H., Briscoe H.W., et al. A Radar Investigation of Venus – Astron. J., 1962, 67, N 1299, c. 181-190.
9. Шапиро И. Радиолокационное определение астрономической единицы. В кн.: Фундаментальные постоянные астрономии, 1967, М., Мир, с. 209-254.
10. Muhleman D.O., Holdridge D.B., Block N. The Astronomical Unit Determined by Radar Reflections from Venus - Astron. J., 67, N 1299, c. 191-213.
11. Мюльман Д.О. Связь между системой астрономических постоянных и радиолокационными измерениями астрономической единицы. В кн.: Фундаментальные постоянные астрономии, 1967, М. Мир, с.181-208.
12. Tolchelnikova- Murri S.A. The Doppler Observations of Venus Contradict the SRT. In “Galilean Electrodynamics”, v. 4, № 1, c. 3-6.
13. Tolchelnikova- Murri S.A. On the Derivation of Classical Formulae for the Longitudial Doppler Effect In. “Galilean Electrodynamics”, v. 5, № 6, с. 116-117.
14. Толчельникова-Мурри С.А., Зинченко М.В. К проблеме учёта аберрации света. В кн.: Проблемы пространства, времени, тяготения, С.-Пб., Политехника, с. 245-260.
15. Толчельникова-Мурри С.А., Чубей М.С. Звёздная аберрация при возросшей точности наблюдений и при больших скоростях движения наблюдателя. В кн.: Проблемы пространства, времени. Движения, т.1, 1997, С.-Пб. “Искусство России”, с. 92-100.
Дата установки: 17.07.2012
[