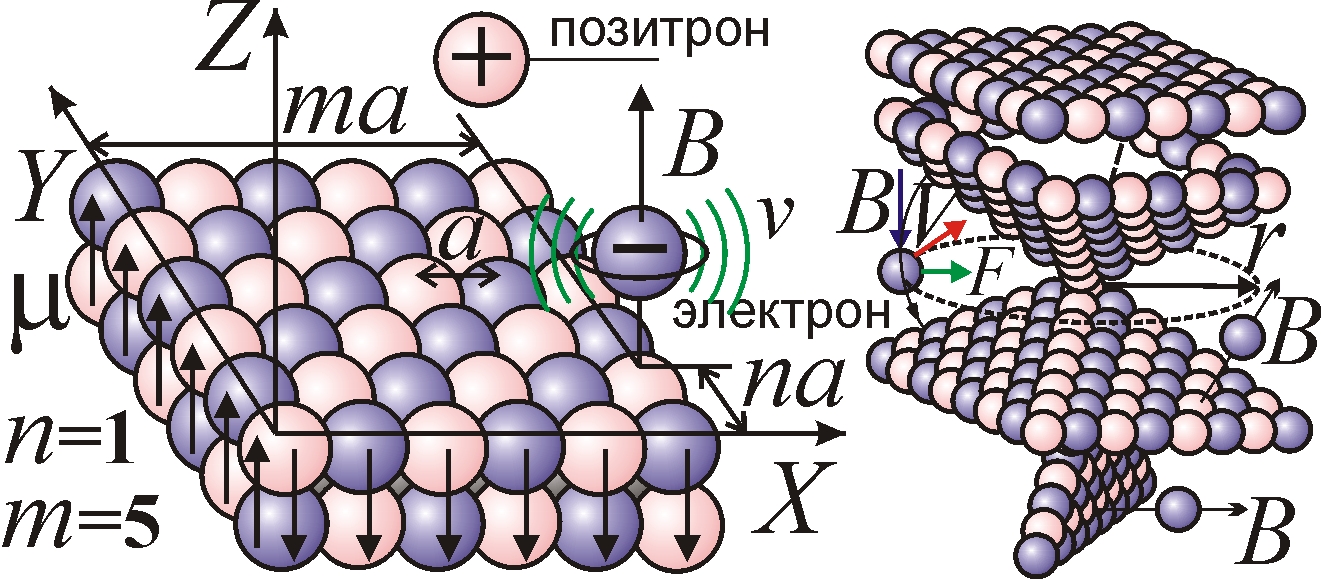
Рис. 1. Схема генерации спектра атома водорода и строение атомного остова.
[вернуться к содержанию сайта]
В настоящее время общепринята квантовая модель атома. Однако она не объясняет ряд эффектов [1–4], ведёт к теоретическим парадоксам [5] и математическим трудностям расчёта спектров многоэлектронных атомов [6]. Формулы квантовой механики приводят к расходимостям и бесконечностям, например, при анализе поля электрона и при учёте в спектре энергий нулевых колебаний в виде энергии hν/2, существующей на любой частоте ν и стремящейся к бесконечности при росте ν. То есть, квантовая физика ведёт к тем же парадоксам, которые в начале XX в. заставили отказаться от классической физики при анализе спектра теплового излучения и “ультрафиолетовой катастрофы” – бесконечного роста энергии в области высоких частот ν. Поэтому обратимся к анализу классической магнитной модели атома, предложенной В. Ритцем [7] и Дж.Дж. Томсоном [8] в начале XX в. – одновременно с квантовой. Эта модель объясняла спектры и решала все парадоксы классической физики в рамках классической механики [7, 9].

Рис. 1. Схема генерации спектра атома водорода и строение атомного остова.
Согласно магнитной модели атома, электроны занимают ряд устойчивых положений-узлов в атомном остове-ядре (рис. 1). При внешних воздействиях электроны массы M и заряда e начинают вращаться возле положений равновесия в магнитном поле B атома, излучая на циклотронной частоте ω = eB/M своего вращения. Ряд узлов (положений равновесия электронов) соответствует узлам сетки периода a вдоль осей X и Y, у которых магнитные поля B1 = μμ0/2πr0y2 и B2 = μμ0/2πr0x2 перпендикулярны к плоскости сетки и противонаправлены. Здесь μ – магнитный момент электрона, μ0 – магнитная постоянная, r0 – классический радиус электрона. Такую структуру узлов и поля B = B1 – B2 могут формировать цепочки электронов и позитронов, образующих подобие кристаллической решётки [9]. Вопреки теореме Ирншоу, такие системы зарядов стабильны при малых отклонениях от закона Кулона [8]. Примером такой плоской решётки служит графен, где атомы углерода образуют слой, вдоль которого электроны движутся по узлам решётки.
Электроны колеблются лишь на частотах, соответствующих магнитному полю B в узлах. Как показал В. Ритц, это объясняет линейчатые спектры водорода и металлов [7]. Так, спектр атома водорода в магнитной модели естественно получается в виде набора частот ω = eB/M = (1/y2 – 1/x2)eμμ0/2πr0M, где x = ma и y = na – координаты электрона, а период a порядка размера атома водорода ~10–10 м. Отсюда спектр частот водорода ν = ω/2π = Rс(1/n2 – 1/m2), где R – постоянная Ридберга, с – скорость света в вакууме, n и m – целые числа. Интенсивность спектральных линий определяется степенью устойчивости положений электронов в узлах. Чем устойчивей узел, тем выше процент атомов с электронами, расположенными в соответствующих узлах и тем выше интенсивность излучения соответствующей спектральной линии.
Магнитная модель атома естественно объясняет эффекты Зеемана и Штарка [9, 10]. В эффекте Штарка электрическое поле E смещает электроны от положений равновесия. Соответственно значению поля B' в новом положении меняется и частота ω' = eB'/M. В зависимости от расположения электронов в атоме, дипольные моменты атомов принимают несколько возможных значений и направлений по отношению к оси атомного остова. Поэтому внешнее поле, ориентируя атомы, смещает электроны в разных направлениях и в разной степени, отчего каждая спектральная линия расщепляется на несколько, с близкими частотами и разными направлениями колебаний (поляризации): в этом суть эффекта Штарка [10]. Это объясняет экспериментальный факт, выявленный ещё И. Штарком: неоднородное электрическое поле разделяет поток атомов на несколько потоков, в зависимости от величины дипольного момента, и каждый поток излучает лишь одну спектральную компоненту [10]. В согласии с магнитной моделью атома, и вопреки квантовой, интенсивность линий зависит от направления поля E к вектору скорости пучка атомов.
Эффект Зеемана Ритц объяснил наложением на внутриатомное поле B внешнего поля ΔB [7]. В новом поле B' = B ± ΔBsinθ меняются частоты колебаний электронов ω' = eB'/M. Т.к. магнитный момент атомов сонаправлен с ΔB и ориентируется, в зависимости от размещения электронов, под разными углами θ к плоскости колебаний электронов, то их частоты принимают лишь ряд значений ω', в зависимости от типа линии, атома и поля ΔB. В итоге каждая линия спектра расщепится на ряд близких с разными поляризациями, с чем и связан эффект Зеемана [10]. Согласно Ритцу, это объясняет нормальный и аномальный эффект Зеемана, где максимальное значение Δω = eΔB/M, вопреки теории Лоренца (Δω = eΔB/2M).
Магнитная модель объясняет и структуру таблицы Менделеева, представляя остов атома в форме бипирамиды, рёбра которой образованы магнитными осями [9]. Такой остов в виде пустотелого многогранника формируется при росте электрон-позитронной решётки в электрическом и магнитном поле ядра, по аналогии с формированием снежинок [11], фуллеренов, белков и белковых оболочек вирусов. Электроны заполняют остов плоскими квадратными слоями растущей площади и ёмкости 2n2. Это объясняет, почему числа элементов в периодах №1–7 (рис. 2) – это удвоенные квадраты: 2·12, 2·22, 2·22, 2·32, 2·32, 2·42, 2·42. Каждый слой соответствует периоду. После заполнения слоя начинает заполняться следующий, соответствующий следующему периоду. Так объясняются свойства инертных газов, лантаноидов и актиноидов, для которых квантовая модель атома не объясняет атипичные валентности [9].
Магнитная модель естественно объясняет и фотоэффект. Магнитные оси создают бочкообразную структуру поля B (рис. 1): оно перпендикулярно средней плоскости остова атома и равно B = μ0μ/πr0r2. На электрон, летящий по орбите радиуса r, действует сила Лоренца F = eVB = e2νμ0μ/r0r = MV2/r (с учётом V = 2πrν). Отсюда энергия электрона MV2/2 = νeμ0μ/r0, где eμ0μ/r0 = h, т.е. W = hν. Эти электроны вылетают из атома при облучении светом частоты ν, вызывающим резонансную раскачку, сход электрона с орбиты и вылет из атома с сохранением энергии W = hν. Объясняет модель и планковский спектр излучения и эффект Комптона [9].
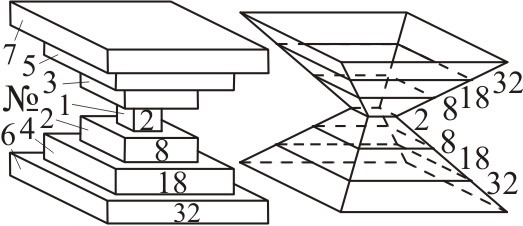
Рис. 2. Схема остова, слоёв атома.
Модель Ритца классически объясняет свойства газов и твёрдых тел [9], включая металлы и полупроводники. Так, спад теплоёмкости при охлаждении объясняется не квантовым вымерзанием степеней свободы, а упорядочением, ростом числа связей атомов при охлаждении. В твёрдом теле образуются всё более крупные конгломераты атомов – жёсткие молекулы, где атомы колеблются как одно целое с энергией ~3kT, где k – постоянная Больцмана. С падением температуры T число N отдельных молекул и атомов тела снижается, за счёт слияния, и теплоёмкость CV = dU/dT = 3Nk падает. Возле абсолютного нуля остаётся одна жёсткая молекула, включающая весь кристалл с энергией ~kT и CV = k ≈ 0, вместо обычной молярной теплоёмкости CV = 3kNa = 3R, т.к. k/R = 1/Na << 1. Это классически объясняет спад теплоёмкости до нуля. У свинца атомы связаны слабо, отсюда его пластичность и CV = 3R даже при T ~ 50 K. Зато у твёрдого алмаза и бериллия CV < 3R даже при T ~ 500 К. И лишь при T > 1000 К их теплоёмкость CV = 3R, ввиду разрушения связей. Т.е. при T ниже температуры Дебая ΘD нет отклонений от классического закона Дюлонга-Пти CV = 3R, если пересчитать теплоёмкость для нового числа молекул. А классически ΘD – это температура TS = WS/k, при которой кинетическая энергия атомов ~kT равна энергии WS их полностью насыщенных связей. Поэтому TS = ΘD определяет скорость звука, коэффициенты упругости, проводимости, и велика у твёрдых тел с высоким WS (бор, алмаз, кремний), но мала у свинца, щелочных металлов.
Модель объясняет также механизм генерации и усиления света фиксированной частоты в твердотельных лазерах, в полупроводниковых светодиодах. Например, если электроны проходят в полупроводнике разность потенциалов U, приобретая энергию W = eU, то при захвате магнитной ловушкой атома они начинают вращаться в поле B остова с фиксированной частотой ν = W/h, излучая на этой частоте (рис. 1).
Отметим ряд возможных применений магнитной модели в микроэлектронике. Например, атомы охлаждённого вещества, не испытывая соударений и внешних воздействий, смогут длительно сохранять электроны в узлах. Это позволит записывать и хранить информацию на атомарном уровне или использовать атом как триггер, переводя электроны в заданные узлы решётки pump-импульсом лазера. Считывание информации производят probe-импульсом с частотой, соответствующей данному узлу. Присутствие электрона в узле выявят по резонансному отклику электрона. В качестве рабочего вещества для таких устройств удобны атомы переходных элементов, включая атомы редкоземельных элементов, с богатым спектром частот, т.е. вариантов размещения электронов в атоме. Не случайно в лазерной технике в качестве активных центров используют элементы переходных групп – хром, эрбий, иттербий, неодим и т.д.
На некоторых типах атомов, где электроны с трудом занимают отдельные узлы, но легко их покидают (генерируя запрещённые линии), можно устроить аналоги диодов и транзисторов. Тогда атом с набором узлов будет работать как микросхема, ячейка памяти. Более надёжны элементы на электронах внутренних оболочек, с резонансными частотами в рентгеновской области (их частоты ν выше, ввиду меньшего шага a), т.к. на них не влияют соседние атомы и температура. Ансамбль атомов образует кристалл рекордного быстродействия, малых размеров и низкого энергопотребления. Переключение элементов, считывание и запись информации осуществит луч лазера, послойно сканирующий кристалл. Более удобен ВУФ- или рентгеновский лазер, облучающий наноразмерную область и поатомно сканирующий образец [12]. Т.к. рентген-микроскопия достигла разрешения в один атом, то X-лучи особенно удобны для записи и считывания информации с отдельных атомов. В кристалле с рёбрами ~1 см число элементов ~1023.
Описание таких устройств возможно и на языке квантовой физики, где узлам и излучению электронов в них соответствуют энергетические уровни и переходы. А квантовые компьютеры отчасти аналогичны рассмотренным атомарным компьютерам. Другое применение магнитной модели – создание трёхмерных изображений-голограмм в воздухе. Для этого следует переводить молекулы воздуха в возбуждённое метастабильное состояние, пропуская воздух через область облучения УФ-лучами или лазерными pump-импульсами, а затем облучая воздух в заданных точках probe-импульсом, ведущим к высвечиванию запасённой энергии. Обновление воздуха в области экспонирования позволит формировать динамические картины – движущиеся изображения, объёмные фильмы, для реализации 3D-телевидения.
Кристаллическая магнитная модель атома объясняет и свойства атомного ядра, представляя его в виде квазикристалла из протонов и нейтронов, в свою очередь имеющих форму электрон-позитронных кристаллов, где позитроны e+ и электроны e– чередуются как ионы Na+ и Cl– в кристаллах соли (рис. 3). В нейтроне числа электронов и позитронов одинаковы, а в протоне позитронов на один больше, чем электронов, отсюда его положительный заряд. Тогда ядерные силы сцепления нуклонов, как показал В. Мантуров, электрической природы – это силы притяжения электронов и позитронов на гранях [9, 13].
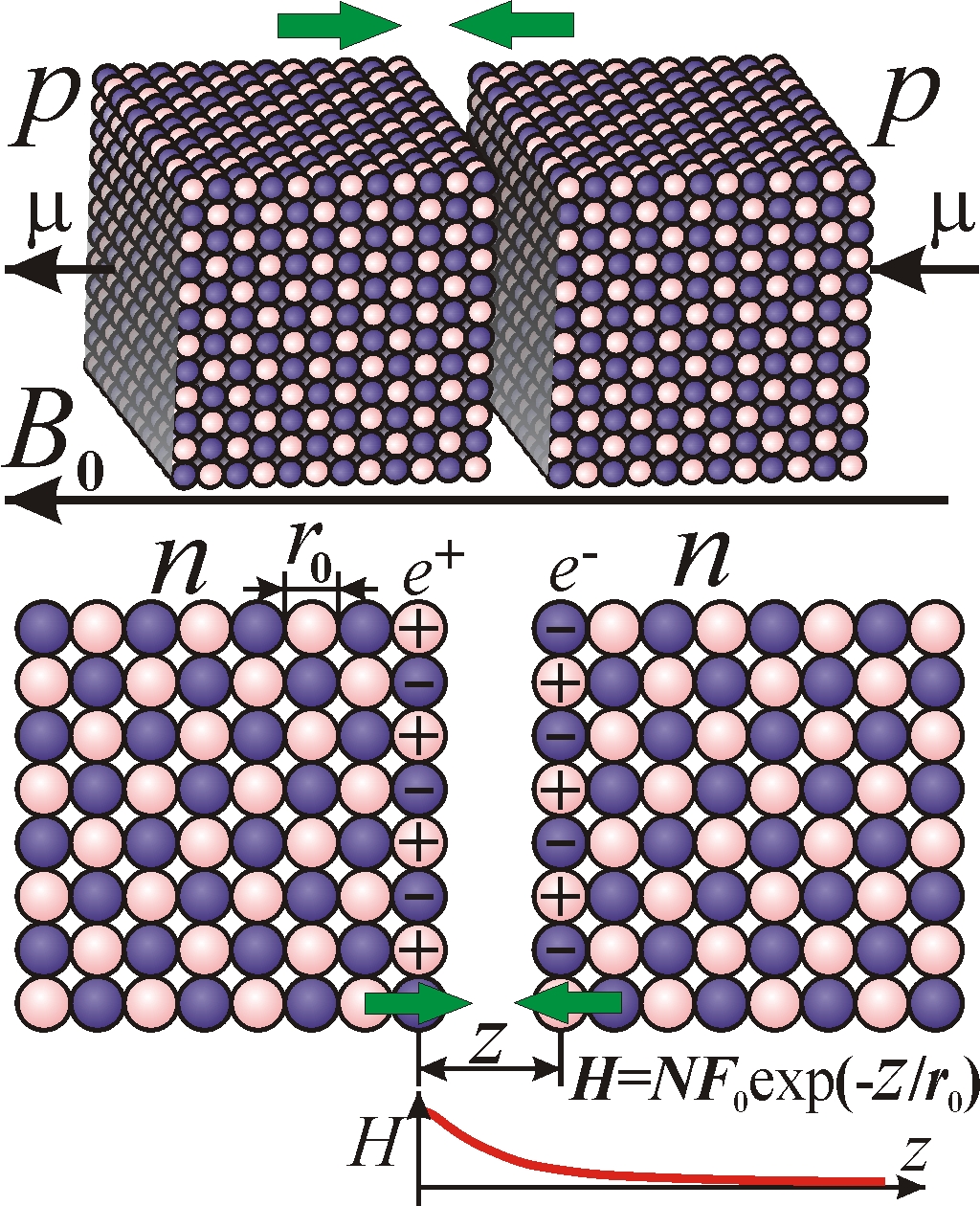
Рис. 3. Синтез ядер в поле B и природа ядерных сил.
Эта модель протона, нейтрона и других элементарных частиц объясняет значения их масс, размеров, заряда, магнитного момента, механизм взаимодействий и распадов. Так, ядерное взаимодействие двух протонов, превышающее их кулоновское отталкивание,– это прямое следствие их мультипольного взаимодействия. Если два протона p в форме кубических кристаллов контактируют гранями, так что напротив электронов окажутся позитроны и наоборот, их притяжение превысит кулоновское отталкивание протонов (рис. 3). Как показывает расчёт [9], сила притяжения H экспоненциально убывает при росте дистанции z меж гранями: H ≈ F0Nexp(–z/r0), где F0 – элементарная сила притяжения электрона к позитрону на расстоянии порядка r0, а N – число частиц, образующих каждую грань (для нуклонов N ~ 100). То есть ядерная сила H в 100 раз интенсивней кулоновского взаимодействия, и быстро убывает с расстоянием, в согласии с опытом. Та же сила притяжения H возникнет между двумя нейтронами n, и между протоном p и нейтроном n, имеющими близкие массы, размеры и формы.
Итак, кристаллическая модель нуклонов объясняет все свойства ядерных сил: равенство их в связях типа p-p, n-n, n-p; высокую интенсивность; короткодействующий характер и быстрый спад с расстоянием (ввиду мультипольного взаимодействия), насыщение (взаимодействуют грани соседних нуклонов). Модель приводит к значению радиуса действия ядерных сил ~r0 (классического радиуса электрона), чего квантовая физика не объясняет. Прочность связей типа p-p, n-n чуть выше, чем n-p (энергия спаривания, повышающая стабильность чётно-чётных ядер), т.к. у протонов и нейтронов от малой разницы в размере граней число связей N и сила H максимальны при контакте однотипных частиц, ввиду равенства граней.
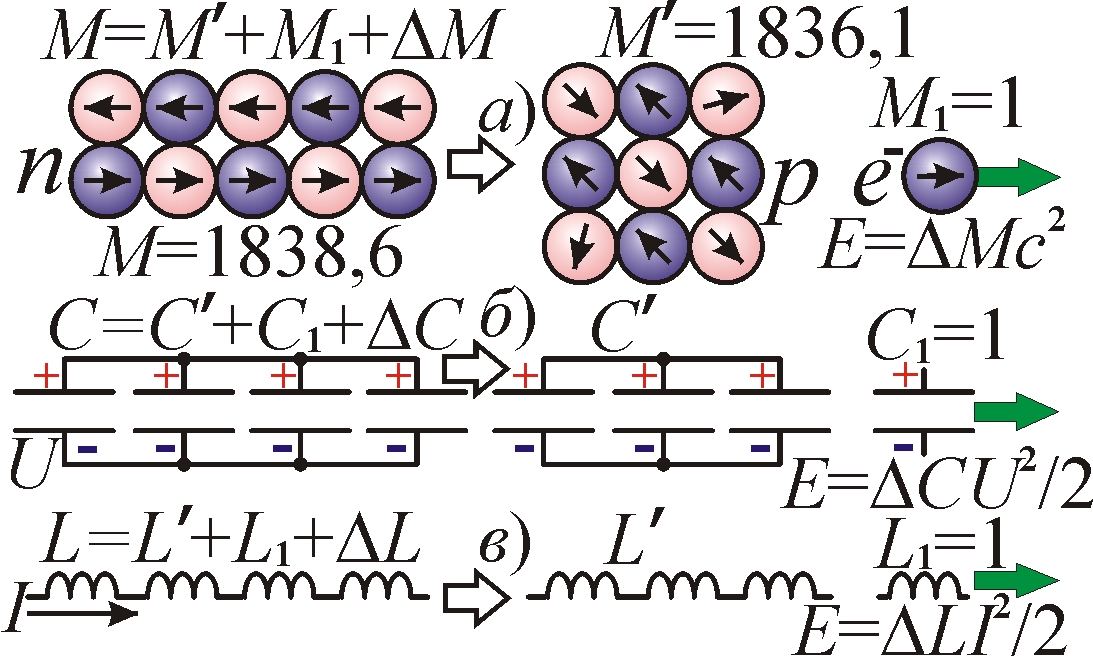
Рис. 4. Природа дефекта масс в реакциях типа n → p + e.
Поскольку шаг r0 электрон-позитронной решётки в 105 раз меньше шага a атомного остова, ядерные частоты колебаний ν в 108–1010 раз больше частот оптических атомных спектров, то есть лежат в гамма-диапазоне, в согласии с опытом. Размещение электронов или протонов в узлах электрон-позитронного “кристалла” открывает ещё один способ записи и обработки информации – не на атомном, а на ядерном уровне. Информация записана в виде координат электронов или протонов в ядре. Т.к. энергии связи в ядрах много выше, чем в атомах, то для хранения информации не обязательно охлаждать вещество до температур близких к абсолютному нулю. Таким образом, можно построить сверхъёмкие носители информации и ядерные компьютеры, функционирующие при комнатной температуре.
Электрическая природа ядерных сил объясняет энергетику ядерных реакций и обнаруженный в них дефект масс. Как показал Ритц [9], опираясь на идеи Лоренца, взаимодействие зарядов при их ускорении приводит к появлению не скомпенсированной электромагнитной силы, т.е. к появлению добавочной инертной массы. Отталкивающее взаимодействие зарядов создаёт положительную инертную массу, а притягивающее – отрицательную. Тогда присоединение или отделение частиц и связанных с ними зарядов изменяет массу частиц, ядер не только на величину присоединённой или отделённой части, но и на величину электромагнитной массы ΔM, связанной с их взаимодействием. Этот дефект массы ΔM пропорционален выделенной или поглощённой в реакции энергии ΔW = ΔMc2 – соотношение, полученное в XIX в. Дж.Дж. Томсоном ещё в рамках классической физики. Так и в электростатике энергия W = CU 2/2 и общая ёмкость C складывается из собственных энергий и ёмкостей конденсаторов и из малых взаимных энергий и ёмкостей ΔC, от взаимодействия обкладок конденсаторов (рис. 4). Извлечение конденсатора единичной ёмкости снижает общую энергию и ёмкость цепи больше, чем на единицу. Эта выделенная энергия взаимодействия ΔW = ΔCU 2/2 пропорциональна “исчезнувшей” паразитной ёмкости ΔC.
То же верно для цепи с индуктивностями L. Не зря инерционную роль ёмкости C и индуктивности L в контурах сравнивают с ролью массы M груза на пружине. Так и при отделении электрона от нейтрона, тот, став протоном, меняет форму и энергию взаимодействия ΔW образующих его электронов и позитронов и связанную с ней электромагнитную добавку массы ΔM = ΔW/c2. Изменение структуры протона, образованного из нейтрона, следует из различия их магнитных моментов в 1,5 раза. То есть различаются распределения моментов электронов и позитронов, в сумме дающих магнитный момент нуклона.
Нуклоны в ядре, как электроны в магнитной модели атома, уложены в форме двойной пирамиды, где нейтронные слои чередуются с протонными (рис. 5). Это объясняет магические числа нуклонов, образующих особо стабильные сочетания: 2, 8, 14, 20, 28, 50, 82, 126 [14]. Значения 2, 8, 20 – это удвоенные пирамидальные числа вида n(n + 1)(n + 2)/3. Прочие числа находятся как удвоенная сумма n-го треугольного числа и (n – 2)-го пирамидального: n(n + 1) + n(n – 1)(n – 2)/3 = (n3 + 5n)/3. Действительно, у ядер выявлены свойства, говорящие о кристаллической структуре и пирамидальной форме ядра [15, 16]. Пирамида может обладать квадратным основанием в случае кубических нуклонов [9], либо треугольным, если спаренные нуклоны имеют форму ромбододекаэдров, соединяясь в подобие пчелиных сот [11].
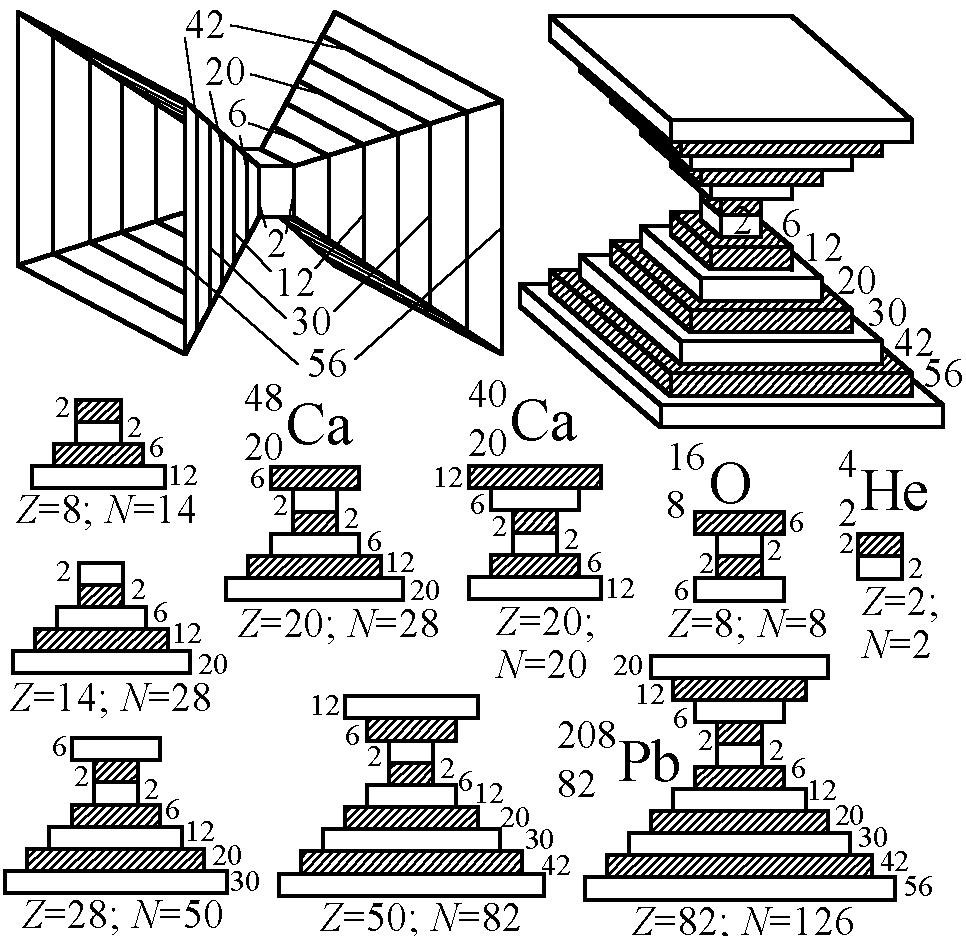
Рис. 5. Схемы и ёмкости нуклонных слоёв в ядрах: p – тёмные, n – белые.
Гипотезу легко проверить методом Лауэ: облучая атомы гамма-лучами с длиной волны λ < 10–15 м, по дифракционной картине можно установить шаг и тип кристаллической решётки. Мощное электрическое поле и лазерное излучение может вести к распаду таких ядер, при достижении порога E ~ e/4πε0r02 ~ 1019 В/см, при котором поле E разделяет электроны и позитроны, приводя к дезинтеграции частиц, распаду ядер, нарушая баланс сил притяжения и отталкивания (рис. 6). Для нестабильных ядер лазерное облучение и сильные поля E будут менять скорость распада. Такие эффекты, подтверждающие электрическую природу ядерных сил, обнаружены в экспериментах [17, 18]. Повысить КПД таких процессов можно, ориентируя ядра электрическим или магнитным полем и действуя лазерным полем в направлении наименьшей интенсивности сил связи между зарядами ядер [19]. Также можно рассекать ядерный “кристалл” по “плоскостям спайности” “лазерным скальпелем”, последовательно разрывая связи, создавая дислокации и другие дефекты, как в реальных кристаллах облегчающие деформацию и разрыв.
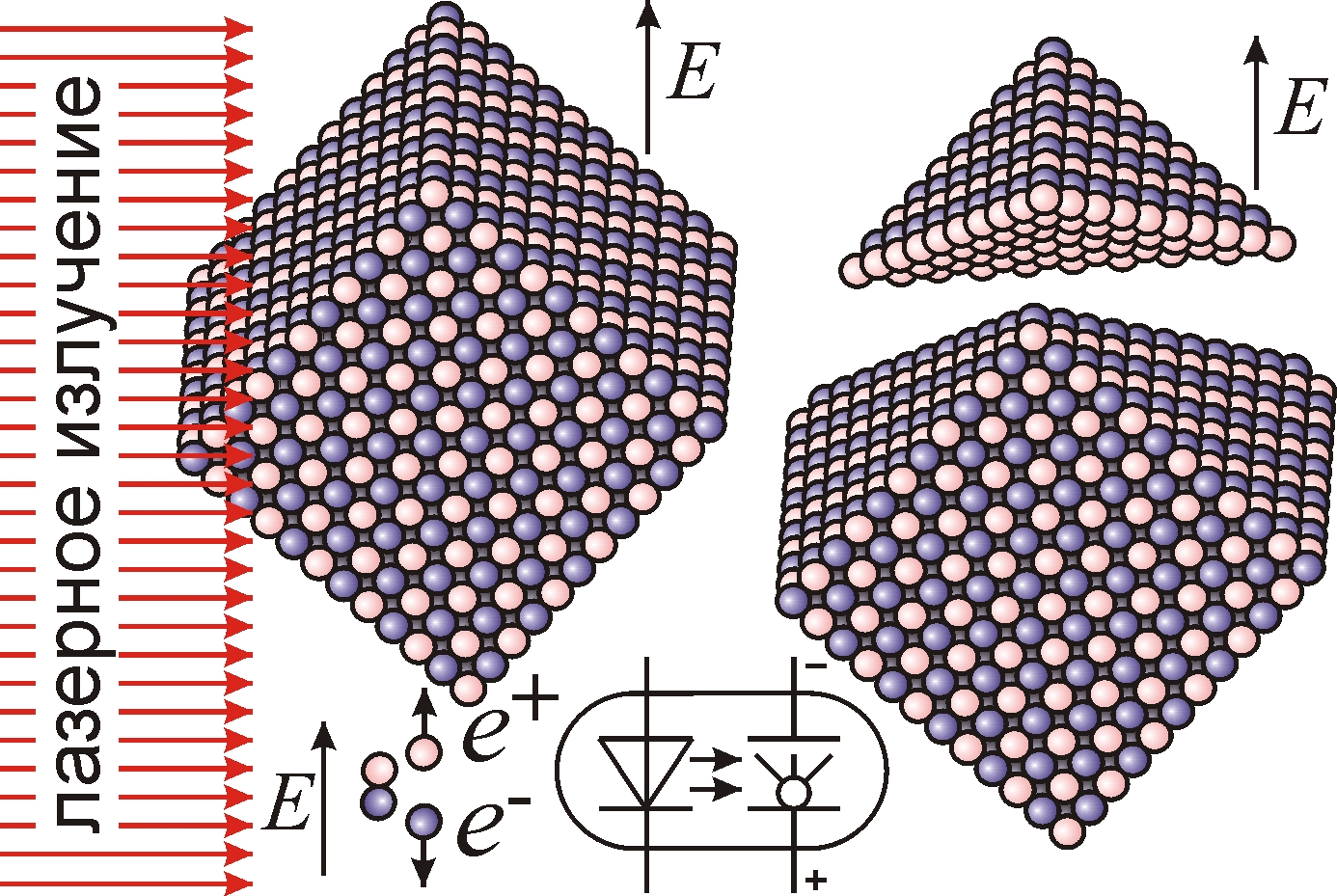
Рис. 6. Разделение частиц лазерным полем и реактоптрон.
Модель позволяет осуществить и реакции ядерного синтеза, если соединять ядра, ориентируя их для максимизации ядерных сил и плавно сближая пондеромоторными силами в лазерном поле. Применение для этих целей полупроводниковых лазеров и KLM-лазерных микрочипов позволит реализовать компактные и почти неисчерпаемые источники энергии (реактоптроны, рис. 6), встроенные в микросхемы, для их автономного питания. В таком источнике, усиливая α- или β-распад [18], дабы излучённые одним электродом α-частицы или электроны осаждались на другом, можно создать электродвижущую силу, регулируемую интенсивностью света. Микропроцессор не потребует усиленной защиты от излучений, т.к. проникающая способность α- и β-лучей мала.
Итак, подобно атомным вихрям и шестерням в теории Максвелла, напомнившим современникам станки и заводы, в магнитной модели атом и атомное ядро напоминают электронные приборы (циклотрон, гиротрон, рупорную антенну и т.д.), полупроводниковые кристаллы, где по узлам решётки перемещаются заряды. Магнитная модель атома не только объясняет свойства атомов, ядер, но и открывает пути создания перспективных электронных устройств и источников питания для микроэлектроники.
Литература:
1. Гринштейн Дж., Зайонц А. Квантовый вызов. М.: Интеллект, 2008.
2. Фаддеев Л.Д., Якубовский О.А. Лекции по квантовой механике для студентов-математиков. Л., 1980.
3. Макки Дж. Лекции по математическим основам квантовой механики. М.: Мир, 1965.
4. Нейман И. Математические основы квантовой механики. М.: Наука, 1964.
5. Маслов В.П. Квантование термодинамики и ультравторичное квантование. М., 2001, 384 с.
6. Фриш С.Э. Оптические спектры атомов. М.–Л.: Физматлит, 1963. 640 с.
7. Ельяшевич М.А., Кембровская Н.Г., Томильчик Л.М. // УФН. 1995. Т. 165, №4. С. 457–480.
8. Thomson J.J. // Phil. Mag. 1919. P. 418–447.
9. Семиков С.А. Баллистическая теория Ритца и картина мироздания. Н. Новгород: Пресс-контур, 2009.
10. Семиков С.А. // Инженер. 2015. №5–6. С. 16.
11. Кеплер И. О шестиугольных снежинках. М.: Наука, 1982. 192 с.
12. Игнатов А.Н. Оптоэлектроника и нанофотоника. СПб.: Лань, 2011. 544 с.
13. Мантуров В.В. // Техника-молодёжи. 2006. №2. С. 2–5.
14. Сивухин Д.В. Атомная и ядерная физика. Т. 2. М.: Наука, 1980.
15. Dudek J., Gozdz A., Schunck N., et al. // PRL. 2002. V. 88, №25, P. 252502.
16. Dudek J., Curien D., Dubray N., et al. // PRL. 2006. V. 97. P. 072501.
17. Запретные превращения элементов // Химия и жизнь. 2015, №8. С. 27–31.
18. Симакин А.В., Шафеев Г.А. // Квантовая электроника. 2011. Т. 41, № 7. С. 614–618.
Дата установки: 18.10.2015
[вернуться к содержанию сайта]