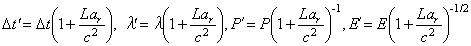[вернуться к содержанию сайта]

РАДИОФИЗИКА
УДК 535.1

ОБ ЭФФЕКТЕ ТРАНСФОРМАЦИИ ДЛИНЫ ВОЛНЫ, ДЛИТЕЛЬНОСТИ И МОЩНОСТИ ЛАЗЕРНЫХ ИМПУЛЬСОВ ПРИ РАССЕЯНИИ НА УСКОРЕННО ЛЕТЯЩИХ ЧАСТИЦАХ

© 2013 г. C.А. Семиков
Вестник ННГУ, 2014, №1(2), с. 180–185

Нижегородский госуниверситет им. Н.И. Лобачевского
sergey-semikov@yandex.ru

    Эффект трансформации длительности электромагнитных сигналов от ускоренно движущегося источника был предсказан В. Ритцем в 1908 г. в его баллистической теории света [1]. Как показал анализ [2–4], эта теория не противоречит известным экспериментам [5, 6]. Согласно теории Ритца, в вакууме источник дополнительно сообщает свою скорость v свету, испущенному относительно источника со стандартной скоростью света c, а относительно приёмника – со скоростью c + v. При ускоренном движении источника к приёмнику волновые фронты, получая в моменты испускания всё большие скорости, догоняют друг друга, сокращая длину волны λ и длительность импульса Δt. Если ускорение источника направлено от приёмника, гребни световых волн расходятся, удлиняя λ и Δt. Из кинематики и закона сохранения следуют преобразования Δt, λ, мгновенной мощности P и поля E импульсов света [4]:

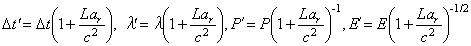,                (1)

где a_r – лучевое ускорение источника, L – путь света. Эффект (1) и назван эффектом Ритца.

    Обычно эффект мал, так как в знаменателе (1) – квадрат скорости света. И на лабораторных дистанциях L ~ 1 м, даже при экстремальных ускорениях источника a_r ~ 10⁷ м/с², когда (λ' – λ)/λ ~ 10^–10, эффект (1) нельзя выявить спектральными методами. Но он регистрируется по эффекту Мёссбауэра – по сдвигу частоты γ-лучей от ускоренных источников [4–6].

    Эффект заметней на космических дистанциях L. Так, у галактик ускорения в видимых участках ядер направлены от нас (a_r > 0), и длины волн λ' росли бы пропорционально дистанциям L галактик. Эффект (1) подобен хаббловскому закону красного смещения λ' = λ(1 + LH/c). Измеренный коэффициент H = 74 (км/с)/Мпк (постоянная Хаббла) близок к расчётному коэффициенту a_r/c ~ 70 (км/с)/Мпк, найденному по ускорениям a_r = V²/R галактик при типичных для них окружных скоростях V ~ 200 км/с и радиусах ядер R ~ 0.002 Мпк [4].

Как показал Дж. Фокс [2], от переизлучения межзвёздным галактическим газом с показателем преломления n свет теряет избыток скорости и на дистанции l = λ/2π(n – 1) приобретает скорость переизлучающего газа, галактическое вращение которого и задаёт далее величину эффекта (1). Для разных λ толщина переизлучающего слоя l различна, и для них определяющим оказывается лучевое ускорение газа a_r = V²/(R + l) на разных радиусах R + l. Это различие объясняет выявленную разницу красных смещений в радио- и оптическом диапазоне [7]. Для разных длин волн λ_i оптического спектра, отвечающих спектральным линиям разных элементов, l – тоже разная и зависит от показателя преломления n соответствующего газа. Общий показатель преломления n стремительно растёт возле резонансных частот f_0i = c/λ_i спектральных линий:

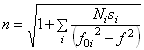,                        (2)

и для них длины переизлучения l_i = λ_i/2π(n – 1) сильно снижены, причём в разной степени, так как в межзвёздном газе разнятся концентрации N_i атомов разных элементов и коэффициенты s_i, характеризующие массы, заряды и силы осцилляторов. Поэтому красные смещения одних и тех же галактик, оцененные по разным линиям f_0i разных элементов, могут заметно разниться. Зависимость n от номера элемента и потенциала ионизации объясняет и наблюдаемое различие красных смещений галактик в линиях щелочных элементов и железа [8].

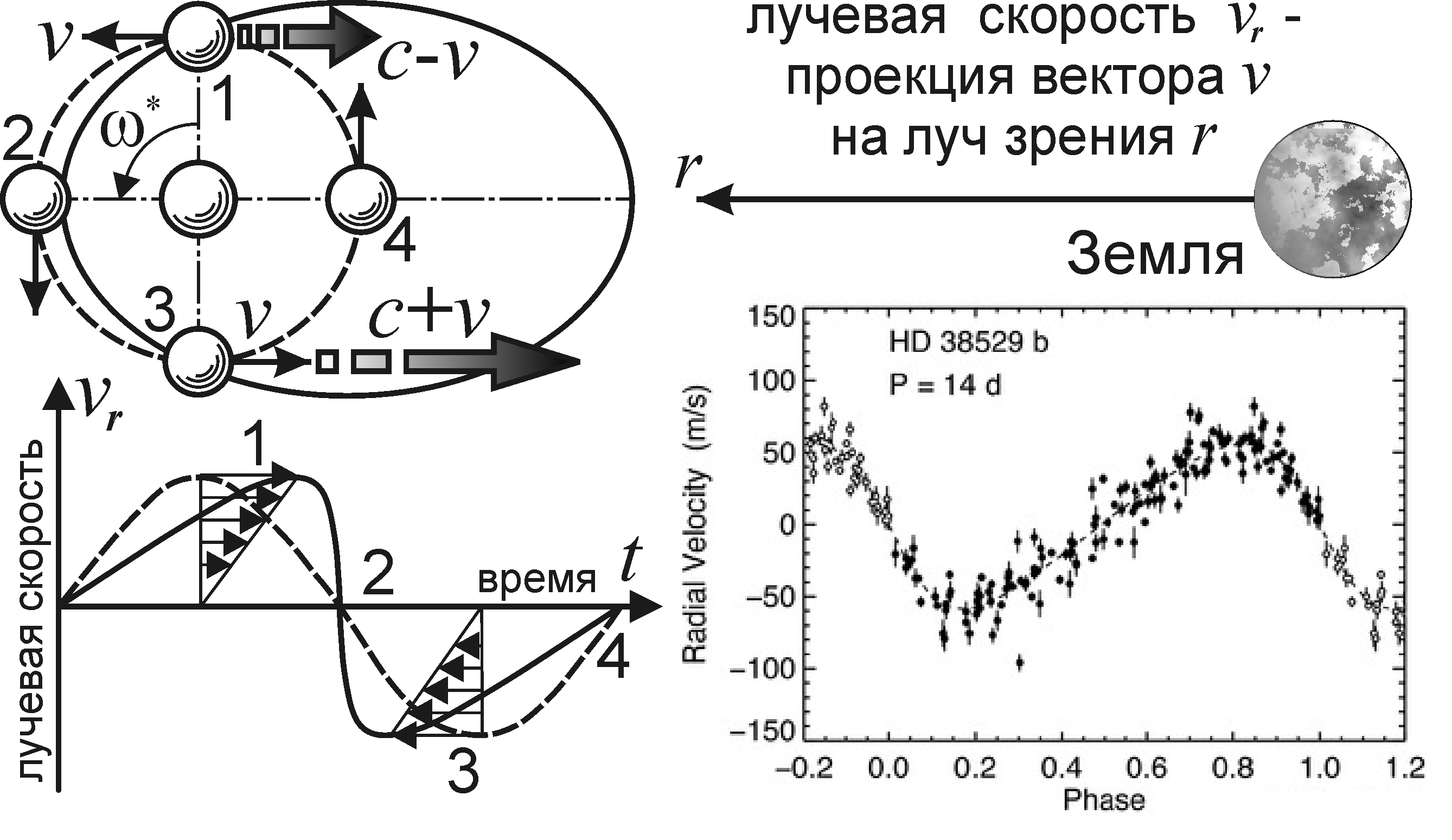
    Исторически первой стала проверка баллистической теории именно в космосе. Так, у звезды с круговой орбитой скорость v, сообщённая свету, исказит видимое движение и синусоиду графика лучевых скоростей v_r(t), придав ей пилообразную форму, в первом приближении подобную графику v_r(t) эллиптической орбиты, вытянутой к Земле (рис. 1). В 1913 г. астрономы [9] выявили это искажение в виде эффекта Барра,– преобладания звёзд с орбитами, вытянутыми к Земле,– с долготами периастра ω* возле 90° [4]. Эффект Барра заметен также у экзопланет, орбиты которых не могут иметь высоких эксцентриситетов ε и неоднородного распределения по ω*. Например, экзопланеты WASP-18b и WASP-33b столь близки к своим звёздам, что должны обладать ε = 0. Поэтому кривые v_r(t) этих систем, отвечающие эксцентриситетам ε = 0.01 и 0.174, считают искажёнными, скажем, приливными эффектами [10]. Проще объясняет искажения теория Ритца, предсказавшая эффекты [9], открытые у WASP-18b и WASP-33b, где ω* ≈ 90° [10], а орбитальные скорости v достаточны для искажений. Другие аномалии экзопланет тоже нашли простое объяснение в баллистической теории [11, 12].

    Искажённая кривая лучевых скоростей соответствует эллиптической орбите лишь в первом приближении, а отклонения, как отметил Э. Фрейндлих [9], имеют вид гармоник орбитального периода, реально выявленных у двойных звёзд и экзопланетных систем. У последних гармоники интерпретируют как реальное существование экзопланет с периодами, относящимися к основному как 1:2, 1:3, 1:4 и т.д. Согласно [13], половине открытых планет присущ орбитальный резонанс 1:2. Теоретически он возможен, но редок, и форму графиков v_r(t) проще объяснить модуляцией скорости света, исказившей синусоиду графика лучевых скоростей и породившей гармоники, как в клистроне, модулирующем скорость электронов.

    В лаборатории, на дистанциях L ~ 1 м, для изменения Δt, λ и P в разы в (1) требуется La_r/c² ~ ±1 и a_r = ±c²/L ~ ±10¹⁷ м/с². Это ускорение легко сообщить электронам, излучающим или переизлучающим свет в синхротронах, где возможно аналогичное искажение профиля электромагнитной волны от летящего по орбите радиуса R электрона, излучающего тогда не только на циклотронной частоте f_c, но и на кратных частотах Hf_c (рис. 2.а, б). Интенсивность и номер H высших гармоник росли бы при росте скорости v электрона и пути L света в вакууме. Мощности излучения на частоте f_c и её гармониках сравнимы, когда ускорение электрона a = v²/R достигает порога a₀ = с²/L ~ 10¹⁷ м/с² (при L ~ R ~ 1 м), то есть при v ~ с. Действительно, при v ~ с электроны, кроме излучения частоты f_c, генерируют её гармоники в форме синхротронного излучения. Отношение сигнал/шум гармоник растёт при выводе излучения через вакуумные каналы, длина которых для видимого излучения L ~ 1 м, а для жёсткого рентгеновского – L ~ 100 м [14], ввиду роста номеров H и мощности гармоник при росте L.

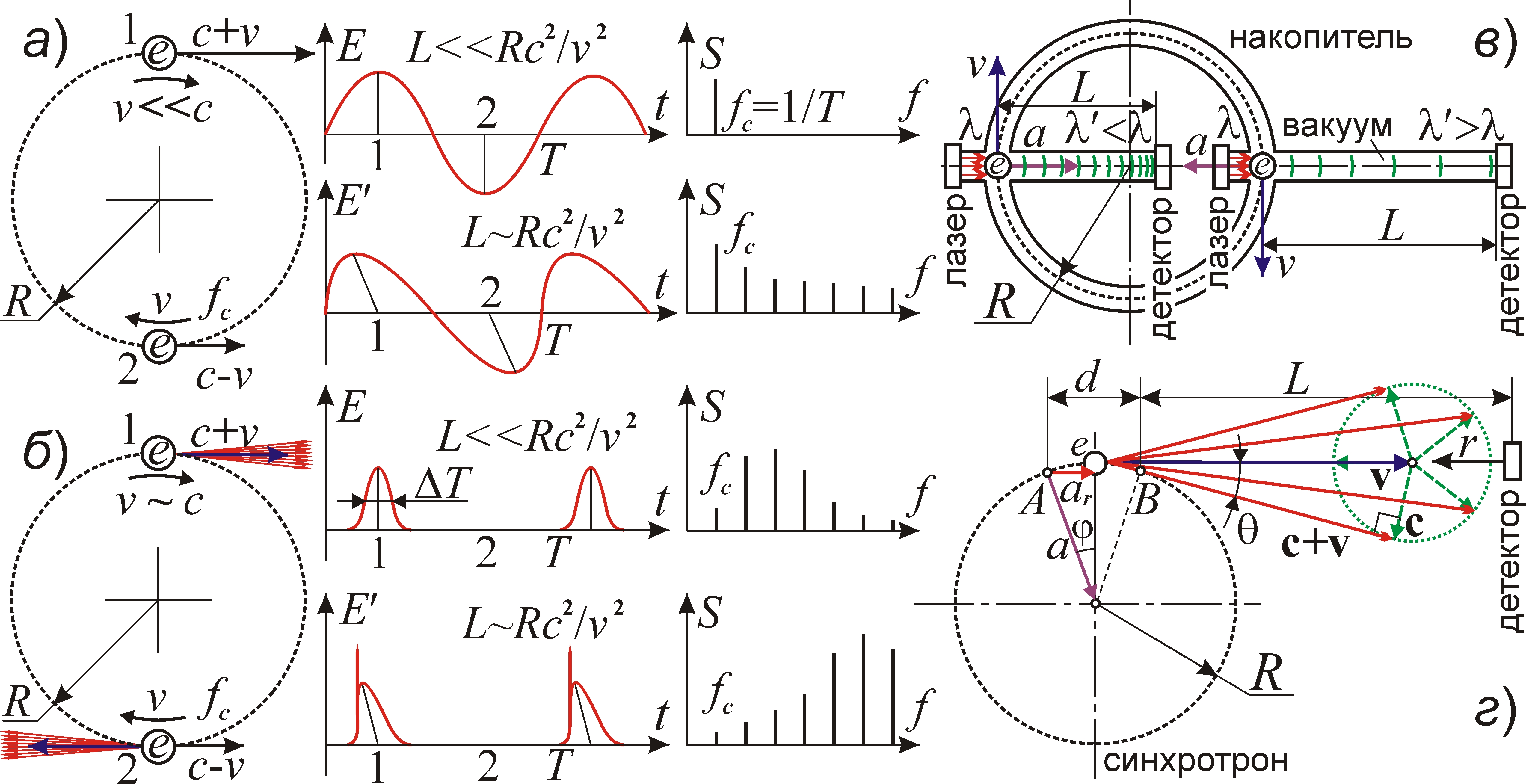
    Другие свойства синхротронного излучения тоже согласуются с теорией Ритца [4, 15, 16], основанной на классической механике, где нет релятивистского роста массы m и предела скорости v. Поэтому в синхротронах импульс электронов mv = eBR ≈ mγc, измеренный по радиусу R их орбит в магнитном поле B, соответствует скорости v = eBR/m ≈ γc, где γ ≈ eBR/mc >> 1 – измеренный гамма-фактор [15]. При добавлении скорости v электрона к скорости c его излучения (рис. 2.г) оно вылетает вдоль вектора v в пределах конуса с углом полураствора θ = arcsin(c/v) ≈ 1/γ [15, 16]. Импульс излучения соответствует пролёту электроном участка орбиты d ~ Rθ ~ R/γ, с которого излучение попадает в детектор на расстоянии L [14]. Из начала A интервала d свет дойдёт за время t_A = (d + L)/(c + v), из конца B – через время t_B = d/v + L/(c + v) после излучения в A. Длина импульса ΔT = t_B –t_A ≈ d/cγ² ≈ R/cγ³, в согласии с [14]. Аналогично, длительность импульса излучения из ондулятора длины d выразится как ΔT ≈ d/cγ². Поэтому замеры ΔT, скажем, в установке “FLASH”, где ΔT ≈ 25 фс ~ d/cγ² [17], не противоречат теории Ритца. То есть релятивистская и баллистическая теории предсказывают сходные характеристики θ(γ) и ΔT(γ) синхротронного излучения [14]. Сделать выбор между теориями можно лишь путём прямых замеров скорости частиц из синхротронов [4]. В пользу баллистической теории свидетельствует и открытое по синхротронному излучению электронов их случайное движение в ондуляторах [18]. Теория Ритца давно предсказала это “броуновское” движение зарядов под ударами своего рода квантов электрического поля [1, 19].

    Обычно гармоники синхротронного излучения объясняют тем, что его регистрируют в виде коротких импульсов длительностью ΔT, отчего спектр и формируют гармоники Hf_c, вплоть до частот f ~ 1/ΔT ~ γ³c/R (рис. 2.б). Но при этом интенсивность высших гармоник мала. А с учётом эффекта Ритца (1), особенно при a_r = -с²/L, профиль импульса E(t) исказится, обретая особенности в виде уступов и пиков, тем более высоких, чем они ближе к середине импульса и чем меньше угол φ точки излучения, где a_r = -a₀ (рис. 2.г). Это вызовет рост интенсивности гармоник и неограниченный рост их номеров H. Лучевое ускорение a_r = -asinφ, где sinφ ~ sinθ ~ 1/γ, и условие a_r = -с²/L генерации жёсткого излучения реализуется при L = R/γ²sinφ ~ R/γ. Тогда при малых γ жёсткое излучение можно получить, удлинив канал L или сократив радиус R, чем и пользуются на практике. Поскольку при уменьшении φ < θ пик растёт, то дальнейшее увеличение L = R/γ²sinφ наращивает интенсивности высших гармоник.

    В синхротроне эффект Ритца позволит преобразовывать не только собственное излучение электронов, но и рассеянное ими внешнее лазерное излучение. Обычно лазерные импульсы, рассеянные электронами, преобразуют эффектом Комптона при γ >> 1 [20], что требует мощных ускорителей и большого расхода энергии, то есть КПД трансформации мал. Эффект Ритца позволит трансформировать излучение даже при γ ~ 1 в ускорителях и накопителях малой мощности с низкими синхротронными потерями, раз уже при v ~ с ускорение электронов a ~ a₀ ~ 10¹⁷ м/с² (при L ~ R ~ 1 м). При γ ~ 1 рассеянное излучение электрона не обладает острой направленностью синхротронного излучения, и степень трансформации ритц-эффектом максимальна для излучения, идущего вдоль вектора ускорения a электрона.

    Поскольку при v ~ с время τ ~ R/v пролёта банча электронов через область облучения – порядка наносекунды, то и длительность лазерных импульсов требуется не выше: Δt ≤ τ. Удобен генератор пикосекундных лазерных импульсов с частотой повторения, равной частоте обращения электронных сгустков (~10 МГц) и ускоряющего поля в синхротроне или накопителе электронов (рис. 2.в). Сохраняя a ~ a₀ (v²/R ~ с²/L), габариты установки можно сократить, пропорционально уменьшив L и R до сантиметров. А снизив радиус орбиты R до 0.1 мм, без изменения базы L ~ 1 м, скорость электронов можно снизить до v ~ с(R/L)^1/2 ~ 0.01с (достижимой в электронной пушке), уменьшив габариты и расход энергии на разгон электронов и генерацию магнитного поля. Поскольку за период оптического поля (~ 1 фс) лучевое ускорение электронов на орбите почти не меняется, то профиль волны не искажается, и гармоник не образуется, а спектр импульса смещается как целое по диапазону частот.

    Ускорение a₀ ~ 10¹⁷ м/с² электронам может сообщать и электрическое поле E, которое при наложении в течение малого времени t ~ 1 пс разгоняло бы электроны до скоростей v << с при малом расходе энергии [4]. В поле E ускорение a = Ee/m электрона (где e/m = 1.76·10¹¹ Кл/кг) достигает 10¹⁷ м/с² уже при E ~ 10⁶ В/м. Эффект Ритца можно реализовать в вакуумной камере, где пучок электронов в поле E получает ускорение ~10¹⁷ м/с², а лазерное импульсное излучение с длиной волны λ и длительностью импульса Δt ~ 1 пс фокусируется на пучке и переизлучается электронами. Их свет, пролетая в вакууме дистанцию L ~ 1 м до светофильтра (блокирующего свет длины волны λ), попадает в спектрометр или детектор, которые при справедливости эффекта Ритца зарегистрируют сигнал иных длительностей Δt' и длин волн λ' (1). Меняя L в таких установках ([4] и рис. 2.в), удастся плавно перестраивать длину волны из оптического в СВЧ, терагерцовый, ИК-, УФ-, рентгеновский или гамма-диапазон так же легко, как при перестройке длины волны в генераторе радиочастот.

    При этом длительность импульса Δt' можно сжать до нуля в ходе пропорционального сжатия периода колебаний, длин волн света, как при сжатии гребней мехов гармошки. То есть, нет спектральных ограничений длительности Δt': её можно сделать сколь угодно малой, а мощность P' – сколь угодно высокой. Тогда импульс, сохранив свою энергию, выродится в дельта-функцию в ходе абсолютной фазовой фокусировки без принципиальных ограничений [4]. Раз сжатие импульса и концентрация света идут на длине L в вакууме, а не в среде, то нет и материальных ограничений P' за счёт нагрева, пробоя среды, поглощения, нелинейных эффектов.

    Электроны, атомы и наночастицы может ускорять и давление света p = 2I/c (рис. 3). Оно сообщает частице радиуса r ~ 10^–9 м, плотности ρ ~ 10³ кг/м³ и массы M = 4πr³ρ/3, ускорение a = pπr²/M ~ I/ρcr ~ 10¹⁷ м/с² уже при интенсивности I ~ 10¹⁶ Вт/см², достижимой в фемтосекундных импульсах, способных ускорять и электроны пондеромоторной силой [20]. Лазерный свет, ускоряя частицы, переизлучался бы ими, далее преобразуясь ритц-эффектом.

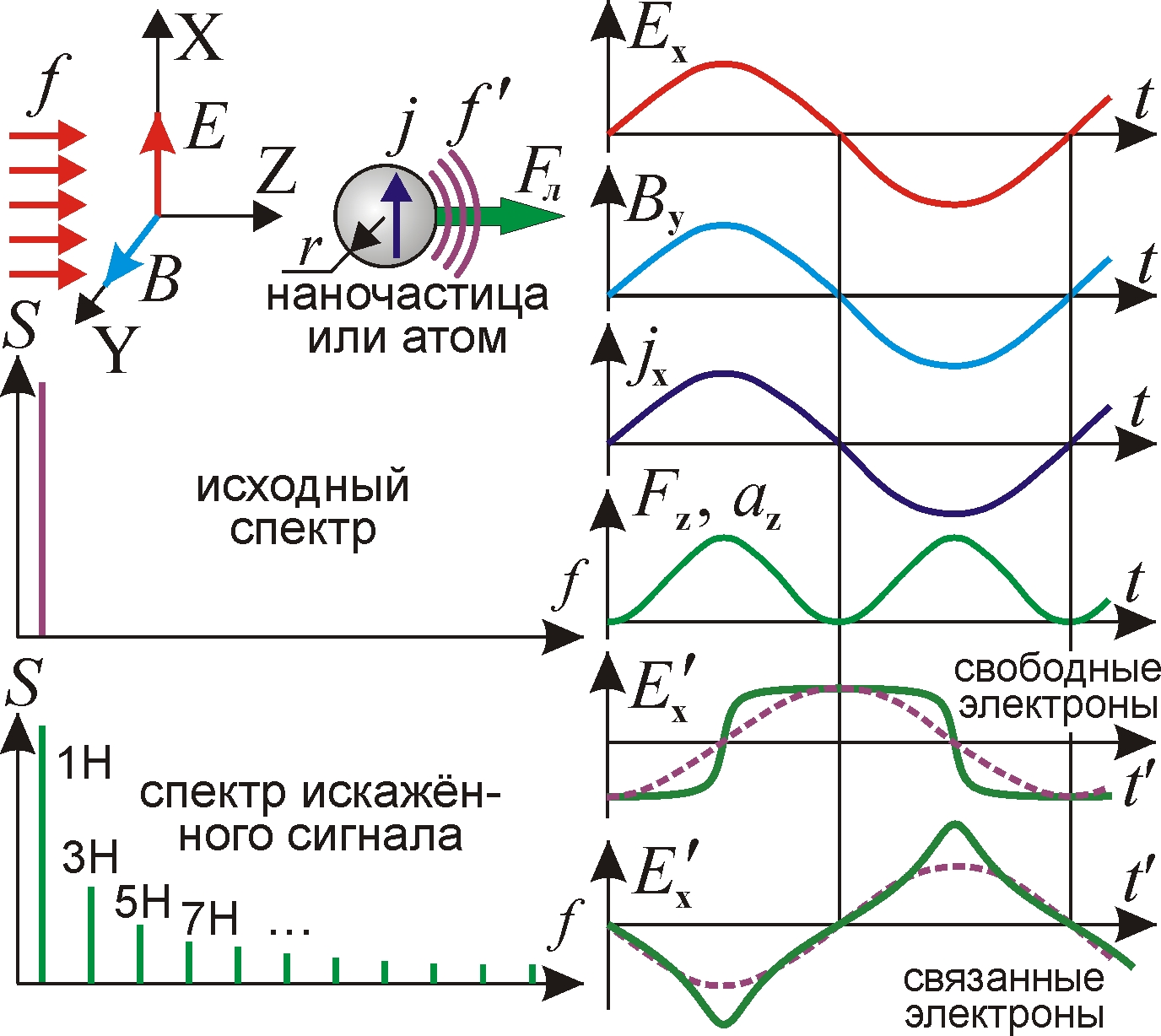
    Обычно давление света данной интенсивности на частицу считают постоянным ввиду его усреднения по времени и поверхности макрообъектов. Но для частиц размером менее длины волны λ сила давления света осциллирует на удвоенной частоте f колебаний светового поля. Переменное давление, модулируя ускорение источника и величину эффекта Ритца (1), исказит профиль излучаемой волны, формируя нечётные гармоники f [21]. Гармоники возникают уже при I << I₀, а при I ~ I₀ мощности, заключённые в гармониках Hf и исходном излучении частоты f, сравнимы. Гармоники реально регистрируют в генераторах аттосекундных импульсов, где в фокусе фемтосекундного лазера атомы и наночастицы под действием светового давления получают гигантские ускорения, вплоть до 10²³ м/с² [20]. Выходит, регистрируемые при этом импульсы рентгеновского излучения аттосекундной длительности могут быть и преобразованными эффектом Ритца (1) фемтосекундными оптическими импульсами.

    Рассмотрим генерацию гармоник в поле E(t) = E₀sin(w t) и B(t) = B₀sin(w t) линейно поляризованной волны. Сила Лоренца давления света на частицу радиуса r и проводимости s

F_л(t) ~ r³j(t)B(t) = r³s E₀B₀[1 – cos(2w t)]/2                    (3)

быстро меняется от осцилляций поля B(t) и плотности тока j(t) = s E(t) в частице, модулируя с частотой 2w её ускорение a = F_л(t)/M. Тогда профиль волны, переизлучённой электронами проводимости (рис. 3, штриховая линия), исказится, приняв форму типа “меандра” (рис. 3, сплошная линия): E'(t) = E₀[cos(w t) – cos(3w t)/3 + cos(5w t)/5 – …]; а у волны, переизлучённой связанными электронами,– форму типа “треугольника”: E'(t) = E₀[cos(w t) + cos(3w t)/9 + cos(5w t)/25 + …]. Спектр образуют нечётные гармоники частоты f вплоть до предельной f_max, синтезирующей самый острый участок профиля.

    В опытах спектр аттосекундных импульсов, формируемых фемтосекундными импульсами в струе газа и при абляции поверхности, образован как раз нечётными гармониками [20]. За резким спадом мощности первых гармоник идёт медленное убывание – “плато”, подобное асимптотическому убыванию 1/H гармоник “меандра” с обрывом на частоте f_max. Реализацию данного механизма можно проверить, изучив зависимость спектра импульсов от дистанции L, наращивающей искажения E'(t). А сжатие импульса, повышая интенсивность I, вызовет рост частот выше значений Hf от постоянной компоненты a и силы давления (3), усреднённой по времени: F_л ~ r³s E₀B₀/2 [4, 6]. Подобный рост частот Hf при сжатии импульсов реально открыт [22]. При падении лазерного луча на поверхность отражённый свет рассеивается на испаряемых ионах, колеблемых уже электрическим полем E(t) световой волны в плоскости падения. Кулоновская сила eE много больше F_л, и даже при I << I₀ эффективность генерации гармоник должна быть выше и зависеть от угла падения и поляризации падающего света.

    Расчёт выполнен для линейно поляризованного света. У циркулярно поляризованного света давление не осциллирует, создавая постоянное ускорение частиц, т.е. циркулярно поляризованный свет не создаёт гармоник частоты f, а может лишь наращивать её по эффекту Ритца (1). Действительно, как показал опыт, гармоники генерирует только линейно, а не циркулярно поляризованный свет. Но циркулярно поляризованное излучение позволит наблюдать преобразование частоты по эффекту Ритца в чистом виде при I ~ I₀ ~ 10¹⁶ Вт/см².

    Для частиц размером менее микрона оценку I₀ следует уточнить, поскольку металл такой толщины прозрачен для света, передающего частице лишь малую часть своего импульса, пропорциональную числу электронов в частице. Последнее означает, что сила давления света F_л растёт как r³, и a не зависит от r: a = F_л/M ~ r³s E₀B₀/r r³ ~ 2s m ₀I/r , откуда I₀ ~ 10¹⁴ Вт/см² (для a ~ a₀). При увеличении размера r частицы ускорение может даже расти ввиду изменения свойств вещества при переходе от микро- к макромасштабам. Это объяснит более эффективную генерацию гармоник при облучении наночастиц, а не атомов, например, серебра [22]. Для частиц размером в нанометры и эта оценка I₀ неточна: при поперечнике порядка десяти атомов сказывается дискретная структура вещества, велики краевые эффекты и ЭДС зарядов, наведённых полем E(t), а давление Лапласа, сжимая частицу, сильно меняет её проводимость s и другие свойства.

    Выяснить основной механизм генерации аттосекундных импульсов можно, изучив зависимость спектра от расстояния L и ускорения a_r (зависящего от I) [4, 21]. Подтверждение эффекта Ритца на основе (1) позволит повысить эффективность трансформации излучения.

    Благодарю за обсуждение профессоров М.И. Бакунова и Н.С. Степанова.

Дата установки: 29.05.2014
[вернуться к содержанию сайта]

W