[вернуться к содержанию сайта]
…В то же время над проблемой смещения перигелия вместе с многочисленными астрономами работали и некоторые физики, пытавшиеся выяснить, нельзя ли объяснить смещение с помощью измененного закона тяготения Ньютона. Этим занимались различные учёные, начиная с Вильгельма Вебера, выдающегося специалиста XIX в. в области электродинамики, и кончая молодым швейцарским физиком Вальтером Ритцем, умершим в 1909 г. С началом XX в. возникла и стала развиваться новая физика. Стало очевидным фундаментальное значение теории относительности и её главного раздела — эйнштейновской специальной теории относительности.
Выражения законов тяготения, учитывающих зависимость от скорости, содержат члены, которые определяются не только расстоянием между телами, но и скоростью этих тел. Можно считать, что эти члены добавляют небольшую величину к обычной ньютоновой силе, так что смещение перигелия получается даже в случае единственной планеты, обращающейся вокруг Солнца. Законы тяготения, учитывающие зависимость от скорости, сыграли более важную роль в исследовании аномального смещения перигелия Меркурия, чем законы, рассмотренные в гл. 5. Во всяком случае, они привлекли внимание некоторых астрономов, поскольку предсказывали существенное смещение перигелия, что давало надежду полностью объяснить аномалию, присущую движению Меркурия. Другим стимулом их применения послужил быстрый прогресс электродинамики. По мере того как развитие этой науки сопровождалось формулировкой новых законов взаимодействия, исследовались и эквиваленты этих законов в теории тяготения. Чем больших успехов достигала электродинамика, тем более обоснованными казались новые законы тяготения.
Сторонники концепции дальнодействия в электродинамике считали, что взаимодействие между удалёнными электрически заряженными частицами имеет фундаментальный характер, и выражали его в виде некоторого закона изменения силы с расстоянием.
Предполагалось, что действие распространяется со скоростью света, и в баллистических теориях для его передачи были предназначены некоторые гипотетические частицы. Считалось, что эти частицы движутся со скоростью, равной сумме скорости света и собственной скорости их источника. Такое представление противоречит специальной теории относительности, согласно постулату которой скорость распространения света постоянна и не зависит от скорости источника света. Начало этому направлению электродинамики, основанному на концепции дальнодействия, положил Вильгельм Вебер, опубликовавший в 1846 г. фундаментальный закон взаимодействия, названный его именем. Другие такие законы были сформулированы позже Гауссом, Риманом и Клаузиусом, и для каждого из них были созданы эквиваленты в теории тяготения. Исследовалась даже возможность использования в этой теории другого, конкурирующего направления электродинамики максвелловской теории поля. На рубеже столетий Ритц предложил сложный закон для силы взаимодействия электрически заряженных частиц, также исходя из концепции дальнодействия. Исследуя его гравитационный эквивалент, он показал, что такой закон позволяет полностью объяснить смещение перигелия Меркурия. Вскоре Ритц разработал гораздо более общую теорию, применимую для широкого круга явлений. Однако вскоре после её опубликования Ритц скончался, и лишь немногие специалисты проявили интерес к этой теории. На основании доводов астрономического характера она была отвергнута, поскольку включала предположение о переменности скорости света. К этому времени была опубликована и другая теория гравитации, основанная на принципе дальнодействия. Теория Гербера привлекла некоторое внимание, когда оказалось, что предсказываемое ею движение перигелия планеты в точности соответствует результату, следующему из общей теории относительности, однако её никогда не считали серьёзным конкурентом последней.
Начало всем этим теориям было положено в девятнадцатом столетии работой Вильгельма Вебера. Поскольку связь между электродинамическими и гравитационными законами была столь сильной, важно обрисовать развитие электродинамики, прежде чем перейти к приложениям в теории тяготения.
…Итак, вместо взаимодействия частица-частица (действие на расстоянии) стали рассматривать взаимодействия частица-поле и поле-частица. Однако некоторые ставили под сомнение необходимость введения полей и считали, что следует ограничиться использованием "чистых" теорий дальнодействия в их модифицированной форме. Новым решающим понятием стал запаздывающий потенциал, – потенциал, распространяющийся с конечной скоростью. Это понятие, соответствующее идеям Гаусса, высказанным им в переписке с Вебером, было введено Риманом и Лоренцем. Уравнения Максвелла могут быть получены при использовании запаздывающих скалярного и векторного потенциалов и определений Е и Н через их посредство. Понятие запаздывающего потенциала было обобщено Льенаром (1898 г.) и Вихертом (1900 г.) на случай движущихся частиц, и Льенар вывел соответствующие выражения для Е и Н в 1903 г. Шварцшильд получил формулу для силы взаимодействия двух частиц, соответствующую результатам Льенара. Позже, в 1908 г., Ритц опубликовал приближённый вариант этой формулы пренебрегая членами порядка выше 1/с2. В окончательном виде указанная формула выглядит следующим образом:
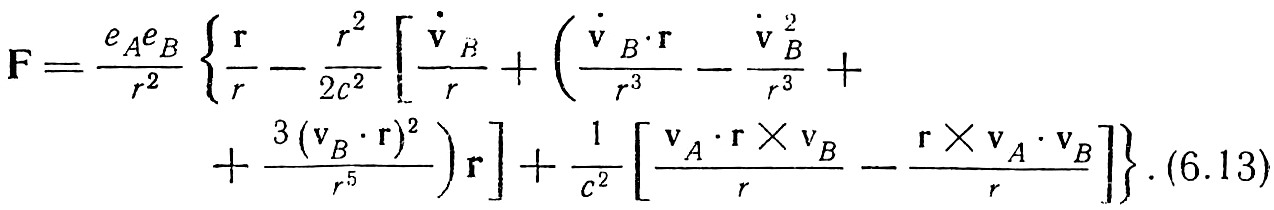
Здесь F – нецентральная сила, а действие и противодействие не равны друг другу.
Выше были рассмотрены пять выражений для закона силы взаимодействия, полученные Гауссом, Вебером, Риманом, Клаузиусом и Ритцем. Все они исследовались в то или иное время как возможная замена ньютонова закона всемирного тяготения в небесной механике. Проследим историю этих исследований, учитывая, что зависимость, отличающаяся от закона обратных квадратов, даёт движение перигелия.
Вначале была предпринята попытка использовать закон Вебера в теории движения планет. В 1864 г. Зеегерс защитил в Гёттингене свою диссертацию, в которой орбитальное движение планет и возмущения рассматривались на основе этого закона [323]. Не исключено, что диссертация была написана под руководством самого Вебера. По мнению Вебера, измерения постоянной с, выполненные им совместно с Кольраушем, свидетельствовали о том, что в отношении движения планет его закон без заметного различия можно принять в качестве закона гравитационного взаимодействия [378]:
"Далее из найденного большого значения константы с вытекает интересное следствие, что такую динамическую составляющую можно также прибавить к силе взаимодействия тяготеющих тел, причём такое добавление не оказывает ни малейшего заметного влияния на движение небесных тел".
Подход, использованный Максвеллом, был необычным для теории тяготения. В электродинамике его теория была доминирующей, хотя и не настолько, чтобы помешать убежденным сторонникам дальнодействия развивать своё направление, вершина которого была отмечена формулой Льенара–Шварцшильда и теорией Ритца. В то же время применение подхода Максвелла к проблеме тяготения не вызывало особого интереса.
Наиболее совершенная теория, основанная на концепции дальнодействия, была опубликована в начале нашего века молодым швейцарским физиком Вальтером Ритцем [307]. В течение всей жизни он отличался слабым здоровьем и в 1909 г. умер молодым в возрасте 31 года. Он был сокурсником Эйнштейна по Цюриху и большую часть своей работы выполнил в Гёттингене. Полученный Ритцем модифицированный закон тяготения, в отличие от рассмотренных нами выше, при специальных предположениях давал полную величину наблюдаемого смещения перигелия Меркурия. Кроме того, Ритц надеялся разработать общую теорию, охватывающую гравитационные и электромагнитные явления. В 1909 г. он высказал основные принципы построения такой теории, в которой тяготение получалось как проявление остаточного эффекта, обусловленного членами высокого порядка в законе силы самой электродинамической теории. Ритц умер вскоре после опубликования этой статьи, и его идеи не получили дальнейшего развития.
Теория Ритца является баллистической, т. е. действие переносится гипотетическими частицами со скоростью, равной сумме скоростей света и источника. Эта теория [307] даёт фундаментальную силу взаимодействия, определённую уравнением (6.13). Предложенный Ритцем вариант формулы для случая тяготения записан следующим образом:
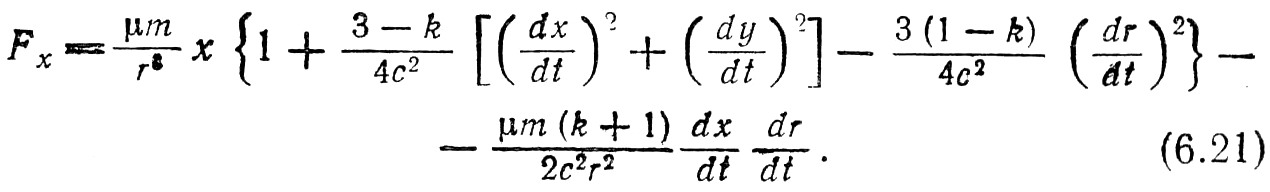
Постоянная k в формуле (6.21) остаётся неопределённой. Ритц получил следующие значения для смещений перигелиев за столетие: Меркурий – (k+5)·3,6''; Венера – (k+5)·0,7''; Земля – (k+5)·0,3''. Согласование со значением 41'' для Меркурия даёт k= 6,4, и в результате получается, что смещение перигелия за столетие должно составлять 41'' для Меркурия, 8'' для Венеры и 3,4'' для Земли. Как можно показать, отсюда следует движение лунного перигея 0,09'' в столетие, согласующееся с теорией движения Луны Брауна. Ритц полагал, что полученные им значения смещения перигелия для Венеры и Земли слишком велики, хотя они почти совпадали со значениями, найденными в общей теории относительности. Относительно недавно Фокс [121] предложил более общую методику оценки величины k. По его мысли, если расширить теорию Ритца, включив в неё анализ тонкой структуры спектра водородного атома, то отсюда можно получить значение k. Однако предложенный метод не позволяет сразу решить проблему, поскольку нет никаких оснований считать, что постоянные, фигурирующие в законах электродинамики и теории тяготения, должны иметь одни и те же значения. Выражение, определяющее отклонение светового луча в гравитационном поле, не зависит от k, поэтому указанный метод неприменим.
Ритц [308] высказал некоторые идеи о связи гравитации с электродинамикой, но и это не помогло. По его мысли, гравитационные силы должны определяться членами высокого порядка, но соответствующие коэффициенты остались неопределёнными, и со смертью Ритца его теория была оставлена. Ритц считал, что атом состоит из положительных зарядов, обращающихся вокруг центрального отрицательного заряда. В соответствии с этой картиной электростатическое взаимодействие между двумя нейтральными телами отсутствует, но члены, зависящие от скорости и ускорения, не равны нулю. Ритц использовал относительные скорости и классическую кинематику и подверг критике теории Лоренца (теорию, разработанную в 1900 г. и основанную на идеях Цельнера, а также теорию лоренц-инвариантов), которые предсказывали нулевые силы из-за использования абсолютных скоростей и неклассической кинематики. Как нашёл Ганс, из теории Ритца следовали возможность существования гравитационного экрана, а также условие неподвижности положительных зарядов.
Члены второго порядка в формуле Ритца, определяющей силу тяготения, зависят от квадрата скоростей зарядов. Отсюда вытекает возможность температурной зависимости, что, согласно Ритцу, “противоречит наблюдениям”. На самом деле было проведено мало опытов для проверки общепринятого предположения о независимости гравитационного взаимодействия от температуры. В 1916 г. П. Е. Шоу из Ноттингема (Великобритания) заявил об открытии температурной зависимости [336]. В качестве теоретического обоснования такой зависимости Шоу ссылался на теорию материи Ми [246], волновую теорию Морозова [249] и на некоторые идеи Бора [33], но не упоминал работы Ритца. Несколько ранее, в 1905 г., Пойнтинг и Филлипс нашли слабое доказательство изменения веса тела с изменением его температуры, а в 1906 г. аналогичные результаты были получены Саузерном. Новизна эксперимента Шоу состояла в том, что он изменял температуру большей массы, находящейся в специальном приборе Бойса, в интервале 20–240°С и получил на основе довольно шаткого доказательства экспериментальную модификацию закона обратных квадратов в виде
F=G(1+αθ)Mm/d2, (6.22)
где θ — температура бóльшей массы М. Измеренное значение температурного коэффициента α равнялось +1,2·10-5 на 1 °С. Вслед за этим на страницах журнала “Нейчур” началась длительная дискуссия по поводу результатов, полученных Шоу [203, 204]. Лармор считал, что несогласие с опытом должно получиться в случае кометы, нагревающейся при приближении к Солнцу. Если бы инертная масса кометы возрастала, то в соответствии с законом сохранения количества движения её скорость должна была уменьшаться, приводя к возмущениям орбитального движения. Шоу отвечал на это, что уравнение (6.22) справедливо лишь в случае, когда нагревается тело большей массы. Другой, более основательный аргумент Лармора состоял в том, что, согласно электродинамической теории, приращение δт равно
δ
m=δE/c2=kδT/c2≈10–35δTи “мало до необнаружимости”, а также гораздо меньше значений α в уравнении (6.22). На это Шоу предложил объяснение температурной зависимости на основе волновой теории [337, с. 401]:
“Сила притяжения, зависящая от температуры, обусловлена колебаниями фарадеевских силовых трубок, перемещаемых взад-вперёд молекулами в процессе их колебательного движения. Картина напоминает вытекающую из волновой теории тяготения Чаллиса, согласно которой тела в колеблющейся среде взаимно притягиваются, если их фазы совпадают”.
Он получил закон силы, аналогичный выведенному Пойнтингом и Филлипсом, который в случае большой массы М и малой массы т сводился к уравнению (6.22). Линдеман и Бартон опубликовали своё совместное письмо, в котором наряду с критическими замечаниями по адресу некоторых следствий из результатов Шоу содержалась похвальная оценка его эксперимента. Дискуссия окончилась в 1917 г., но вопрос был закрыт в 1922 г., когда Шоу и Дэви повторили эксперимент и обнаружили, что температурная зависимость на самом деле отсутствует. Вину за ошибочный результат 1916 г. они возложили на дефекты в экспериментальной установке.
Чтобы избежать слабой температурной зависимости в своём законе силы взаимодействия, Ритц решил выбрать произвольные постоянные так, чтобы избавиться от соответствующих членов второго порядка. К членам более высоких порядков это возражение не относилось, как писал Ритц [308]: “...при условии, что межатомные скорости велики по сравнению со скоростями теплового движения, что представляется возможным a priori”.
Таким образом, Ритц получил фундаментальный закон Ньютона до члена четвёртого порядка, сделав вполне правдоподобное допущение, что масса тела пропорциональна числу вращающихся зарядов, содержащихся в нём. Члены шестого порядка должны были учитывать смещение перигелия Меркурия (и, в какой-то мере, отклонение света звёзд в гравитационном поле Солнца) при подходящих числовых значениях постоянных, хотя такое определение было бы ограниченным из-за необходимости исключить члены второго порядка. Ритц обратился также к рассмотрению членов третьего, пятого и других порядков, считая, что они, возможно, вносят вклад в гравитацию, поскольку и эти члены содержали неопределённые постоянные. Он пришёл к выводу, что “...объяснение аномалии Меркурия и определение гравитационной постоянной путём электромагнитных измерений, несомненно, можно осуществить, исходя из законов электродинамики, когда последние станут известны с более высокой точностью. При любой гипотезе гравитация должна быть, по существу, следствием динамического строения атомов” [308, с. 490].
Ритц умер в 1909 г., оставив лишь скупые наброски своей теории тяготения. Независимо от того, была ли принята эта теория и применялся ли предложенный Ритцом закон силы взаимодействия, её признание зависело от приемлемости исходной электродинамической теории. Последняя же была отвергнута из-за несоответствия данным эксперимента, хотя, как утверждал Фокс [120, 121], окончательные доказательства против теории Ритца были получены лишь в 1960-х годах. Фоксу фактически пришлось модифицировать эту теорию, поскольку из неё следовало, что скорости гипотетических частиц не изменяются при прохождении через материальную среду. Поскольку это противоречило результатам опыта Физо, Фокс ввёл вполне естественное изменение [121, с. 4]:
“Когда световая волна приводит в движение заряды, имеющиеся в среде, они в свою очередь излучают новые волны, центры распространения которых движутся в вакууме со скоростью зарядов среды”.
Фоксу удалось таким образом объяснить результаты всех оптических экспериментов, которые, казалось, опровергали теорию Ритца. Для этого он обратился к “...так называемой теореме погашения Эвальда и Озеена, которая показывает, как внешнее электромагнитное возмущение, распространяющееся в вакууме со скоростью света, в веществе полностью сводится на нет, уступая место вторичному возмущению, которое распространяется с соответственно меньшей скоростью” [34, с. 70].
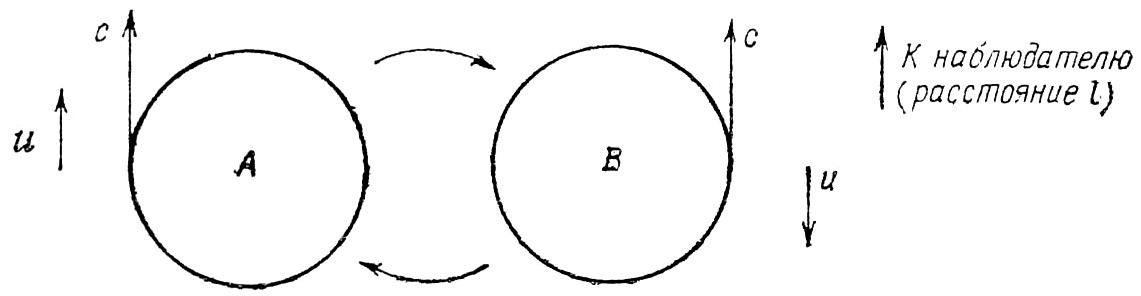
Рис. 6.1. Компоненты двойной звезды, обращающиеся вокруг центра масс.
Эта теорема показывает, что эксперименты по измерению скорости света от конкретного источника неизменно сводятся к измерению скорости распространения света, типичной для некоторой промежуточной материальной среды. Эффекта, предсказываемого теоремой погашения, можно избежать лишь в том случае, когда “частота электромагнитного излучения настолько высока, что электроны атомов не могут следовать за ней”. Такое условие выполняется в случае γ-лучей, и Фокс принял результаты выполненных в 1964 г. экспериментов с γ-лучами энергией 6 ГэВ, как наилучший аргумент против теории Ритца и в пользу постулата о постоянстве скорости света относительно движущегося источника.
Теория Ритца рассматривалась как серьёзный конкурент специальной теории относительности. Один из наиболее широко известных аргументов против теории Ритца появился как результат исследований в астрономии. Этот аргумент, основанный на наблюдениях двойных звёзд, был сформулирован в 1913 г. де Ситтером [81], хотя его основная идея была опубликована ранее Комстоком [65].
“Если эмиссионная теория света верна, то скорость света от звезды, находящейся в положении А, будет с+u, а в положении В должна быть с–u. Следовательно, звезда должна наблюдаться в положении А через l/(с+u) секунд после фактического прибытия в эту точку, а в положении В – через l/(с–u) секунд. Вследствие этого видимое время половины оборота, соответствующее перемещению звезды из А в В, должно быть равно Δt–l/(с+u)+l/(с–u)=Δt+2ul/с2, где Δt – действительное время полуопорота по орбите, которую для простоты можно считать круговой. С другой стороны, кажущееся время следующего полуоборота, соответствующее перемещению из В в А, будет составлять Δt–2ul/с2. Для большинства спектроскопических двойных величина 2ul/с2 сравнима с Δt по порядку, а в ряде случаев имеет даже большее значение. Следовательно, если бы эмиссионная теория света была верна, то без поправок за переменную скорость света нам едва ли удалось бы найти, что параметры орбитального движения звёзд соответствуют законам Кеплера, как это наблюдается в действительности. Безусловно, сказанное является очень сильным аргументом против эмиссионной теории” [365, с. 24–25].
Аргументация де Ситтера в том же году встретила возражения со стороны Фрейндлиха [122] и Гутника [144]. Фрейндлих указал, что переменная скорость света в первом приближении должна проявиться в трансформации видимой орбиты в кеплеровский эллипс, у которого линия апсид совпадает с лучом зрения, а периастр направлен в сторону от Земли. Он добавил, что указанный эффект действительно уже наблюдался Барром в 1908 г., хотя и допускал, что возможно иное его объяснение, например космогоническое следствие расположения Солнца вблизи центра Млечного Пути.
Де Ситтер [82] ответил короткой заметкой, повторив свою аргументацию и отметив, что для типичной звезды влияние любой переменности скорости света должно быть очень малым. Однако Фокс, исходя из теоремы погашения, показал, что аргументы де Ситтера не бесспорны. Свет от всех внеземных источников при своём распространении проходит через неоднородную среду: межзвёздный газ, земную атмосферу, стеклянные линзы в лаборатории. Более того, как было показано Отто Струве, большинство тесных двойных звёзд окружены газовыми оболочками, которые не вращаются с компонентами двойной и потому также изменяют скорость светового излучения. Струве и Хуанг [351] выдвинули гипотезу, призванную объяснить эффект Барра. Они предположили, что неравномерное распределение наблюдаемых значений долгот периастров обусловлено искажением кривых лучевой скорости, которое вызвано влиянием потоков выброшенного газа, обращающихся вокруг компонентов двойной. Однако эта гипотеза была не настолько обоснованна, чтобы считаться безусловно общепринятой. В качестве альтернативы оставалось возможным использование теоремы погашения с учётом влияния межзвёздного газа и других факторов, чтобы спасти теорию Ритца.
Таким образом, опровергнуть теорию Ритца оказалось труднее, чем думали в период развития общей теории относительности. Сам Ритц относился критически к применению законов электродинамики, таких, как закон Вебера, в теории тяготения, поскольку они не позволяли полностью объяснить аномальное смещение перигелия Меркурия, а также получить (и даже надеяться на это) значение гравитационной постоянной из электрических или магнитных измерений. Теория Ритца открывала возможность достичь этих целей, и он сам считал её успех “весьма вероятным”. Окончательному утверждению общей теории относительности способствовало обнаружение двух других эмпирических эффектов, которые наряду с аномальным смещением перигелия Меркурия стали “классическими” испытаниями справедливости этой теории, а именно красного смещения линий в спектре источника излучения, находящегося в гравитационном поле, и отклонения световых лучей вблизи массивных тел.
Гравитационное красное смещение, согласно теории относительности, представляет собой следствие замедления течения времени в гравитационном поле. Однако его можно получить, используя простую модель фотона. Если фотон массой m переносится из области с потенциалом Р в область пренебрежимо малого потенциала, то он теряет энергию mР. Поскольку, согласно специальной теории относительности, Е= тс2, фотон теряет энергию, равную РЕ/с2, так что относительная потеря составляет dE/E=Р/с2 или относительное красное смещение dν/ν=-Р/с2, что соответствует общей теории относительности. Таким образом, все теории такого рода предсказывают существование красного смещения, и на этом основании невозможно сделать выбор между ними.
Отклонение света, согласно общей теории относительности, вытекает из зависимости скорости света от гравитационного потенциала. Однако такое отклонение получается также и в том случае, если фотон рассматривать как частицу. Ещё в 1801 г. Зольднер представил решение этой задачи, исходя из закона Ньютона, и получил результат, составляющий половину значения 1,75'', следующего из общей теории относительности. Сравнительно недавно в работе [274, с. 544] были даны общее выражение электродинамического закона силы взаимодействия, а также выражения для смещения перигелия и отклонения светового луча, соответствующих этой силе. Сравнение сил, следующих из этого общего выражения и закона Ритца, позволяет найти значения коэффициентов. Таким образом, можно показать, что отклонение светового луча, соответствующее закону Ритца, составляет 3/4 от предсказываемого теорией относительности, или 1,31''. В настоящее время, хотя подтверждение предсказания общей теории относительности нельзя считать совершенно окончательным, просмотр полученных результатов убеждает, что значение 1,31'' никоим образом не имеет преимуществ по сравнению со значением 1,75'' [195]*. Экспедиция Гринвичской обсерватории на Принсипи, состоявшаяся в 1919 г., получила значение 1,61''±0,40'', а австралийская экспедиция 1922 г. (Додвелл и Дэвидсон) получила 1,77''±0,40''. Однако, хотя результаты обеих экспедиций не опровергают теорию Ритца, предпочтение следует отдать общей теории относительности. Другие значения, например полученные экспедицией Гринвичской обсерватории в Собраль (1919 г.), подтвердили справедливость общей теории относительности, а более поздние экспедиции, где производились измерения отклонения света, дали значения больше 1,75''. Таким образом, теория Ритца, в которой использовалась формула взаимодействия, отличающаяся от ньютонова закона обратных квадратов, к 1922 г. была окончательно опровергнута. Однако этот факт остался незамеченным её современниками, поскольку она и раньше пребывала в забвении, возможно, не совсем заслуженно.
В течение первых двух десятилетий нашего века теория Ритца и общая теория относительности имели конкурента. Это была гипотеза, которая не претендовала на всеобъемлющее объяснение гравитации и электродинамики, но давала простую формулу гравитационных сил, позволяющую без введения произвольных постоянных и исключения каких-либо членов полностью объяснить смещение перигелия Меркурия. Такая формула была предложена Паулем Гербером…
…Предложенный Гербером закон взаимодействия обладает замечательным свойством: если положить v равной скорости света, то предсказываемое им смещение перигелия Меркурия составит 41''. Для Венеры соответствующее значение равно 8'', как следует из закона Ритца и общей теории относительности, а значения для других планет и лунного перигея достаточно малы, чтобы согласоваться с наблюдениями…
…Получение потенциала составляет существенную часть теории Гербера, поскольку его формула (6.24) выведена при рассмотрении влияния, которое конечное время распространения оказывает, во-первых, на расстояние и, во-вторых, на количество полученного потенциала. Во втором случае возможна интерпретация в рамках представлений Ритца о гипотетических частицах: чем быстрее поглощающее тело движется по направлению к излучающему, тем больше частиц "собирает" оно, и аналогично, чем быстрее движется излучающее тело, тем быстрее движутся излучаемые им частицы и тем больше их поглощается в единицу времени. Однако детали этого процесса представить трудно…
…Как было показано, этот закон приводил к такому же выражению для смещения перигелия, как и общая теория относительности. Однако теория Гербера была применима лишь к гравитации и вне этой области ни о чем не говорила. Поэтому для создания полной физической картины её требовалось дополнить, в частности, теорией электродинамики. Во время появления общей теории относительности это могла быть либо теория Лоренца, либо специальная теория относительности, но, как мы увидим в следующей главе, обе эти теории приводили к одной и той же зависимости массы от скорости. Эта зависимость, учитываемая в рамках "ньютонианской" теории, приводила к значению 1'' в столетие для смещения перигелия Меркурия**. Как уже отмечалось в гл. 4, де Ситтер в 1913 г. показал, что это значение вполне укладывалось в рамки общепринятого тогда объяснения аномалии на основе ньютоновой теории, если исходить из гипотезы Зеелигера о зодиакальном свете и слегка уменьшить плотность пылевого вещества. Это релятивистское движение перигелия необходимо учитывать и в приложении к теории тяготения. В общей теории относительности это подразумевается, так как она включает в себя специальную теорию относительности. Это молчаливо предполагалось и в незаконченной теории Ритца 1909 г., поскольку последняя должна была охватывать как электродинамику, так и гравитацию и предусматривать изменение массы и другие следствия электродинамической теории Ритца [274, с. 620]. При использовании в 1908 г. формулы Ритца в качестве чисто гравитационного закона следовало бы добавить смещение за счёт электродинамического эффекта, но поскольку соответствие вычисленной величины аномалии наблюдениям устанавливалось путём принятия специальных предположений, это обстоятельство не опровергало закона Ритца. Однако кажущееся преимущество формулы Гербера, не требующей подгонки постоянных, в данном случае обратилось против неё, так как и здесь требуется добавить релятивистский эффект, что в совокупности приводит к смещению перигелия Меркурия, равному 49'' в столетие. В то время как небольшая заниженность расчётного значения по сравнению с наблюдаемым может быть приписана малому сжатию Солнца или наличию пылевого вещества внутри орбиты Меркурия, даже небольшой избыток объяснить очень трудно. Никто не отваживался утверждать, что Солнце на самом деле вытянуто вдоль оси вращения, а значение смещения, равное 42'' в столетие, если и оспаривалось, то поправки вносились в сторону его уменьшения. Таким образом, закон Гербера не обеспечивал верного предвычисления смещения перигелия.
Вторая причина, по которой закон Гербера следовало бы отвергнуть, – это эффект отклонения световых лучей в гравитационном поле Солнца. Правда, в то время его существование подвергалось сомнению. Ранее уже обсуждалось отклонение света в гравитационном поле Солнца в соответствии с теорией Ритца. Мы считали световой луч состоящим из частиц, проходящих вблизи массивного тела. Аналогичный подход можно повторить и при исследовании закона Гербера…
…Приведённые соображения следует рассматривать как явное опровержение закона Гербера. Ранние результаты наблюдений солнечных затмений не принесли окончательного подтверждения общей теории относительности [195]. Экспедиция в Собраль 1919 г. получила значение 1,98''±0,16'', свидетельствующее в пользу этой теории в том смысле, что соперничающие теории Нордстрема и "ньютонианская" предсказали соответственно полное отсутствие эффекта и отклонение, равное 0,87''. Полученные данные также подтверждали превосходство общей теории относительности над теориями Ритца и Гербера, которые предсказывали значения 1,31'' и 2,62'' соответственно. Однако более поздние измерения привели к результатам, которые превышают значение, предсказываемое теорией Эйнштейна.
Хотя концепции дальнодействия всё ещё эпизодически появляются, общая теория относительности занимает настолько прочное положение, что при обсуждении теорий тяготения повсюду используется принятая в ней терминология. Развитие общей теории относительности и её связь с аномальным смещением перигелия Меркурия рассматриваются в следующей главе, которая по содержанию будет резко отличаться от данной. Ряд теорий, рассмотренных в этой главе, завершается теориями Гербера и Ритца. Однако теория Гербера, имевшая плохую научную репутацию, игнорировалась специалистами, если не считать немногих её сторонников, руководимых сомнительными целями. Теория Ритца была встречена в штыки, несмотря на её верные научные истоки, так как была до некоторой степени произвольной, и ценность её как теории тяготения была под вопросом. Ни одна из этих теорий не выдержала проверки на классических эффектах, подтверждающих общую теорию относительности, а измерения эффекта отклонения световых лучей явились для них камнем преткновения.
Выдвигались и другие теории гравитации, исходящие из свойств эфира. В отличие от пульсационных теорий, где причиной, вызывающей притяжение и отталкивание тел, считались короткопериодические потоки эфира, в них рассматривались вековые потоки. Ещё в 1853 г. Риман показал, что поток эфира в “большую вселенную” через каждую частицу может дать эффект притяжения [87, с. 443; 305, с. 503], однако теоретически эту идею обосновал в 1891 г. Карл Пирсон, до того опубликовавший несколько работ по пульсационной теории.
Первая из них была посвящена практическому применению теории – исследованию движения судов [277]. Уже в следующей статье, написанной в том же 1883 г. и прочитанной в Кембриджском философском обществе в 1885 г., Пирсон представил детально разработанную теорию тяготения. Выведенный им закон притяжения напоминал закон Клеро, но включал дополнительный член, пропорциональный r–5, и обладал рядом новых свойств. Оказалось, что благодаря изменениям периодов пульсаций под влиянием других соседних тел масса тяготеющего тела должна немного меняться. Отсюда следовало, например, что, измеряя плотность Земли и используя в эксперименте различные материалы, мы должны получать разные результаты. Пирсон полагал, что от этого сомнительного вывода можно избавиться, рассматривая вместо массы в законе тяготения другие функции; правда, он указывал на “опыты Бейли, [где] средняя плотность, полученная в серии экспериментов с шарами на крутильном стержне, различалась в зависимости от вещества шаров” [279, с. 115]. Из теории также следовала зависимость массы от температуры, которая якобы наблюдалась Шоу в 1916 г. (см. гл. 6).
Вторая часть работы была более интересной [278]***. Она была направлена против Томсона, который в 1884 г. предложил модель атома, состоящего из “материального ядра, окруженного рядом материальных сферических оболочек, объединённых упругими силами”, и Линдемана, который в 1888 г. опубликовал результаты изучения механической модели атома Томсона. Цель Пирсона состояла в том, чтобы “...показать, что полученные Линдеманом результаты никоим образом не зависят от структуры оболочечной модели атома Томсона; что, далее, представление о пульсациях сферического атома гораздо лучше, чем оболочечная модель, объясняет химическое соединение и распад; как показано в моей первой работе, оно бросает некоторый свет на химические силы, силы сцепления и даже гравитацию” [278, с. 60].
В 1891 г. Пирсон отказался от пульсационной интерпретации в пользу “эфирных струй”, хотя больше этот предмет он не затрагивал [280]. В 1870 г. о силах, возникающих между источниками и стоками жидкости, и об аналогии с гравитацией говорил Томсон, но Пирсон, исходя из этой идеи, построил серьёзную модель [280, с. 309]:
“Представления о струях эфира в качестве динамической модели атома, во всяком случае, весьма просты. Однако действие одной группы струй на другую приводит к уравнениям, сложность которых вполне можно сравнить со сложностью самой Природы... Как показано, и закон тяготения, и теория потенциала более естественно вытекают из теории струй эфира, чем из пульсационных теорий”.
Об оболочках и упругих силах он писал [280, с. 310]:
“Атомы и молекулы Томсона – Линдемана выглядят сложными механизмами, вызывая вполне естественное отвращение философского рассудка к дуалистической теории Вселенной”.
Его собственная теория была монистической [280, с. 312]:
“...первичной субстанцией является жидкая невращающаяся среда, а атомы или элементы материи суть струи этой субстанции. Откуда взялись в трёхмерном пространстве эти струи, сказать нельзя; в возможности познания физической Вселенной теория ограничивается их существованием. Может быть, их возникновение связано с пространством более высокой размерности, чем наше собственное, но мы о нём ничего знать не можем, мы имеем дело лишь с потоками в нашу среду, со струями эфира, которые мы предложили именовать “материей”.
Для скорости потоков эфира Пирсон получил выражение в виде ряда. Он содержал постоянный член, ответственный за тяготение, периодические члены, связанные с химическим сродством и связью, и другие колебательные члены, описывающие оптические и электрические явления. Гравитационный потенциал имел вид
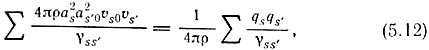
где ρ – плотность среды, as – радиус сферы s, 0vs – средняя скорость потока эфира через поверхность сферы s, γss' – расстояние между сферами s и s', qs – средний темп переноса эфира струёй через поверхность s, т. е. qs= 4πas2ρ·0vs. Определяя массу как средний темп переноса эфира, Пирсон вывел закон обратных квадратов [278, с. 314]. Потенциальная энергия по существу представляет собой кинетическую энергию эфира. Под струями можно понимать источники и стоки эфира – это и будут уже известные нам “положительные” и “отрицательные” массы.
На вопрос, куда, согласно этой теории, течёт эфир и откуда он истекает, ответ дал Шотт [319]. Его предположение непосредственно опиралось на объяснение узости спектральных линий; пытаясь разобраться в этом, Джинс был вынужден предположить существование сил неизвестной природы, действующих между электронами, в то время как Рэлей дал лишь неполный ответ на вопрос, исходя из кинематических соображений. Трудность заключалась в том, что для кольца электронов атома “строго стационарное движение невозможно, если считать, что электрон не меняется, и исключить все силы неэлектромагнитного происхождения... Предполагая, что радиус электрона медленно меняется, эту трудность можно преодолеть” [319, с. 23].
Идея “раздувающегося” электрона как источника эфира согласуется с теорией Пирсона; Шотт вывел закон обратных квадратов, но с зависящей от времени постоянной тяготения. Сам Шотт не считал свою теорию особенно успешной, но её поддержал Тунцельман. Он ввёл дополнительное предположение о деформации электрона с изменением скорости, полагая, что зависящий от скорости поток эфира может привести к смещению перигелиев.
Однако и в теории Шотта требовалась “большая вселенная”, ибо нужно было объяснить, почему электрон испытывает вековое расширение (это расширение можно было бы интерпретировать как одну из фаз долгопериодических пульсаций электрона); по мнению Тунцельмана, причина расширения состоит в общем уменьшении давления эфира во Вселенной. И хотя в принципе его можно было бы объяснить внутренними причинами (подобно тому как в общей теории относительности расширение Вселенной вытекает из уравнений поля), пришлось обратиться к уменьшению давления эфира на границе Вселенной, вызванному воздействием какого-то фактора во “внешней вселенной”.
Рассмотрим ещё одну из теорий тяготения – теорию Лесажа. Она впервые появилась в 1782 г. и в 1883 г. была фактически возрождена Томсоном, когда он показал, как можно обойти выдвинутое Максвеллом возражение против этой теории, позднее использованное Пуанкаре [359]. Она вызвала противоречивые отклики. Так, Джон Гершель считал её “слишком абсурдной, чтобы её можно было воспринимать всерьёз” [357], в то время как Тейт (последователь Томсона) утверждал, что это “единственное приемлемое решение [проблемы объяснения тяготения] из всех предложенных до сих пор” [357].
Теория Лесажа ответила на ряд вопросов, оставшихся за рамками нашего обсуждения, которые касались аргумента о связи трёхмерности пространства с законом обратных квадратов. Правда, этот аргумент не давал никаких указаний на характер зависимости силы от масс. Он не позволял ответить и на вопрос, почему большое и малое тело могут иметь равные веса. Если тело с расстояния r от силового центра перенести на расстояние 2r, то, как легко видеть, исходя из трёхмерности пространства, сила притяжения уменьшится вчетверо. Однако если тело, оставаясь на том же расстоянии, вдруг изменит форму и займёт бóльшую долю поверхности сферы радиуса r, его вес отнюдь не увеличится в той же пропорции. Более того, он вообще не возрастёт, что противоречит отмеченному выше соображению, касающемуся размерности пространства. Теория Лесажа разрешала это противоречие или создавала такое впечатление.
В понимании Лесажа материя состоит из неделимых частиц в форме сетчатых ячеек с “прутьями” очень малой толщины, а всё пространство во всех направлениях с очень большими скоростями пронизывают корпускулы – переносчики гравитации, которые очень редко сталкиваются друг с другом. Изолированное тело, помещённое в пространство, будет находиться в покое, поскольку “бомбардировка” прутьев корпускулами симметрична, и потому получаемые со всех сторон импульсы одинаковы. Если к нему приблизить другое тело, то оно станет “затенять” первое тело от корпускул, летящих по направлению от второго тела. Равновесие нарушится, и тела будут стремиться друг к другу, как если бы они взаимно притягивались [359, с. 323]:
“Не надо быть очень искушенным в математике, чтобы вывести отсюда все законы тяготения, как локальный, так и универсальный (и, следовательно, законы Кеплера и т. п.), со всей точностью, которую обеспечивают нам наблюдаемые явления. Следовательно, эти законы – неизбежное следствие принятого строения материи”.
В закон тяготения входит масса тела, так как тело тем массивнее, чем из большего числа ячеек (и “прутьев”) оно состоит и, следовательно, чем больше испытывает столкновений с корпускулами. Изменение формы тела его веса не меняет, поскольку при этом не меняется число составляющих его ячеек.
Корпускулы в теории Лесажа считались абсолютно жёсткими. Чтобы теория “работала”, их скорость в результате столкновений с “прутьями” должна уменьшаться, следовательно, гравитационное взаимодействие со временем должно постепенно ослабевать. Однако, по мнению Лесажа, никаких трудностей это не создает, если только процесс протекает достаточно медленно ****. Абсолютно жёсткие корпускулы не будут испытывать отдачи после столкновения, они “прилипнут” к бомбардируемому телу. Постоянство массы тел при этом “налипании” можно было бы объяснить ничтожностью массы корпускул, но Лесаж полагал, что после столкновения корпускулы “стекают” с тел. Если они абсолютно жёсткие, большая часть их энергии должна уходить на нагревание. Как показал Максвелл [242], в результате такой бомбардировки тела нагрелись бы до белого каления, а Томсон несколько раньше писал, что “рост температуры был бы вполне достаточен для плавления и испарения любого твёрдого тела, в равной степени большого или малого, в считанные доли секунды” [359, с. 329]. Томсон заменил эти частицы абсолютно упругими “вихревыми атомами”. Поскольку при абсолютно упругих столкновениях кинетическая энергия не теряется, указанное препятствие исчезает; однако если скорость корпускул остаётся неизменной, эффект тяготения не возникнет. Томсон предположил, что на самом деле кинетическая энергия поступательного движения корпускул при столкновениях уменьшается и часть её переходит в энергию колебаний. Она, в свою очередь, может вновь перейти в энергию поступательного движения, что и должно обеспечивать прежний уровень тяготения. В поддержку такого предположения Томсон привлек принцип Клаузиуса, согласно которому в системе взаимодействующих упругих корпускул отношение колебательной и вращательной энергии к энергии поступательного движения постоянно. После столкновения с телом этот баланс должен нарушаться, но затем в ходе межкорпускулярных столкновений вскоре восстанавливаться.
Во второй половине XIX в. теория Лесажа в разных вариантах анализировалась многими учёными, в том числе Изенкраэ, Боком, Рысанеком, Яролимеком и Престоном. Престон [295] считал гравитационные корпускулы чем-то сродни молекулам газа, предполагая, следовательно, что они подчиняются кинетической теории, предписывающей для них равномерное распределение по всем направлениям. Опираясь на анализ движения Нептуна и используя упомянутую идею и её следствия, Рысанек [311] получил оценку скорости частиц 2,7·1012 – 5,4·1017 м/с. Престон пытался обойти отмеченное Максвеллом противоречие по-другому, без обращения к принципу Клаузиуса: он считал, что, если бесконечно увеличить число корпускул и тем самым уменьшить передаваемую каждой корпускулой энергию, можно избежать вывода о заметном повышении температуры тел [296, с. 151]. Однако этот аргумент малоубедителен без количественной оценки, подтверждающей эффективность указанного механизма тяготения. Престон отмечал, что, согласно теории Томсона, действие тяготения распространяется лишь до тех расстояний, где энергия поступательного движения корпускул успевает полностью восстановиться. Это обстоятельство само по себе не опровергало теорию, ибо закон обратных квадратов был “проверен” лишь до расстояния порядка 30 а. е. (между Солнцем и Нептуном), а предполагаемое отсутствие тяготения между звёздами лишь увеличило бы устойчивость Вселенной. Мы уже видели в гл. 4, как Зеелигер использовал теорию Лесажа для объяснения устойчивости Вселенной и решения гравитационного парадокса; однако он обошёлся без идеи Престона, приняв, что существует поглощение гравитации.
В 1897 г. Фарр нашёл новое слабое место этой теории [113]. Теоретически поглощение гравитации должно было быть очень малым, и не только по той причине, что оно не наблюдается (предполагавшаяся величина поглощения в масштабах межпланетных расстояний была бы незаметной), но и потому, что после некоторого критического значения массы (когда ещё все корпускулы “видны”) тяготение уже не зависело бы от массы тела. Высказывая своё возражение, Фарр опирался, в частности, на результат Нернста, согласно которому молекулы жидкости вблизи точки кипения при атмосферном давлении занимают около 0,3 всего объёма. Эта доля настолько велика, что экранировка должна быть непомерно большой. Конечно, этот аргумент убедителен в том случае, если молекулы рассматривать как твёрдые и непрозрачные для гравитационных корпускул частицы.
В 1905 г. Джордж Дарвин [71] дал математическое описание теории Лесажа. Он привёл следующее выражение для силы притяжения между двумя сферами, полученное с учётом и нормальных, и тангенциальных составляющих сил, возникающих при столкновениях:
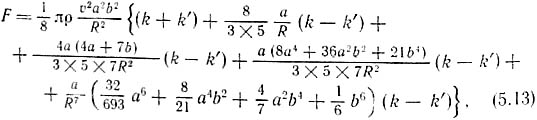
где ρ – плотность среды, и – скорость корпускул, a и b – радиусы сфер, R – расстояние между их центрами, k и k' – коэффициенты упругости (k' – для тангенциальной составляющей), причём для идеально неупругих столкновений k=1, а для идеально упругих k=2. Это выражение не совсем совпадает с законом обратных квадратов, но сводится к нему, если положить k=k'. В общем случае действие и противодействие не равны, поскольку a и b входят в формулу несимметрично, но, считая все сферы “элементарными частицами” одного размера, можно избавиться и от этого затруднения. Однако полученный закон для силы является приближённым, поскольку при его выводе Дарвин пренебрёг отражёнными частицами. В принципе закон Дарвина предсказывает смещение перигелия, но так как величина коэффициента при R–3 имеет порядок радиуса “элементарной частицы”, это смещение крайне незначительно.
Если и казалось, что Дарвин придал теории Лесажа некое подобие “респектабельности” (сам он так не считал*****), то Пуанкаре [286, 287, с. 203–216] окончательно опроверг эту теорию. Он количественно рассчитал давно предполагавшийся эффект нагревания гравитирующих тел. Связав нагревание с сопротивлением, испытываемым телами, и используя примерно тот же аргумент, что и Лаплас, Пуанкаре показал, что скорость корпускул должна быть в 24·1017 раз больше скорости света; если так, то за счёт взаимодействия с ними Земля получала бы в 1020 раз больше энергии, чем излучает Солнце. Не лучше обстояло дело и с неидеально жёсткими корпускулами или волновым вариантом теории (рассмотренным Дарвиным и Томмасиной), где вместо корпускул действовало лучистое давление (давление Максвелла – Бартоли). Итак, теория Лесажа оказалась несостоятельной [87, с. 433]:
“Тот факт, что столь искусственная гипотеза с таким большим количеством слабых мест, подвергаясь анализу столь известных учёных, существовала в течение более чем двух столетий и теперь должна с достоинством умереть, послужит созданию у читателей впечатления о крайней сложности проблемы динамического представления гравитационного действия”.
Так писал о теории Лесажа Тунцельман. Хотя все теории, о которых мы говорили, оказались в конечном счёте ошибочными, они отражали и сложность природы самого тяготения, и стремление учёных разобраться в нём, а не просто принять закон обратных квадратов или какой-либо другой из подходящих законов. Всё это и привело Эйнштейна к созданию общей теории относительности. Несмотря на ошибочность, эти теории воспринимались серьёзно. Я рассмотрел их по той причине, что только с их помощью можно a priori оценить степень правдоподобности гипотезы Холла или же найти иные пути для объяснения движения перигелия Меркурия. Как мы увидели, ни одна из рассматриваемых теорий не дала формулы для силы, соответствующей гипотезе Холла. Это обстоятельство, а также рассмотренные выше аргументы в пользу закона обратных квадратов наводят на мысль, что гипотеза Холла уже с самого начала была маловероятной.
* Приводимые ниже данные опубликованы более детально вместе со ссылками в таблице на с. 58 работы [195].
**Разумеется, ньютонова теория несовместима со специальной теорией относительности, поскольку в отличие от последней в ней предполагается бесконечная скорость распространения гравитационного действия. Теория Гербера в этом отношении совместима со специальной теорией относительности.
*** Здесь Пирсон ссылался на Балтиморские лекции Томсона и работу Линдемана [223].
**** Постепенное ослабление гравитации в таких условиях отметил и Лесаж, указав на него как на слабое место теории. Он говорил: “Итак, тяготение, а вместе с ним и весь мир должны были бы уже закончить своё существование. Ответ. Согласен, но поскольку это препятствие ничего не приносит, чтобы мир пришёл к своему концу быстрее, чем сам по себе, то его следует считать ничтожным” [359, с. 328].
***** Дарвин предварил своё “Введение в динамическую астрономию” [73] обзором ряда теорий тяготения. Говоря об аргументах Максвелла против теории Лесажа, он добавлял: “Лорд Кельвин, однако, указал путь обхода этой фундаментальной трудности... . С другой стороны, тяготение не может передаваться на бесконечность и действует лишь в ограниченной области пространства. В дальнейшем я не стану касаться этой концепции. Во всяком случае, по моему мнению, ни один из людей науки не склонен считать, что она выводит на верную дорогу”. Он писал об эксперименте Бьёркнеса: “Какими бы занимательными и интересными ни были эти рассуждения и опыты, мне не кажется, что они могут привести к рабочей гипотезе о природе тяготения”. И далее об идеях Осборна Рейнольдса: “Хотя и нельзя считать, что Рейнольдс хорошо излагает свои взгляды, его достижения в науке таковы, что теория требует внимательного подхода” (Рейнольдс [304, с. 205] в 1903 г. вывел закон обратных квадратов для тяготения).
33. Bohr N. On the constitution of atoms and molecules. Phil. Mag. 26, 1–25, 1913.
34. Born M., Wolf E. Principles of optics. Pergamon Press, London 1959. [Имеется перевод: Борн М., Вольф Э. Основы оптики. – М., Наука, 1970.]
65. Comstock D. F. A neglected type of relativity. Astronomical consequences of the assumption that the velocity of light depends on the source velocity. Phys. Rev., 30, 267, 1910.
71. Darwin G. The analogy between Lesage's theory of gravitation and the repulsion of light. Proc. R. Soc. A76, 387–410, 1905.
73. Darwin G. Introduction to dynamical astronomy. Sci. Pap. (Cambridge), 5, 9–15, 1916.
81. De Sitter W. Ein astronomischer Beweis für die Konstanz der Lichtgeschwindigkeit. Phys. Z., 14, 429, 1913.
82. De Sitter W. Über die Genauigkeit, innerhalb welcher die Unabhängigkeit der Lichtgeschwindigkeit von der Bewegung der Quelle behauptet werden kann. Phys Z., 14, 1267, 1913.
87. De Tunzelmann G. W. A treatise on electrical theory and the problem of the universe. Chap. 18, 362. Charles Griffin, London, 1910.
113. Farr С. С. On an objection to LeSage's theory of gravitation. Trans. Proc. N. Z. Inst., 30, 118–120, 1897.
120. Fox J. G. Experimental evidence for the second postulate of Special Relativity. Am. J. Phys., 30, 297–300, 1962.
121. Fox J. G. Evidence against emission theories. Am. J. Phys., 33, 1–17, 1965.
122. Freunlich E. Zur Frage der Konstanz der Lichtgeschwindigkeit. Phys. Z., 14, 835—838, 1913.
144. Guthnik P. Astronomische Kriterjen für die Unabhängigkeit der Fortpflanzungsgeschwindigkeit des Lichtes von der Bewegung der Lichtquelle. Astr. Nachr., 195, 265–270, 1913.
195. Kluber von H. The determination of Einstein's light-deflection in the gravitational field of the sun. Vistas. Astr, 3, 45–77, 1960.
203. Larmor J. Nature (Lond.), 97, 321, 421, 1916.
204. Larmor J. Nature (Lond.), 99, 44–45, 1917.
223. Lindemann F. A. Über Molekular Physik. Versuch einer einheitlichen dynamischen Behandlung der physikalische und chemischen Kraften. Schr. phys.-ökon. Ges. Konigsberg, 29, 31–81, 1888.
242. Maxwell J. C. Atom. In Encyclopaedia Britannica (9th edn.) 1875.
246. Mie G. Grundlagen einer Theorie der Materie, Chap. 5, Die Gravitation, Annln. Phys., 40, 25–63, 1913.
249. Морозов Н. А. Журн. русс. хим. общества, 40, 23–35, 1908.
274. O'Rahilly A. Electromagnetic theory. Dover Publications, New York, 1965.
277. Pearson K. On the motion of the spherical and ellipsoidal bodies in fluid media. Q. J. pure appl. Math., 20, 60–79, 184–211, 1885.
278. Pearson K. On a certain atomic hypothesis. Part II. Proc. London math. Soc, 20, 38–63, 1888–1889.
279. Pearson K. On a certain atomic hypothesis. Trans. Camb. phil. Soc, 14, 71–120, 1889.
280. Pearson K. Ether squirts. Am. J. Math., 13, 309–362, 1891.
286. Poincaré H. La dynamique de l'électron. Rev. gén. Sci. pures appl., 19, 386–402, 1908.
287. Poincaré H. Les limites de la loi de Newton. Bull. Astron., 17, 121–269, 1953.
295. Preston S. T. On some dynamical conditions applicable to LeSage's theory of gravitation. Phil. Mag. (Ser. 5), 4, 206–213, 364–375, 1877.
296. Preston S. T. Comparative review of some dynamical theories of gravitation. Phil. Mag. (Ser. 5), 39, 145–159, 1895.
304. Reynolds O. The submechanics of the universe. Cambridge University Press, 1903.
305. Riemann B. Gesammelte mathematische Werke (ed. H. Weber). Teubner Leipzig, 1876.
307. Ritz W. Recherches critiques sur l'électrodynamique générale. Ann. Chim. Phys., Ser. B, 13, 145–275, 1908.
308. Ritz W. Die Gravitation. Scientia, 5, 241–255, 1909.
311. Rysanek A. Versuch einer dynamischen Erklärung der Gravitation. Repert. Phys., 24, 90–114, 1888.
319. Schott G. A. On the electron theory of matter and the explanation of fine spectrum lines and of gravitation. Phil. Mag. (Ser. 6), 12, 21–29, 1906.
323. Seegers С. De motu perturbationibusque planetarum secundum logem electrodynarnicam Weberianam solem ambientum. Inaugural Diss. Göttingen, 1864.
336. Shaw P. E. The Newtonian constant of gravitation as affected by temperature. Phil. Trans. r. Soc. Lond., Ser. A, 216, 349–392, 1916.
337. Shaw P. E. Nature (Lond.), 97, 400–401, 1916.
351. Struve O., Huang S.-S. Close binary stars. Occas. Notes, R. Astr. Soc. 3 (19), 161–188, 1957.
357. Taylor W. B. Kinetic theories of gravitation. Smithson. Rep. (Wash.) 205–282, 1876.
359. Thomson W. On the ultramundane corpuscles of LeSage. Phil Mag (Ser. 4), 45, 321–332, 1873.
365. Tolman R. С. The theory of the relativity of motion. University of California Press, Berkeley, 1917.
378. Weber W., Kohlrausch R. Elektrodynamische Maassbestimungen insbesondere Zuruckfahrung der Stromintensitats-Messungen auf mechanisches Maass. Abh. k. sächs. Ges. Wiss. (Lpz.), 5, 265, 1857.
Дата установки: 21.03.2010
[вернуться к содержанию сайта]