[вернуться к содержанию сайта]

ПОРЯДОК В МИКРОМИРЕ
(напечатано в журнале "Инженер" №7-8, 2011)

    Часто приходится слышать, будто микромир – это мир хаоса, беспорядка, где царит суматоха, случайные метания и распады частиц. Похожее впечатление произвёл бы и мегаполис в час пик: "случайно" мечущиеся пешеходы, безумные потоки людей и машин, шум, гам, аварии. Но стоит подняться на сотню-другую метров над городом, и в этом "хаосе" обнаружится порядок и ритмичность, закономерные движения машин и людей, выпускаемых одними зданиями и поглощаемых другими, кристально чёткая сетка улиц, периодичные ячейки кварталов из многоугольников зданий, прямолинейные цепочки фонарей и т.д. А по краям города увидим медленную "кристаллизацию" новых зданий. Так и микромир с его частицами при взгляде с высоты – это образец порядка и кристальной чёткости. Идеально похожие атомы, ядра, элементарные частицы напоминают типовые здания-многогранники с гранями-стенами, утыканными периодичной решёткой окон. Словно дома, возведённые по одному плану, частицы одного типа имеют идентичные характеристики: размер, форму, массу, время жизни (расчётный срок эксплуатации) и прочие свойства. Чем же объяснить этот идеальный порядок микромира, граничащий с "хаосом" и "случайным" поведением частиц?

    На этот вопрос давно ответили атомисты Древней Индии, которые считали, что наименьшие элементарные частицы (электроны и позитроны) соединяются попарно, а затем эти пары сливаются в более крупные конгломераты, образуя периодичные структуры в виде новых частиц [1]. Кратность заряда любой частицы заряду электрона e означает, что именно из электронов e^– и позитронов e⁺ составлена всякая частица, а заряд её связан с избытком одних над другими, или равен нулю при равенстве их числа. Факт вылета электронов и позитронов из частиц при распаде или ударе доказывает, что из них построены все частицы. Это кристаллическое строение частиц-зданий, собранных из стандартного числа однотипных кирпичиков, и задаёт их стандартные свойства (заряд, массу, размер, форму, прочность, срок жизни). В Древней Греции Платон тоже считал атомы-элементы стандартными телами в форме правильных многогранников, кристаллизующихся из мельчайших частиц двух типов. И Демокрит, Эпикур, Лукреций объясняли характерные свойства атомов их стандартной формой и весом, ибо каждый атом набран из одинаковых точечных частиц-амер, уложенных чёткими рядами. Те же взгляды отстаивал М.В. Ломоносов. Говоря о стандарте формы и веса частиц данного типа, он предвосхитил даже открытие изотопов и изомеров: "Однородными я называю те корпускулы, которые равновелики и подобны по фигуре… они могут иметь некоторое несходство фигуры и неравенство, но настолько незначительные, что ими можно пренебречь и не принимать их во внимание при отыскании причины ощутительной разницы в сцеплении. Например, если масса одной корпускулы относится к массе другой, как 1000 к 999, а по отношению к фигуре – если две корпускулы обладают фигурой пирамиды, стоящей на квадратном основании, и одна имеет угол к основанию, равный 52° 31', а вторая 52° 30' [2]". Так же и Дж. Томсон, открывший электроны – атомы электричества, считал, что атомы и другие частицы образованы из тысяч электронов и противоположно заряженных частиц (позитронов), связанных в пары и образующих пространственные кристаллические комплексы [3].

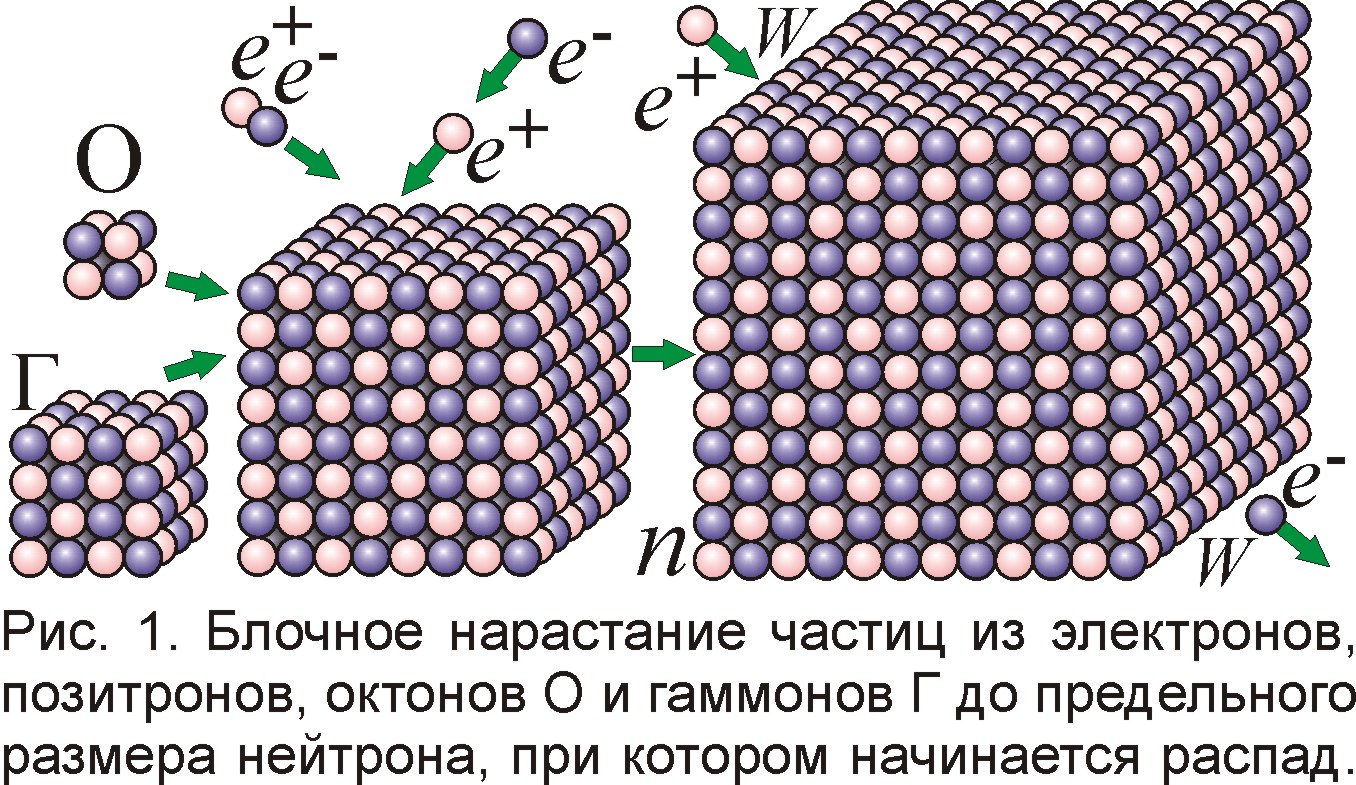
    То есть атомисты давно поняли, что идентичные свойства атомов, элементарных частиц обусловлены их правильным кристаллическим строением и сходством форм. Так и простые кристаллы обладают не только идентичными физическими, химическими, оптическими свойствами, но и равенством форм и углов граней. В россыпи кристаллов находим те же сотни близнецов, как среди стандартных атомов и частиц (например, протонов). Впрочем, у одних кристаллов шире одни грани, у других – другие, кристаллы можно вырастить разного веса и размера, а у элементарных частиц и ядер массы фиксированные. Казалось бы, раз их образуют позитроны e⁺ и электроны e^–, связанные кулоновскими силами в кристаллы (вроде кристаллов соли из ионов Na⁺ и Cl^–), то почему они растут лишь до фиксированного размера (рис. 1)? Дело в том, что при неком критическом размере частицы становятся нестабильными, подобно ядрам тяжелей урана, отсутствующим в природе. Тяжёлые ядра нестабильны по причине сильного кулоновского отталкивания их частей. Это верно и для элементарных частиц. Если частица устойчива, стабильна, то при выводе её из равновесия, скажем при делении от толчка, её части вновь слипнутся за счёт притяжения. А если частица нестабильна, то при её делении части улетают всё дальше за счёт отталкивания. С ролью устойчивости все знакомы с детства: когда строили башню из кубиков, та рушилась, достигнув характерного размера, по превышении которого теряла устойчивость. А потому в городке, возведённом ребёнком, все здания имеют ограниченный размер. То же видим и в мире частиц, где функцию гравитации, разрушающей слишком большие дома, выполняет слабое взаимодействие.

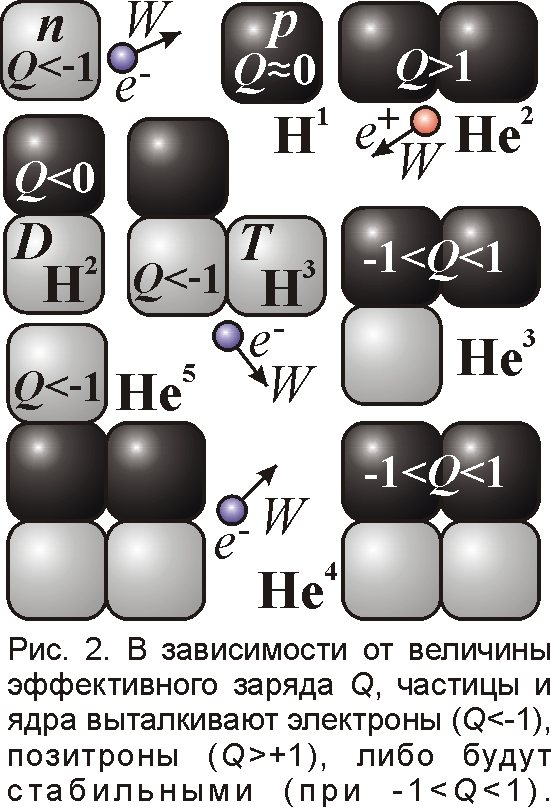
    Взять, к примеру, нейтрон n. Казалось бы, раз он нейтрален, его части не должны отталкиваться. Но если нейтрон содержит 920 электронов и 920 позитронов (в сумме образующих массу нейтрона ~1840), то они могут отталкиваться при малой асимметрии взаимодействий [4]. Так, если электрон отталкивает другой электрон с силой всего на 0,11 % большей силы F притяжения электрона к позитрону, то 920 электронов и 920 позитронов, образующих нейтрон, отторгают электрон с силой W=920F·0,0011=1,012F. Если один из электронов нейтрона отделится, то избыточный позитрон из оставшихся 920e⁺ и 919e^–, притягивая электрон с силой F, не сможет его удержать: сила отталкивания W=1,012F больше притяжения на 0,012F. То есть нейтрон нестабилен и распадается в среднем за 15 минут на протон и электрон (рис. 2). Ясно, почему масса нейтрона жёстко фиксирована. Если вес нейтральной частицы меньше, чем у нейтрона,– например 1820, и она содержит 910 электронов и 910 позитронов, то вылетевший электрон притянется назад с силой 910F–909·1,0011F=0,0001F. Поэтому нейтральная частица не теряет, а наращивает свою массу, притягивая всё новые позитроны и электроны, пока её масса не достигнет массы нейтрона, после чего частица начнёт распадаться (рис. 1). Тем более должна распадаться, и гораздо быстрее, более тяжёлая нейтральная частица, например Λ⁰-гиперон, с весом 2184 и временем жизни 2,6·10^–10 с.

    А почему же стабилен протон p с массой, почти как у нейтрона n? Просто заряд протона положителен (он содержит лишний позитрон, имея состав: 920e⁺ и 919e^–), и если его покинет электрон, то два избыточных позитрона притянут его назад с силой 920F–918·1,0011F=0,99F. У позитрона сила притяжения к электрону уже на 0,11 % больше силы отталкивания от другого позитрона [4]. Поэтому, если позитрон вдруг оторвётся от протона, то оставшаяся нейтральная система из 919 электронов и 919 позитронов притянет его с силой W=919·1,0011F–919F=1,011F. В этом причина стабильности протона и асимметрии нашего мира, где много протонов и электронов, но почти нет антипротонов и свободных позитронов. Все позитроны пребывают в связанном состоянии. Притянутые нейтральными частицами, они образуют стабильные положительные протоны и ядра. Зато электроны отталкиваются нейтральными частицами, то есть антипротоны, содержащие избыточный электрон,– нестабильны. Оттого так много свободных электронов. Физики-ядерщики не заметили нестабильности антипротона, поскольку не наблюдали его в течение секунд, необходимых для распада. Антипротоны, рождённые в ускорителях, летят с огромными скоростями и сразу гибнут в столкновениях с протонами, не прожив отпущенного им срока.

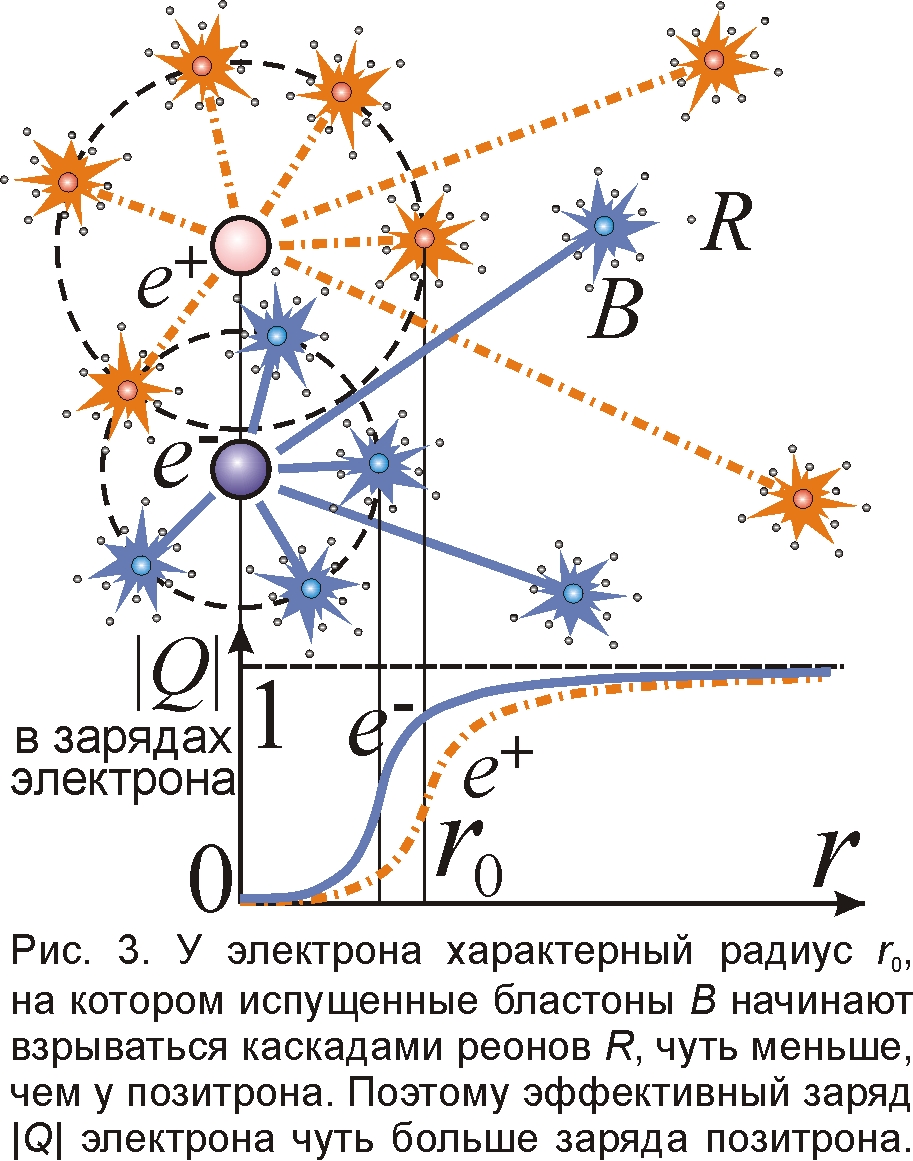
    Избыточные силы отталкивания электронов и притяжения позитронов нейтральными частицами называют силами слабого взаимодействия W, хотя они – обычные электрические силы, вызванные малой асимметрией воздействий и нарастающие вместе с массой частицы. Чем же обусловлена эта асимметрия? По баллистической теории Ритца [4], электрическое притяжение и отталкивание вызвано ударами микрочастиц – реонов R, выстреленных электронами, и ареонов, выстреленных позитронами (рис. 3). Тогда заряд – это полный поток материи от источника поля, то есть число испускаемых им частиц-реонов, пересекающих в единицу времени сферу, окружающую заряд. Напряжённость электрического поля – это плотность этого потока: число частиц, ежесекундно пронизывающих единичную площадку этой сферы. Полный поток частиц от электрона и позитрона одинаков: их заряды равны по модулю, но противоположны по знаку, поскольку электрон испускает материю (реоны), а позитрон – антиматерию (ареоны). Но это в случае, если размеры электрона и позитрона точечные. Реальный же их размер r₀ – порядка 10^–15 м: их заряд как бы размазан по сфере радиуса r₀. Это возможно, если электрон выбрасывает не отдельные реоны, а собранные в пачки-бластоны B, наподобие осколочных, кассетных снарядов, взрывающихся на расстоянии r₀ от электрона каскадами реонов (так и снаряд фейерверка выбрасывает осколки, вспыхивающие на отдалении сверкающей сферой). Но у электрона и позитрона радиус r₀ сферы распада бластонов может чуть разниться. То есть заряды электрона и позитрона "размазаны" в пределах сфер разных радиусов r₀. И на расстоянии порядка r₀=10^–15 м потоки, воздействия от электрона и от позитрона слегка разнятся, словно эффективный заряд Q электрона больше заряда позитрона на 0,11 % (эта оценка может быть исправлена при более точном анализе).

    Тогда нейтрон, где поровну электронов и позитронов, имеет минусовой эффективный заряд Q: его части отталкиваются, и он распадается, выбрасывая электрон. Зато протон, где позитронов на один больше, обладает почти нулевым эффективным зарядом Q: его части притягиваются, вот протон и стабилен. Так и в химии есть стабильные, стойкие соединения, а есть нестойкие. Скажем, водород из-за своей реактивности встречается лишь в связанном виде, подобно позитронам, запертым в протонах. Зато в природе много свободного кислорода, окутывающего Землю атмосферой, подобно атмосфере электронов вокруг атома. Также много ионов кислорода O^2– и водорода H⁺ связано вместе в молекулах воды, подобно электронам e^– и позитронам e⁺, связанным в пары, образующие океан элементарных частиц.

    Неравенство электрона и позитрона объясняет не только асимметрию мира, природу слабого взаимодействия и распада нейтрона, но и обретение им стабильности в ядрах. Так, соединив нейтрон с протоном, получим стабильное ядро дейтерия H², где нейтрон устойчив (рис. 2). Если электрон случайно отделится от ядра, то два избыточных позитрона притянут электрон с такой силой, что он снова упадёт на ядро (так и Λ⁰-гиперон обретает в ядре повышенную стабильность [5]: положительный заряд ядра удерживает электроны e^– и пионы π^– в гипероне). Если добавить к ядру дейтерия ещё нейтрон, то возникшее ядро трития H³ получит минусовой эффективный заряд Q<-1, который вытолкнет электрон из нейтрона. Но если добавить к тритию ещё протон, образовав ядро гелия He⁴, нейтрон снова стабилизуется.

    Если нейтрон обретает в ядре стабильность, то протон, напротив, может её утратить из-за отталкивания позитронов положительным ядром. Так, соединив два протона, получим нестабильное ядро гелия-2, которое тут же теряет один позитрон от распада протона, и становится ядром дейтерия (рис. 2). Но, дополнив два протона нейтроном, получим стабильное ядро гелия-3, поскольку добавочное притяжение W позитрона нейтроном не позволит ему улететь. Ещё стабильней ядро гелия-4 из двух протонов и нейтронов, крепко держащих позитроны в ядре. А положительный заряд двух протонов удерживает электроны в нейтронах, эффективно противостоя их отталкиванию W. Но если добавим к ядру ещё один нейтрон, то притяжение ядра He⁵ уже не сможет перебороть силу отталкивания W электрона пятью нуклонами. Так и у последующих элементов стабильность ядра определяется балансом сил электрического притяжения и отталкивания. Вот почему каждый элемент имеет лишь ограниченное число стабильных изотопов: заметное нарушение баланса сил, баланса нейтронов и протонов ведёт к отделению от ядра электронов или позитронов. Стабильны лишь те ядра, у которых, как у протона, эффективный заряд Q на поверхности близок к нулю, не превосходя по модулю единицу (за единичный заряд в ядерной физике принят заряд электрона). У нестабильных ядер эффективный заряд – около единицы и выше. Это объясняет, почему энергия электронов и позитронов, вылетающих из этих ядер, составляет порядка МэВ [6]: такова энергия взаимодействия E=e²/4πε₀r двух единичных зарядов e на расстоянии порядка радиуса ядра r≈10^–15 м. То есть примерно такую энергию и должно сообщать вылетевшему электрону или позитрону кулоновское отталкивание ядра с единичным эффективным зарядом Q.

    Точный расчёт значений Q и стабильности ядер сложен. Ведь их задаёт не только состав ядра, но и его геометрия, форма, так как кулоновские силы F спадают пропорционально квадрату расстояния, а силы W слабого взаимодействия убывают гораздо быстрее (оттого взаимодействие и названо слабым, что даже на расстоянии r₀ оно составляет лишь 0,11 % от кулоновского, а при отдалении вообще теряется на его фоне, становясь в миллиарды раз слабее [6]). Асимметрия элементарных сил притяжения и отталкивания быстро исчезает по мере отдаления: силы выравниваются. Ведь на некотором удалении взорвутся уже все испущенные бластоны, и полные потоки частиц от электрона и позитрона сравняются и перестанут меняться с расстоянием (рис. 3). Вот почему уже на атомных масштабах эта асимметрия не заметна, нейтрон не воздействует на заряды (его эффективный заряд Q обнуляется), а эффективный заряд протона вырастает до единицы. Лишь на расстояниях порядка ядерных эта асимметрия существенна, и потому очень важно взаимное расположение нуклонов в ядре. Чем ближе протоны к нейтрону, тем больше кулоновская сила F, удерживающая там электрон, но ещё быстрей растёт отталкивающая сила W. А нейтроны, чем ближе к протону, тем крепче удерживают в нём позитрон, отталкиваемый другими протонами. То есть размещение нуклонов, особенно во внешних слоях ядра, сильно влияет на его устойчивость. Вот почему есть ядра-изомеры, имеющие одинаковый протон-нейтронный состав, но отличающиеся стабильностью и периодом полураспада из-за различной формы, геометрии ядра [6-9].

    Геометрия частиц объясняет и то, почему энергия электронов, вылетающих при бета-распаде ядер и нейтронов, не постоянна, а образует непрерывный спектр. Просто электроны отделяются от разных участков ядер и нейтронов. Так, если нейтрон имеет форму кубика, то нужна разная энергия, чтобы отщепить от него частицу из уголка-вершины, из ребра, или из грани. С изменением расстояния до центра кубика меняется и отталкивающая сила, разгоняющая электроны до разных энергий, вплоть до некого предельного значения. Ещё больше вариантов отделения электрона в ядре, имеющем сложную форму. То есть сплошной спектр энергий электрона получается без гипотезы о нейтрино, якобы уносящем часть энергии электрона. Ведь если электрон отделяется от разных участков ядра, забирая разную энергию, то и оставшаяся в ядрах энергия различна: ядра остаются в возбуждённом состоянии. Когда ядра перестраиваются в состояние с наименьшей энергией, эта избыточная энергия выделяется в виде гамма-излучения, имеющего высокую проникающую способность. Возможно, это гамма-излучение и принимают за нейтринное излучение бета-распадов [6].

    Итак, ядра из начала таблицы Менделеева распадаются в основном за счёт отделения электронов и позитронов. А ядра из конца таблицы распадаются на два ядра под действием сил кулоновского отталкивания. При этом образуются ядра из середины таблицы Менделеева, либо отделяется ядро гелия, оставив ядро с зарядом и номером на две единицы меньше исходного. А порой из ядер вылетают и отдельные протоны (ядра водорода), либо нейтроны, порой связанные в пары [6]. Есть и ряд стабильных, устойчивых ядер. Такая устойчивость при размерах много больше, чем у нейтрона, объясняется так же, как устойчивость зданий из кубиков, если складывать их не один на другой, а пирамидой, увеличив площадь основания. Тогда высоту башен можно значительно увеличивать. Именно такие пирамиды, сложенные из кубиков-нуклонов, и представляют собой ядра атомов по гипотезе В. Мантурова [7, 8].

    Деление ядер происходит, когда кулоновские силы отталкивания превысят ядерные силы притяжения частей ядра. Ядерные силы тоже имеют электростатическую природу и обусловлены периодичным кристаллическим строением частиц-нуклонов – протонов и нейтронов [7-10]. Образующие их электроны и позитроны, расположенные в шахматном порядке, встают друг против друга, когда нуклоны касаются гранями. Электроны и позитроны, выстроенные правильными рядами и обменивающиеся выстрелами реонов и ареонов (словно батареи пушек двух галионов перед сцеплением в абордажном бою), и порождают ядерные силы H сцепления двух нуклонов (рис. 4). Именно это позволяет протону удерживать возле себя незаряженный нейтрон и одноимённо заряженный протон. Та же сила связывает вместе два нейтрона, несмотря на их нейтральность. Эта ядерная связь напоминает водородную связь молекул воды, которые хоть и нейтральны, тоже слипаются. Просто молекула воды, содержащая положительные ионы H⁺ и отрицательный ион O^2–,– это электрический диполь, который одним концом притягивает молекулы H₂O за ионы водорода, а другим – за ионы кислорода. Именно эти водородные связи выстраивают молекулы воды в изящные ледяные кристаллы снежинок. Так и ядерные силы взаимодействия нуклонов выстраивают их в чёткие кристаллы ядер. Странно, что физики, построив капельную модель ядра на этой аналогии ядерных сил и сил сцепления (когезии) молекул воды [5], не осознали, что ядерные силы вызваны притяжением электрических диполей из электронов и позитронов, образующих элементарные частицы. И лишь В. Мантуров объяснил на этой основе все особенности ядерных сил [7]. Так, у молекул воды притяжение заметно лишь на расстоянии порядка размера молекулы-диполя и быстро спадает с удалением. В этом же причина короткодействия и насыщения ядерных сил: каждый нуклон притягивает лишь ближайших, смежных соседей.

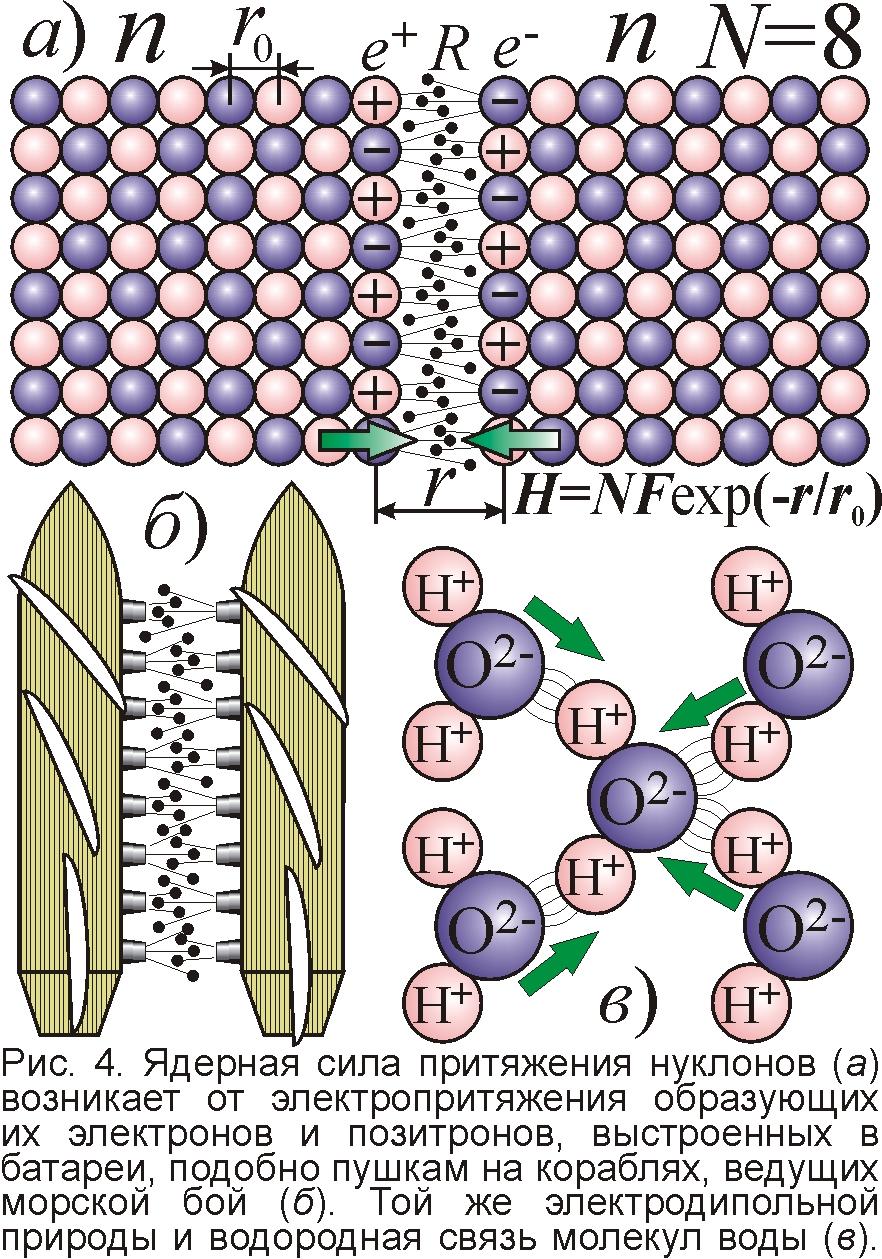
    Это объясняет огромную величину ядерных сил, способных удержать вместе два протона и более. На расстоянии r близком к радиусу r₀ электрона сила H связи двух граней, образованных из N электронов и позитронов, составляет порядка NF=Ne²/4πε₀r² и экспоненциально спадает с удалением граней [8]. Поэтому сила H эффективно противостоит кулоновскому отталкиванию двух протонов F=e²/4πε₀r², даже при дистанции меж ними порядка 5r₀. Ведь если протон составлен из 1836 электронов и позитронов, образующих кубик с габаритами примерно 12x12x12 частиц, то каждая грань содержит N≈12x12=144 частицы. Почти во столько раз (на два порядка) ядерные силы интенсивней кулоновских, как показал опыт. Значит, ядерная энергия – это обычная энергия электровзаимодействия. При соединении, синтезе ядер выделяется электростатическая энергия притяжения граней нуклонов, а если ядра делятся, то выделяется электростатическая энергия отталкивания заряженных ядер. Кулоново отталкивание и разгоняет ядра, придавая им энергию в ядерных взрывах и реакторах [10].

    Раз ядерная энергия электрической природы, то почему же нам внушают, что энергия образуется из массы M по формуле E=Mc²? Оказывается, Эйнштейн ложно истолковал смысл этой классической формулы, найденной задолго до него Дж. Томсоном [3], Лоренцем и Хевисайдом. В теории относительности формула стала выражать эквивалентность массы и энергии, словно тело с ростом скорости и энергии наращивает массу. На деле же формула E=Mc² выражает лишь связь электромагнитной энергии E и так называемой электромагнитной массы M: вот откуда множитель c² – квадрат скорости электрических воздействий. Ещё Лоренц показал, что инертная масса M электрона может быть электромагнитной природы: при ускорении a одноимённо заряженные части электрона (рис. 5.а), неодинаково отталкивая друг друга, порождают тормозящую, инертную силу F_эм=Ma [11, 12]. Отсюда нашли классический радиус электрона r₀=e²/4πε₀Mc², задающий его массу M, размер нуклонов, ядер и радиус действия ядерных сил. А энергия, выделяемая при сближении электрона и позитрона до расстояния r₀,– это энергия их электровзаимодействия E=e²/4πε₀r₀=Mc², а не энергия "аннигиляции материи" [7, 10-12]. Частицы не исчезли, а слились в нейтральную пару из двух сцепленных противоположностей, как в знаке Инь и Ян (рис. 5.в). Но электромагнитная масса такой пары и впрямь снизится на величину ΔM, пропорциональную выделенной энергии E, ведь при ускорении системы e⁺e^– разница сил притяжения разноимённых зарядов уже не тормозит, а толкает пару в сторону ускорения, занижая величину инертной массы пары [11].

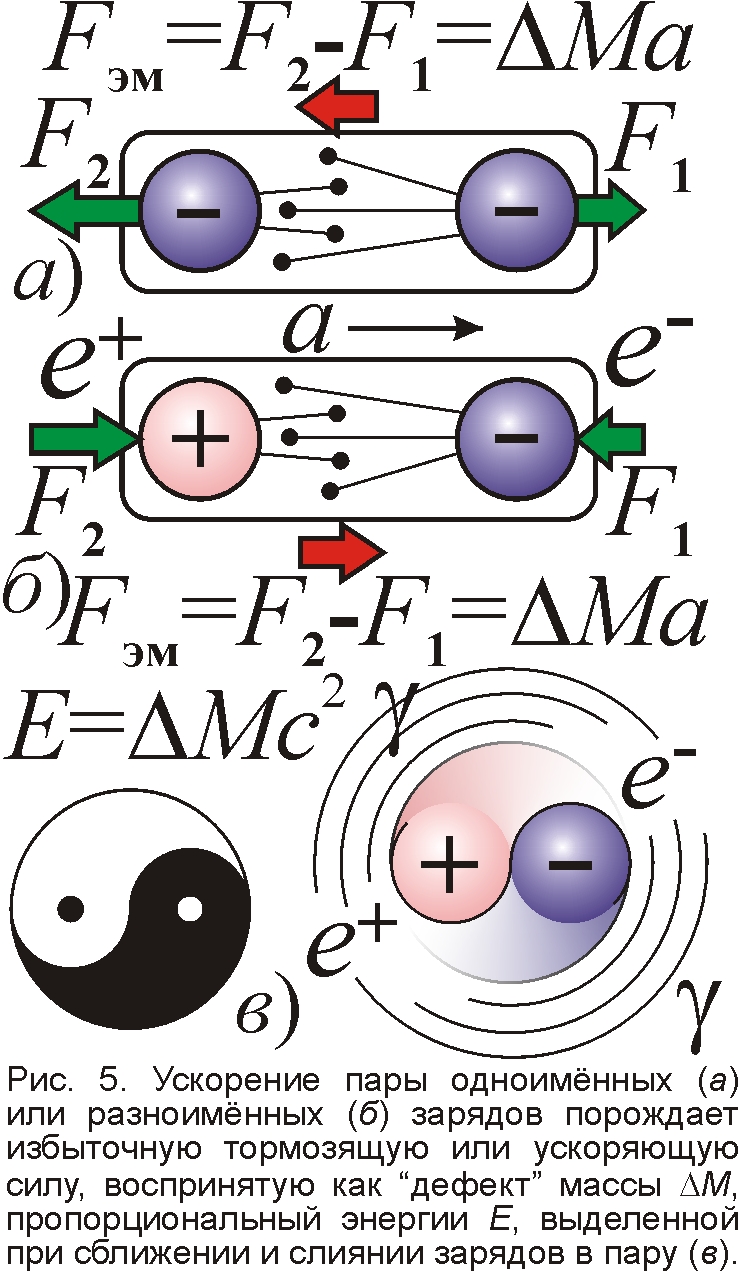
    Это объясняет, почему при слиянии двух ядер, скажем дейтерия, масса возникшего ядра меньше суммы масс исходных, а "пропавшая" масса ΔM (дефект массы) пропорциональна выделенной энергии E=ΔMc². Всё дело в электромагнитной массе. Когда два ядра соединятся гранями своих нуклонов, так что электроны одной грани встанут рядом с позитронами другой (рис. 4), то притяжение разноимённых зарядов двух ядер породит небольшую силу F_эм=ΔMa, толкающую ядро в сторону ускорения и вызывающую мнимое снижение его инертной массы на ΔM (рис. 5.б). Дефект масс именно мнимый, поскольку на деле в реакции количество материи не менялось: число нуклонов, электронов и позитронов сохранилось. А "дефект массы" ΔM и впрямь связан с выделяемой в реакции электростатической энергией E=ΔMc², поскольку сближение зарядов произошло до расстояния r порядка радиуса электрона r₀. То есть масса, как мера количества материи, не исчезала, а выделившаяся энергия – это не энергия уничтожения массы, а электростатическая энергия взаимодействия зарядов. Такие классики электродинамики как Томсон, Лоренц, Хевисайд, Ритц прекрасно это понимали, когда выводили формулу E=ΔMc², применимую лишь к электромагнитной массе и энергии. "Заслуга" же Эйнштейна лишь в том, что он "приватизировал" эту формулу, извратив её смысл и подстроив под свою теорию относительности. Не зря Резерфорд, которому мы обязаны открытием ядерных реакций, изучал их без помощи СТО, считая её бессмысленной и бесполезной. О том же говорил и руководитель Резерфорда Дж. Томсон, поддержавший баллистическую теорию Ритца [3]. Да и сам Резерфорд первым применил в ядерной физике баллистическую аналогию, уподобив вылетающие при распадах частицы и ядра снарядам. Ядра гелия, выстреленные атомами, совсем как ядра из пушек, бьют по мишеням-атомам. Хоть масса элементарных частиц и ядер мала [13], но их скорости огромны, так что сравнение частиц со снарядами не только естественно, но и зримо, если вспомнить гигантскую энергию ядерного взрыва, по сути, кинетическую энергию разлетающихся микрочастиц.

    Выходит, все успехи ядерной физики связаны исключительно с применением классической формулы E=ΔMc², но никак не с теорией относительности или квантовой механикой, которые до сих пор не объяснили толком, из чего состоят элементарные частицы, почему их масса, заряд и другие характеристики именно такие, а не иные. Кванторелятивистские теории, вопреки распространённому мнению [13], не объясняют микромир, а дают лишь формальное и неполное описание уже известного [5]. Зато баллистическая теория предлагает механическое объяснение всех феноменов и загадок микромира, включая стабильность частиц. Частицы, ядра, атомы, молекулы устойчивы по той же причине, по какой не разрушаются при ударах модели молекул из шариков химического набора: прочность связи частиц больше сил ударов, но если её превысить, частицы делятся: квантовые законы здесь ни при чём. Такую условную неделимость атомов принимали, видимо, и древние атомисты, раз считали атом состоящим из ещё меньших частиц-амер, отделить которые проблематично.

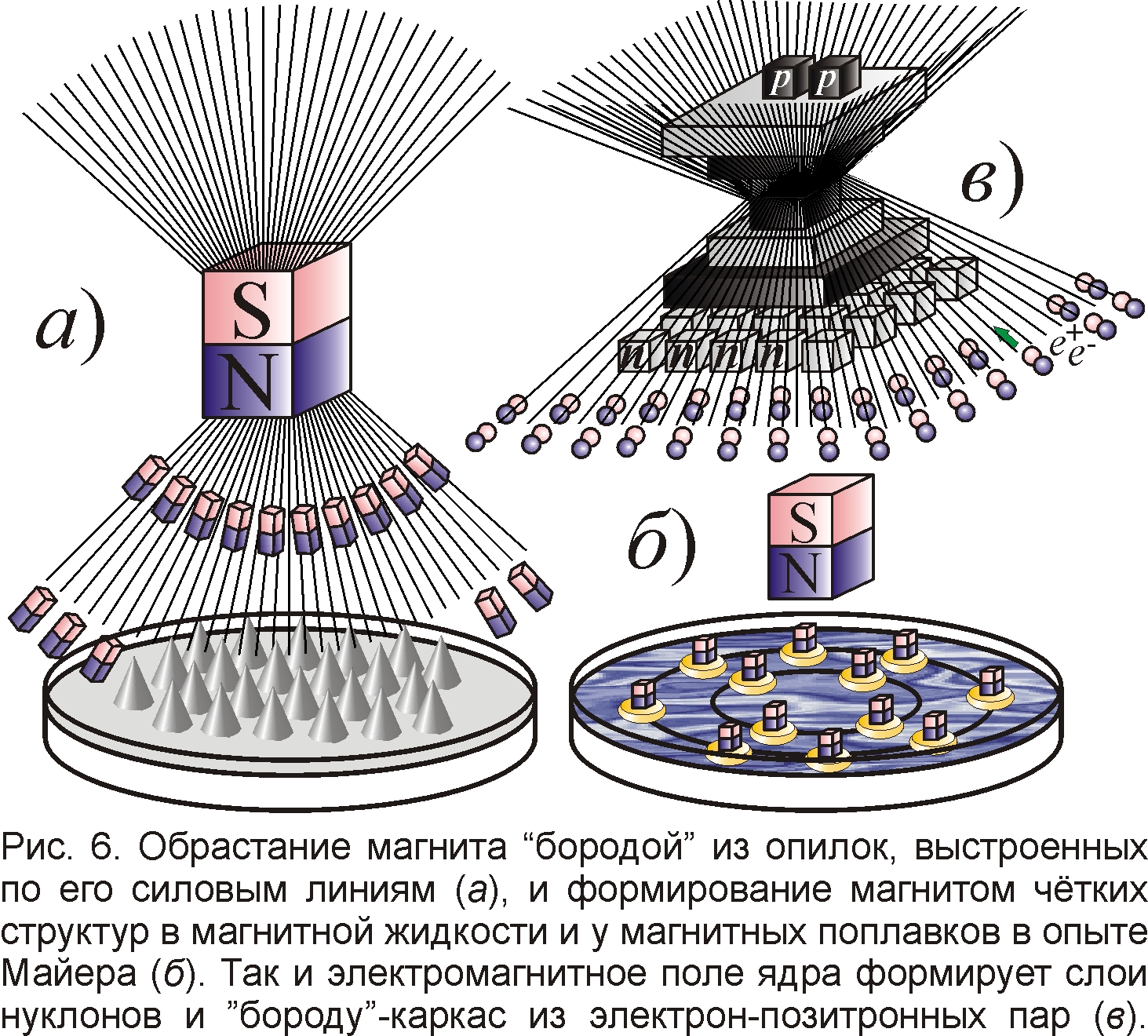
    Итак, выполнение в ядерных реакциях электродинамической формулы E=ΔMc² доказывает не теорию относительности, а электрическую природу ядерных сил и энергий E, а дефект масс ΔM обусловлен не собственной массой ядер, а электромагнитной массой от взаимодействия их частей. Малость дефекта масс доказывает, что он связан именно со способом измерения массы – это дефект весов, а материя сохраняется. Впрочем, есть и реакции типа распада пионов, мюонов, где "теряется" заметная или вся масса [9-12]. Но и здесь потеря массы мнимая, если её уносят нейтральные, трудноуловимые частицы. Эта идея привлекалась ещё Ван-ден-Бруком и Ридбергом для объяснения дефекта масс ядер [10], но, похоже, главная причина всё же во взаимодействии электрон-позитронных решёток ядер, а добавочная масса ядерного каркаса не существенна. Сам же бипирамидальный ядерный каркас явно существует. Если он и не вносит заметного вклада в массу ядер, то играет важную роль в формировании нуклонных слоёв [8, 9]. Эти слои, поочерёдно заполненные протонами и нейтронами (рис. 6, 7), реально выявлены в виде неоднородностей ядра [5]. Образован же ядерный каркас электрон-позитронными парами, потерявшими вес от взаимодействия (рис. 5.в).

    В виде ответа на вопрос о формировании ядерного каркаса [13] можно привести опыт Майера с плавающими в воде магнитами. Вокруг большого магнита магнитные поплавки собираются в стандартные конфигурации в виде многоугольников, расположенных оболочками (рис. 6). Уже Дж. Томсон приводил этот опыт в качестве иллюстрации формирования стандартных электронных оболочек атома [3]. Так же и нуклоны образуют чёткие последовательные слои с заданным числом частиц в слоях. Ядро своим электромагнитным полем кристаллизует вокруг себя бипирамидальный каркас из витающих вокруг электрон-позитронных пар. Аналогично магнит, помещённый под стекло или в жидкость с железными опилками, формирует на полюсах две конических "бороды" из опилок, напоминающих два раструба-пирамиды ядра. Заряженные протоны стремятся расположиться возможно дальше друг от друга и потому симметрично заполняют оба раструба. Под действием ядерных сил частицы, словно атомы кристаллов, выстраиваются в чёткие прямоугольные и квадратные слои, а потому вместо двойного конуса формируется двойная пирамида. В свою очередь бипирамидальный каркас влияет на размещение нуклонов, отчего те кристаллизуются расширяющимися слоями, словно ярусы сосны или ёлки, выросшие из конической шишки-каркаса и заключённого в ней семени-ядра. Так и ядерный каркас вырастает далеко за пределы ядра, задавая и слоистую бипирамидальную структуру электронных слоёв. Образование периодичных решёток не раз наблюдали в опытах с магнитами, скажем при воздействии на магнитную жидкость, или в сверхпроводнике в виде кристаллической решётки абрикосовских вихрей магнитного порошка. То, что частицы в ядре расположены упорядоченно, занимая всегда одни и те же положения, заданные масштабом кристаллической решётки ядерного каркаса, подтверждают и стандартные гамма-спектры возбуждённых ядер. Фиксированные частоты этих спектров заданы собственными частотами колебаний заряженных частиц ядра (электронов и протонов) в его магнитном поле, обладающем в каждом узле решётки характерным значением. Так же и магнитные поплавки в опыте Майера при малом отклонении колеблются каждый со своей стандартной частотой. Этот магнитный механизм Дж. Томсон и В. Ритц приводили в качестве модели, объяснявшей стандартные спектры атомных частот [3, 8].

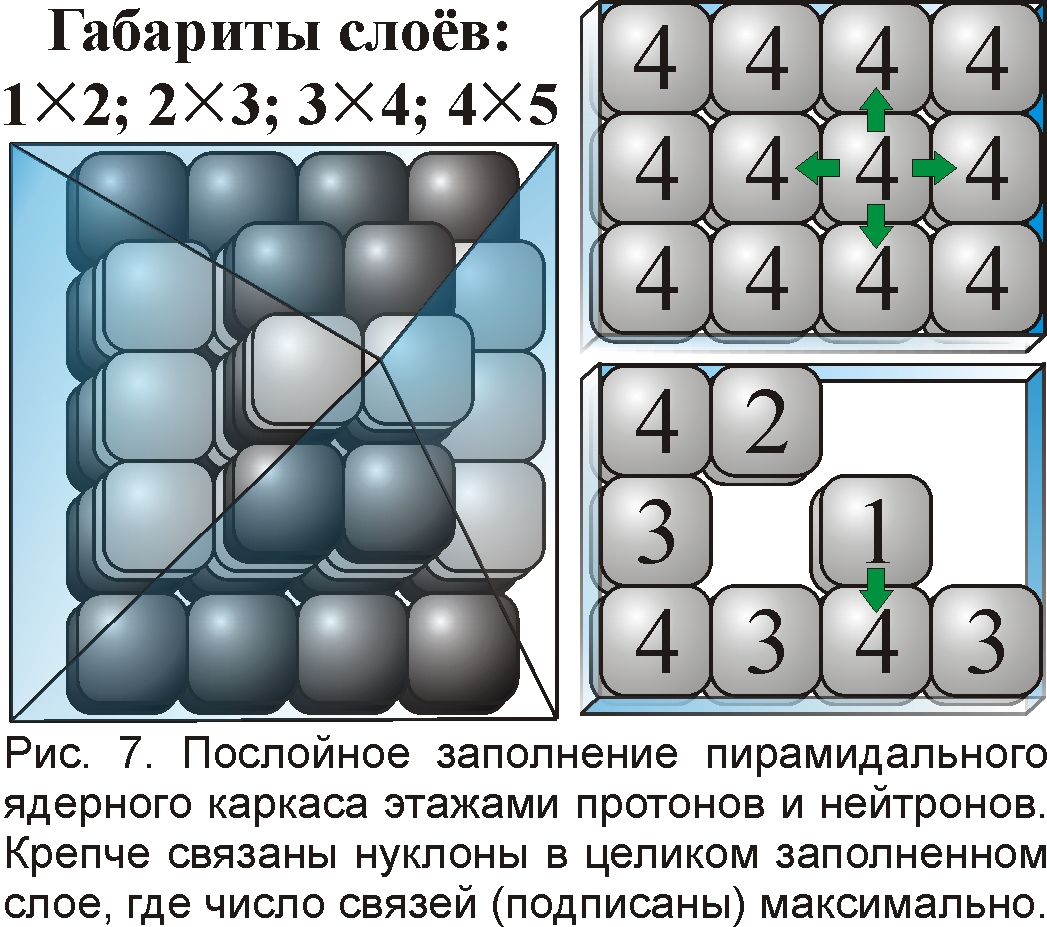
    Электрическая природа ядерной энергии позволяет понять, почему наиболее прочны и стабильны ядра с магическими числами нуклонов, и почему при их синтезе получаются наибольшие энергии и "дефекты масс" [8, 9]. Когда протоны и нейтроны составляют плотные упаковки с наименьшей поверхностью, то число связей N каждого нуклона максимально (рис. 7). Такие ядра наиболее прочны и стабильны: нуклоны в них крепко связаны, образуя целиком укомплектованные нуклонные слои, не имеющие выступов и зазоров, с минимальной свободной поверхностью и максимальной поверхностью контакта, пропорциональной общему числу связей N, которое наращивает энергию ядерных связей H=NF и "дефект" массы. Оттого у магических ядер, где таких связей больше всего, велики дефекты масс и выделяемые энергии, а также прочности. Примерно так, оконный проём, заложенный кирпичами, трудней всего пробить, если кирпичи заполняют его целиком, поскольку каждый кирпич крепко зажат, и со всех сторон связан цементом (площадь контакта максимальна). Но если кладка выщерблена, и не хватает всего одного кирпича, сломать её много проще. Кстати, ещё Ломоносов показал, что элементарные частицы сцеплены тем прочней, чем больше площадь контакта их граней, а силы их сцепления объяснял давлением, ударами микрочастиц [2].

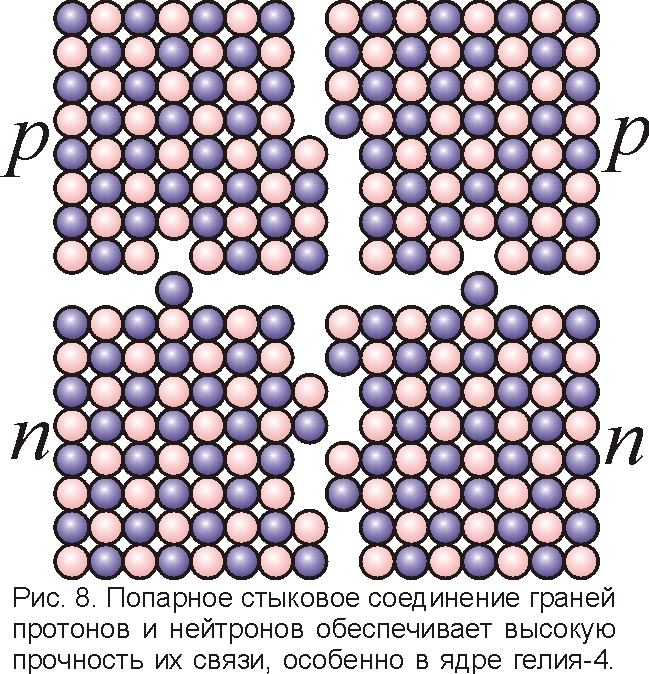
    Итак, правильная форма нуклонов и завершённых нуклонных слоёв максимизирует энергию связи и объясняет их высокую стабильность. В этом же причина устойчивости ядер с чётным числом протонов и нейтронов, имеющих, вероятно, форму не совсем идеальных кубиков, а с микро-выступами и впадинами на гранях, что ещё крепче связывает их друг с другом, наподобие шипового соединения деревянных деталей (рис. 8). Выступы одного нейтрона попадают в пазы другого. То же и у протонов, снабжённых выступами иной формы. При этом растёт площадь контакта, число N связей и их общая сила H=NF, а электроны и позитроны на этих выступах теряют способность легко отрываться, будучи зажаты меж нуклонами. Это объясняет, почему протоны и нейтроны соединяются попарно, почему они образуют отдельные слои, обладающие повышенной прочностью. У протонов могут быть и выступы для стыковки с нейтронами. Так что два протона и два нейтрона могут сцепиться, наподобие 4-х паззлов с эмблемы "Microsoft Office", формируя ровный квадрат с минимальной поверхностью, лишённый выступов, с которых обычно "выпрыгивают" электроны и позитроны, а потому обладающий наибольшей энергией связи, прочностью и наименьшей массой. Не зря такие сочетания двух протонов и двух нейтронов, образующих ядро гелия-4,– самые прочные и сохраняют эту связь даже внутри более крупных ядер, отделяясь при распаде как одно целое, в виде альфа-частицы (рис. 9). Наличие выступов и впадин на кубе нуклона понятно, если его образуют не только 27=3x3x3 кубиков-гаммонов Г, но и 6 частиц-октонов O (рис. 1), формирующих наслоения на его гранях [9]. Итак, у нуклонов, где каждому электрону отвечает свой позитрон, связь устроена по принципу "электромагнитный ключ-замок", давно открытому в структурной химии. Именно так попарно сцеплены электростатическими силами и цепочки нуклеотидов в молекуле ДНК, подходящие друг другу по форме.

    Изучим теперь роль формы и "дефекта масс" на примере нейтрона (схематично изображённого на рис. 10), с его массой в 1838,6 масс электрона. Почему при отрыве электрона от нейтрона возникает протон с массой 1836,1 электронных? Казалось бы, раз отделился всего один электрон, масса должна снизиться на единицу (до 1837,6), а она падает на 2,5 масс электрона. На деле инертная масса уменьшается не только за счёт удаления электрона, но и за счёт того, что он перестал взаимодействовать с электронами и позитронами, образующими нейтрон. В сумме это взаимодействие отталкивающее (рис. 1), то есть завышает инертную массу нейтрона (рис. 5.а). Значит, электрон вносит в нейтрон, кроме собственной инертной массы, добавочную электромагнитную массу ΔM, вызванную его взаимодействием с элементами нейтрона. А при распаде масса нейтрона снижается и на единичную массу электрона, и на вызванную им электромагнитную добавку массы. Так и в электроцепи энергия E=Cu²/2 и общая ёмкость C складывается не только из собственных энергий и ёмкостей конденсаторов, но также из малых взаимных энергий и ёмкостей ΔC (называемых ещё паразитными), обусловленных взаимодействием обкладок каждого конденсатора с другими. Извлечение одного заряженного конденсатора единичной ёмкости снижает общую энергию и ёмкость цепи больше, чем на единицу. Эта энергия взаимодействия, исчезающая при отделении конденсатора, выделяется в виде его кинетической энергии и тепла, причём она пропорциональна "исчезнувшей" паразитной ёмкости ΔC. Здесь ёмкость C – это точный аналог массы M.

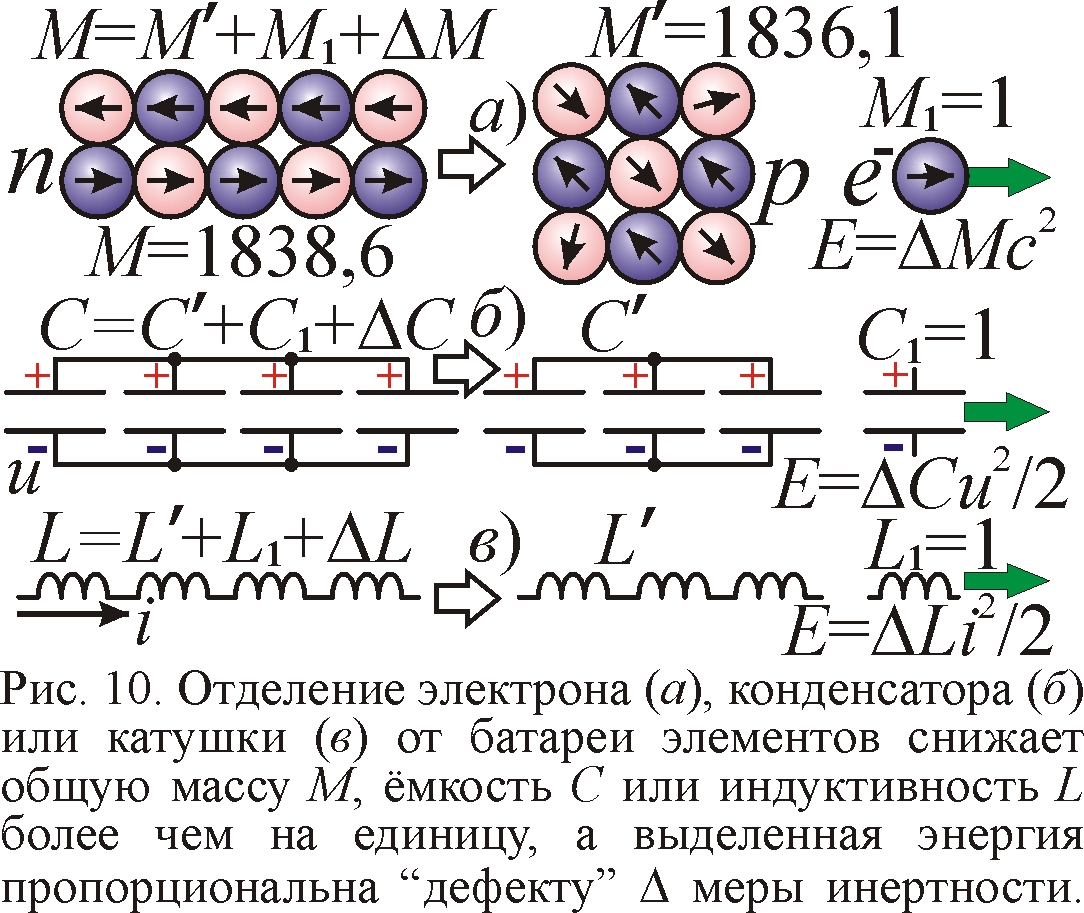
    То же верно и для цепи, где общая индуктивность L складывается из собственных и взаимных индуктивностей катушек, а полная энергия цепи E=Li²/2 включает в себя и энергию взаимодействия катушек, которая пропорциональна паразитной индуктивности ΔL и выделяется при удалении одной из катушек. Не зря инерционную роль ёмкости C и индуктивности L в колебательном контуре всегда сравнивали с ролью массы M груза, колеблющегося на пружине. При отделении электрона от нейтрона, тот, став протоном, меняет вдобавок и форму, и энергию взаимодействия образующих его электронов и позитронов, а значит и вызванную этим взаимодействием энергию и электромагнитную добавку массы (аналогично, удаление конденсатора или катушки меняет распределение напряжений u и токов i в цепи). То, что нейтрон, став протоном, перестраивает структуру, видно из того, что их магнитные моменты отличаются в 1,5 раза. То есть разнятся распределения электронов и позитронов, ориентации их магнитных моментов, в сумме дающих магнитный момент нуклона (рис. 10).

    Как известно, магнитный момент электрона примерно в тысячу раз больше момента протона и нейтрона, что вызвано взаимной компенсацией магнитных моментов электронов и позитронов [10]. Малейший сдвиг электронов и позитронов в кристаллической решётке нуклона, а тем более удаление одного из них, заметно меняет этот баланс, даже если электроны и позитроны сместятся или повернутся на ничтожную величину. То, что нуклоны состоят из сотен электронов и позитронов, магнитные моменты которых скомпенсированы, подтверждает открытие больших магнитных полей нуклона в момент разрушения (когда разделяются его части, нейтрализующие магнетизм друг друга, см. "Инженер" 2009, №2, с. 4), а также рассеяние нейтронов ферромагнитными образцами, где выявлено "намагничивание" нейтронов [7]. Внешнее поле ориентирует сонаправленно магнитные моменты электронов и позитронов, образующих нейтрон, отчего тот заметно наращивает магнитный момент. Именно так кусок железа, обладающий ничтожным магнетизмом, намагничивается внешним полем, поскольку магнитные моменты атомов, обычно нейтрализующие друг друга, устанавливаются параллельно. Но со временем намагниченность исчезает за счёт теплового колебания атомов железа, хаотизирующего их магнитные моменты. Так же рассогласуются в нейтроне и магнитные моменты электронов, позитронов, колеблющихся под ударами реонов.

    Те же удары реонов вызывают распады ядер и частиц. Ведь под ударами реонов электроны и позитроны колеблются, словно ионы в кристалле соли. Это "тепловое" дрожание частиц напоминает квантовую неопределённость их положений, но имеет классическую природу. Подобные тепловые колебания атомов, ядер и электронов под действием ударов микрочастиц, снующих со скоростью света, приводились Максвеллом и Пуанкаре в качестве аргумента против теорий Лесажа и Ритца [14]. Но, если размер реонов мал, эти колебания тоже малы, ввиду усреднения ударов. К тому же электрон под ударами реонов не наращивает свои "тепловые" колебания бесконечно, ибо не только поглощает вместе с реонами энергию, но и столько же отдаёт, когда испускает их обратно. Зато "тепловые" колебания электронов под ударами микрочастиц легко объясняют ядерные распады, как показал ещё Дж. Томсон [3], и "туннельный эффект", путём классической трактовки принципа неопределённости [10].

    "Неопределённость", "случайность", "спонтанность" ядерных распадов – это вещь мнимая и носит классический вероятностный характер. Распады строго детерминированы, предопределены. Так, если выстроить на полу много однотипных домиков-пирамид из карт или кубиков, то они тоже будут, один за другим, разваливаться,– казалось бы, спонтанно, в случайные моменты, по тому же экспоненциальному закону, что и ядра. Но реально каждый распад домика или ядра связан с внешними воздействиями (вибрациями, порывами ветра реонов), носящими случайный характер и, в момент сильных всплесков-флуктуаций (превышающих прочность домика или ядра),– разрушающими его. Более прочные типы домов имеют большее время жизни и период "полураспада", и в спокойной обстановке простоят столетия, но всё равно однажды рухнут от редких, но сильных флуктуаций в виде землетрясений, ураганов и т.п. Так же и ядра подвержены "случайным" ударам судьбы (самые прочные ядра ждут рокового случайного толчка миллиарды лет), и элементарные частицы распадаются под ударами реонов и ареонов в момент превышения предела прочности частицы. Причём распадаются не только нестабильные частицы с массой большей массы нейтрона, но и частицы-мезоны, масса которых ниже. Ведь чем меньше частица, тем меньше в ней связей N, тем проще их разорвать. И даже сами электроны, позитроны и бластоны выбрасывают реоны и ареоны в ходе распада под ударами реонов и ареонов, налетающих со всех сторон.

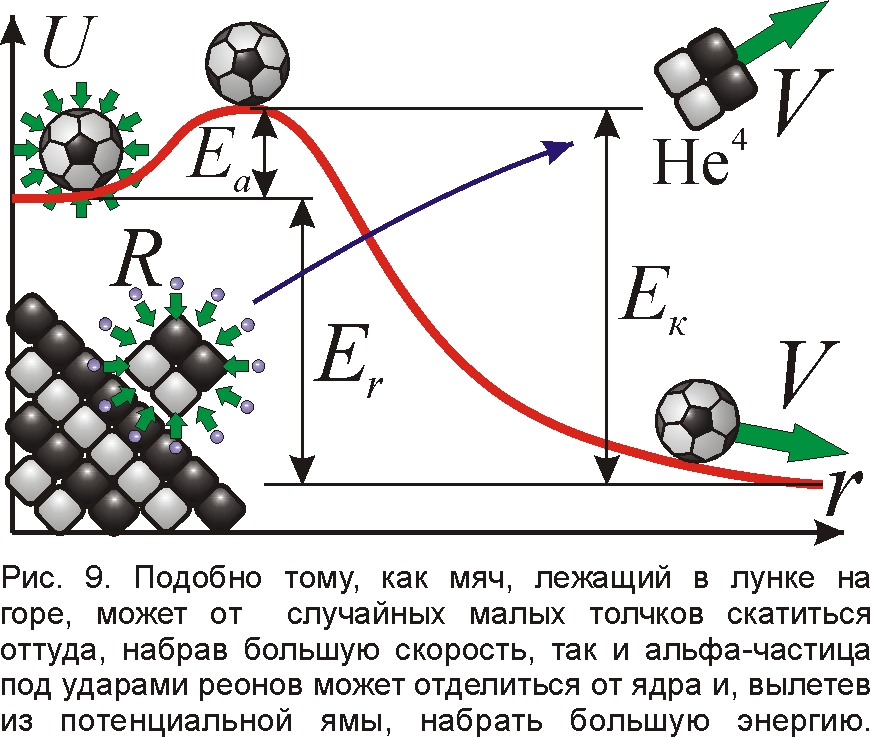
    Той же природы и "туннельный" эффект в альфа-распаде. Вылетающую α-частицу ни к чему считать волной, вводя неопределённость её положения и энергии в ядре. Необходимую для отрыва энергию активации α-частице сообщают случайные удары реонов, вынуждающие части ядра дёргаться, наподобие броуновских частиц. Так и в химических реакциях энергию активации молекулам обычно сообщают случайные удары атомов, вызывающие тепловые колебания молекул, временами их разрывающие. Подобные тепловые колебания частиц под ударами реонов, предсказанные Ритцем [14], сообщают энергию активации и ядерным реакциям распада. Когда совокупная энергия ударов превысит энергию активации E_a, α-частица оторвётся и дальнейший её разгон произведёт кулоновская сила, отдающая потенциальную энергию E_к. Ядро, вылетающее из потенциальной ямы под действием случайных ударов, напоминает поведение мяча, лежащего в неглубокой лунке на горе и в "случайный" момент времени слетающего с горы под действием "хаотичных" порывов ветра (рис. 9). По законам статистики вероятность P получения ядром в единицу времени энергии активации резко убывает с ростом этой энергии P~exp(–E_a/E₀). Это напоминает максвелловское распределение, где роль средней тепловой энергии kT атомов играет средняя энергия реонов E₀. Если энергия активации E_a велика, то распады происходят крайне редко: ядра имеют большой период полураспада T_1/2~1/P~exp(E_a/E₀). Поскольку для ядер с близкими зарядами кулоновская энергия E_к почти одинакова [6, 10], то при снижении энергии активации E_a выделяемая в реакции энергия E_r=E_к–E_a, полученная альфа-частицей, растёт. Ничтожный прирост энергии α-частиц от уменьшения E_a вызовет сильное снижение периода полураспада T_1/2. Тем самым нашёл простое классическое объяснение экспериментально открытый закон Гейгера-Неттола T_1/2~exp(D/E_r^1/2), без привлечения квантовой теории α-распадов Гамова [6].

    Таким образом, как верно отмечали древние атомисты, во главе с Демокритом, в мире всё закономерно, подчинено строгому порядку. Распады лишь кажутся хаотичными, происходящими в случайный момент времени у случайных ядер. Реально же моменты распада и жертвы распада, заранее предопределены и даже предсказуемы, если знать распределение реонов. Примерно так и "хаотичное" движение броуновских пылинок вызвано, по Демокриту, ударами атомов, а значит тоже предсказуемо, если знать распределение атомов и их скоростей. Так что, вопреки квантовой механике, в микромире царит такой же строгий порядок и детерминизм, как в механике нашего обыденного мира. Лишь незнание природы и условий распадов, а также их статистический характер рождает иллюзию случайности. Но последовательное применение классической физики позволяет навести порядок и в микромире.

1. Мюллер М. Шесть систем индийской философии. М.: Искусство, 1995.
2. Ломоносов М.В. Избранные философские произведения. М., 1950.
3. Томсон Дж. Дж. Электричество и материя. М.-Л.: ОГИЗ, 1928.
4. Семиков С. Альтернативная электродинамика // Инженер. 2009. №№8-9.
5. Черногорова В.А. Беседы об атомном ядре. М.: Молодая гвардия, 1976.
6. Сивухин Д.В. Атомная и ядерная физика. Ч. 2. М.: Наука, 1989.
7. Мантуров В.В. От кристаллических нуклонов и ядер к разгадке распределения простых чисел. М., 2007.
8. Семиков С. Атомный кристалл-пирамида // Инженер. 2009. №3.
9. Семиков С. Геометрия – ключ к микромиру // Инженер. 2008. №2.
10. Семиков С. Ядерная энергия и структура частиц // Инженер. 2010. №№4-5.
11. Семиков С. О природе массы и времени // Инженер. 2006. №5.
12. Семиков С. Масса и строение частиц // Инженер. 2006. №11.
13. Подольный Е. Судный день для Альберта Эйнштейна // Инженер. 2011. №2.
14. Роузвер Н.Т. Перигелий Меркурия от Леверье до Эйнштейна. М.: Мир, 1985.

Дата установки: 01.08.2011
[вернуться к содержанию сайта]

W