[вернуться к содержанию сайта]

МАГНИТНЫЙ КЛЮЧ К МИКРОМИРУ

    Атом давно считают открытой книгой: якобы все загадки микромира уже решены и строение атомов и субатомных частиц известно [2]. Но в последние годы обнаружен ряд явлений, в корне противоречащих представлениям об устройстве атомов и элементарных частиц [3]. Так, обнаружен ряд аномалий при рассеянии высокоэнергичных протонов. Открыты высокотемпературные сверхпроводники среди ферромагнетиков, хотя магнетизм всегда препятствовал сверхпроводимости [4]. Эти сюрпризы в поисках учёных напоминают опыты Эдисона, перебравшего тысячи сортов древесины, прежде чем найти подходящий материал для нити в лампе накаливания. А истинный изобретатель лампы – Лодыгин сразу нашёл подходящую угольную, а затем и вольфрамовую нить накала. Так и учёные, случайно обнаружив сверхпроводимость и другие свойства, обычно обескураживаются, как столяр Джузеппе, открывший удивительные свойства полена. Такие сюрпризы при поиске методом “научного тыка” возникают от незнания структуры атомов и их конгломератов. Оттого пока и нет фантастических устройств, типа левитаторов, портативных реакторов и т.д. Но такое знание даёт баллистическая теория (БТР) и магнитная модель атома Ритца, открывающая все тайны микромира как магнитный ключ [5]. А путеводной нитью в лабиринте атома станет спектроскопия, зародившаяся, когда Ньютон пробил отверстие в ставне и разложил свет в спектр. Так что начнём путешествие к центру атома, продолжив расшифровку рун атомных спектров, начатую Кирхгофом и Бунзеном в те же 1860-е годы, когда жюль-верновский герой, расшифровав руны древнего алхимика А. Сакнуссема, предпринял путешествие к центру Земли.

    Рассмотрим в качестве пробного камня эффект Зеемана. Ранее показали, что магнитная модель атома прекрасно объясняет эффект [5]. Напомним, эффект Зеемана состоит в расщеплении каждой спектральной линии на ряд компонент. Но число, положение и интенсивности компонент часто не соответствуют прогнозам квантовой теории. Поэтому вводят новые модели и их уточнения, чтобы добиться соответствия, а в теории Ритца всё получается само.

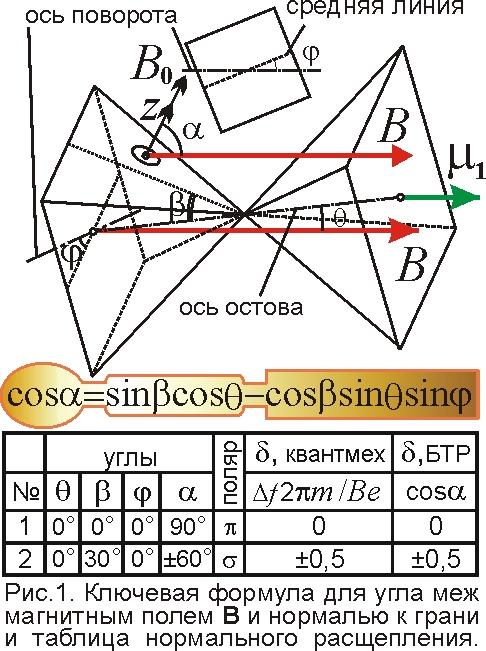
    По теории Ритца эффект Зеемана обусловлен наложением внешнего магнитного поля B на внутриатомное поле B₀ бипирамидального остова атома (рис. 1). Тогда электрон, крутящийся в магнитном поле атома B₀ с фиксированной частотой f₀=eB₀/2πm, меняет частоту вращения на f=e(B₀+B_z)/2πm. Проекция поля B_z=Bcosα на нормаль z к плоскости вращения электрона может принимать ряд значений, в зависимости от ориентации атома к внешнему полю и от того, на какой грани сидит генерирующий электрон. Соответственно, вместо одной линии, генерируется ряд линий с близкими частотами [5]. Ранее обсудили генерацию триплета Лоренца – трёх линий в простом эффекте Зеемана. Даже здесь квантовая теория делает ряд промашек. Так, квантовая теория предсказывает, что при наблюдении вдоль магнитного поля видно всего две линии, а на деле видны три линии, в согласии с магнитной моделью [5], но излучение центральной линии не поляризовано, и мала её интенсивность, поскольку её генерируют электроны на перегородке остова, где электрон может оказаться с вероятностью 1/3. Кроме того, у электрона, летящего по круговой орбите, по диаграмме направленности интенсивность излучения в плоскости орбиты в два раза ниже, чем в поперечном. А при изучении через поляризаторы, измеряющие циркулярную поляризацию, интенсивность ещё снижается. Случайное движение электронов от узла к узлу и соответствующие интенсивности спектральных линий можно рассчитать методом Монте-Карло.

    А теперь исследуем более сложные картины расщепления, например в спектр натрия, детально изученном спектроскопистом Р. Вудом, не уступавшем в плане озорства и детективных поисков деревянному человечку [6]. Жёлтая линия натрия D₁ расщепляется на 4 компоненты. Дело в том, что у типа атомов натрия, который генерирует данную линию, остовы во внешнем магнитном поле ориентируют оси не вдоль поля B, а под углом θ, ввиду наличия у остова, кроме собственного магнитного момента, магнитного момента электронов, и общий момент μ₁ направлен под углом θ к оси остова (рис. 2). В итоге, пирамидальный атомный остов в поле B поворачивается вокруг диагонали квадратного основания на угол θ, и у электронов, сидящих на двух смежных боковых гранях генерируется частоты f=f₀(1±B₁/B₀), а у электронов на двух других гранях f=f₀(1±B₂/B₀), где проекции B₁=Bcosα₁, B₂=Bcosα₂. Тогда вместо одной, возникают 4 близких линии почти равной интенсивности, поскольку размещения электрона на всех четырёх гранях остова равновероятны, как равны вероятности вытащить данную масть из колоды карт, часто складываемых пирамидой, типа остова атома. По разнице частот легко найти B₁, B₂ и углы α и θ (рис. 2). При таких углах α понятно, почему линии, соответствующие α₁=72°, имеют продольную полю B π-поляризацию, а α₂=50° – поперечную σ-поляризацию. Т.к. α₁≠90°, α₂≠0° и остов может вращаться вокруг B, у линий можно наблюдать и слабые σ- и π-компоненты.

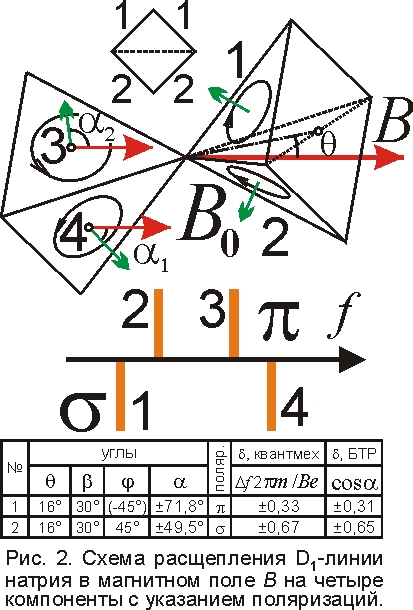
    Оценим строго величину расщепления. Угол между гранью и осью бипирамиды β=30° [5], и эта ось повёрнута на угол θ к полю B, вокруг оси вращения, расположенной в основании одной из пирамид под углом φ к средней линии квадратного основания (рис. 1). Тогда из тригонометрии легко найти, что угол α между нормалью z и полем B есть cosα=sinβ·cosθ–cosβ·sinθ·sinφ. Это золотое соотношение из пяти элементов даёт ключ к пирамиде атома и расчёту величины расщепления Δf=eBcosα/2πm, при любом повороте остова по полярному углу θ и азимутальному углу φ. Если считать, что смещения Δf близкие к расчётным по квантмеху, получим для линии D₁ следующие углы φ, α и расщепления δ=Δf2πm/eB=cosα (рис. 2). Видно, что расчётные значения δ не совпадают с известными. И действительно, точные измерения показали отклонения от квантового расчёта: немного нарушается кратность (правило Рунге) и нарушается симметрия смещения линий. Это показывает преимущества классической модели. Впрочем и она несовершенна, т.к. предсказывает симметричные смещения. Просто в расчёте не учли магнитный момент самого излучающего электрона, его момент при сложении с моментом остова, в зависимости от грани, даёт немного разный суммарный момент μ₁. Т.е. разным положениям электрона соответствует немного разные углы θ. Соответственно, немного изменятся и углы α, нарушив симметрию.

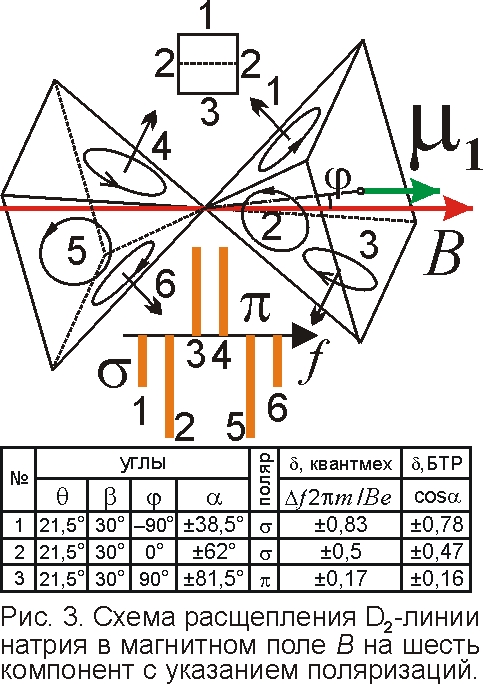
    Другая линия дублета – D₂ расщепляется на 6 компонент, поскольку остов поворачивается уже вокруг средней линии квадратного основания пирамидального каркаса на угол α₂. Соответственно, на верхней грани остова поле B₁=Bcosα₁, на двух противоположных боковых гранях B₂=Bcosα₂, на нижней B₃=Bcosα₃. В итоге, у двух средних спектральных линий, соответствующих B₂, яркость будет в два раза выше, т.к. у электрона вероятность оказаться на них в два раза выше, чем на верхней или нижней. Понятны и поляризации линий (рис. 3). Кроме того, интенсивность зависит от угла α, поскольку диаграмма направленности для излучателя в виде вращающегося заряда даёт максимумы в направлении перпендиклярном к плоскости орбиты заряда, а при выделении данной поляризации π или σ теряется часть интенсивности. Для π-поляризации максимум интенсивности достигается при α близком к 90°, а для σ – при α близком к 0°. По диаграмме направленности, усредняя по всем углам поворота остова вокруг линии поля B, легко найти точное значение интенсивности линий. Видно, что найденные смещения не совсем совпадают с расчётными по квантмеху. И действительно, точные измерения показывают, что смещения линий не совсем соответствуют теории квант.

    У других элементов возможно расщепление линий дублетов на большее число компонент. Так, если атомный остов повёрнут на малый угол θ₃ относительно линии, не совпадающей ни с диагональю квадратного основания остова, ни со средней линией, тогда у всех четырёх боковых граней углы к полю B будут чуть отличаться друг от друга и от значения при θ₃=0°. Соответственно, каждая линия триплета Лоренца преобразуется в четыре линии, соответствующие разным граням, или перегородкам, на которых расположен генерирующий электрон (рис. 4). Именно такая картина расщепления и наблюдается [7].

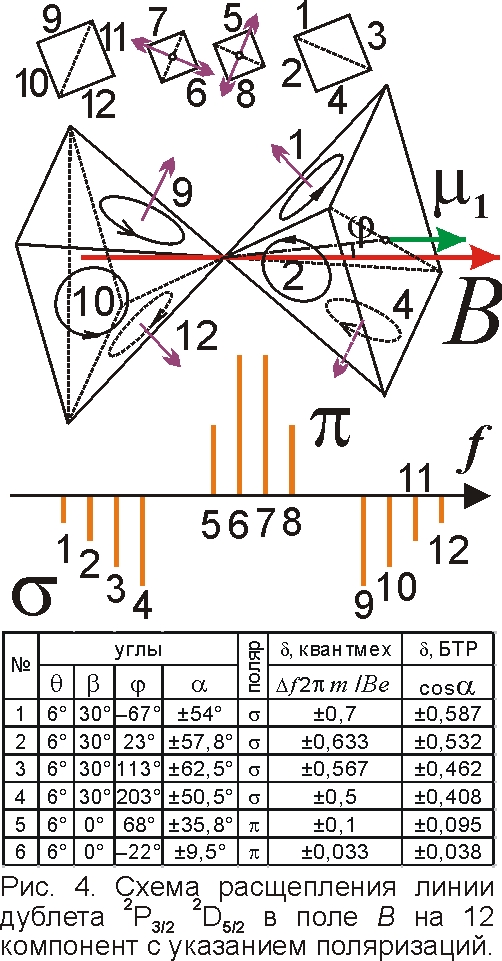
    Компоненты, расположенные ближе к исходной частоте f₀, поляризованы вдоль поля (π-поляризация), т.к. плоскость, в которой вращаются электроны, почти параллельна полю (α≈90°). А компоненты, расположенные дальше от f₀, имеют поперечную к полю σ-поляризацию. В магнитной модели это естественно, т.к. сдвиг частоты Δf=eBcosα/2πm, и чем меньше угол α к полю B, тем ближе поляризация к поперечной σ и тем больше сдвиг частоты Δf. Так магнитная модель элементарно объясняет, почему поляризация такая, а не иная, чего квантовая механика не может. При этом нет строгих границ между одной и другой поляризацией, но, начиная с некого угла α, одна начинает преобладать над другой. Это хорошо видно в эффекте Зеемана, наблюдаемом по адсорбционному спектру – есть области, в которых присутствуют сразу компоненты с π- и с σ-поляризацией. Да и в спектре излучения есть линии на границе, у которых есть обе составляющих π- и σ- [7]. Значит, электрон движется по окружности, и мы лишь выделяем поляризатором компоненты этого движения и излучения.

    В случае триплетов атом уже может принимать два положения по отношению к внешнему полю: одно – когда момент остова сонаправлен с полем B, второе – когда остов наклонён под углом θ к полю B. Триплеты обычны для элементов второй группы – цинка, кальция. Это естественно: два их внешних электрона могут располагаться либо на противоположных боковых гранях, либо на смежных. В первом случае поперечные моменты компенсируют друг друга (μ₁ направлен вдоль оси остова) и остов устанавливается вдоль поля B – наблюдается лоренцев триплет. Во втором случае поперечные моменты не скомпенсированы (μ₁ направлен под углом θ к оси) и атом повёрнут под углом θ к полю B, что ведёт к расщеплению как для дублетов. В итоге спектры от двух типов атомов складываются, и вместо каждой из трёх линий триплета наблюдается либо одна, либо три, либо пять, в зависимости от того какие картины расщепления складываются. А у дублетов элементов 1-й группы, например, натрия, единственный внешний электрон может создать единственную ориентацию момента μ₁ в атоме, поэтому все линии спектра генерирует один тип атомных остовов.

    Для атомов VI и VII групп – с 6-ю и 7-ю внешними электронами, например у хрома, йода, расщепление ещё сложнее [7, 8]. Тут следует учесть, что атом во внешнем поле поворачивается, как барабан в “Поле чудес”, множеством способов, в зависимости от того, как направлены магнитные моменты электронов, дающие в сумме момент μ₁. И этим разным сочетаниям соответствует разная ориентация атомов в пространстве. Т.е. каждому типу атомов отвечает свой спектр, что легко проверить, разделяя атомы неоднородным магнитным полем и исследуя их спектры отдельно [5]. В итоге атомы, излучавшие пучок расщеплённых линий распадутся на пучки атомов, каждый из которых генерирует свою линию или группу линий.

    Во всех случаях расщеплённые компоненты смещены от центральной, как считают, на строго фиксированные интервалы частот, относящиеся к частоте Лармора eB/4πm как небольшие рациональные числа по правилу Рунге. А фактически точные измерения спектров показали, что правило не выполняется строго [7]. Частоты чуть отличаются от расчётных из квантовой механики, как показывают точные измерения приборами высокого спектрального разрешения, например интерферометром Фабри-Перо [9]. Ведь cosα лишь иногда случайно совпадает с рациональными числами (скажем для углов α в египетских треугольниках), например cos60°=1/2. Кстати, грани остова наклонены к оси бипирамиды не обязательно на β=30°, но возможно и на 35°, если остов из половинок октаэдра – двух четырёхгранных пирамид, сложенных не основаниями, а вершинами. Угол α можно определить прецизионным измерением величины расщепления. Пока же малые несовпадения величины расщепления с расчётной списывают на неточности измерений поля B, Δf и неточности квантовых моделей.

    Проверить модель расщепления можно, принудительно ориентируя остовы атомов в заданном направлении. Ведь обычно остовы ориентируются магнитным полем на фиксированные θ и φ, и промерять зависимость Δf от θ и φ нельзя. Но если электрическим полем E сориентировать остов, обладающий дипольным моментом, а магнитным B – лишь менять частоту генерации электронов в узлах, тогда можно, поворачивая остов в разные стороны и наблюдая изменение числа, поляризации и интенсивности компонент, проверить правильность гипотезы. Другой способ – наблюдать эффект Зеемана на линиях поглощения в кристаллах (например, ксенотита и тизонита [10]). Тогда генерирующие атомы, строго ориентированные в кристаллической решётке, матрице кристалла, будут поворачиваться вместе с кристаллом (рис. 5). Поворачивая кристалл, можно наблюдать разные типы эффекта Зеемана, и такой анизотропный эффект Зеемана реально обнаружен в ряде кристаллов [11], например для ионов тербия в матрице алюмината и граната [12]. Более того, наблюдая кристалл в поперечном взгляду магнитном поле с разных сторон, можно изучить зависимость интенсивности расщеплённых компонент от углов φ, θ и угла поворота остова к наблюдателю, а у атомов газа можно наблюдать лишь усреднённую картину. Аналогичный эффект возможен у кристаллов и в отношении электрического поля: обнаружится эффект Штарка, зависящий не только от атомов кристалла и поля E, но и от углов поворота кристалла в поле E. И такой анизотропный эффект Штарка реально обнаружен в кристаллах, подтвердив правильность модели [2, 13]. Это напоминает анизотропию полена: по одним направлениям оно расщепляется легко, а по другим – нет. Так можно детально изучить механизм атома, устроенного наподобие мудрёных швейцарских часов или часов нижегородского мастера И. Кулибина в виде яйца [14]. Часы Кулибина представляли собой две соединённых перемычкой половинки, типа двух половинок остова атома, со сложной начинкой-ядром, где крутились, наподобие электронов, сотни мелких колёсиков, показывая время и раскрывая причудливый спектр кукольного представления. Такие механизмы – предки современных роботов-автоматов были весьма популярны в Европе той эпохи, как показывает пример диснеевского мультфильма “Пиноккио”, где мастер Джепетто (аналог папы Карло и нашего Кулибина) строил такие механизмы.

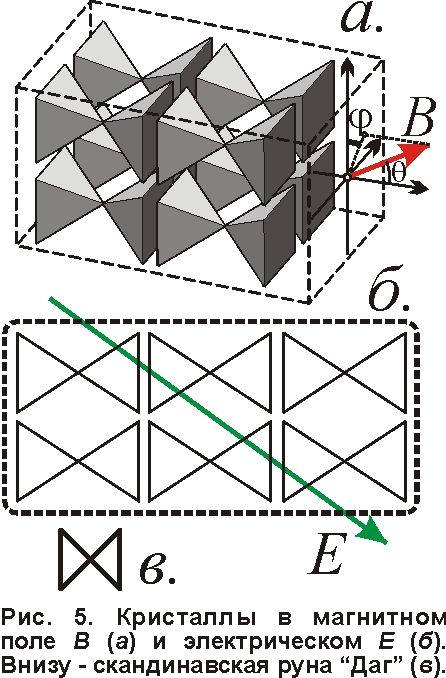
    Магнитная модель атома объясняет и эффект парамагнитного резонанса – он обусловлен электронами, расположенными на биссектрисе грани, где внутриатомные магнитные поля B₀ скомпенсированы [5, 15]. Если выделить два соседних или два противолежащих ребра бипирамиды, тогда образуется крестовина, напоминающая крест (вагу марионеток) с отходящими от неё невидимыми нитями силовых линий магнитного поля, управляющими электронами, которые крутятся в магнитном поле и генерируют излучение. На биссектрисе угла этой крестовины поля B₀ скомпенсированы, но во внешнем поле B электроны могут колебаться с частотой f=eB_z/2πm, и при воздействии излучения такой частоты f СВЧ-диапазона возникнет резонансное поглощение излучения. Кроме внешнего поля электрон находится также в слабом поле других электронов и ядра, которое специфично для разных атомов: у каждого атома свой индивидуальный портрет спектра резонансных частот. Так, методом парамагнитного резонанса устанавливают химический состав среды – входящих в неё атомов.

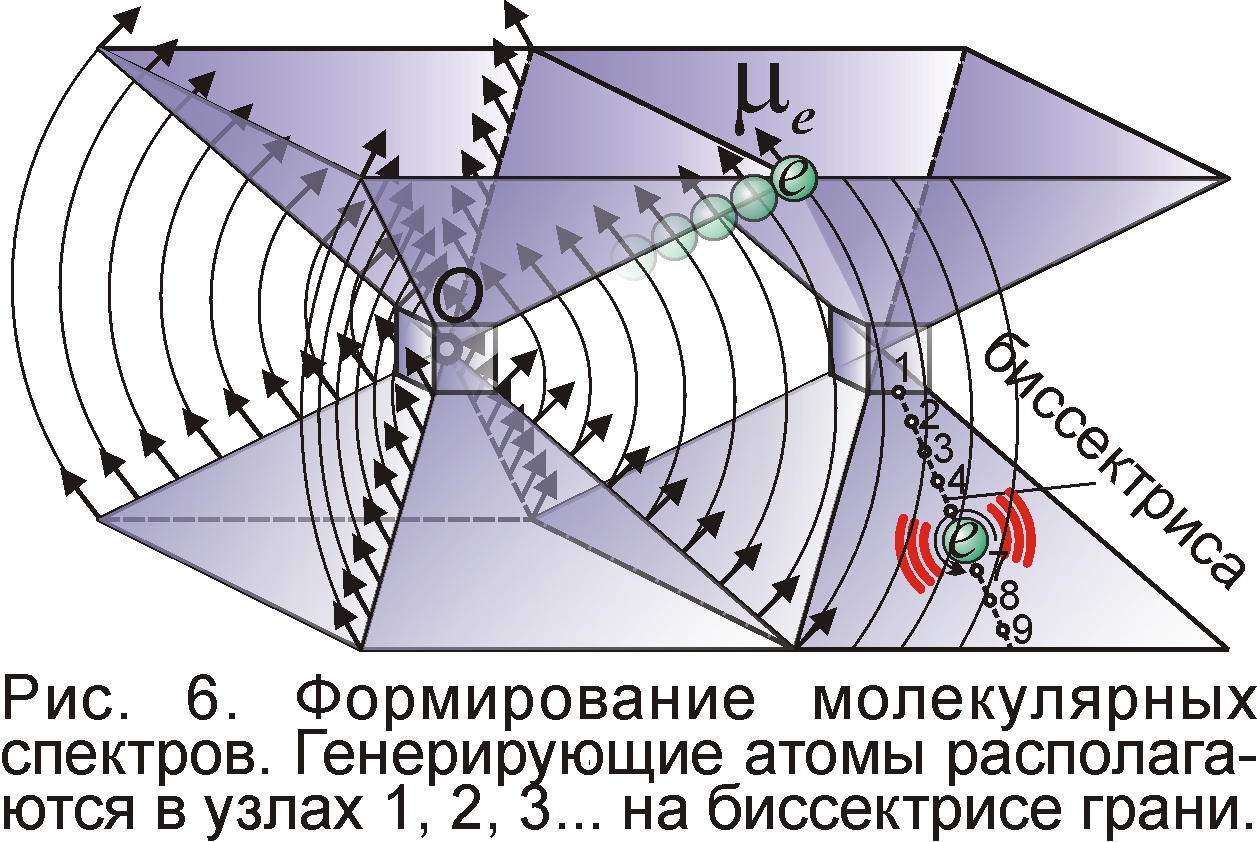
    У молекул спектры сложнее и становятся полосатыми, причём каждая полоса представлена на деле набором очень близких линий. Такой спектр тоже генерируют электроны на биссектрисе грани, обычно “молчащие” из-за нулевого поля B₀, но “просыпающиеся” в поле соседнего атома (рис. 6). Поскольку источник поля достаточно отдалён, в соседних узлах на биссектрисе поперечное к грани магнитное поле мало и меняется от узла к узлу примерно на одну и ту же величину ΔB_z. Поэтому молекулярный спектр (его называют вращательным) почти эквидистантный, т.е. все линии в спектре отстоят друг от друга почти на одну и ту же величину Δf=eΔB_z/2πm и расположены в ИК-диапазоне. Светлые и тёмные полосы спектра чередуются, как в штрихкоде. Величина Δf меняется либо в удалённых узлах, где поле ΔB_z заметно спадает, либо в других сериях, где магнитное поле соседнего атома иначе ориентировано от другого расположения соседнего атома. При этом разные атомы с электронами в одном и том же узле генерируют чуть разные частоты, т.к. кроме магнитного поля остова, электроны оказываются в поле соседних атомов молекулы, в зависимости от расположения в них электронов создающие чуть разные добавочные поля B_mi<<B_z. Поэтому вместо одной линии f=eB_z/2πm виден частокол линий с частотами f_i=e(B_z+B_mi)/2πm, т.е. молекулярная полоса, ширина которой тем больше, чем больше разброс поля B_mi,– чем дальше электрон от центра. И точно, полосы расширяются к границе серии, т.е. при увеличении номера полосы, номера узла вдоль биссектрисы. В твёрдых телах, при соединении многих атомов, линий становится столь много, что они сливаются в непрерывный спектр, что объясняет закон Планка распределения энергии в спектре чёрного тела, как сумму излучений от узловых электронов, генерирующих фиксированные частоты в узлах, словно ноты – на нотных строках, и орбитальных электронов, летящих по траекториям, свивающимся наподобие скрипичного ключа.

    Неточным может быть и значение постоянной Планка h, измеренное, скажем, в фотоэффекте. Ведь, в зависимости от типа атомов могут немного меняться расстояния между диполями, образующими магнитные оси, а также направления элементарных магнитных моментов у зарядов, образующих эти оси. В итоге меняется магнитное поле, в котором вращаются электроны по орбитам вокруг остова атома и вокруг узлов на гранях. Действительно, значения h, измеренные в фотоэффекте или из постоянной Ридберга R для водородоподобных атомов или атомов щелочных металлов, немного отличаются от табличного h, причём не только от разной массы ядер. А поправки к R, полученные в рамках квантовой электродинамики, в БТР получаются от разного размещения в остове зарядов – этих элементарных q.

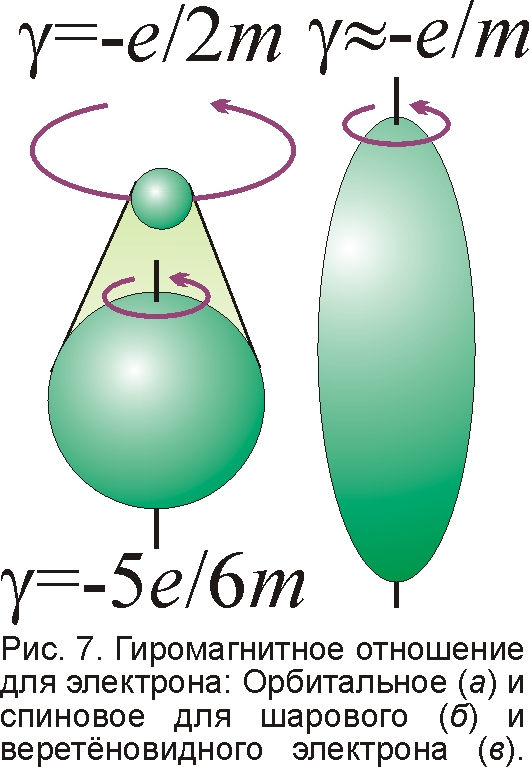
    Другая аномалия – гиромагнитное отношение для электрона. Как показывает расчёт для заряда, движущегося по орбите, отношение магнитного момента к моменту импульса всегда равно -e/2m. Но для спинового момента, т.е. магнитного момента электрона, обусловленного его осевым вращением, гиромагнитное отношение оказалось в два раза больше: γ=-e/m, вопреки расчётам (рис. 7). Баллистическая теория и магнитная модель атома элементарно решают эту загадку. Ведь электрон излучает реоны только с поверхности. А раз испускание реонов и ведёт к появлению электрического воздействия заряда, этот заряд распределён по поверхности, а масса электрона распределена во всём объёме. В итоге, для электрона в форме шара момент импульса равен N=2mr²ω/5, а магнитный момент при интегрировании по сфере μ=-eωr²/3. Отсюда гиромагнитное отношение γ=μ/N=-e5/6m, что уже близко к измеренному гиромагнитному отношению для электрона. Если же электрон имеет форму эллипсоида, вытянутого вдоль оси вращения, тогда отношение может стать сколь угодно близким к γ=-e/m. Причём малое отличие коэффициента в γ перед e/m от единицы в меньшую сторону реально наблюдается в экспериментах Барнетта и Эйнштейна-де Гааза [16]. Отметим, что ещё в начале прошлого века некоторые учёные, например Абрагам, нашли расчётное значение γ=-e5/6m из представления электрона шариком, если его масса электромагнитной природы – гипотеза, подробно исследованная Ритцем. Ввиду отличия формы электрона от шаровой его магнитный момент отличается и от магнетона Бора μ_H=eħ/2m: μ≈1,00012·μ_H. Эта разница сложно выражается в квантовой электродинамике через постоянную тонкой структуры α. А в классической магнитной модели атома и электрона это отличие и сама величина α – это просто следствие несферичности электрона (α выразится через отношение полуосей электрона).

    Правильное понимание природы магнитного поля атома имеет ключевое значение и для понимания магнитных и сверхпроводящих свойств материалов. Прежде отмечали, что магнитными свойствами должны обладать элементы чётных периодов, у которых происходит заполнение электронами слоя вдоль периметра верхней части бипирамидального остова, напоминающего колпак с кисточкой [15, 17]. Напомним, электроны постепенно заполняют уровень по свёртывающейся квадратной спирали, типа антенны в магнитных карточках, служащих ключом-пропуском в метро. Электроны поочерёдно заполняют сначала целиком верхний слой, затем нижний, затем снова верхний и т.д., дабы минимизировать энергию взаимодействия с положительным ядром в центре остова, и с магнитным полем остова. Именно по отношению к направлению его магнитного поля можно говорить о верхе или низе. Этим способом магнитная модель предсказала ферромагнетизм даже у тех элементов, у которых магнетизм не ожидали [3]. С другой стороны, исходя из свойств таблицы Менделеева, можно предположить аналогичные свойства у элементов нечётных периодов тех же групп (Si, P, S, Mo, Ru, Rh, Pd, актиноиды). Действительно, у ряда таких элементов обнаружен ферромагнетизм или антиферромагнетизм, например у актиноидов, включая уран, нептуний, плутоний и т.д. [18]. Специфические магнитные свойства можно ожидать, например, у соединений серы.

    Поскольку магнетизм и сверхпроводимость – родственные явления [3], у этих элементов можно предположить и сверхпроводящие свойства [17]. Действительно, многие лантаноиды – это не только ферромагнетики, но и сверхпроводники [19]. Да и актиноиды – торий, протактиний, уран и ряд соединений Th, Pa, U оказались сверхпроводниками [4, 19]. Сверхпроводимость можно также ожидать у соединений плутония. Такие высокотемпературные сверхпроводники очень нужны в электронике и робототехнике, ибо позволяют создать простые переключатели-реле (ключи на контакте Джозефсона). Действительно, именно на криоэлектронных схемах из криотронов предлагают строить устройства искусственного интеллекта, как в рассказах А. Азимова и А. Кларка [20]. На нелинейной магнитной связи, доменной структуре, обладающей памятью, возможно и создание новых типов думающих машин – где процессы не цифровые, а аналоговые, как в нейронах мозга и фильме “Короткое замыкание”. Появится ли в таких машинах ещё и магнитная совесть – это вопрос, но думать, самообучаться они смогут. Комбинации сверхпроводник-магнит станут основой для роботов, части которых дистанционно удерживаются и перемещаются как у марионеток, но роль невидимых нитей играют силовые линии магнитного поля и радиоволны для передачи команд [17], а роль управляющего креста (вага) играет микросхема с отростками выводов. Наверняка, есть вещества, переходящие в сверхпроводящее состояние и при нормальных условиях, при комнатной температуре, чем можно объяснить древние парящие статуи и летающий транспорт на сверхпроводниках, парящих в магнитном поле [17], как в фильме “Путешествие к центру Земли”. Однако, все эти драгоценные древние знания вместе с моделью строения атома, сверхпроводящих свойств ферромагнетиков и антиферромагнетиков канули в Лету, погрузились под воду с Атлантидой [21], словно остров в жюль-верновской повести “Приключения дядюшки Антифера”, или затерялись в снегах гор, как Обручевская “Земля Санникова” и “Плутония”.

    Но вернёмся к обсуждению известных кандидатов в сверхпроводники и ферромагнетики. Взять тот же плутоний: применение его в качестве магнитного и сверхпроводящего материала особенно перспективно, ведь у плутония шесть кристаллических модификаций и шесть степеней окисления [20], т.е. он образует широкий спектр кристаллов и соединений, обладающих уникальными свойствами. Хотя у самого плутония сверхпроводимость пока не обнаружена, ряд его соединений оказались сверхпроводниками с критической температурой T_c на порядок выше, чем у соединений аналогичных элементов. И на основе плутония стремятся создать новый класс сверхпроводников. В некотором роде эти случайно открываемые “волшебные” вещества – высокотемпературные сверхпроводники, которые при T_c>20 °C позволят создать новые типы роботов, подобны оживляющему порошку из сказки А.М. Волкова “Урфин Джюс и его деревянные солдаты” (у неё тоже был западный прототип – сказка Л.Ф. Баума “Страна Оз” и русская сказка “Летучий корабль”, где “дрова” оживили “боевых дроидов” [22]). И в сказках Волкова строили “боевых дроидов” за счёт свойств нового вещества. Кстати, эта сказка о четырёхсекторной стране тоже насыщена символикой кристаллического пирамидального четырёхгранного атома, с жёлтой линией натрия в качестве ключа [21].

    Итак, магнитная модель атома обладает огромной прогностической силой. Расщепление спектральных линий в эффекте Зеемана, открывая путь к строению атома, открывает и способы расщепления ядра. Ведь, к эффекту Зеемана приводит не только внешнее магнитное поле, но и поле ядра. Это обнаруживается по эффекту Мёссбауэра, позволяющему изучить тонкую структуру рентгеновских и гамма-спектров. Сам эффект Мёссбауэра тоже связан с магнетизмом. Например, ядро кобальта Co превращается в ядро железа Fe при захвате электрона с K-оболочки атома, где электрон обладает строго фиксированной энергией. Поэтому при ускорении ядром, вращаясь в магнитном поле B₀ остова, он излучает на фиксированной частоте, которая выдерживается с точностью до 10^–12. Соседние атомы, например в кристалле гематита (Fe₂O₃) немного меняют энергию электрона и величину поля В, причём рядом способов, в зависимости от расположения остова. В итоге линия мёссбауэровского поглощения тоже расщепляется [23]. Не исключено, что и расщепление ядра плутония удастся осуществить, управляя внутренними и внешними магнитными полями, влияющими на структуру ядра и его стабильность. Так, именно магнитная бипирамидальная модель атома и ядра объясняет почему тяжёлые ядра делятся на части отношение масс которых близко к золотому сечению – числу Фидия – Ф=1,618 [24] – это отношение масс двух пирамидок ядра, т.е. соседних магических чисел [15, 21]. Не зря числу Ф имело магический, сакральный смысл.

    Отметим, что в основном с помощью магнитного поля и осуществляют проникновение в тайны микромира, ведь магниты применяют в приборах для извлечения энергии излучения атома, скажем в мазерах. Мазеры природного происхождения обнаружены и в космосе. Например, вокруг звёзд типа мирид (Омикрон Кита – Мира), есть область, излучающая интенсивные радиолинии газа, совсем как земные мазеры. Эта область образует кольцо вокруг звезды. Ведь по эффекту Ритца обычно переизлучает свет центральной звезды газ, расположенный в пределах сечения эллипсоида плоскостью, т.е. как раз в пределах кольца [22].

    Самое интересное – наблюдение эффекта Зеемана в спектрах звёзд. Предполагают, что удвоение линий и сильная поляризация излучения в спектре поляров и магнитных звёзд, а также белых карликов связана с эффектом Зеемана, например, у звезды EUVE J0317-855. Но скорее поляризация вызвана движением звёзд – размытием их изображений и электронных орбит. Поэтому например у β Лиры поляризация меняется синхронно с орбитальным движением и изменением видимой формы звёзд. Конечно, у звёзд есть магнитные поля, но небольшие, порядка обнаруженных у Солнца. У далёких звёзд за счёт ускорения от силы Лоренца в этих полях, происходит сильное смещение частоты излучения попеременно в большую и меньшую сторону. Это и ведёт к симметричному уширению линий белых карликов, ряда красных карликов и сверхгигантов [25]. Если бы уширение происходило лишь за счёт дисперсии лучевых ускорений на поверхности звезды оно получалось бы асимметричным – только в красную сторону, вопреки наблюдениям. Такой эффект обнаружен также у галактик в диапазоне красных смещений 0<Z<2 [26], в эмиссионных линиях, для которых эффект Ритца особенно велик, так как они почти не переизлучаются средой. Что причина в эффекте Ритца, подтверждает и рост ширины линий пропорционально красному смещению Z, т.е. расстоянию r. Особенно сильно эффект выражен для квазаров и сейфертовских галактик, у которых ширина эмиссионных линий Δλ~(0,01–0,1)λ, т.е. близка к их смещению Δλ~Zλ [27].

    Так же и переменная поляризация, аномальные свойства магнетаров, пульсаров и источников гамма-всплесков (GRB) связаны, видимо, не с магнетизмом этих звёзд, а с эффектом Ритца, вызывающим иллюзорные вспышки в гамма-диапазоне и вариации их периода. Так, у источника в созвездии Рыб, вспыхнувшего в 1979 г. [26] пульсации блеска, очевидно, были вызваны орбитальным вращением звезды. Поэтому в согласии с теорией Ритца наблюдалась резкая вспышка, а затем плавное угасание с осцилляциями переменного периода [28].

    Но главная замочная скважина, скрывающая все тайны космоса, находится в ядре, точнее в керне, в центре Галактики – в радиоизлучающем объекте Sgr A*, где, как полагают, находится сверхмассивная чёрная дыра. Полагают, что её тяготение, как мощный магнит, приводит к быстрым движениям звёзд возле центра Галактики (рис. 8). Причём гигантские скорости звёзд устанавливают как по видимому движению, так и по спектрам, которые вполне соответствуют наблюдаемому движению звёзд [29]. Но можно рассмотреть и другие объяснения быстрых движений в центре Галактики. Тем более отсутствие сверхмассивных тел в центре нашей и других галактик подтверждает спектр излучения этих участков, который соответствует крайне разреженному газу, судя по наличию в спектре запрещённых линий [7, с. 374]. А сверхмассивная чёрная дыра вызывала бы аккреции межзвёздного газа, повышение его концентрации и температуры. Кроме того, она вела бы к быстрой прецессии, повороту орбит звёзд, более быстрому, чем у Меркурия. Но такие эффекты не обнаружены.

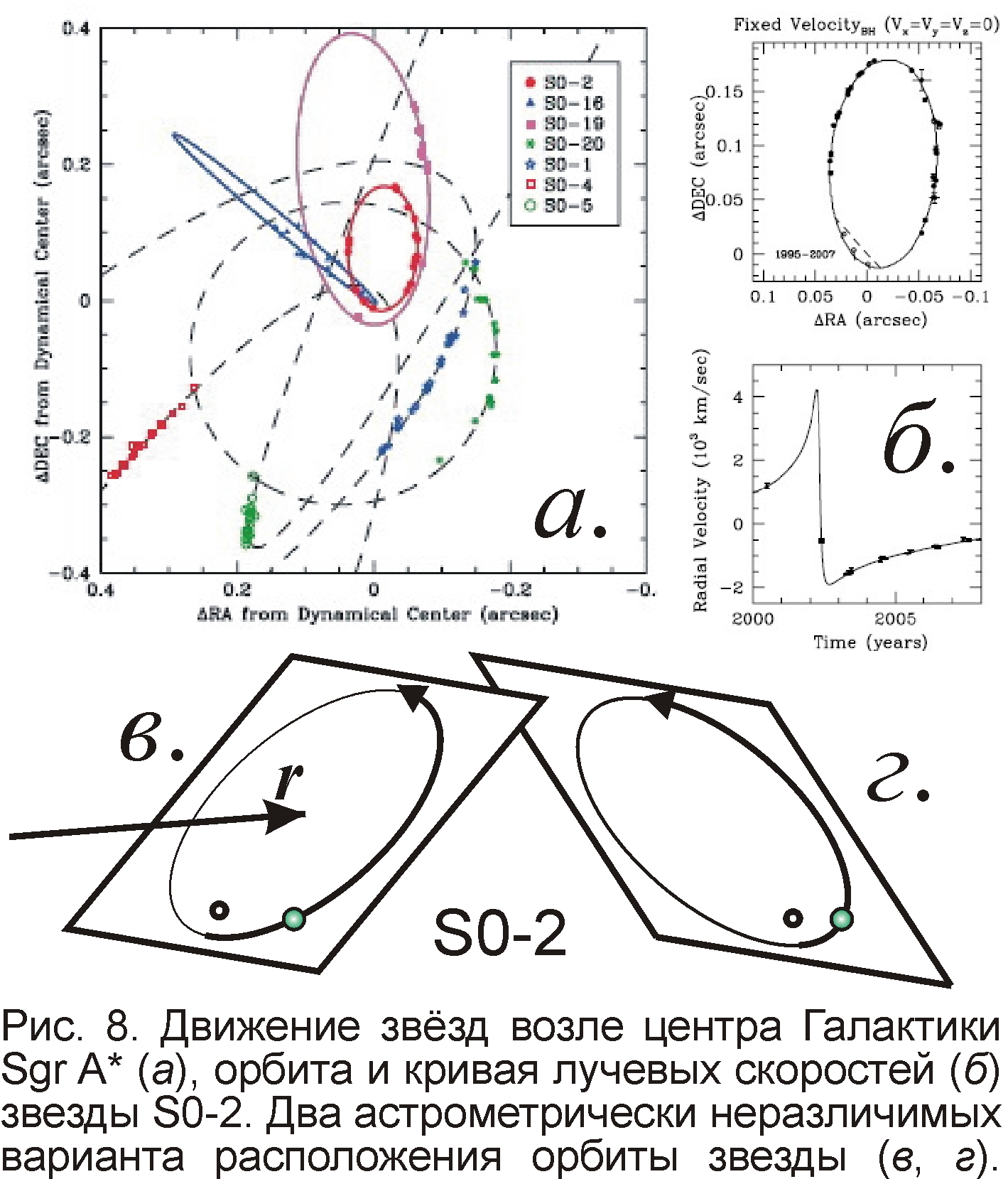
    Поэтому естественней предположить, что наблюдается иллюзорный рост скорости видимого движения звёзд за счёт их движения с ускорением близким к критическому a_с≈-a₀=-c²/r. Например, если звёздная система с массивной центральной звездой движется с лучевым ускорением -a₀ в поле тяготения другой массивной звезды или звёздного скопления. Предпримем путешествие к центру Галактики и рассчитаем во сколько раз ускоряется видимое движение звезды, если (1+ra_с/c²)=b<<1, т.е. коэффициент компрессии g, показывающий, во сколько раз убыстрено по сравнению с истинным видимое движение, будет равен g=dt/dt'=1/b>>1. В случае предельного сближения ускорения с критическим -a₀ возникнет режим сверхмодуляции частоты (СЧМ), когда малые модуляции скорости света с'=c–V_r, вызванные собственными движениями звёзд с лучевой скоростью V_r, вызовут гигантские вариации частоты. В общем случае период световых колебаний преобразуется как

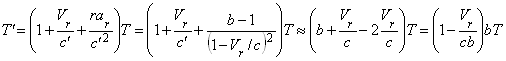    .     (1)

    Таким образом, движение звёзд выглядит ускоренным в g=1/b раз, так что измеренная астрометрически трансверсальная скорость звёзд V_t'(t)=V_tT/T'=V_t(t)/b. А лучевая скорость, измеренная спектроскопически, если исследовать относительные смещения линий от их средних положений, составит V_r'(t)=-V_r(t)/b. Таким образом, в обоих случаях происходит иллюзорный рост скорости в g раз, но во втором случае расчётное направление скорости становится обратным. Казалось бы, это приведёт к несоответствию наблюдаемого астрометрически движения и измеренного спектроскопически. На деле от неопределённости угла i=i₀ наклонения орбиты, поскольку наблюдается только проекция орбиты и видимого движения на картинную плоскость (рис. 8), им могут соответствовать два неразличимых варианта расположения орбиты i=i₀ и i=-i₀. И каждому положению звезды будут отвечать два возможных значения лучевой скорости V_r'=V_r0 и V_r'=-V_r0. Таким образом, в элементах орбиты, определённых астрометрически и спектроскопически, нет противоречий, но вместо истинного угла i=i₀ получат ложное значение i=-i₀, которому соответствует значение лучевой скорости V_r'=-V_r0.

    Несоответствие можно выявить по спектру звезды, в котором удаётся чётко выделить спектр поглощения и излучения межзвёздного газа [27]. Если для истинной орбиты с i=i₀ наиболее далёкой точке соответствует наиболее интенсивный спектр поглощения межзвёздного газа, для ложной орбиты с i=-i₀ тому же движению звезды на картинной плоскости соответствует наиболее близкое расположение звезды и слабый спектр поглощения газа, что будет означать неверное значение i и обращение знака лучевой скорости. А если измерять не на относительное смещение спектральных линий, а абсолютное, можно тоже найти несоответствие, ведь из формулы (1) при T'<<T по эффекту Доплера требуется лучевая скорость V_r'~-c. Итак, наблюдается огромное смещение спектральных линий, которое не замечают потому, что неверно отождествляют спектральные линии. Видимо, регистрируемые спектральные линии гелия и брома на деле соответствуют низкочастотному излучению дальнему ИК- и радиолиний водорода и гелия, смещённых ритц-эффектом в ближний ИК-диапазон.

    Если измеренные астрометрически и спектроскопически движения звёзд возле галактического центра иллюзорно ускорены эффектом Ритца в g=1/b~400 раз, тогда истинные скорости окажутся много меньше, а орбитальные периоды – много больше расчётных. Например, у звезды S0-2, вместо измеренной скорости V_r'~4000 км/с, найдём, что истинная скорость V_r~10 км/с, а орбитальный период не P'=15 лет, а P=6000 лет. Тогда масса центральной звезды получится не M'~4·10⁶M_¤ , а M=M'/g²~25M_¤ , т.е. величина типичная для звёзд главной последовательности класса O и B. При этом характерные массы звёзд-спутников составят ~0,1M_¤ . Чтобы звёздная система двигалась в течение такого времени P~6000 лет с ускорением близким к критическому a_с≈-a₀=-c²/r, она должна лететь в поле тяготения шарового скопления, расположенного от звезды на расстоянии R~100000 а.е. и имеющего массу M~10⁷M_¤ . Такая система может включать 10⁶ звёзд с массой ~10M_¤ . При этом шаровое скопление может иметь размер ~10000 а.е., ведя к движению центральной звезды с периодом P~10000 лет.

    Такие массивные скопления как раз типичны для центра Галактики, в керне, где концентрация звёзд максимальна. Да и сам центр служит центром тяготения, способным обеспечить критическое ускорение a_с≈-a₀. Действительно, по известному распределению масс [25, с. 197], внутри шара радиуса R возле центра (в керне) Галактики m(R)=kR, где k=10⁷M_¤ 1/пк. Отсюда критическое расстояние R_с найдётся из условия равенства ускорения на поверхности шара критическому a₀=Gm/R_с². Откуда R_с=Gkr/c²=1,5·10¹⁴ м=1000 а.е. Это значение R_с в пределах порядка соответствует размерам орбит S0-2 и других звезд, движущихся вокруг центрального объекта [29]. Таким образом, в пределах шара радиуса R_с=1000 а.е. в центре Галактики многие объекты, облетающие центр, обладают ускорением порядка критического. Отсюда – возникающие по эффекту Ритца активность, вспышки, быстрые движения, ионизирующие излучения в центре нашей и других галактик. Так астрономы-релятивисты превратили центр Галактики в Поле чудес в Стране дураков, где из одной звезды “вырастают” миллионы масс Солнца. На деле все явления можно объяснить классическим движением обычной звёздной системы по орбите вокруг центра Галактики или другой звёздной системы.

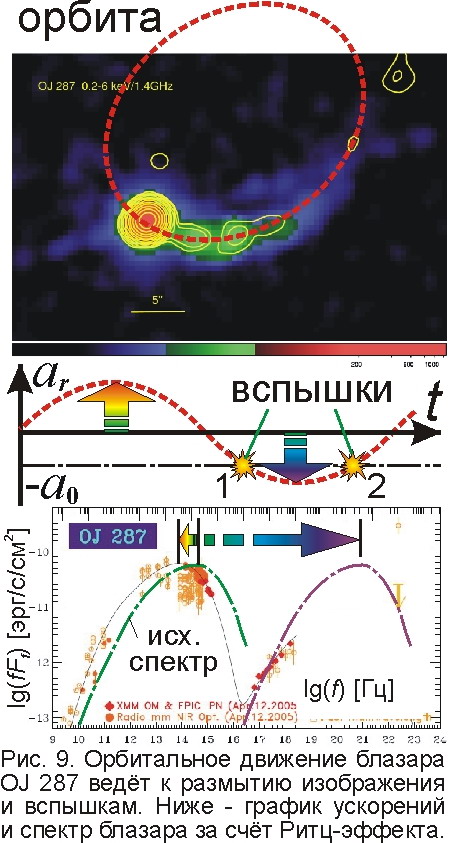
    Такой двойной сверхмассивной чёрной дырой считали и блазар OJ 287, чем объясняли его вспышки при пересечении одной дырой аккреционного диска другой. Но это могут быть и две простые звёздные системы, меняющие яркость по эффекту Ритца при движении по орбите. Эта орбита даже видна: вдоль неё размыто изображение блазара (рис. 9) и расщеплено на три – такое умножение изображений в электродинамике тоже предсказал Ритц. Причём движение по орбите с периодом 12 лет приводит к типичной вспышке дважды за период. Интересно, что астрофизики получают похожие кривые блеска на основе биминг-эффекта – меняющего яркость релятивистского эффекта Доплера у движущихся с огромной скоростью плазменных джетов [30], словно борода развивающихся в стороны от вращающейся звезды [21, 22, 28]. Сверхсветовые скорости OJ 287 и его джетов – это тоже следствие ускорения видимых процессов эффектом Ритца. Не зря OJ 287 называют розетским камнем астрофизиков [31]: именно этот блазар проливает свет на иероглифы спектров блазаров. Спектр всех блазаров содержит два отчётливых максимума – в видимом диапазоне и в рентгеновском. В рамках эффекта Ритца происхождение их очевидно: звёзды в системе блазара движутся по орбитам с ускорением близким к критическому и значительную часть орбитального периода их ускорение максимально a_r≈a₀=c²/r или минимально a_r≈-a₀. Соответственно, у части звёзд частота излучения снижена примерно в два раза (f'=f/2), а у другой части – примерно в тысячу раз увеличена по эффекту Ритца f'=f/(1+a_r/a₀)>>f. Результирующий спектр блазара – это сумма двух спектров – обычного теплового, но с в 2 раза меньшей цветовой температурой звёзд и рентгеновского – повторяющего оптический, но смещённый в рентгеновский диапазон (рис. 9). И точно, спектр представлен суммой двух спектров, близких к тепловым, и максимумы их примерно равны, т.к. время излучения звёзд в обоих положениях примерно равное. Так сказочные объекты (типа нейтронных звёзд и т.д.) из сказочной материи эффект Ритца магическим образом превращает в обычные звёзды, хотя сам эффект и породил иллюзию активности этих объектов.

    Таким образом, современные сказки о тёмной материи и сверхмассивных чёрных дырах и т.д. порой ещё более фантастичны, чем прежние мифы о мире, плавающем в океане на спине гигантской черепахи с четырьмя слонами на панцире, как образно показано в фильме “Цвет волшебства”. Прежние представления будут даже менее фантастичны, если под океаном понимать космос, под вселенским диском и черепахой – Землю или галактику, а под четырьмя слонами – фундамент мироздания атом с его четырьмя гранями, на которых обитают электроны. На одной древней гравюре есть изображение человека, пробивающего по совету Дж. Бруно на краю мира отверстие в куполе небосвода и видящего за ним совсем иную картину явлений – изнанку иллюзорного кукольного представления, разыгрывающегося на небосводе. Так и БТР, пробивая световой барьер и хрустальные сферы атома, вскрывает истинные причины явлений, позволяя увидеть явления в истинном свете. Возможно, именно Дж. Бруно стал прототипом для образа Буратино у А.Н. Толстого, поскольку совсем как “Пиноккио” Коллоди родился и жил в Италии, скитался по свету, сея революционные идеи, стремясь освободить людей от догм, кстати, как и сам Коллоди – участник национально-освободительного движения. И Буратино чуть не разделил учаcть Бруно, которого сожгли на костре. А роль инквизиции, конечно, сыграл Карабас-Барабас с его плёткой и костром. Для самого же Коллоди прототипом Пиноккио, видимо, стал Сирано де Бержерак – носатый поэт, много сочинявший в стиле бурлеска [22] и напропалую коловший острым словом и шпагой.

    Ключом к переосмыслению микромира и мегамира (космоса) служит магнитная модель атома, гармоничная, как часы или лира. Не зря атом издавна сравнивали с музыкальным инструментом, органом, шарманкой, музыкальной табакеркой [6, с. 102]. По мифу Орфей как раз с помощью лиры спустился в подземный мир и путешествовал там, словно атомная подземная лодка из фильма “Ядро”. Так лира сыграла роль ключа к этому миру. Не исключено, что мифопредставление об Аиде (греческом аде) – это символическое изображение микромира (атома, отсюда созвучие) или мегамира (ядра Галактики), а лира – это древняя модель, символ атома. Да и в библейском мифе, рассмотренном, например у Данте, ад (так же как рай) состоял из 7 уровней (кругов) [32], что соответствует 7 уровням атома, на которых расположены электроны (отсюда 7 периодов таблицы Менделеева). Так же и в греческих мифах подземное царство многоэтажное – под Аидом располагался Тартар. А в русских сказках под медным (или железным) располагалось серебряное царство, а под ним – золотое. Совсем как элементы Cu, Ag, Au расположены в длиннопериодной таблице Менделеева один под другим в периодах, соответствующих заполнению электронами этажей-уровней атомного остова. Кстати, и в русской сказке Садко путешествовал в подводном царстве, как атомная подводная лодка, благодаря гуслям, которые тоже могли символизировать модель атома [7]. Выходит, древнее представление об аде,– это лишь стилизованное представление о микромире вечного хаоса, атомного огня, ядерных реакций. Так же как расположенная за очагом микродверца в сказках о Буратино или об Алисе Л. Кэррола [28]. Чтобы открыть и пройти в эту дверь, требовалось уменьшиться, изменить ненадолго атомарную структуру. Знание устройства атома как раз позволит строить такие подземные лодки, проникающие сквозь горные породы, как в рассказе Г. Гаррисона “Проникший в скалы”. Ведь атомы – это почти на 100 % пустое пространство, где на долю ядра и электронов приходится мизерная доля объёма, поэтому раскачивая электроны, атомные остовы внешним полем, можно “протискивать” твёрдые тела сквозь скальную породу [3]. Вероятно, такое символичное описание микромира есть и в матричном варианте квантовой механики. Матрица как раз напоминает структурой атомную плоскость, где числа расположены в ячейках, узлах. А микромир подобен миру фильма “Матрица” – цифрового мира магнитных матриц памяти, где значения координат, моментов меняются дискретно, по строгим правилам, как в программах, первые из которых разработала Ада Лавлейс (Байрон) как раз в те годы, когда возникла спектроскопия.

    Символика атома встречается и в народных промыслах. Узоры на русских рубашках, гармошках и т.д. из ромбов и встречных треугольников очень напоминают пиксельную структуру атома. Так же и в играх типа крестиков-ноликов, рендзю, точек, происходящих от древних игр, типа шахмат и го, может быть отражено дискретное строение атома с узлами, в которых могут располагаться и прыгать частицы двух типов – отрицательные электроны или положительные ядра и позитроны, образующие сложные конфигурации [15, 33]. Совершенство, изящество часового механизма атома и устройства микрочастиц настолько удивительны, что создают иллюзию того, будто они, как и сама модель атома, сконструированы в начале времён каким-то искусным мастером типа Кулибина. Отражение этой модели атома можно видеть и в скандинавских рунах, скажем в руне “Dag”, как раз означающей “свет”, “середина дня, лета”, ведь атом – это элементарный излучатель света, центр, основа мироздания. Не случайно руна “Dag” – последняя, расположена внизу алфавита: так и атомы, ядра лежат в фундаменте мироздания. Так что руны не зря служат ключом к подвальным этажам мироздания в романах Жюль-Верна и Р. Толкиена. Кстати, и первая буква русского алфавита “A” изначально могла означать основу мира – атом (вспомним Å [5]), а последняя буква кириллицы “Я”, напоминающая в древнем написании (в буквице – “Ижа” æ [34]) руну “Dag”, могла символизировать ядро [28]. Могли буквы символизировать и отдельные элементы, тем более точки у многих букв (ё, i) напоминают Ленгмюровские обозначения электронов у атомного остова. Да и сама древнеславянская азбука-буквица 7×7 [34] и алфавит санскрита напоминают таблицу Менделеева, в которой элементы обозначены буквами (в исходных алфавитах число букв доходило до 100, как в таблице – элементов). Учёный исходно так и строил таблицу – как матрицу 7×7. Причём алфавит – это матрица универсальная, типа магического квадрата, дающая ключ и к микромиру, и к космосу [33, 34, 35], отсюда алхимические соответствия элементов и планет. Поэтому азбука, изначально полученная Буратино от папы Карло, уже сама по себе была ключиком к мирозданию, если бы он только знал. В качестве такой азбуки “с чудными цветными картинками” и ключом – символическим изображением строения электронов, атомов, протонов, микромира и космоса, может выступать и астрокнига И. Левитт [36]. Модель атома и ядра можно усмотреть и в египетских пирамидах [5, 37], и даже в символике с обложки и диска журнала “Химия и жизнь” (он как раз посвящён анализу свойств атомов и соединений). Да и редакция журнала расположена в Москве в здании Института египтологии, среди корпусов химических институтов.

    Таким образом, баллистическая теория и магнитная модель атома раскрывают не только тайны строения атома и космических объектов, но и позволяют понять устройство элементарных частиц, в том числе для выделения скрытой в них гигантской энергии, как подробнее рассказано в докладах автора на Международной конференции [38] и научно-технических миниконференциях [39, 40]. Итак, именно баллистическая теория и магнитная модель атома приносят освобождение от паутины догм, навязанных кукловодами, манипулирующими сознанием своих марионеток. А магнитная модель атома служит тем магнитным ключом, который открывает заключённому разуму путь к свободе мысли, науки и выход энергии микромира – атомного очага, за которым скрыта дверца атомного ядра.