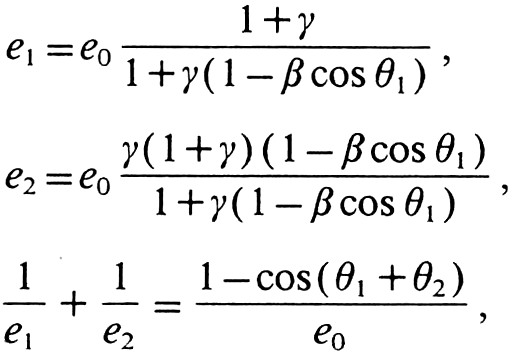 (2)
(2)[вернуться к содержанию сайта]
Представлен критический анализ опыта Саде, выполненного для проверки второго постулата специальной теории относительности Эйнштейна. Показано, что этот эксперимент является некорректным и неубедительным.
Автором был представлен обзор экспериментов, которые были выполнены в целях проверки второго постулата специальной теории относительности. Опыты Саде [1] и Альвагера [2] являются двумя тестами, которые теорема погашения не лишает законной силы [3]. Саде использовал гамма-лучи, порождаемые аннигиляцией позитронов на лету, тогда как Альвагер использовал гамма-лучи, порождаемые распадом π0 мезонов. Результаты опыта Альвагера следует интерпретировать лишь как тест на самосогласованность, поскольку скорость π0 мезона не измерена напрямую, но определена из релятивистской кинематики.
Саде заявляет, что два гамма-луча должны идти под углами θ1 и θ2 к линии движения позитрона, так что
0<θ1<π, π<θ2<3π/2. (1)
Саде рассматривает два гамма-луча. Один из этих лучей обладает составляющей скорости в направлении полёта позитрона, а другой обладает составляющей скорости в противоположном направлении. Если скорость гамма-лучей складывается со скоростью центра масс (электрона и позитрона), согласно классическому векторному сложению, то у одного из них скорость будет выше скорости света, а у другого скорость будет ниже скорости света.
Чтобы проверить условие (1), Саде расположил детекторы гамма-лучей под углами θ1 и θ2 к направлению, заданному источником позитронов 64Cu и мишени из Перспекса [марка оргстекла], поскольку он предполагал, что направление полёта позитрона в момент аннигиляции совпадало с направление 64Cu-Перспекс.
Саде также использовал два отдельных канала, которые гарантировали, что в многоканального анализатора достигают только те гамма-лучи, энергии которых заключены между 0,511 и 0,65 МэВ. Ниже показано, что если эти два гамма-кванта имеют энергию между 0,511 и 0,65 МэВ, то направление полёта позитрона не совпадает с направлением 64Cu-Перспекс, и углы θ1 и θ2 не соответствуют условию (1).
Как мы теперь знаем [4], позитрон входит в вещество и аннигилирует с вероятностью, растущей вместе с ростом количества потерянной им энергии за счёт взаимодействий в веществе. Это означает, что позитрон меняет направление движения при входе в вещество.
При выборе двух гамма-лучей следует принять во внимание энергии e1 и e2 этих двух гамма-лучей, поскольку они зависят от углов θ1 и θ2, согласно соотношениям [5]
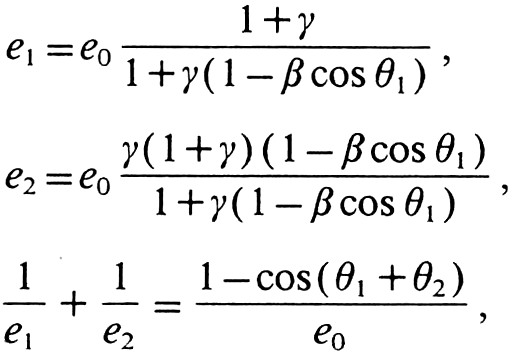 (2)
(2)
где e0=m0c2, β=v/c, γ=(1–β2)–1/2, и m0 – масса покоя электрона, v – скорость позитрона в лабораторной системе отсчёта, и c – скорость света.
Используя соотношения (2), можно показать, что углы θ1 и θ2 двух гамма-лучей, рассматриваемых Саде, обладая энергией между 0,511 и 0,65 МэВ, изменяются между минимальной и максимальной величинами, которые зависят от энергии позитрона (Eβ). Углы θ1 и θ2 имеют одинаковые предельные величины, поскольку энергии e1 и e2 заключены между одинаковыми значениями. На рис. 1 возможные величины угла θ1 показаны в заштрихованной области. Эти величины располагаются примерно между 52°,5 и 89°,9.
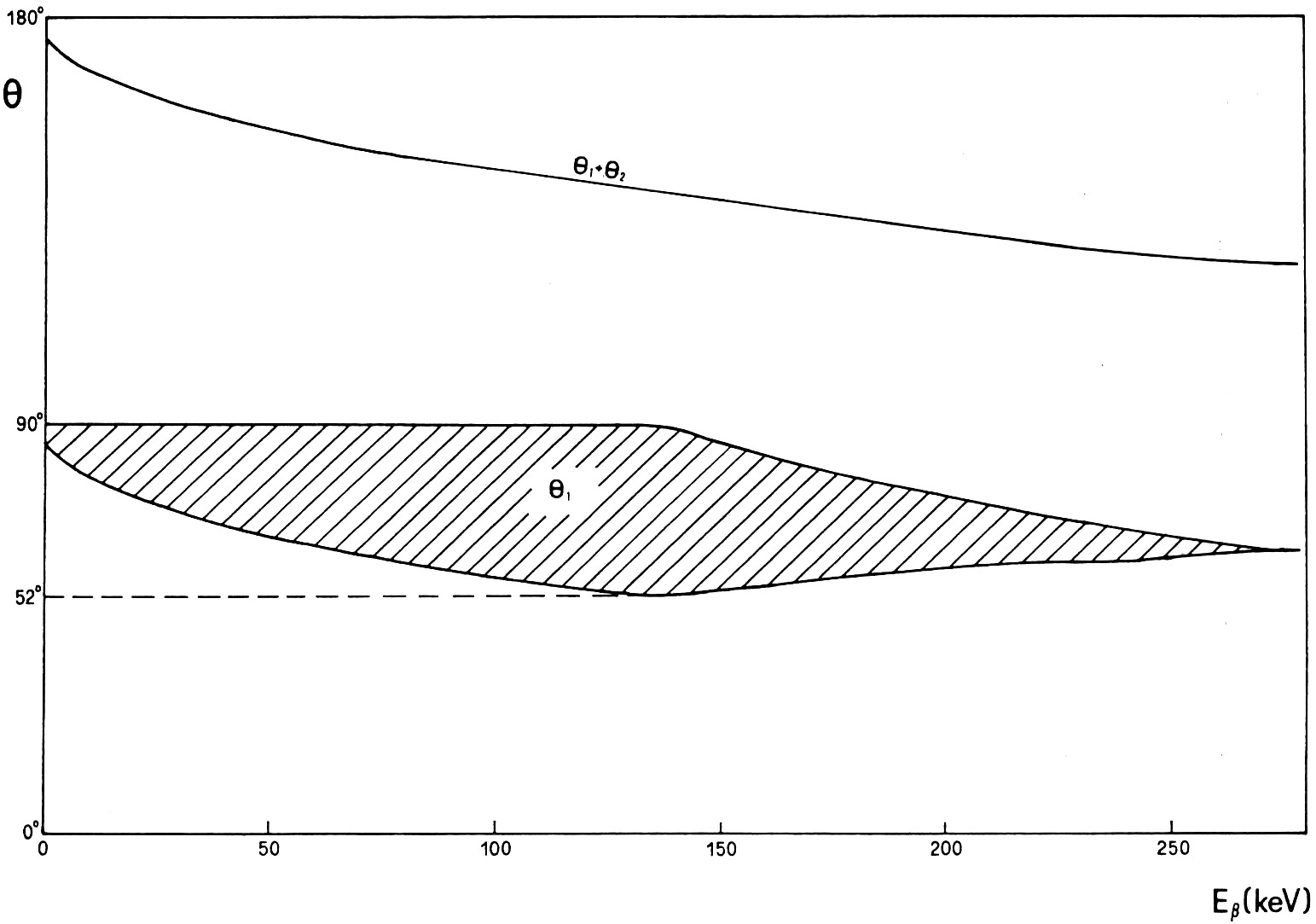
Рис. 1. Угол θ1+θ2 между двумя счётчиками как функция энергии Eβ позитрона, если энергии двух гамма-лучей лежат в интервале между 0,511 и 0,65 МэВ. Заштрихованная область представляет все величины угла θ1, образованного одним гамма-лучом и направлением полёта позитрона, как функция Eβ.
На рис. 2 показан угол, в пределах которого ограничено направление полёта позитрона, если e1 и e2 лежат между 0,511 и 0,65 МэВ. Поэтому экспериментальная установка Саде отбирает только те пары гамма-лучей, оба из которых обладают составляющей скорости в направлении полёта позитрона в момент аннигиляции. Это противоречит группе условий (1), поэтому опыт Саде ошибочен и бездоказателен.
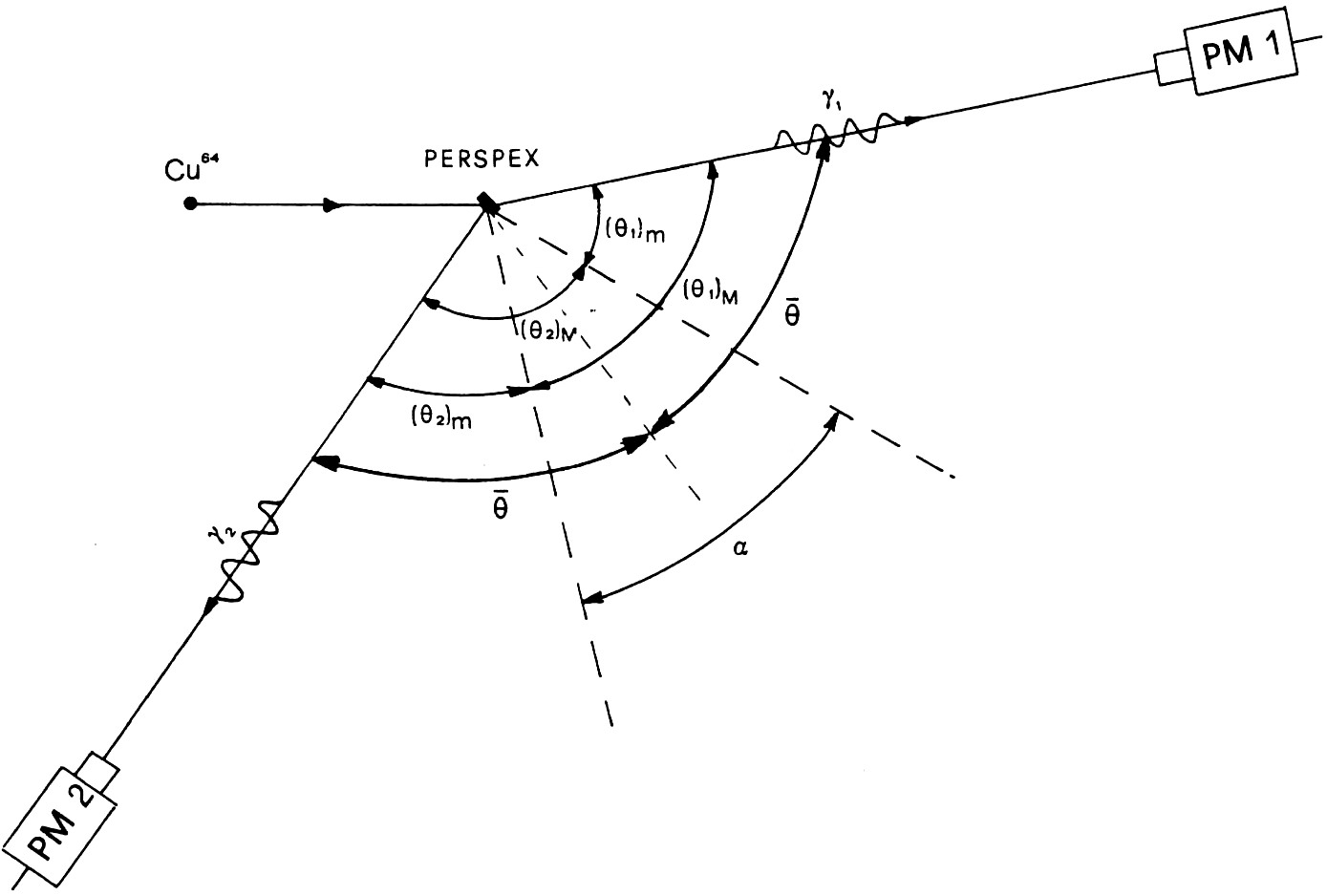
Рис. 2. Расположение двух детекторов гамма-лучей, источник 64Cu и слой перспекса, в котором имела место аннигиляция, как предполагает Саде. α – угол, в пределах которого ограничено направление полёта позитрона, согласно соотношениям (2), если энергии двух гамма-лучей – те же, что и в опыте Саде; (θ1)m, (θ2)m и (θ1)M, (θ2)M,– соответственно, минимальные и максимальные величины углов θ1 и θ2 у лучей γ1 и γ2.
Для условия
52°,5<θ1, θ2<89°,9
результат, который Саде получил из его эксперимента, не позволяет сделать выбора между классическим и релятивистским сложением векторов.
Если скорость гамма-лучей складывается со скоростью источника, согласно классическому сложению векторов, то пары гамма-лучей, отобранных устройством Саде, могут быть разделены на следующие группы (см. рис. 2): пары гамма-лучей, порождаемых аннигиляцией позитронов, направление полёта которых ограничено в пределах угла ō –(θ1)m, где ō =(θ1+θ2)/2, и пары гамма-лучей, порождаемых позитронами, направление полёта которых ограничено в пределах угла (θ1)M– ō. В первом случае луч γ2 отстаёт от луча γ1 на время Δt, такое что 0≤Δt≤ΔtM, где Δt=0, если θ1=θ2= ō, и Δt=ΔtM, если θ1=(θ1)m. Во втором случае луч γ2 опережает луч γ1 на время Δt, такое что 0≤Δt≤ΔtM, где Δt=0, если θ1=θ2= ō, и Δt=ΔtM, если θ1=(θ1)M. Таким образом, пик временнóго спектра аннигиляции в полёте имел бы место в точке Δt=0.
Если два гамма-луча движутся с одинаковыми скоростями, согласно второму постулату специальной теории относительности, то эти два гамма-луча достигают детекторов за одинаковое время после прохождения одинаковой дистанции между детекторами и точкой аннигиляции. Поэтому пик временнóго спектра аннигиляции в полёте тоже получится в точке Δt=0 в случае релятивистского сложения векторов. Различие между этими двумя спектрами состоит в том, что временной спектр аннигиляции для классического сложения векторов скоростей является более широким, чем спектр аннигиляции для релятивистского случая. Ширина временнóго спектра аннигиляции в полёте больше чем 2(ΔtM)Max, где (ΔtM)Max – максимальная задержка между этими двумя гамма-лучами, и она возникает, когда луч γ1 движется под углом θ1=52°,5 или под углом θ1=89°,9, и это соответствует задержке порядка ±(ΔtM)Max=0,08 нс. Ширина временного спектра аннигиляции в полёте больше примерно 0,16 нс, что меньшее разрешения по времени τ=0,25 нс оборудования Саде.
Итак, Саде не показал, складывается ли скорость гамма-лучей со скоростью источника согласно классическому сложению векторов, или согласно преобразованиям Лоренца. Автор предлагает повторять этот эксперимент.
[1] D. Sadeh, Phys. Rev. Lett. 10 (1963) 271.
[2] T. Alvager, F.J.M. Farley, J. Kjeliman and I. Wallin, Phys. Lett. 12 (1964) 260.
[3] J.G. Fox, Am. J. Phys. 30 (1962) 297.
[4] S. Berko and F.L. Hereford, Rev. Mod. Phys. 28 (1956) 299.
[5] J.M. Jauch and F. Rohrlich, The theory of photons and electrons (Addison-Wesley, Reading, 1955) pp. 263-274. [Дж.М. Джауч и Ф. Рохлих, Теория фотонов и электронов (Эддисон-Уэсли, Ридинг, 1955) cc. 263-274]
Дата установки: 28.08.2013
[вернуться к содержанию сайта]