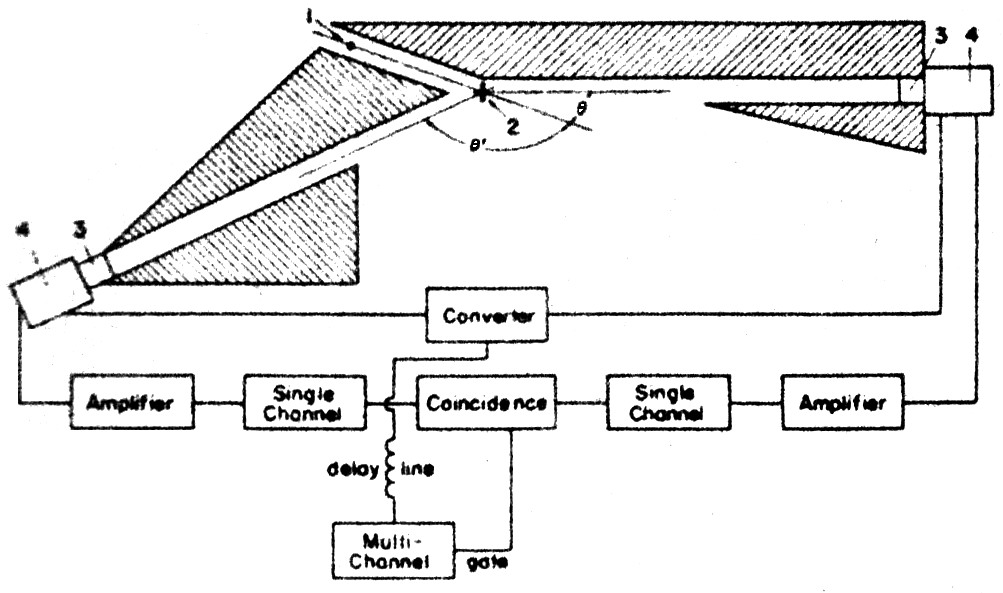
FIG. 1. Experimental arrangement. (1) Cu64 source; (2) Perspex;
(3) NaI(Tl) crystals; and (4) 56-AVP photomultiplier. Shaded area: lead shielding.
[вернуться к содержанию сайта]
During the last 50 years many experiments have been performed1 to prove that the velocity of light is constant and does not depend on the velocity of the source from which it is emitted. A paper published recently2 claims that these experiments do not, in fact, prove the constancy of the velocity of light) but rather they suggest the possibility that light emitted from a moving source does not travel directly to the measuring equipment; instead, it may be scattered by electrons in the neighborhood of the source, so that it is the scattering electron that must be regarded as the moving source. In an experiment which appears to support this theory, the interference fringes produced by light passing through moving glass were observed.3 These fringes showed a shift with respect to those produced when the glass was at rest. According to the author this proved that the velocity of the glass which scattered the light added on to the velocity of the light, and it cast doubt on all previous experiments.
In the opinion of Fox,2 "there may not exist any sure experimental evidence for the second postulate of special relativity." To overcome the problem of the scattering of light it would, according to Fox, be worthwhile to test the second postulate, using gamma rays. The only experiment which measured whether the velocity of gamma rays is dependent on the velocity of the source used gamma rays from bremsstrahlung4; but the conclusions are not sufficiently clear.2
In our experiments we used the annihilation in flight of positrons. In the annihilation the center-of-mass system of the positron and electron moves with a velocity close to ½c, and two gamma rays are emitted. In the case of annihilation at rest, the two gamma rays are emitted at an angle of 180° and their velocity is c. In the case of annihilation in flight, the angle is smaller than 180° and depends on the energy of the positron. If the velocity of the gamma ray adds on to the velocity of the center of mass according to classical vector addition, and not according to the Lorentz transformation, then the gamma ray traveling with a component of motion in the direction of the positron flight will have a velocity greater than c, and that having a component in the opposite direction will have a velocity smaller than c. If it is found that the two gamma rays reach the counters at the same time for equal distances between the counters and the point of annihilation, this would prove that even for a moving source the two gamma rays travel with the same velocity.
We used a 20-curie Cu64 positron source produced in the reactor. The source, in the shape of a disc 0.1 mm thick and 2 cm in diameter, was placed at one end of a lead collimator (see Fig. 1), and at the other end was placed a 1-mm thick layer of Perspex in which the annihilation took place. A 1½-in.×1½-in. crystal of NaI(Tl), coupled to a 56-AVP photomultiplier, was placed 60 cm from the Perspex, at an angle θ of 20° to the motion of the positrons. A similar arrangement was set up at an angle θ' of 135° to the motion of the positrons. A time-to-amplitude converter converted the time differences to pulse heights, and single channels ensured that the only gamma rays gating the multichannel analyzer were those between 0.511 MeV and 0.65 MeV (the energy range of the annihilation-in-flight gamma rays from our source).

FIG. 1. Experimental arrangement. (1) Cu64 source; (2) Perspex;
(3) NaI(Tl) crystals; and (4) 56-AVP photomultiplier. Shaded area: lead shielding.
The stability of the electronic system was tested before and after the experiment and found to be less than one channel, i.e., less than 0.25 nsec. The multichannel analyzer was time-calibrated by measuring the annihilation at rest taking different distances between the source and the crystals.
Since no experimental work has been done on the relation between positron energy and the angles θ and θ' of the gamma rays, we calculated these angles for positron energies between 200 keV and 600 keV. The question which arises is how this calculation should be performed. The accepted way is to transform from the center-of-mass system, in which the gamma rays move at an angle of 180°, to the laboratory system. As relativistic velocities are involved, a Lorentz transformation should be performed, but if the second postulate of the special theory of relativity is being tested one cannot base oneself on it and must revert to the Galilean transformation, that is, the classical addition of vectors. The former method gives an angle of 155.5° for Eβ=300 keV, and the latter gives 157° (for θ=20°). The angles subtended by the counters at the point of annihilation were together 6° in our experiments (between 152° and 159°), so that the problem of which transformation to use does not arise.
Table I gives the velocities of the gamma rays in the θ and θ' directions for different positron energies, as calculated by classical vector addition.
|
Eβ (MeV) |
θ + θ ' |
V/c |
V'/c |
|
0.6 |
150° |
1.41 |
0,63 |
|
0.5 |
155° |
1.38 |
0.66 |
|
0.4 |
155.5° |
1.37 |
0.67 |
|
0.3 |
157° |
1.36 |
0.68 |
|
0.2 |
160° |
1.32 |
0.70 |
Table I. Velocities of the gamma rays calculated according to classical vector addition. E
β is the positron energy; θ+θ', the angle between two counters; and V and V', the velocities of the gamma rays as they would be if they added on to the velocity of the source according to classical vector addition. It is clear from this table that in choosing a certain angle we also chose the energy of the positrons.The upper curve in Fig. 2 gives the spectrum of times recorded for annihilation at rest, i.e., recorded at 180°. The position of the peak is indicated by the dashed line on the right. If in the case of annihilation in flight the velocity of the gamma rays were constant, the peak would occur in the same place. The dashed line on the left marks the place where the peak would be if the velocity of the gamma rays added on to the positron velocity by classical vector addition. The lower curve gives the experimental results obtained for annihilation in flight.
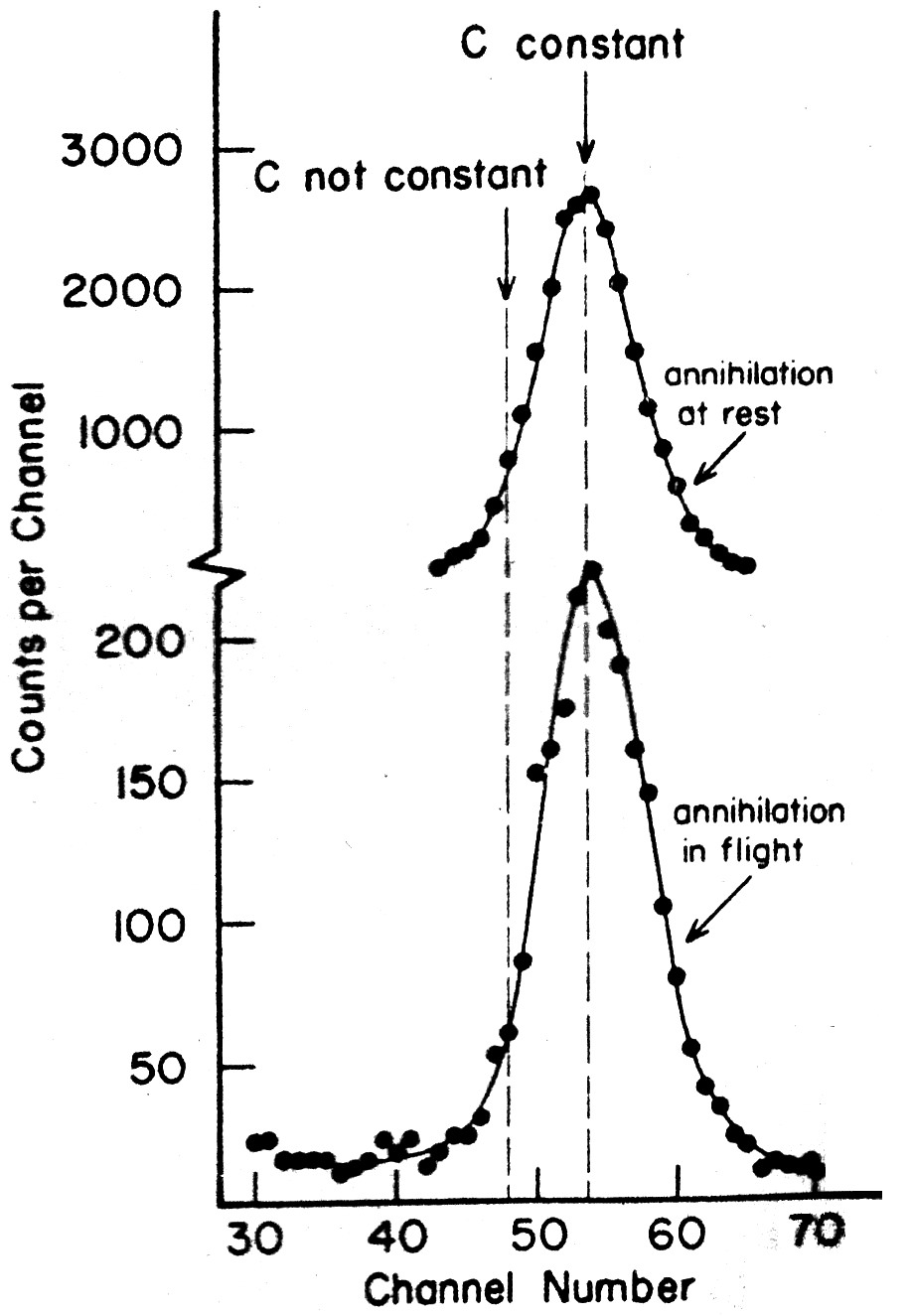
FIG. 2. Time spectrum of annihilation in flight and at rest. Dashed lines show position of peak for c constant and c not constant. The peak of the lower curve would have coincided with the dashed line on the left if the velocity of the gamma rays added on to the velocity of the positrons.
In order to check that annihilation in flight was being measured and not annihilation at rest, a second measurement was performed without the Perspex and no peak was obtained at all. We also calculated that the number of counts fitted well with what is known of the number of annihilations in flight.5,6 The experiment was repeated four times under four different sets of conditions (varying θ, θ', and channel number), and the same results were found.
It is clear from the graph that the velocity of the gamma rays is constant (±10%), in accordance with the second postulate of the special theory of relativity, and does not add on to the velocity of the source.
см. также критические замечания А.Г. Баранова и М. Ло Савио по поводу опыта
Дата установки: 21.08.2013
[вернуться к содержанию сайта]