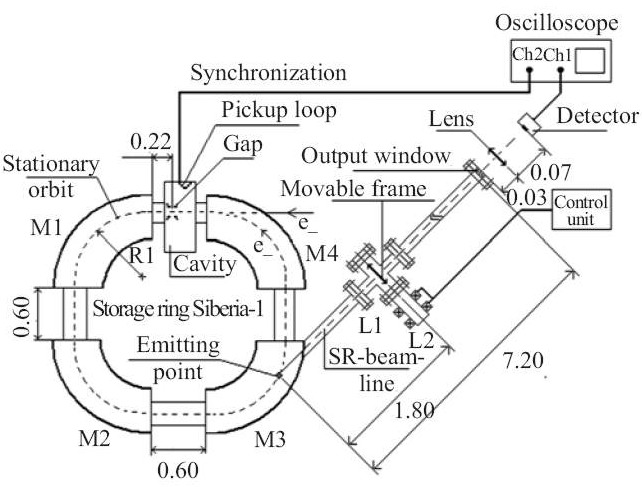
Рис. 1. Схема эксперимента: М1-М4 – поворотные магниты; L1, L2 – катушки магнитного привода каретки. Расстояния указаны в метрах
[вернуться к содержанию сайта]
∆ Физико-технический институт им. А.Ф. Иоффе РАН, С.-Петербург, Россия
○ Научно-исследовательский центр "Курчатовский институт", Москва, Россия
□ Санкт-Петербургский государственный университет, Санкт-Петербург, Россия
Поступила в редакцию 4 июля 2011 г.
После переработки 14 июля 2011 г.
Осуществлено прямое измерение скорости светового импульса от ультрарелятивистского электронного сгустка. Найденная скорость с точностью до 0.3% совпадает с табличным значением скорости света в вакууме. Полученный результат может рассматриваться в качестве наиболее прямого экспериментального подтверждения второго постулата специальной теории относительности А. Эйнштейна.
1. Введение. Утверждение о независимости скорости света от скорости источника было выдвинуто Альбертом Эйнштейном [1] в качестве второго постулата его знаменитой специальной теории относительности (СТО). Обоснованию этого постулата в течение последнего столетия было посвящено множество астрономических наблюдений и экспериментальных исследований, см., например, последние обзоры [2]. Многократно на протяжении этого времени постулат подвергался сомнениям со ссылками на недостаточную точность измерений, что, как правило, было связано с малой скоростью v движения источника по отношению к скорости света c. В настоящей работе мы прямо измерили скорость света от источника, движущегося с ультрарелятивистской скоростью, и нашли, что эта скорость, как и постулировал Эйнштейн, не отличается от табличной скорости света в вакууме.
2. Описание установки и план эксперимента. В основу эксперимента было положено использование синхротронного излучения (СИ) сгустка релятивистских электронов, движущихся со скоростью, очень близкой к скорости света c, по искривлённой траектории в магнитном поле поворотного магнита накопителя электронов. В этих условиях легко померить скорость испущенного света в безукоризненном лабораторном вакууме.
В соответствии с наиболее популярной среди критиков СТО корпускулярно-баллистической гипотезой Ньютона-Ритца [3-5] скорость света, испускаемого сгустком электронов вперёд по касательной к траектории, должна быть равна удвоенной скорости света от неподвижного источника. Это весьма грубый эффект, обнаружение которого (в случае его существования) не потребовало бы специальных ухищрений, имея в виду высокую интенсивность СИ.
Источником СИ служил накопитель электронов Сибирь-1 в Курчатовском центре синхротронного излучения НИЦ КИ [6]. Общая схема эксперимента показана на рис. 1. Магнитная система электронного накопителя, формирующая замкнутую орбиту электронов, состоит из четырёх поворотных 90-градусных магнитов (М1-М4), разделённых четырьмя прямолинейными промежутками длиной по 60 см. Радиус R равновесной орбиты электронов в поворотных магнитах равен 1 м. Индукция магнитного поля на равновесной орбите равна 1.5 Т при номинальной энергии электронов 450 МэВ. Синхротронное излучение, создаваемое релятивистскими электронами в поворотных магнитах, имеет широкий спектр от инфракрасного и видимого до рентгеновского диапазона с характеристической длиной волны 61.3 Å. Оно приводит к потерям энергии в 3.69 кэВ на оборот каждым электроном. Для компенсации потерь в промежутке № 1 накопителя находится высокочастотный (ВЧ) резонатор. Подводимая к нему ВЧ-мощность создаёт на ускоряющем зазоре резонатора напряжение с амплитудой 15 кВ и с частотой 34.53 МГц, равной частоте обращения электронного сгустка в накопителе. Распределение продольной плотности электронов в сгустке является гауссовым со стандартным размером a=0.30 м.

Рис. 1. Схема эксперимента: М1-М4 – поворотные магниты; L1, L2 – катушки магнитного привода каретки. Расстояния указаны в метрах
Ось канала вывода СИ, являясь касательной к равновесной орбите в магните М3, идёт под углом 30° к оси прямолинейного промежутка №4, следующего за магнитом М3. То есть точка излучения (начало отсчёта длины пути СИ вдоль оси канала) находится на расстоянии πR/3 от входного торца магнита М3. Длина канала от точки излучения до выходного сапфирового окна 7.2 м. Камера накопителя и канал вывода СИ составляют один вакуумный объём.
За выходным окном установлена собирающая линза, фокусирующая изображение пучка СИ на окно детектора излучения. В качестве детектора используется кремниевый фотодиод типа PIN Hamamatsu S5972 (область спектральной чувствительности 0.32-1 мкм, полоса частот 500 МГц, эффективная площадь чувствительной зоны 0.5 мм2).
Напряжение, создаваемое фототоком диода на нагрузке (50 Ом), поступало на первый вход двухканального осциллографа Tektronix TDS 3052C (полоса 500 МГц). На второй вход осциллографа подавался непрерывный синусоидальный ВЧ-сигнал синхронизации с измерительной петли резонатора. Чтобы исключить ошибку, вызванную различными фазовыми сдвигами сигналов, их транспортировка осуществлялась по однотипным помехозащищённым (с двойным экраном) коаксиальным кабелям одинаковой длины.
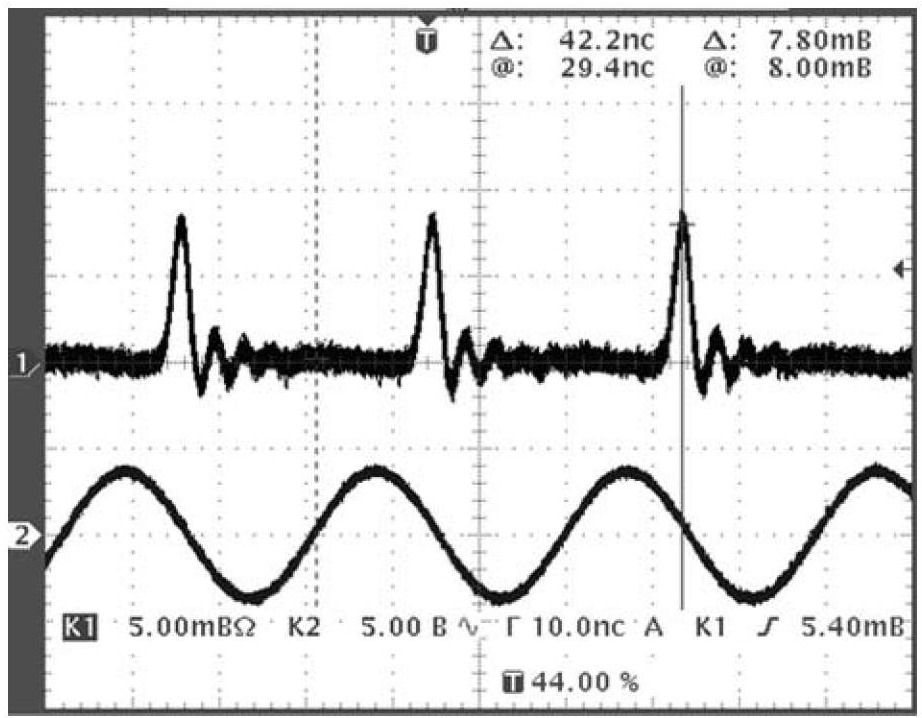
Рис. 2. Осциллограмма импульсов СИ (канал 1) и сигнал синхронизации (канал 2)
На рис. 2 представлена фотография с экрана осциллографа. Скорость развёртки соответствует 10 нс в большом делении. На рис. 3 приведена подобная осциллограмма, растянутая во времени в 2.5 раза и подвергнутая цифровому усреднению для подавления шумов. Рис. 3 даёт представление о достижимой точности измерений.
Как видно, оптический сигнал по форме и длительности весьма близок к идеальной ожидавшейся картине – периодической последовательности гауссовых импульсов с шириной на полувысоте 2.35 нс (см. врезку на рис. 3, где на сигнал фототока наложен расчётный контур оптического импульса). Единственным отличием выступает "звон" на заднем фронте импульсов фототока, связанный с колебательными процессами в цепях фотодетектора. Эта помеха, однако, не мешает решению поставленной задачи.
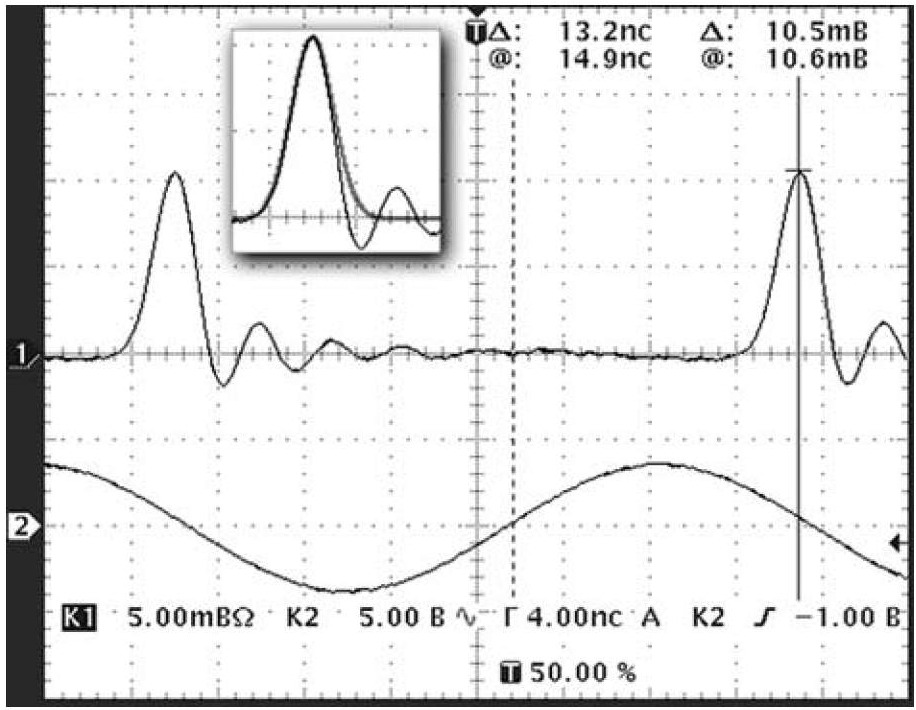
Рис. 3. Растянутая в 2.5 раза во времени и усреднённая осциллограмма. На вставке на осциллограмму СИ наложен гауссов контур, соответствующий неискажённой форме импульса (жирная кривая)
Эксперимент был запланирован в двух версиях. Первая версия предусматривала оперативное перекрытие светового пучка в канале вывода СИ стеклянной пластинкой, закреплённой на подвижной каретке и вводимой в луч с помощью магнитного привода. По логике баллистической гипотезы преломляющая пластина рассматривается в качестве вторичного и уже неподвижного источника света. Поэтому участок канала вывода СИ от пластины до выходного окна свет должен проходить со скоростью c (вместо 2c в отсутствие пластины). Длина участка l равна 5.4 м (см. рис. 1), так что перекрытие пучка СИ стеклянной пластиной должно было бы привести к задержке во времени оптических сигналов на 9.0 нс.
Вторая версия эксперимента предусматривала прямое измерение скорости импульса СИ путём деления длины участка ΔL=7.2 м выводного канала до выходного сапфирового окна на время τ прохождения импульса. Это время можно измерить с помощью осциллографа, используя сигнал синхронизации с учётом его расчётного фазового сдвига относительно момента прохождения электронного сгустка мимо окна выводного канала СИ.
3. Результаты эксперимента. В первой версии измерялся сдвиг оптических импульсов во времени при введении в луч СИ стеклянной пластинки. Сдвиг не был обнаружен с точностью около 0.05 нс. (Задержка, связанная с преломлением света в тонкой пластинке, пренебрежимо мала.)
Во второй версии эксперимента была непосредственно измерена скорость импульса СИ. Она оказалась равной 2.99·1010 см/с, что всего лишь на ~0.3% ниже табличной скорости света в вакууме. Среднеквадратическая случайная ошибка измерения оценена величиной ~±0.2%. Систематическая ошибка определяется точностью измерения длин траектории электронного пучка и луча СИ и не превышает ±0.5%. Детали вычисления и измерения величины т приведены в нашем предварительном сообщении [7].
4. Заключение. В этой работе осуществлено (насколько нам известно, впервые) прямое измерение скорости света, испущенного релятивистским источником. Полученные результаты несовместимы с баллистической гипотезой Ритца, предполагающей галилеевское сложение скорости света со скоростью источника. Показано, что введение стеклянной пластинки в пучок света от ультрарелятивистского источника не меняет скорости света с точностью до долей процента, в то время как по логике гипотезы Ритца эта скорость после прохождения неподвижного окна должна была бы упасть вдвое. Этот эксперимент верифицирует ранее существовавшие астрономические свидетельства справедливости второго постулата СТО (см., например, [8, 9]), которые систематически подвергались сомнению критиками СТО со ссылкой на преломляющее воздействие межзвёздного газа. Дополнительно прямое измерение скорости светового импульса СИ в вакууме привело к величине, совпадающей с табличным значением скорости света с точностью до 0.3%. Результаты измерений могут рассматриваться в качестве наиболее прямого (и окончательного) доказательства справедливости второго постулата СТО.
Идея нашего эксперимента восходит к С.И. Вавилову, который был озабочен защитой СТО ввиду ожидавшейся в конце 40-х годов прошлого века кампании политической атаки на новую физику. Вавилов поручил своему докторанту A.M. Бонч-Бруевичу [10] подготовить и осуществить прямое измерение скорости света от быстрого атомного пучка. Из-за недостаточных технических возможностей того времени реализовать этот план не удалось (более подробно история вопроса изложена в [7]).
Авторы выражают благодарность оперативному персоналу источника СИ ускорительно-накопительного комплекса Сибирь за помощь в проведении экспериментов, чл.-корр. РАН Квардакову В.В. за внимание к работе, директору НИЦ КИ Ковальчуку М.В. за предоставление возможности проведения экспериментов.
Работа выполнена при частичной финансовой поддержке РФФИ (грант #11-02-00538-а) с использованием оборудования ЦКП КЦСИиНТ НИЦ "Курчатовский институт".
1. A. Einstein, Ann. der Phys. 17, 891 (1905).
2. Г.Б. Малыкин, Опт. и спектр. 107, 624 (2009); 109, 1018 (2010).
3. W. Ritz, Ann. de Chim. et de Phys. Ser.8, 13, Février., 145 (1908).
4. W. Kantor, JOSA 52, 978 (1962).
5. О.М. Дуплищева, И.И. Шпирка, Результаты экспериментальных исследований М.И. Дуплищева закономерностей явления излучения и распространения света в Пространстве, Днепропетровск: АРТ-ПРЕСС, 2008, 35 с.
6. A. Filipchenko, V. Korchuganov, Yu. Krylov et al., NIM, A 448, 8 (2000).
7. E.Б. Александров, П.А. Александров, В.С. Запасский и др., УФН 181, №12 (2011).
8. W. de Sitter, Phys. Zeit. 14, 29 (1913).
9. E.Б. Александров, Астроном, журн. 42, 676 (1965).
10. A.M. Бонч-Бруевич, УФН 171, 1087 (2001).
Дата установки: 18.10.2011
[вернуться к содержанию сайта]