К настоящему времени обнаружен ряд космических объектов, у которых орбитальный период быстро меняется. Как правило, эти вариации интерпретируют по эффекту Доплера как результат вариаций орбитальной лучевой скорости тел, входящих в систему. Яркий пример – спутники Юпитера, у которых ещё в XVII веке открыли изменение орбитального периода, задолго до открытия эффекта Доплера [1]. Но в редких случаях изменение столь велико, что его нельзя объяснить доплер-эффектом при типичных скоростях V << c. Кроме того, часто наблюдаются чрезвычайно короткие орбитальные периоды, которые на порядки меньше теоретически возможных. Далее рассмотрим это явление с точки зрения альтернативных эффектов изменения периода, например, с позиций эффекта Ритца – гипотетического эффекта, предсказанного в 1908 г. Ритцем на основе баллистической теории [2, 3] и обоснованного в XXI веке на примере ряда астрономических эффектов, включая аномалии красного смещения в спектрах галактик и квазаров [3–5] и закономерности эффекта Барра [6].

    Суть эффекта состоит в следующем. Рассмотрим источник, излучающий световые сигналы через малый интервал времени dt и удаленный от приёмника на расстояние r. Свет источника, испущенный в момент t, достигнет приёмника в момент t' = t + r/c', где c' – скорость света в вакууме. Время dt' между приёмом двух световых сигналов найдётся дифференцированием t' по t:

.                        (1)

    Здесь рассмотрен общий случай, когда скорость света c' играет роль не константы c (как в СТО), а переменной, как в общей теории относительности (ОТО) и теории Ритца [2, 7]. Второе слагаемое в (1) характеризует эффект Доплера dt' = (1 + V_r/c')dt, т.к. ∂r/∂t = V_r – лучевая скорость источника относительно приёмника, а третье слагаемое характеризует изменение длительности сигналов за счёт вариаций скорости света. Данный эффект

,                            (2)

следует из баллистического принципа c' = с + V (классическое сложение скоростей [1, 7]), по которому скорость света c' меняется от добавления скорости V источника (в противоположность СТО, где в вакууме всегда c' = с). Отметим, что на данный момент нет экспериментов (включая анализ Де Ситтера и опыт Е.Б. Александрова), которые однозначно б доказали ошибочность баллистического принципа [3, 5, 8]. И напротив, есть ряд астрономических наблюдений, эффектов, закономерностей, свидетельствующих в пользу теории Ритца [3, 6, 8–10]. Из баллистического принципа в направлении приёмника скорость света c' = с – V_r, где V_r – лучевая скорость источника (проекция V на луч зрения – на радиус-вектор r источника). Дифференцируя ∂c'/∂t = -∂V_r /∂t = -a_r (где a_r – лучевое ускорение источника – проекция вектора a на r) и подставляя в (2), при V_r << c, найдём

.                            (3)

    Природа эффекта очевидна: согласно баллистической теории, ускоряемый источник в каждый последующий момент сообщает свету новую скорость, и последовательные сигналы (или фронты световых волн), испущенные с разными скоростями, догоняют друг друга (сокращая длину волны λ), либо расходятся (наращивая λ), приходя к приёмнику чаще или реже. Из преобразования интервалов dt (3), периода T световых колебаний T' = Tdt'/dt и закона сохранения энергии света, найдём для изменения исходной длины волны λ' = cT', частоты света f' = 1/T', длительности импульса Δt', и его интенсивности I' (по сравнению с интенсивностью I света от такого же, но неподвижного источника), преобразованные параметры (штрихованные) по сравнению со статическими (нештрихованными) в той же системе:

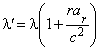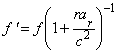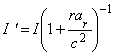, , , .        (4)

    Эффекты (3) и (4), дополняющие эффект Доплера, далее будем называть эффектом Ритца, т.к. формула (3) выведена швейцарским физиком В. Ритцем в 1908 г. [2, с. 251]. Возможным подтверждением эффекта служит красное смещение z = (λ' – λ)/λ в спектрах галактик, тоже пропорциональное расстоянию r галактик, с соответствующим растяжением длительности процессов в галактиках [3–5]. Из (1) при V_r << c следует преобразование в сумме от эффектов Доплера и Ритца

, .                    (5)

    Доплер-эффект dt' = (1 + V_r /c)dt легко регистрируется в лаборатории, а эффект Ритца (3) обнаружить существенно сложнее, ввиду малости ra_r /c² << 1. Но на космических дистанциях r порядка светового года малые ускорения a_r ~ c²/r ≈ 9,5 м/с² могут менять видимую длительность процессов и длину волны в разы. Этим, в частности, можно объяснить короткие частые вспышки пульсаров, которые могут представлять собой обычные двойные звёзды, значительно меняющие частоту f'(t) и интенсивность излучения I'(t) по эффекту Ритца (4) при вариациях лучевого ускорения a_r(t) [4, 10, 14].

    Если эффект (4) имеет место, и видимое движение звёзд искажается, тогда, кроме отмеченного искажения, произойдёт дополнительное к эффекту Доплера смещение спектральных линий по закону (4). Общее изменение периода и длины волны спектральной линии задано формулой (5). Таким образом, красное смещение z представлено суммой смещений по эффекту Доплера и по эффекту Ритца:

.                        (6)

    Интерпретируя это смещение как чисто доплеровское, получают при спектральных измерениях не совпадающее с истинным V_r расчётное значение лучевой скорости

.                  (7)

где V_r^* – дополнительная мнимая лучевая скорость, обусловленная эффектом Ритца.

    Для графиков лучевых скоростей звёзд, движущихся по круговой орбите, эффект Ритца приведёт к изменению орбитальной фазы звезды. Истинная лучевая скорость звезды задана выражением V_r = -Ksin(2πt/P). А при учёте ускорения a_r = dV_r/dt = –(2πK/P)cos(2πt/P), вносимая эффектом Ритца добавочная мнимая (кажущаяся) скорость составит V_r^* = ra_r/c или V_r^* = la_r/c (в случае переизлучения света межзвёздным газом на длине l [3, 8]). Отсюда найдём, что расчётная скорость задана выражением

,                (8)

где сдвиг по фазе φ = arctg(2πl/Pc), а расчётная амплитуда лучевой скорости

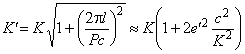,                        (9)

в приближении параметра e' = πlK/Pc² << 1. Кроме того, произойдёт искажение наблюдаемого графика лучевых скоростей V_r'(t'), если в качестве времени брать не время t в системе источника, а время t' в системе земного наблюдателя. Тогда график лучевых скоростей V_r'(t') будет соответствовать не круговой, а приблизительно эллиптической орбите с эксцентриситетом e' (см. подробнее о параметре e' в [6]).

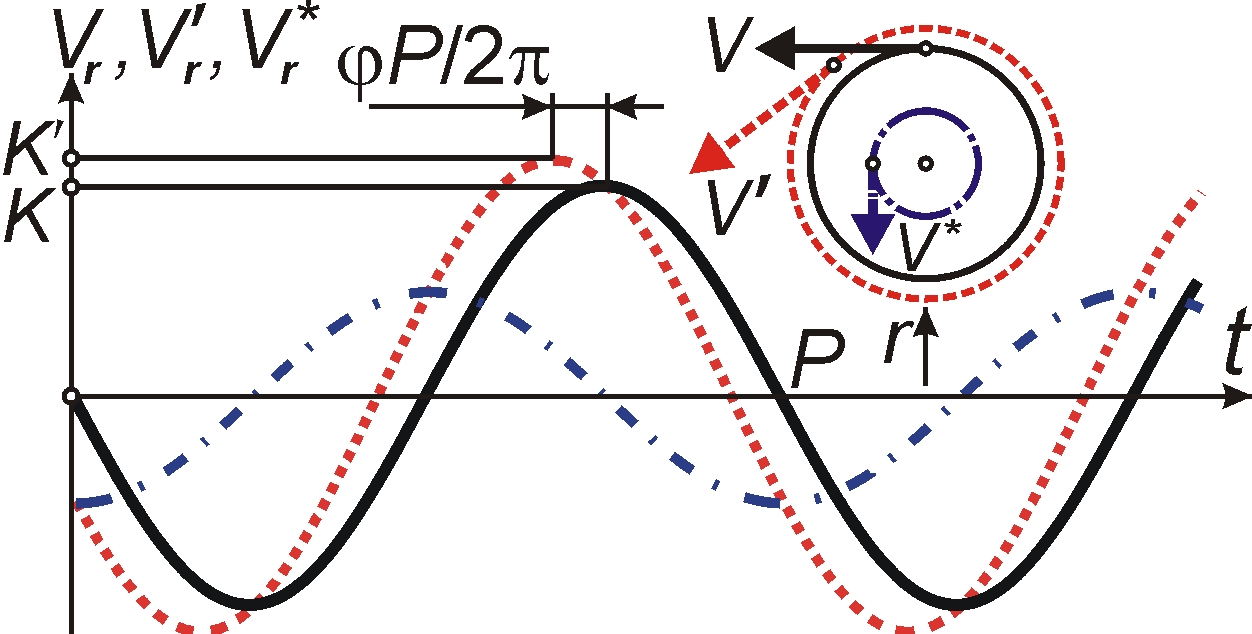
Рис. 1. Схема искажения доплеровской кривой лучевых скоростей V_r(t) (сплошная линия) от дополнительного сдвига частоты по эффекту Ритца в виде кривой мнимых лучевых скоростей V_r^*(t) = la_r/c (штрих-пунктирная линия) и соответствующие круговые орбиты. Результирующая кривая спектральных смещений (пунктирная линия) дает ложную доплеровскую скорость V_r'(t) = V_r(t) + V_r^*(t).

    Смещение по фазе графика лучевых скоростей V_r'(t) (Рис. 1) будет заметно у спектрально-двойных звёзд, наблюдаемых одновременно как затменно-двойные. Теоретически затмение звезды с круговой орбитой наблюдалось бы в момент наибольшего её удаления в фазе кривой лучевых скоростей 0. Если кривая смещена эффектом Ритца, затмение произойдёт с запозданием на разность фаз φ, достигающую π/2 (или в орбитальной фазе Φ = φ/2π = 0.25 в астрономических обозначениях),– в предельном случае, когда смещение спектра обусловлено в основном эффектом Ритца. Фазовые несоответствия кривых блеска и лучевой скорости реально открыты, например у υ Андромеды [11], а также у ряда тесных двойных звёзд, что обычно интерпретируют по гипотезе неоднородного распределения яркости по поверхности звезды. Эффект обнаружен также у двойного пульсара PSR 1957+20, у которого затмение наступает в орбитальной фазе Φ = 0.25 [12], совпадающей с предельным значением Φ, при котором вариации периода пульсара почти целиком обусловлены эффектом Ритца.

    Если пара звёзд в кратной системе движется с общим ускорением a_r в поле тяготения третьей звезды, тогда в соответствии с (4) будет меняться наблюдаемый орбитальный период P' системы по сравнению с истинным P. Но, в отличие от доплер-эффекта (например для спутников Юпитера), сокращение измеренного периода P' по эффекту Ритца будет значительным при достижении a_r критической величины |a_r| ~ a₀ = c²/r. Причём период P' может уменьшаться на порядки и быстро меняться при a_r ≈ -a₀  и малых вариациях a_r возле -a₀ как

,

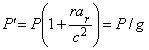где g – коэффициент компрессии, сжатия масштаба времени.

    Подобный эффект наблюдался у рентгеновского пульсара GX 1+4, период P₁' пульсаций которого в течение 15 лет сокращался, пока в 1985 г., достигнув минимума, не стал столь же быстро нарастать (рис. 2). Для объяснения этих вариаций P₁' формально приняли, что магнитные поля и трение вращающегося газового кольца, ускорявшего вращение звезды, стало тормозить её вращение [13]. Но до сих пор не выяснены причины смены направления при сохранении величины момента сил трения, который огромен, т.к. за 10 лет он в 2 раза повысил гигантскую энергию вращения пульсара, а затем столь же быстро затормозил вращение. Ритц-эффект элементарно объясняет эти вариации как иллюзорные [14], если предположить, что пульсар с периодом P₁ входит в кратную систему, двигаясь вокруг главной звезды с большим орбитальным периодом P₂ = 2π/ω и орбитальным лучевым ускорением a_2r. Сначала в ходе орбитального движения звезды (приблизительно по круговой орбите) ускорение пульсара a_2r = a₂cos(ωt) приближалось к -a₀, сокращая регистрируемый период P₁' = P₁ + P₀cos(ωt), а затем стало отдаляться от -a₀, наращивая P₁', где P₀ = P₁ra₂/c². Масштаб времени dt' = dt/g сжат пропорционально коэффициенту компрессии g, откуда t' = t + P₀sin(ωt)/ωP₁. Т.е. график наблюдаемых вариаций P₁'(t') представляет собой трохоиду (укороченную циклоиду). Возле минимума (заострения трохоиды) P₁' меняется почти линейно, как у GX 1+4 [15]. Аналогичные вариации наблюдались у пульсара 4U0900-40 [16, с. 594]. Небольшие отклонения точек от трохоиды связаны, вероятно, с малыми вариациями a_r в поле тяготения спутников, соответственно меняющих P₁' (так наблюдается дополнительная регулярная вариация P₁' с периодом в 304 сут [18], соответствующих орбиальному периоду гипотетического спутника), а также с тем, что истинное движение пульсара происходит не по круговой, а по эллиптической орбите. Для точного совмещения теоретической и экспериментальной кривой P'(t') и определения параметров орбиты пульсара следует произвести на ЭВМ перебор параметров e, a, ω орбиты, минимизирующий сумму квадратов отклонений экспериментальных точек от теоретической кривой, либо представлять зависимость a_2r(t) в виде полинома, ряда, подбирая коэффициенты по методу [17]. При минимальном периоде P₁' ≈ 100 с звезда перестала излучать рентгеновские лучи. В рамках баллистической теории это – следствие выросшей степени компрессии g, переводящей оптическое излучение звезды уже не в рентгеновский, а в гамма-диапазон. Но в гамма-лучах звезду на тот момент не исследовали, и её гамма-переменность остаётся под вопросом.

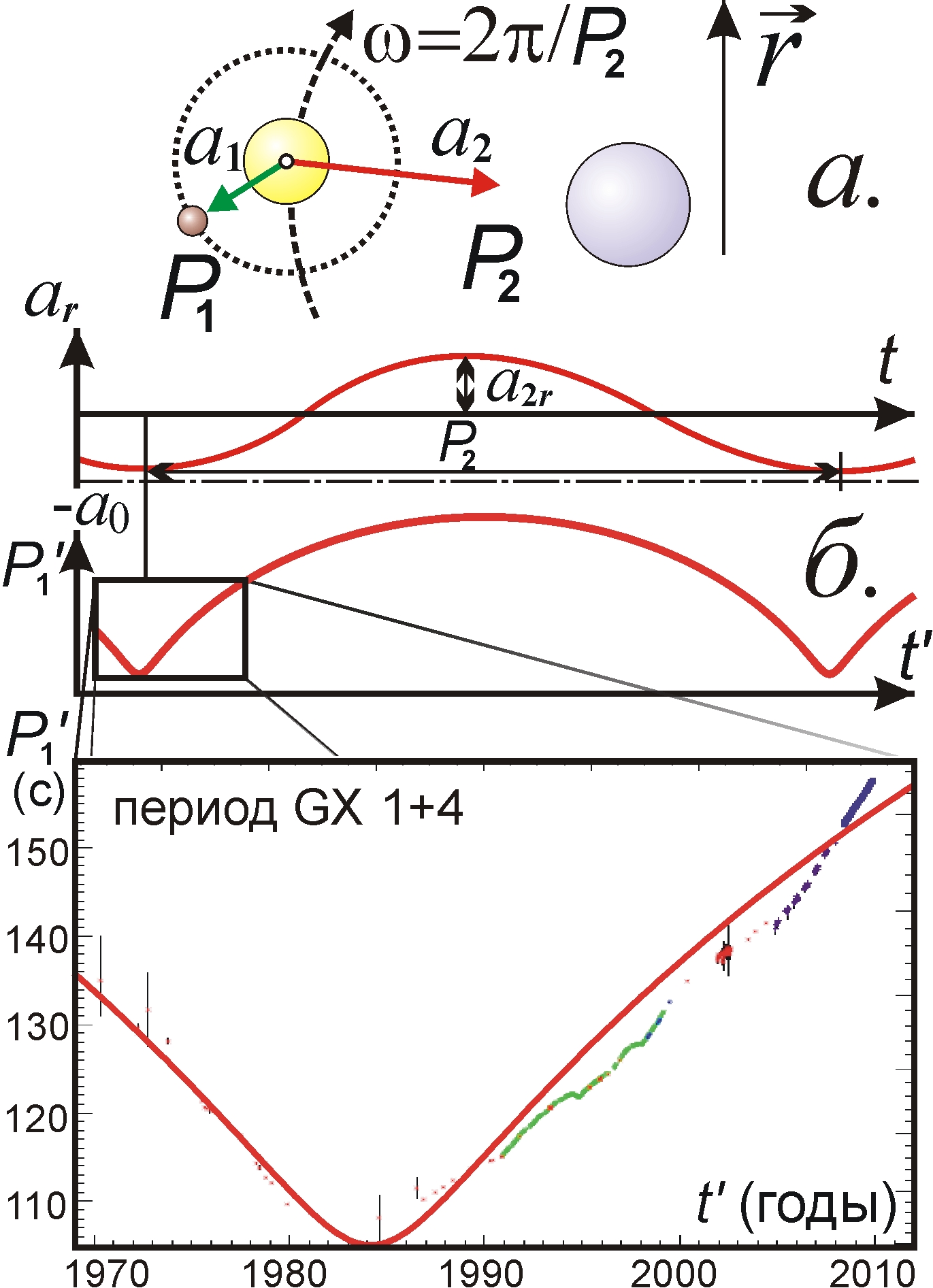
Рис. 2. Возможное строение системы пульсара GX 1+4 (а) и вариации его периода P₁' за счёт ускорения звезды и эффекта Ритца (б). Сплошная линия P₁'(t') – теоретическая кривая (моделирование по эффекту Ритца), точки с интервалами погрешностей – результат измерений периода [13, 15].

    Сами вспышки (вариации I'(t)), очевидно, обусловлены регулярной компрессией света двойной звезды по эффекту Ритца (4). Это подтверждает пример пульсара GX 5-1, у которого мощность вспышек нарастает пропорционально интегральной светимости звезды, как у ряда других пульсаров и переменных звёзд [14]. Колебания лучевого ускорения могут быть связаны либо с орбитальным движением двойных звёзд, либо с пульсацией их поверхности. Так, у звёзд типа β Большого Пса, β Цефея и пекулярных Ap-звёзд главной последовательности, у которых открыты осцилляции блеска с периодом 5–20 минут, механизм переменности может быть комбинированным. Т.е. яркость варьирует за счёт малых пульсаций атмосферы звезды и за счёт эффекта Ритца, усиливающего малые осцилляции яркости I'. Так, в атмосфере Солнца открыты пятиминутные колебания [16, с. 301]. Сами по себе столь быстрые колебания не способны привести к заметному изменению радиуса, температуры и истинной яркости звезды, и колебания блеска нельзя объяснить в рамках теории пульсаций. Но модуляция лучевой скорости атмосферы звезды (с амплитудой 100–200 м/c) ведёт по эффекту Ритца к заметным вариациям яркости, как показал С. Девасиа [19]. Такие короткопериодные осцилляции блеска с периодом в несколько минут реально наблюдаются у ряда звёзд, например у V391 Пегаса, у белых карликов [16, с. 142]. Т.к. амплитуда осцилляций блеска высока, наиболее вероятная их причина – эффект Ритца. У пульсаров, движущихся вокруг главной звезды с ускорением a_r ≈ -a₀, орбитальный период (P ~ 1 сут) или пульсационный период (P ~ 1 мин) компрессируется до P' по эффекту Ритца (4), уменьшаясь в миллионы раз (g ~ 10⁶). Это объясняет также бимодальность в распределении периодов P' пульсаров, т.е. группирование периодов возле значений порядка секунд и миллисекунд.

    Другим примером служит объект T5X2 (пульсар IGR J17480-2446 в скоплении Terzan 5), у которого тоже обнаружена переменность блеска в рентгеновских лучах: помимо обычных пульсаций с частотой 11 Гц, наблюдаются квазипериодичные осцилляции (QPO) с частотой порядка мГц [20]. В течение одного месяца у T5X2 период квазипериодичных осцилляций сократился с 1000 до 200 с, а затем снова вырос до 1000 с (рис. 3). Рост частоты колебаний блеска в 5 раз (с 1 мГц до 5 мГц) сопровождался пропорциональным нарастанием средней рентгеновской яркости в 5 раз. Как видно из рис. 3, максимум рентгеновского блеска точно соответствует максимальной частоте колебаний блеска. Это естественно интерпретировать как проявление эффекта Ритца (4): приближение ускорения системы к критическому (как на рис. 2) сопровождается пропорциональным ростом частоты колебаний блеска и интенсивности в 4–5 раз, согласно ф-ле (4). Видимо, близость ускорения a_r к критическому -a₀ и делает T5X2 рентгеновским источником, преобразуя свет звезды главной последовательности в рентгеновский диапазон.

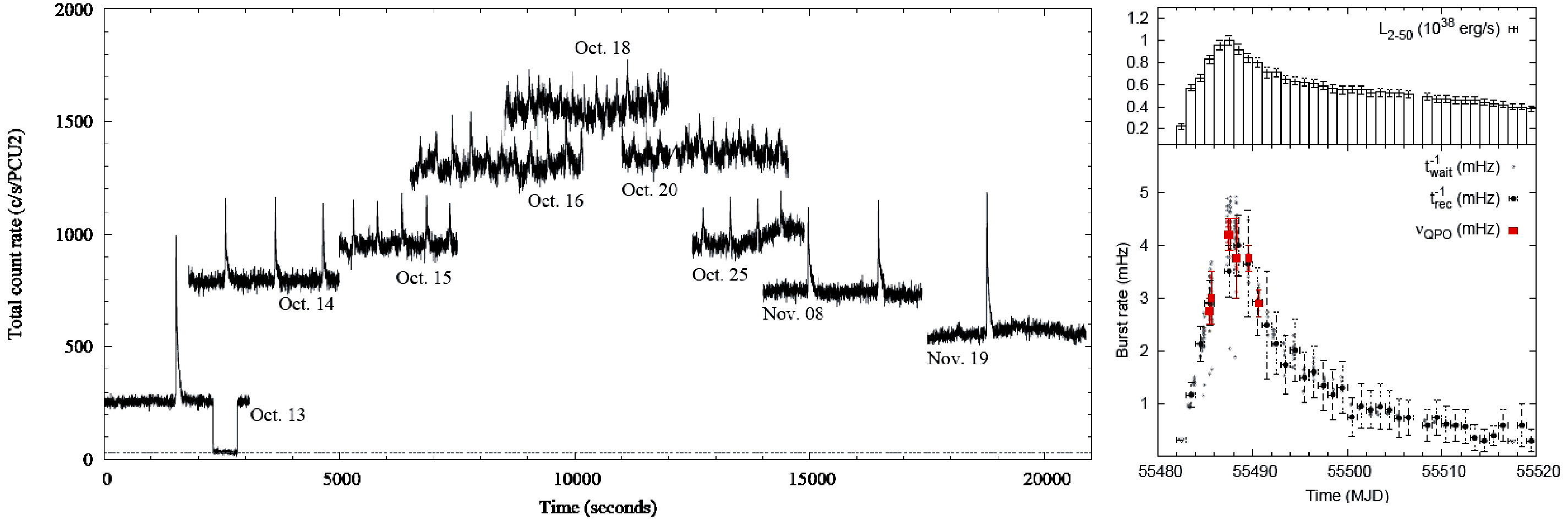
Рис. 3. Слева – график колебаний рентгеновской яркости объекта T5X2 (IGR J17480-2446) в 2010 г. Справа – графики колебаний средней рентгеновской яркости и частоты QPO вариаций блеска [20].

    Параллельный рост интенсивности и цветовой температуры (частоты спектрального максимума) рентгеновского излучения обнаружен также у пульсара IGR J18245-2452 [21]. Отметим, что у него пульсации рентгеновского блеска имеют вид почти идеальных синусоид. Это свидетельствует о колебаниях, обусловленных движением звезды по круговой орбите с лучевым ускорением a_r, меняющимся по гармоническому закону. По эффекту Ритца при малой глубине модуляции a_r(t) относительно уровня -a₀ (m << 1) это ведёт к колебаниям блеска по гармоническому закону [14].

    Подобное иллюзорное ускорение процессов, вероятно, наблюдается и в случае других аномально быстрых движений или аномально быстрых изменений, например в центре нашей Галактики [10, 22]. В частности, в районе галактического центра – радиоисточника Sgr A* наблюдаются аномально быстрые движения звёзд возле гипотетической сверхмассивной чёрной дыры с массой M' ~ 4×10⁶M¤ . Предполагают, что именно сверхмассивная чёрная дыра и создает силы тяготения, достаточные для удержания быстрых звёзд на широких орбитах. Причём гигантские скорости звёзд устанавливают как по видимому движению, так и по спектрально измеренной кривой лучевых скоростей, которая достаточно точно соответствует наблюдаемому движению звёзд [23, 24]. Однако можно рассмотреть и другие объяснения аномально быстрых движений в центре Галактики, тем более, что другие факты противоречат существованию там сверхмассивной чёрной дыры. Отсутствие сверхмассивных тел в центре нашей и других галактик подтверждает спектр излучения этих участков, который соответствует крайне разреженному газу, судя по наличию в спектре запрещённых линий [25, с. 374]. Присутствие сверхмассивных чёрных дыр вызывало б аккрецию на них межзвёздного газа, т.е. повышение его концентрации и температуры. Кроме того, не наблюдается релятивистской прецессии – смещения периастров орбит, которое в гигантском поле тяготения происходило б намного быстрее, чем у Меркурия.

    Таким образом, сверхбыстрые движения звёзд в центре Галактики вряд ли вызваны тяготением сверхмассивной чёрной дыры. Естественней предположить, что наблюдается иллюзорный рост скорости видимого движения звёзд за счёт движения звёздной системы с лучевым ускорением a_с близким к критическому a_с ≈ -a₀. Например, если звёздная система с массивной центральной звездой движется с ускорением a_с ≈ -a₀ в поле тяготения другой массивной звезды или звёздного скопления.

    Решим задачу строго и рассчитаем во сколько раз ускоряется видимое движение звезды, если (1 + ra_с/c²) = b << 1, т.е. коэффициент компрессии g, показывающий, во сколько раз убыстрено по сравнению с истинным видимое движение, будет равен g = dt/dt' = 1/b >> 1. В случае предельного сближения ускорения с критическим -a₀ будет наблюдаться эффект сверхмодуляции частоты (СЧМ), когда малые модуляции скорости света с' = c – V_r, вызванные собственными движениями звёзд с лучевой скоростью V_r, приводят к гигантским вариациям частоты. В общем случае из (5), если учесть с' ≠ c и считать собственные орбитальные ускорения звёзд малыми (т.е. их результирующее лучевое ускорение a_r ≈ a_с), период световых колебаний преобразуется как

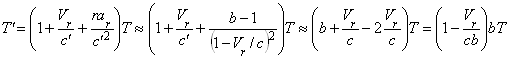.                (10)

    Таким образом, движение звёзд выглядит ускоренным в g = 1/b раз, так что измеренная астрометрически трансверсальная скорость звёзд V_t'(t) = V_tT/T' = V_t(t)/b. А измеренная спектроскопически лучевая скорость, если исследовать относительные смещения линий от их средних положений, составит V_r'(t) = -V_r(t)/b. Таким образом, в обоих случаях происходит иллюзорное увеличение скорости в g = 1/b раз, но во втором случае расчётное направление скорости становится обратным. Казалось бы, это приведёт к несоответствию наблюдаемого астрометрически движения и измеренного спектроскопически движения звёзд. Однако фактически, от неоднозначности угла i = i₀ наклонения орбиты, поскольку наблюдается только проекция орбиты и видимого движения на картинную плоскость (рис. 4), им могут соответствовать два астрометрически неразличимых варианта расположения орбиты i = i₀ и i = -i₀. Соответственно, каждому расположению звезды будут отвечать два возможных значения лучевой скорости V_r' = V_r0 и V_r' = –V_r0. Таким образом, в элементах орбиты, определённых астрометрически и спектроскопически, не будет противоречий, но вместо истинного угла i = i₀ получится ложное, противоположное значение i = -i₀, которому соответствует противоположное по знаку значение лучевой скорости -V_r0.

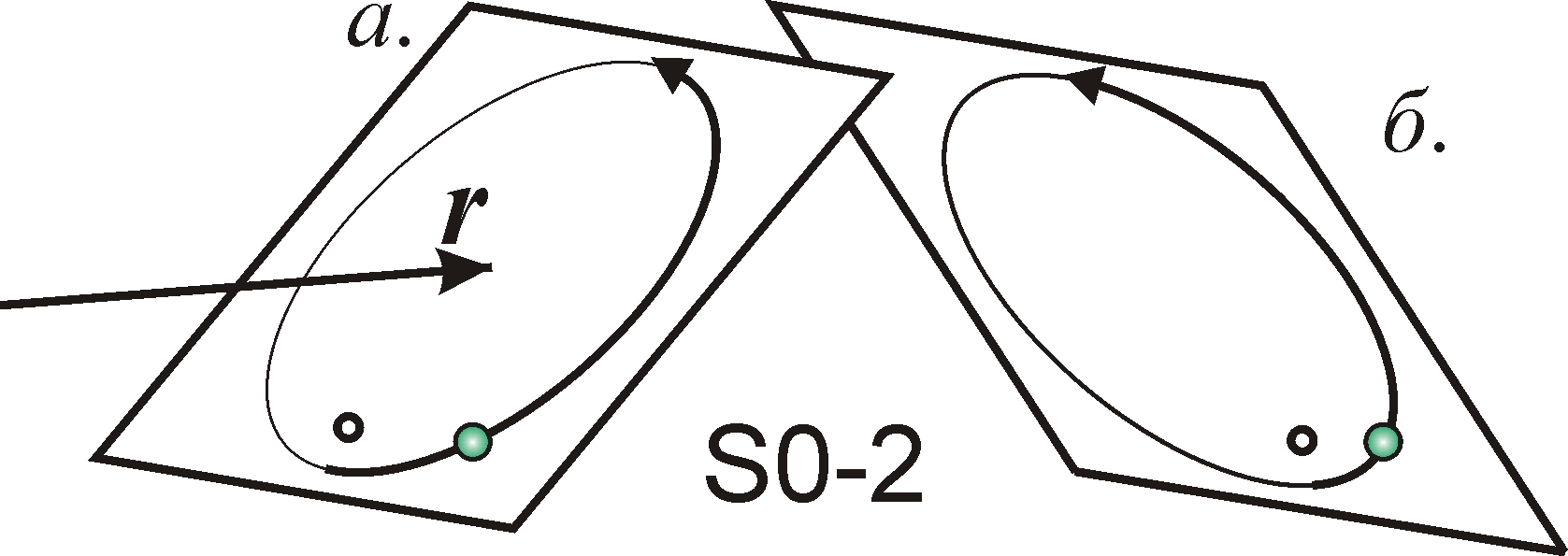
Рис. 4. Два варианта расположения орбиты S0-2 (а и б) по отношению к лучу зрения r, соответствующие одинаковому видимому движению звезды S0-2 на картинной плоскости, но противоположным по знаку кривым лучевых скоростей V_r(t).

    Тем не менее, несоответствие можно выявить, исследуя спектр звезды, в котором удается чётко выделить спектр поглощения и излучения межзвёздного газа [24]. Если для истинной орбиты с i = i₀ наиболее далекой точке (V_r = 0 и убывает) будет соответствовать наиболее интенсивный спектр поглощения межзвёздного газа, то для ложной орбиты с i = –i₀ тому же движению звезды на картинной плоскости соответствует наиболее близкое расположение звезды и наименее интенсивный спектр поглощения газа. Таким образом, если картина вариаций спектра поглощения будет обратной к ожидаемой, или если у некоторых звёзд затмения центральной звездой происходят в нерасчётные моменты времени, это будет означать, что i определено неверно, и наблюдается обращение знака лучевой скорости. Кроме того, если ориентироваться не на относительное смещение спектральных линий, а на абсолютное, можно будет тоже обнаружить несоответствие, т.к. из формулы (10) при g ~ 10³ по эффекту Доплера получится мнимая лучевая скорость V_r' ~ -c. Таким образом, наблюдается огромное смещение спектральных линий, которое не обнаруживают исключительно от неверного отождествления спектральных линий. Видимо, регистрируемые спектральные линии гелия и брома на деле соответствуют низкочастотному излучению дальнего ИК-диапазона и радиолиний водорода и гелия, смещённых ритц-эффектом в ближний ИК-диапазон.

    В случае, если измеряемые астрометрически и спектроскопически движения звёзд возле галактического центра иллюзорно ускорены эффектом Ритца в g = 1/b ~ 400 раз, тогда истинные скорости окажутся много меньше, а орбитальные периоды – много больше расчётных. Например, у звезды S0-2, вместо измеренной скорости V_r' ~ 4000 км/с, найдём, что истинная скорость V_r ~ 10 км/с, а орбитальный период не P' = 15 лет, но P = 6000 лет. Соответственно, масса центральной звезды получится не M' ~ 4·10⁶M_¤, а M = M'/g² ~ 25M_¤ , т.е. величина типичная для звёзд главной последовательности классов O и B. При этом характерные массы звёзд-спутников, движения которых наблюдают, составят порядка 0.1M_¤ , что типично для красных карликов. Чтобы звёздная система двигалась в течение такого времени P ~ 6000 лет с лучевым ускорением близким к критическому a_с ≈ -a₀, она должна лететь в поле тяготения шарового скопления, расположенного от звезды на расстоянии R ~ 100000 а.е. и имеющего массу M ~ 10⁷M_¤ . Такое скопление может состоять из 10⁶ звёзд с массой ~10M_¤ . При этом шаровое скопление может иметь размер ~10000 а.е. и будет приводить к движению центральной звезды с периодом P ~ 10000 лет. Таким образом, отпадает надобность в центральной чёрной дыре, а наблюдаемые явления можно объяснить движением обычной звёздной системы по орбите вокруг крупного звёздного скопления.

    Такие массивные плотные скопления как раз типичны для центральной области Галактики – керна, в котором концентрация звёзд максимальна. Да и сам центр служит центром тяготения, способным обеспечить критическое ускорение a_с ≈ -a₀. Действительно, по известному распределению масс в керне [16, с. 197], шар радиуса R с центром в центре Галактики обладает массой M(R) = kR, где k ≈ 10⁷M_¤ пк^–1. Отсюда критическое расстояние R_c найдётся из ускорения на поверхности шара такого радиуса равного критическому a₀ = GM/R_c². Откуда R_c = Gkr/c² = 1.5×10¹⁴ м = 1000 а.е. Это значение R_c в пределах одного порядка соотносится с измеренными полуосями орбит S0-2 и других звёзд, движущихся вокруг центрального объекта [23, 24]. Таким образом, внутри шара такого радиуса в центре галактики многие объекты, летящие вокруг центра, будут обладать ускорением порядка критического a₀. В итоге, эффект сверхмодуляции частоты позволяет элементарно интерпретировать активность центров галактик в виде вспышек и иной быстрой переменности блеска и спектра во всем диапазоне электромагнитных волн, а также позволяет объяснить аномально быстрые движения в центре нашей (Sgr A*) и других галактик.

    Показано, что гипотетический эффект Ритца, который следует из классических преобразований для скорости света от движущегося источника, объясняет ряд эффектов, включая красное смещение галактик, быстрые изменения частоты света звёзд, искажение формы графика лучевых скоростей и видимого движения двойных звёзд и экзопланет, а также быстрые изменения их периодов. Эффект элементарно объясняет наблюдаемые аномалии графиков лучевых скоростей и кривых блеска у двойных звёзд, пульсаров и экзопланет. Предсказанный на основе теории Ритца эффект сверхмодуляции частоты света элементарно объясняет аномально быстрые движения звёзд в центре Галактики, возле гипотетической сверхмассивной чёрной дыры. Также эффект сверхмодуляции частоты естественно объясняет активность ядер галактик – быструю переменность блеска и спектра ядер, в том числе в радио-, рентгеновском и гамма-диапазонах.

    Материалы статьи доложены на 36-х Научно-футурологических чтениях 7 августа 2014 г. [26], на 68-ой научно-технической конференции-семинаре НТОРЭС в ННГУ 18 октября 2016 г. [27] и на XX научной конференции по радиофизике 13 мая 2016 г. [28]. Автор выражает благодарность профессору Нижегородского госуниверситета М.И. Бакунову за критические замечания и дискуссии, уточнившие обоснование эффекта Ритца. Кроме того, автор выражает признательность за обсуждение и организацию семинара в ИПФ РАН по эффекту Ритца сотрудникам ИПФ РАН В.В. Кочаровскому и Г.Б. Малыкину. Отдельную благодарность автор выражает А.М. Чепику, своими конструктивными замечаниями и уточнениями способствовавшего установлению эффекта сверхмодуляции частоты.

СПИСОК ЛИТЕРАТУРЫ

Дата установки: 24.03.2017
[вернуться к содержанию сайта]