[вернуться к содержанию сайта]
Исследуется ориентация линий апсид орбит спектрально-двойных звёзд, содержащихся в каталогах А. Бечваржа и А. Бэттена. Устанавливается преимущественная концентрация за картинной плоскостью периастров звёзд с периодом Р>20d и лучевой скоростью Vr<0. Обнаруживается наличие галактической ориентации линий апсид этих звёзд.
Даётся возможная интерпретация В-эффекта и Е-эффекта. Доказывается теорема о расположении линии апсид в плоскости, перпендикулярной вектору возмущающей силы. Показывается, что в результате взаимодействия звёзд с межзвёздной средой проекции линий апсид орбит двойных звёзд на плоскость галактического экватора ориентируются параллельно большой оси их галактических орбит.
Высказывается предположение о том, что короткопериодические и долгопериодические двойные звёзды отличаются направлением взаимного обращения компонентов.
ON GALACTIC ORIENTATION OF SPECTRAL DOUBLE-STARS ORBITS, by E. F. Brazhnikova, M. M. Dagaev, V. V. Radzievsky. – The orientation of orbits apsid lines of spectral double-stars c
ontained in the A. Bečvář's and A. Batten's catalogues is investigated. It is established that periastrons of the spectroscopic binaries with periods Р>20d and radial velocity Vr<0 are mostly concentrated behind the tangent plane. The galactic orientation of the apsid lines of these stars is discovered.В 1908 г. Барр [1] впервые обратил внимание на несимметричность распределения периастров орбит спектрально-двойных звёзд относительно картинной плоскости: у периастров орбит более ярких компонентов* имеется явно выраженная тенденция находиться за картинной плоскостью, проведённой через центр масс бинарной системы. Следуя работам [2, 3], будем для краткости называть этот феномен В-эффектом. Его подтверждению и интерпретации посвящён ряд работ [2–15].
В настоящей статье мы подтвердим существование В-эффекта у долгопериодических пар и попытаемся дать ещё одну возможную интерпретацию этого феномена.
Для исследования В-эффекта были отобраны из каталогов Бечваржа [16] и Бэттена [17] все спектрально-двойные звёзды с периодом Р>20d и надёжными значениями долготы периастра ω. Звёзды, орбиты которых, по утверждению Бэттена [17], определены неуверенно, использованы не были.
Статистическая обработка элементов орбит 164 звёзд из каталога Бечваржа [16] и 130 звёзд из каталога Бэттена [17] проводилась раздельно. Полученные результаты оказались сходными и поэтому материалом для настоящей статьи послужили данные более нового каталога Бэттена.
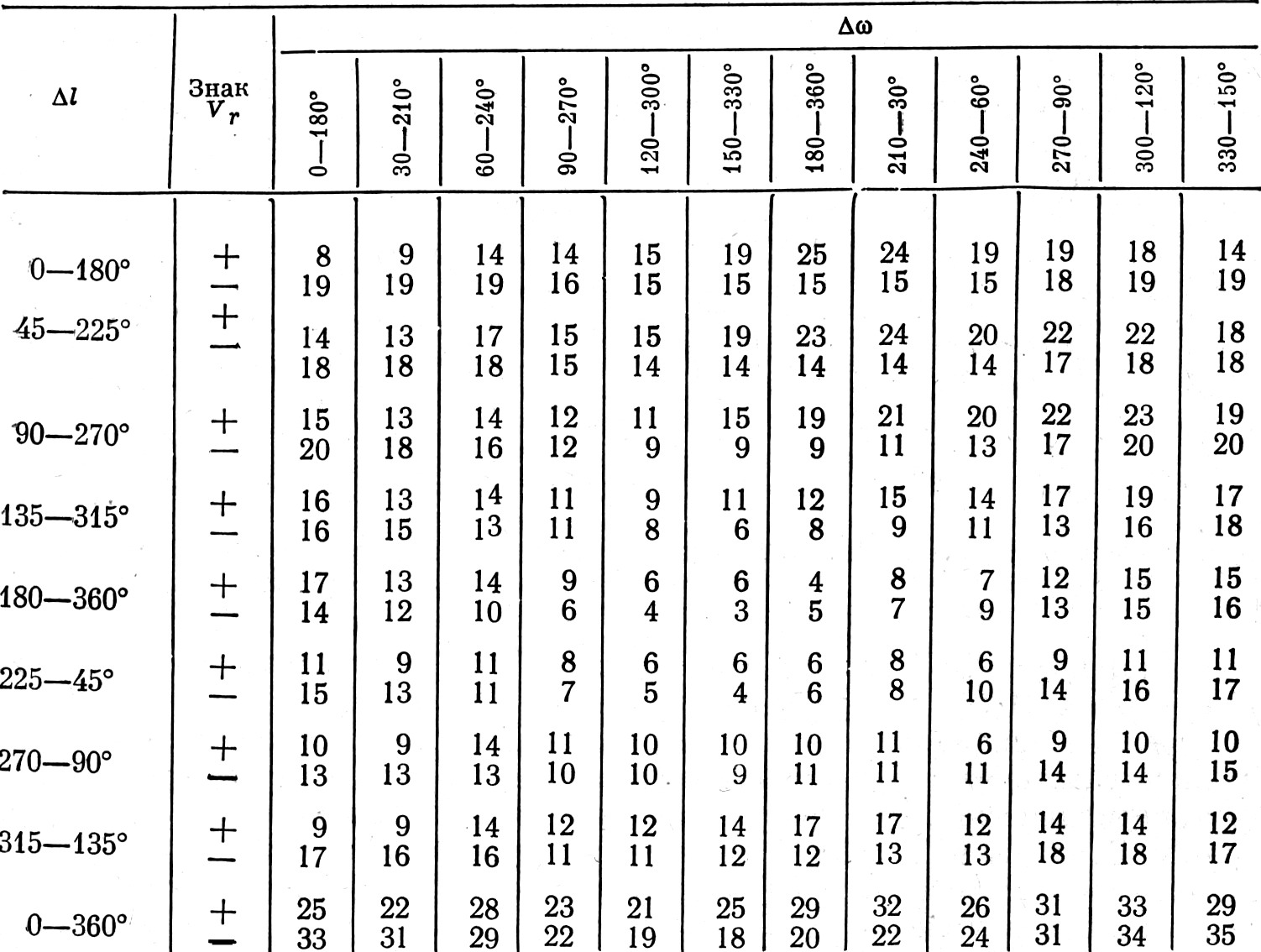
Таблица 1
Распределение звёзд по долготе периастра и галактической долготе
Для каждой звезды были определены галактические координаты в новой системе (долгота центра Галактики l0=0°) по таблицам [18] и расстояние r в парсеках по параллаксам, приводимым в [16]. Для небольшого числа звёзд с неизвестными тригонометрическими параллаксами расстояния вычислялись по видимой m и абсолютной звёздной величине М, заимствованной из работы Аллена [19], с учётом среднего поглощения по Бархатовой [20]. Видимая величина m переменных звёзд бралась в максимуме блеска. Следует отметить, что неточность в вычислении расстояния по модулю (m–М) не является существенной для полученных нами результатов, поскольку знание r необходимо лишь для определения знака лучевой скорости звёзд Vr. Зависящая от r поправка Оорта оказалась незначительной и практически не привела к изменению знака Vr. Лучевые скорости были исправлены за движение Солнца к апексу и освобождены от эффекта Эйнштейна, равного в среднем 1 км/сек.
Для анализа В-эффекта мы использовали метод статистического осреднения по полукругу, описанный одним из авторов [21].
Как и в работах [2, 3], будем называть величиной В-эффекта в направлении долготы ω отношение
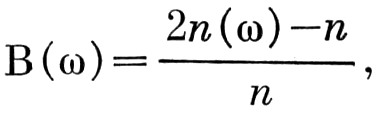 (1)
(1)
где n(ω) – число звёзд с долготой периастра (ω±90°), а n – полное число звёзд. Очевидно, при равномерном распределении периастров В(ω)=0 для всех значений ω. Если все периастры находятся за картинной плоскостью, то В(90°)=1 и В(270°)=-1.
Кривые зависимости В(ω) от ω можно строить при любом интервале Δω (мы приняли Δω=30°).
По данным наблюдений построена первая половина кривых, а вторая половина, приведённая для наглядности, непосредственно вытекает из первой переменной знака ординат.
На рис. 1 пунктирной линией изображена функция В(ω) для всех 130 звёзд. Как видно из этой кривой, В-эффект не является ярко выраженным. Картина, однако, существенно меняется после изъятия 23 звёзд с галактической широтой b>45° и b≤–45°. В табл. 1 даётся распределение оставшихся 107 звёзд по долготе периастра ω и галактической долготе l. Кривая В(ω), построенная по данным последних двух строк табл. 1 (на рис. 1 – сплошная линия), уже чётко показывает наличие В-эффекта и свидетельствует о существовании повышенной концентрации периастров долгопериодических спектрально-двойных звёзд в полусфере с вершиной ω=30°. Здесь их в 1.7 раза больше, чем в противоположной полусфере.
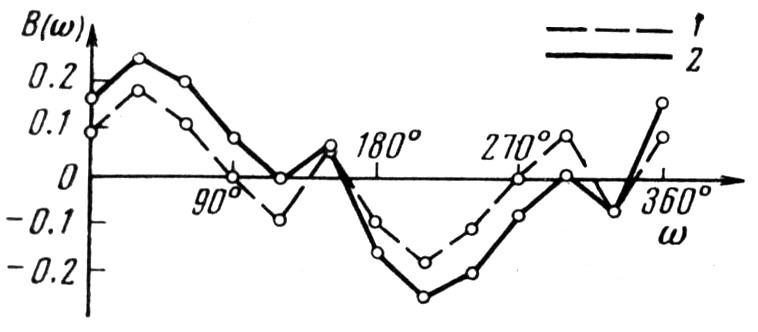
Рис. 1. Графики В(ω): 1 – для 130 звёзд с Р>20d; 2 – для 107 звёзд с Р>20d и |b|≤45°
Для дальнейшего исследования мы объединили звёзды в две группы по знаку их лучевой скорости Vr. Звёзд с Vr>0 оказалось 54; их средняя звёздная величина m=4m.65. Звёзд с Vr<0 оказалось 53 (m=4m.73).
Кривые В(ω), построенные отдельно для этих двух групп (рис. 2), обнаруживают следующую закономерность: у звёзд с Vr<0 (на рис. 2 – сплошная линия) периастры находятся преимущественно за картинной плоскостью (у 62 % от числа этих звёзд), амплитуда В-эффекта резко возрастает и регулярность кривых становится несомненной; у звезд с Vr>0 такой резко выраженной концентрации периастров не наблюдается.
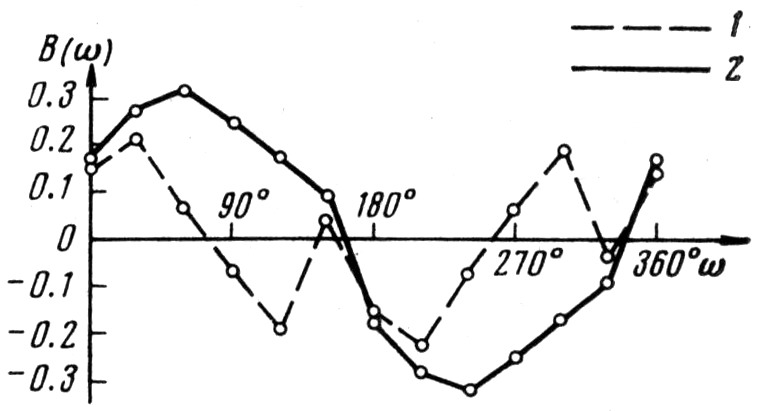
Рис. 2. Графики В(ω): 1 – для 54 звёзд с Vr>0; 2 – для 53 звёзд с Vr<0
Возникает вопрос о связи ориентации линий апсид орбит спектрально-двойных звёзд с их галактическим движением. С целью ответа на него выделим группу звезд с Vr>0, интересную наличием второго максимума (рис. 2), и объединим эти звёзды в две подгруппы по галактической долготе 0°<l≤180° (n=33) и 180°<l≤360° (n=21). Кривые В-эффекта для этих двух подгрупп, изображённые на рис. 3, не оставляют сомнения в природе В-эффекта: он не связан с какими-то локальными процессами внутри бинарных систем, а вызывается определённой галактической ориентацией линий апсид орбит двойных звёзд.
Как видно из рис. 3, периастры звезд, расположенных в направлении галактического движения центроида (l=90°), концентрируются перед картинной плоскостью [В(90°)<0], в то время как у звёзд, находящихся в противоположной половине неба (l=270°), преобладает концентрация периастров за картинной плоскостью [В(90°)>0]. Следовательно, периастры и тех и других находятся в антиапексиальной полусфере с точки зрения их движения вокруг ядра Галактики. Вторичный небольшой максимум на рис. 2 обусловлен менее многочисленными наблюдениями звёзд южной полусферы.
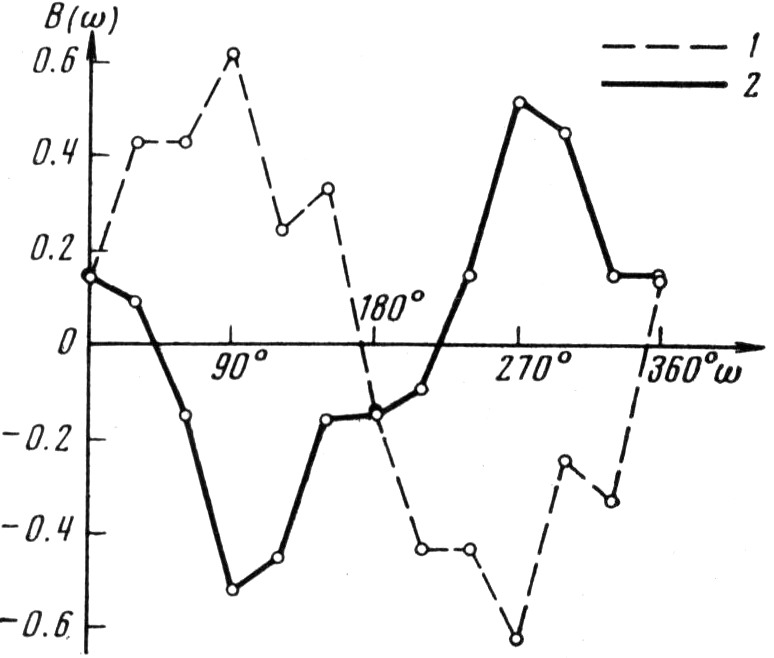
Рис. 3. Графики В(ω): 1 – для 21 звезды с Vr>0 и 180°<l≤360°; 2 – для 33 звёзд с Vr>0 и 0°<l≤180°
Для анализа ориентации периастров относительно плоскости круга галактической широты введём понятие Е-эффекта, определяемого величиной
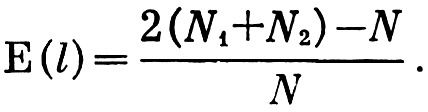 (2)
(2)
В этой формуле N1 – число звёзд, имеющих галактическую долготу (l±90°) и долготу периастра 0°<ω≤180°; N2 – число звёзд с галактической долготой [(l+180°)±90°] и долготой периастра 180°<ω≤360°; N – полное число звёзд, из которых выбраны звезды N1 и N2.
Нетрудно видеть, что сумма N1 и N2 даёт число звёзд, периастры которых находятся по одну сторону от плоскости круга галактической широты с долготой l. При Е(90°)>0 преобладают периастры в апексиальной половине галактического движения и, наоборот, при Е(90°)<0 – в антиапексиальной половине.
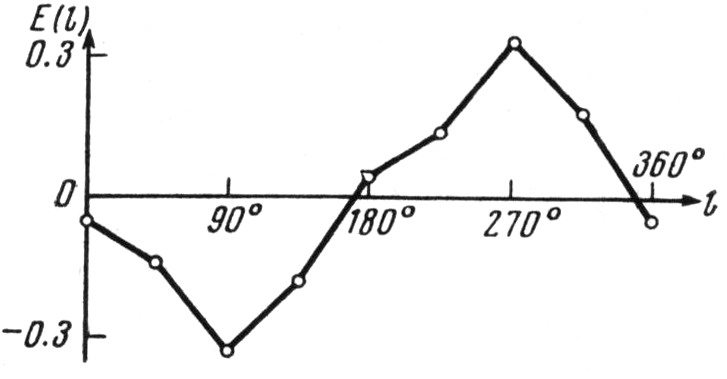
Рис. 4. График Е(l) для 107 звёзд с Р>20d и |b|≤45°
На рис. 4 приведён график Е-эффекта для звёзд, вошедших в таблицу 1. Наличие уверенно выраженного минимума E(l) при l=90° говорит о том, что среди долгопериодических спектрально-двойных звёзд преобладают пары, периастры ярких компонентов которых в среднем направлены точно против галактического движения.
Обработка аналогичных материалов, выполненная для короткопериодических спектрально-двойных звёзд, показала, что такие звёзды, наоборот, движутся вокруг ядра Галактики вперёд периастрами. Для них Е-эффект достигает максимума при l=135°. Звёзды, находящиеся в этом направлении (а таких большинство), имеют периастры преимущественно за картинной плоскостью (положительный В-эффект).
Оба эффекта (В и Е) могут найти объяснение, если опираться на следующую теорему: “В поле постоянной по величине и направлению силы, действующей на один из компонентов бинарной системы с небольшим эксцентриситетом, линия апсид этой системы стремится расположиться в плоскости, перпендикулярной к вектору силы, таким образом, чтобы компонент, подверженный её действию, проходил через свой периастр, двигаясь в направлении вектора силы”.
Для доказательства этой теоремы воспользуемся результатами работы [22], в которой даются изменения элементов оскулирующей орбиты спутника под действием постоянной по величине и направлению силы светового давления Солнца, с учётом весьма малого эффекта Пойнтинга–Робертсона. Если из выражений, полученных в [22], исключить члены, обусловленные эффектом Пойнтинга–Робертсона, то останется лишь эффект действия постоянной силы Р0, природа которой может иметь любой характер.
Сохраняя обозначения работы [22], выпишем изменения оскулирующих элементов за I период:
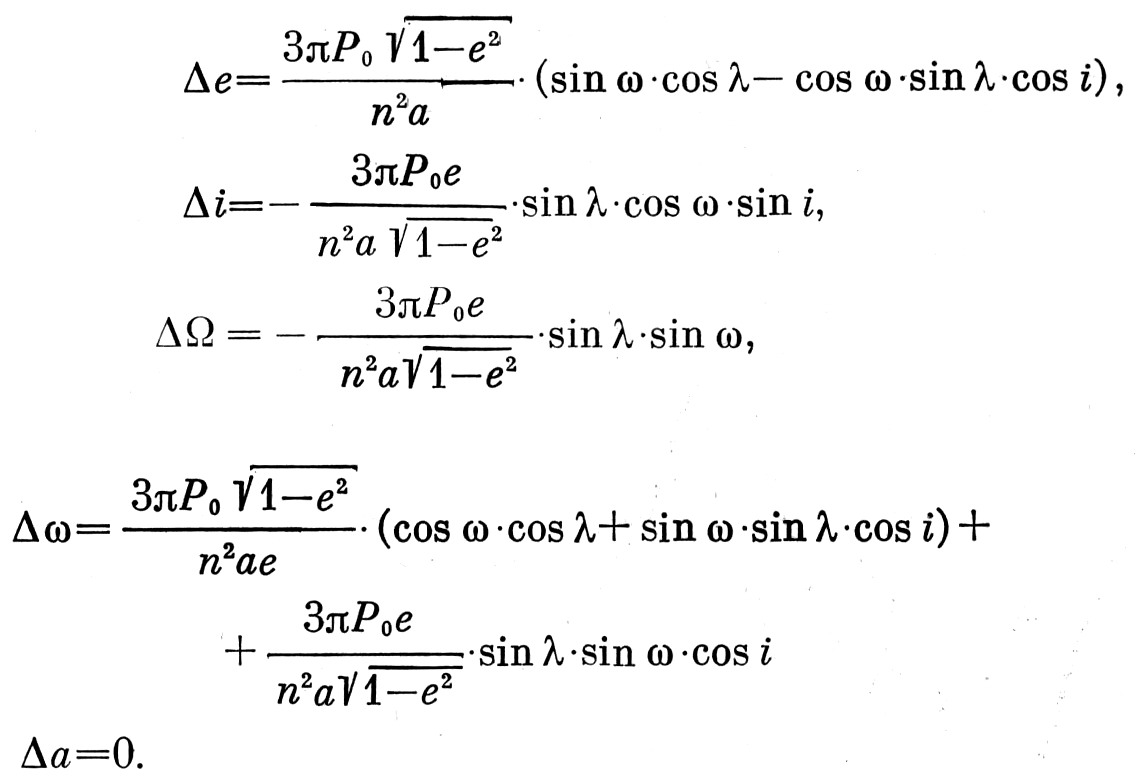 (3)
(3)
Нетрудно видеть, что при е=0.1 скорость изменения долготы периастра на 2 порядка превосходит скорость изменения остальных элементов орбиты. Поэтому в первом приближении можно положить e=const, i=const, Ω=const, а среднюю за период P=2π/n скорость изменения долготы периастра представить в виде
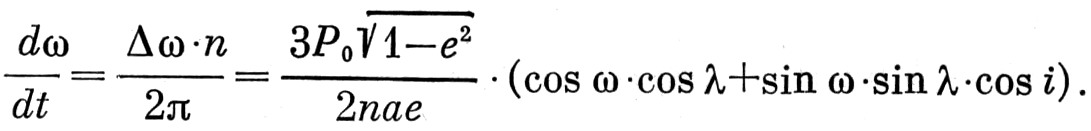 (4)
(4)
Напомним, что в равенстве (4) λ – угол между узлом Ω и Солнцем, а в общем случае это угол между узлом и точкой приложения вектора силы.
Из рис. 1 работы [22] легко определить угол ψ между направлением вектора силы и направлением на периастр:
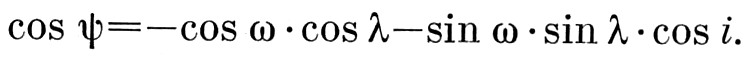 (5)
(5)
Подставляя (5) в (4), получим
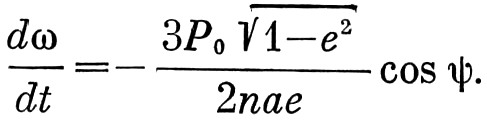 (6)
(6)
Формула (6) выражает скорость изменения ω, отсчитанной от любой точки орбиты. Поэтому она сохраняет силу и при отсчёте от узла, образованного орбитой с картинной плоскостью. Как видно из (6), долгота периастра перестаёт изменяться при cosψ=0, т. е. когда периастр попадает в плоскость, перпендикулярную вектору силы. При cosψ≠0 периастр движется к той точке, через которую компонент проходит в направлении действия силы.
Посмотрим теперь, какая возмущающая сила может играть роль основного динамического фактора, определяющего ориентацию линий апсид орбит двойных звёзд. Ещё в 1932 г. Моисеев [23], развивая работы Нольке [24] и Моро [25], показал, что вследствие гравитационной фокусировки за холодной звездой, движущейся в однородной среде, образуется значительное уплотнение (“хвост” Нольке), вызывающее гравитационное торможение звезды. В 1950 г. Агекян [26] нашёл, что звезда, отталкивающая своим излучением космические пылинки с силой, превосходящей их притяжение, испытывает действие ускоряющей силы, которая у звёзд высокой светимости ранних спектральных классов может на несколько порядков превышать силу их гравитационного торможения.
Компоненты спектрально-двойных звёзд имеют относительно короткие периоды обращения. Поэтому их взаимодействие с пылинками, находящимися на расстояниях, значительно превышающих размеры орбит, можно изучать в рамках ограниченной фотогравитационной задачи трёх тел [27], считая тела конечной массы неподвижными.
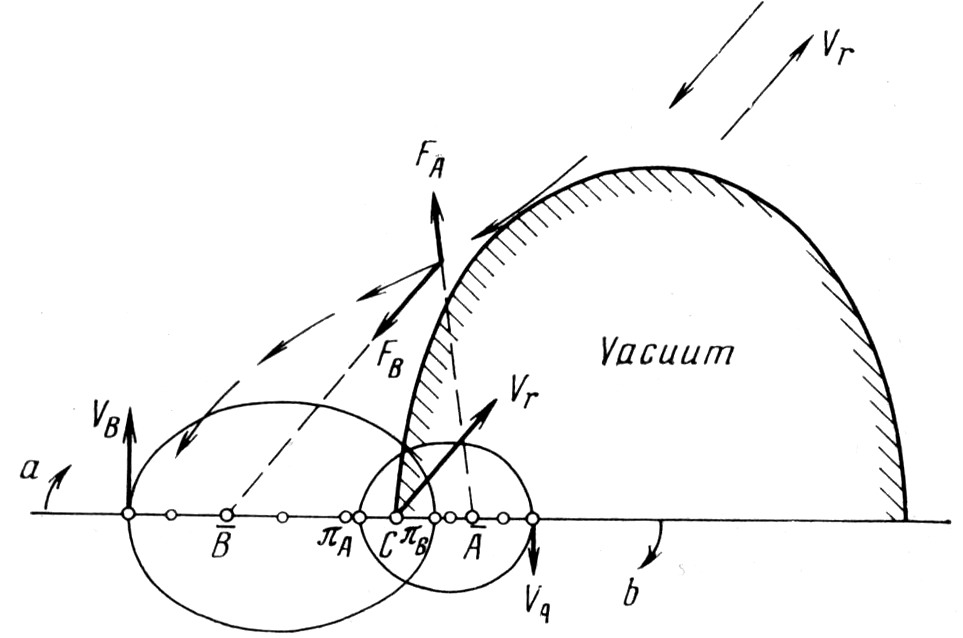
Рис. 5. Поверхность нулевой скорости и направление встречного потока частиц в задаче двух неподвижных центров; πА – периастр яркого компонента; πB – периастр слабого компонента; Ā и В – среднее по времени положение компонентов А и В; Vr – вектор скорости центра масс системы; FA и FB – силы, действующие на пылинку со стороны звёзд А и В (в их среднем положении); стрелки а и b показывают направление вращения линии апсид
В работах [3] и [28] показано, что среднее по времени положение каждого компонента двойной звезды соответствует точке, лежащей посредине между центром эллипса и противоположным фокусом орбиты (рис. 5). Если считать, что компоненты пары покоятся в точках своих средних положений, то поверхность нулевой скорости для пылинок, отталкиваемых ярким компонентом, но притягиваемых слабым, будет иметь вид приблизительно такой, как показано на рис. 5, на котором даётся сечение этой поверхности плоскостью орбиты, полученное на основании интеграла энергии [27] для пылинок, удовлетворяющих условиям FA<0, FB>0 и |FA|=FB. В этом случае пылинки, накапливаясь у апекса яркого компонента A, будут затем “стекать” в сторону его спутника В, образуя мощный тормозящий поток. Разность ускоряющей силы яркого компонента и тормозящей силы слабого компонента и может создать ту силу, которая, как это видно из формулы (6) при cosψ≈l, способна вращать линию апсид с угловой скоростью, соизмеримой со скоростью галактического вращения звезд.
Если бы вектор скорости звезды, движущейся по эллиптической галактической орбите, существенно менял своё направление относительно неподвижной системы отсчёта, то действие такой силы не успело бы вызвать соответствующей ориентации линий апсид орбит двойных звёзд. Но в действительности, как это показано в работе [29], основной компонент ỷ вектора скорости тела, движущегося по эллиптической орбите, всегда направлен в одну и ту же сторону относительно среды, движущейся в каждой точке пространства с соответствующей круговой скоростью V0, причём этот компонент всегда направлен в сторону движения тела в перицентре.
Параллельный большой оси орбиты компонент скорости
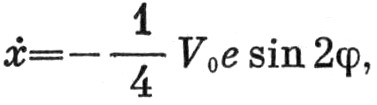 (7)
(7)
а перпендикулярный ему компонент
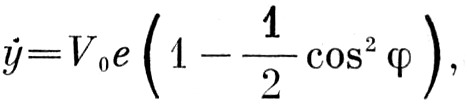 (8)
(8)
что даёт средние значения 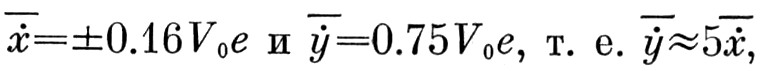 и, следовательно, является основным компонентом скорости.
и, следовательно, является основным компонентом скорости.
Основываясь на доказанной теореме и результате, вытекающем из формул (7) и (8), мы приходим к следующему заключению.
В результате взаимодействия двойных звёзд с межзвёздной средой линии апсид их орбит стремятся занять положение в плоскости, перпендикулярной плоскости галактического экватора и параллельной большой оси их галактической орбиты, таким образом, чтобы при прохождении через периастр яркий компонент двигался в сторону движения всей бинарной системы в перигалактикуме. Отсюда следует, что двойные звёзды от перигалактикума до апогалактикума движутся вперёд периастрами, если направление их собственного обращения является обратным по отношению к галактическому движению. Если же направления обоих движений совпадают, то эту половину галактической орбиты двойные звёзды проходят апоастрами вперёд. Таким образом, можно высказать предположение, что среди долгопериодических звёзд преобладают системы, компоненты которых имеют взаимное обращение, совпадающее по направлению с их галактическим движением, в то время как среди короткопериодических пар доминируют движения в противоположную сторону.
Поступила в редакцию 30 января 1974 г.
Всесоюзное астрономо-геодезическое общество при Академии наук СССР
* В дальнейшем речь будет идти только об орбитах более ярких компонентов.
1. J. M. Barr, J. Roy. Astron. Soc. Canada, 2, 70, 1908.
2. Э. Ф. Бражникова, Уч. зап. Горьковск. пед. ин-та, вып. 123, 248, 1970.
3. Э. Ф. Бражникова, Астрон. ж., 47, 149, 1970.
4. Р. В. Куницкий, Русск. астрон. ж., 1, 43, 1924.
5. О. Struve, A. Rogo, Astron. Nachr., 234, 297, 1929.
6. R. G. Aitken, The Binary Stars, 1935.
7. O. Struve, Popular Astron., 56, 348, 1948.
8. O. Struve, Publ. Astron. Soc. Pacifies, 60, 160, 1948.
9. E. L. Scott, Astrophys. J., 109, 194 and 446, 1949.
10. V. M. Blanco, A. D. Williams, Publ. Astron. Soc. Pacifies, 61, 93, 1949.
11. M. P. Savedoff, Astron. J., 56, 1, 1951.
12. M. Jaschek, С. Jaschek, Z. Astrophys., 44, 18, 1957.
13. Э. Ф. Бражпикова, С. В. Бабинчук, Астрон. ж., 42, 678, 1965.
14. А. Н. Batten, Publ. Astron. Soc. Pacifies, 80, 85, 1968.
15. A. H. Batten, J. Roy. Astron. Soc. Canada, 62, 344, 1968.
16. A. Bečvář, Atlas coel
i II - katalog 1950.0, Praha, 1964.17. A. H. Batten, Publ. Domin. Astrophys. Observ., Victoria, В. С., 13, 119, 1967.
18. Annals of the Observation of Lund, 15, 1961.
19. К. У. Аллен, Астрофизические величины, Пер. с англ., ИЛ, М., 1960.
20. К. А. Бархатова, Астрон. ж., 26, 251, 1949.
21. В. В. Радзиевский, Бюл. Всес. астрон.-геодез. об-ва, 6, 16, 1949.
22. V. Radziewsky, J. Chernikov, Bull. Astron. Čechosl.,
16, 1, 1965.23. N. Moisseiev, Atti Reale Accad. Naz. Lincei, Rendiconti, Ser. 6, 15, 135, 1932.
24. F. Nölke, Abhandl. d. Natur. Ver. Bremen, 20, 29, 1909.
25. T. Moreux, Origine et formation des mondes, Paris, 1922.
26. Т. А. Агекян, Докл. АН СССР, 75, 361, 1950.
27. В. В. Радзиевский, Астрон. ж., 27, 250, 1950.
28. Э. Ф. Бражникова, В. В. Радзиевский, Астрон. ж., 47, 650, 1970.
29. Э. Ф. Бражникова, М. М. Дагаев, В. В. Радзиевский, Астрон. ж., 46, 610, 1969.
Дата установки: 18.04.2013
[вернуться к содержанию сайта]