[вернуться к содержанию сайта]

    § 6. Разложение скоростей. Нахождение по данной сложной скорости скоростей слагаемых движений называется разложением скоростей. Вопрос о разложении, вообще говоря, неопределёнен. Определённым он становится лишь тогда, когда становятся известными некоторые данные, относящиеся к скоростям, на которые желают разложить данную скорость. Решим задачу об определении относительной скорости.

Фиг. 43.

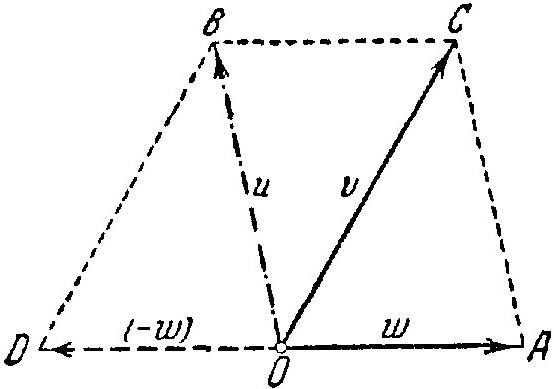
    Пусть абсолютная скорость точки О есть v (фиг. 43), переносная же скорость есть w. Чтобы найти u – скорость относительного движения этой точки, соединим концы векторов А и С и из точки О проведём линию ОВ параллельно АС, а из С ведём СВ параллельно АО. Тогда получим параллелограмм ОВСА с диагональю ОС, равной v, и со стороной ОА, равной w, другая сторона этого параллелограмма ОВ и представит собою искомую относительную скорость u.

    Эту же скорость можно получить иным образом. Отложим от точки О скорость w в противоположную сторону, так, чтобы вектор OD равнялся w, и соединим точку D с В; получим: BD=ОС, как отрезки между равными и параллельными линиями. Фигура ODBC будет параллелограмм, и по его построению видно, что искомая величина – относительная скорость u – есть его диагональ. Отсюда вытекает следующее правило для определения относительной скорости. Относительную скорость получим, складывая по правилу параллелограмма абсолютную скорость и скорость влечения, взятую в противоположную сторону.

    П р и м е р 1. Определить направление дождя относительно вагона конно-железной дороги, движущегося со скоростью w.

Фиг. 44.

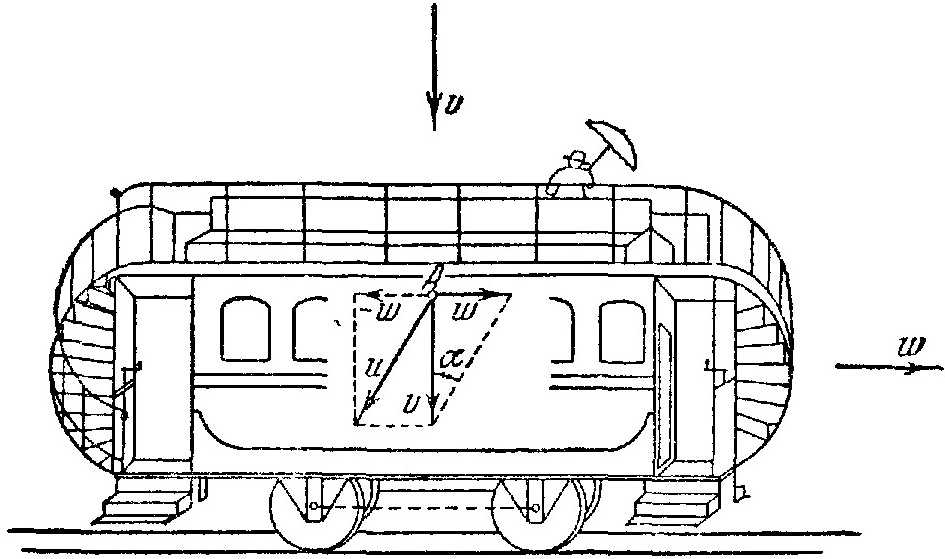
    Предположим, что скорость падения дождя равна v. Чтобы узнать относительную скорость дождя, надо в точке А (фиг. 44) приложить в обратную сторону скорость w и эту величину сложить с v; диагональ полученного таким образом параллелограмма и даёт относительную скорость дождя, а также и относительное его направление по уравнению

tgα=w/v.

    Из этого уравнения получается угол α, образуемый относительной скоростью с абсолютной. Под таким углом, следовательно, должен наклонить свой зонтик пассажир, сидящий на империале вагона, чтобы лучше всего предохранить себя от дождя.

    П р и м е р 2. Такова же, по существу своему, и задача об аберрации света, решаемая в сферической астрономии. Явление это, открытое Брадлеем в 1728 году, состоит в том, что, благодаря годичному движению Земли и немгновенности распространения света, звёзды всегда кажутся нам несколько отклонёнными в сторону этого движения.

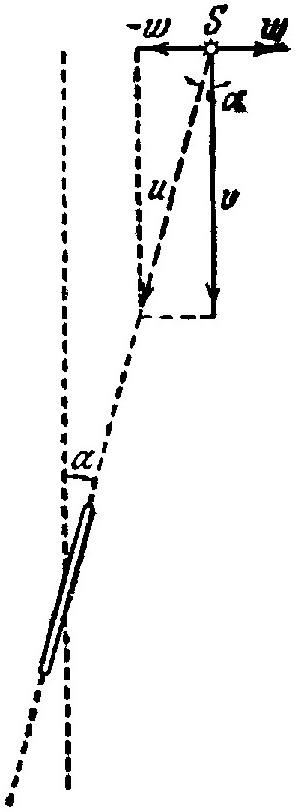
    Рассмотрим, например, тот случай, когда звезда расположена в полюсе эклиптики (фиг. 45). Мы имеем два движения: движение луча звезды со скоростью v и движение Земли со скоростью w. Чтобы найти направление луча света к наблюдателю (относительную скорость), нужно к скорости распространения света по общему правилу разложения движений придать скорость движения Земли с обратным знаком.

Фиг. 45.

    Обращаясь к чертежу (фиг. 45), мы видим, что для того, чтобы увидать звезду в поле зрения, астрономическую трубу приходится поставить не по направлению действительного положения звезды, а с небольшим наклоном в сторону движения на некоторый угол α, величина которого определится из равенства:

tgα=w/v.

    Подставив приблизительные значения (w=30 км/с и v=300000 км/с), получим:

tgα=30/300000=1/10000,

или α приблизительно равняется 20''.

Дата установки: 25.09.2011
[вернуться к содержанию сайта]

W