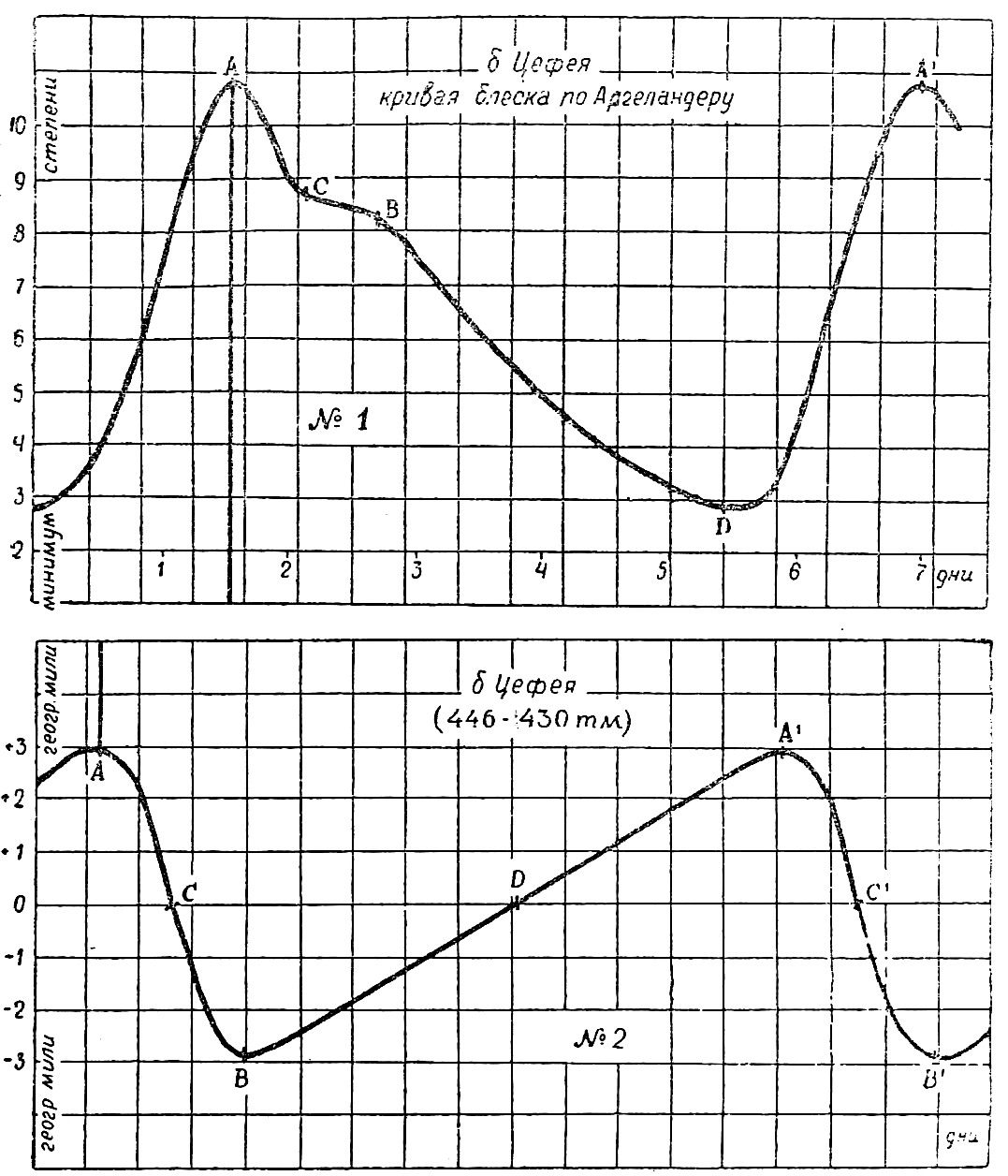
Черт. 1 и 2.
[вернуться к содержанию сайта]
Араго был первым, поставившим вопрос о дисперсии в небесных пространствах, т.е. вопрос о том, движутся ли лучи разного цвета с одинаковой скоростью или с различными скоростями.
Араго показал, что в случае дисперсии переменные звёзды должны с изменением блеска менять также свой цвет. Если дисперсия в небесных пространствах имеет тот же знак, как в прозрачных средах, например в стекле, т.е., если красные лучи имеют наибольшую скорость, а фиолетовые – наименьшую, то звезда должна получать голубой оттенок во время ослабления блеска и красный – во время усиления блеска.
Не найдя нигде указаний на изменение цвета переменных звёзд, Араго заключил, что дисперсии в небесных пространствах не существует.
Метод Араго нельзя признать удобным, так как определение цвета звёзд – трудное дело, и даже такой искусный наблюдатель, как И.Ф. Шмидт, делает значительные ошибки при этих определениях.
В качестве примера можем привести до сих пор неразрешённый окончательно вопрос об изменении цвета звезды “альфа” Большой Медведицы; некоторые считают это изменение действительным, другие его не признают совершенно.
Многочисленные наблюдения И.Ф. Шмидта [1] показывают, что переменные звёзды во время ослабления блеска чуть-чуть краснее, чем во время его возрастания. Если эти изменения цвета действительно зависят от дисперсии, то следует считать её обратной, т.е. что лучи фиолетовые двигаются быстрее красных.
Для исследования дисперсии можно с удобством воспользоваться звёздами, лучевые скорости которых периодически изменяются в течение нескольких дней. В настоящее время известно достаточно большое число подобных звёзд, например, α Близнецов, α Девы, β Возничего, β Персея, β Лиры, δ Цефея, η Орла и др.
Из них четыре последние – переменные.
Предположим, что луч длины волны λ от некоторой звезды достигает Земли на а минут раньше, чем луч длины волны λ'. Измерим отдельно лучевые скорости звезды по смещению линий λ и λ' и построим для этих линий кривые лучевых скоростей. Тогда мы найдём, что эти кривые совершенно одинаковы, но все точки кривой λ' имеют абсциссы (по оси абсцисс мы откладываем время) на а минут больше, чем соответствующие точки кривой λ, т.е. вся кривая λ' сдвинута относительно кривой λ на а минут вправо.
Это смещение должно возрастать с увеличением расстояния звезды и разности между длинами волны λ и λ'.
Произведённые до сих пор наблюдения не позволяют подробно заняться этим вопросом отчасти потому, что они недостаточно точны, и отчасти вследствие того, что они выполнены в узкой области спектра.
Некоторые наблюдения А.А. Белопольского над β Лиры позволяют думать, что дисперсия в небесных пространствах обратная, т.е., что скорость луча возрастает с убыванием длины волны, но недостаточное количество этих наблюдений заставляет быть осмотрительным при этих заключениях.
Сделаем следующие предположения относительно дисперсии:
1) дисперсия обратна;
2) она возрастает с увеличением длины волны.
Теперь мы рассмотрим, какие последствия вытекают из этих предположений.
Если мы имеем переменную звезду с коротким периодом, то наблюдаемая кривая изменения её блеска не соответствует действительному изменению. Лучи разного цвета достигают Земли в каждый момент в различных фазах их яркости, и наблюдаемая кривая блеска есть результат сложения действительных кривых, соответствующих каждому лучу в отдельности. Если дисперсия достаточно велика, то изменение блеска, в действительности происходящее в течение нескольких часов, может растянуться на весь период, и затменная переменная звезда может дать непрерывную кривую, как у δ Цефея и η Орла (черт. 1 и черт. 3).
Известно, что не существует оранжевых звёзд, принадлежащих к типу Алголя.
Пользуясь вторым предположением, мы можем объяснить этот факт следующим образом: так как дисперсия сильно возрастает с приближением к красным лучам спектра, последние должны резко изменить кривую блеска. Красные и оранжевые лучи белых звёзд, каковы звезды типа Алголя, относительно слабы, и, следовательно, их действие не очень чувствительно; действительная кривая блеска может достаточно хорошо сохранить свою форму.

Черт. 1 и 2.
Красные и оранжевые лучи звёзд оранжевых, каковы δ Цефея и η Орла, достаточно интенсивны, чтобы сделать кривую блеска непрерывной.
Как мы увидим далее, изменение блеска δ Цефея и η Орла зависит от затмения и, следовательно, их кривые при отсутствии дисперсии должны были бы походить на кривую Алголя с той разницей, что они имели бы кроме главного минимума ещё вторичный, соответствующий затмению менее яркой составляющей. Точки С кривых 1 и 3 соответствуют этим вторичным минимумам, изменённым, как мы полагаем, вследствие дисперсии.
Черт. 2 и черт. 4 представляют кривые радиальных скоростей δ Цефея и η Орла согласно А.А. Белопольскому. Если мы поместим кривые 2 и 4 под кривыми 1 и 3 таким образом, что абсциссы точек А совпадут (это сделано на чертежах), тогда точки С кривых 2 и 4, где радиальные скорости равны нулю, соответствуют вторичным минимумам С кривых 1 и 3. Вторичные максимумы В (1 и 3) соответствуют максимумам отрицательных скоростей В (2 и 4). Главные минимумы D (1 и 3) соответствуют точкам D (2 и 4), где радиальные скорости обращаются в нуль.
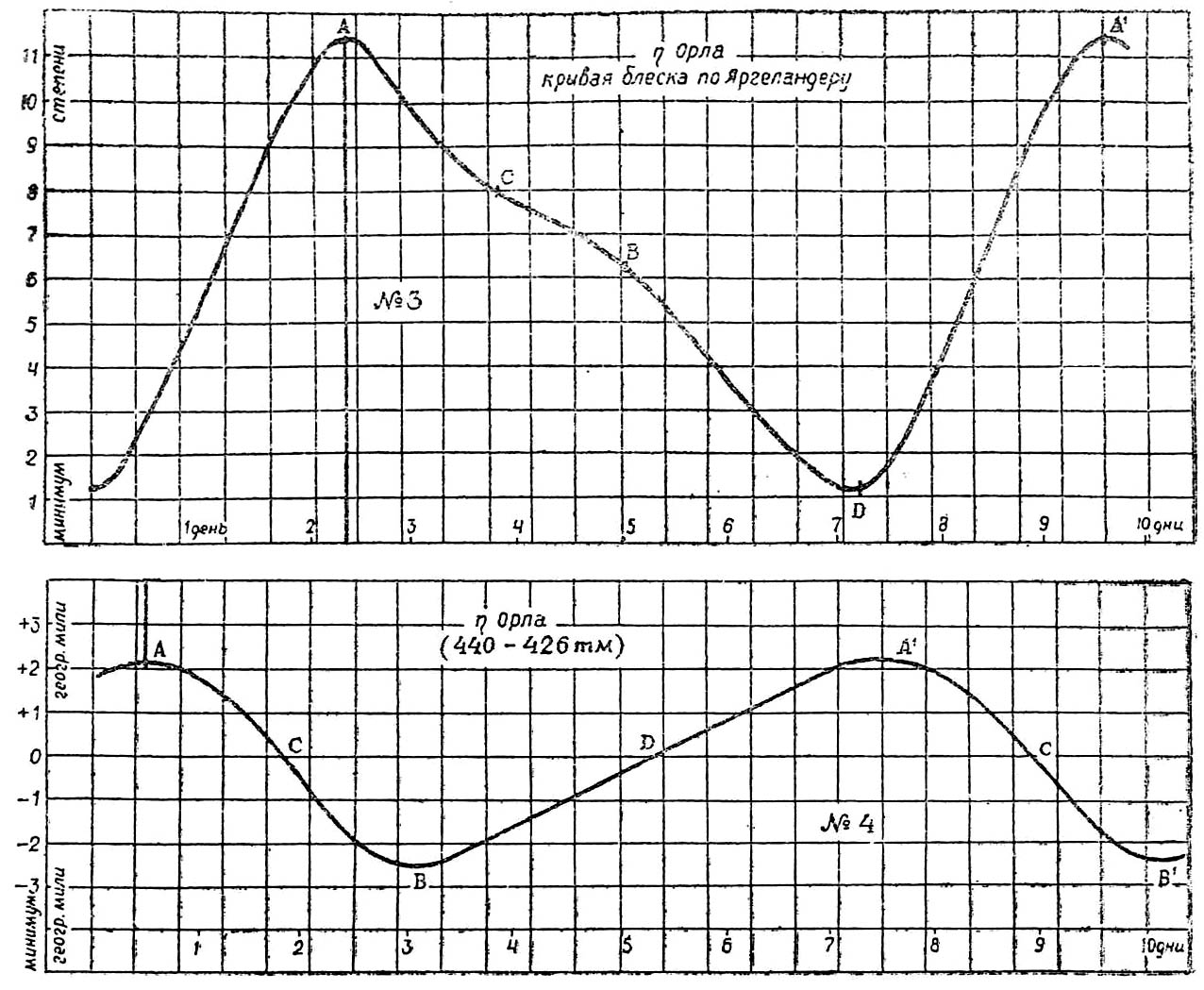
Черт. 3 и 4.
Небольшое несогласие этих совпадений возможно уничтожится позднейшими и более точными наблюдениями.
Мы должны теперь объяснить, почему кривые 1 и 3 отстают относительно кривых 2 и 4.
Согласно сказанному, минимумы D (1 и 3) соответствуют ближе всего действительному минимуму наиболее ярких лучей (приблизительно 600 mμ).
По этой причине минимумы D (1 и 3) должны запаздывать относительно точек D кривых 2 и 4, так как последние получены посредством более коротких длин волн (446–426 mμ). Запаздывание кривой 1 относительно кривой 2 равно 26 часам, а запаздывание кривой 3 относительно 4 – 46 часам.
Согласно с изложенной теорией звезда типа Алголя должна перейти в звезду типа δ Цефея по мере того, как цвет её изменяется от белого к оранжевому.
Если дисперсия существует, то распределение яркости в спектре переменной звезды должно изменяться периодически с изменением её блеска.
Дисперсия может дать новый способ определения расстояний спектроскопически-двойных и переменных звёзд.
Если мы определим, что разность хода лучей одной звезды составляет а минут, а другой звезды – b минут, то расстояния этих звезд относятся как а:b.
Зная расстояние одной подобной звезды, мы можем найти расстояния всех других, о которых идёт речь.
Допуская, например, что распределение яркости в спектрах δ Цефея и η Орла одинаково, и, замечая, что кривые 2 и 4 получены приблизительно с помощью одинаковых лучей, мы можем заключить, что расстояние η Орла в 46/26 = 1,77 раза больше, чем расстояние δ Цефея.
Мы позволяем себе надеяться на то, что более глубокое изучение отмеченных звёзд не замедлит полностью разрешить затронутый вопрос.
[1] И.Ф. Шмидт. Астрономические известия (Astronomische Nachrichten), т. 93, стр. 88).
Мемуары Общества итальянских спектроскопистов. Том XXVII, 1898 г. (Метоriе della Societa degli spettroscopisti Italiani, vol XXVII, 1898).
Начиная с Ньютона было предложено много способов для решения этой проблемы.
В своих знаменитых мемуарах “О дисперсии света” (Прага, 1836) Коши не допускает дисперсии в пространстве, так как “...иначе звёзды представлялись бы нам не в виде блестящих точек, а в виде ярких и очень узких полос, которые обнаруживали бы различные оттенки солнечного спектра” (стр. 185). Дело идёт, несомненно, о постоянной аберрации, которая изменялась бы от одного цвета к другому. Однако даже если бы разность скоростей крайних лучей была велика и достигала одной двухсотой части всей скорости, то угол между этими лучами равнялся бы всего 0'',1.
Араго указал на способ, несравненно более чувствительный, привлекая внимание к наблюдению цвета переменных звёзд. Но в последнее время найдено много других причин периодического изменения цвета переменных, и метод Араго сделался поэтому очень сложным.
Рэлей в 1881 г. [1] указывал на то, что сравнение скорости света, полученной по способу аберрации, с одной стороны (индивидуальная скорость волн), и по спутникам Юпитера, с другой (скорость групп волн), не оставляет места допущению дисперсии в пространстве, возвещённому Форбсом и Юнгом [2], которые допустили для пустоты, на основании своих опытов по методу Фуко, избыток скорости голубых лучей по сравнению с красными приблизительно на 2%.
Форстер указал на то, что для звёзд, имеющих большую скорость перпендикулярно к лучу зрения, влияние дисперсии растянуло бы их в спектры. Чувствительность этого способа сравнима с таковой в методе Коши, он впервые применён Гоманном [3].
Я приступил к проблеме дисперсии в 1896 г. и несколько позднее указал два различных способа [4]. Первый состоит в сравнении фаз орбитального движения спектрально-двойных звёзд; эти фазы вычисляются по смещениям различных линий возможно более удалённых в спектре. Не имея тогда приборов необходимых для применения этого способа, я заметил, что можно сравнивать фазу орбитального движения (наблюдаемого обычно в области Нγ звёзд спектрально-двойных и переменных в то же время с формой их блеска (наблюдаемого визуально, в области 560 mμ).
Допуская, что нулевые скорости должны соответствовать минимуму блеска, я применил этот способ к звездам δ Цефея и η Орла, что мне дало очень большие смещения (26 и 46 часов соответственно) и в таком смысле, что дисперсия была бы обратна таковой для прозрачных сред.
В той же статье я указал на возможность сравнения между собой расстояний до звёзд в том случае, если бы предполагаемая дисперсия была реальной.
В 1900 г. Шварцшильд [5] публикует результаты своих фотографических наблюдений переменных η Орла и β Лиры. Сравнение этих кривых с кривыми, наблюдёнными визуально, не дало заметного сдвига, который превосходил бы погрешности наблюдения (±5 часов для β Лиры и 6 часов для η Орла). Таким, образом, моё объяснение взаимного смещения кривых спектральных и фотометрических не подтвердилось. В настоящее время известно аналогичное смещение для 10 звёзд типа δ Цефея, и его объяснение следует искать в самой природе этих звёзд [6].
Во время моего первого пребывания в Медоне, в 1898–1899, я производил опыты спектрофотометрирования переменных звёзд визуальным способом, все с целью изыскания дисперсии. Но, применяя обычный метод призм, я натолкнулся на трудности, практически непреодолимые, и пришёл к более простым спектро-фотометрическим способам, которые были применены мною впоследствии.
В 1903 г. Белопольский начал в Пулкове систематические наблюдения β Возничего с целью применения спектрального метода к изысканию дисперсии. Около 50 этих спектров было изучено Белопольским; эти самые спектры и другие в таком же числе были изучены мною другим способом. Мы пришли к одинаковому заключению, а именно, что фаза синей орбиты (соответствующей 450 mμ) опережает таковую орбиты фиолетовой, соответствующей 400 mμ) на 10–20 мин.; средняя ошибка этого сдвига равна приблизительно половине самого сдвига2.
В начале 1906 г. я предпринял в Пулкове фотографические наблюдения блеска переменных звёзд через светофильтры с окрашенной желатиной, которые я смог изготовить таким образом, что они пропускают последовательно 8 различных областей спектра, от красной до ультрафиолетовой. Это и есть вышеупомянутый простой способ.
Для начала я изучил звезду типа Алголя RT Персея и W Большой Медведицы,
Вот результаты, полученные по способу ступеней, перенесённых на фотографическую пластинку:3
RT Персея (период: 20 ч. 23 мин. 10 сек.). Изучена в лучах 560 mμ и 430 mμ. Звёзд сравнения 34. Продолжительность изменения блеска 3 часа и 2 часа соответственно. Минимум кривой 560 mμ идёт впереди другого на 4 минуты.
W Большой Медведицы (период: 4 ч. 0 мин. 13,2 сек.). Изучена в лучах 625 mμ (оранжевых), 490 mμ (голубовато-зелёных) и 380 mμ (ультрафиолетовых). 13 звёзд сравнения. Кривые, оранжевая и ультрафиолетовая, весьма похожи. Кривая голубовато-зелёная мало надёжна. Оранжевый минимум опережает ультрафиолетовый на 10 минут. Кроме того, установлено большое различие в цветах звёзд сравнения.
Итак, три звезды β Возничего, RT Персея и W Большой Медведицы) дали сдвиг в одинаковом смысле, а именно: лучи с более длинной волной приходят раньше лучей с более короткой волной.
Важно отметить, что наблюдения Нордмана, доложенные Академии 24 февраля, дают сдвиг в том же смысле для β Персея и λ Тельца.
В моих методах и в методе Нордмана дело идёт о наблюдении групп волн в смысле, указанном Рэлеем [7] и Гуи [8]. Обозначая скорость группы волн через U и таковую индивидуальных волн через V, мы имеем известное соотношение:
U = V – λdV/dλ. (1)
Допустим для межзвёздной среды закон дисперсии
V0/V = a + b/λ2, (2)
где V0 обозначает скорость света в среде, не обладающей дисперсией, а и b суть положительные постоянные; из уравнений (1) и (2) получаем следующую зависимость:
dU = 3dV.
При выводе этой формулы мы приняли аV/V0 = 1, что справедливо, если пренебречь малыми величинами второго порядка.
Следовательно, если найденные сдвиги происходят от дисперсии, то они в три раза больше тех, которые были бы вычислены на основании показателей преломления, дающих V.
Таким образом, эти способы в три раза более чувствительны, чем предполагалось ранее, и следует разделить все наблюдённые сдвиги на 3, чтобы получить дисперсию в обычном смысле, т.е. дисперсию индивидуальных волн.
Если бы дисперсия в пространстве следовала закону V = α + βλ, где α и β суть постоянные, мы имели бы U = α, и такая дисперсия совершенно ускользала бы от наблюдения нашими методами [9].
Некоторые наблюдения оптического и фотографического блеска звёзд подтверждают указанные результаты, давая место предположению о существовании в пространстве избирательного поглощения света, которое увеличивается с галактической широтой и с уменьшением длины волн [10]; отсюда вытекают также возможность допустить различие дисперсии на разных галактических широтах.
Резюмируя можно сказать, что первые результаты обнадёживают, и что исследования космической дисперсии стоят на верном пути. В частности, принятый мною метод, основанный на фотографической регистрации со светофильтрами, хорошо поддаётся дальнейшему развитию, так как с металлическими зеркалами можно продвинуться в ультрафиолет до 300 mμ, с одной стороны (см. работы Гёггинса), и, с другой стороны, до области красной и даже инфракрасной.
Выбрав подходящие переменные звёзды, представляется возможным оценить моменты фаз с точностью в несколько десятков секунд времени.
1. R a y l e i g h. Nature, London, vol. XXIV, p. 382.
2. F o r b e s and Y u n g. Proceedings of the Royal Society of Edinbourgh, 1881-82.
3. H. H o m a n n. Beitrage zur Untersuchung der Sternbewegungen. Inaug. Dissert. Berlin, 1885.
4. O. T i k h о f f. Memoria della Societa degli Spettroscopisti Italiani, vol. XXVII. 1898.
5. S c h w a r z s c h i l d. Publicationen der von Kuffner'schen Sternwarte in Wien, Bd. V, 1900.
6. Lick Observatory Bulletin, № 118.
7. R a y l e i g h. The Theory of Sound, vol. I, № 191 and Suppl.
8. G o u y. Comptes Rendus, Paris, vol. XCI, p. 877; vol. CI, p. 502; vol. CIII, p. 244. et Journal de Mathématique pures et appliquees, vol. VIII, p. 395. Paris, 1882.
9. G o u y. Annales de Chemie et de Physique, vol. XVI, p. 283. Paris, 1889.
10. J.C. K a p t e y n. Bulletin de la Carte du Ciel, vol. II. p. 131.
Доклады Парижской академии (Comptes Rendus), Париж. Заседание 16 марта 1908 г., т. 146, стр. 570-574.
Дата установки: 03.09.2014
Последнее обновление: 18.10.2014
[вернуться к содержанию сайта]