[вернуться к содержанию сайта]

О происхождении спектров и закона Планка
Сэр Дж. Дж. Томсон,
Обладатель "Ордена за заслуги",
Президент Королевского Общества ¹

On the Origin of Spectra and Planck's Law.
By Sir J. J. Thomson, O.M., P.R.S.
Статья из журнала Phil. Mag. 1919 г. Стр. 418-447
(см. оригинал статьи на сайте www.ivanik3.narod.ru)
Перевод на русский – С.Семиков, 2011

    Результаты исследований числа электронов в атомах различных элементов показывают, что строение этих атомов, если выражаться в терминах электрических зарядов, имеет в некоторых случаях очень простой характер. Атом водорода, например, как полагают, содержит всего один электрон и один положительный единичный заряд. Напрашивается вопрос, если электроны и положительный заряд расценивать как центры сил, изменяющихся обратно пропорционально квадрату расстояния, не возникнет ли потенциальная возможность объяснить свойства атома законами механики. Объяснение некоторых из этих свойств, например, таких как удельная диэлектрическая постоянная [диэлектрическая проницаемость – С.Семиков] газа, формирование молекул соединением с другими атомами, будет ли это водород или некий иной элемент, по-видимому, могут существовать в пределах этой очень простой системы. Существуют, однако, другие свойства, о которых этого нельзя сказать. Наиболее яркий среди них – это спектр, излучаемый газом. Водород, как известно, может испускать несколько спектров. Однако для нашей цели достаточно обратиться лишь к наиболее известным: второму спектру [видимо, серия Лаймана – С.С.], который содержит чрезвычайно большое число линий, простираясь далеко в ультрафиолет, и к так называемому "четырёх-линейчатому спектру" [серия Бальмера – С.С.], который, как есть все причины верить, включает в себя бесконечное число линий, частоты которых связаны простым численным соотношением, обнаруженным Бальмером. Колебания, которые испускались бы единственным электроном, помещённым возле положительного единичного заряда, не имели бы такого характера. Принимая обычный закон взаимодействия между двумя зарядами, получим, что для того, чтобы атом пребывал в устойчивом состоянии, электрон должен описывать орбиту вокруг положительного заряда. Период обращения электрона будет зависеть от его расстояния от этого заряда, и если оно непрерывно меняется, то с периодом вращения происходит то же самое, а значит спектр, частоты которого заданы этими периодами, был бы непрерывным. Если заряды рассматривать просто как центры обратно квадратичных сил, то нет никаких причин для сохранения некоторых из этих орбит как возможных и для пренебрежения другими. М-р Бор в его теории спектров предполагает, что единственно возможные орбиты – это те, для которых отношение энергии электрона к его угловой скорости есть кратное определённой единицы. Однако это не является следствием динамических соображений. Это скорее арифметический, чем динамический вывод, и если он справедлив, то это должен быть результат действия сил, существование которых не было доказано. Исследование таких сил было бы задачей величайшего интереса и значения.

    При помощи этого правила и последующего, по которому, когда электрон переходит с одной орбиты на другую, он генерирует излучение с частотой, пропорциональной разности энергий электрона на двух орбитах, м-р Бор получает выражение, которое даёт с замечательной точностью частоты линий в четырёх-линейчатом спектре водорода. Однако я думаю, будет справедливо заметить, что для многих умов арифметический базис этой теории кажется намного более удовлетворительным, чем физический.

    Колебания, которые создают спектр по этой теории, не соответствуют частоте какого-либо вращения или колебания в атоме, когда он пребывает в стационарном и нормальном [невозбуждённом – С.С.] состоянии. То что в нормальном атоме есть нечто, что может колебаться на частоте линий или, во всяком случае, на частоте некоторых из линий спектра, видимо, доказано почти неопровержимо экспериментами профессора Вуда и м-ра Бэвана со спектрами поглощения паров щелочных металлов. Эти пары дают в спектре поглощения чёткие тёмные линии, совпадающие по положению с линиями главной серии спектра металла. Так, например, профессор Вуд получил 48 из этих линий в спектре поглощения паров натрия, а м-р Бэван – 24 для калия, 30 для рубидия, 24 для цезия. Острота и интенсивность этих линий спектра поглощения, создаваемых сравнительно холодными парами, столь велика, что крайне трудно поверить, будто они не обязаны своим появлением эффекту резонанса, вызванного системами в нормальном атоме, имеющем периоды колебаний, идентичные с таковыми у линий поглощения, причём в нормальном атоме есть вибраторы с тем же периодом, что и некоторые из периодов в излучающем атоме. Имеются, однако, линии в побочных сериях спектра излучения, которые не обнаруживаются в спектре поглощения: таким образом, казалось бы, получается, что некоторые из атомов в светящемся газе отличаются от атомов в нормальном газе, поскольку электроны вибрируют с разными периодами в этих двух случаях. Спектр поглощения, однако, слишком сложен, чтобы доказать, что это не может быть объяснено колебаниями нескольких электронов под влиянием их собственных отталкиваний и притяжений, оказываемых на них положительным зарядом, если эти притяжения и отталкивания следуют простому закону обратных квадратов.

    Хотя в любом исследовании равновесия электронов и положительных зарядов естественно начинать с предположения, что притяжение между положительным и отрицательным зарядами изменяется обратно пропорционально квадрату расстояния, следует иметь ввиду, что нет никакого прямого свидетельства со стороны эксперимента, которое подтвердило бы справедливость этого закона на расстояниях, сопоставимых с теми, которые отделяют электроны и положительные заряды в молекуле. Измерения и явления, которые предоставляют подтверждение закона обратных квадратов, относятся к расстояниям, которые огромны по сравнению с атомными расстояниями. Если c₁, c₂, c₃ имеют величину порядка атомных расстояний, то нет никаких экспериментов, проведённых на данный момент, которые позволили бы выбрать между силой вида l/r² и силой вида

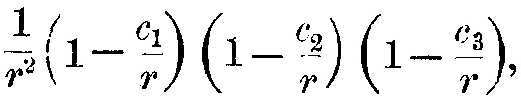
и всё же на атомных расстояниях две силы совершенно несходны, вторая меняется от притяжения к отталкиванию и обратно к притяжению, поскольку r последовательно принимает величины c₁, c₂, c₃, и т.д.

    Если положительная часть атома образована из отдельных единиц, то отталкивание между ними не может продолжаться до расстояний порядка тех, которые имеются в этой части атома, иначе атом, содержащий несколько таких единиц, взорвался бы.

    Поэтому, я буду рассматривать следствия, вытекающие из предположения, что силовое поле вокруг положительного заряда, при изменении обратно пропорционально квадрату расстояния на больших расстояниях от атома, всё же меняется в самом атоме туда и обратно между притяжением и отталкиванием. Чтобы обосновать наши идеи, предположим, что выражение для силы содержит множитель sincu/cu, где u=l/r, и r – расстояние от центра. Когда r велико по сравнению с c, то sincu/cu – единица, так что этот множитель не влияет на силу на больших расстояниях. Внутри атома, если атомные размеры сопоставимы с c, будет ряд положений равновесия, определяемых из условия cu=nπ или r=c/nπ, где n – целое число. Таким образом, даже если имеется только один положительный заряд и один электрон, то в атоме могут быть однократно бесконечные атомные серии с электроном на расстояниях от центра, представленных выражением r=c/nπ. Периоды колебаний электронов относительно этих положений были бы различны, так что набор таких атомов мог бы генерировать бесконечное число линий и в адсорбционных и в эмиссионных спектрах [спектрах поглощения и излучения – С.С.]. Каждая линия генерировалась бы определённым типом атомов. Яркость линии зависела бы, наряду с другими причинами, от числа атомов того типа, который генерирует данную специфическую линию. Теория дисперсии позволяет, если известна связь между показателем преломления и длиной волны, вычислять количество систем, которые колеблются с любым характерным периодом. Бэван применил этот метод, чтобы найти число атомов в парах натрия, которые могли бы колебаться в унисон с различными линиями в главной серии этого металла. Он нашёл, что число атомов, которые могут излучать или поглощать D линию, составляет приблизительно двенадцатую часть от общего числа атомов, тогда как приблизительно лишь один из 1000 может генерировать дублет 3303, и приблизительно один из 5500 – дублет 2852.

    Таким образом, число атомов, соответствующих линии в главной серии, очень быстро уменьшается вместе с номером, задающим положение линии при увеличении серии. И, хотя могут существовать различные типы атомов, основное их большинство имеет один тип.

    Замечательно, что примерно лишь 9 процентов атомов натрия относятся к типу, дающему линии в видимой части главной серии. Это означает, что, возможно, самая сильная линия в серии окажется линией в инфракрасном диапазоне. Атом одного типа физическими или химическими процессами может быть преобразован в атом другого типа. Таким образом, если бы атом с электроном в точке P был ионизован, он стал бы положительно заряжен и притянул бы электрон извне. Однако этот электрон мог бы осесть в другой точке равновесия Q, образуя иной тип атома.

    Видимо, эти различные типы атомов различаться и в других отношениях, нежели период колебаний электронов. Они, например, отличились бы по их диэлектрическим проницаемостям, так что соотношение различных типов отличалось бы в разных участках быстро меняющегося электрического поля. Кроме того, атомы одного типа могли бы с большей готовностью соединяться с атомом другого элемента, чем атомы другого вида. Так что, если газ в спектральной трубке был постепенно поглощён химическим способом, например, как кислород поглощается натрием, то относительная интенсивность линий в конце процесса не могла бы быть той же самой, что и в начале. Или, с другой стороны, если спектр элемента получен путём разделения соединения, например, как в случае, когда спектры щелочных металлов получены при помещении той или другой их соли в пламя горелки Бунзена, то относительная интенсивность линий могла бы зависеть от характера соли. Уже упомянутый эксперимент Бэвана показал, что число атомов, дающих более коротковолновые линии главной серии, росло при увеличении температуры паров натрия. Я отмечал много лет назад, что величина показателя преломления гелия показывает, что лишь малая часть атомов гелия может вибрировать с частотой любой характерной линии в спектре гелия. Множество примеров переменности относительной интенсивности различных линий в одном и том же спектре приведено в "Спектроскопии" Кайзера. Поскольку процессы, которые заставляют газ светиться, также ионизуют газ и тем самым позволяют атому одного типа преобразовываться в другой тип, не кажется возможным, что каким-либо процессом фракционирования мы сможем получить газ, содержащий атомы только одного типа, а потому генерирующий спектр, состоящий из одной линии при всех условиях возбуждения.

    Электрическое поле внутри атома состоит, согласно только что принятому представлению, из чередующихся оболочек притягивающих и отталкивающих сил, положения, где притяжение сменяется отталкиванием, являются положениями, где сила исчезает, и где электрон мог бы находиться в равновесии. Расстояния этих положений равновесия от центра находятся в арифметической прогрессии.

    Теперь перейдём к рассмотрению природы сил, которые действуют на электрон и заставляют его колебаться на частотах спектральных линий. Как увидим, можно постулировать бесконечное число законов электрической силы, которая могла бы вызывать ряд частот колебаний, представленных законом Ридберга.

    Мы можем также вообразить, что в дополнение к электрическому полю внутри атома имеется также магнитное поле, и что частоты колебаний электронов заданы магнитными, а не электрическими силами. Электрон, находясь в магнитном поле, описывает спираль вокруг силовых линий магнитного поля, совершая вращение за период 2π/(He/m), где H – напряжённость магнитного поля, e – заряд, и m – масса электрона. Таким образом, он испускает излучение частоты He/2πm, которая не зависит от энергии электрона. Поскольку эта энергия уменьшается, радиус спирали, описываемой электроном, уменьшается, но частота колебаний неизменна. Таким образом, если бы магнитная сила была преобладающей в определении колебаний электронов, то частоты колебаний, выдаваемые различными типами атома, были бы

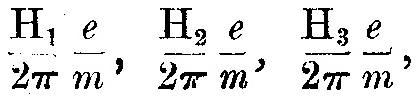
где H₁, H₂, H₃ – величины магнитной индукции в различных точках равновесия. Предположим, теперь, что величина H в точке равновесия на расстоянии r от центра равна μ(a²-r²),– распределение силы магнитного поля, которое a priori не запрещено, раз это внутренняя часть равномерно заряженной сферы с электричеством и вращением как у твёрдого тела.

    Поскольку положения равновесия заданы условием sinc/r=0, т.е. c/r=nπ или r= c/nπ, где n – целое число, то величина индукции магнитного поля в положениях равновесия, а значит, и частота колебаний в этих положениях, будет пропорциональна

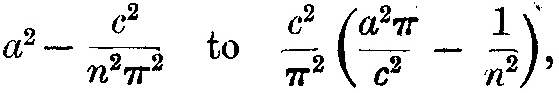
и таким образом формировалась бы серия бальмеровского типа. Если, кроме того, положение r=a, где магнитная сила исчезает,– это также положение, где исчезает электрическая сила, c/a=mπ, где m – целое число, и выражение для частоты переходит в С(1/m²–1/n²), где C – константа, а m и n – целые числа.

    Перед тем как перейти к подробному обсуждению этого выражения, рассмотрим тип атома, который необходим, чтобы удовлетворить предположению, которое мы сделали в вышеприведённом исследовании. Этот атом состоит из поля электрической силы, которое может быть рассмотрено как составленное из ряда оболочек притягивающей и отталкивающей силы, поочерёдно следующих друг за другом, радиусы границ этих оболочек, на которых электрон может находиться в равновесии, подчиняются арифметической прогрессии. На поле электрической силы налагается поле магнитной силы, тоже организованной в оболочки, внешняя граница магнитного поля совпадает с местом, где электрическая сила исчезает. Если рассмотреть атом, находящийся в условиях, которые могут возникать в сильных электрических разрядах или в других методах генерации спектров, то внешние слои этого магнитного поля могут отделиться, и граница магнитного поля подойдёт близко к центру, так что, фактически, получится случай, который можно было бы назвать магнитной ионизацией атома, и атом восстановит своё нормальное магнитное состояние, когда электрический разряд, и т.п., прекратится. Таким образом, атомы в светящемся газе обладают двойным разнообразием, одно является результатом различных положений электронов в атоме, а другое происходит от вариаций магнитной границы атома. Первое многообразие порождало бы различные линии в одной и той же спектральной серии, второе порождало бы множество различных серий, большинство которых будет испускаться только особым типом атомов, возникающих при пропускании электрического разряд сквозь газ.

    Пока мы рассмотрели лишь случай, когда в атоме находился только один электрон, так что положением равновесия был участок, где сила притяжения к положительному заряду исчезала. Если же количество электронов больше единицы, то положение равновесия находится не там, где сила притяжения к положительному заряду исчезает, а там, где эта сила, действующая на какой-либо электрон, уравновешивает силу отталкивания от других электронов. Это сместит положение равновесия, и вместо того чтобы задаваться условием sincu=0, или cu=nπ, оно будет задано условием cu=n(π+δ), где δ – это величина, зависящая и от отталкивания электронов и, возможно, также от n.

    Поскольку частоты колебаний пропорциональны a²-r², то теперь они будут пропорциональны

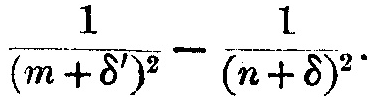
    Рассмотрим теперь различные типы спектральных серий, которые могут возникать на базе этого представления.

    Общая особенность спектров заключается в том, что серии состоят не из одинарных линий, а из серий дублетов, или триплетов.

    Они не ограничиваются каким-либо частным типом серий, но возникают как в главных, так и в побочных сериях, хотя закон для разности частот различен. В главных сериях разность частот между компонентами дублета уменьшается так же, как уменьшается длина волны, в то время как в побочных сериях разность частот постоянна.

    Две компоненты дублета возникают от разных электронов. Как показал Вуд, одна из D линий натрия может быть возбуждена без другой, и, кроме того, эффект Зеемана для одной линии дублета совершенно отличается от эффекта Зеемана для другой линии.

    Следует ожидать появления дублетов или триплетов, когда вместо единственного электрона имеет место кольцо электронов или несколько электронов, расположенных в углах многогранника, если их распределение не является совершенно симметричным относительно центра. Таким образом, если б, например, имелось кольцо из четырёх электронов, расположенных не в углах квадрата, а в углах прямоугольника [параллелограмма – С.С.], длины диагоналей которого слегка различаются, то два электрона находились бы на большем расстоянии от центра, чем другие два, так что магнитное поле, а значит и частота, будет меньше для первой пары электронов, чем для второй. И, поскольку переменная часть магнитного поля, пропорциональная r², исчезала бы в центре, то предельная частота, которая соответствует колебаниям электронов возле центра, была бы одинаковой для каждой пары электронов. Таким образом, получим серию дублетов, ведущих себя, подобно сериям дублетов в главных сериях.

    Мы видели причину, по которой первая побочная серия [диффузная серия – С.С.] приписывается колебаниям электрона в атоме, где магнитная граница сползала до положения, занятого внешним кольцом электронов в атоме того типа, который излучает главную серию. Если конфигурация кольца слегка асимметрична, то для магнитной границы у атомов, генерирующих первую побочную серию, можно ожидать того же.

    Если это так, то часть магнитного поля, которая не зависит от r, различается в разных направлениях, а потому величина первого члена в скобках выражения для частоты

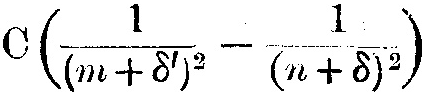
различалась бы для электронов, находящихся на разных радиусах, идущих из центров атомов. Так что предельная частота электронов, расположенных на этих радиусах, будет различной, и линии дублета не стали бы ближе по мере уменьшения длины волны.

    Кроме того, направления, в которых электроны, дающие главные серии, выпирали бы, и вдоль которых колебания имели бы меньшую частоту, будут теми направлениями, в которых магнитная граница выпирает из атомов, дающих первую побочную серию. Направления, где магнитные границы выпирают, соответствуют местам, где постоянный член в скобках максимален и, следовательно, вдоль таких направлений частота максимальна.

    Таким образом, линия с большей длинной волны в дублете главной серии аналогична линии с меньшей длиной волны в дублете первой побочной серии. Это находится в согласии с поведением дублетов в спектрах щелочных металлов, поскольку, если более преломляемая [более коротковолновая – С.С.] линия пары более интенсивна в главной серии, то в первой побочной серии, более преломляемая линия слабее, тогда как эффект Зеемана для более преломляемых линий в главной серии аналогичен эффекту Зеемана для менее преломляемых [более длинноволновых – С.С.] в первой побочной серии.

    В спектрах щелочных металлов члены 1/(n+μ)², 1/(m+μ)², которые появляются в выражениях для серий, приближаются в некоторых случаях к 1/(n+1/2)² и к 1/n² – в других, где n – целое число. Так получалось бы, если б положения, где электроны находятся в равновесии, были заданы уравнением sin2x=0, а не sinx=0, тогда решение уравнения будет 2x=pπ, где p – целое число. Если p – чётное целое число, то это решение можно записать в виде x=nπ, а если нечётное, то x=(n+1/2)π, где n – целое число. Таким образом, если обозначим первые решения через "S", а вторые – через "C" , и допустим, что магнитная граница атома может совпадать с C- или c S-решением, то можно получить следующие типы серий. Я назову постоянный член в скобках выражения Ридберга границей серии, и обозначу его L_s или L_c, согласно тому, соответствует ли он S- или C-решению. Далее, переменную часть обозначим через S_s или S_c, согласно тому, находятся ли электроны, генерирующие колебания, в положении равновесия, соответствующего S- или C-решению соответственно.

    Серии могут быть представлены в виде

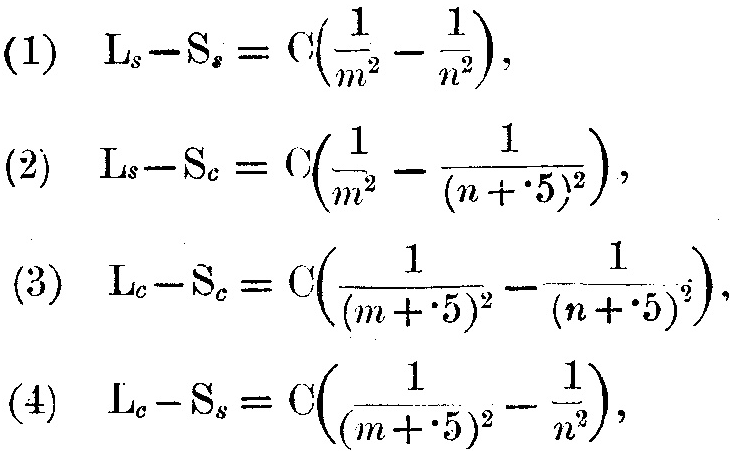
где L_s и L_c могут иметь разные величины, соответствующие разным положениям магнитной границы.

    Отсюда видно, что разность частот двух линий в сериях типа (1) или (3) будет равна частоте линий в другой серии того же типа.

    Разность между частотами любых двух линий в серии типа (2) будет частотой линии в другой серии типа (3).

    Разность между частотами любых двух линий в серии типа (4) будет частотой линии в другой серии типа (1).

    Таким образом, если взять линии, принадлежащие любой серии, то полный спектр газа будет содержать линию, частота которой равна разности частот этих двух линий серии.

    Необходимо помнить, что эти две линии должны быть отобраны из той же самой серии, если эти две линии выбраны из спектра наугад, то не должно быть линии, частота которой равна разности частот этих двух линий.

    Представление, по которому колебания, вызывающие излучение, определяются магнитными силами, приводит к закону Планка, и даёт физическую основу для квантовой теории, если принять простое соотношение между электрической и магнитной силой.

    Предполагая, что электрическому полю сопутствует магнитное, а магнитная индукция B сонаправлена с электрической силой R и связана с ней соотношением

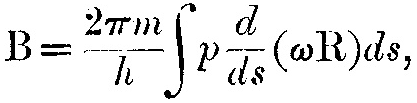
где ds – элемент электрической силовой линии, ω – сечение силовой трубки, m – масса электрона, h – постоянная Планка, и p определяется уравнением dp/ds=-1/ω.

    Когда сила вызвана единственным положительным зарядом, то можно положить p=1/r, ω=r², где r – расстояние от заряда.

    Отметим, что, когда закон силы сводится к закону обратных квадратов, ωR постоянно, и B исчезает.

    При интегрировании по частям получим

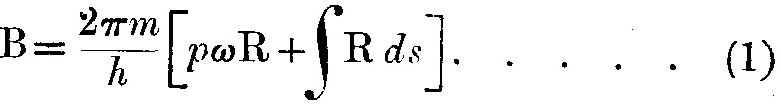
    Следовательно, если B₁, B₂ – это величины B в двух положениях равновесия, где R исчезает, то

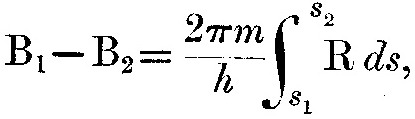
или, если w – это работа, совершаемая электроном при перемещении из одного положения в другое,

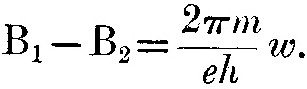
    Если n₁, n₂ – частоты колебаний электрона в двух положениях

    Следовательно

    Таким образом, если электрон переходит из положения, где магнитная сила исчезает, к другому положению равновесия, то частота колебаний равна w/h, где w – энергия, преобразованная в излучение. Таким образом, переход потенциальной энергии в энергию излучения согласуется с законом Планка.

    Принимая соотношение между электрической и магнитной силой, данное в предшествующих исследованиях, легко найти такой закон изменения электрической силы, при котором частоты колебаний электронов были бы связаны соотношением, подобным выражению для Ридберговских серий.

    Таким образом, например, предположение, что сила R, с которой положительный заряд действует на электрон, даётся уравнением

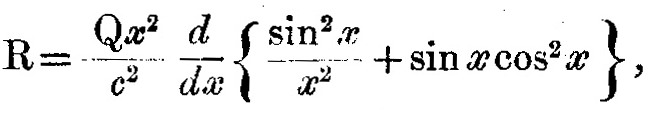
где x=c/r. Когда x мало, то есть когда r велико, это выражение сводится к

так что это даёт правильную величину силы на большом расстоянии от атома. Кроме того, когда x велико, положения равновесия даются соотношениями

cos x=0, или x=(2p+l)π/2,

где p – целое число.

    Поскольку

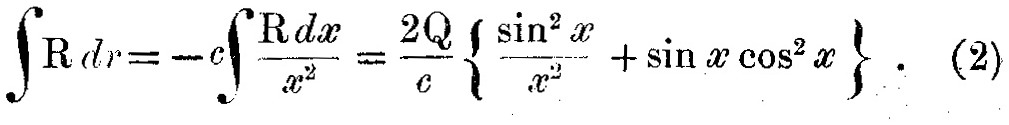
    В положении равновесия из уравнения (1) видно, что поскольку sin²x=l,

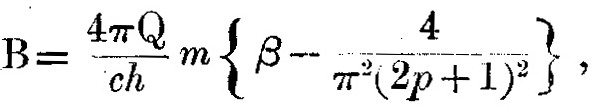
где β – константа. Если магнитная индукция исчезает в точке равновесия, где p=p₀,

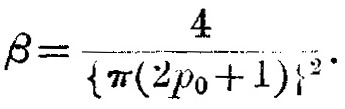
Следовательно, частота колебаний n даётся уравнением

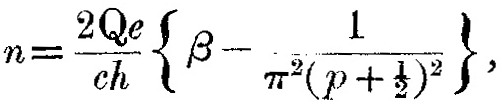
которое может быть записано в форме

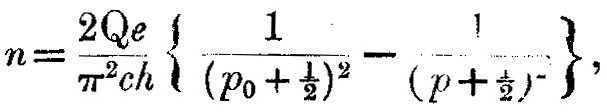
типа Ридберговских серий.

    Если

то коэффициент переменного слагаемого такой же, как в теории Бора.

    Линии в спектре дают лишь информацию о величине магнитного поля во множестве изолированных точек. Даже в совокупности с тем условием, что на больших расстояниях электрическая сила должна выражаться как Qe/r², они не могут предоставить достаточно данных, чтобы однозначно определить закон изменения силы, и, фактически, мы можем без труда найти различные выражения для R, которые всё же дали бы те же самые серии спектральных линий.

    Величина c, которая входит в выражения для R и B внутри атома, имела бы размерность длины, и если это универсальная константа, т. е. величина одинаковая для всех атомов, то имелась бы некоторая стандартная длина, встречающаяся во всех атомах или в окружающей их среде. В этом случае, поскольку величина c не изменяется от атома к атому, частота колебаний будет пропорциональна Q, положительному заряду в атоме. Эксперименты Мозли с длиной волны характеристического спектра рентгеновского излучения, даваемого различными элементами, показали, что частоты пропорциональны квадрату, а не первой степени положительного заряда, если принять дополнительное предположение, что положительный заряд пропорционален атомному номеру. По этой причине мы должны предположить, что Q/c пропорционально Q², так что c=c'/Q, где универсальной константой является c', а не c.

    Поскольку c' имеет размерность длины, умноженной на электрический заряд, то она представляет собой момент электрического диполя, и если её принять в качестве универсальной константы, то следует предположить, что электрические дублеты с постоянными моментами частично формируют атомы всех элементов или среды, которая их окружает.

    Можно вычислить величину c или c', если знать количество работы, требуемой для перемещения электрона от одного из его положений равновесия на бесконечно большое расстояние от атома. Поскольку мы видим из уравнения (2), что, если положение равновесия электрона отвечает условию x=π/2, то эта работа равна

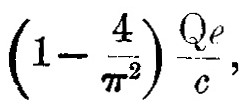
или, если работа выражена как Ve, где V – потенциал, через который должен пройти заряд e, чтобы приобрести это количество энергии, то

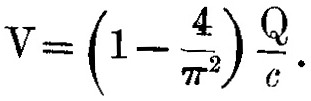
    Если взять потенциал ионизации в качестве меры V, то для атома водорода V=11 вольт и Q=e, откуда найдём, принимая e=4,7×10^–10, V=11/300,

c=7,7×10^-9,

и c'=c×Q=3,6×10^-18.

    Если вычислить c' из соотношения

то получим c'=3,97×10^-18.

    Это отличается примерно на 10 процентов от величины, рассчитанной из потенциала ионизации. Определение этого потенциала для атома водорода едва ли является достаточно точным, чтобы исключить возможность погрешности в 10 процентов, так что величина 3,97×10^-18 для c' допустима. Эта величина сделала бы численные постоянные в соотношениях для серий согласующимися с величиной, даваемой теорией Бора, которая даёт значения частот, соответствующие наблюдениям.

    Потенциал ионизации обычно измеряется как разность потенциалов, через которую должны пройти катодные лучи, чтобы суметь ионизировать газ.

    Однако, если атом, как мы предположили, является областью интенсивных магнитных сил, то возможно, что энергия, которой должны обладать катодные лучи, дабы ионизировать газ, не могут измерять энергию, которую катодные лучи должны отдать электрону, чтобы позволить ему покинуть атом, а скорее измеряют энергию, которой катодные лучи должны обладать, чтобы проникнуть достаточно глубоко в атом и достичь того электрона, который должен быть освобождён.

    Кроме того, во многих случаях ионизации катодными лучами электроны вылетают с конечным запасом кинетической энергии, которая не зависит от энергии катодных лучей. Если это так, то потенциал ионизации выше линейного интеграла электрической силы от начального до конечного положения электрона.

    Когда спектр газа возбуждён ударами катодных лучей, то первый процесс, который происходит – это выброс электронов из атома. С нашей точки зрения это не вызывает излучения, соответствующего линиям спектральных серий. Оно возникает благодаря второму процессу, возвращению электронов к ионизированному газу, для замещения тех электронов, которые были испущены. Эти электроны являются не высокоэнергичными катодными лучами, а медленными электронами, произведёнными ионизацией атомов, и энергия, которая преобразуется в излучение – это та энергия, которую эти электроны приобретают при падении в положения равновесия. Из некоторых экспериментов, которые я провёл с излучением, вызванном бомбардировкой вещества катодными лучами, я заключаю, что намного большая часть энергии лучей сконцентрирована в излучении определённой длины волны, поскольку я нашёл, что, когда энергия катодных лучей постепенно изменялась, характер излучения на некоторых этапах заметно не изменялся, тогда как на других этапах увеличение энергии катодных лучей производило значительное увеличение в жёсткости излучения. Это – именно то, что происходило бы, если б это излучение было смесью определённых типов (a, b, c, d ……) характеристических излучений мишени, бомбардируемой катодными лучами. Тип a не возбуждался, если энергия катодных лучей не превышала e₁, b не возбуждался, если энергия не превышала e₂, и так далее. Таким образом, когда энергия катодных лучей заключена между e₁ и e₂, излучение будет ограничено типом a, и оно станет смесью типов a и b, как только энергия катодных лучей превысит e₂. Когда она превысит e₃, добавится тип излучения c, и так далее.

    Когда электроны попадают в положения равновесия и вращаются вокруг магнитных силовых линий, то энергия, приобретаемая ими при падении, постепенно преобразуется в энергию излучения, и электрон постепенно приходит в состояние покоя.

    Если f – ускорение электрона, то темп, в котором он испускает энергию, есть

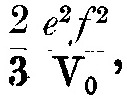
где e – заряд электрона и V₀ – скорость света.

    Если H – напряжённость магнитного поля, v – скорость электрона, то, когда орбита перпендикулярна напряжённости магнитного поля, то

f=Hev/m=2πnv,

где n – частота колебаний электронов, когда она задана магнитным полем. Подставляя эту величину в f, найдём, что темп, в котором энергия испускается электроном, равен

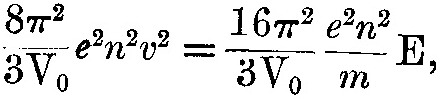
где E – кинетическая энергия электрона. Следовательно, если теряемая электроном энергия полностью переходит в излучение, получим

    Таким образом E=c·exp(–kt).

    Теперь                       e/m=1,78×10⁷,

e=1,6×10^-20,

отсюда                           k=5×10^-22 n²,

и фактическое время, уходящее на снижение энергии до значения в 1/e от её начальной величины, составит 10²²/5n².

    Таким образом, если колебания имеют частоту 5,1×10¹⁴ D линии в спектре натрия, то это время равно 7,7×10^–9 секунд, и длина цуга, испускаемого за это время составила бы примерно 4 миллиона длин волн. Если длины волн составляют 10^-8 см, обычно такой порядок даёт L-серия характеристического рентгеновского излучения платины, то время составило бы 1/4,5×10¹⁵, а испускаемый цуг включал бы примерно 660 длин волн. Таким образом, если спектральные линии являются результатом действия магнитных сил, то они могут ожидаться состоящими из цугов, содержащих очень большое число длин волн, обратно пропорциональное частоте колебаний.

    Рассмотрим поток энергии излучения, частично проходящей сквозь металл. За счёт магнитных полей, созданных атомами, в металле будут магнитные поля, достигающие в некоторых точках очень высоких значений, и падающие до предельно низких – в других точках. И в очень широких пределах изменения магнитного поля можно найти точки, где напряжённость магнитного поля имеет любую заданную величину. Если во всех таких точках можно обнаружить электрон, то кусок металла будет системой, содержащей вибраторы любых возможных периодов, заключённых в очень широком интервале.

    Кажется весьма вероятным, что в металле электроны не все расположены непосредственно в пределах атомов, но что некоторые из них отделены, помогая созданными ими силами заставить атомы соединиться и сформировать твёрдое тело. Тогда, если положения этих отделённых электронов будут точно скоординированы с интенсивностью магнитного поля, то эффект будет почти такой же, как будто эти электроны случайно распределены в магнитном поле. И можно ожидать найти некоторые электроны в участках, где напряжённость магнитного поля имела бы любую заданную величину в широких пределах изменения. Кусок металла будет в таком случае системой рассмотренного вида, позволяющей вибраторам реагировать на любые колебания в пределах широкого диапазона частот. Таким образом, если бы свет любой частоты, между границами этого диапазона, падал на металл, то он нашёл бы отдельные электроны, у которых частота колебаний в магнитном поле в точках, где они расположены, равнялась бы собственной частоте света, и они бы приобрели высокую скорость. Чтобы электрон стал свободным, он должен добраться до области, где магнитная сила исчезает, поскольку, как можно легко доказать, воздействие магнитного поля на электрон, смещённый из положения равновесия, такое же, как в случае притяжения электрона к точке, равного Be/m, помноженному на смещение электрона. Предположим, что P – точка, где магнитная индукция исчезает, и где, следовательно, электрон может стать свободным. Предположим, что Q – точка, из которой электрон выходит, чтобы освободиться в точке P. Чтобы добраться из Q в P, он должен приобрести количество энергии, равное w, где w – работа, требуемая для перемещения электрона из Q в P против электрического поля. Если эта энергия приобретается за счёт излучения, то это должен быть резонанс, дабы излучение, от которого берётся энергия, имело частоту свободных колебаний электрона в точке Q. Так как сила магнитного поля исчезает в P, то по уравнению (2) эта частота будет равна w/h. Таким образом, электрон в Q, поглощая энергию частоты n, может освободиться в точке P с запасом потенциальной энергии, равной hn.

    Это вызвало бы хорошо известный фотоэффект. Если бы в Q от излучения поглотилось количество энергии, меньшее чем w, то электрон не смог бы освободиться. После того, как излучение прошло бы насквозь, эта энергия стала бы снова излучаться электроном в Q, вибрирующим в магнитном поле вблизи Q с частотой n. Таким образом, поглощённое излучение снова бы испускалось в виде излучения той же самой частоты, и не произошло бы никакого превращения энергии. Для того чтобы энергия преобразовалась, нужно сообщить Q энергию, равную w. И поскольку w=hn, мы получим результат, даваемый квантовой теорией, так что преобразование энергии излучения в потенциальную или кинетическую энергию происходит определёнными квантами, каждый из которых равен hn.

    Объяснение фотоэффекта допускает возможность обнаружения в металле электрона с собственной частотой n, где n может быть любым заданным числом в пределах широкого диапазона величин. В связанной системе типа металла это кажется вероятным. И примечательно, что в металлах фотоэлектрические эффекты происходят в совершенно иных масштабах, чем фотоэффекты в газах. Так, Хьюгес [Hughes] не обнаружил никакого следа ионизации, когда ультрафиолетовый свет полностью поглощался паром цинкового этила, хотя, когда тот же самый свет падал на цинковую пластину, он вызывал поток электронов в миллион раз превышающий тот, который мог быть зафиксирован, если бы он появился из паров цинка. Ультрафиолетовый свет очень малой длины волны, несомненно, производит ионизацию в газах, тогда как одно из наиболее характерных свойств лучей Рентгена – это их интенсивная ионизация газов. Однако следует помнить, что, как показывают полосы поглощения в ультрафиолете у газов типа CO₂ и O₂, газы во многих участках спектра ультрафиолетового света способны давать спектр непрерывный вблизи многих частот, и поэтому, возможно, содержат электроны, способные свободно колебаться в широком диапазоне частот. С другой стороны, важно помнить, что число ионизированных атомов составляет чрезвычайно малую часть от числа атомов в газе. Их число, конечно, изменяется вместе с интенсивностью ионизующего излучения; но при обычных условиях лабораторной работы число атомов, ионизуемых в секунду – намного меньше, чем 1/10¹² от числа атомов, подвергнутых облучению. Или, выражаясь иначе, отдельный атом был бы ионизирован не чаще, чем примерно раз в сотню тысяч лет.

    Далее, в газе атомы входят в столкновение и могут формировать кратковременные ассоциации, и, пока они пребывают в этом состоянии, естественные частоты сдвинуты на значение, которое меняется от одной пары атомов или молекул к другой. Следовательно, если берём во внимание эти пары, то обнаружим в газе электроны, собственные частоты которых не просто равны частотам свободного атома, но непрерывно расширяются до диапазона частот, который можно обнаружить в парах. Таким образом, пока длится диапазон частот электрона, газ эквивалентен куску металла. Верно, что в газе число электронов, способных колебаться на частотах, которые можно назвать аномальными, составляет очень малую часть от общего числа электронов. Но мы видим, что, если электрон входит в это состояние раз в сотню тысяч лет, то будет возможно сделать эту долю больше полной доли ионизации в газе. Эффект, оказываемый сближением атомов на расширение диапазона частот, проявляется в огромном уширении некоторых линий, когда давление газа повышено. Если принять представление, по которому в газе можно ожидать найти электроны с частотами, непрерывно меняющимися в широком диапазоне, хотя число таких электронов, обладающих частотами отличными от нормальных собственных частот, может быть очень мало, то можно применить к газам рассуждение, которое мы использовали для фотоэффекта в металлах, и принять в качестве вывода, что энергия испускаемого электрона будет пропорциональна частоте излучения, которое снабдило его энергией. Другими словами, что энергия в корпускулярном излучении будет пропорциональна частоте первичного рентгеновского излучения. Эксперименты, произведённые до настоящего времени по вырыванию электронов лучами Рентгена, совместимы с этим законом.

    Атом, из которого удалён электрон, будет испытывать нехватку электрона, когда тот освободится из атома, с которым был временно связан, и сможет испустить излучение, когда электрон попадёт в него, заместив тот, который был потерян. Теперь атом свободен, так что излучаемые им колебания имеют нормальную частоту, которая может быть частотой излучения, придающего электрону энергию для выхода. Таким образом, характер рентгеновского излучения, возбуждённого первичным излучением, не будет зависеть от природы излучения, но исключительно – от природы атома. С другой стороны, природа корпускулярного излучения будет зависеть исключительно от природы первичного излучения, а не от природы атома. Эти выводы находятся в согласии с известными свойствами рентгеновского излучения.

    Кроме того, мы видим, что каждый испущенный электрон будет соответствовать одной единице энергии характеристического излучения атома. Оно будет испускаться, когда электрон попадает в атом, дабы заместить электрон, который был испущен. Таким образом, независимо от энергии испускаемого электрона, энергия в соответствующем характеристическом излучении будет постоянной.

    Далее, энергия испускаемого электрона увеличивается вместе с частотой лучей. Следовательно отношение энергии в корпускулярном излучении к энергии в характеристическом излучении будет увеличиваться с жёсткостью первичного рентгеновского излучения. Также видим, что, когда частота первичного рентгеновского излучения равна частоте характеристического излучения, энергия в корпускулярном излучении будет равна энергии в характеристическом.

    В предшествующем обсуждении мы пренебрегли возможностью высокоэнергичных электронов, выброшенных лучами Рентгена, возбуждать при их соударении с атомами характеристическое излучение вещества. Оправданием этому служит то, что в некоторых экспериментах, которые я выполнил по возбуждению лучей Рентгена катодными лучами, я обнаружил, что энергия рентгеновского излучения была сконцентрирована в очень мягком типе излучения, и что лишь очень малая часть энергии катодных лучей была преобразована в тип излучения, сопоставимый по жёсткости с тем, который возбуждает корпускулярное излучение, сравнимое по скорости с катодными лучами, которые его произвели.

    Когда электрическая сила меняется с плюса на минус, как это происходит внутри атома по нашей гипотезе, то количество энергии, которую надо сообщить электрону, чтобы он добрался из одной точки P в другую Q, может быть много больше чем где R – сила, действующая на электрон, ds – элемент его пути. Поскольку распределение потенциала может тогда иметь вид кривой, типа представленной на рис. 1, где электрон не может добраться из P в Q, если не преодолеет пик R. Чтобы сделать это, он должен получить энергию, представленную отрезком RM, которая может быть намного больше, чем которая представлена отрезком QN. В случае подобном этому электрон, выпущенный из P, достигнет Q с конечным количеством кинетической энергии, измеренной разностью между RM и QN.

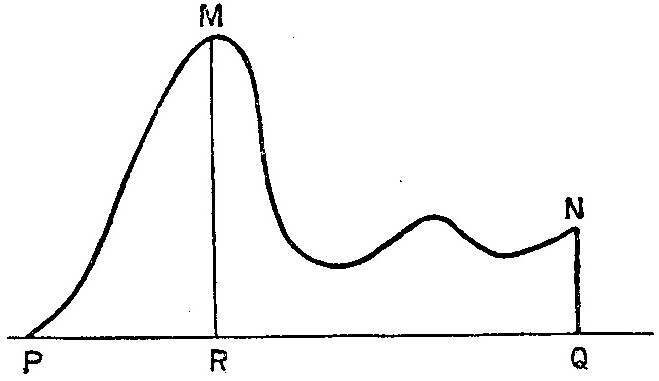
Рис. 1.

    В периодически меняющемся электрическом поле рассмотренного типа мы предполагаем, что можно ожидать максимальную величину RM приблизительно равной удвоенному QN. Работа, производимая между двумя точками равновесия, соответствует B₁-B₂, где B₁ и B₂ – значения магнитной индукции в двух точках.

    Далее, если численное значение силы магнитного поля в точке P – не ниже, чем значение в любой другой точке, расположенной ближе к поверхности атома, то максимально возможная отрицательная величина B₂ будет – B₁. А поскольку B₁, в первом приближении, изменяется гармонически, то B₂ может ожидаться близкой к этой величине. Таким образом, B₁–B₂ будет иметь в качестве своего максимального значения 2B₁, то есть энергия, которую надо сообщить электрону, чтобы он преодолел препятствие, подобное пику R, составляет удвоенную величину от увеличения потенциальной энергии, которую электрон получает, идя в точку Q, где B₂ принято исчезающе малым. Таким образом, когда электрон выходит из атома в точке Q, он будет обладать кинетической энергией, равной половине энергии, сообщённой ему в точке P.

    Предположим, что атом ионизируется излучением, частота которого – n, где n также является частотой характеристического излучения атома. Испускание электрона начинается при поглощении количества энергии, равного 2hn, от которой после освобождения электрона сохраняется в качестве кинетической энергии hn – эта энергия проявляется как энергия корпускулярного излучения. Другая половина энергии проявляется затем как характеристическое излучение, когда электрон падает в атом, чтобы занять место удалённого. В этом случае энергия корпускулярного излучения равна энергии характеристического.

    Затем предположим, что частота n₁ падающего излучения отличается от n, частоты характеристического излучения. Поглощение энергии будет иметь место, когда атом временно соединился с другим атомом, таким образом, что силы между атомами изменили частоту электрона с n на n₁. Поглощение энергии электроном теперь – 2hn₁, из неё hn₁ проявляется в качестве энергии корпускулярного излучения. Атом, восполняющий электрон после того, как он снова стал свободным, отдаёт hn единиц характеристического излучения. Разность

2hn₁–h(n+n₁)=h(n₁–n)

останется в атомах, приводя к их отделению с бóльшим количеством энергии, чем они имели, когда были вместе. Часть β этой энергии могла бы быть преобразована в медленное корпускулярное или мягкое рентгеновское излучение.

    Таким образом, выброс высокоэнергичного электрона будет сопровождаться следующими энергетическими эффектами:

    Энергия в корпускулярном излучении =hn₁.

    Энергия в характеристическом излучении =hn.

    Энергия в мягком рентгеновском излучении =βh(n₁–n).

    Корпускулярное излучение вызывает характеристическое излучение в отношении n₁ к n и, таким образом, неограниченно нарастает с увеличением n₁. Если включить мягкое рентгеновское излучение с корпускулярным, и во многих экспериментах они бы не различались, то отношение корпускулярной энергии к характеристической энергии будет

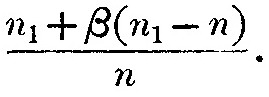
    Представление о том, что, когда электрон поглощает энергию излучения, то является составной частью системы, в которой он колеблется в унисон с излучением, не лишено трудностей. Оно требует, например, концентрации энергии световой волны в некоторых точках, вместо однородного распределения по фронту волны. Однако оно имеет большое преимущество, поскольку объясняет электрические эффекты, производимые освещением, без внесения в нашу концепцию света изменений, которые вызывают трудности в отношении обычных оптических явлений типа интерференции или рассеяния. Но их бы не затронула гипотеза резонанса.

    В пользу этой гипотезы говорит следующее:

    До сих пор мы предполагали, что резонанс вызван периодами свободных колебаний электронов в одном атоме, изменёнными за счёт соседства другого атома. Однако можно предположить, что тот же самый результат может быть вызван процессами, происходящими непосредственно в пределах атома и независимых от соседних атомов. Для атомов любого вещества, кроме водорода, содержащих больше одной положительной единицы заряда, если масса каждого положительного заряда равна заряду атома водорода, то число положительных зарядов будет равно атомному весу. Если атом электрически нейтрален, то где-нибудь внутри него должно иметься равное число электронов. Эксперименты показывают, однако, что лишь примерно половина из электронов свободны производить какие-либо независимые эффекты, другая половина должна быть связана с положительными зарядами. Если бы среди этих положительных зарядов за большие промежутки времени порой происходили бы изменения, аналогичные, хотя и в сильно уменьшенном масштабе, тем, которые происходят в радиоактивных веществах, электроны могли бы временно отделяться от этих зарядов, хотя и не так, как в радиоактивных веществах, и не с такой энергией, с какой электроны вылетают из атома в форме высокоскоростных β-лучей. Однако смещение электронов в нерадиоактивных веществах меняло бы частоту колебаний электронов в атоме, и создало бы небольшой запас атомов, частоты которых неодинаково отличались бы от частот в нормальном атоме и резонировали бы с колебаниями, на которые обычный атом не будет реагировать.

    Мы предположили, что периоды колебаний электронов определяются исключительно магнитными силами. Но даже если эти силы просто преобладают, то электрические силы, которые им сопутствуют, до некоторой степени изменят периоды, и смогут преобразовать период, который, если пренебречь этими силами, соответствовал одной линии,– в несколько линий, отделённых крайне малыми интервалами.

    Возможно, стоит указать на одно возражение, часто выдвигаемое против колебаний, обусловленных только электростатическими силами. А именно, что при таких силах исходные уравнения движения дают квадрат частоты, тогда как соотношения, заданные законами спектральных серий, затрагивают непосредственно частоту, а не её квадрат, и не применимы ко всем типам электростатической силы. Если, например, силу, действующую со стороны положительного заряда на электрон, представить как Ce(dφ/dr)², где C – константа и φ – функция r, тогда один набор положений равновесия определился бы из условия φ=0. И если ξ – это смещение от одного из этих положений, то уравнение движения

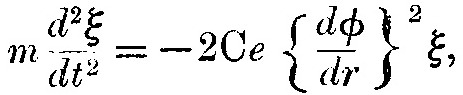
где {dφ/dr} – величина dφ/dr в положении равновесия.

    Частота колебаний, представленных этим уравнением, равна

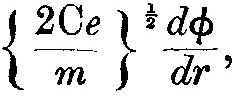
так что этот случай имеет сходство с тем, где колебания заданы магнитной силой, поскольку первая степень частоты даётся простым выражением без квадратных корней в переменной части. Подбором величины φ мы можем получить серии частот Ридберговского типа.

    Когда на электрон в магнитном поле действуют электрической силой, магнитные силы отклонят его, как только он придёт в движение, и он не будет двигаться по направлению электрической силы. Таким образом, если плоско поляризованный луч света, в котором вектор электрического поля параллелен оси x, падает на электрон, то он придаст электрону, вместе с ускорением по x, ускорение параллельное y и z. Ускорения, параллельные y и z, создадут рассеянные волны, которые не будут исчезать вдоль оси x. Теперь мы знаем, что в случае видимого света или Рентгеновских лучей свет, рассеянный в этом направлении, в нормальных случаях составляет крайне малую величину. А раз это так, то необходимо выяснить, совместим ли этот вывод с наличием сильных магнитных полей внутри атома.

    Пусть электрическая сила в волне параллельна x и равна Ecospt. Пусть ξ, η, ζ, будут смещениями электрона параллельно x, y, z, и a, b, c – будут компонентами вектора магнитной индукции внутри атома. Тогда уравнения движения, если мы учитываем возвращающие электрические силы, пропорциональные смещению, имеют вид

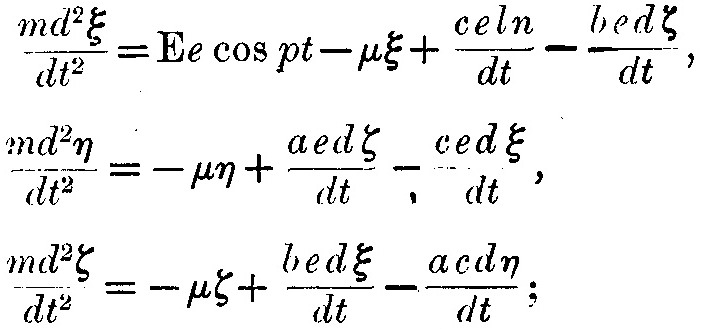
решение этих уравнений, если ξ, η, ζ изменяются как exp(pt), есть

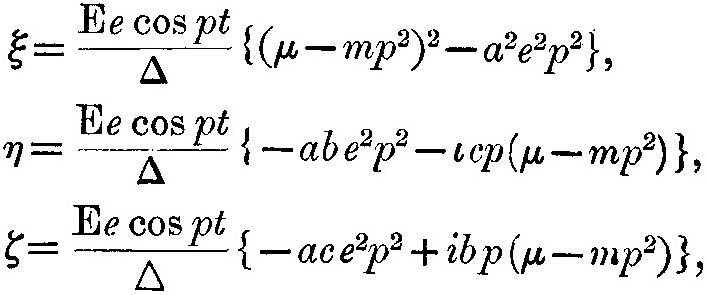
где                Δ=(μ–mp²)³+(μ–mp²)e²(a²+b²+c²).

    Отсюда видно, что смещения электрона идут не совсем в направлении электрической силы. Но из формы уравнений видно, что, если mp² или очень мало или очень велико по сравнению с μ, то смещение поперёк направления силы бесконечно мало по сравнению со смещением вдоль него. В теории рассеяния видимого света mp² принято малым по сравнению с μ, тогда как для лучей Рентгена оно принято большим, так что магнитное поле не влияло бы заметно на эти типы излучений.

    Если есть несколько электронов, центр конфигурации которых совпадает с центром атома, и если ось x – главная ось, то Σab, Σac, Σc и Σb исчезают, и рассеянное излучение будет идти в том же направлении, как это получается из обычной теории для немагнитного атома. Эффект поперечных смещений, если б электроны в одном атоме были расположены несимметрично, так что Σab, и т.д., все бы не исчезали, и если бы все отдельные атомы ориентировались точно так же, то это привело бы к вращению плоскости поляризации у плоско поляризованного света, проходящего через собрание атомов. Этот эффект, однако, исчез бы, если б атомы ориентировались случайным образом.

    Поэтому, видимо, в рассеянии света атомами газа или во вращении плоскости поляризации света нет ничего, несовместимого с существованием сильного магнитного поля внутри атома.

    Если б доминирующими силами внутри атома были магнитные, то заряженная частица, движущаяся сквозь атом, отклонялась бы. Но поскольку сила, действующая на движущуюся частицу в его магнитном поле, всегда перпендикулярна к направлению движения частицы, то частица ни потеряла бы, ни приобрела энергию. Столкновения были бы такими, которые обычно называют упругими, дабы отличить их от тех, в которых есть потеря энергии, и которые называются неупругими.

    Эксперименты Франка и Герца показывают, что в некоторых случаях, например, в аргоне и азоте, электрон может сталкиваться с очень большим количеством атомов без потерь энергии, и в случаях, где электроны не могут произвести много столкновений перед захватом и прикреплением к атому, эффекты, по-видимому, совместимы с представлением, по которому такие столкновения идут как упругие, и что альтернативой являются захваты или освобождения без потерь энергии.

    Поскольку частота колебаний электрона пропорциональна магнитному полю, то это свидетельствует, что на неё может влиять внешнее магнитное поле. На неё также влияло бы внешнее электрическое поле, так как оно сместит положения равновесия. Рассмотрение этих эффектов следует, однако, оставить до следующего раза.

Примечания:

1 Доложено автором.

Дата установки: 06.05.2011
Последнее обновление: 27.03.2012
[вернуться к содержанию сайта]

W