[вернуться к содержанию сайта]

    Преобразования Галилея решающим образом основаны на предположении, что промежутки времени во всех системах отсчёта одинаковы: Δt=Δt'. Это не означает, что если сейчас в Нью-Йорке 10 часов, то 10 часов должно быть и в Милуоки; но это значит, что если некоторый процесс продолжается 10 секунд в одной системе отсчёта, он будет продолжаться 10 секунд и в другой системе отсчёта. Это предположение представляется настолько очевидным, что не заслуживало бы и упоминания, если бы на самом деле оно не было ошибочным. Вскоре мы увидим, почему предположение о равенстве интервалов времени ошибочно. А пока отметьте, что это предположение прямо ведёт к заключению, что относительные скорости складываются алгебраически. Именно этот пункт и беспокоил больше всего Эйнштейна в начале нашего столетия.

    Эйнштейна занимала одна проблема, связанная с законами электромагнетизма, выражаемыми уравнениями Максвелла. Мы будем изучать их в главе 22. Они предсказывают, что электромагнитное излучение распространяется с вполне определённой скоростью – скоростью света. Однако уравнения ничего не говорят о том, в какой системе отсчёта эта скорость будет именно такой. По всей видимости, уравнения справедливы в любой системе отсчёта и во всех системах отсчёта. Следовательно, в вакууме свет всегда распространяется только с этой скоростью, равной 3,0·10⁸ м/с.

    Природа вещей такова, что скорость света универсальна и имеет одно и то же значение независимо от скорости источника света или скорости наблюдателя, выполняющего её измерение. Что это, гипотеза или экспериментальный факт? И то, и другое.

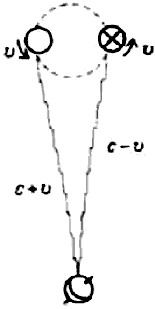
    Многие эксперименты показали, что скорость света не зависит от относительной скорости источника и наблюдателя. Например, на небе можно наблюдать множество двойных звёзд. Когда партнёры, составляющие двойную звезду, с большой скоростью обращаются один вокруг другого, мы видим их сначала как двойную звезду, затем как одиночную, когда один из партнёров проходит позади другого, и затем снова как двойную. В таких случаях мы располагаем источниками света, которые с большими скоростями движутся то к нам, то от нас (когда они движутся один вокруг другого), и эти источники света со строгой периодичностью включаются и выключаются (когда они заходят друг за друга). Если бы свет от той из звёзд, что удаляется от нас, распространялся медленнее, мы наблюдали бы запаздывание в наступлении её затмения передней звездой. Если бы свет от приближающейся к нам звезды распространялся быстрее, наблюдаемый эффект, в самом деле, был бы очень необычным.

    Объяснение наблюдаемого поведения двойных звёзд может состоять только в том, что свет всегда распространяется с одной и той же скоростью независимо от скорости источника, как если бы свет представлял собой некоторый вид волнового движения в неподвижном пространстве. В конце концов, именно так происходит распространение звука в воздухе. Наблюдатель получает при измерении одну и ту же скорость звука, издаваемого свистком поезда, независимо от того, с какой скоростью поезд приближается к нему или удаляется (хотя высота тона может изменяться). Если это объяснение применить и к свету, то наблюдатель на Земле смог бы обнаружить изменение скорости света, вызванное движением Земли в пространстве. Если бы световые волны распространялись в некоторой заполняющей космическое пространство среде подобно звуковым волнам, распространяющимся в воздушной среде, то скорость света в направлении движения Земли отличалась бы от скорости света в перпендикулярном направлении.

стр. 273
Ответы на вопросы

    11-15. Скорость наблюдаемого нами света всегда равна 3,0·10⁸ м/с. Однако цвет приходящего от квазара света изменяется.

    11-16. Наблюдаемый эффект зависел бы от расстояния между нами и двойной звездой. (Почему?) Если бы свет от звезды распространялся быстрее при её приближении к нам, чем при удалении от нас, нам бы казалось, что звезда проводит лишь очень короткое время в положении затмения. Такое могло бы также случиться и тогда, когда одна звезда большая, а её партнёр – малая. Но тогда движение партнёра казалось бы неправильным. В конце концов могли бы появляться ложные звёзды – звёзды-призраки: иногда двойная звезда выглядела бы как тройная. Отметьте также, что экспериментальные наблюдения за двойными звёздами доказывают, что в вакууме свет любого цвета распространяется с одинаковой скоростью. В противном случае двойные звёзды, попадающие в положение затмения, были бы видны быстро изменяющими свою окраску – замечательно интересный эффект, если бы он наблюдался. Но он не наблюдается.

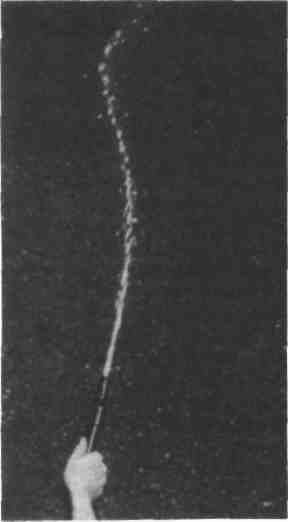
    4. Струя воды из шланга даёт довольно точную аналогию линий электрического поля. Если перемещать шланг очень медленно (в сравнении со скоростью струи) в перпендикулярном к струе направлении, получается модель линий поля, выходящих из медленно движущегося электрического заряда. (Игнорируйте тот факт, что струя воды следует параболической траектории в вертикальной плоскости из-за силы тяжести. Наблюдайте только за горизонтальной проекцией струи.) Струя из шланга образует прямую линию, выходящую из наконечника и перпендикулярную к направлению движения. Если, однако, перемещать наконечник с ускорением, на струе образуется излом. Этот излом имеет ясно выраженную составляющую, перпендикулярную к основному направлению струи.

    Особенно впечатляющий эффект можно получить, двигая наконечник перпендикулярно к струе туда и обратно по гармоническому закону. По струе будут перемещаться извивающиеся волны.

    Отметьте в особенности, что размах волн увеличивается с увеличением расстояния от наконечника. Иллюстрация этого эффекта приведена на фотографии. Чтобы лучше понять излучение ускоренного заряда, стоит выполнить эту простую демонстрацию своими руками.

    Сам Максвелл не решал своих уравнений, чтобы показать, что ускоренные заряды “стряхивают” с себя электромагнитную энергию. Детальный расчёт сложен, но можно приближённо разобраться в ситуации на основе модели линий поля. Поля, которые обнаруживают себя на некотором расстоянии от движущегося электрического заряда, были созданы этим зарядом в предшествующие моменты времени. Когда заряд движется с постоянной скоростью (но при условии, что она значительно меньше скорости света), Электрическое поле E в некоторой удалённой точке будет постепенно изменяться по модулю и направлению, как показано на рисунке.

    Магнитное поле в этой точке при движении заряда остаётся неизменным по направлению, но постепенно изменяется по модулю. Чтобы поддерживать движение заряда с постоянной скоростью, не требуется подводить энергию, и заряд не теряет энергии, когда он увлекает за собой линии электрического и магнитного полей.

    Чтобы ускорить заряд в направлении движения, к нему требуется приложить силу, и поэтому должна совершаться работа, Часть затрачиваемой при этом энергии излучается в форме электрического и магнитного полей, которые несут сообщение о внезапном изменении скорости источника.

    Проанализируем поле, создаваемое в удалённой точке электрическим зарядом, который сначала покоился, а затем внезапно получил ускорение a вертикально вверх на короткий промежуток времени δt. Его скорость к концу этого периода ускорения равна v=aδt. Затем он продолжает свободное движение вверх с этой скоростью v. Рассмотрим линию электрического поля, которая выходит из заряда в горизонтальном направлении. Даже после того, как заряд начал движение, электрическое поле в отдалённой точке остаётся постоянным и горизонтальным. Никакой информации о том, что заряд начал движение, ещё не поступило в эту точку. В момент времени T, равный расстоянию от заряда до этой точки, делённому на скорость света, поле начинает изменять направление. К моменту времени T+δt электрическое поле изменится так, что оно будет направлено вдоль прямой, выходящей из положения заряда в момент T+δt.

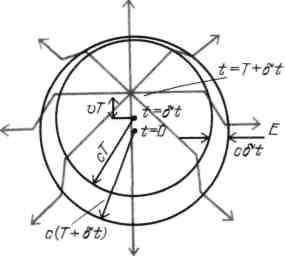
    В течение промежутка времени от Т до T+δt направление электрического поля в удалённой точке наблюдения резко изменяется. Посмотрим, как всё это выглядит, и изобразим линии электрического поля, как показано на рисунке. За пределами круга радиусом c(T+δt) линии поля направлены вдоль прямых, радиально расходящихся из начального положения заряда при t=0. Никакая информация о движении заряда ещё не вышла за пределы этого круга. Внутри меньшего круга радиусом cT линии поля направлены радиально из точки, где находится заряд в данный момент времени t=T+δt. Оба круга радиально расширяются со скоростью света. Между ними находится промежуточная область, где линии поля имеют большую составляющую, перпендикулярную к радиальному направлению. (Заметьте, что линии поля должны быть непрерывны, поэтому при переходе из внутренней сферы каждая линия должна соединяться с соответственной линией за пределами наружной сферы.) Линия поля в этом “изломе” имеет не то направление, которое примет поле после того, как импульс минует точку наблюдения. То направление изменится очень незначительно, поскольку источник перемещается лишь на небольшое расстояние vT, в то время как световой сигнал проходит расстояние cT. Поэтому в конце концов линия поля изменит направление лишь на небольшой угол порядка v/c.

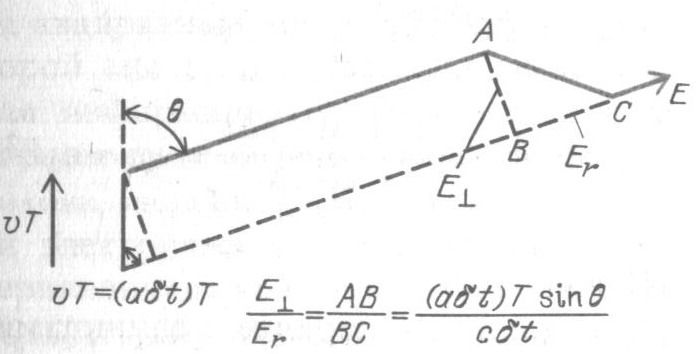
    В изломе горизонтальной линии поля отношение поперечной составляющей напряжённости поля к радиальной составляющей, как видно из следующего рисунка, равно

    E_┴/E_r=vT/cδt=aδtT/cδt=aT/c.

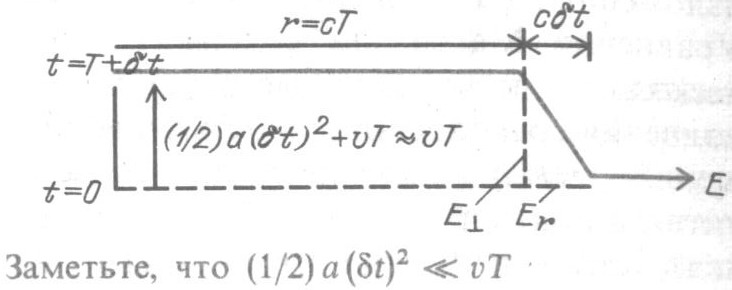
    Радиальная составляющая представляет собой просто поле точечного заряда и даётся законом Кулона:

    E_r=kq/r².

    Следовательно, поперечная составляющая напряжённости электрического поля равна

    E_┴=E_raT/c=kqaT/r²c.

    Расстояние от движущегося заряда до точки наблюдения равно r=сТ, откуда Т=r/c. Подстановка этого значения Т даёт следующее значение для поперечной составляющей электрического поля:

    E_┴=kqar/r²c²=kqa/c²r.

    Напомним, что эта поперечная составляющая электрического поля несёт информацию о том, что заряд подвергается ускорению. Она и пропорциональна ускорению заряда, но, что более замечательно, она обратно пропорциональна лишь первой степени расстояния. Почему же некоторая часть электрического поля, зависящего обратно пропорционально квадрату расстояния, убывает обратно пропорционально первой степени этого расстояния? Если вы пристально наблюдали за поведением струи воды из шланга при движениях наконечника в стороны туда и обратно, то должны были заметить, что поперечная компонента возрастала с увеличением расстояния от наконечника. Этот эффект показан на фотографии, помещённой на с. 302. С аналитической точки зрения заметьте, что поперечная компонента пропорциональна времени, в течение которого распространяется сообщение от источника до точки наблюдения. Это непосредственно связано с тем фактом, что резко сдвинутое поле в точке наблюдения направлено вдоль прямой, выходящей из точки, где находится равномерно движущийся заряд в данный момент времени. Чем больше время распространения сигнала T, тем дальше вверх успевает сдвинуться заряд и поэтому тем больше сдвиг линии электрического поля и тем больше его поперечная компонента.

    Поперечная составляющая электрического поля – излом на линии поля – зависит также от угла между линией поля и направлением ускорения. Мы рассмотрели случай, когда линия поля перпендикулярна к ускорению и эффект максимален. Если бы мы наблюдали за поведением линии поля, направленной в ту же сторону, что и ускорение заряда, то не обнаружили бы никакого эффекта. Независимо от модуля ускорения такая линия электрического поля сохраняет своё направление, и поэтому здесь не будет поперечной компоненты. Модуль поперечной составляющей поля зависит от синуса угла между направлением ускорения и направлением наблюдения, как показано на этом рисунке. Окончательная формула для поперечной составляющей напряжённости электрического поля имеет вид

    E_┴=kqasinθ/c²r.

    Поскольку обычные электрические и магнитные поля, создаваемые уединёнными зарядами или диполями, или электрическими токами, убывают обратно пропорционально второй или третьей степени расстояния, то единственным полем, которое можно обнаружить на больших расстояниях от источника, будет создаваемая ускорением составляющая напряжённости поля, зависящая от обратной величины первой степени расстояния. Отметьте, прежде всего, что эта часть поля перпендикулярна к прямой, выходящей из источника. Далее, этот поперечный излом уносится наружу со скоростью света. Как мы уже видели раньше, такой импульс электрического поля должен сопровождаться импульсом магнитного поля, которое перпендикулярно к электрическому полю и также к направлению распространения. Плотность энергии в таком импульсе пропорциональна квадрату электрического или магнитного поля. Поэтому излучаемая ускоренно движущимся зарядом энергия должна быть пропорциональна квадрату заряда, квадрату ускорения и обратно пропорциональна квадрату расстояния от источника. Свет, приходящий к нам от карманного фонарика или от удалённой звезды, пропорционален 1/r², если под “светом” понимать поступающую от источника энергию, которую можно зарегистрировать. Поскольку испускаемая ускоряемым вдоль прямой линии зарядом энергия пропорциональна sin²θ, заряд излучает преимущественно в перпендикулярных к ускорению направлениях.

    В антенне радиопередатчика электроны приводятся в движение вверх и вниз вдоль вертикальной линии, образующей резонансную цепь. Линия имеет длину l в каждую сторону от точки, где к антенне подводится мощность. Электрический заряд совершает простое гармоническое колебание, при котором положение центра заряда даётся выражением y=lsinωt. При этом скорость центра заряда равна

    v =Δy/Δt=ωlcosωt.

    Ускорение этого заряда равно

    a=Δv/Δt=-ω²lsinωt.

    22-5. Возможный способ решения этой задачи – представить себе линии поля как траектории фотонов, выбрасываемых электрическим зарядом. Для такой модели математическая аналогия с движением струи из шланга становится точной. К моменту времени δt заряженная частица набрала скорость v. Чтобы фотон был выброшен в перпендикулярном к скорости частицы направлении (в этом случае он достигнет наблюдателя), он должен начать движение, имея компоненту скорости назад, равную v (поскольку он испускается источником движущимся вперёд со скоростью v). Когда фотон достигает наблюдателя, он будет казаться прибывшим вдоль прямой, выходящей из положения заряда в момент времени T+δt.

    22-6. Поскольку ускорение электрического заряда, совершающего простое гармоническое движение, пропорционально квадрату частоты, а испускаемая энергия пропорциональна квадрату ускорения заряда, излучаемая энергия должна быть пропорциональна четвёртой степени частоты. Следовательно при одной и той же мощности излучения низкочастотные радиоисточники требуют гораздо больших токов, циркулирующих в передатчике, чем высокочастотные источники.

стр. 254
Дополнительный материал
Относительный характер электрического и магнитного полей

    При изучении второго раздела электромагнитных явлений мы описали действия электрических зарядов, движущихся мимо нас с постоянной скоростью. Как мы видели в главе 11, когда наблюдатели в двух различных системах отсчёта измеряют одно и то же явление, они могут использовать одни и те же законы – при условии, что они правильно выполняют преобразования расстояний и промежутков времени. Попробуем поставить мысленный эксперимент с электрическими зарядами и опишем его результаты в двух различных системах отсчёта, движущихся друг относительно друга с постоянной скоростью.

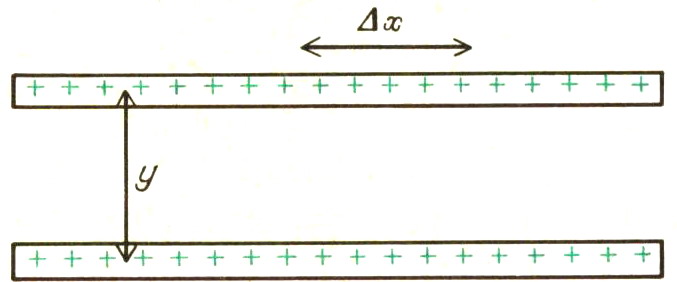
    На этом рисунке показаны две бесконечные линии, разделённые расстоянием y, каждая из которых имеет равномерный статический заряд с линейной плотностью λ: λ=Δq/Δx. На с. 159 было рассчитано электростатическое поле, создаваемое линейным зарядом. Оно равно

    E=λ/2πε₀y.

    Действующая на другой провод сила просто равна произведению его полного заряда на электрическое поле, создаваемое первым проводом. Поэтому сила взаимодействия двух проводов в расчёте на единицу длины равна

    F_y/Δx=λ²/2πε₀y.

    До сих пор мы предполагали, что заряды неподвижны не только по отношению друг к другу, но и по отношению к нам, наблюдателям. Теперь посмотрим, что происходит, если эти же заряженные стержни равномерно движутся вправо вдоль оси x со скоростью v. Как мы видели в главе 11, длины движущихся тел сокращаются. Может оказаться, что метровый стержень, скреплённый с движущимися проводами, для нас будет иметь длину только 50 см. Однако не существует никакого релятивистского уменьшения действительного числа зарядов. Заряд образован определённым числом электронов, и это число не зависит от скорости наблюдателя. Однако линейная плотность заряда действительно изменяется, поскольку λ=Δq/Δx. Если мы наблюдаем, что отрезок единичной длины сокращается вдвое, то это означает, что плотность заряда возрастает вдвое, поскольку мы бы насчитали то же самое число зарядов на сократившемся отрезке, как и в том случае, когда эти заряды были неподвижны.

    Дальше мы будем снабжать нулевым индексом все величины, относящиеся к движущимся телам и измеренные в движущейся системе отсчёта. Такие значения были бы получены при измерении наблюдателем, “оседлавшим” стержни и движущимся вместе с находящимися на них зарядами. Символы без нулевого индекса относятся к величинам, которые мы получаем при измерении, когда ведём наблюдение за проносящимися мимо нас стержнями. Соотношение длин, например, даётся формулой

    Измеряемая нами линейная плотность заряда равна

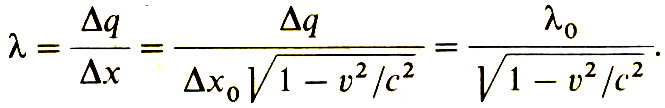
    Раз уж мы получаем при измерении бóльшую линейную плотность заряда, чем наблюдатель, оседлавший стержни, давайте сравним силу отталкивания между проводами, как она получается при измерении двумя наблюдателями. Измеряемое нами значение силы на единицу длины равно F_y/Δx. Значение силы на единицу длины, измеряемое оседлавшим провод наблюдателем, равно

    F_y0/Δx₀=λ₀²/2πε₀y,

тогда

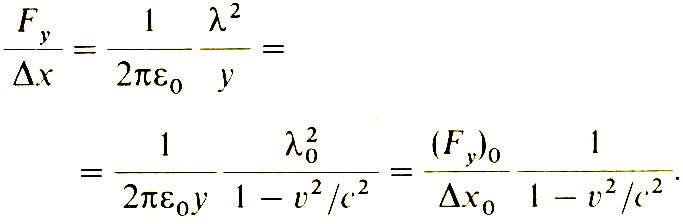
    Очевидно, что мы и движущийся наблюдатель расходимся во мнениях о значении силы отталкивания между проводами. Здесь есть серьёзная трудность, ибо этот результат привёл бы к разным предсказаниям для одного и того же события. Подсчитаем это расхождение между двумя системами наблюдателей:

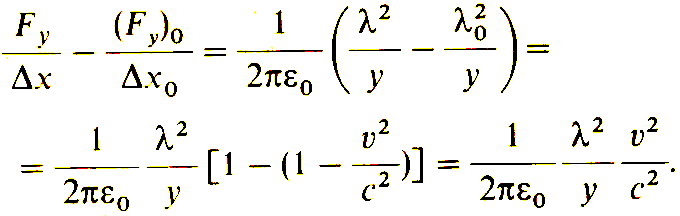
    При обычных скоростях отношение v/c очень мало, поэтому может показаться, что разногласия двух наблюдателей не очень велики, хотя и имеется некоторое расхождение. Продолжим это обсуждение. Обратите внимание, что хотя заряды неподвижны по отношению к наблюдателю, связанному с проводом, они движутся по отношению к нам, и поэтому создают электрический ток. Этот ток равен I=λv (I=Δq/Δt, λ=Δq/Δx). Поэтому мы можем переписать расхождение наблюдений в виде

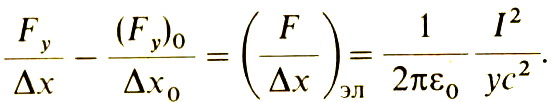
    У нас имеется ещё одно расхождение. Когда мы наблюдаем два параллельных тока, мы знаем, что между ними существует сила притяжения. Магнитная сила между двумя проводами равна

    (F/Δx)_M=μ₀I²/2πy.

    Таким образом, имеется два расхождения между результатами наших измерений и измерений наблюдателя, связанного с движущимся проводом. Он видит одну лишь силу электростатического отталкивания. Мы видим бóльшую силу электростатического отталкивания, потому что измеряемая нами линейная плотность заряда больше. Но мы видим также силу притяжения, обусловленную магнитным взаимодействием. Что касается движущегося наблюдателя, то для него нет никакого магнитного поля.

    Если сила, отнесённая к единице длины, измеряемая двумя наблюдателями, имеет разные значения, наблюдатели предсказали бы разные события для одного и того же явления.

    Подобное противоречие было бы крушением наших научных методов. Например, что если измеряемое нами магнитное поле оказалось бы достаточно сильным, чтобы вызвать сближение проводов? (В действительности для принятого нами расположения сила отталкивания всегда должна быть больше, чем сила притяжения. Однако существует ситуация, называемая “пинч-эффектом”, когда движущиеся с большой скоростью пучки и в самом деле сближаются. Но чтобы пинч-эффект происходил, между токами должны также находиться нейтрализующие заряды.)

    Можно избежать противоречия между двумя наблюдателями, сказав, что наблюдаемая нами добавочная сила отталкивания должна быть как раз равна добавочной магнитной силе притяжения. Это условие выполняется, если

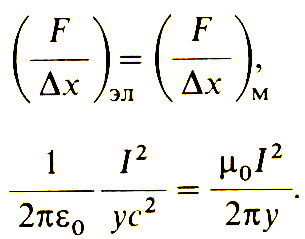
    Эти выражения равны друг другу, если

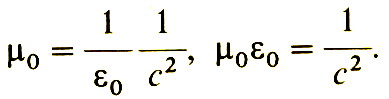
    Электрическая (ε₀) и магнитная (μ₀) постоянные представляют собой константы, измеряемые в статических ситуациях. Значение электрической постоянной находится на основе измерения полей и геометрических размеров какого-либо конденсатора; числовое значение магнитной постоянной выбрано в эксперименте, который служит определением ампера. Подставим эти значения в наше уравнение:

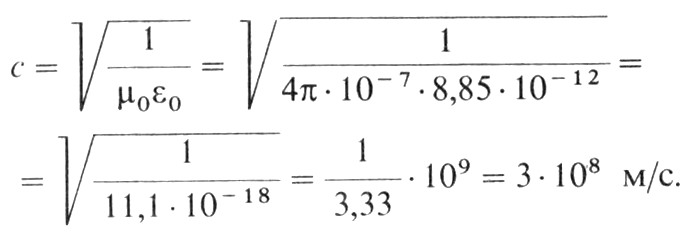
    Это равенство действительно удовлетворяется. Поразительно, но свойства статических электрического и магнитного полей связаны со скоростью света!

    Будем ли мы наблюдать электрическое поле или магнитное поле, зависит, очевидно, от нашей скорости по отношению к источникам. Электрическое поле для одного наблюдателя может стать магнитным полем для другого. Оказывается, что магнетизм представляет собой просто релятивистский эффект, значение которого зависит от квадрата отношения относительной скорости к скорости света. Можно ожидать, что это явление будет обнаружено только у субатомных частиц, разогнанных до скоростей, близких к скорости света; но мы уже видели, что магнитные явления могут наблюдаться с обычными проводами, подключенными к сухому элементу. Электроны в таком потоке дрейфуют со скоростью в доли миллиметра в секунду. Почему же нам удаётся построить мощные электродвигатели, действие которых основано на столь слабом эффекте?

    Магнитное поле, создаваемое дрейфом электронов в проводе, и в самом деле чрезвычайно малó по сравнению с электрическим полем, создаваемым тем же самым зарядом. Однако электрон в проводе не одинок. Все отрицательные и положительные заряды присутствуют в нём парами, так что обеспечивается полная электростатическая нейтральность. Магнитное поле, обусловленное дрейфовой скоростью каждого отдельного электрона, хотя оно и мало, не подвергается компенсации. В расчёте на каждый ампер в проводе 6·10¹⁸ электронов дрейфуют мимо данной точки за каждую секунду. Поле отдельного электрона мало, но число таких вкладов огромно. В результате получается воздействие, которое можно обнаружить в мире явлений, относящихся к нашим обычным человеческим масштабам. Всякий раз, когда вы чувствуете магнитную силу, вы наблюдаете на опыте следствия частной теории относительности.

Дата установки: 11.03.2011
Последнее обновление: 18.03.2011
[вернуться к содержанию сайта]

W