[вернуться к содержанию сайта]
Цель данного сообщения – показать, как можно от известных спектральных серий элемента прийти к новым сериям, которые представляются точно без введения каких-либо новых констант для всех серий и линий, недавно обнаруженных Ленардом, Коненом (Konen), Гагенбеком (Hagenbach), Сандерсом (Saunders), Моллом (Moll), Рэмеджем (Ramage) и Бергманом. Новый комбинационный принцип находит также применение и к другим спектрам, в частности к гелию и щёлочноземельным металлам. Также представим более тесную связь с атомным весом, чем та, что была известна до настоящего времени.
В наиболее удобном виде предложенная мной формула серии гласит (1
):(1) 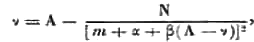
где ν – волновое число в вакууме, N – универсальная константа,
m – целое число, A – граница серии; α и β - константы. Для малых величин m ν может стать отрицательным, что должно быть учтено в члене β(A–ν). Κонстанты α и β характеризуют порядок серии: они эквивалентны двум сериям с различными константами.Также имеем приближённо
(2) 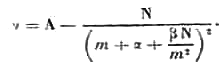
Используем для краткости обозначение
(3) 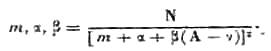
Пусть, например, константы α и β принимают значения
d и δ для первой из пары побочных серий ("диффузная серия" согласно терминологии Ридберга). Для второй побочной серии (ридберговские "резкие серии") пусть их значения будут s и σ. Для главных серий пусть эти величины будут p1, π1 и p2, π2. Для щелочных металлов весьма приближённо π1=π2 (2).Если первая побочная серия имеет спутника [спектральный дублет – С.С.], с другим набором величин,
d' и δ', то применяется вторая главная линия, где опять же приближённо δ=δ'.Выражение для трёх серий может теперь быть записано так (там же
, p. 291):Главная серия:
±ν = (1,5,
s, σ) – (m, pi, πi) (i = 1, 2; m = 2, 3, 4, ... , p1 > p2).Вторая побочная серия:
±ν = (2,
pi, πi) – (m, s, σ) (i = 1, 2; m = 1,5; 2,5; 3,5, ... ).Первая побочная серия:
|
|
(первая главная линия и сателлит) |
|
(вторая главная линия) |
Константа, разделяющая линии дублета, есть ν
1 = (2, p1, π1) – (2, p2, π2). На основании данных наблюдений доступных на данный момент, можно отметить следующие моменты (3):1. В уравнении главной серии при замене 1,5 на большие числа – 2,5; 3,5, ... ; и в уравнении побочных серий при замене 2 на более высокие числа – 3, 4, 5, ... , новые линии дадут результат, который не раз наблюдался. Это предсказывал уже Ридберг.
2. Для каждого терма (
m, α, β) εсть минимальное значение m (а именно, 3 для первой побочной серии; 1,5 для второй побочной серии, согласно примечанию из моей уже упомянутой диссертации), которое является основным числом. Если придаём m ещё меньшие значения, то следовало бы ожидать более интенсивную линию, однако на практике эта линия не наблюдалась. Я уже показал (4), что ни в одном спектре рассматриваемая линия не соответствует номеру n=2 первой побочной серии, настолько уверенно, насколько наблюдения способны ответить на этот вопрос.3. Если составим из этих термов новую комбинацию (1,5,
s, σ) – (3, d, δ), ςо получим новые линии, которые наблюдались у He, K, Rb, но которые всё ещё не выявлены у Na и Li. Для щёлочноземельных металлов они попадают в инфракрасную область. Рассчитанная для He величина ν=26244,86, наблюдаемая величина – 26244,78.4. В случае Li и Na также наблюдалась комбинация (2, p1, π1) – (m, p1, π1); (2, p2, π2) – (m, p2, π2); m=3, 4, ... .
5. Если составляем комбинацию (3,
d, δ) – (m, p1 – p2, π1 – π2); m=4, 5, ... , то получаем инфракрасную серию, найденную Бергманом (5) для K, Rb, Cs и соответствующие линии для Li, Na, He, которые были неизвестны.Для Rb и Cs первая побочная серия имеет спутника, так что мы получали в итоге вторую серию (3,
d', δ') – (m, p1–p2, π1–π2), которая располагается возле первой и имеет постоянное смещение относительно неё, как показали наблюдения Бергмана и ещё ранее Сандерса для Cs. Тогда как для Rb линии не могут быть выявлены. Основной номер для этого недавно образованного терма (m, p1–p2, π1–π2) будет m=4.6. Существует также следующая комбинация:
(2, pi, πi) – (m, p1–p2, π1–π2) (i= 1, 2; m= 4, 5, ...).
У Na цвет пары переходит в ультрафиолет. Соответствующая пара у Cu и серии линий, которые были найдены Ленардом, Коненом и Гагенбеком у Li и Na, приведена здесь.
(4, p1–p2, π1–π2) – (m, p1–p2, π1–π2).
7. Подробных исследований, вроде тех, что существуют для щелочных металлов, недостаточно для щёлочноземельных металлов в инфракрасной области. И главные серии не наблюдались, показывая, что проверка комбинационного принципа, в том виде, который до сих пор применялся, в настоящее время не может быть выполнена. Другие обстоятельства, однако, указывают, что справедливо и следующее: в первой побочной серии, из серии триплетов с двумя спутниками, мы должны ввести новые термы (
m, p3, π3), (m, d'', δ'') с p1>p2>p3. В первом приближении мы можем пренебречь π1–π2, π2–π3 и рассчитать p1–p2, p2–p3 из границ побочных серий, несмотря на то, что главная серия не наблюдалась. Тогда p1–p2 будет в два раза больше, чем p2–p3, и две разности волновых чисел (обозначенных Ридбергом как ν1 и ν2) естьν
1= (2, p2, π2) – (2, p1, π1), ν2= (2, p2, π2) – (2, p3, π2).Здесь часто наблюдаются двойные линии, отстоящие на величину ν
1, и триплеты с расстоянием ν1 и ν2 вне серии. Этого следовало ожидать уже из комбинационного принципа, но только если (2, pi, πi) связано с какой-либо величиной (m, α, β). Эти дублеты и триплеты должны, таким образом, принадлежать сериям, которые завершаются в той же точке (2, pi, πi), что и уже известная побочная серия, но в которой лишь несколько термов достаточной интенсивности должны быть заметны.Далее оказалось возможным найти уравнение второй побочной серии для сильных ультрафиолетовых пар линий у Ca, Sr, Ba, для которых разница волновых чисел ν' в два раза больше, чем ν
1, и из элементов этих двойных линий образовать соответствующие разности констант p, принимая π1–π2=0. Это расстояние [между линиями – С.С.] отличается от расстояния в серии триплетов всего примерно на 15 %. В том же, но более точном вычислении два значения, вероятно, совпали бы, что соответствовало бы комбинационному принципу.Наконец, побочные серии близких триплетов были недавно найдены у Ca и Sr Фоулером (Fowler) и Сандерсом. Из границ этих серий опять же могут быть образованы разности
p'1–p'2, p'2–p'3. В пределах точности они совпадают с рассчитанными из спутниковых и главных линий первой побочной серии d–d', d'–d'', так что здесь имеются новые комбинации.Кроме того, обнаруживается преимущество в отношении связи с атомным весом, для ввода константы в формуле волновых чисел, несмотря на то, что это можно считать только приближением. Хорошо известно, например, что отношение ν
1 к квадрату атомного веса μ практически не меняется в пределах группы химически связанных элементов; но зато оно сильно меняется от группы к группе, от 31,6 у Cs до 187,0 у Tl. Мы вводим (p2–p1)/μ2 вместо ν1/μ2, и вариации становятся намного меньше.Несоответствия, которые всё ещё остаются, вероятно, должны частично исчезнуть в формуле серии, особенно в случае пренебрежения величиной π
1–π2, что, конечно, не допустимо для Al, In и Tl. Знание главных серий этих элементов позволило бы нам принять решение в отношении этого.
Согласно выводам Ридберга (
Rapports du Congres de Physique, t. II, Paris, 1900)Известно, что с увеличением атомного веса серии быстро ослабевают, так что наблюдаются только те линии, которые соответствуют наименьшим номерам последовательности. В то же время количество разных серий увеличивается (даже Mg показывает серию двойных линий и простых линий в дополнение к серии триплетов) и число комбинаций увеличивается. Таким образом, мы наконец пришли к спектру, в котором можно обнаружить большое количество
разностей характерных констант. Мне кажется весьма вероятным, что так называемые спектры второго класса, которые показывают такое поведение – это спектры с очень многими комбинациями и с весьма незначительно развитыми сериями.Вычисление величины (
m, α, β) предполагает знание элементов серии в формуле, в которую она входит. Эти элементы могут быть определены с большой точностью, за исключением случая, когда наблюдается несколько диффузных (размытых) линий. Это также почти не зависит от непостоянства, выходящего за рамки строгой формы уравнения серии. Для случаев, упомянутых под номерами (1), (3), (4), мы действительно должны вычислять исключительно разности и суммы наблюдаемых волновых чисел. Точность здесь, естественно, всё ещё высокая. Но с другой стороны константы, входящие в терм (m, p1–p2, π1–π2), могут быть изменены на 20 процентов без существенного увеличения разницы между вычислением и наблюдением. На степень малости этой разности влияние констант p1–p2, π1–π2, относительно невелико по сравнению с m, и серия идёт рядом с серией Бальмера, особенно у Li, Na и He. Для большого атомного веса наблюдения до настоящего времени крайне неточны, чтобы они могли дать что-то определённое в этом вопросе.В статье, которая недавно вышла (6
), я показал, что мы можем упомянуть системы наиболее простого вида, для которых вся энергия чисто электромагнитная, и которые рассматривают формулу Бальмера, законы спектральных серий, аномальный эффект Зеемана и т.д. Колебания вида![]()
производятся магнитным полем от
m–2 элементарных магнитов, которые повёрнуты друг к другу и идентичны между собой: в дополнение к этому магнитному ряду электрон подчиняется только жёстко заданным комбинациям. Подобное положение дел хорошо применимо и к другим спектрам. Таким образом, более высокие номера последовательностей в определённой мере соответствуют более высоким магнитным полимеризациям, которые постепенно становятся менее устойчивыми, вот почему линии уширяются с увеличением номера последовательности, а также постепенно становится всё более слабыми. Интенсивные движения, вроде тех, что возникают в электрической искре, также оказываются неблагоприятными для стабильности, поэтому в искре серии обрываются на более низких номерах последовательности, чем в электрической дуге.Магнитное поле в атоме во всех спектрах может быть рассмотрено, как производимое двумя полюсами противоположного знака, которые по отдельности могут занимать различные положения в атоме. В случае водорода, эти точки расположены на равных расстояниях на прямой линии. По-видимому, мы можем более широко сформулировать принцип, согласно которому простые линии зависят или определяются положением этих полюсов в атоме. В (
m, α, β)– (m, α', β') κаждый из термов представляет собой влияние одного полюса; и, как мы показали ранее, возможные положения отдельных полюсов допускают весьма различные комбинации полюсов в парах.Что касается некоторого минимума, предписанного номеру последовательности
m, — который возникает в случае неизвестных процессов вибрации, — то этот метод представления утверждает лишь, что полюса магнита удерживаются структурой атома на некотором минимальном расстоянии от электрона, колеблющегося в пределах атома. Эта идея представляется весьма вероятной.Гёттинген, июнь 1908.
Примечания:
(1) Inaug.-Diss. Auszug, Ann. der Physik, t. XII, 1903, p. 264; OEuvrеs, I, p. 1.
(2) Там же, с. 291; OEuvres, I, p. 52.
(3) Другие подробности читатель сможет найти в статье, уже вышедшей в Physikalische Zeitschrift. OEuvres, IX, p. 141.
(4) OEuvres, VII. p. 98, et VIII, p. 137.
(5) Inaug.–Diss., Jena, 1907; также C. Runge, Physik. Zeitschr., t. IX, 1908, p. 1.
(6) Magnetishe Аtomfelder und Serienspektren (OEuvres, VII, p. 98).
Дата установки: 23.12.2008
[вернуться к содержанию сайта