[вернуться к содержанию сайта]

АТОМНЫЙ МАГНИТ И СПЕКТРАЛЬНЫЙ КОД АТОМА
(напечатано в журнале "Инженер" №5-6, 2015)

    Учёные, узревшие в начале XIX в. загадочные чёрточки спектральных линий атомов, оказались в положении египтологов, пытавшихся в те же годы расшифровать иероглифы. Ведь строение атомов, которое не рассмотришь в увеличительное стекло, требовалось постичь, не зная смысла их спектрального штрих-кода, помогающего идентифицировать атомы, как товары – на кассе, или как человека – по отпечаткам пальцев [1]. Египтологам в расшифровке помог розеттский камень, но такого ключа не было у “атомологов”. По замечанию одного из них, В. Ритца, “Спектральные измерения с крайней точностью дают нам в руки многочисленные документы, но, к несчастью, они написаны иероглифами, которые мы не умеем расшифровывать” [2, 3]. И всё же Ритц разгадал этот ребус, а розеттским камнем стал магнит – “камень любви”. Ведь первая модель атома, предсказавшая спектры атомов, в том числе водорода и щелочных металлов, была не планетарной, а магнитной, и выдвигалась в начале XX века В. Ритцем и Дж. Томсоном – современниками героев книг Конан-Дойла. Несмотря на успехи, эта модель забыта ввиду ранней гибели Ритца и суеверий квантовой механики. Ряд свойств атомов и их соединений до сих пор не понят, а новые исследования выявляют всё больше неувязок с официальной квантовой версией. Поэтому обратимся к дедуктивному методу Ритца [3] и классической магнитной модели – магнитному ключу к загадкам материи.

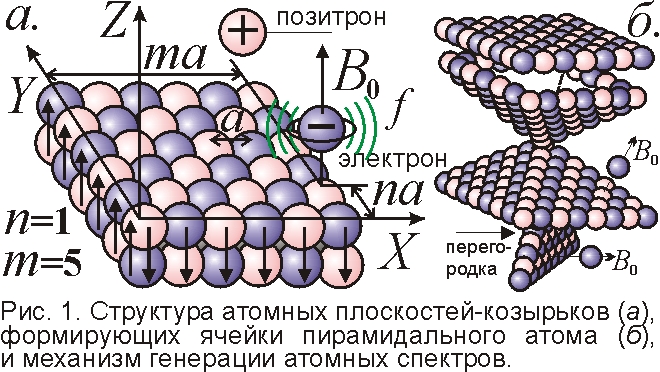
    Напомним, Ритц и Томсон представляли атом в виде системы зарядов, где электроны (открытые Томсоном) занимают лишь устойчивые положения в узлах атома, как шахматные фигуры на клетках магнитной шахматной доски. Вот и атом с сеткой узлов образует два симметричных козырька, закрывающих электроны (рис. 1). Представление об узлах дают железные опилки-диполи на доске, образующие в поле подковообразного магнита ёжик периодичных сгущений, игл, где положения частиц устойчивы. Так и поле атомного ядра формирует V-образный атомный остов из ряда электрон-позитронных диполей (динамид, предсказанных И. Штарком), кристаллизуя их из электрон-дырочного вакуума, признанного наукой [4]. По сути, атом – это компактное массивное ядро, окружённое невесомой оболочкой, наподобие кометы Чурюмова-Герасименко, ядро которой при сближении с Землёй в 2015 г. изучил зонд “Розетта”. Согласно Ритцу, атом аналогичен полимерам из повторяющихся элементов [3]. Предсказывал эти первоэлементы в форме “протила” (нулевого элемента) и Менделеев, и У. Крукс – английский химик, вышедший на след электрона с помощью трубки Крукса и открывший элемент таллий методом спектрального анализа. Видимо, прототипом юного Шерлока Холмса – неординарного химика, искавшего вещества по еле уловимым следам, и был Крукс, знакомый Конан-Дойлу по Лондонскому обществу спиритизма [5].

    Магнитное поле атома плавно меняется вдоль осей, но раз электроны в атоме ютятся лишь возле узлов, магнитное поле для них принимает ряд дискретно меняющихся от узла к узлу значений B₀. Электроны прилипают лишь к узлам магнитных листков-граней (рис. 1), как крупицы чернил в лазерном принтере – к заряженным точкам-пикселам магнитного барабана. В итоге, частоты вращения электронов возле узлов меняются дискретно, образуя дискретный спектр частот f – линейчатый спектр атома: вращаясь с частотами f=eB₀/2πM, электроны массы M и заряда e излучают на них. По этим частотам можно выявить атомы в ничтожной концентрации. В классической физике, где величины меняются плавно, прежде не удавалось понять спектры. Вот и придумали безумную по словам Н. Бора квантовую физику, где всё скачет, меняется дискретно. Но дискретность материи, её частиц, образующих узлы “кристаллической решётки” атома, допускает скачкообразное изменение параметров и в классике. Так и “квантование” наследственности, генов (тоже отображаемых полосками), как показали Уотсон и Крик, обусловлено не мистикой, а “атомами” генома – кодом ДНК.

    Ещё в 1908 г. Ритц первым предсказал неизвестную прежде серию Ритца-Пашена и весь спектр водорода f=Rc[1/n²–1/m²], где R=1,1·10⁷ м^–1 – постоянная Ридберга, c=3·10⁸ м/с – скорость света [3, 6, 7], считая, что атом излучает данную частоту f в зависимости от узла с целыми координатами n и m, занятыми им в сетке атома (рис. 1). Атомы подобны кристаллическим ПЗС-матрицам фотокамер, микрочипам ЭВМ, карт памяти и флэшек, где информация разложена по полочкам в двумерной матрице из ячеек-транзисторов: наличие заряда там соответствует “1”, а отсутствие – “0”. Вот и атом, в зависимости от размещения зарядов, излучает разный спектральный код. В будущем это позволит создать элементы памяти размером с атом: идеально для этого подходят охлаждённые многоэлектронные атомы редкоземельных элементов. Как во флэшке, внешнее воздействие, скажем электрический разряд, сбрасывает, перезаписывает информацию: электрон смещается и излучает новую частоту.

    Длительное воздействие разрядов проявляет спектральные линии, прежде скрытые [8]. Видимо, разряд повреждает “кристалл” атома, меняя внутриатомные поля, образующие новые линии. Атомы в разрядах ионизуются, теряют часть электронов, эффективный заряд Z_ef остова атома растёт, меняя расстояния меж узлами a=a₀/Z_ef (рис. 1), где a₀~0,53·10^–10 м – характерный размер атома [9, 10]. Так и разные магниты образуют сетки узлов разного шага. Соответственно меняются поля и частоты f=Rca₀²(1/y²–1/x²)=RcZ_ef²(1/n²–1/m²). Если атомы не подвержены воздействиям, например, в межзвёздном газе, электроны могут вечно пребывать в одном узле, а номера n и m достигают сотен. В отсутствие столкновений кристаллическая решётка атома разрастается, а электроны, заняв удалённые от ядра малоустойчивые позиции с номерами n и m~100, долго там остаются, высвечивая запрещённые линии с n и m, нарушающими правила отбора квантовой механики. На деле эти линии не противоречат букве классических законов, но обычно их яркость мала от малоустойчивости электронов в узлах.

    Интенсивность линии, как отмечал Ритц, определяется устойчивостью данного положения электрона в атоме (рис. 1), т.е. процентом атомов с таким размещением электронов. Поэтому яркость линий убывает при росте n и m для далёких от ядра электронов [7]. А ширина линий растёт, поскольку колебания и дефекты решётки, а значит и вариации частоты линий, растут с удалением от ядра. Магнитная модель атома позволяет рассчитать интенсивности свечения линий более естественно и строго, чем квантовая теория с коэффициентами Эйнштейна, матрица которых образует подобие шахматной доски, где коэффициенты соответствуют интенсивностям линий, излучаемых электронами разных клеток (рис. 1). Согласно британскому археологу Дж. Нидэму, аналогия магнита и шахмат ещё глубже: в Индии и Китае магнитный компас и шахматы составляли одно целое – движение фигур на доске, как электронов – в атоме, задавалось случайным образом с помощью костей и стрелок [11].

    Магнитная модель объясняет и опыт Штерна-Герлаха, показавший, что, кроме величины поля B, дискретно меняется и направление магнитного момента μ атома. В опыте поток атомов серебра в неоднородном магнитном поле разбивался на два потока (рис. 2). Казалось, это невозможно, поскольку во внешнем поле магнитный атом колеблется, а планетарный атом – прецессирует [9], и их магнитные моменты μ не могут установиться вдоль поля. Но ведь и стрелка компаса в магнитном поле колеблется, а затем замирает из-за сил трения, ориентируясь вдоль поля B. Казалось, летящий атом, в отличие от стрелки, ничто не тормозит. Но и атом подвержен трению, только уже радиационному [12]: колеблющийся с частотой f электрический заряд или диполь излучает на частоте f своих колебаний. Оттого при парамагнитном резонансе атомы и связанные с ними электроны, влетая в магнитное поле, начинают колебаться с частотой f и излучать на ней. На излучение и тратится энергия колебаний, пока атом, как стрелка, не установит момент μ вдоль поля B. Отсюда эффект магнитного охлаждения: в магнитном поле атомы отдают тепло, излучают энергию своих колебаний в поле B.

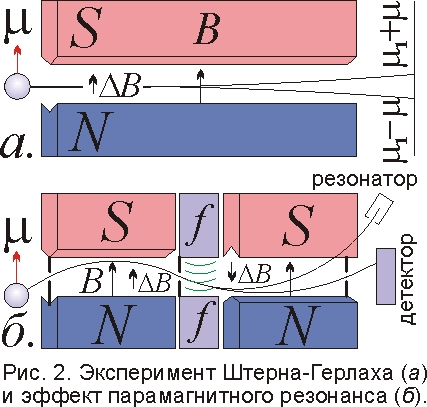
    В атоме серебра один свободный электрон. У атомного остова – свой магнитный момент μ₁. При этом в атоме магнитное поле B₀ в разных точках имеет разную величину и направленность, отчего у электрона магнитный момент μ либо сонаправлен с моментом остова (μ₁+μ), либо противонаправлен (μ₁–μ). Следовательно, результирующий магнитный момент у двух типов атомов отличен на 2μ, и неоднородное магнитное поле сепарирует два типа атомов на два потока (рис. 2). Если валентных электронов больше, их магнитные моменты образуют больше комбинаций, и поле B расщепляет пучок атомов на большее число компонент.

    Электрон, крутясь возле узла, создаёт добавочный магнитный момент, как у витка с током. Неоднородное магнитное поле отклоняет такие атомы иначе, чем атомы с неподвижными электронами. Это позволяет измерять радиочастоты f колебаний электронов в атоме методом парамагнитного резонанса: атомы со стандартным магнитным моментом проходят сквозь систему магнитов и диафрагм. Но радиоизлучение частоты f вызывает резонансную раскрутку электронов: за счёт избыточного магнитного момента магнитное поле сильней отклоняет атомы, и те минуют детектор (пунктир на рис. 2.б). Сходный принцип применяют в мазерах – стандартах радиочастоты. Для отбора атомов, например, водорода, излучающих на частоте f=1,4 ГГц, их пучок пропускают через неоднородное магнитное поле B, по-разному отклоняющее атомы, излучающие и поглощающие энергию. Электроны, излучающие при вращении, создают добавочный магнитный момент, и поле B отклоняет их сильнее, направляя в резонатор, где атомы водорода излучают энергию на частоте f (рис. 2). Итак, парамагнитный резонанс и мазерный эффект – это классические следствия магнитной модели атома.

    Объяснил Ритц и эффект Зеемана – расщепление в магнитном поле B каждой линии спектра на ряд компонент [6]. Поле B ориентирует остовы атомов и, налагаясь на внутриатомное поле B₀>>B, меняет его до B₀±B_z, где B_z=Bcosα – проекция внешнего поля на ось z, перпендикулярную грани (рис. 1, 3). Грани наклонены на 30° к оси остова, откуда α=60° и B_z=B/2, а на перегородке B_z=0. В итоге, у части атомов частота вращения электронов останется f=eB₀/2πM, у части вырастет до f=e(B₀+B_z)/2πM, а у части снизится до f=e(B₀–B_z)/2πM, и кроме линии f=eB₀/2πM, появятся две смещённых на Δf₀=±eB/4πM, в согласии с опытом. Грани с наклоном 30° к оси, при взгляде на атом сбоку (рис. 1, 3), имеют вид равносторонних треугольников. Так вот, начав изучать древние символы – янтры, обнаружишь поразительное сходство с пирамидальным атомом в виде встречных равносторонних треугольников.

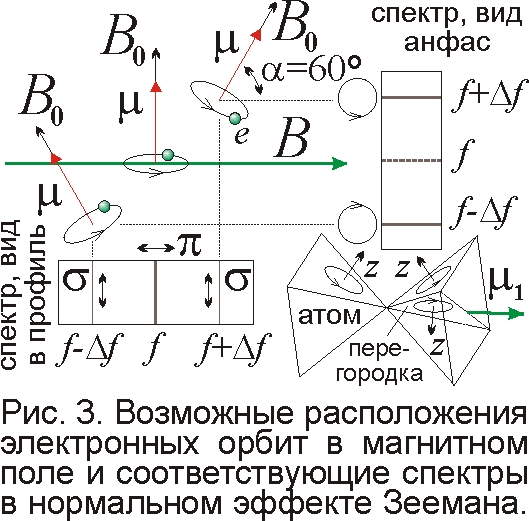
    Электроны на гранях вращаются поперёк линий поля B, и при взгляде сбоку у их излучения – поперечная полю линейная σ-поляризация. А часть электронов – на перегородке, вдоль которой направлено поле B, здесь уже поперечное к B₀ (рис. 3). Оно не меняет частоту вращения электрона, и излучение поляризовано вдоль B. При взгляде вдоль поля излучение частот f–Δf₀ и f+Δf₀ циркулярно поляризовано по и против часовой стрелки: именно в эти стороны вращаются электроны при взгляде анфас. Но разную поляризацию линий не объясняет квантовая механика, где электроны подобны туману, а не летают по орбитам. Три линии соответствуют не одному атому, как в модели Лоренца, а разным типам атомов. Проверить магнитную модель можно, разделяя эти три типа атомов неоднородным магнитным полем.

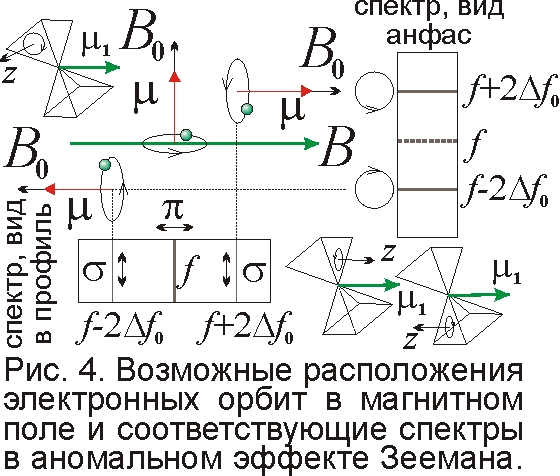
    Известен и аномальный эффект Зеемана, состоящий в расщеплении спектральных линий на большее число компонент. Он обычен для многоэлектронных атомов. Эффект противоречил модели Лоренца, но элементарно следовал из магнитной модели атома [6]. Раз электронов в атоме более одного, то и сортов атомов больше: кроме электрона, излучающего частоту f, есть валентные электроны, размещённые на разных гранях. Магнитные моменты μ этих электронов меняют момент атома μ₁, так что он может принимать разные направления по отношению к оси атома (рис. 4). Поэтому внешнее поле B, вдоль которого ориентируются атомы, как стрелки компаса, образует разные проекции B_z=Bq/p на вектор внутриатомного поля B₀, где q и p≥q – целые числа, сопоставимые с валентностью – числом свободных электронов. Следовательно, вместо одной линии, появится ряд линий, смещённых на Δf=±eB_z/2πM=±eBq/p2πM от основной. Такую картину и наблюдают: сдвиги Δf между линиями растут пропорционально B и, по закону Рунге, составляют рациональные дроби от нормального смещения: Δf=Δf₀2q/p. В прежних моделях атома было неясно, почему в аномальном эффекте Зеемана Δf может в 2 раза превышать обычный лоренцев сдвиг Δf₀=eB/4πM, скажем, у железа [13]. Но триплеты с Δf=eB/2πM естественно возникают в модели Ритца, если поле B точно сонаправлено или противонаправлено B₀ (рис. 4): тогда q=p и Δf=2Δf₀. Действует и закон Престона: число компонент каждой линии и сдвиг меж ними зависит лишь от типа спектральной серии, не завися от m и номера Z элемента. Каждой спектральной серии отвечает своё размещение электронов, и поле B одинаково ориентирует атомы однотипных элементов. Оттого и картина расщепления у них одинакова.

    Ритц, объяснив эффект Зеемана, связал его и с расщеплением каждой линии на несколько в отсутствие поля B (тонкая структура линий). По магнитной модели в многоэлектронных атомах, вместо одиночных линий (синглетов), возникают двойные (дублеты, как у натрия), триплеты и мультиплеты. Это объяснил ещё Лармор: на излучающий электрон действует, кроме поля остова B₀, поле других электронов B_e [6]. Оно наращивает либо снижает поле B₀, и электрон вращается и генерирует свет чуть большей или меньшей частоты. Легко рассчитать расщепление линий атомов. Если в атоме один валентный (свободный) электрон, как у натрия и других щелочных металлов, тогда поле B_e запертых на уровнях электронов либо увеличит, либо уменьшит поле атома, и каждая линия расщепится на две. Так, яркая жёлтая линия натрия представляет собой дублет D₁ и D₂, соответствуя размещению электрона в ближнем к ядру узле (рис. 5), удалённом на r~a₀~10^–10 м [9, 10]. Отсюда B_e~μ₀μ/2r³, где μ=9,3·10^–24 Дж/Тл – магнитный момент электрона, и Δf~eB_e/2πM~2·10¹¹ Гц [9], что порядка измеренного Δf~5·10¹¹ Гц. Тонкое расщепление отличается от теоретического, т.к. магнитные поля электронов складываются, и вклад в Δf даёт лишь проекция поля B_z.

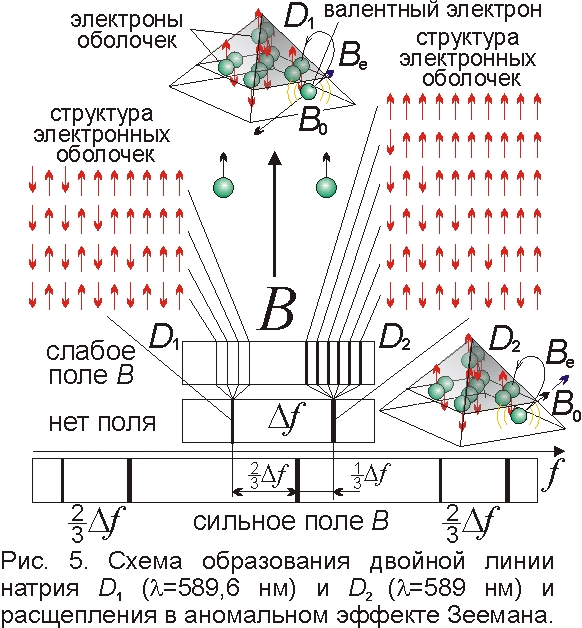
    Магнитный атом открывает и смысл главного “иероглифа” – α≈1/137 – постоянной тонкой структуры, характеризующей расщепление α~Δf/f~1/10². По сути, это отношение магнитного поля B_e одиночного электрона к полю B₀ остова из сотен зарядов того же момента μ. Из геометрии атомной пирамиды и следует простое число 137. Расщепление, разница частот Δf растут с номером элемента [4, 13], поскольку растёт число и общее магнитное поле электронов остова. А при отдалении от ядра магнитное поле уменьшается, отчего при росте m снижается Δf. Если в атоме свободных электронов два и более, тогда, в зависимости от их положения, получится больше комбинаций магнитных полей, и больше линий, отвечающих разным типам атомов. Интенсивность расщеплённых линий пропорциональна доле атомов с соответствующим размещением электронов. Воздействие соседних электронов позволяет объяснить также спектры других многоэлектронных атомов, например, проблемный для квантовой механики спектр гелия. Он во многом подобен спектру водорода, содержа ряд близких спектральных линий: λ=389 нм (близко к H_ζ), λ=1279 нм (близко к P_β) и т.д. Ведь и спектр ионов гелия He II, содержащих по одному электрону, повторяет спектр водорода, но с множителем Z²=4. В атоме гелия второй электрон лишь искажает спектр, и ряд линий расщепляется на три компоненты, отчего спектр гелия представлен синглетами и триплетами.

    Во внешнем поле B каждая линия дублета натрия расщепляется по эффекту Зеемана на ряд компонент. Их число задано числом возможных ориентаций магнитных моментов электронов (рис. 5). От разных комбинаций D₁-линия натрия расщепляется на 4, а D₂ – на 6 компонент. Если же поле B велико и сопоставимо с атомным B₀ и с полями соседних электронов, каждая линия расщепится всего на три, даже в многоэлектронных атомах. Причина в том, что внешнее поле B ориентирует все магнитные моменты связанных электронов вдоль оси, и по отношению к B магнитный момент излучающего электрона может принимать лишь три положения (рис. 3). При этом величина тонкого расщепления Δf~eB_e/2πM снижена в полтора раза, ввиду уменьшения поля B_e электронов, моменты которых сонаправлены с B, а их поля почти компенсируют друг друга (рис. 5). При этом центральная компонента не расщепляется, поскольку поля электронов B_e сонаправлены с B и перпендикулярны к B₀ (рис. 3). Эффект Зеемана в сильных полях был открыт в 1912 г. руководителем Ритца из Тюбингена – Ф. Пашеном и Э. Баком. Ориентацию электронов полем B подтверждает и нарушение правила Рунге: при росте поля смещения линий становятся асимметричными. Меняются и интенсивности спектральных линий [13], т.к. магнитное поле смещает электроны. Это объясняет и появление запрещённых линий: малоустойчивые узлы в сильном поле B обретают устойчивость, наращивая процент атомов с электронами в этих узлах и яркость соответствующих линий.

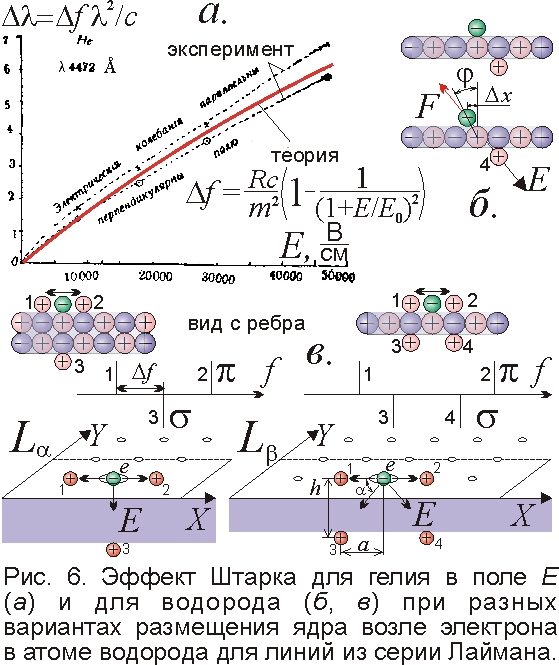
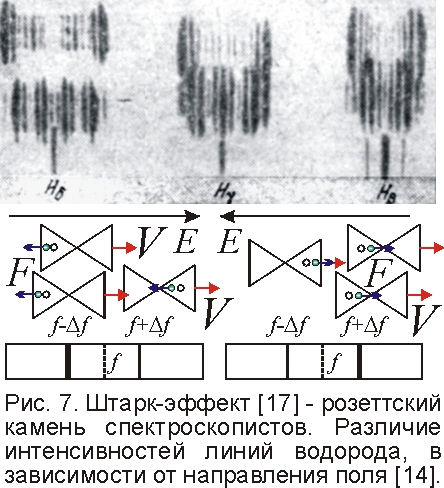
    Аналогично объясним эффект Штарка – расщепление линий в электрическом поле E. Эффект был предсказан учителем Ритца В. Фойгтом и открыт И. Штарком в 1913 г., но ряд его особенностей долго оставался загадкой. А в теории Ритца всё было кристально ясно ещё в 1908 г. Поскольку электроны образуют в атомах разные конфигурации, у атомов разнятся величины и направления дипольных моментов (рис. 6), и во внешнем поле E разные атомы ориентируются по-разному. В итоге, проекции поля E на плоскость XOY орбиты электрона разнятся (рис. 1), и разнятся смещения Δx электрона в поле E. Словно шахматные фигуры на магнитной доске, все электроны чуть сместятся от центров клеток, причём тем сильней, чем больше наклон доски. В разных атомах электроны, смещаясь от узла в разных направлениях на разные дистанции Δx, окажутся в магнитных полях B₀, отличных на малую величину ΔB~B₀Δx/a, крутясь в них и генерируя излучение разных частот, разнящихся на Δf=eΔB/2πM~fΔx/a. Интенсивность линии определяется долей атомов с данным размещением электронов. Это следует из обнаруженной Штарком разницы интенсивностей линий f-Δf и f+Δf: 1-ая линия на 30% ярче, если поле E сонаправлено со скоростью V атомов водорода, а если противонаправлено – ярче 2-ая [14]. В ускоряемых атомах водорода электроны, как пассажиры автобуса, скучиваются сзади, и в первом случае поле E ещё сильней тянет их назад, от ядра (Δx>0), где ниже B₀, а частота – f-Δf. В обратном поле E электроны смещаются вперёд (Δx<0), где выше B₀, а частота – f+Δf (рис. 7). В квантовой теории разницы нет, и этот факт не афишируют.

    Ритц отмечал, что электрон в положение равновесия возвращает квазиупругая сила F=kΔx, и Δx=eE/k. Для водорода смещённая частота f´=Rc[1/n²–1/(m+Δx/a)²], и сдвиги частот Δf пропорциональны E. Действительно, плоскости атома, как грани пирамид, образованные из стандартных блоков, составлены из чередующихся зарядов (рис. 1, 6), и электрон на такой плоскости возвращает к узлу сила Кулона F_К=e²/4πε₀z² нижележащего заряда e⁺, где z~h/2 (возможно, z<<h). Её проекция на плоскость колебаний электрона F=F_Кsinφ≈F_К2Δx/h=kΔx (рис. 6). В итоге Δf~fΔx/a=feEh/2F_Кa=wE, где w=πε₀fh³/2ea. Если атом многоэлектронный, внешнее поле ориентирует атом не вдоль линии электрон-ядро, а в направлении общего дипольного момента атома, а электрон смещает составляющая поля E_x и E_y. Следовательно, для атомов с разными электронными конфигурациями значения E_xy и сдвиги частот Δf=wE_xy получаются разными.

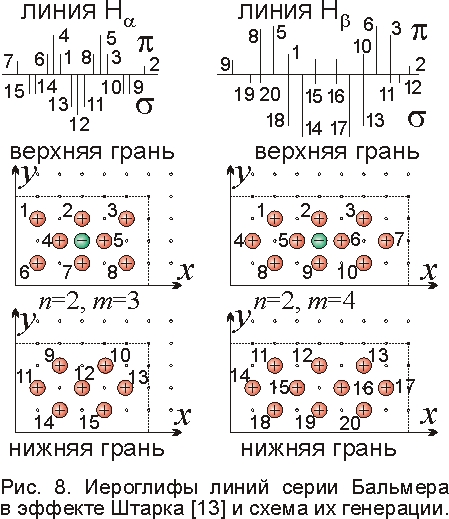
    Простейшая картина эффекта Штарка наблюдается для атома водорода, где всего один электрон. Положительный протон расположен в одном из узлов внутри прямоугольника, в центре которого – излучающий электрон. Всего N=(2n–1)(2m–1) узлов и возможных размещений заряда (рис. 6, 8). Соответственно, каждая линия расщепится не более чем на N компонент. Если заряд расположен на той же грани, что электрон, поле E, ориентируя атом, установится вдоль плоскости колебаний электрона, и, смещая его, образует линии поляризованные вдоль поля (π-компоненты). А если положительный заряд расположен на обратной грани, поле E поперечно плоскости колебаний электрона, формируя линии поперечной поляризации (σ-компоненты). Поскольку заряды опорной грани чередуется в шахматном порядке, положительные заряды могут размещаться лишь в узлах, где n+m – нечётное. Несмещённая центральная σ-компонента есть только для таких n+m, когда заряд расположен точно под электроном (в этом случае зарядовая плоскость должна быть двухслойной, рис. 6, 8).

    Наблюдается именно такая картина происшествия [4, 13]: магнитная модель точно предсказывает число, поляризацию и сдвиги Δf компонент. В частности, меньший сдвиг Δf~wEcosα у σ-компонент в серии Лаймана обусловлен наклоном поля Е к грани: сдвиг электрона компонентой поля E_x=Ecosα – меньше, чем для π-компонент (E_x=E). Для линии L_β эта разница в два раза (cosα≈1/2), откуда толщина плоскости h≈2a (рис. 6). Это соответствует модели атома Ритца, где шаг частиц, образующих грань, определяет и толщину h, и расстояние a между узлами. Симметричные линии возникают от симметрично размещённых зарядов, противоположно смещающих электрон. Картина не вполне симметрична, поскольку равные и противоположные смещения заряда полем E меняют магнитное поле и частоту Δf чуть по-разному, и положения заряда обладают разной устойчивостью. На рис. 8 более яркие линии изображены длиннее: они соответствуют размещению зарядов ближе к осям или электрону e. Итак, магнитная модель – это не просто догадка, а гипотеза, объясняющая все без исключения факты.

    Связь эффекта Штарка с разницей дипольных моментов атомов легко проверить, измеряя отклонение пучка атомов в неоднородном электрическом поле. Уже Штарк наблюдал расщепление пучка атомов на компоненты: каждой из них отвечала своя спектральная линия [14, 16]. Поэтому сам Штарк предложил простую картину эффекта, допустив деформацию электронных оболочек во внешнем поле E и соответственные изменения частоты колебаний электронов в атоме. Поляризацией Штарк объяснил и расщепление пучка атомов в поле E. И точно, сдвиг частоты Δf=f´–f=Rc[1/m²–1/(m+eE_x/ka)²]: такую зависимость (рис. 6) и наблюдал Штарк для гелия [14]. При Δx/a=eE_x/ka<<1, получим Δf≈Rc[2eE_x/mka–3(eE_x/mka)²]/m². При росте E линии сдвинутся не симметрично (преобладает красное смещение – спад f от вычета E_x²), в согласии с опытом [13]. Если E велико (E_x~ka/e), возникает квадратичный Штарк-эффект: Δf нарастает как E². Если E мало (E_x<<ka/e), тогда Δf≈2RceE/m³ka≈E8πε₀Rca²/em³~wE, где w~5·10⁵ Гц·м/В. И точно, для водорода при E~5·10⁶ В/м открыт линейный сдвиг частоты Δf≈4·10¹² Гц [14], т.е. w~8·10⁵ Гц·м/В – порядок верный.

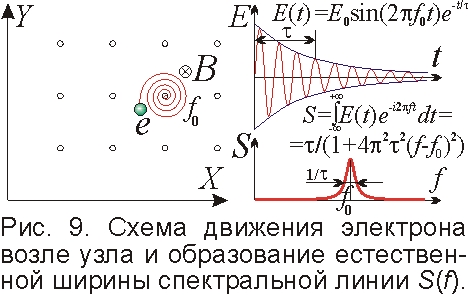
    Эффект Штарка объясняет и уширение спектральных линий. Электрические поля соседних электронов, атомного остова и соседних атомов сдвигают электроны от равновесных положений в каждом атоме по-разному. В итоге атомы генерируют спектральные линии чуть разных частот, образующих при наложении уширенную спектральную линию. Особенно выражен эффект для молекул, образующих, вместо линий,– полосы (наборы близких расщеплённых линий, раскрытых Ритцем). Для отдельного атома спектральная линия заметно уже. Но и она имеет естественную ширину от неоднородностей электрического и магнитного поля, отчего частота в каждом узле чуть зависит от амплитуды. К тому же электрон в атоме, вращаясь в магнитном поле остова, при потере энергии на излучение, сокращает витки орбиты за характерное время τ (рис. 9). В. Вин напрямую измерил это мгновение горения атомов τ~10^–8 c [17]. Из теории сигналов ширина спектральной линии Δf≥1/τ [12, 17]. Но в квантовой теории и этот классический вывод трактуют по принципу неопределённости: произведение неопределённостей энергии кванта ΔE=hΔf и времени Δt~τ, не меньше постоянной Планка h, получая Δf≥1/τ.

    Расщепление линий открыто и в ядерных спектрах по эффекту Мёссбауэра. В зависимости от конфигураций электронов в атоме и соединений, образуемых атомами, меняются γ-спектры ядер [4]. Но в ядре заряды расположены теснее (a<<a₀), и роль поля, созданного электронами, мала: расщепление – много меньше. Итак, модель атома Ритца не только проще, наглядней, но и шире, предсказывая все особенности эффектов Зеемана и Штарка. Оба эффекта служат ключом, открывающим тайные пружины атома, этого чёрного ящика, музыкальной табакерки, механизм издания звуков которой надо раскрыть, не заглядывая внутрь.

    Объясняет магнитная модель и спектры щелочных металлов (рис. 10), представленные сериями линий – резкой (s – sharp), главной (p – principal), диффузной (d – diffuse) и фундаментальной (f – fundamental). Как серии фильма, они содержат общие элементы, канву, перекликаясь одна с другой по комбинационному принципу Ритца [3, 7]. От названий серий и произошло деление электронных этажей атома на s, p, d, f-уровни. Эти 4 буквы, вместе с номерами n и m, стали первыми разгаданными символами атомного шифра, понятыми ещё в рамках классической физики. При случайном выборе этих букв электроном, движущимся по атомной плоскости, как по планшету медиума, “буквы” складываются в “слова” – в спектр атома. Ещё Демокрит и Лукреций сравнили атомы с буквами алфавита, из которых строится всё. Атомный остов с узлами, куда попадают электроны, подобен шифровальной маске Штирлица, собирающей буквы в слова,– в стройные спектральные серии, проявляемые спектроскопом – декодирующей шифровальной маской. Да и сами серии на спектрограммах, как на криптограммах, выявляют особой маской с прорезями, типа перфокарты [13], называя расшифровкой линий [17].

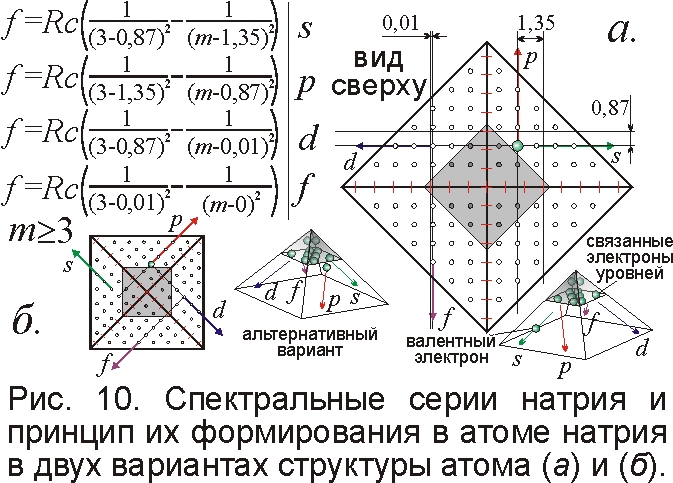
    Расшифруем четыре спектральные серии щелочных металлов, например лития и натрия (рис. 10). Кстати, они помогли раскрыть одно преступление в сфере общепита Р. Вуду – коллеге Ритца, прозванному “Шерлоком Холмсом” за разгадку тайн золота Тутанхамона спектральным методом [18]. Да и модель атома из магнитных шариков, формирующих в магнитном поле сетку стабильных узлов, предложил Р. Вуд [18] и Дж. Томсон [19]. Как показал Ритц [3, 6, 7], серии щелочных металлов f=Rc[1/(n+μ'+b'/n²)²–1/(m+μ+b/m²)²] подобны сериям водорода [17], отличаясь лишь малыми поправками μ, b, μ', b', индивидуальными для металлов. А согласно Холмсу, именно мелочи решают всё, и с этого момента рассмотрим всё подробней.

    Судя по всему, зарядовая сетка с узлами, где сидят электроны, устроена одинаково у водорода и щелочных металлов. Но в атомах металлов эта сетка деформирована кулоновскими силами других электронов. Наличие поправок означает, что излучающий электрон смещается от обычного положения (рис. 1, 10), и его расстояние до осей уже y=a(n+μ'+b'/n²) и x=a(m+μ+b/m²). Постоянное смещение на aμ и aμ' вызвано деформацией остова атома. Смещение сетки узлов от магнитных осей-рёбер пирамиды на aμ и aμ' и влечёт изменение спектра. У атомного остова в форме пирамиды четыре грани, отсюда – четыре серии: каждой отвечает размещение электрона на определённой грани (рис. 10). Кстати, на древнетибетских эмблемах света виден именно такой узор – крест и точки внутри. В отсутствие воздействий электроны лежат лишь на p-грани, и спектр поглощения представлен лишь главной серией. Внешнее воздействие перебрасывает электроны на другие грани, приводя в колебания и проявляя в спектре излучения. Причём линии s-серии – резкие, а линии d-серии – размытые (отсюда название), ибо на этих гранях узлы менее стабильны. Если главная и резкая серия состоят из двойных линий, то диффузная и фундаментальная – из тройных: внешнее поле меняет направление магнитных моментов электронов, и они образуют три комбинации поля. Ритц установил, что поправки μ и μ' одних серий соответствуют поправкам других. Здесь комбинационный принцип следует из равенства смещений узлов соседних граней (рис. 10).

    Таким образом, электроны сидят на 4-х линиях узлов, словно ноты на нотных строках, где каждому положению ноты соответствует свой звук. Так и электроны, в зависимости от положения на строчках сетки атомного вещания, излучают свет соответствующей частоты, как струна скрипки, гитары издаёт разный звук, в зависимости от прижатого лада. Кстати, Ритц до магнитной разрабатывал струнную и пластинную модель атома, представляя атом в виде заряженной струны или пластинки, излучающей набор частот. Ритц иллюстрировал это на примере фигур Хладни из песчинок [6, 20], как электроны в атоме, собирающихся в устойчивых узлах пластин от трения смычка, извлекающего звуки разной частоты из пластин и струн. Если скрипка не настроена, натяжение или длина струны отличны от номинальных, скрипка фальшивит – возникает звук искажённой частоты. Так фальшивит и атомный инструмент при деформации атома, изменении притяжения электрона и смещении его от положения равновесия (как в эффекте Штарка, или от поправок μ и μ') меняется частота излучения. Уже Ломоносов предсказал в диссертации деформацию атомов-пирамидок, их малые различия [21]. Не зря он же восстановил искусство мозаики – сложения картин-головоломок из цветных камешков, как тел – из атомов, связанных гранями, следуя Ньютону и Кеплеру.

    Переменные поправки к x=am и y=an, составляющие Δx=ab/m² и Δy=ab'/n², снижаются при росте m и n, то есть при удалении от магнитных осей. Очевидно, эти смещения электрона от узла вызваны электрическим притяжением ядра – эффект аналогичный штарк-эффекту. Составляющие кулоновской силы F_x~Z_efe²/4πε₀x² и F_y~Z_efe²/4πε₀y² уравновешивает упругая сила в узле F_x=kΔx и F_y=kΔy, откуда Δx=Z_efe²/4πkε₀a²m² и Δy=Z_efe²/4πkε₀a²n², то есть b≈b'≈Z_efe²/4πkε₀a³≈Z_efh³/a³. Итак, внешние и внутренние поля меняют структуру атома, что даёт ключ к созданию экзотичных типов атомов и к превращению одних атомов в другие в мощных электрических разрядах, как в повести К. Дойла “Открытие Рафлза Хоу”, основанной на идеях У. Крукса. Так, получение атомов в метастабильных состояниях в электроразрядах открыло эпоху лазеров, а что ещё грядёт! Ведь уже есть данные о реакциях ядерного синтеза и распада в электронных пучках и разрядах молний [22]. Не случайно Кюри и Курчатов до прихода в ядерную физику занимались теорией магнетизма. А Крукс изобрёл модификацию алмазов, придавая им радиацией зелёную окраску, что делает их пригодными в лазерной физике [23]. Да и модификация воды магнитами, открытая советским физиком Р.Я. Берлагой, получает объяснение в магнитной модели атома. Возможно, в древности под “философским камнем” подразумевали именно магнит, позволяющий управлять свойствами материалов и открывающий путь превращения одних элементов в другие.

    Спектры изотопов водорода и водородоподобных атомов отличаются и значением постоянной R=R_H/(1+M/M_N), где R_H=e⁴M/8ε₀²h³c [4, 10], поскольку при неподвижном центре масс движется и электрон массы M, и ядро массы M_N. В квантовой механике этот результат получен не вполне строго, т.к. ядро не смещалось для электрона, размазанного в виде сферического облака. Вообще квантовая механика нашпигована парадоксами и мистикой, которые Холмс всегда изгонял. Ведь для непосвящённого формулы с пси-функциями (Ψ), задающими по М. Борну вероятность обнаружить электрон в точке, выглядят сущей абракадаброй типа “пляшущих человечков”. А теория Ритца – рациональна: беря за основу детерминизм классической механики, она позволяет рассчитать спектры всех элементов. Зато квантовая механика и теория Бора, как шутят физики, не объясняет даже спектр бора – пятого элемента.

    Ещё одно отличие от водорода – это начало нумерации n и m не с единицы, а с номера периода: 2 – для лития, 3 – для натрия и т.д. [13]. Так, в атоме натрия заполнено два электронных слоя, и электроны в них, как пассажиры в набитом двухэтажном автобусе, блокируют узлы с n=1 и 2 (рис. 10). Ведь электроны заполняют атомный остов, словно мёд – пирамидальное дно пчелиных сотов, а воск аналогичен электрон-позитронному каркасу атома. Ещё Кеплер в “Трактате о шестиугольных снежинках” сравнил атомы и царящий у них кристальный порядок с сотами. А узловые электроны занимают лишь свободные ячейки атомных сот, и, крутясь возле них, как пчёлы в танце, передают зашифрованную в полосках спектра информацию о координатах и направлении полёта (направлении поляризации) [13].

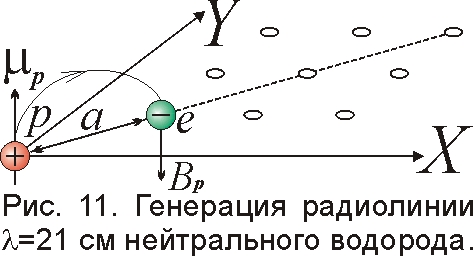
    А что будет, если n и m совпадут (например, n=m=1), и электроны расположатся в узлах на биссектрисе (пунктир на рис. 11)? В этих узлах поле остова скомпенсировано, и частота колебаний f близка к нулю. Но, кроме поля остова, есть ещё поле ядра – протона B_p=μ₀μ_p/2a₀³, где μ_p=1,4·10^–26 Дж/Тл – магнитный момент протона, a₀≈0,53·10^–10 м – масштаб атома [9, 10]. Отсюда частота колебаний электрона f=B_pe/2πM, а длина излучаемой волны λ=c/f=4πMca₀³/μ₀μ_pe≈0,2 м. И точно, у атомов водорода открыто излучение на длине волны – 21 см, связанное с влиянием на электрон магнитного поля ядра, хотя по квантовой механике эта линия – запрещённая. Предполагают, что инопланетные цивилизации именно на этой длине волны отправляют закодированные сообщения, достигающие нас спустя века.

    Итак, магнитная модель атома в виде пирамиды позволяет разгадать иероглифы атомных спектров. Да и главная буква спектроскопистов Å (ангстрем=10^–10 м – мера длины волны и атома) напоминает пирамиду и египетский символ анкх – ключ к тайнам жизни и смерти. Возможно, в Древнем Египте знали об атомах с их пирамидально-слоистой структурой, отражённой в строении пирамид, этих посланных к грядущим цивилизациям символов вечности, нерушимости, внутренней гармонии (типа золотого сечения), как основных атрибутов атома [24]. Ведь слово “Атум” в Египте символизировало вечность, первооснову всего, гору-пирамиду, типа полярной горы Меру. А седые пирамиды могли работать как АЭС с последующим захоронением. Не зря идею трансмутации элементов часто связывают с пирамидами, как в повести П. Коэльо “Алхмимик”. Судя по высказываниям Платона, Пифагора и Демокрита, учившихся у жрецов Египта, оттуда они и завезли в Грецию идею атомов в форме правильных многогранников-пирамидок. Возможно, и под музыкой 7-ми хрустальных сфер Платон и Пифагор подразумевали не звуки солнечной системы, а гармонию спектральных серий атома, на каждом из 7-ми уровней которого электроны колеблются со своими частотами. Кстати, упомянутый Хладни изобрёл прототип стеклянной гармоники в виде пирамиды, конуса из пластин или полусфер, издающих звуки разной частоты в зависимости от уровня. Этот инструмент считают развитием идей о музыке хрустальных сфер. Да и в других музыкальных инструментах (скрипке, свирели, арфе, органе), видимо, отражена структура атома [10]. Но, как в пьесе Пушкина “Моцарт и Сальери”, физики ушли от понимания атома, захотев “гармонию алгеброй поверить”, т.е. – квантовой механикой с её формальным описанием без понимания гармонии атома. И только Ритц, уже смертельно больной в горах Швейцарии начал приближаться к построению “каменного цветка” атома – основы всех минералов.

    Гипотеза пирамидального атома, которую утверждал и кодировал в своих рисунках Леонардо Да Винчи, позволяет, кроме спектров, объяснить магнитные свойства сложенных из атомов веществ. Так, она предсказала все элементы-ферромагнетики [10, 25], включая те, у которых магнитных свойств не предполагали: кислород, углерод, азот. И точно, сильнейший ферромагнетик – это соединение азота с железом: его магнитная проницаемость превысила предел, поставленный квантовой теорией. Твёрдый кислород оказался ярким антиферромагнетиком. И даже графит обладает ферромагнетизмом, который приписывали его примесям.

    Кстати, из магнитной модели следует связь магнитных свойств со сверхпроводимостью [25]. Действительно, в последние годы открыт ряд ферромагнетиков-сверхпроводников [26], что в квантовой физике было полной неожиданностью, ведь магнетизм обычно мешал сверхпроводимости. Следовательно, модель Ритца прокладывает мост от магнитных свойств атома к свойствам вещества. А квантовая механика не смогла предсказать сверхпроводимость ни у ферромагнетиков, ни у керамических сверхпроводников. В итоге физики ищут сверхпроводники наугад, чуть ли не с помощью медиумов [26], хотя ещё Шерлок Холмс учил, что гадать – это вредная привычка. Надо рассуждать логически, по примеру Ритца [6, 27]. В свою очередь открытие новых магнетиков и сверхпроводников, понимание их природы, через эффект Шарля-Серла и Барнетта, прокладывает путь к созданию антиграв-устройств и антиграв-веществ [25], типа драгоценного левиума из повести “Сокровища громовой луны”.

    Ритц, как Шерлок Холмс, последовательно рассмотрел весь спектр версий [27], гипотез устройства атома, исключая одну за другой по уликам (отпечаткам-спектрам) и находя узловые моменты, пока не пришёл к единственно верной магнитной модели атома. Напротив, официальная наука, словно Лестрейд и полиция, развивала ложную планетарную версию устройства атома и “духов” – призрачных электронных орбиталей. Стремясь гипотезами квантовой механики совместить с опытом модель атома в виде набора сферических электронных оболочек, физики уподобились сторонникам птолемеевой модели строения мира в виде набора прозрачных сфер. При каждом новом несоответствии они игнорировали факты, либо придумывали новую сферу, а в квантовой механике добавляли новое квантовое число, вопреки совету Холмса, учившего не подгонять факты под гипотезу. По части описания свойств атома не было разницы между моделями, и приняли формальную квантовую механику, как некогда – систему Птолемея. Но, обнаружив пороки теории Птолемея, учёные первыми приняли теорию Коперника. Вероятно, так примут и магнитную модель, вернувшую век назад затерянный мир атома. Ведь Ритц решил загадку спектров элементов – элементарно.

1. Торвальд Ю. Век криминалистики. М.: Прогресс, 1984.

2. Суворов С.Г. О чём рассказывает свет. М.: Воениздат, 1963.

3. Ритц В. // Вестник опытной физики и элементарной математики. Вып. 489. 1909 г., с. 206.

4. Сивухин Д.В. Атомная и ядерная физика. М.: Наука, 1986.

5. Дойл А.К. История спиритизма. М.: AUM, 1999.

6. Ельяшевич М.А., Кембровская Н.Г., Томильчик Л.М. // УФН. Т. 165. 1995. №4.

7. Ritz W. On a New Law of Series Spectra // Astroph. Journal. V. XXVIII. 1908. №3, p. 237.

8. Роговский Е. // Журнал Русского Физико-Химического Общества. Т. 40(2). 1908 г.

9. Матвеев А.Н. Атомная физика. М.: Высшая школа. 1989.

10. Семиков С.А. БТР и картина мироздания. Н. Новгород: Перспектива, 2013.

11. Линдер И.М. Шахматы на Руси. М.: Наука, 1975.

12. Петров В.М. Мифы современной физики. М.: Либроком, 2012.

13. Фриш С.Э. Оптические спектры атомов. М.–Л. Физматлит, 1963.

14. Рабинович А. // Вестник опытной физики и элементарной математики. 618. 1914 г., с. 132.

15. Сивухин Д.В. Оптика. М.: Наука, 1980.

16. Нобелевские премии по физике. 1901–1921. М.: УФН, 2002, с. 355.

17. Ландсберг Г.С. Оптика. М.: Наука, 1976.

18. Сибрук В. Роберт Вуд. М.: Наука, 1980.

19. Thomson J.J. On the Origin of Spectra and Planck's Law // Phil. Mag. 1919. p. 418.

20. Gander M.J., Wanner G. // SIAM Review. V. 54. 2012. №4.

21. Ломоносов М.В. Избранные философские произведения. М.: Госполитиздат, 1950, с. 65.

22. Кадменский С.Г. Излучение Черенкова как феномен неожиданных открытий // УФН. 2015. №5.

23. Бурмин Г. Царь камней. М.: Детская литература, 1979.

24. Семиков С.А. Атомный кристалл-пирамида // Инженер. 2009. №3.

25. Семиков С.А. Упрямая загадка магнетизма // Инженер. 2012. №11-12.

26. Колмогоров А. Как рассчитать сверхпроводник // Химия и жизнь. 2014. №4.

27. Семиков С. Структура света: самое тёмное дело в истории физики // Инженер. 2008. №5.

Дата установки: 09.05.2015
[вернуться к содержанию сайта]

W