[вернуться к содержанию сайта]

    Два постулата Эйнштейна вначале кажутся противоречивыми. Но, как мы видели, противоречие только кажущееся. Оно обусловлено некритическим использованием преобразований Галилея в условиях быстрого движения, когда справедливость этих преобразований была ещё не удостоверена опытом. Швейцарский физик В. Ритц (1878–1909) на этом основании в 1908 г. отверг второй постулат – постулат независимости скорости света от скорости источника, пытаясь сохранить преобразования Галилея и первый постулат. Мотивом для такого заключения послужило отсутствие прямой экспериментальной информации о справедливости второго постулата.

    Имеет смысл ещё раз, но качественно пояснить взаимную противоречивость постулатов Эйнштейна для галилеевских ИСК. Вообразим две такие системы, выполненные в виде гигантских отражающих, но легко проницаемых сфер, радиусы которых равны световой секунде, т. е. расстоянию, проходимому светом за 1 с (r~3·10⁵ км). Пусть в некоторый момент времени центры сфер, назовём их A и B, совпадают. Этот “радостный миг” отмечается салютом из артиллерийского орудия в системе A. Через 2 с наблюдатель в точке A увидит полностью освещённую поверхность шара. Постулат относительности требует, чтобы для наблюдателя в точке B его сфера осветилась равномерно тоже через 2 с. Роль второго постулата заключается в отрицании влияния на процесс движения салютовавшего орудия. Значит, наблюдатели в точках A и B видят одинаковую сферическую поверхность с центром в разных точках, разделённых расстоянием v·2с, где v – относительная скорость движения сфер.

    Тот же самый разрыв праздничного снаряда с точки зрения законов механики не имеет кажущегося противоречивого описания. Рассмотрим в тех же условиях разлёт осколков снаряда. Пусть в системе A осколки летят во все стороны с одинаковой скоростью. Через секунду (берём произвольный интервал времени) осколки будут находиться на поверхности шара, как для наблюдателя в точке A, так и для наблюдателя в точке B, что удовлетворяет принципу механической относительности. Но требование одинаковости картины разлёта осколков для обоих наблюдателей невыполнимо, так как система A покоится относительно снаряда, а система B движется. Здесь движение снаряда скажется на скорости полёта осколков, т. е. существует зависимость скорости движения осколков от скорости движения снаряда.

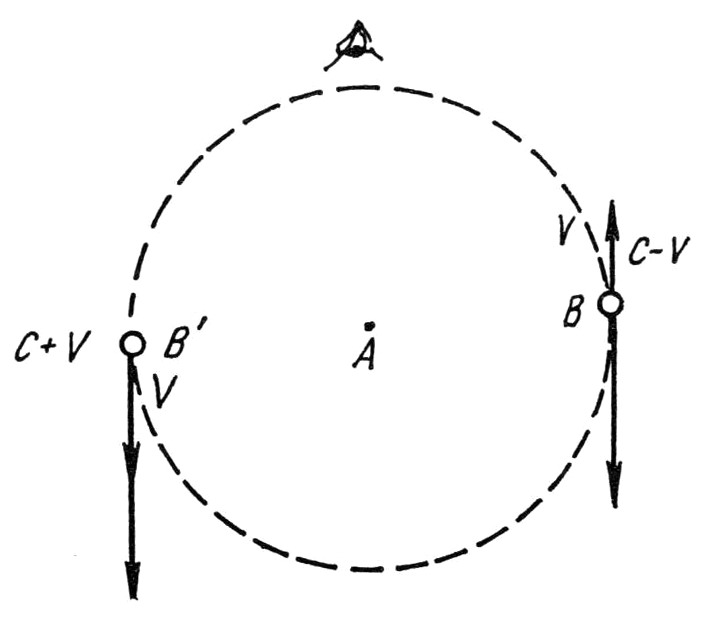
    Гипотеза Ритца как раз и заключалась в переносе этой качественной механической картинки на почву электромагнитной теории. Если принять, как это сделал Ритц, что скорость света, как в механике, зависит от скорости источника частиц, то постулат относительности не будет противоречить преобразованиям Галилея. Преобразования Лоренца не понадобятся. Ритц построил на этой основе своеобразную электродинамику, отличавшуюся от электродинамики Максвелла. Она получила название баллистической гипотезы света из-за приведённого примера, где световой луч вёл себя как осколок. Гипотеза Ритца не стала последовательной теорией потому, что уже в 1913 г. голландец В. Де-Ситтер (1872–1934) указал на факты, явно противоречившие этой гипотезе (к тому времени выяснилось также, что эта гипотеза требует больших усилий и натяжек для объяснения явления аберрации и опытов Физо). Факты относились к астрономии, к наблюдениям двойных звёзд, которые мы упоминали раньше. Подобных пар вокруг солнечной системы много. Эффект Допплера совместно с прямым наблюдением движения позволяет подробно изучать движения пар, их орбиты. Зависимость скорости света от скорости звезды сразу бы отразилась на наблюдаемых явлениях. На рис. 43 дано пояснение возникавших бы в этом случае “фокусов”. Даже очень малые скорости (v ~ 10 км/с) из-за больших расстояний (d>10¹³ км – расстояние до ближайших двойных звёзд) существенно сказались бы. Так, звезда B, движущаяся вокруг звезды A, посылала бы свет со скоростью (c–v) из точки B, а затем со скоростью (c+v) из точки B'. Положение B' звезда занимает позже. Но свет из B' идёт скорее и может приходить одновременно или даже раньше, чем из B. Наблюдение в таких условиях смазывало бы орбиты либо давало дополнительные миражи, звёзды двоились бы, троились и т. д. Но наблюдаемые орбиты хорошо удовлетворяют описанию, вытекающему из механики Ньютона (законов Кеплера).

Рис. 43

    Небольшой расчёт показывает, что явления миражей могли бы наблюдаться в реальных условиях. Если изменение скорости света Δс=v, а время движения света t=d/с, то изменение времени можно найти, дифференцируя формулу tc=d. Тогда

Δtс+Δсt=0

расстояние существенно не меняется, примем его постоянным). Итак, |Δt|=Δсt/с=vd/с²=10·10¹³/10¹¹ (с) ~ 10³ с. Как видно, это хорошо различимые времена. Анализ Де-Ситтера показал, что сложение скоростей света и источника вида (c±kv) привело бы к появлению миражей уже при k≥0,002.

    Величина параметра k служит удобным количественным критерием, который может быть извлечён из опытных данных так, как это сделал Де-Ситтер. Теоретические значения этой величины легко предсказываются. Второй постулат Эйнштейна означает, что k=0 (скорость света не зависит от скорости источника). Гипотеза Ритца требовала k=1. Так что уже результат Де-Ситтера, казалось, не мог быть совместимым без дополнительных гипотез с моделью Ритца. Надо было бы изобретать нечто вроде частичной зависимости скорости испускания света от скорости источника, т. е. вводить типичную гипотезу ad hoc.

    Интересный факт выяснился незадолго до смерти Эйнштейна в беседе с ним физика и историка науки Шенкланда. Великий релятивист отметил, что до 1905 г. он задумывался над баллистической, или эмиссионной, идеей, воплощённой позже в гипотезе Ритца, но отказался от её развития, ибо не смог придумать необходимую модификацию уравнений Максвелла, которую в 1908 г. нашёл Ритц. Как мы сейчас понимаем, наука от этой неудачи Эйнштейна только выиграла, ибо это обстоятельство помогло Эйнштейну свернуть с тупикового пути на правильную дорогу. Смерть помешала Ритцу в попытках детального развития своей гипотезы, к тому же упоминавшиеся принципиальные трудности этой гипотезы сразу породили скептическое отношение к ней. Но тем не менее она стимулировала постановку нескольких интересных экспериментов, позволивших параллельно оценить справедливость второго постулата СТО.

    При обдумывании постановки этих экспериментов выяснилось, что для опытов с замкнутыми световыми путями СТО и модель Ритца не имеют различия, если измерения чувствительны только к эффектам первых порядков по β. В этом отношении ситуация полностью аналогична идентичности предсказаний СТО и теории Лоренца в этом же порядке. И вновь только эксперименты, способные измерять эффекты второго порядка, могли бы как-то помочь. Выяснилось, что эксперимент майкельсоновского типа, но с внеземным источником света удовлетворяет этим требованиям. Классическая схема опыта Майкельсона, очевидно, не могла быть использована – источник света не имел скорости относительно приёмника, поэтому нельзя было и надеяться уловить механическое сложение скоростей света и источника.

    Требовался свет “быстрый”, т. е. его должны были испускать быстро движущиеся источники. Опыты Томашека, поставленные в 1923 г., полностью удовлетворяли этим запросам. В интерферометре майкельсоновского типа сравнивались интерференционные картины, возникавшие от земных и внеземных источников. В качестве последних брались последовательно Солнце, Луна, Юпитер, звёзды – Сириус и Арктур. Все эти объекты имеют разные скорости относительно Земли. Поэтому, согласно Ритцу, следовало бы ожидать разного смещения интерференционных полос. Однако его не было. Случайные смещения полос не превышали 12% ожидаемых по модели Ритца. Это соответствовало ограничению по параметру k (k<0,1), т. е. эти опыты, конечно, были менее суровы по отношению к гипотезе, чем выводы Де-Ситтера. Это объясняется “игрой” эффектов второго порядка. Для получения одинаковых ограничений по параметру k опыты второго порядка должны иметь точность, в 10⁴ раз большую, чем опыты первого порядка. Тем не менее полученный весьма низкий предел k, как увидим в следующем разделе, в чём-то оказался более надёжным, чем результат Де-Ситтера.

    Спустя 30 лет гипотезу Ритца удалось подвергнуть дальнейшим экспериментальным проверкам на основе методики измерения разности фаз двух лучей света. Советские физики М. А. Бонч-Бруевич и В. А. Молчанов в 1956 г. точно измерили время прохождения одинакового расстояния лучами от разных краёв вращающегося Солнца. Мы уже знакомы с измерением этих скоростей на основе эффекта Допплера. В данном опыте известная разница лучевых скоростей на концах солнечного экватора была использована для проверки гипотезы Ритца. Эта разница скоростей должна была бы дать разницу времени прохождения пути длиной 2 км, равную 7,5·10^-11 с, которая определялась по разнице фаз лучей. В результате измерения разница времени прихода лучей оказалась равной (1,4±5)·10^–12 с, т. е. примерно на порядок меньше ожидаемой, что означало ограничение k<0,1, как и в опыте Томашека.

    В этом эксперименте, поставленном по идее известного советского оптика С. И. Вавилова (1891–1951), был использован качественно новый эффект первого порядка по β. Его своеобразие заключалось в том, что измерялось время прохождения светом фиксированной базисной линии в одном направлении. Свет модулировался ультразвуком с частотой модуляции около 12,4 МГц. Фазометр позволял сравнить разницу фаз второй гармоники модулятора и света, прошедшего базисную линию. Эффект, как мы увидим в главе 5, имеет неинтерференционную природу, пропорционален βu/c, т. е. не относится прямо к эффектам второго порядка. В этом его существенная новизна.

    Так как прямое измерение величины k давало довольно слабое ограничение (k<0,1), а результат Де-Ситтера, как, впрочем, и результаты прямых экспериментов, подверглись впоследствии критике с несколько неожиданной стороны, то волна проверок второго постулата СТО продолжалась. В 1965 г. она получила несколько неожиданный всплеск после публикации результатов американца В. Кантора. Он занялся проверкой гипотезы Ритца на основе напрашивающегося изменения предыдущих источников света. Надо просто ввести в установку быстро движущийся земной источник света. Таким источником Кантору служили две тонкие прозрачные пластинки 3 и 3' (рис. 44), укреплённые на одном диаметре диска 4, который мог быстро вращаться (линейная скорость центра пластинок была около 47 м/с). Эти пластинки и были источниками света, после того как они освещались синхронизированными вспышками от источника s. Синхронизация позволяла попадать свету на пластинки 3 и 3' в моменты их движения по ходу или против хода луча. Разделение на два луча 1 и 1' обеспечивалось полупрозрачной пластинкой 5. Толщина пластинок – источников света – выбиралась очень малой (2·10^-3 см) для исключения возможного увлечения света. Система зеркал 6, 7, 8, 9 позволяла свести вновь в интерферометре лучи 1 и 1' и наблюдать интерференционную картину. Высота пучков света выбиралась так, чтобы часть пучка 2 и 2' проходила и под пластинами. Это было сделано для того, чтобы иметь эталонную интерференционную картину, с которой можно было бы сравнивать картину от движущихся пластин. Кантор ожидал, что, по гипотезе Ритца, c'=c±kv (k=l) сдвиг полос достигнет 0,74 ширины. Опыт показал сдвиг полос величиной 0,5 ширины полосы, что соответствовало k=0,33, т. е. как будто было получено качественное подтверждение гипотезы Ритца.

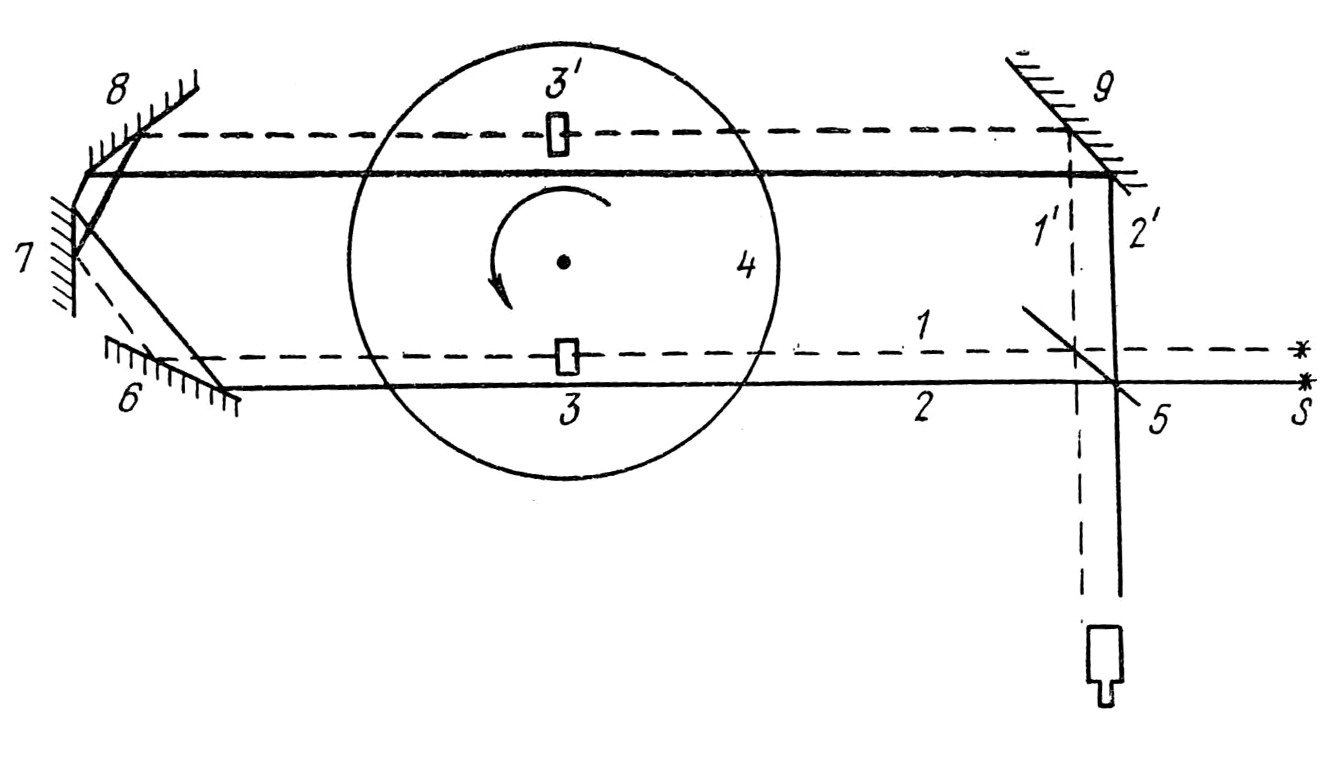
Рис. 44

    Естественно, такой результат не мог не вызвать многочисленных проверочных опытов. Не будем подробно останавливаться на их описании. Просто суммируем их результаты, анализируя параллельно качественные особенности проведения любого такого опыта. Неоднородность скоростей света по радиусу пластинки (очевидно, чем ближе точка прохождения света к центру диска, тем большую линейную скорость света можно использовать для сложения либо вычитания скорости пластинки) должна была вызывать поворот фронта волны. Этот поворот доступен наблюдению, причём телескоп позволял измерять углы порядка 0,5'', т. е. половину угловой секунды. Для значения k, полученного Кантором, этот поворот был бы около 13''. Отсутствие подобного поворота ограничило k<0,025, т. е. “эффект Кантора” сразу же стал экспериментально противоречивым. Кроме того, было показано, что “эффект” мог быть вызван температурными изменениями. Эксперимент был повторен другими экспериментаторами в глубоком вакууме для исключения температурных и других влияний. Вновь “эффект” отсутствовал. Вывод, сделанный в результате этой группы проверок, k<0,006. В них изменялись условия синхронизации вспышек света, брался монохроматический свет лазеров для улучшения картинки интерференции, менялись длины плеч интерферометра, использовалось последовательное изменение вращения диска. И неизменно авторы всех последующих экспериментов получали отрицательные результаты – отсутствие сдвига полос, который наблюдал Кантор.

    Вспоминая значение k, полученное Де-Ситтером, внимательный читатель мог бы спросить здесь: а нельзя ли было сразу привлечь результаты астрономических оценок для выражения недоверия эксперименту Кантора? Без сомнения, такая точка зрения была выдвинута при обсуждении результатов Кантора. Но здесь выяснилось, что как доводы Де-Ситтера, так и результаты Кантора не учитывали возможного влияния среды, в которой распространялся свет. О том, как она влияет и как можно избавиться от этого влияния, читатель узнает из следующего раздела, а пока можно сделать простой вывод – даже неудачные эксперименты (в период выяснения причин их неудачи) в какой-то мере служат прогрессу науки, вызывая постановку новых проблем либо открывая новые грани в старых. Ошибаются отдельные люди, физика же неуклонно движется вперёд, анализируя ошибки и суммируя достижения, закрепляя всё это в своих положительных выводах.

    О гипотезе Ритца после “канторовского бума” не следовало бы даже упоминать, если бы не обычная история, почти каждодневно встречающаяся в физике. Нет людей более недоверчивых, чем физики. В этом, возможно, один из залогов её постоянного процветания как передовой науки вот уже в течение более четырёх веков. Любой факт проверяется физической научной общественностью тщательно и дотошно. И очень часто критический взгляд на факты заставляет либо их пересматривать, либо вообще от них отказываться, когда выясняется, что они были псевдофактами, т. е. лишь казались фактами. Частенько, что мы ещё увидим, сами критики оказываются совершенно неправыми.

    Люди с критическим отношением к какому-либо вопросу получили хлёсткое название “адвокаты дьявола”. В физике эти “адвокаты” весьма часто играли положительную роль, так что к приспешникам “физического сатаны” их относить не совсем разумно. Например, одним из самых знаменитых физических “адвокатов дьявола” в первой трети нашего века был известный австрийский физик П. Эренфест (1880–1933), работавший в России 5 лет с 1907 г. и часто навещавший Советский Союз в последующие годы. Эренфест стоял у истоков организации всемирно признанной советской школы теоретической физики. Он мог бы сделать гораздо больше, если бы царское правительство уделяло больше внимания развитию физической науки в России. Талантливый физик не смог устроиться на постоянную работу и был вынужден уехать в Голландию, где стал преемником Г. Лоренца на кафедре университета в Лейдене.

    Эренфест сыграл выдающуюся роль “адвоката дьявола” для А. Эйнштейна и великого датского физика Н. Бора (1885–1970), сильно способствовав развитию как СТО, так и квантовой теории. Такие люди никогда не переводились в физике. К их числу принадлежит и известнейший советский физик Л. А. Арцимович (1902–1976). Его знакомство с физикой состоялось в Белоруссии, где он закончил физико-математический факультет университета. Затем он стал аспирантом и впоследствии ближайшим сотрудником знаменитого “отца советской атомной промышленности” И. В. Курчатова (1901–1958). Трудно переоценить ту роль, которую сыграл Л. А. Арцимович как “адвокат дьявола” в физике, но в то же время и как один из самых страстных организаторов и вдохновителей управляемых термоядерных исследований в СССР и за рубежом. Своей конструктивной и последовательной критической оценкой собственных результатов он сильно содействовал безошибочному движению по сложному пути получения управляемых термоядерных реакций.

    Нашлись “адвокаты дьявола” и у доводов Де-Ситтера. При анализе эксперимента Кантора американцем Д. Фоксом была выдвинута весьма правдоподобная критика всей аргументации Де-Ситтера. Фокс подметил, что излучение оптического диапазона, на которое опирался в своём анализе Де-Ситтер, приходит на Землю через межзвёздную среду. В ней излучение рассеивается, начальная волна поглощается и заменяется перерассеянной волной, излучаемой атомами межзвёздной среды, так что скорость света в этой среде совсем не зависит от происхождения, а определяется лишь его фазовой скоростью. Для того чтобы это происходило, т. е. чтобы свет успел “забыть” о своём происхождении, нужна долгая дорога. Она зависит от длины волны света. Длина пути “забывания” обратно пропорциональна длине волны излучения и равна двум световым годам для оптического диапазона, т. е. свет от всех двойных звёзд, находящихся не ближе 4–5 световых лет от нас, должен начисто “забывать” о своём прошлом и не может служить источником информации о тонких деталях разницы скоростей своих родителей – двойных звёзд.

    Вызов “адвоката дьявола” был принят. Изумительная изобретательность физиков помогла всё-таки выйти с честью из этой запутанной ситуации. Как это часто бывает, помогли новые открытия, новые объекты, излучение которых не имело приведённого “дефекта”. В эксперименте Кантора проблема забывания тоже существовала и была в какой-то степени решена проверочными измерениями в глубоком вакууме. Хотя световой путь у Кантора был мал по сравнению с межзвёздным путём, плотность воздуха несравнима с плотностью межзвёздной среды, где на 1 см³ приходится менее 10^-5 частиц. В воздухе это число, грубо говоря, порядка 10¹⁹ частиц в 1 см³. Довольно простое по замыслу, но трудное по непосредственному исполнению решение проблемы для эффекта Кантора было найдено. Глубокий вакуум (≈10^-6 мм рт. ст.) в контрольных опытах служил не только уменьшению температурных влияний, но параллельно удалением большей части молекул воздуха из аппарата способствовал исключению фактора “забывания” своего происхождения светом из числа причин, как будто бы мешающих проявиться принципу Ритца.

    С удалением молекул из межзвёздной среды дело обстояло, казалось бы, безнадёжно. Но тут выручило вот какое обстоятельство. Видимый свет охотно поглощается молекулами воздуха и молекулами, находящимися в межпланетной среде. “Невидимый свет” – рентгеновское излучение и жёсткие γ-лучи очень слабо поглощаются атомами и молекулами. Это связано с тем, что у атома и молекулы энергетические уровни расположены на расстояниях порядка десятков электрон-вольт друг от друга (1 эВ эквивалентен разности частот 1,6·10¹⁵ Гц), а рентгеновские лучи и γ-кванты имеют заметно большие энергии (десятки кэВ). Поэтому они не могут заставить квантовую систему – атом или молекулу – поглотить себя с возбуждением. Вероятность же распада атома за счёт такого поглощения мала. Всё это приводит к тому, что длина “забывания” в межзвёздной среде у этих квантов невидимого света очень велика по сравнению с оптическими квантами. Для рентгеновских квантов с энергией 70 кэВ эта длина составляет несколько десятков тысяч световых лет (3·10¹⁷ км). Так как астрофизики обнаружили достаточно большое число рентгеновских излучателей в этой области, то изучение законов их движения должно было снять все ограничения “светового забывания”.

    Что же это за излучатели и как можно определить их движение?

    В 1968 г. астрофизические наблюдения за небом с помощью радиотелескопов обнаружили так называемые пульсары, источники пульсирующего радиоизлучения. Как оказалось, это нейтронные звёзды с плотностью вещества, равной ядерной плотности, имеющие излучающее пятно – магнитный полюс пульсара. Вращение звезды заставляет пульсировать поток излучения для далёкого наблюдателя. Частота пульсаций совпадает, конечно, с частотой вращения звезды, причем эти частоты постоянны или медленно изменяются по определённому закону. Пульсары в радио-, оптическом и “невидимом” рентгеновском диапазонах представляют собой весьма точные часы, “развешанные” природой достаточно часто в галактике и за её пределами. Но особенно важно то, что рентгеновские пульсары часто встречаются в бинарной звёздной системе и вращаются вокруг общего центра масс двух звёзд. К тому же характеристика излучения пульсара несёт на себе отпечаток пройденного излучением расстояния, т. е. расстояния до пульсаров хорошо известны. По этим данным можно определить угловое положение источника на орбите. Эту же величину определяют из наблюдений затмений в бинарной системе. Если скорость “невидимого” света не зависит от скорости пульсара, то оба положения должны точно совпадать. Гипотеза Ритца, как мы сейчас увидим, вызвала бы беспорядок в наблюдаемых закономерностях движения.

    Для того чтобы увидеть, какие особые явления возникают при c'≠c (c' – наблюдаемая скорость света, c – скорость света от неподвижного источника), рассмотрим движение обеих звёзд бинарной системы на расстоянии D от Земли (рис. 45). Звёзды вращаются вокруг общего центра масс по круговым орбитам с угловой частотой ω и периодом T=2π/ω. Пусть источник A испускает импульсы постоянной частоты. Проекция радиуса r на луч зрения при вращении источника A меняется по закону r'=rsinωt', где t' – время в системе покоя точки O. Тогда скорость источника меняется по закону dr'/dt', как это следует из определения скорости. Итак, v=dr'/dt'=rωcosωt', так как производная функции sinωt' равна ω×cosωt'. Но линейная скорость связана с угловой простым соотношением v=rω, тогда v'=vcosωt'.

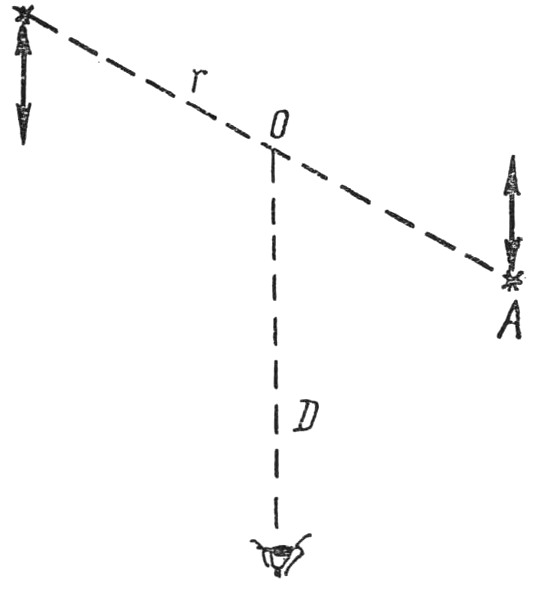
Рис. 45

    Импульс, испускаемый источником A в момент t', прибудет на Землю в момент

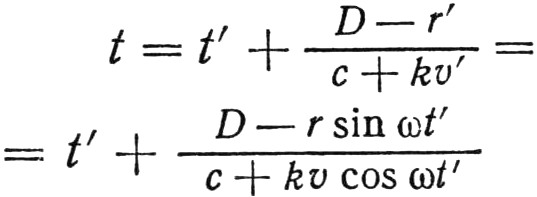
в том случае, если верна гипотеза Ритца в частичном виде (k≠1), т. е. когда скорость источника частично складывается со скоростью света для приёмника, не движущегося вместе с излучателем. В этой формуле следует учесть условия r<<D и v<<c. Тогда, используя, как и раньше, приближённую формулу 1/(1+α)=1–α, получим

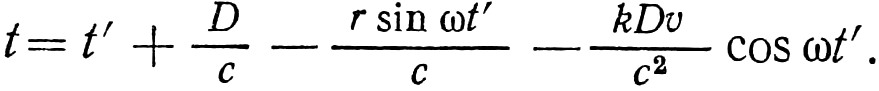
    Найдём производную по t':

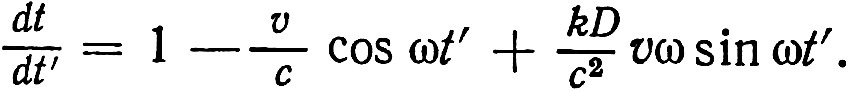
    В том случае, когда последний член формулы мал, а это произойдёт при kDvω/c²<<1, время приходов импульсов излучения на Землю следует простому гармоническому закону, выражаемому первыми двумя слагаемыми правой части формулы. Если записать это выражение на языке частот в системе покоя точки O и системе покоя приёмника, то получится простая гармоническая зависимость эффекта Допплера. Заметный вклад последнего члена, когда kDvω/c²~1, нарушает эту гармонию. Возможны случаи, когда приёмник регистрировал бы импульсы, прибывающие от более чем одного положения источника A на орбите в одно и то же время t. Отсутствие наблюдения таких событий означает, что kDvω/c²<<1, т. е. k<<Tc²/2πDv.

    Сведём в небольшую таблицу наблюдаемые параметры трёх бинарных рентгеновских источников и полученные значения верхней границы k (см. табл. 4).

Таблица 4

Объект наблюдения	v, км/с	D, кпс	T, сут	k
Геркулес Х-1	169	6	1,70	7·10-5
Кентавр Х-3	415	8	2,09	2·10-5
Малые Магеллановые облака Х-1	299	61	3,89	8·10-6

    Латинской буквой X в первом столбце обозначен рентгеновский источник, цифры относятся к порядковому номеру источников в созвездии. Данные столбца D приведены в килопарсеках, 1 кпс=3,08·10¹³ км.

    Согласно приведённым данным, параметр k ограничен сильнее, чем у Де-Ситтера. Более детальный анализ дал k<10^–9, причём в этом анализе трудность с “забыванием” исключена. Такова в настоящее время количественная оценка гипотезы Ритца и одновременно справедливости второго постулата Эйнштейна.

    В период некоторой растерянности, вызванной результатом Кантора, были проведены проверки гипотезы Ритца для земных источников с излучениями “невидимого света”. В этих опытах излучение было жёстким γ-излучением. Его поглощение воздухом во много раз меньше поглощения рентгеновских квантов. Поэтому в этих опытах “забывания своей родословной” квантами при нормальных лабораторных путях не происходит.

    За период 1963–1965 гг. различными исследователями было проведено несколько подобных экспериментов с разными источниками γ-излучения. Группа шведских учёных под руководством Т. Альвагера измеряла различие скоростей γ-квантов, испускаемых неподвижными и движущимися ядрами. Шведские физики оригинально решили проблему источников. Они облучали пучком α-частиц с энергией 14 МэВ, ускоренных в циклотроне, мишени из углерода C¹² и кислорода O¹⁶. Поглощением α-частиц ядра мишеней возбуждались, приобретая одновременно некоторую кинетическую энергию отдачи. Получались возбуждённые ядра C¹²* и O¹⁶*, причём уровень возбужденного ядра углерода находился на 4,43 МэВ выше основного невозбуждённого уровня ядра, а кислорода – на 6,13 МэВ. Возбуждённые ядра обладают большой разницей во времени снятия возбуждения. Так, ядро C¹²* имеет период полураспада (время, за которое половина возбуждённых частиц исчезает, превращаясь в невозбуждённые ядра) 6,5·10^-14 с, а ядро O¹⁶* – 1,2·10^-11 с. Такая разница во времени жизни проявлялась в том, что ядро C¹²* излучало γ-квант до замедления и полной остановки, а O¹⁶* испускало γ-квант уже после остановки. Это различие в движениях было обнаружено с помощью эффекта Допплера, который дал среднюю скорость ядра C¹²* в момент излучения (1,8±0,2) 10^-2 с, а ядра O¹⁶* – 0.

Рис. 46

    Приёмники излучения регистрировали γ-кванты от обеих мишеней М₁, М₂ (рис. 46), которые располагались в пучке α-частиц на расстоянии d=0,3 м друг от друга и могли меняться местами. Первый контрольный приёмник находился на расстоянии 1 м от второй мишени, основной – 5 м. На рис. 47 приведены данные эксперимента для двух импульсов ускоренных α-частиц. Этим импульсам соответствуют две пары пиков, контрольный приёмник давал пики, нарисованные пунктиром. Сигналы контрольного приёмника сдвинуты с помощью специальной линии задержки относительно основных сигналов. Верхний спектр – впереди установлена мишень с C¹², нижний – O¹⁶. Когда скорость света не зависит от скорости источника, то Δ=0=τ₁–τ₂–(Δ₁–Δ₂), где (Δ₁–Δ₂) – разница времени контрольного приёмника, (τ₁–τ₂) – основного. Когда есть сложение скорости ядра углерода и света, расстояние S между приёмниками γ-кванты пройдут в первом случае быстрее, чем во втором, т. е.

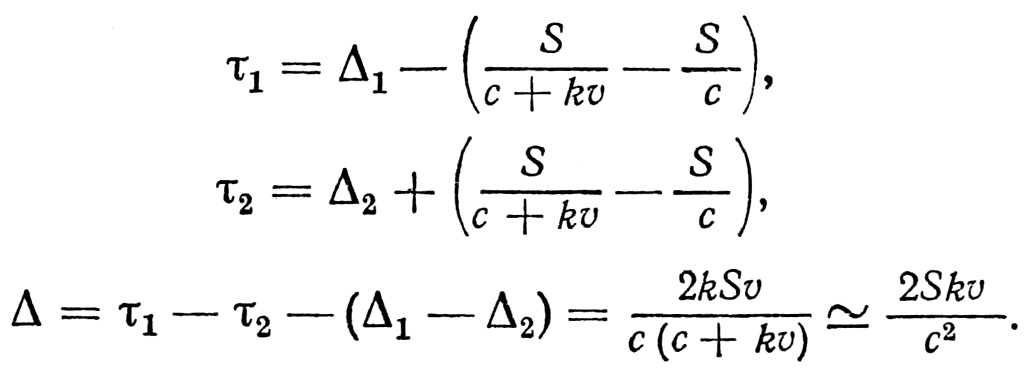
    В условиях эксперимента Δ=2k·4·10^-2/3·10⁸~k·0,5·10^-9 с=k·0,5·нс. Эксперимент дал значение Δ_экс=(–0,2±0,2) нс, т. е. очень слабо ограничил величину k (для утроенной ошибки k<0,8).

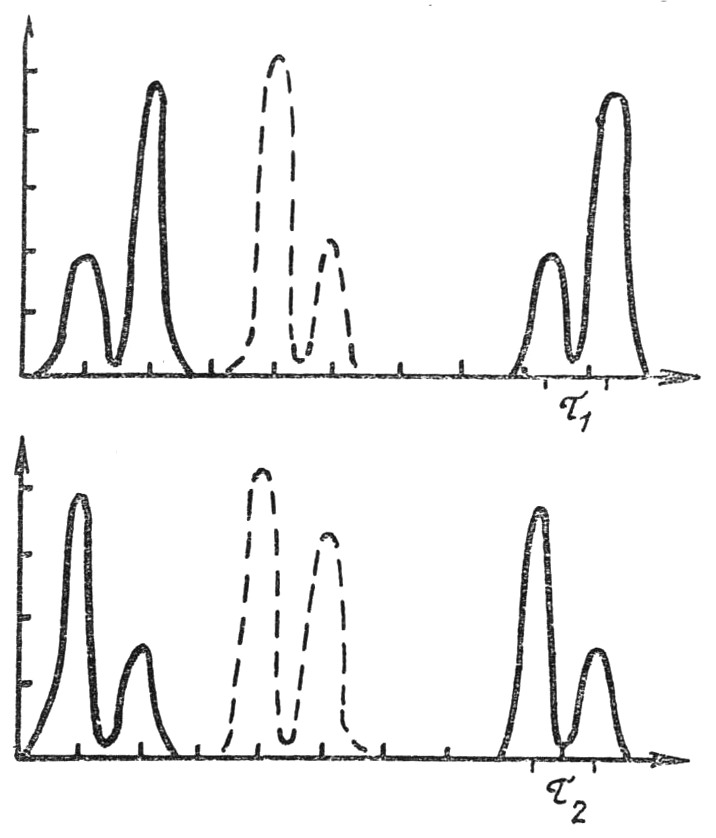
Рис. 47

    Более строгими по ограничению были работы, в которых изучалось время пролёта двух γ-квантов, рождённых в результате аннигиляции электрон-позитронной пары либо распада π⁰-мезонов, нестабильных элементарных частиц. Процесс превращения электрона и позитрона в два γ-кванта, процесс аннигиляции e^–+e⁺→2γ, активно происходит при попадании движущихся позитронов в вещество. Торможение позитрона может его остановить до процесса аннигиляции. Тогда по закону сохранения импульса γ-кванты должны разлетаться под углом 180° друг к другу. Аннигиляция движущегося позитрона с электроном вещества в лабораторной ИСК приводит к тому, что γ-кванты разлетаются под углами, меньшими 180°, хотя в системе покоя центра тяжести позитрона и электрона разлёт происходит также под углом 180°. Схема установки изображена на рис. 48. Позитроны со скоростью 0,89c вылетали из источника позитронов (изотоп меди Cu⁶⁴). В пластинке 1 из оргстекла толщиной 1 мм происходила аннигиляция в полёте. На расстояниях 0,6 м помещались два сцинтилляционных счётчика 2 и 3, которые по моменту возникновения световой вспышки в веществе сцинтиллятора регистрировали время появления γ-кванта в приборе.

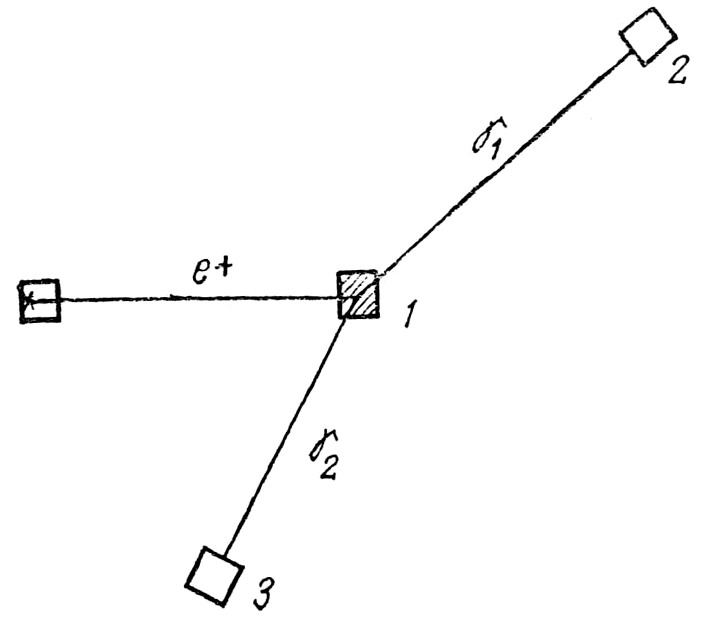
Рис. 48

    Если бы скорости света и источника складывались (источником здесь служил аннигиляционный процесс, скорость движения центра масс e^– и e⁺ играла роль скорости источника, она была равна 0,6 с), то первый γ-квант имел скорость 1,6 с, а второй – 0,6 с при углах вылета 20° и 130° к пучку e⁺. Разность времени прилёта γ-квантов была бы равна 2 нс. Разницу, большую 0,2 нс, аппаратура не зарегистрировала, меньшие разницы не могли измеряться, ибо разрешающая способность прибора была равна 0,2 нс. Для параметра k этот эксперимент дал ограничение k<0,1.

    Аналогичные эксперименты измеряли время прихода двух γ-квантов от движущегося π⁰-мезона. Эта частица распадается чрезвычайно быстро (за время ~10^-16 с) на одну пару γ-квантов; π⁰-мезоны большой энергии получались при бомбардировке мишени из бериллия ускоренными протонами. Если один γ-квант, вылетающий при распаде π⁰-мезона, летел вдоль движения π⁰, а второй – против, то разницу времени прилёта можно было бы зафиксировать счётчиком. В этих опытах ограничения для k получены значительно лучшие (k<10^–5).

    Все эти эксперименты отвергают гипотезу Ритца с k=1 и подтверждают второй постулат СТО. Количественная оценка выражается числами, заметно меньшими единицы (от 10^-4 до 10^-9), для излучений очень широкого спектрального диапазона.

Дата установки: 28.05.2011
[вернуться к содержанию сайта]

W