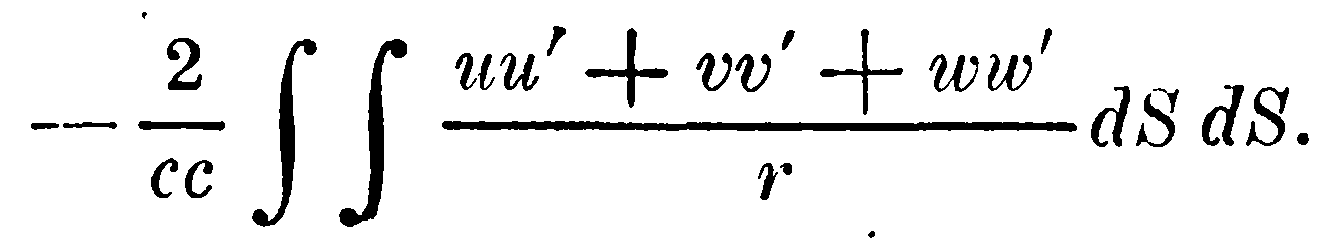
[вернуться к содержанию сайта]
Королевскому обществу я позволю себе сообщить одно замечание, которое приводит в тесную связь теорию электричества и магнетизма с теорией света и лучистой теплоты. Я установил, что электродинамические действия гальванических токов могут быть объяснены, если исходить из допущения, что действие электрической массы на другие совершается не мгновенно, а распространяется по направлению к ним с постоянной скоростью (в пределах возможных ошибок наблюдений равной скорости света). При этом допущении дифференциальное уравнение распространения электрической силы – то же самое, что и уравнение распространения света и лучистой теплоты.
Пусть S и S' – два проводника, которые не находятся в состоянии относительного движения и через которые проходят постоянные гальванические токи; ε – масса электрической частицы в проводнике S, в момент времени t находящейся в точке (x, у, z); ε' – масса электрической частицы в проводнике S', в момент времени t находящаяся в точке (x', у', z'). По поводу движения электрических частиц (которое предполагается в каждом элементарном объёме проводника взаимно противоположно направленным для положительных и отрицательных частиц) я сделаю следующее предположение: в любой момент положительные и отрицательные частицы распределены таким образом, что, какова бы ни была функция f(x, у, z) с непрерывными частными производными, суммы
∑ε
f(x, у, z), ∑ε'f(x', у', z'),распространённые на все частицы, могут быть пренебрегаемы по отношению к таким же суммам, распространённым только на положительные или только на отрицательные частицы.
Это допущение может быть выполнено разнообразными способами. Предположим, например, что проводники имеют кристаллическое строение, так что одно и то же относительное распределение электричества повторяется периодически через определённые расстояния, бесконечно малые по отношению к размерам проводников; тогда, если обозначим через β длину такого рода периода, то рассматриваемые суммы будут бесконечно малыми порядка cβn в случае, если функция f и её производные непрерывны до порядка n–1 и бесконечно малыми порядка e–c/β, если они непрерывны все [1].
Пусть через u, v, w обозначены в точке (x, у, z) в момент времени t компоненты по трём осям удельной силы тока в механической мере, через u', v', w' – то же в точке (x', у', z'); пусть, затем, r – расстояние между этими точками, а c – константа, значение которой определили Кольрауш и Вебер. Тогда, как показывают наблюдения, потенциал силы, с которой S воздействует на S', равен
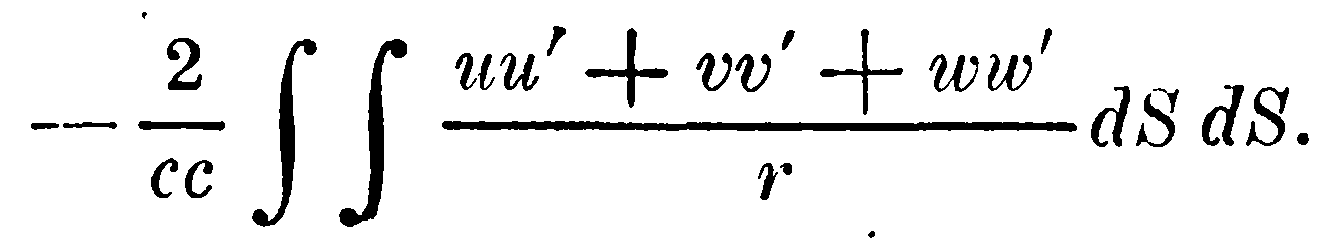
Если, вместо удельной силы тока, ввести произведения скоростей на удельные плотности и после этого, вместо произведений на объёмные элементы, – содержащиеся в них массы, то это выражение примет вид
![]()
причём то изменение r2 за время dt, которое проистекает от движения ε, обозначено через d, а то, которое проистекает от движения ε', — через d'.
Отнимая отсюда выражение
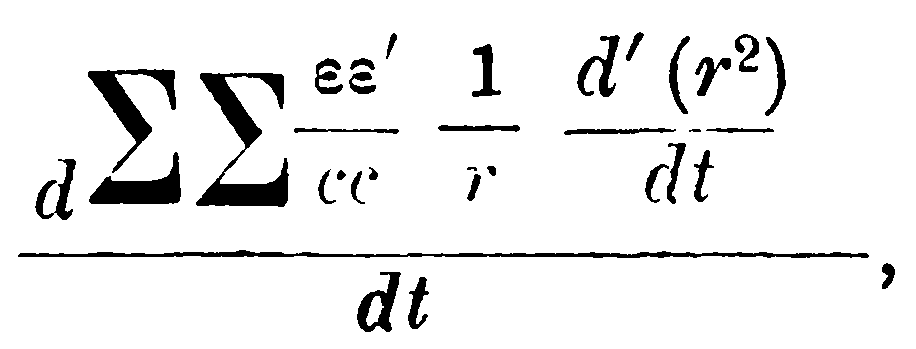
которое можно считать равным нулю, как это видно из суммирования по ε, мы получим новое выражение
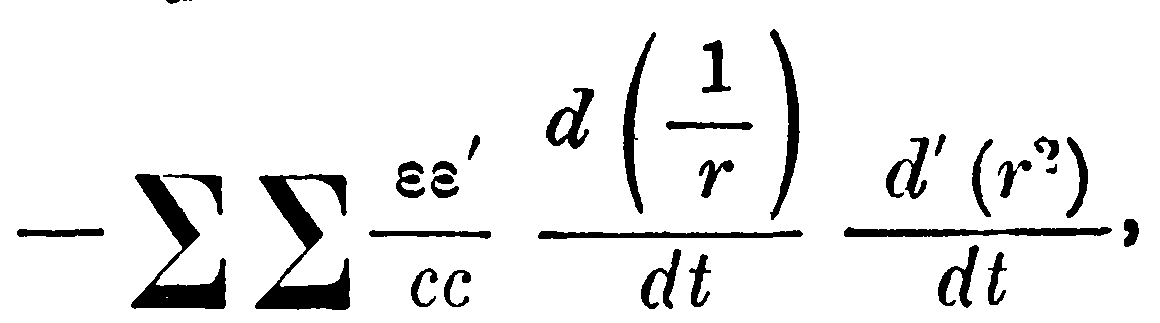
а это последнее, после прибавления выражения
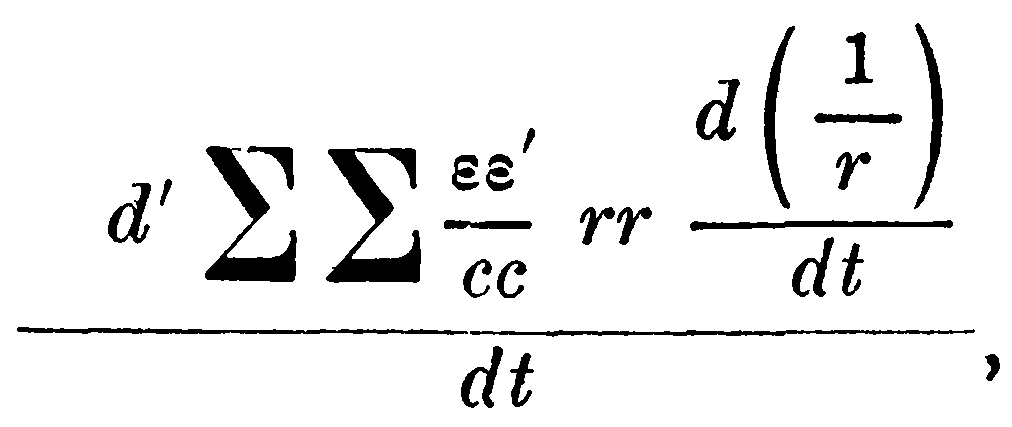
которое можно считать равным нулю, как это видно из суммирования по ε', принимает вид
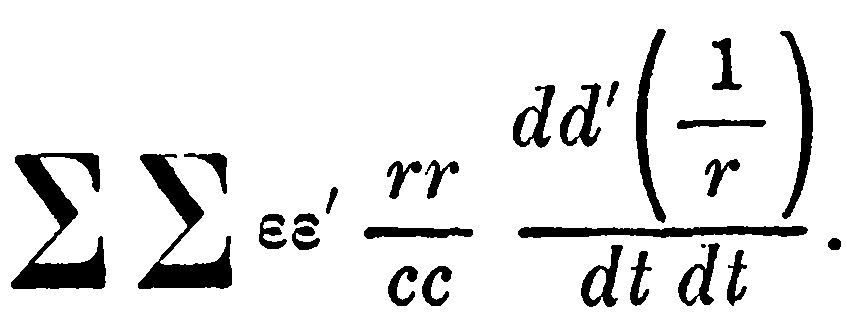
Согласно предположению, которое до настоящего времени всегда принималось при изучении электростатического действия, потенциальная функция U как угодно распределённых электрических масс определяется уравнением
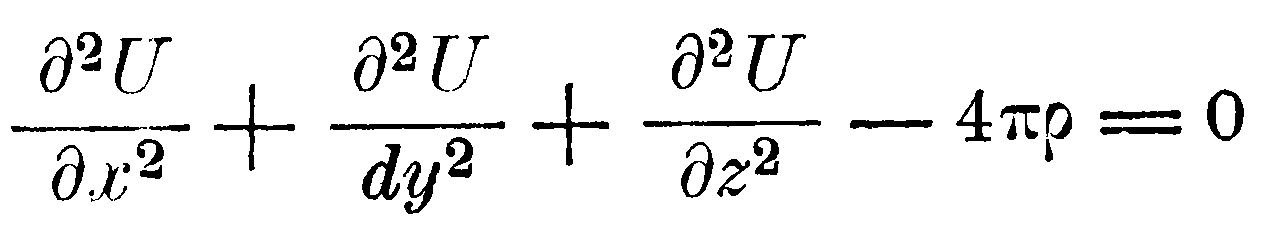
[ρ
– плотность в точке (x, у, z)] и условием, что U непрерывна и на бесконечном расстоянии от действующих масс постоянна. Частный интеграл уравнения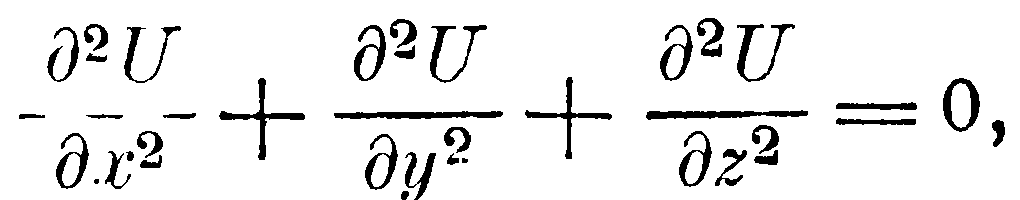
который непрерывен всюду, кроме точки (x', у', z'), имеет вид
f(t)/r,
и эта функция есть потенциальная функция точки (x', у', z'), если в момент времени t здесь находится масса –f(t).
Я сделаю, однако, иное допущение, а именно, буду считать, что потенциальная функция U определяется уравнением
![]()
так что потенциальная функция массы –f(t), помещённой в точке (x', у', z'), в момент времени τ будет
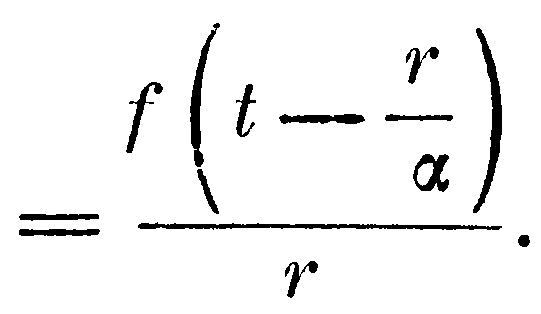
Если обозначим через xt, уt, zt координаты массы ε в момент t, а через xt'', уt'', zt'' – координаты массы ε' в момент t', и положим для краткости
![]()
то потенциал воздействия ε на ε' в момент t будет
![]()
Потенциал воздействия всех масс ε проводника S на все массы ε' проводника S' за время от 0 до t поэтому будет равен
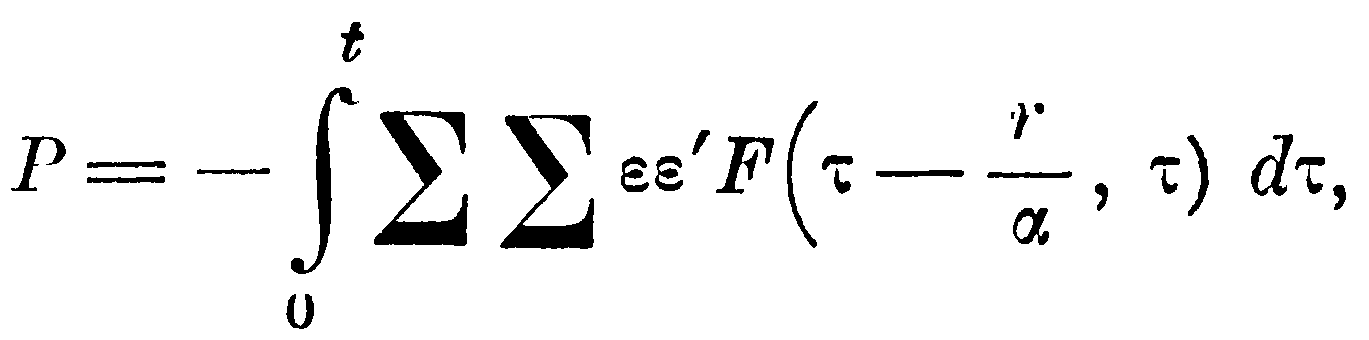
где суммы распространены на все массы обоих проводников.
Так как в каждом элементарном объёме проводника движение положительных и отрицательных частиц электричества взаимно противоположно, то после дифференцирования по t функция F(t, t') приобретает свойство менять знак вместе с ε, и точно так же после дифференцирования по t' приобретает свойство менять знак вместе с ε'. Поэтому, при наших предположениях относительно распределения электричества, распространённая на все электрические массы сумма ∑∑εε'Fn'(n)(τ, τ), где верхний значок обозначает дифференцирование по t, нижний – по t', только в том случае не будет бесконечно малой по отношению к сумме такого же вида, распространённой на массы лишь одного знака, если n и n' – оба нечётные.
Допустим теперь, что за время распространения силы от одного проводника к другому электрические массы совершают лишь очень маленький путь, и рассмотрим действие на протяжении промежутка времени, по сравнению с которым время распространения бесконечно мало. В таком случае в выражении P можно, прежде всего, заменить
![]()
через
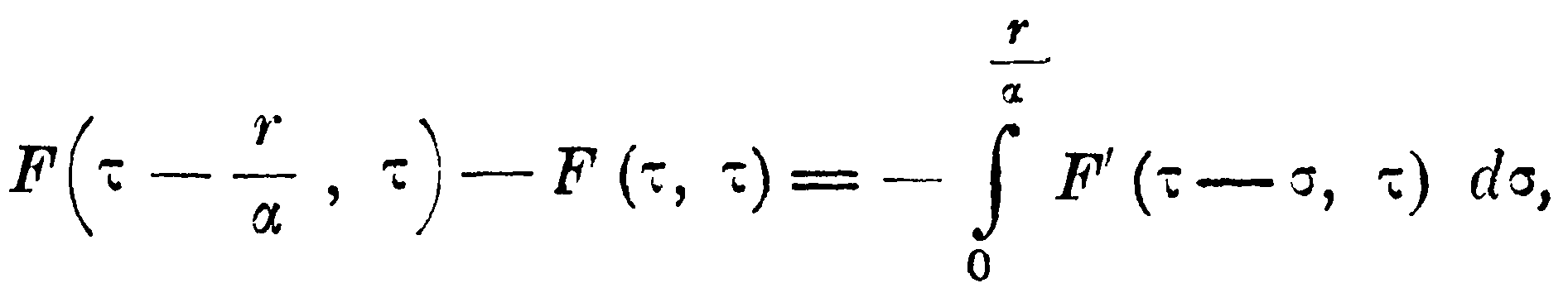
так как суммой ∑∑εε'F(τ, τ) можно пренебречь; тогда получается:
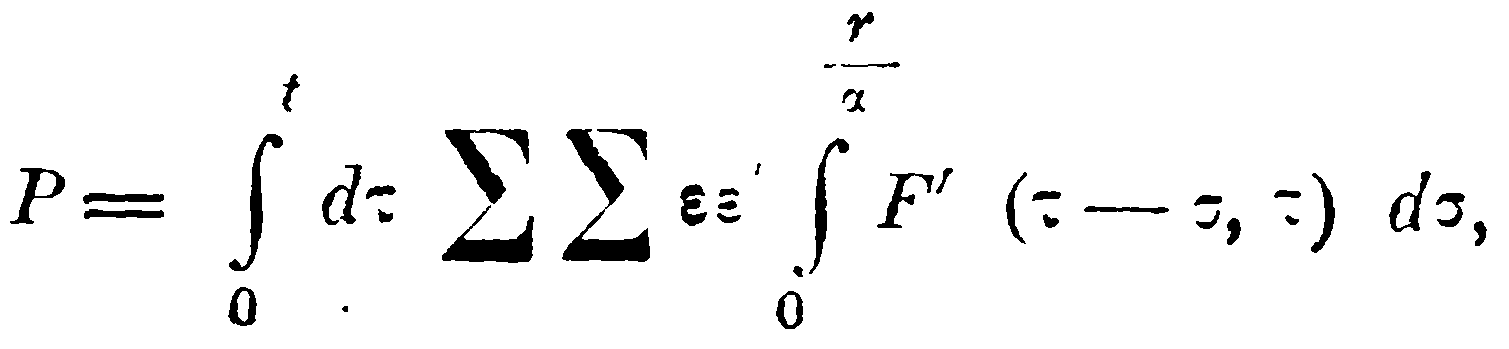
или, после перемены порядка интегрирования и замены τ на τ+σ,
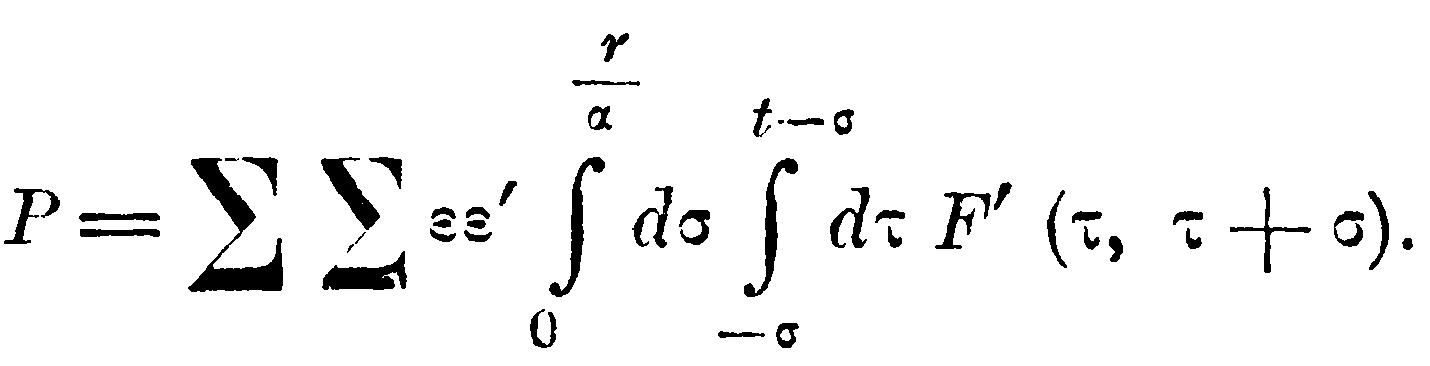
Если во внутреннем интеграле пределы поставим от 0 до t, то в результата на верхней границе прибавится выражение
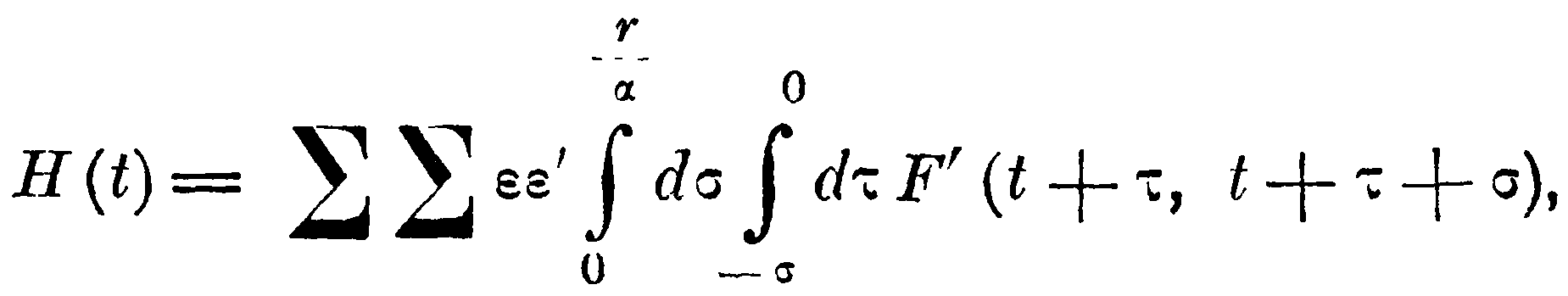
а на нижней – вычтется такое же выражение, но при значении t=σ. Поэтому
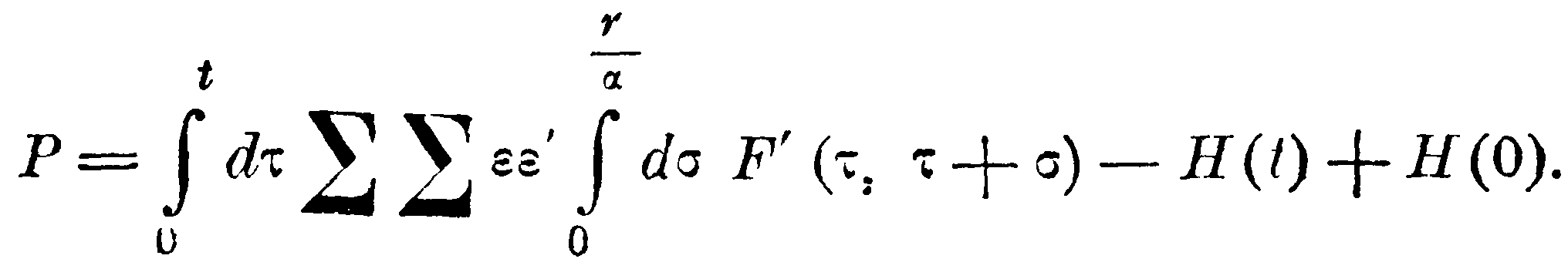
В этом выражении можно заменить F'(τ, τ+σ) через F'(τ, τ+σ)–F'(τ, τ), так как суммой
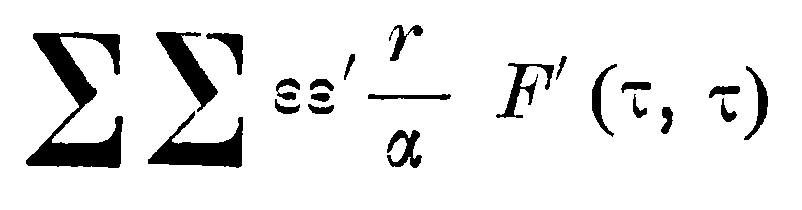
можно пренебречь. Тогда в качестве множителя при εε' будет стоять выражение, меняющее свой знак как вместе с ε, так я вместе с ε', так что, при суммировании члены взаимно не уничтожаются, а бесконечно малыми долями отдельных членов можно пренебречь. Таким образом, заменяя
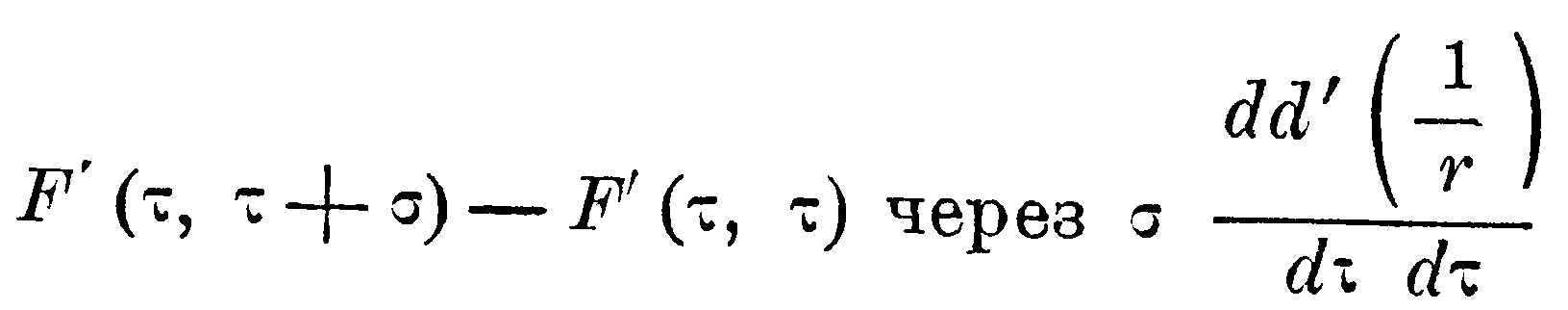
и выполняя интегрирование по σ, мы получаем, с отбрасыванием бесконечно малой доли:
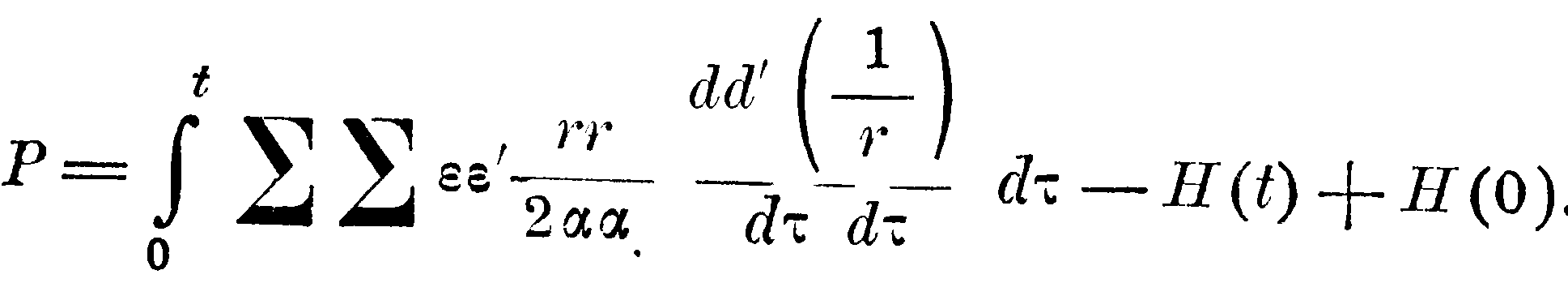
Легко видеть, что величинами H(t) и H(0) также можно пренебречь; в самом деле,
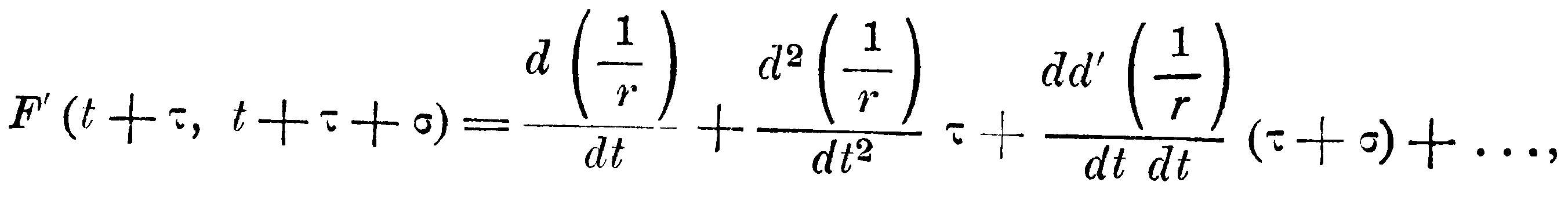
следовательно,
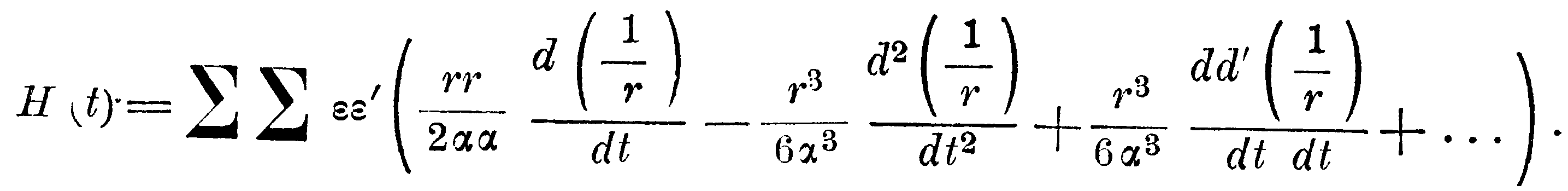
Здесь только первый член множителя при εε' того же порядка, что и первый член в выражении для P, но и он, при суммирования по ε', даёт величину, которой можно пренебречь.
Итак, значение P, которое следует из нашей теории, совпадает с полученным из опыта, а именно,
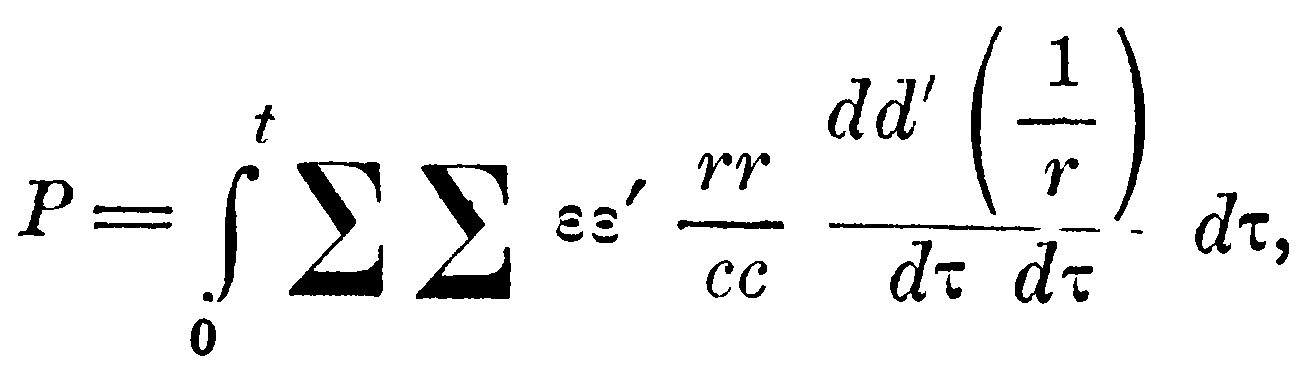
если только положим αα= cc/2.
По определению Вебера и Кольрауша оказывается, что
c= 439 450·106 миллиметр/секунда,
откуда следует, что
α= 41 949 г
еографическая миля/секунда,тогда как для скорости света из наблюдений Буша и Брадлея над аберрацией было получено число 41 994, а из прямых наблюдений Физо – число 41 882.
В Собрании сочинений Римана мы находим следующее примечание Вебера:
“Эта статья была представлена Риманом 10 февраля 1858 г. Гёттингенскому Научному обществу (на рукописи имеется соответствующая пометка секретаря общества), но позднее была взята обратно. Будучи опубликована уже после смерти Римана в Annalen der Physik und Chemie, т. CXXXI, она подверглась критике со стороны Клаузиуса (там же, т. CXXXV), который в основном сделал такое возражение:
В силу сделанных предположений сумма
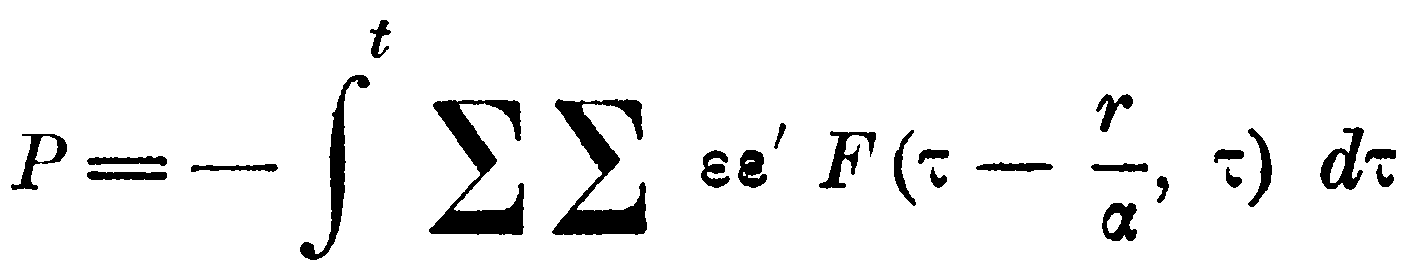
должна иметь бесконечно малое значение. Если же позднее получаемое для неё значение не оказывается бесконечно малым, то причину этому следует видеть в некоторой оперативной ошибке. Именно, Клаузиус усматривает ошибку в незаконной перестановке пределов интегрирования.
Это возражение (говорит дальше Вебер) кажется мне обоснованным, и вместе с Клаузиусом я полагаю, что отмеченная несообразность не укрылась от Римана, и потому он взял работу обратно.
Хотя существенная часть римановой дедукции таким образом отпадает, я всё же решился включить статью в собрание сочинений, так как не могу взять на себя суждение о том, не содержится ли здесь зародыш дальнейших плодотворных идей в этой чрезвычайно интересной области”.
С другой стороны, R. Rеiff и A. Sommerfeld в статье, помещённой в Enzyklopädie d. Math. Wiss. (V, 12), подробно излагают содержание работы Римана и, указывая на критику Клаузиуса, вместе с тем особо отмечают то обстоятельство, что потенциал Римана согласуется с потенциалом Неймана, если положить α2=c2/2, где c – константа Вебера-Кольрауша, т. е. если принять α равным скорости света. “Интерес римановой теории, – заключают эти авторы, – зависит, во-первых, от последнего обстоятельства, позволяющего видеть в Римане предшественника Максвелла, и, во-вторых, от того, что современная теория электронов в некотором смысле снова приводит к римановой форме элементарного потенциала”.
[1] к стр. 444.
К этим не вполне очевидным соображениям можно присоединить следующую формальную иллюстрацию. Ограничиваясь линейным случаем, допустим, что частицы расположены в точках νβ(–∞<ν<+∞), причём масса равна +1 или –1, смотря по тому, будет ли ν чётным или нечётным. С помощью трансформации
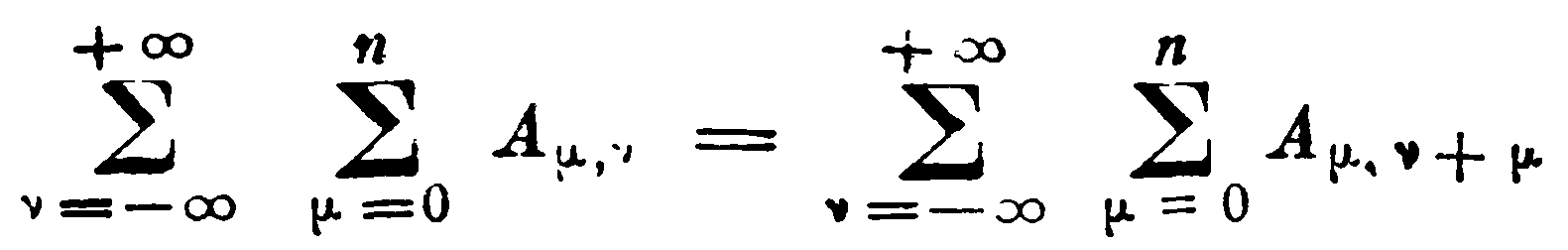
получим, предполагая непрерывность (и абсолютную интегрируемость в бесконечных пределах) функции f(n)(x):
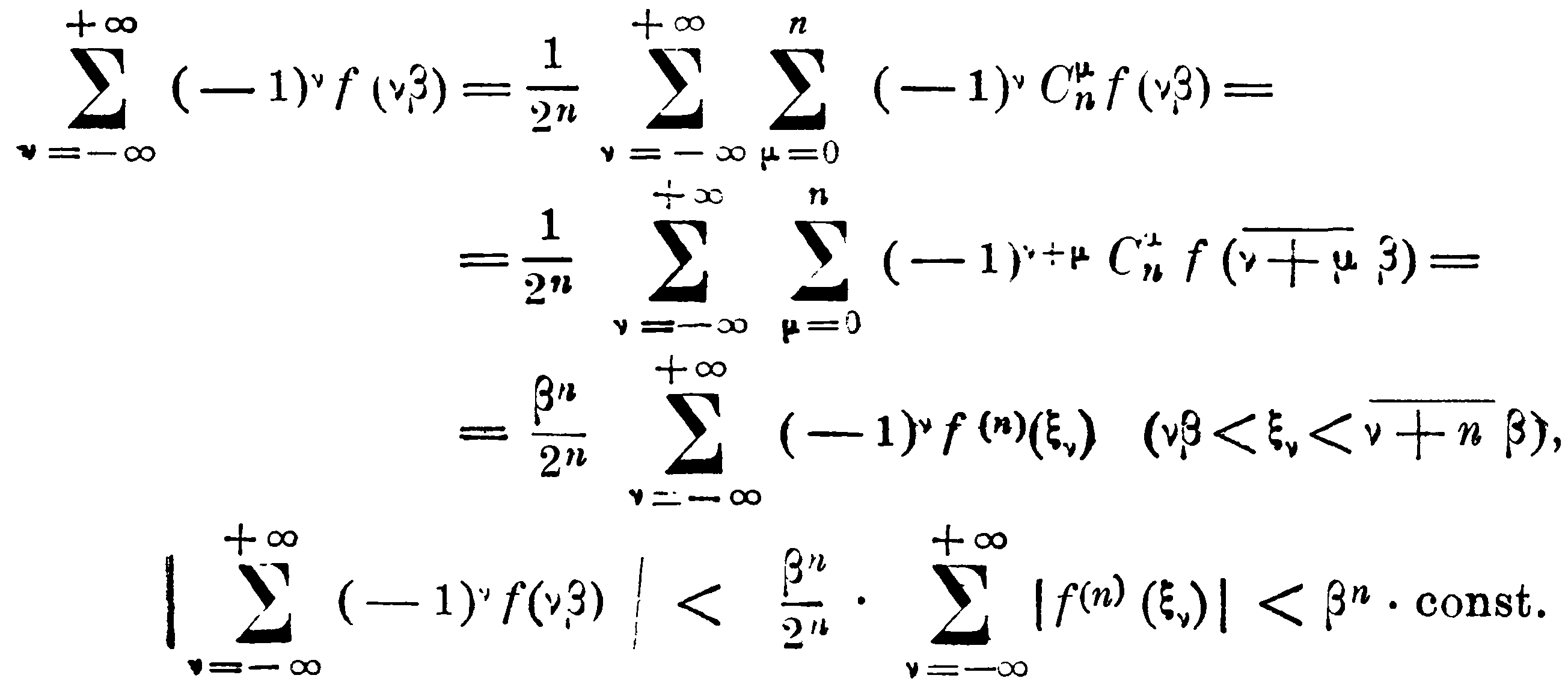
Nec mea dona tibi studio disperta fideli
Intellecta prius quam sint, contempta relinquas
Lucretius 1).
Своей задачей н а у к а о п р и р о д е имеет – охватить и логически истолковать природу посредством точных п о н я т и й.
Роль понятий, посредством которых осуществляется логическое истолкование природы, заключается не только в том, чтобы в каждый момент дополнять восприятия, но и в том, чтобы предусматривать заранее необходимость или – если система понятий ещё не окончательно построена – вероятность будущих восприятий; таким образом, можно установить, что является “возможным” (также – что является “необходимым”, пли чему противоположное невозможно), и степень возможности (“вероятности”) каждого события, которое признано возможным, может быть вычислена математически, если только введённые понятия достаточно точны.
Если действительно наступает то, что согласно этим понятиям является необходимым или вероятным, то сами понятия этим контролируются и на таком контроле посредством опыта основывается доверие, которое мы им оказываем. Если же случается нечто такое, что согласно понятиям не должно быть ожидаемо, т. е. является невозможным или невероятным, то возникает задача: так дополнить, или, если нужно, видоизменить понятия, чтобы в дополненной или улучшенной системе понятий воспринятое нами перестало быть невозможным или невероятным. Дополнение или улучшение системы понятий есть “объяснение” неожидавшегося восприятия. Такого рода процесс делает наше понимание природы постепенно всё более полным и правильным, но вместе с тем ведёт нас всё глубже за поверхностную видимость явлений.
История “объясняющих” наук о природе (насколько мы можем её проследить) показывает, что таким именно и был действительный путь развития наших знаний. Системы понятий, лежащие в их основе в настоящее время, возникли в результате постепенного преобразования прежних систем, и причину, в силу которой были совершаемы переходы к новым системам, всегда можно найти в некотором противоречия или некоторой невероятности, которые обнаруживались при прежних способах объяснения явлений.
Таков процесс образования новых понятий, насколько он является доступным нашему наблюдению.
Но Гербарт доказал, что и все те из числа понятий, служащих для объяснения мира, возникновения которых мы не можем проследить ни в истории, ни в нашем собственном развитии (так как они внедряются незаметно, вместе с усвоением речи), – если только они представляют собою нечто большее, чем выражение связи между простыми ощущениями – могут быть выведены из того же источника, и потому нет необходимости выводить их (как категории у Канта) из особых свойств человеческой души, независимых от всякого опыта.
Такое доказательство их происхождения из непосредственных восприятий важно для нас потому, что только оно выясняет их значение удовлетворительным с точки зрения науки способом.
––––––––––––––––––––––––
Как только образовано понятие вещей, “существующих для себя” при размышлениях по поводу изменения, которое противоречит понятию “существования для себя”, возникает задача, насколько возможно сохранить и оправдать это уже введённое понятие. Отсюда возникает одновременно понятие непрерывного изменения и понятие причинной связи.
Пусть наблюдается переход некоторой веши из одного состояния в другое, причём не обнаруживается никакого скачка, т. е. внезапного изменения. Дополняя восприятие, можно или принять, что переход совершается посредством очень большого, но конечного числа скачков недоступных по своей малости нашему восприятию, или же допустить, что рассматриваемая вещь переходит из одного состояния в другое через все промежуточные ступени. Наиболее сильное основание для последнего допущения заключается в стремлении насколько возможно сохранить понятие “существования для себя”. Конечно, невозможно себе представить в действительности переход через все промежуточные ступени, но подобного рода затруднения, как уже было замечено, встречаются в сущности и для всех других логических понятий.
Вместе с тем, в согласии с ранее введённым и оправдываемым посредством опыта понятием “существования для себя”, мы заключаем, что вещь осталась бы тем, чем она была, если бы не прибавилось нечто новое. Отсюда возникает потребность искать причину всякого изменения.
–––––––––––––––––––––––
I. В каком случае наше понимание мира мы считаем истинным?
“В том случае, если совокупность наших представлений соответствует совокупности вещей”.
Элементы нашего представления о мире существенно отличны от соответствующих элементов представляемой реальности. Они – нечто в нас; элементы реального – нечто вне нас. Но связи между элементами в представлении и элементами в реальном должны быть одинаковы, если представление истинно. Истинность представления не зависит от степени тонкости представления, – не зависит от того, соответствуют элементы представления большим или меньшим частям реального. Но связи должны отвечать друг другу: не может быть в представлении непосредственного взаимодействия двух элементов, если в действительности имеется лишь опосредствованное взаимодействие. В этом случае представление считается ложным и нуждается в исправлении; напротив, если элемент представления заменяется группой мелких элементов, причём его свойства следуют отчасти из более простых свойств мелких элементов, отчасти же – из их отношений, и таким образом, частично становятся доступными нашему пониманию, то наше проникновение в связь вещей от этого становится глубже, но при этом нет необходимости прежнее понимание рассматривать как ложное.
II. Каким образом устанавливается связь вещей?
“Из связи явлений”.
Представление о вещах, доступных чувственному восприятию, в определённых пространственно-временных соотношениях есть то, что является результатом сосредоточенного размышления о природе или д а ё т с я в качестве такового. С другой стороны, к а ч е с т в е н н ы е признака вещей, как цвет, звук, тон, запах, вкус, теплота или холод, есть нечто заимствованное только из наших ощущений, вне нас не существующее.
Итак, то, из чего должна быть познаваема связь вещей, есть к о л и ч е с т в е н н ы е, пространственно-временные соотношения между вещами, доступными чувственному восприятию, а также соотношения интенсивности в признаках и их качественные различия.
Из размышлений над наблюдаемой связью этих соотношений и должно возникнуть познание связи вещей.
I. То, к осуществлению чего стремится нечто действующее (ein Agens), должно содержаться в самом понятии действующего; его действие (Action) не может зависеть ни от чего другого, кроме его собственной сущности.
II. Это требование удовлетворено, если действующее стремится сохранить или восстановить само себя.
III. Но такого рода действие невозможно мыслить, если действующее есть вещь, нечто сущее, а возможно лишь, если оно есть состояние или отношение. Если налицо имеется с т р е м л е н и е что-то сохранить или восстановить, то должны быть возможны отклонения, и притом различных степеней, от того, что сохраняется или восстанавливается; и это последнее, если упомянутому стремлению противостоят иные стремления, может быть сохранено или восстановлено в большей или меньшей степени. Но степеней бытия нет никаких, степенные различия мыслимы лишь в состояниях или отношениях. Следовательно, если нечто действующее стремится с а м о с е б я сохранить или восстановить, оно должно быть состоянием или отношением.
IV. Указанного рода действие некоторого состояния, разумеется, может быть направлено только на такие вещи, которые способны находиться в том же состоянии. Но на какие вещи оно направлено и существует ли оно вообще, об этом нельзя судить, исходя из самого понятия действующего 2).
Очень правильно замечает Кант, что, анализируя понятие вещи, нельзя заключить, что она существует, или что она есть причина чего-нибудь другого, и что, таким образом, понятия бытия и причинной связи – не аналитические и могут быть почерпнуты только и з о п ы т а. Но когда он дальше приходит к необходимости принять, что понятие причинной связи предшествует всякому опыту и обусловливается свойствами познающего субъекта, сводя, таким образом, причинность просто к правилу временной последовательности, в силу которого всякому явлению, рассматриваемому как; причина, может быть сопоставлено в с я к о е д р у г о е, рассматриваемое как следствие, – то это уже означает вместе с водой выплёскивать из корыта и ребёнка. (Конечно, надлежит устанавливать причинные связи, исходя из опыта; но мы не вправе отказаться от обязанности исправлять и дополнять наше понимание наблюдаемых явлений последующим размышлением.)
–––––––––––––––––––––––
Слово “гипотеза” имеет теперь несколько иной смысл, чем у Ньютона. Теперь называют гипотезой всё, что мы прибавляем к наблюдениям после их обдумывания.
Ньютон был далёк от нелепой мысли, будто бы объяснение явлений может быть получено путём абстракции.
Ньютон: Et haec de deo; de quo utique ex phaenomenis disserere ad philosophiam experimentalem pertinet. Rationem vero harum gravitatis proprietatum ex phaenomenis nondum potui deducere, et hypotheses non fingo. Onicquid enim ex phaenomenis non deducitur, hypothesis vocanda est 3).
Arago, Oeuvres complètes, т. 3, 505: une fois, une seule fois, Laplace s'élança dans la région des conjectures. Sa conception ne fut alors rien moins qu´une cosmogonie 4).
Лаплас отвечает на вопрос Наполеона, почему в его Méc. céleste не упоминается имя бога: Sire, je n'avais pas besoïn de cette hypothèse 5).
––––––––––––––––––
Различие, которое Ньютон делает между законами движения (или аксиомами) и гипотезами, не кажется мне основательным. Закон инерции есть гипотеза: если бы материальная точка была одна во всём мире и двигалась бы в пространстве с некоторой определённой скоростью, то эту скорость она сохраняла бы постоянно.
Свободное движение системы материальных точек m1, m2, … с прямоугольными координатами x1, y1, z1; x2, y2, z2, ... , при воздействии сил, параллельных трём осям, X1, Y1, Z1; X2, Y2, Z2, ... , совершается согласно уравнениям
![]()
Этот закон можно выразить следующим образом: ускорения определяются из условия обращения в minimum выражения
![]()
действительно, эта функция ускорений принимает своё наименьшее значение 0, если ускорения заданы по формулам (1), т. е. все величины d2xi/dt2–Xi/mi, … равны нулю, и только в этом случае она принимает наименьшее значение; в самом деле, если бы одна из этих величин, например d2xi/dt2–Xi/mi, оказалась отличной от нуля, то d2xi/dt2 можно было бы изменять непрерывно таким образом, что абсолютное значение этой величины и, следовательно, её квадрат – уменьшался. И функция тогда становилась бы меньше, при условии, что остальные ускорения оставались бы неизменными.
Эта функция ускорений отличается от выражения
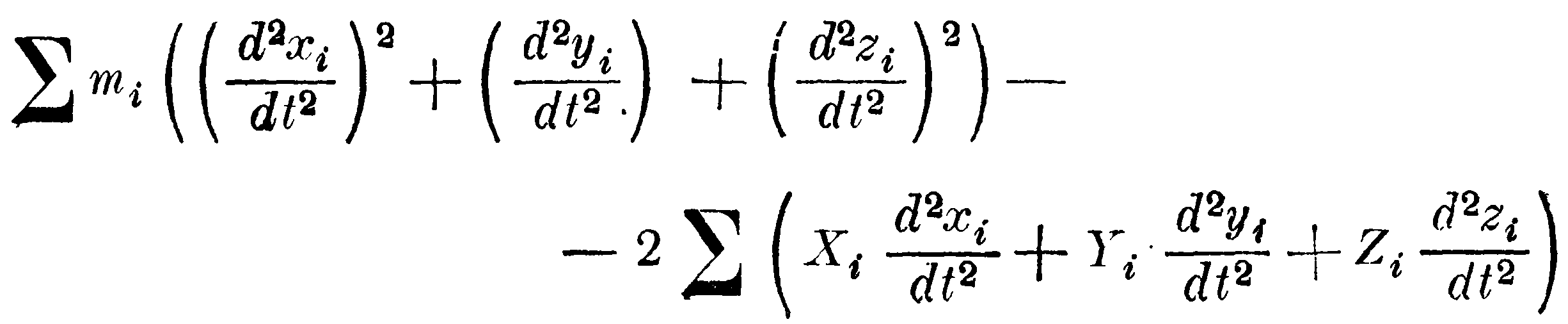
только константой, т. е. величиной, не зависящей от ускорений.
Пусть силы обусловливаются притяжениями и отталкиваниями точек и являются функциями их расстояний; именно, пусть i-я и i'-я точки, находясь на расстоянии r, отталкиваются с силой fi,i'(r) или притягиваются с силой –fi,i'(r). Тогда, как известно, компоненты сил являются частными производными от функции координат всех точек
![]()
где Fi,i'(r) обозначает функцию, производная которой равна fi,i'(r), и где i, i' пробегают всевозможные пары значений.
Подставим эти значения компонент
Xi=∂ρ/∂xi, Yi=∂ρ/∂yi, Zi=∂ρ/∂zi,
в указанную выше функцию ускорений и умножим на dt2/4 (отчего положение максимумов и минимумов не изменится); тогда получится выражение, которое только на величину, не зависящую от ускорений, отличается от выражения
![]()
Предполагая, что положение и скорости точек в момент времени t заданы, положение их в момент t+dt определяется из условия, чтобы это выражение было возможно меньше. Итак, имеется некое стремление к тому, чтобы это выражение было минимальным.
Полученный закон может быть выведен из тех воздействий, которые должны обращать в минимум отдельные члены этого выражения, если допустим, что противостоящие друг другу стремления выравниваются таким образом, чтобы сумма величин, которые отдельные воздействия стремятся сделать возможно меньшими, обратилась в минимум.
Предположим, что массы точек m1, m2, ... , mn относятся как целые числа kl, k2, ... , kn, так что mi= kiμ; тогда мы увидим, что выражение, которое должно быть обращено в минимум, состоит из величин
![]()
(для всех частиц μ) и величины –Pt+dt. Следуя Гауссу, станем рассматривать величину
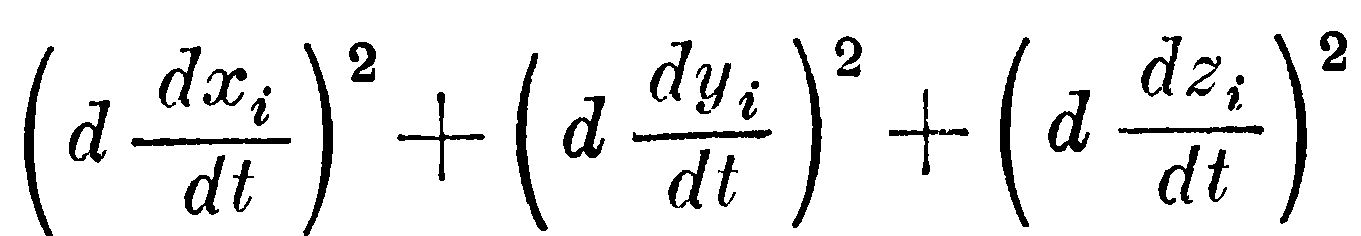
как меру отклонения движения массы μ в момент t+dt от движения её в момент t; в таком случае разложение общего воздействия по каждой отдельной массе даёт воздействие, которое должно сделать возможно меньшим отклонение её движения в момент t+dt от движения в момент t, т. е. стремление сохранить её движение, и, кроме того, воздействие, которое должно сохранить возможно малое значение величины –P.
Это последнее воздействие разлагается на стремления сохранить возможно малые значения отдельных членов суммы ![]() , т.е. на притяжения и отталкивания между всякими двумя толчками, что привело бы нас к обыкновенному выводу законов движения из закона инерции и притяжений и отталкиваний; но оказывается, как будет разъяснено в дальнейшей статье о тяготении, что для всех известных явлений природы упомянутое воздействие может быть выведено и из взаимодействия двух соседних элементов пространства.
, т.е. на притяжения и отталкивания между всякими двумя толчками, что привело бы нас к обыкновенному выводу законов движения из закона инерции и притяжений и отталкиваний; но оказывается, как будет разъяснено в дальнейшей статье о тяготении, что для всех известных явлений природы упомянутое воздействие может быть выведено и из взаимодействия двух соседних элементов пространства.
Хотя заглавие этой статьи едва ли вызовет у большинства читателей благоприятное к ней расположение, мне всё же показалось, что оно наилучшим образом выражает содержащуюся в ней идею. Здесь поставлена задача проникнуть в сущность явлений природы глубже, чем то было сделано Галилеем и Ньютоном в области астрономии и физики. Правда, для астрономии приведённые ниже соображения не принесут непосредственно практической пользы, но, как я надеюсь, это обстоятельство не лишит следующие строки интереса в глазах их читателей…
Основание для общих законов движения весомого вещества в том виде, в каком они сформулированы Ньютоном во введении в его Principia, следует искать во внутреннем состояний весомых частиц. Постараемся, исходя из нашего собственного внутреннего опыта, по аналогии судить об этом состоянии. В наше сознание постоянно вступают некоторые “массы представлений” и очень скоро из него снова исчезают. Наблюдая постоянную деятельность нашей души, мы видим, что в основе каждого её акта лежит нечто “остающееся”, таковым проявляющее себя по особым причинам (усилие памяти), но не оказывающее длительного влияния на наши восприятия. Таким образом, постоянно (при каждом психическом акте) “остающееся” входит в нашу душу, но не оказывает длительного влияния на мир восприятий. Итак, в основе всякого акта нашей души лежит “остающееся”, вступающее в нашу душу при этом акте, но в тот же момент окончательно исчезающее из мира явлений.
Исходя отсюда, я делаю такую гипотезу: пространство наполнено некоей материей, непрерывно устремляющейся в весомые атомы и там исчезающей из осязаемого мира.
Говоря короче, в весомых атомах материя из осязаемого мира постоянно переходит в неосязаемый. Причину исчезновения материи следует видеть в непосредственно предшествующем возникновении в атомах некоторой неосязаемой субстанции, так что весомые тела являются как бы местом соприкосновения осязаемого и неосязаемого миров 6).
На основе этой гипотезы мы сейчас объясним явление всемирного тяготения. Сила тяготения, как известно, определена в каждой точке пространства, если для этой части пространства задана потенциальная функция всех весомых масс, т. е. такая функция P, что сумма весомых масс, заключённых внутри замкнутой поверхности S, равна ![]() .
.
Допустим, что материя, наполняющая пространство, есть однородная несжимаемая жидкость без инерции и что в каждый весомый атом в равные промежутки времени втекают равные и пропорциональные массе атома количества материи; тогда, очевидно, давление, испытываемое атомом [пропорционально скорости движения материи в точке местонахождения атома].
Таким образом, действие всемирного тяготения на весомый атом зависит от давления материи, наполняющей пространство, в непосредственной окрестности атома.
Из нашей гипотезы неизбежно вытекает, что материя, наполняющая пространство, должна распространять колебания, которые мы воспринимаем как свет и теплоту.
Рассмотрим плоско-поляризованный луч и обозначим через x расстояние некоторой его точки от постоянного начального положения, через y – элонгацию точки в момент времени t; так как при всех обстоятельствах скорость распространения колебаний в пространстве, свободном от частиц весомой материи, почти постоянна (равна α), то равенство
y=f(x+αt)+φ(x–αt)
должно быть выполнено по меньшей мере с очень большой точностью.
Допуская, что оно выполняется совершенно точно, мы получим
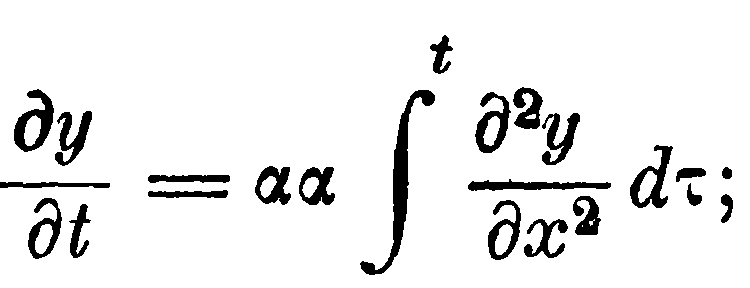
очевидно, не противоречит опытным данным и равенство
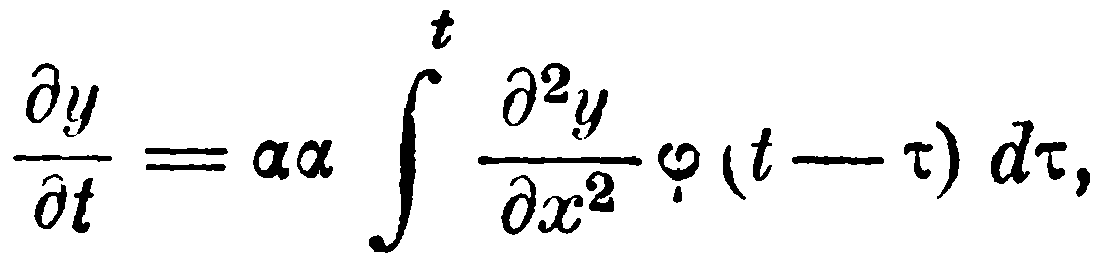
если φ(t–τ) и не при всех положительных значениях t–τ равно единице (с увеличением t–τ стремится к нулю), лишь бы на достаточно большом промежутке времени мало отличалось от единицы.
Определим положение некоторой точки нашей материи в момент t посредством прямоугольной координатной системы, и пусть x, y, z — координаты переменной точки О. Подобным же образом, пусть x', y', z' – координаты точки О' также в прямоугольной системе. Тогда x', y', z' – функции x, y, z, и ds'2= dx'2+ dy'2+ dz'2 есть однородное выражение второй степени относительно dx, dy, dz. Согласно известной теореме можно (и притом единственным образом) найти три линейных выражения
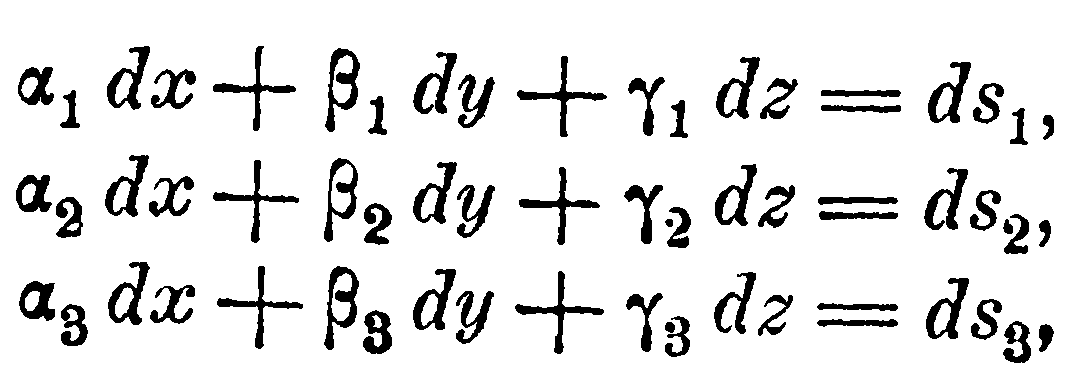
таких, что
![]()
тогда как
![]()
Величины G1–1, G2–1, G3–1 называются главными расширениями частицы в О при переходе от первой формы ко второй; я обозначу их через λ1, λ2, λ3.
Я допускаю, дальше, что различие между предшествующей формой частицы и её формой в рассматриваемый момент времени порождает силу, стремящуюся изменить форму частицы таким образом, что влияние предшествующей формы (caeteris paribus) тем меньше, чем раньше до момента t она имела место, а влиянием формы в достаточно удалённые моменты можно вовсе пренебречь. Тогда силы, которые стремятся уменьшить λ1, λ2, λ3, могут быть рассматриваемы как линейные функции λ1, λ2, λ3; именно, вследствие однородности эфира сила, стремящаяся уменьшить λ1, есть функция λ1, λ2, λ3, не меняющаяся при перестановке λ2 и λ3, а остальные силы получаются из неё посредством перестановки λ2 и λ1, λ3 и λ1, и потому общий момент этих сил равен
![]()
или же, при изменённых значениях констант,
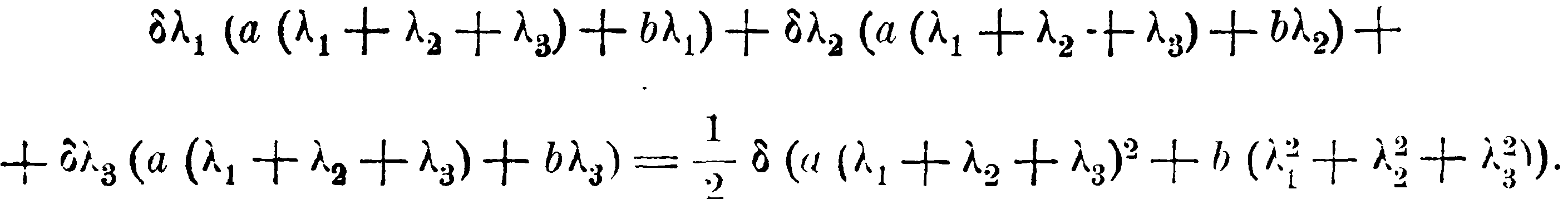
С другой стороны, момент сил, стремящихся изменить форму бесконечно малой частицы в О, можно рассматривать как результирующий из сил, которые стремятся изменить длину линейных элементов, заканчивающихся в О. Так мы получаем следующий закон: если dV' есть объём бесконечно малой частицы в О в момент t, а dV' – объём той же частицы в момент t', то сила, стремящаяся удлинить ds, возникающая вследствие различия двух состояний, представляется формулой
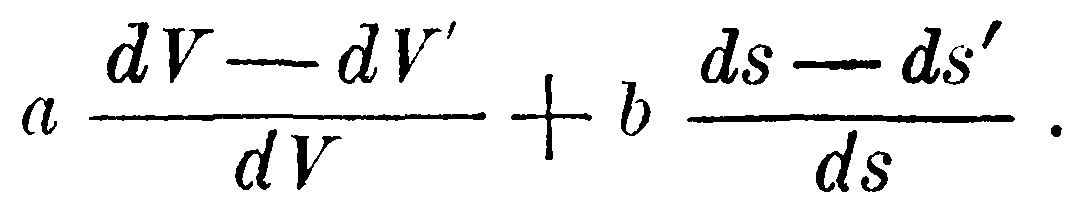
Первая часть этого выражения происходит от силы, с которой частица сопротивляется изменению объёма без изменения формы; вторая – от силы, с которой линейный элемент сопротивляется изменению длины.
Нет никаких оснований предполагать, что действия обеих причин изменяются во времени по одному и тому же закону; поэтому, собирая вместе воздействия всех предшествующих моменту t форм частицы на изменение линейного элемента ds, мы получаем значение δds/dt, равное
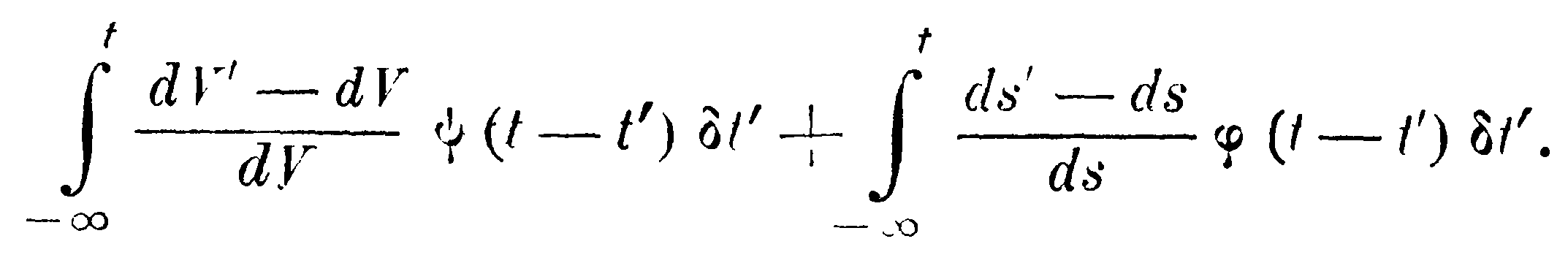
Каковы же должны быть функции ψ и φ, чтобы тяготение, свет и лучистая теплота могли передаваться пространственной материей?...
––––––––––––––––––
Действия весомой материи на весомую материю сводятся
1) к силам притяжения и отталкивания, обратно пропорциональным квадратам расстояний,
2) к свету и лучистой теплоте.
Оба класса явлений могут быть объяснены, если допустим, что всё бесконечное пространство наполнено однородной материей, каждая частица которой воздействует только на своё окружение.
Математический закон, лежащий в основе этих явлений, можно себе представлять разложенным
1) на сопротивление, оказываемое частицей изменению объёма,
2) на сопротивление, оказываемое физическим линейным элементом изменению длины.
На первом основывается тяготение и электростатическое прптяжение и отталкивание, на втором – распространение света и теплоты, а также электродинамическое или магнетическое притяжение и отталкивание.
Данное Ньютоном объяснение движения падающих тел и небесных тел заключается в принятии следующих допущений:
1) Существуют бесконечное пространство, обладающее свойствами, указываемыми в геометрии, и весомые тела, изменяющие своё положение в нём не иначе, как непрерывно.
2) В любой момент всякая весомая точка имеет нечто, определённое по величине и направлению и обусловливающее её движение (материя в состоянии определённого движения). Мерой движения является скорость 7).
Объясняемые посредством этих допущений явления ещё не ведут к допущению различных масс весомых тел.
3. В любой момент во всякой точке пространства существует нечто определённое по величине и направлению (сила ускорения), что сообщает находящейся там весомой точке – какова бы она ни была – определённое движение, складывающееся геометрически с движением, которым она уже обладает.
4. В каждой весомой точке существует нечто определённое по величине (абсолютная сила тяготения), что порождает во всякой точке пространства силу ускорения, обратно пропорциональную квадрату расстояния от этой весомой точки и пропорциональную присущей этой точке абсолютной силе тяготения; эта сила ускорения складывается геометрически со всеми другими силами ускорения, приложенными к этой точке 8).
Существующую согласно 3 в каждой тачке пространства определённую по величине и направлению силу ускорения я пытаюсь объяснить движением некоей субстанции, наполняющей всё бесконечное пространство, а именно, допускаю, что направление её движения совпадает с направлением силы ускорения, а скорость её пропорциональна величине силы ускорения. Эту субстанцию можно представлять себе как физическое пространство, точки которого движутся в геометрическом пространстве.
На основании этого допущения все воздействия весомых тел на весомые тела передаются в пустом пространстве посредством названной субстанции. Таким образом, формы движения, лежащие в существе света и теплоты, посылаемых небесными телами, суть не что иное, как формы движения этой субстанции. Но названные явления, именно тяготение и распространение света сквозь пустое пространство, – единственные, которые должны были бы быть объяснены только движением этой субстанции.
Я допущу дальше, что действительное движение субстанции в пустом пространстве составляется из движения, которое должно быть допущено для объяснения явления тяготения, и из движения, которое должно быть допущено для объяснения явления света.
Дальнейшее развитие следствий, вытекающих из этой гипотезы, распадается на две части, поскольку требуется исследовать
1) законы движения субстанции, позволяющие дать объяснение явлений,
2) причины, объясняющие само возникновение этого движения.
Первая задача – математическая, вторая – метафизическая. По поводу последней я сразу же замечу, что движение субстанции не следует пытаться объяснять притяжением и отталкиванием её частиц. Такого характера объяснения широко применяются в физике не вследствие их очевидности (особой разумности) и – кроме электричества и тяготения – не вследствие их особой лёгкости, а вследствие того обстоятельства, что закон всемирного тяготения Ньютона – вопреки ожиданиям его творца – так долго не допускал более глубокого объяснения 9).
Пусть прямолинейные координаты некоторой точки пространства обозначены x1, x2, x3, соответствующие в момент времени t компоненты скорости движения, обусловливающего явления тяготения, – через u1, u2, u3, а компоненты скорости движения, обусловливающего явления света, – через w1, w2, w3; наконец, компоненты скорости истинного движения – через v1, v2, v3, так что v= u+w. Как обнаружится из самих законов движения, если субстанция в определённый момент оказывается всюду одинаково плотной, то эта плотность сохраняется и в любой момент; поэтому в дальнейшем плотность принимается равной единице.
Сила тяготения в каждой точке определяется потенциальной функцией V, частные производные которой ∂V/∂x1, ∂V/∂x2, ∂V/∂x3 являются компонентами силы, и эта функция V определяется следующими условиями (с точностью до постоянного слагаемого):
1. dx1 dx2 dx3(∂2V/∂x12+∂2V/∂x22+∂2V/∂x32) вне притягивающих тел = 0, а для некоторого элемента весомого тела имеет неизменное значение, а именно равно произведению –4π на абсолютную величину силы притяжения, которую ему следует приписать согласно теории притяжения и которую мы обозначим через dm.
2. Если все притягивающие тела заключены в конечной части пространства, то на бесконечно большом расстоянии r от некоторой точки величины r∂V/∂x1, r∂V/∂x2, r∂V/∂x3 бесконечны малы.
Согласно нашему предположению ∂V/∂x=u, и потому
![]()
Таким образом, мы получаем
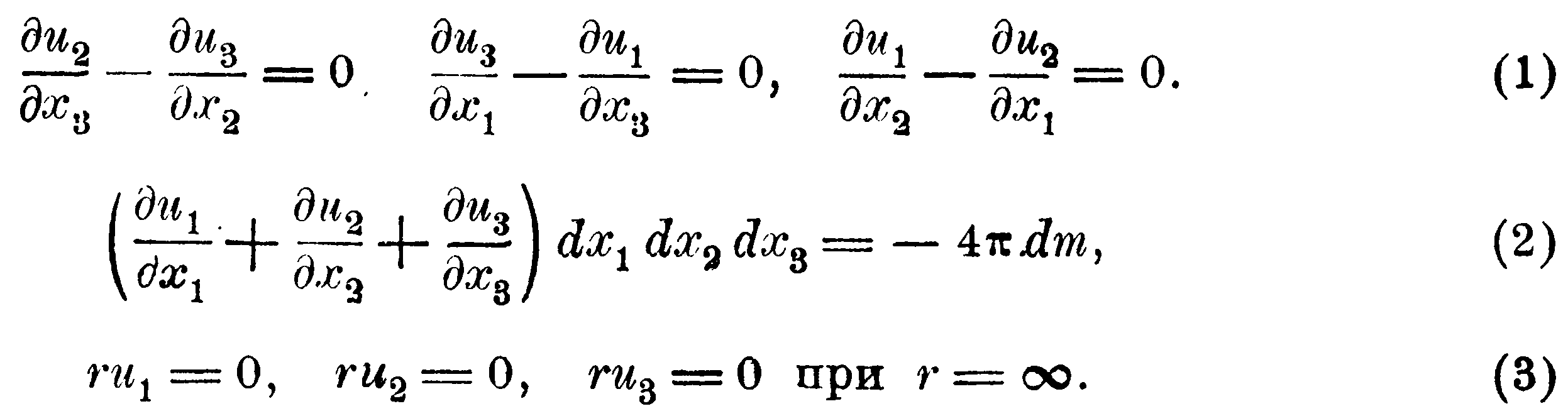
Обратно, величины u, удовлетворяющие этим условиям, являются компонентами силы тяготения. В самом деле, условия (1) свидетельствуют о возможности найти функцию U такую, что dU= u1dx1+ u2dx2+ u3dx3, откуда следует ∂U/∂x=u, а остальные дают тогда U= V+const.10).
2. Движение, обусловливающее явления света
Движение, которое нужно допустить в пустом пространстве для объяснения явления света, может быть рассматриваемо (на основании одной теоремы), как составленное из плоских волн, т. е. таких движений, для которых вдоль каждой плоскости из некоторой системы параллельных плоскостей (волновых плоскостей) форма движения – одна и та же. Для каждой плоской волны движение совершается (как можно cудить на основании опыта) параллельно плоскости волны, причём сама волна распространяется при любой форме движения (т. е. какого бы рода ни был свет) с постоянной скоростью c перпендикулярно к плоскости волны.
Пусть ξ1, ξ2, ξ3 – прямоугольные координаты точки пространства, причём первая перпендикулярна, остальные – параллельны плоскости волны, и ω1, ω2, ω3 – параллельные им компоненты скорости в рассматриваемой точке в данный момент времени t; тогда
∂ω
/∂ξ2=0, ∂ω/∂ξ3=0.Согласно опыту, во-первых, ω1= 0; во-вторых, движение составляется из двух движений, распространяющихся со скоростью c: одного – направленного в положительную сторону, другого – направленного в отрицательную сторону от плоскости волны. Обозначая через ω' компоненты скорости первого движения, через ω'' – компоненты скорости второго, мы видим, что ш не меняются при увеличении t на dt и ξ1 на cdt, а ω'' – при увеличении t на dt и ξ1 на –cdt, и притом ω= ω'+ ω''. Отсюда следует:
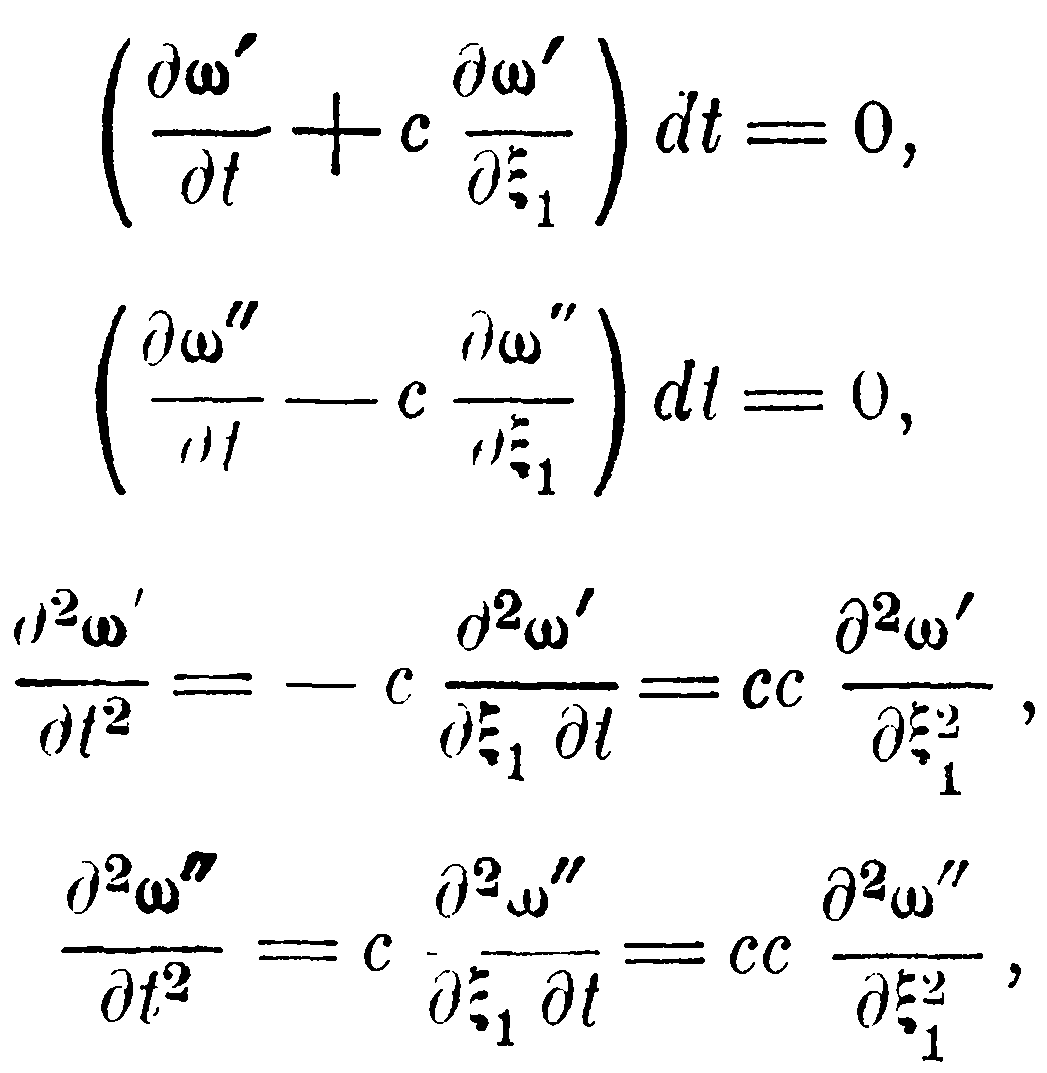
так что
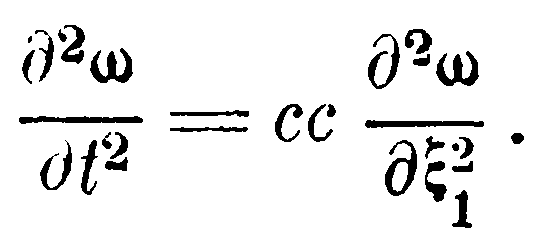
Из этих равенств вытекают следующие симметрические:
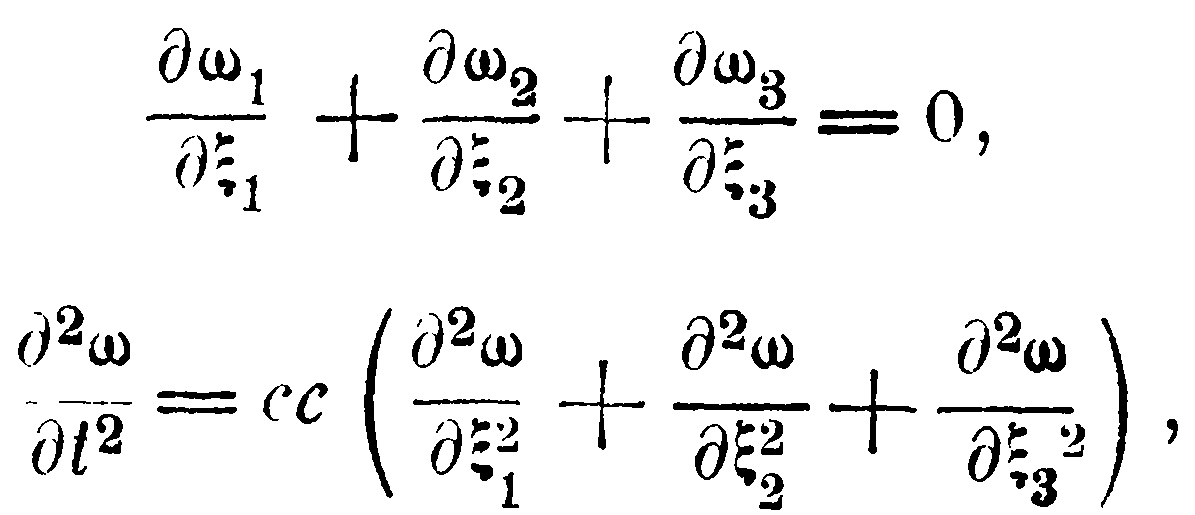
которые при переходе к первоначальной системе координат сохраняют свой вид, а именно:
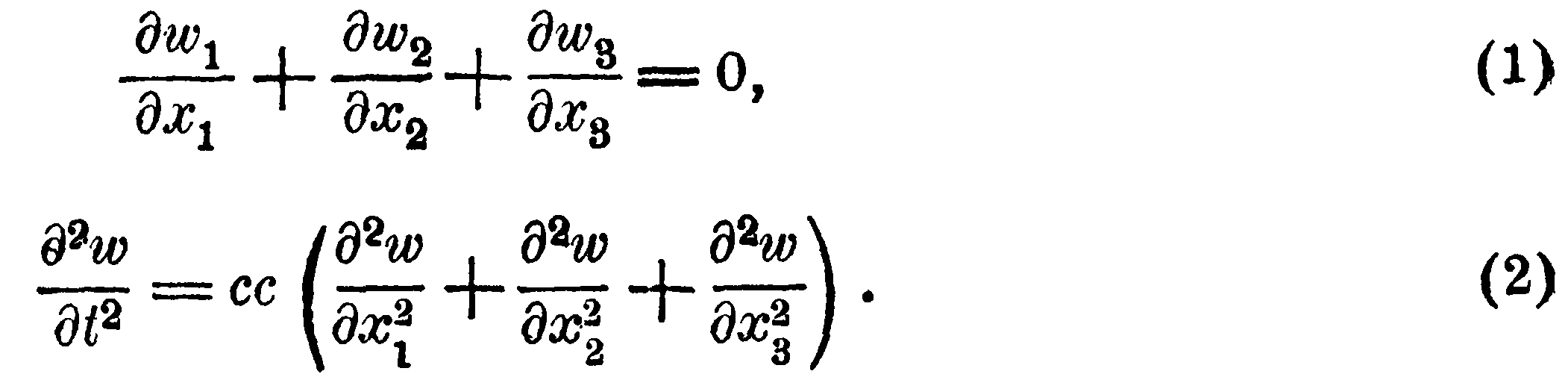
Эти уравнения выполняются для всякой плоской волны, проходящей через точку (x1, x2, x3) в момент t и, следовательно, для всякого движения, составленного из подобных волн.
3. Движение, обусловливающее оба рода явлений
Из полученных уравнений для u и w вытекают следующие уравнения для v, т. е. законы движения субстанции в пустом пространстве:
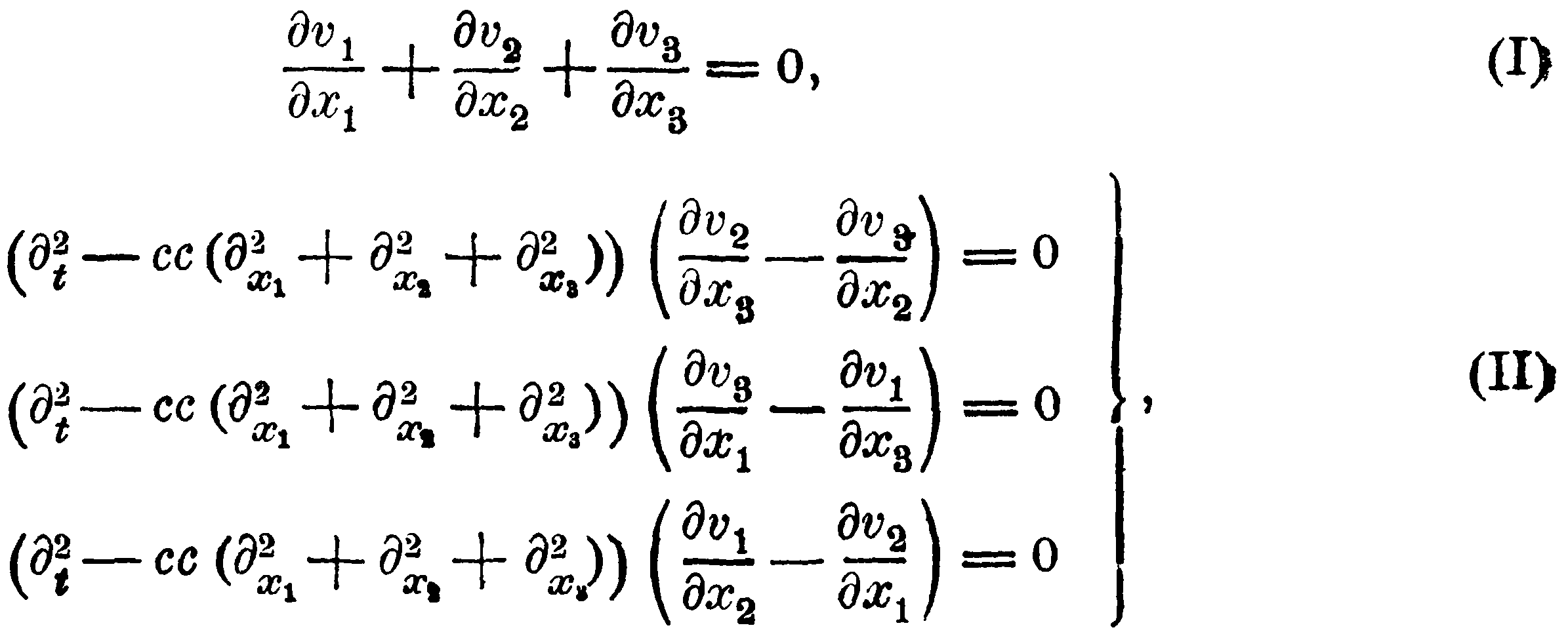
как нетрудно установить, выполняя все операции.
Эти уравнения показывают, что движение любой точки субстанции зависит только от движений в соседних точках и в непосредственно-предшествующие моменты времени, так что причина движения полностью содержится в движениях окрестности.
Уравнение (I) доказывает ранее высказанное утверждение, что плотность субстанции остаётся неизменной; в самом деле, выражение
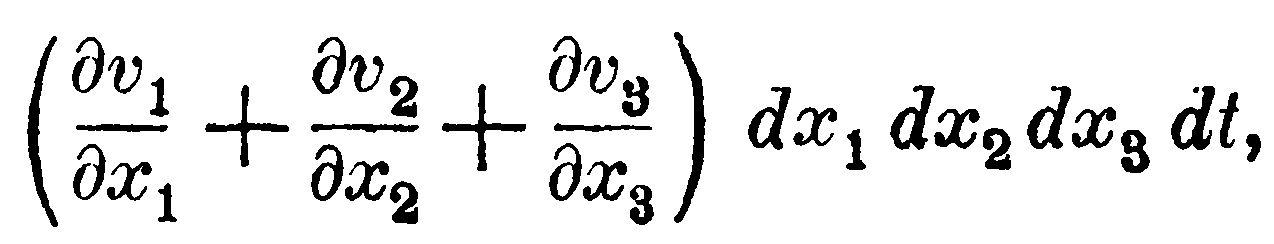
которое вследствие этого уравнения = 0, представляет количество субстанции, вливающейся за время dt в элемент объёма dx1dx2dx3, и потому содержащееся в этом элементе количество субстанции остаётся неизменным.
Условия (II) означают, что
![]()
есть полный дифференциал dW. Мы получаем:
![]()
и, следовательно,
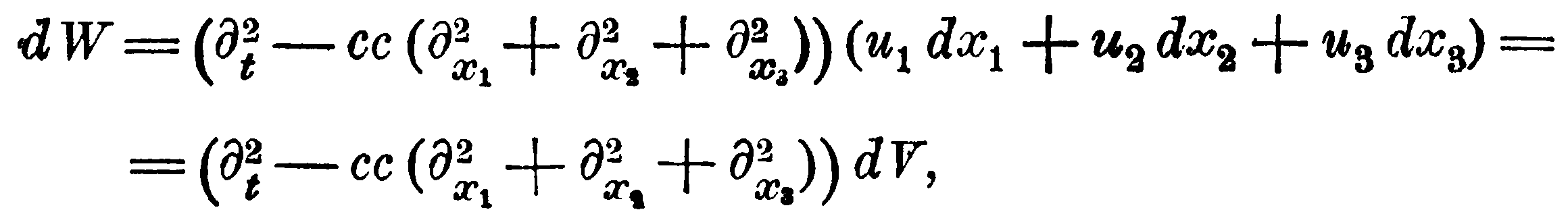
или, так как (∂2x1+∂2x2+∂2x3)dV=0, то =d(∂2V/∂t2).
Закон этих движений можно охватить требованием, чтобы вариация интеграла
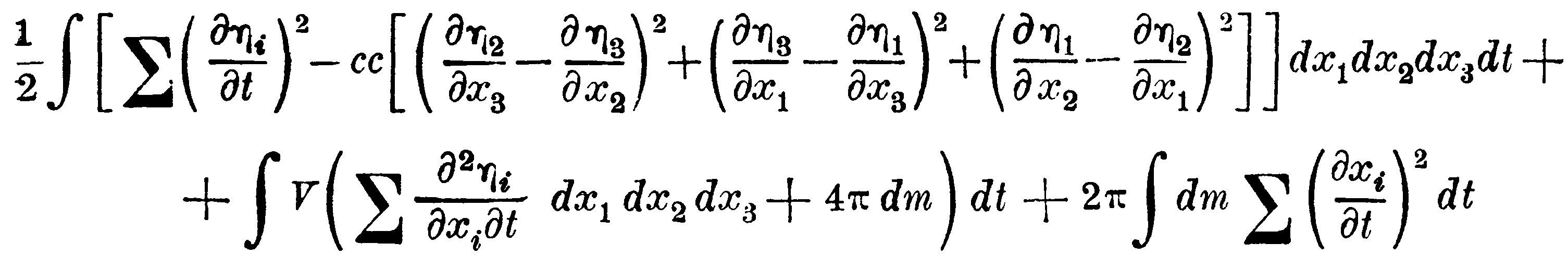
(при надлежащих условиях на границе) обращалась в нуль.
Здесь первые два интеграла берутся по всему геометрическому пространству, а последние – по всем весомым телам; и нужно определить координаты каждого весомого элемента как функции времени, а η1, η2, η3, V – как функции x1, x2, x3, t, таким образом, чтобы всякая вариация их, удовлетворяющая условиям на границе, вызывала только вариацию интеграла второго порядка малости.
Тогда величины ∂η/∂t (=v) будут компонентами скорости движения субстанции, а V будет равно потенциалу в момент t для точки (x1, x2, x3).
В “Riemann's Werke” Вебер предпосылает “Фрагментам” введение, существенную часть которого мы здесь воспроизведём.
Философские размышления, результаты которых здесь излагаются, занимали Римана, как можно судить по оставленному им наследию, на протяжении большой части его жизни. Время возникновения отдельных отрывков едва ли может быть установлено вполне точно. Сохранившиеся наброски отнюдь не приведены автором к виду связного, готового для печати изложения, хотя некоторые места указывают, что Риман кое-когда и предусматривал таковое; при отсутствии детализации всё же они достаточны, чтобы в общих чертах характеризовать позицию Римана по отношению к вопросам психологического и натурфилософского порядка и установить направление его исследований. Какое значение сам Риман придавал своим философским работам, ясно из следующей заметки:
“Работы, которые меня теперь преимущественно занимают, таковы:
1. Подобно тому как это уже сделано с большим успехом в отношении алгебраических функций, показательных или круговых, эллиптических и абелевых функций, ввести мнимость в теорию также и других трансцендентных функций; для этого уже выполнена в моей диссертации самая необходимая подготовительная работа (см. § 20 этой диссертации).
2. В связи с этим находятся новые методы интегрирования дифференциальных уравнений в частных производных, которые я уже применил с успехом ко многим вопросам из области физики.
3. Главная моя работа относится к новому пониманию известных законов природы – я имею в виду их формулировку с помощью других основных понятий, – причём стало возможным использование экспериментальных данных, касающихся взаимоотношения между теплотой, светом, магнетизмом и электричеством, для исследования их взаимной связи. К этому меня побудило, главным образом, изучение сочинений Ньютона, Эйлера и – с другой стороны – Гербарта. Что касается последнего, то к самым ранним исследованиям Гербарта, результаты которых изложены в его диссертациях (защищённых 22 и 23 октября 1802 г.), я смог примкнуть почти безоговорочно, но от дальнейшего хода его философских размышлений должен был отклониться в одном существенном пункте, чем и обусловливается моё особое отношение к его натурфилософской системе и тем утверждениям из области психологии, которые связаны с этой системой”.
Дальше в другом месте мы находим более точные указания по поводу этого пункта:
“Автор является гербартианцем, поскольку речь идёт о психологии и теории познания (методологии и эйдолологии), но он по большей части не может примкнуть к его натурфилософии и к связанным с нею метафизическим дисциплинам (онтологии и синекологии)” ...
В дальнейшем по поводу фрагментов “Тяготение и свет” и “Новые математические принципы натурфилософии”, объединённых под общим заглавием “Натурфилософия”, Вебер отмечает, что в письме от 28 декабря 1853 г. Риман высказывает намерение опубликовать исследование, к которому должен был бы относиться первый из упомянутых фрагментов. Что касается второго, то на подлиннике его имеется дата “1 марта 1853 г.” – таким образом можно думать, что он более раннего происхождения.
) Лукреций. “О природе вещей”, книга I, строки 52–53. Строки 50–53, в переводе Ф.А. Петровского, таковы: Ты же теперь напряги свой слух и свой ум прозорливый,
Освободи от забот, достоверному внемля ученью,
Дабы дары, приносимые мной с беспристрастным усердьем,
Прежде чем их оценить, с презрением прочь не отринул.
Если две вещи a и b вступают в связь по некоторой внешней причине, то или из самой их связи (связанности) или же из изменения её степени может проистекать некоторое следствие c. Проще всего допустить, что c есть следствие их связанности.
Нет необходимости развивать дальше эти соображения. Их принцип заключается в применении предложения: “то, к осуществлению чего стремится действующее, должно содержаться в самом понятии действующего”, но применять его нужно не к объектам, обладающим целым рядом характеристик (как это делали Лейбниц и Спиноза), а к возможно более простым реальным основаниям. И actio и effectus переводятся одним и тем же словом “действие” (Wirkung). Так как гораздо чаще это слово употребляется во втором значении, то легко возникает неотчётливость, когда его употребляют вместо actio, как, например, при обычных переводах “actio aequalis est reactioni”, “principium actionis minimae”. Кант старается облегчить положение тем, что рядом со словами “действие”, “взаимодействие” ставит в скобках латинское “actio”, “actio mutua”. Пожалуй, можно было бы сказать: “сила равна противосиле”, “принцип наименьшего применения силы”. Но так как нет простого перевода для слова “agere”, обозначающего стремление, направленное на что-то другое, то пусть будет мне позволено пользоваться иностранным словом.
) О боге я скажу следующее: о чём и как судить на основании опыта, это относится к экспериментальной философии. Но я ещё не смог объяснить этих свойств тяготения на основании опыта, а гипотез я не создаю. Ибо всё, что не выводится из опыта, должно быть названо гипотезой. ) Один раз – только один раз – Лаплас пустился в область предположений. И то, что возникло в результате его размышлений, было не менее, чем космогонией (Араго). ) Государь, в этой гипотезе я не нуждался. ) В каждый весомый атом вступает в каждый момент определённое количество материи, пропорциональное силе тяготения, и там исчезает.Из психологии, стоящей на почве учения Гербарта, следует, что субстанциальность присуща не душе, а каждому возникающему в нас отдельному представлению.
) Если бы материальное тело было в пространстве одно, оно или не изменяло бы своего положения в нём или же двигалось в пространстве по прямой линии с постоянной скоростью.Этот закон движения не может быть обоснован принципом достаточного основания. То, что тело продолжает своё движение, должно иметь причину, которую следует искать во внутреннем состоянии материи.
) Одна и та же весомая точка в двух различных местах претерпела бы изменения движения, которые по направлению совпали бы с силами, а по величине были бы пропорциональны силам.Отношение силы к изменению движения поэтому всегда одно и то же для определённой весомой точки. Но для различных весомых точек оно различно. Оно называется массой точки.
) Ньютон говорит: “Мысль о том, чтобы способность возбуждать тяготение могла быть неотъемлемым, внутренне-присущим свойством материи, и чтобы одно тело могло воздействовать на другое через пустоту на расстоянии, без участия чего-то такого, что переносило бы действие и силу от одного к другому, – представляется мне столь нелепой, что нет, как я полагаю, человека, способного мыслить философски, кому она пришла бы в голову”. См. третье письмо к Bentley. ) Итак, функция U может быть определена с помощью общих законов движения из опытных данных (при наблюдении относительного движения), но только с точностью до линейной функции координат, так как мы наблюдаем лишь относительное движение.Определение этой функции основано на следующей математической теореме: функция точки V определяется в конечной части пространства (с точностью до постоянного слагаемого), если она не может быть разрывной вдоль некоторой поверхности и если для всякого объёмного элемента задано (∂2V/∂x12+∂2V/∂x22+∂2V/∂x32)dx1dx2dx3 и, кроме того, на границе рассматриваемой части пространства задаётся или сама функция V или её производная при перемещении внутрь по перпендикуляру к поверхности. При этом следует заметить:
1. Обозначая упомянутую производную для элемента границы ds через ∂V/∂ρ, мы должны в последнем случае иметь
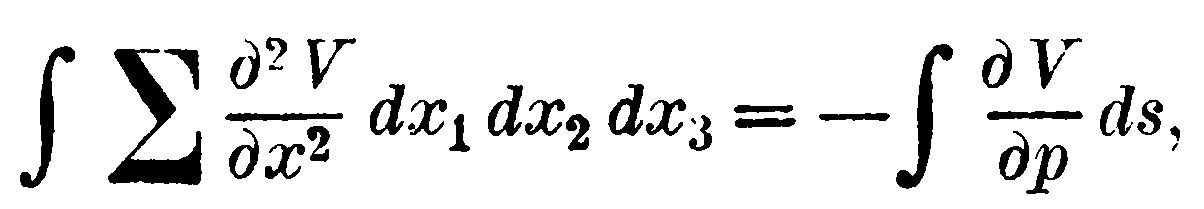
причём интеграл слева берётся по выделенному объёму, а интеграл справа – по его границе; помимо того, в обоих случаях все данные могут быть совершенно произвольными, и потому они необходимы.
2. Если в некотором элементе объёма ∑∂2V/∂x2 обращается в бесконечность, то надлежит произведение заменить через интеграл ![]() , взятый по границе этого элемента.
, взятый по границе этого элемента.
3. Если ∑∂2V/∂x2 имеет отличное от нуля значение только в некоторой конечной части пространства, то условие на границе может быть заменено требованием, чтобы на бесконечно большом расстоянии R от некоторой точки величины R∂2V/∂x2 были бесконечно малыми.
Дата установки: 19.04.2010
[вернуться к содержанию сайта]