[вернуться к содержанию сайта]

    Согласно баллистической теории ускоряемый источник в каждый последующий момент сообщает свету несколько иную скорость, и последовательные сигналы (или фронты световых волн), испущенные с разными скоростями, догоняют друг друга (сокращая длину волны), либо расходятся (наращивая длину волны), приходя к приёмнику чаще или реже. Из преобразования интервалов времени dt и периода T найдём для изменения длины волны λ = cT, частоты света f = 1/T,– новые интервалы, длины волны и частоты, соответственно,

, , .                     (1)

    Эффект (1), дополняющий эффект Доплера, далее будем называть эффектом Ритца: Ритц вывел формулу (1) в 1908 г. [1]. При V_r << c общее преобразование по эффектам Доплера и Ритца

, .                        (2)

    Если доплер-эффект dt' = (1 + V_r /c)dt легко регистрируется в лаборатории, то эффект Ритца (1) обнаружить сложнее, ввиду малости ra_r /c² << 1. Но на дистанциях r порядка светового года малые ускорения a_r ~ c²/r ≈ 9,5 м/с² могут менять видимую длительность процессов в разы.

    Изменение видимой длительности dt' процессов по эффекту Ритца (представляющее собой такую же иллюзию как изменение dt' по эффекту Доплера) приводит также к изменению регистрируемой мощности излучения W'. Действительно, если источник излучил в единичную апертуру фотоприёмника мощность W в течение времени dt, то по закону сохранения энергии Wdt, воспринимаемой за время dt', регистрировалась бы мощность W' = Wdt/dt'. Отсюда, с учётом (1),

.                            (3)

    Итак, лучевое ускорение источника a_r приводит к изменению видимой яркости и мощности W' источника, а колебания a_r вызывают колебания видимой яркости источника, например звезды.

    Если эффект (1) имеет место, и видимое движение звёзд искажается, тогда, кроме отмеченного искажения, произойдёт дополнительное смещение спектральных линий по закону (1). Общее изменение периода и длины волны спектральной линии задано формулой (2). Таким образом, оно представлено суммой смещений по эффекту Доплера и по эффекту Ритца:

.                            (4)

    Интерпретируя это смещение как чисто доплеровское, найдут расчётное значение скорости

,                           (5)

которое отличается от истинного V_r.

    Для графиков лучевых скоростей звёзд, движущихся по круговой орбите, эффект Ритца приведёт к изменению орбитальной фазы звезды. Если истинная лучевая скорость звезды задана выражением V_r = –Ksin(2πt/P), тогда ускорение a_r = dV_r/dt = –(2πK/P)cos(2πt/P), и вносимая им добавочная мнимая (кажущаяся) скорость V_r^* = ra_r/c или V_r^* = la_r/c (в случае переизлучения света на длине l). Отсюда получим, что расчётная скорость задана выражением

,                (6)

где сдвиг по фазе φ = arctg(2πl/Pc), а расчётная амплитуда лучевой скорости

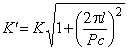.                        (7)

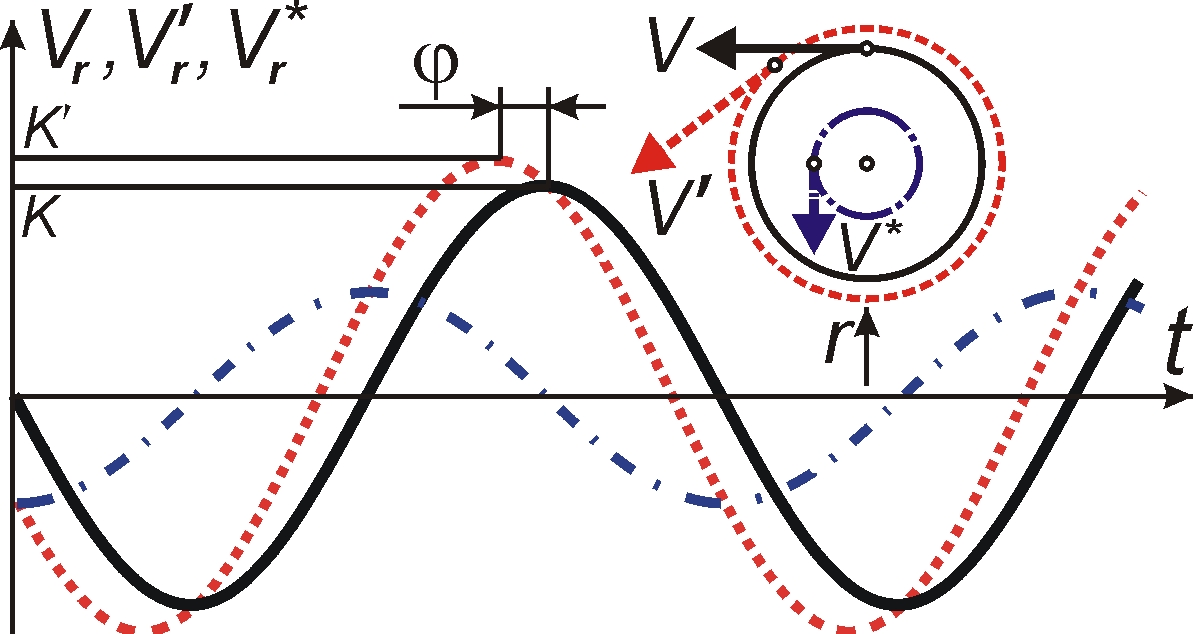
    Фазовое смещение графика лучевых скоростей V_r'(t) (Рис. 1) можно обнаружить у спектрально-двойных звёзд, являющихся одновременно затменно-двойными. Теоретически затмение звезды с круговой орбитой наблюдалось бы в момент наибольшего её удаления в фазе кривой лучевых скоростей 0. Если кривая искажена эффектом Ритца, затмение произойдёт с запозданием относительно фазы 0 на разность фаз φ, достигающую π/2 (или в орбитальной фазе 0,25 – в астрономических обозначениях) в предельном случае, когда смещение спектра обусловлено в основном эффектом Ритца. Несоответствия кривых блеска и лучевой скорости реально открыты, например у звезды υ Андромеды [2, 3]. Тот же эффект отмечен у двойного пульсара PSR 1957+20, у которого затмение наступает в орбитальной фазе 0,25 [4], совпадающей с предельным значением 0,25, при котором вариации периода пульсара целиком обусловлены эффектом Ритца.

    Также у двойного радиопульсара PSR 1957+20 обнаружены плавные колебания оптического блеска и цвета с орбитальным периодом P ≈ 9,17 часа [5], которые тоже могут быть следствием эффекта Ритца (3) и (1). Об этом свидетельствует форма кривой блеска W'(t), соответствующая по эффекту Ритца форме графика лучевых ускорений a_r(t) звезды, движущейся по круговой орбите (как показал метод тайминга), с искажениями, обусловленными ритц-эффектом. Таким образом, ряд аномалий космических объектов свидетельствуют в пользу теории Ритца.

1. Ritz W. // Ann. Chim. Phys. 1908. V. 13. P. 145–275.

2. Семиков С.А. Через поля к экзопланетам // Техника-молодёжи. 2014. №6. С. 28–31.

3. Kürster M. // Astroph. Journal. 2005. V. 622(2). P. 1075–1090.

4. Callanan P.J., Paradijs J.V., Rengelink R. // Astroph. J. 1995. V. 439. P. 928–932.

5. Ryba M.F., Taylor J.H. // Astroph. J. 1993. V. 380. P. 557–563.

Дата установки: 17.07.2016
[вернуться к содержанию сайта]