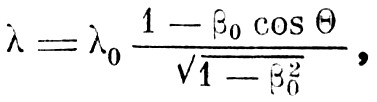 (1)
(1)[
вернуться к содержанию сайта]Проведено критическое рассмотрение экспериментальных работ по прямой проверке релятивистской формулы для эффекта Доплера. Описывается усовершенствованная методика измерений и обработки полученных результатов. Отмечается систематическое расхождение между экспериментальными и расчётно-теоретическими данными. Рассматриваются причины, которые могли бы привести к этим расхождениям.
Эффект Доплера, как известно, заключается в изменении длины волны λ, воспринимаемой неподвижным наблюдателем от движущегося источника колебаний, сравнительно с точно таким же неподвижным источником колебаний с длиной волны λ0
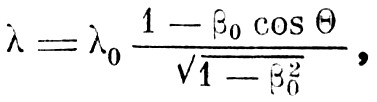 (1)
(1)
где β0=V0/C (V0 – скорость движения источника колебаний, Θ – угол между направлением скорости и направлением наблюдения).
При β0<<1
λ=λ
0(1–β0cosΘ+β02/2). (2)При чисто классическом рассмотрении может быть получен только числитель выражения (1), знаменатель же получается при релятивистском рассмотрении.
Попытки обнаружить эффекты, связанные с множителем (1–β02)1/2, в знаменателе выражения (1), длительное время оставались безуспешными, так как при β0<<1 они чрезвычайно малы.
В 1938 г. Айвсом и Стилуэлом была предложена и осуществлена удачная схема эксперимента, которая подтвердила выражение (1) [1]. В этом эксперименте ионы H2+, ускоренные в “катодной трубке” до 28 кэВ, при столкновении с неускоренными молекулами водорода “разваливались” на свободные протоны и возбужденные атомы водорода. В результате их же столкновений образовывались неподвижные атомы водорода в возбуждённом состоянии. Таким образом, в эксперименте будут наблюдаться две линии: несмещённая (λ0) и смещённая вследствие эффекта Допплера (λ). Айвс предложил проводить измерения одновременно под двумя симметричными углами Θ° и 180°+Θ°. Тогда в направлении движения мы зафиксируем длину волны согласно выражению (2)
λ
1=λ0(1–β0cosΘ+β02/2).Под углом Θ°+180° будет фиксироваться длина волны
λ
2=λ0(1+β0cosΘ+β02/2).Между линиями λ1 и λ2 располагается несмещённая линия λ0. Соответственно написанным выражениям получаем сдвиг в синюю область
Δλ
с=|λ1–λ0|=λ0(β0cosΘ–β02/2)и сдвиг в красную область
Δλ
к=|λ2–λ0|=λ0(β0cosΘ+β02/2).Комбинируя написанные выражения, имеем
Δλ
к+Δλс=2λ0β0cosΘ,Δλк–Δλс=λ0β02. (3)
Таким образом, сложная в экспериментальном отношении задача чрезвычайно точного определения длин волн заменяется более простой – определением асимметрии смещения двух линий относительно центральной. Схема эксперимента Айвса в упрощённом виде показана на рис. 1, a.
В дальнейшем эти же авторы повторили свой эксперимент и довели энергию ионов H2+ до 40 кэВ [2]. Результаты этих работ совпадают: использовалась линия Hβ
с λ0=486.2 нм и Θ=7°.В 1962 г. Мандельберг и Виттен, используя усовершенствованную методику, довели энергию ионов H2+ до 78 кэВ [3]. В этом эксперименте пучок ионов H2+ проходил через отверстия в двух плоских зеркалах, между которыми располагался экран с отверстием для прохождения пучка ионов. Зеркала наклонены к оси пучка под углами 45 и 135°, благодаря этому они отражают свет под углами, близкими к 0 и 180° относительно оси пучка ионов; расстояние между центральными отверстиями в зеркалах 10 см. Давление водорода в камере составляет 400 мкм Hg. Совмещённый световой поток подаётся на щель спектрографа. Эти авторы также подтвердили выражение (1). Схема их эксперимента показана (упрощённо) на рис. 1, б.
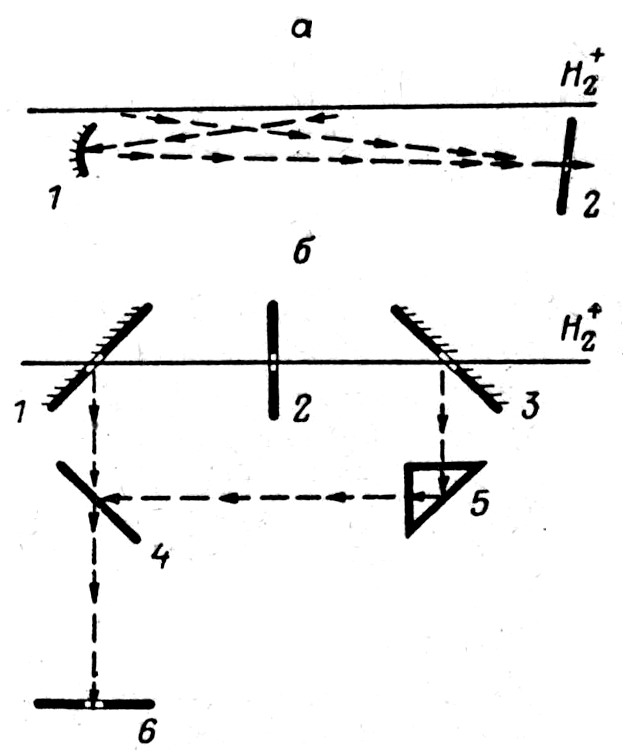
Рис. 1. Оптическая схема экспериментов Айвса (а) и Мандельберга (б).
а: 1 – зеркало, 2 – щель спектрографа; б: 1, 3 – зеркала, 2 – экран,
4 – полупрозрачное зеркало, 5 – призма, 6 – щель спектрографа.
Можно было бы привести ещё ряд работ, подтверждающих наличие множителя 1/(1–β02)1/2 в выражении (1), однако, по мнению авторов, эти работы содержат лишь косвенные подтверждения. Кроме работ [1, 2, 3], не удалось обнаружить в литературе описание прямых экспериментов, посвящённых этому вопросу. И хотя в настоящее время трудно сомневаться в справедливости выражения (1), в экспериментальном отношении работы [1, 2, 3] представляются нам недостаточно убедительными по следующим причинам.
1. Конструкции экспериментальных установок в упомянутых работах таковы, что производится сравнение длин волн, испущенных под углами, близкими к 0 и 180°, относительно пучка ионов из разных областей пространства. Вследствие торможения в атмосфере водорода, напускаемого в рабочую область установки, в разных областях пространства пучку ионов H2+ необходимо приписывать разные β0, что должно приводить к нежелательным побочным эффектам и возникновению ложной асимметрии в положении линий Δλ=λ0β02. Например, используя приведённые в работе [3] расстояния между зеркалами и давление в камере, нетрудно рассчитать эту ложную асимметрию. Результаты представлены на рис. 2. В этих расчётах использовались тормозные способности водорода по данным работы [4]. Этот пример несколько условен, так как области, из которых собирается излучение, не могут быть точно локализованы. Становится непонятным, каким образом авторы работы [3] получили прекрасное согласие своих экспериментальных результатов с расчётными по формуле (1). К сожалению, в работах [1, 2] не указываются конкретные размеры установки и рабочее давление, что не позволило провести оценки ложной асимметрии.
2. В упомянутых работах используются ионы H2+ слишком низких энергий, вследствие чего эффекты, связанные с множителем 1/(1–β02)1/2, малы; в то же время конечные результаты этих работ указываются без экспериментальных погрешностей.
Изложенные причины побудили авторов ещё раз вернуться к вопросу об экспериментальном подтверждении выражения (1).
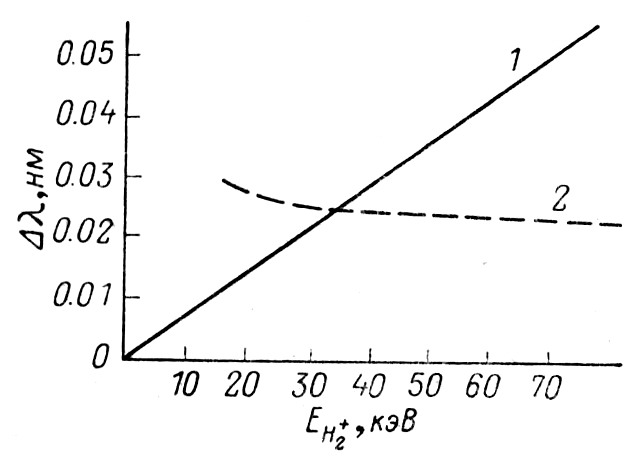
Рис. 2
Расчётная асимметрия Δλ=λ0β02 по формуле (3) и ложная Δλ=λ0Δβ.
λ0=656.28 нм; 1– Δλ=λ0β02, 2– Δλ=λ0Δβ.
В качестве источника ионов H2+ нами использовались ускорители Радиевого института им. В. Г. Хлопина НГ-400 (до 300 кэВ) и ЭГ-5 (до 2000 кэВ). Магнитный анализатор выделял из “прямого” пучка ионов необходимую нам компоненту ионов H2+. Токи пучка ионов H2+ составляли ~50 мкА при энергиях ионов до 300 кэВ и ~10–12 мкА при более высоких энергиях. Так как свечение, вызываемое пучком с такими токами, малоинтенсивно, то для увеличения светосбора нам представилось целесообразным использовать многощелевой коллиматор света жалюзного типа. Такой коллиматор несложно реализовать, если углы наблюдения близки к 90° относительно пучка ионов. В нашем случае эти углы составляют 77 и 257°. Коллиматор состоит из 29 параллельных пластин длиной 116 мм, шириной 20 мм и толщиной 0.2 мм. Расстояние между пластинами 0.5 мм. В центре коллиматора имеется отверстие, через которое проходит пучок ионов H2+. Таким образом, реализуется геометрия, при которой производится наблюдение излучения, образовавшегося в одной и той же области пространства “по” и “против” направления движения пучка ионов.
Проверка параллельности пластин коллиматора показала, что она лучше чем 10–3 рад. В рабочий объём подаётся водород до давлений (4–6)·10–2 мм Hg. Для поддержания высокого вакуума в объёме ускорителя (3·10–6 мм Hg) используется система дифференциальной откачки: между диафрагмами, коллимирующими пучок ионов (диаметр отверстия 5 мм, расстояние между диафрагмами 250 мм), поставлен диффузионный насос. На рис. 3 приведена схема используемой нами установки.
В оптической схеме нашего эксперимента (рис. 4) первоначально использовался дифракционный спектрограф с дисперсией ~4.3 нм/мм, калибровка которого осуществлялась независимо по линиям спектра неона. Данные, относящиеся к энергиям ионов H2+ (2000, 1750, 1500, 300, 250, 200 и 150 кэВ), получены с этим спектрографом и приводятся в работе [5].
В последующих измерениях использовался спектрограф с дисперсией ~2.4 нм/мм, в процессе измерений осуществлялась подсветка спектром неона. Благодаря этому на деловой фотографии получается система реперных линий. Таким образом, выполнены измерения при энергиях ионов H2+: 175, 180, 210, 225, 260 и 275 кэВ.
Излучение под углом 257° с помощью системы из цилиндрической и сферической линз фокусировалось на щель спектрографа. Излучение под углом 77° с помощью такой же системы линз фокусировалось в торец гибкого световода. Второй конец световода соединялся с боковой гранью установленного непосредственно перед щелью спектрографа кубика Люммера, в котором совмещались световые потоки. В полученных фотографиях наблюдается несмещённая Hα линия водорода с λ0=656.28 нм и две смещённые за счёт эффекта Доплера линии, которые несколько расширены по сравнению с несмещённой.
Линии, соответствующие углу наблюдения 77°, менее интенсивны, так как использование гибкого световода связано с дополнительными потерями света. Время экспозиции при энергиях ионов 2000, 1750 и 1500 кэВ составляло ~48 и 6–8 ч в остальных случаях.
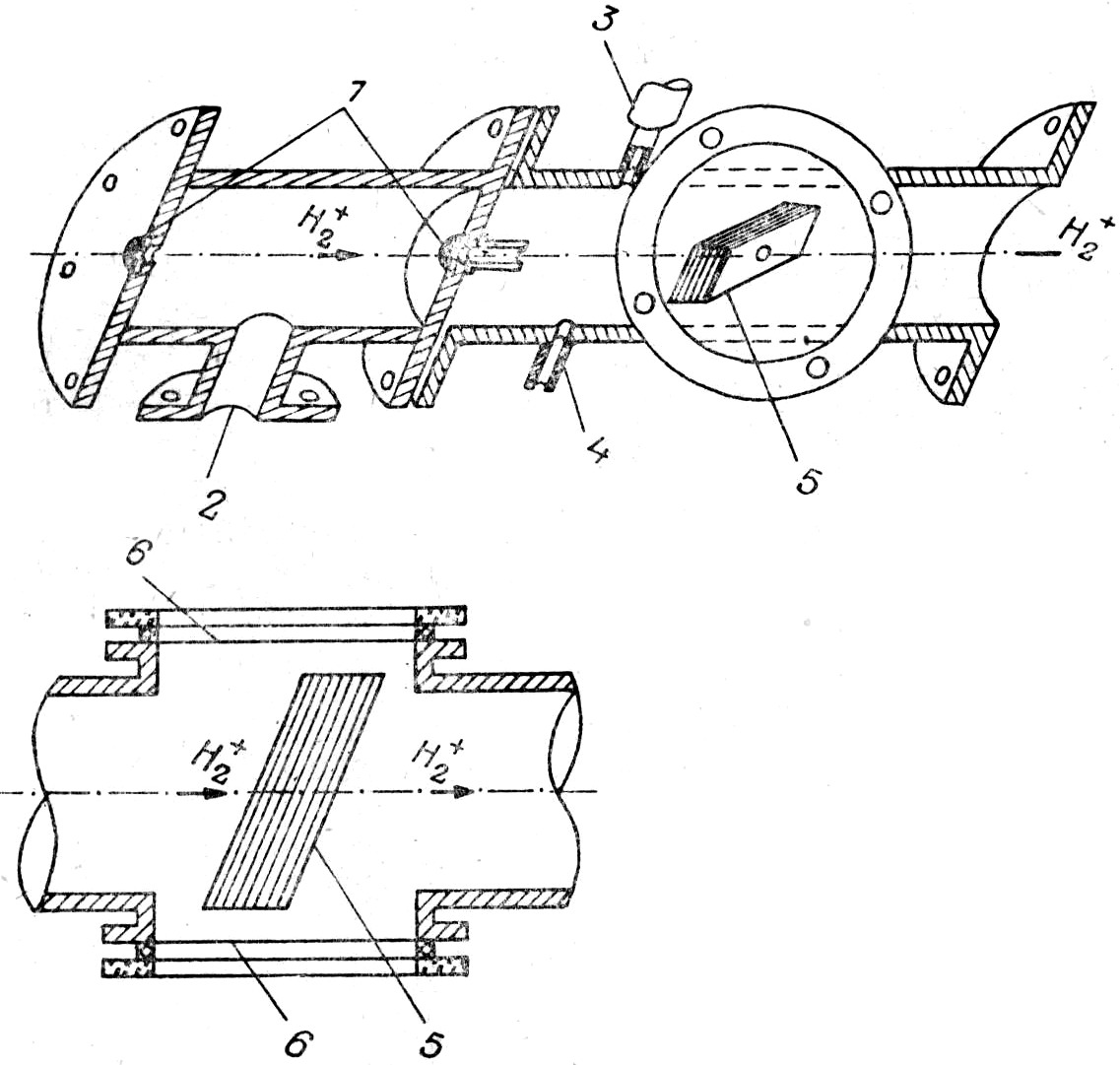
Рис. 3. Схема установки.
1 – коллиматор пучка ионов, 2 – выход к насосу, 3 – термопарная лампа,
4 – напуск водорода, 5 – коллиматор светового потока, 6 – смотровые окна.
На рис. 5 представлен обработанный на микрофотометре спектр, относящийся к энергии ионов H2+ 175 кэВ.
При обработке полученных фотографий высота щели микрофотометра устанавливалась меньше высоты полученных линий. Для каждой фотографии производилось 10 фотометрирований в разных по высоте участках спектра. Определялось в каждом случае положение центра тяжести линий. Затем результаты усреднялись и определялись погрешности (среднеквадратичные). Расстояния между линиями также измерялись под микроскопом, а часть фотографий независимым образом была обработана на компараторе. Результаты оказались близкими друг к другу. В конечном виде результаты представлены в таблице.
В течение всех измерений установка несколько раз разбиралась, при каждой энергии пучка заново осуществлялась его проводка в рабочую область. Показателем неизменности условий проведения измерений может служить значение cosΘ, рассчитанное по формуле (3). Отклонения значений cosΘ лежат в пределах ~10–2, величины, определяемой размерами диафрагм, коллимирующих пучок ионов. Определённый геометрическим путём cosΘ=0.21. Близкое совпадение определённых разными путями cosΘ может служить доказательством того, что ионы H2+ имели действительно ту скорость, которая получается расчётным путём по формуле V=(2E/m)1/2, значения β0 для которой приведены в таблице.
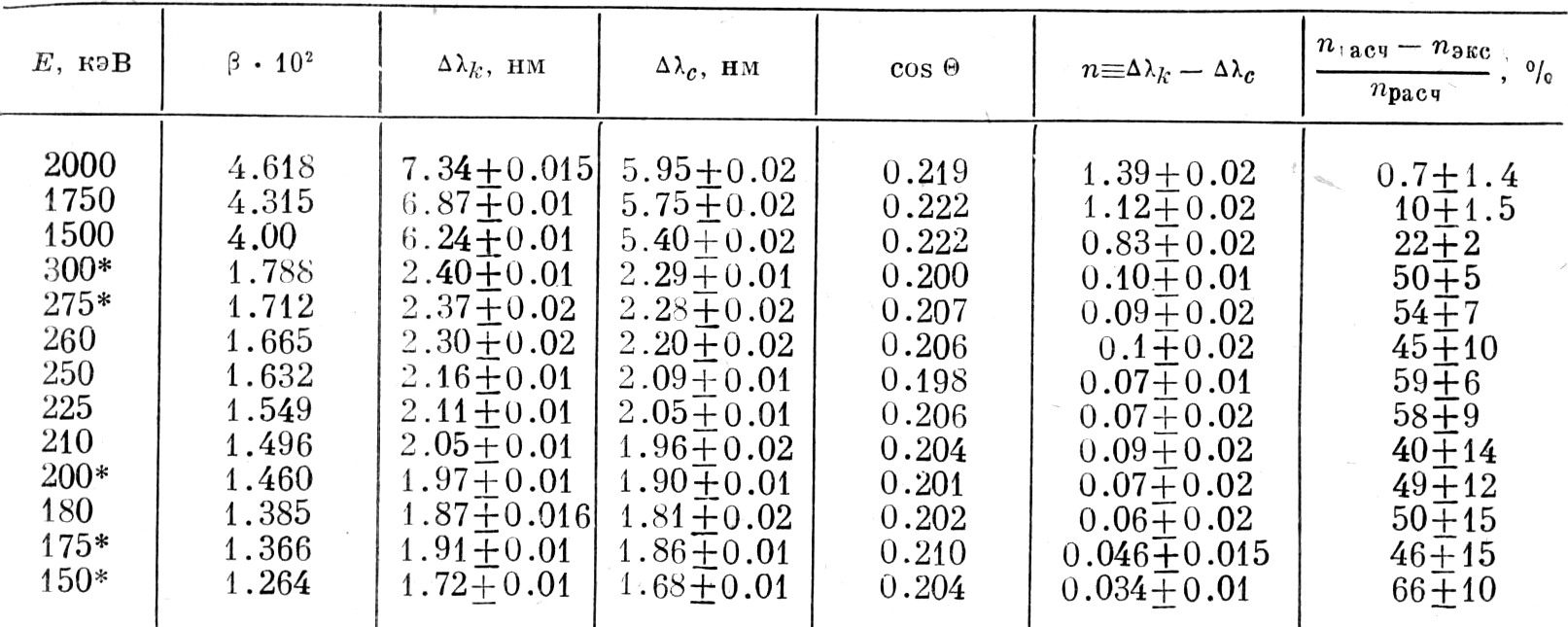
Обращает на себя внимание систематическое отклонение экспериментально измеренной величины nэкс≡Δλк–Δλс от её расчётно-теоретического значения nрасч≡λ0β02. Эти отклонения представлены в таблице величиной nрасч–nэкс/nрасч. На рис. 6 представлены nэкс и nрасч.
В связи с вышеуказанным целесообразно рассмотреть эффекты, которые могли бы привести к подобным отклонениям.
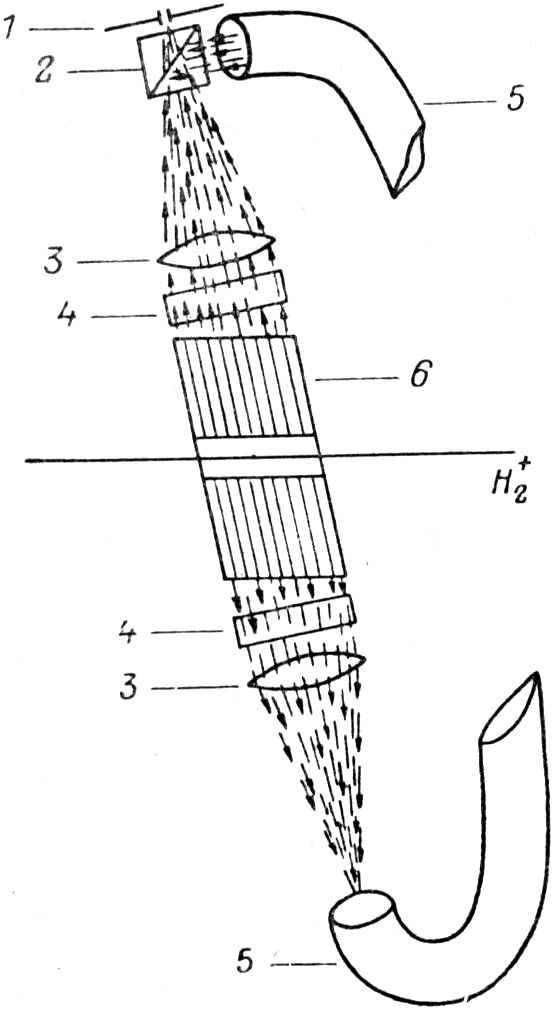
Рис. 4. Оптическая схема эксперимента.
1 – щель спектрографа, 2 – кубик Люммера, 3 – сферические линзы,
4 – цилиндрические линзы, 5 – гибкий световод, 6 – щелевой коллиматор света.
1. Асимметрия в углах наблюдения, т. е. Θназад≠Θвперёд+180°, тогда Δλс=λ0(β0cosΘ–β02/2) и Δλк=λ0[β0cos(Θ+ΔΘ)+β02/2]. Это влечёт за собой появление ложной асимметрии в длинах волн (Δλк–Δλс)ложн=–2λ0β0×sin(Θ+ΔΘ/2)×sinΔΘ/2.
Если перевернуть коллиматор на 180° таким образом, чтобы то его плечо, которое выделяло направление “назад”, стало бы выделять направление “вперёд”, то ложная асимметрия изменит знак. При этом наблюдаемый эффект станет больше теоретического. В таблице звёздочка соответствует измерениям с перевёрнутым коллиматором, когда превышение измеряемого эффекта над теоретическим не наблюдается.
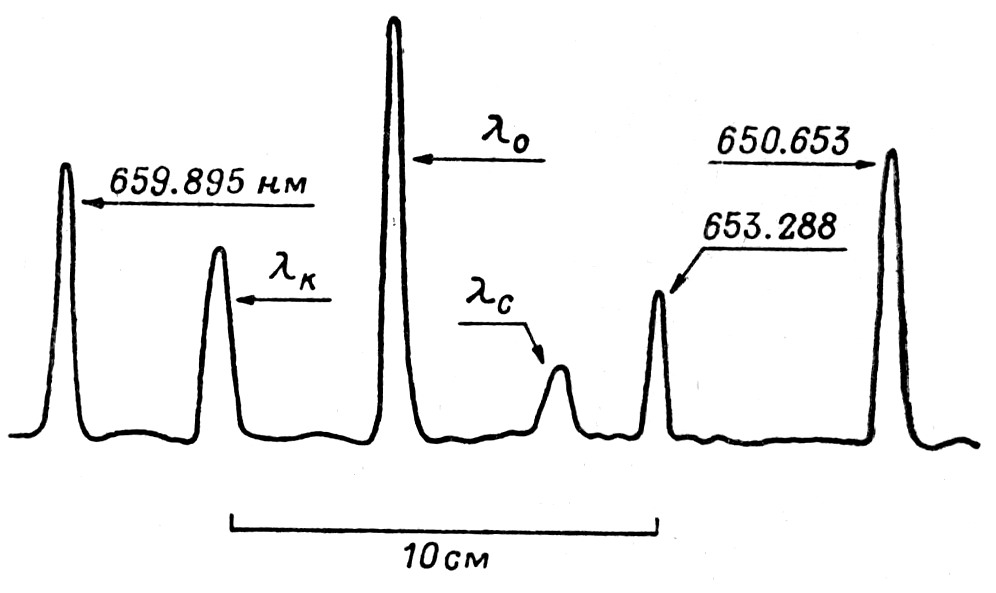
Рис. 5. Микрофотограмма полученного спектра при энергии пучка ионов H2+ 175 кэВ (увеличение 50).
2. Сдвиг величины λ0 может произойти, если та молекула водорода, которую мы считали неподвижной и с которой связывали излучение с длиной волны λ0 в акте рассеяния приобретает некоторую скорость. Среднее значение этой скорости можно определить из условия, что импульс пучка передаётся среде водорода на длине свободного пробега. Так, например, при EH2+=200 кэВ и токе ионного пучка 100 мкА мы получим Vcp=3·104 см/с (длина пробега в водороде принята 3·10–5 см). Эта величина меньше скорости теплового движения при комнатной температуре ~2·105 см/с. В фотографиях, полученных на спектрографе с дисперсией 2.4 нм/мм, калибровочная шкала строится по линиям спектра неона, имеющимся на фотографиях, что даёт возможность определять длину волны λ0. Так, для микрофотографии на рис. 5 λ0=656.279 нм, среднее значение по всем фотографиям λ0=656.2792±0.003 нм, табличное значение λ0=656.28 нм.
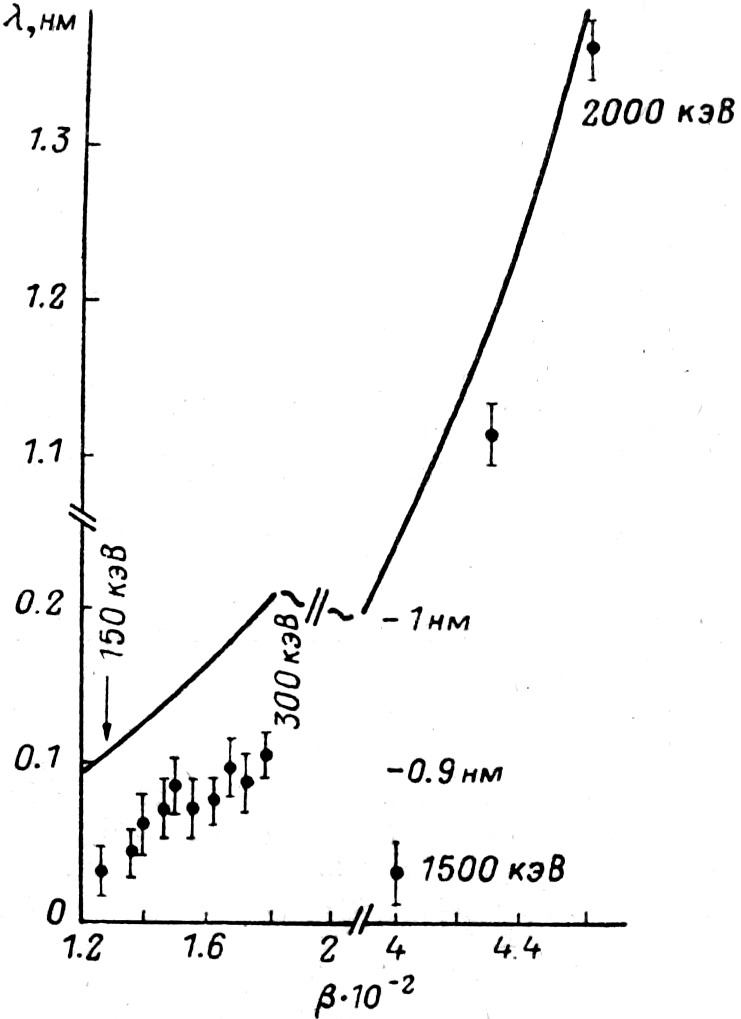
Рис. 6. Экспериментальные результаты в сравнении с их расчётными значениями λ0β02.
Таким образом, ни в рамках предположения о несимметрии углов наблюдения, ни перераспределением скоростей в акте взаимодействия наблюдаемые отклонения экспериментальных величин от расчётно-теоретических объяснены быть не могут. Авторам не удалось найти разумного объяснения полученной ими аномалии. Не исключено, что механизм образования атома водорода в возбужденном состоянии не такой, как принимается нами и в работах [1–3]. В этом направлении была бы желательной постановка независимых экспериментов другой группой исследователей.
Авторы считают своим приятным долгом поблагодарить Ю. И. Островского за участие в постановке измерений, В. И. Вавилкина за участие в измерениях, А. И. Таразевича за изготовление установки. Мы так же признательны М. В. Блинову, Ю. А. Немилову и С. С. Коваленко за поддержку, без которой выполнение данной работы было бы невозможным.
[1] Ives U. Е., Stilwell G. R. // J. Opt. Soc. Amer. 1938. Vol. 28. N 7. P. 215–224.
[2] Ives U. E., Stilwell G. R. // J. Opt. Soc. Amer. 1941. Vol. 31. N 5. P. 369–374.
[3] Mandelberg U. I., Witten L. // J. Opt. Soc. Amer. 1962. Vol. 52. N 5. P. 529–536.
[4] Nucl. Data Tables. Sect. A. 1970. Vol. 7. N 3–4. 233 p.
[5] Победоносцев Л. А., Крамаровский Я. М., Селезнёв Б. К. и др. Препринт Радиевого института им. В. Г. Хлопина. № РИ-199. Л., 1986. 18 с.
Поступило в Редакцию
11 февраля 1988 г.
Дата установки: 10.07.2012
[