[вернуться к содержанию сайта]
Принцип относительности Л о р е н т ц а-Э й н ш т е й н а занял почётное положение в современной физике; ввиду этого, без сомнения, покажется весьма странным утверждение, что этот принцип представляет собою не что иное, как косвенное и замаскированное признание зависимости скорости светового луча от скорости источника света. Между тем, с этой точки зрения, легко объясняются не только факты, лёгшие в основу теории Лорентца-Эйнштейна, что доказывал В. Ритц в 1908 г., и что в настоящее время признают многие европейские и американские учёные; но с этой точки зрения находит себе поразительно простое объяснение и сам принцип относительности: уравнения преобразования Лорентца и, столь импонирующие своей парадоксальностью, выводы новой механики. Теория Ритца, который в сущности возвращается к теории света Ньютона, приспособляя последнюю к современным взглядам на электромагнитную природу света, эта модернизированная теория истечения наталкивается в своём развитии ещё на очень большие трудности 1). Не имея возможности разобрать в настоящей статье этот важный вопрос по существу, мы только попытаемся доказать, что все трудности, выпадающие на долю теории Ритца, должна делить с нею теория Эйнштейна; всё, что противоречит одной из этих двух теорий, противоречит также и другой; всё, что служит подтверждением для одной теории, подтверждает и другую. Иными словами, мы предполагаем доказательство того положения, что между теорией Лорентца-Эйнштейна с одной стороны и теорией Ньютона-Ритца с другой – нет, и не может быть принципиально произведён "experimentum crusis".
В классической механике, неразрывно связанной с именем Ньютона, отрезок длины имеет определённое значение, независимо от того, находится ли он в покое или движении по отношению к наблюдателю; точно так же два события в системе S одновременны или неодновременны, независимо от движения системы. В новой же механике – это считается правильным только приблизительно и только для скоростей очень малых сравнительно со скоростью света. Отсюда вывод: классическая механика представляет из себя частный случай новой механики; она даёт приблизительную картину явлений, совершающихся при малых скоростях. Величина v2/c2, которая входит почти во все формулы принципа относительности, становится ничтожно малой при малых v, вследствие чего формулы принципа относительности превращаются в формулы классической механики. Но это только одно из двух возможных толкований. Уравнения преобразования Лорентца превращаются в уравнения классическое механики не только тогда, когда v очень мало, но и тогда, когда c бесконечно велико. С этой последней точки зрения, классическая механика изображает явления не в том виде, в каком мы их можем наблюдать, но в том виде, в каком они наблюдались бы, если бы скорость света была бесконечно велика. В основных формулах принципа относительности, полученных чисто математически, дедуктивным путём, величина c означает скорость передачи сигнала вообще; полагая эту величину равной бесконечности, тем самым мы превращаем формулы принципа относительности в уравнения классической механики. Следовательно, классическая механика даёт нам картину явлений в том виде, как они могли бы наблюдаться, если бы передача каких-либо сигналов была мгновенной. Иными словами, классическая механика представляет явления такими, как они происходят для некоторого воображаемого наблюдателя, могущего улавливать мгновенную передачу сигналов, например, взаимные возмущения тяготеющих масс.
Которое из двух толкований надо считать правильным? Даёт ли классическая механика приближённое изображение событий, применимое только для малых скоростей движущихся тел, или она даёт совершенно точное изображение событий для каких угодно скоростей, но представляет события в том виде, в каком они должны были наблюдаться, если бы передача сигналов была мгновенной? Без всякого сомнения, никто из творцов классической механики не согласился бы с первым толкованием, наоборот, второе толкование всегда было, если не высказываемой, то само собою подразумевающейся, быть может, подсознательной предпосылкой. Классическая механика всегда представляла явления в том виде, в каком они действительно происходят. Но очевидно, что наблюдать явления в совершенно точном и неискажённом виде можно только в том случае, когда скорость передачи сигналов идеальна.
Допустимо, что в природе не существует скоростей во много раз превосходящих скорость света; более чем вероятно, что не существует исследователя, могущего наблюдать скорость сигналов большую, нежели скорость света. Однако ничто не мешает нам вообразить такого исследователя. По самому свойству нашего ума, наблюдения этого идеального исследователя имеют для нас бòльшую ценность, нежели наблюдения других исследователей. Если бы наши собственные наблюдения разошлись с наблюдениями исследователя, улавливающего мгновенную передачу сигналов, мы не колеблясь, признали бы свои наблюдения неправильными и ввели в них поправки.
Но, как бы ни было, определённый отрезок времени или длины представляет собою некоторую величину и для нашего воображаемого наблюдателя; следовательно, выражение: "величина какого-либо отрезка длины l или времени t для наблюдателя, могущего улавливать бесконечно большую скорость сигнала" – не заключает в себе никакого противоречия как определение.
Теперь, с одной стороны, очевидно, что величина отрезков времени или длины в системе S будет величиной совершенно одинаковой для нашего идеального наблюдателя, независимо от того, находится ли система S в относительном движении, или в относительном покое; масштабы не изменяют своих длин, часы не изменяют своего хода для нашего наблюдателя при изменении скорости движения, так как всякая скорость ничтожна по сравнению с наблюдаемой им бесконечно большой скоростью сигнала. С другой же стороны не может быть сомнения, что картина, наблюдаемая нашим идеальным исследователем, в точности совпадает с представлениями классической механики.
Итак, классическая механика может дать вполне удовлетворительный ответ на вопрос, что подразумевать под величиной отрезка времени или длины в системе S. Величина отрезка времени или длины в системе S будет различна для обычного наблюдателя, и будет находиться в зависимости от относительной скорости системы. Для классической же механики данный отрезок времени или длины при всех условиях будет иметь одно и то же определённое значение, а именно то значение, которое должно было бы наблюдаться, если бы передача световых, или каких-либо иных сигналов сделалась мгновенной. Мы не впадём ни в какое противоречие с духом классической механики, если назовём это последнее значение "абсолютной величиной" данного отрезка времени или длины. Абсолютные величины отрезков, очевидно, легко могут быть вычислены.
В дальнейших рассуждениях мы будем исходить из теории Эйнштейна, и шаг за шагом, сравнивая заключения Эйнштейна с заключениями классической механики, убедимся, что вся теория Эйнштейна построена на косвенном признании зависимости скорости световых лучей от скорости источника света.
–––––––––––––––––––––
С точки зрения принципа относительности пара часов A и B находится в одинаковых фазах, если, при передаче световых сигналов от A к B, часы B в момент получения сигнала показывают как раз середину промежутка времени, необходимого световому лучу для прохождения пути AB туда и обратно. Для классической же механики синхронны те часы одинаковость фаз которых должна была бы обнаружиться с непосредственной очевидностью, если бы передачу сигналов возможно было сделать мгновенной.
Можно доказать, что, если пара часов укреплена в точках A и B движущейся системы S, и если наблюдатели, движущиеся вместе с системой S, поставят часы синхронно по световым сигналам, то такая пара часов будет также синхронна с точки зрения классической механики. Допустим противное: мы имеем пару часов, синхронных с точки зрения классической механики, но для того, чтобы поставить их синхронно по световым сигналам, один из наблюдателей в системе S должен перевести стрелки на своих часах; часы более не будут иметь одинаковый фазы с точки зрения классической механики. Но для классической механики часы не меняют своего хода при перемещении в пространстве, и следовательно, если такую пару часов сблизить на достаточно малое расстояние, на котором время передачи световых сигналов исчезает, то разность фаз часов непременно будет обнаружена; таким образом, наблюдатель в системе S имел бы способ обнаружить неравномерное распространение света, что противоречит принципу относительности.
Теперь предположим, что часы A и B, установленные описанным образом наблюдает исследователь, относительно которого система S движется. Из формулы преобразования Лоренца следует, что часы, синхронные для наблюдателя, движущегося вместе с системой S, для неподвижного наблюдателя обнаружат во-первых определённую разность фаз, и во-вторых – замедленный ход. Следовательно, с точки зрения классической механики, неподвижный наблюдатель совершает ошибку, определяя времена в системе S единицами своей системы; отсюда вывод: времена в движущейся системе надо измерять в единицах этой же системы.
Положим далее, что часы A и B, синхронные с точки зрения классической механики, движутся навстречу друг другу, или же удаляются друг от друга, причём наблюдатель движется вместе с часами A. Очевидно, что наблюдатель рассматривает часы A, как находящиеся в покое, и часы B, как движущиеся: стало быть, он найдёт, что часы B имеют замедленный ход, сравнительно с часами A. Но в момент встречи часы A и B, как синхронные для классической механики, должны оказаться в одинаковых фазах; следовательно, приближающиеся часы наблюдатель должен считать ушедшими вперёд, а удаляющиеся часы отставшими на величину Δt, зависящую от расстояния X между часами, от относительной скорости U и определяемую уравнениями преобразований Лорентца.
Легко доказать также, что с точки зрения классической механики длины в движущейся системе S, нужно измерять в единицах этой системы; измеряя же длины в системе S единицами другой системы, относительно которой система S движется, иными словами, измеряя кинематические длины масштабов в системе S, наблюдатель совершает ошибку. В самом деле, пусть наблюдатели, движущееся вместе с системой S, измеряют длину AB каким-нибудь способом, например, измеряя время, необходимое световому лучу для прохождения длины AB. С точки зрения классической механики, они имеют правильно идущие и находящееся в одинаковых фазах часы в точках A и B, поэтому они могут правильно определить моменты подачи и получения световых сигналов и в определении длины не допустят никакой ошибки. Наблюдатель же, находящийся в другой системе, относительно которой система S движется со скоростью V, измеряя то же расстояние AB, получит величину меньшую в ![]() раз, и, следовательно, ошибочную.
раз, и, следовательно, ошибочную.
Итак, чтобы привести выводы какого-либо наблюдателя в согласие с законами классической механики, надо времена и длины в движущихся системах выражать в единицах этих же систем, употребляя для переоценки формулы преобразования Лорентца.
После этих предварительных замечаний приступим к доказательству положения, что между теориями Ритца и Эйнштейна, невозможно произвести "experimentum crusis".
Обе упомянутые теории распространяют принцип относительности Ньютона на электродинамику; обе теории отвергают мировой эфир и отказываются рассматривать свет как волнообразные возмущения неподвижной среды. В этом обе теории чрезвычайно близки. Но в следующем между ними существует, по-видимому, полная противоположность: Эйнштейн утверждает, что скорость света в пустоте C есть универсальная постоянная, наблюдаемая всегда и при всех условиях. По теории же Ритца, C – это есть скорость удаления поверхности волны от её геометрического центра, а кроме того, световая волна, как целое, обнаруживает движение по касательной к траектории относительного движения источника света. Следовательно, относительная скорость света слагается из этих двух составляющих и поэтому, неравна C для двух тел, движущихся друг относительно друга.
Ввиду этого, сущность опыта, решающего вопрос в пользу той или другой теории, может заключаться только в следующем: нужно измерить скорость световых лучей, испускаемых приближающимся источником света, а также скорость лучей, испускаемых удаляющемся источником, напр., скорость лучей, испускаемых противоположными краями солнечного диска.
Допустим, что "experimentum crusis" произведён, что скорость лучей, вышедших из приближающегося источника света измерена и оказалась равной C; затем измерена скорость лучей, вышедших из удаляющегося источника света, и также оказалась равной C.
Произведём теперь расчёт с точки зрения теории Эйнштейна, а также с точки зрения классической механики.

Рис. 1.
С точки зрения теории Эйнштейна расчёт, по-видимому, очень прост: система S (рис. 1), в которой имеется источник света, движется по направлению от B к A со скоростью V. В момент t', когда источник света находился в точке B, на расстоянии X от A, был дан световой сигнал; сигнал этот достиг точки A спустя время Δt. Скорость света равна C и Δt=X/C.
Но с точки зрения классической механики, весь этот расчёт ошибочен: неверно определён момент подачи светового сигнала, и неверно определена длина пути светового луча; поэтому и величина, полученная для скорости света, должна быть подвергнута переоценке. Переоценка даёт следующее:
1) Время передачи сигнала от источника света до точки A. Величина X представляет собою кинематическую длину отрезка AB; между тем эту длину надо выразить в единицах движущейся системы S. Положим, что длина AB, выраженная в единицах системы S, равна X'.
В таком случае из уравнений преобразования Лорентца вытекает, что часы в системе S ушли вперёд по сравнению с часами, находящимися в точке A, на величину, равную VX'/C2.
Но c точки зрения классической механики – это неверно; иными словами, с точки зрения классической механики момент t' подачи сигнала в системе S наступил позднее, чем следует по расчёту теории Эйнштейна; и время, в течение которого луч прошёл расстояние от S до A, должно быть уменьшено на величину VX'/C2.
Исправленное время передачи сигнала Δt' должно быть равно:
Δ
t'=X'/C–VX'/C2=X'(C–V)/C2……………………(1)2) Путь, пройденный лучом. Так как время t' в системе S наступило позднее, чем следует по расчёту теории Эйнштейна, то в момент, когда система S находились в положении B (рис. 1), часы показывали не t', но время меньшее на величину VX'/C2. В течение этого промежутка времени, двигаясь со скоростью V, система прошла расстояние V2X'/C2. Следовательно, световой сигнал дан не в точке B, но в точке C; и путь, пройденный лучом, также должен быть уменьшен.
AC=X'–V2X'/C2=X'(C2–V2)/C2…………..…………(2)
Чтобы определить действительную скорость луча, надо (2) разделить на (1); при этом очевидно:
C'=AC/Δt'=C+V.
Т.е. относительная скорость света равна скорости удаления поверхности волны от её геометрического центра плюс относительная скорость источника света.
Точно так же, если система S движется в противоположном направлении, и следовательно, удаляется от A, с точки зрения теории Эйнштейна, произойдёт следующее: световой сигнал дан в момент t', когда источник света находился в B (рис. 1); путь луча равен X, время прохождения лучом длины AB равно Δt, скорость света равна С; при этом Δt=X/C.
Переоцениваем все эти величины с точки зрения классической механики. Расстояние AB, выраженное в единицах движущейся системы S, равно X'; из формул преобразования Лорентца следует, что часы в системе S отстали от часов, находящихся в точке A, на величину, равную V2X'/C2. Так как с точки зрения классической механики, это неверно, то момент t' подачи сигнала наступил ранее, чем следует по расчёту теории Эйнштейна, а время передачи сигнала в действительности равно не X/C, но X'/C+VX'/C2=X'(C+V)/C2. Сигнал подан, таким образом не в точке B, но ранее, в точке C, причём AC опять равно X'(C2–V2)/C2. Разделяя длину пути на время, получим для скорости света:
C'=C–V,
т.е. в этом случае величину, меньшую C.
Таким образом, результаты опытов, подтверждающие теорию Эйнштейна, могут быть переоценены с точки зрения классической механики и приведены в согласие с теорией Ритца. Следовательно, и наоборот, результаты опытов, подтверждающие теорию Ритца, нисколько не противоречат теории Эйнштейна и могут быть выражены при помощи формул принципа относительности. Это обстоятельство раскрывает перед нами структуру теории Эйнштейна и смысл, который с точки зрения классической механики, имеют формулы преобразования Лорентца.
Положим, что в точке A (рис. 1) отмечен момент t получения светового сигнала, данного источником света, приближающимся со скоростью V. Спрашивается: на каком расстоянии X от A дан более светлый сигнал, и какому моменту времени t1, на часах, находящихся в точке A, соответствует момент t' подачи светового сигнала? Могут быть сделаны троякого рода допущения:
1) Скорость луча равна C+V. Если это предположите справедливо, то время t1 и расстояние X будут определены согласно с законами классической механики, и принцип относительности получит наиболее простое и законченное выражение: всякая скорость относительна, следовательно, и скорость света.
2) Скорость луча равна C, но в системе, заключающей источник света, время движется иным темпом, понятие о синхронности иное, длины в направлении движения сократились и т. д. В этом случае расстояние X и момент времени t1 будут определены с таким расчётом, чтобы непременно получилась знаменитая "универсальная постоянная" C. В результате получается блестящая и стройная система, представляющая все явления в четырёхмерном пространстве, выводы которой могут быть проведены как угодно далеко, нигде не впадая в противоречие. Но в своей сущности эта грандиозная система построена на том предположении, что скорость света зависит от скорости источника. Если это предположение окажется неверным, тогда "новая механика" непременно встанет в противоречие с фактами и потерпит крушение.
3) Всякое третье предположение противоречит распространению принципа относительности на оптику.
Рассмотрим ещё формулы сложения скоростей Эйнштейна. Можно убедиться, что эти формулы не противоречат правилу параллелограмма скоростей, но сами получены по правилу параллелограмма.
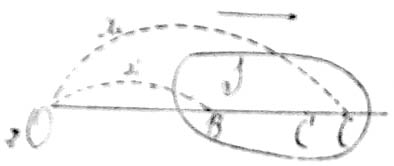
Рис. 2.
В положительном направлении по оси X-ов со скоростью V относительно точки O движется система S; а точка B движется относительно системы S со скоростью U также в положительном направлении от O к C по оси X (рис. 2).
Абсциссы OB и OC точек B и C в момент t'1 равны X'1 и X'2. В момент t'2 точка B догонит точку C. Скорость U точки B относительно C равна (X'2–X'1)/(t'2–t'1), и скорость W точки B относительно O равна U+V. Времена и длины выражены в единицах системы S; часы в точках B и C синхронны; весь расчёт произведён с точки зрения классической механики. С точки зрения теории Эйнштейна этот расчёт надо переоценить следующим образом:
Скорость U преувеличена. В случае S понятие о синхронности иное, нежели в O. Точка B находится позади точки C в направлении движения, и следовательно, часы в B ушли вперёд по сравнению с часами в C на величину V(X'2–X'1)/C2, но несмотря на это считаются в системе S синхронными.
Поэтому момент t'1 взят позднее, чем следует, и промежуток времени t'2–t'1 должен быть увеличен на V(X'2–X'1)/C2.
Когда часы в B показывали момент t'1, часы в C показывали меньшее время и, стало быть, точка C имела меньшую абсциссу, не X'2, но X'2–V2(X'2–X'1)/C2; стало быть, расстояние X'2–X'1 должно быть уменьшено на V2(X'2–X'1)/C2. Исправленная скорость U' точки B относительно C равна:
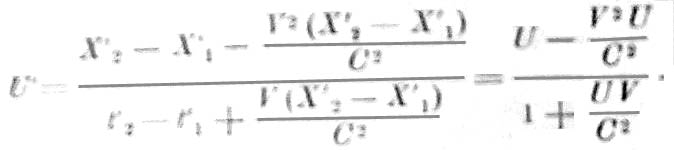
Чтобы найти теперь W' – скорость точки B относительно O, надо сложить скорости V и U' по правилу параллелограмма.
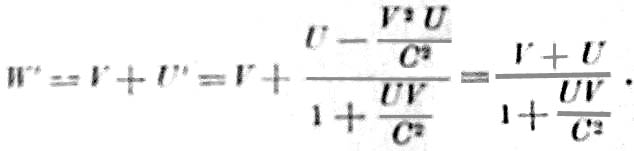
То есть мы получаем формулу Эйнштейна.
Если бы системы S и точки C не существовало и наблюдалась бы только относительная скорость точек B и O, то не впадая в противоречие, с точки зрения Эйнштейна мы опять должны получать скорость W'. Отсюда можно сделать важный вывод. Всякую наблюдённую скорость W' можно разложить по правилу параллелограмма на две составляющие, из которых, по крайней мере, одна будет меньше действительной, с точки зрения классической механики. Но этот вывод можно было представить a priori, так как градации всевозможных скоростей от нуля до бесконечности, допускаемой классической механикой, по теории Эйнштейна соответствуют скорости от нуля до C.
В общих чертах мы разобрали структуру теории Эйнштейна. В настоящее время невозможно, конечно, предсказать, удержится ли в науке эта теория. Если теория Эйнштейна сохранит своё господствующее положение, то теория Ритца всё-таки будет полезна, как вспомогательное представление, при разработке наиболее трудных вопросов о непрямолинейном и неравномерном движении, которые в теории Эйнштейна разработаны ещё очень мало. Как должны меняться времена, длины и проч. в системах, движущихся по криволинейным траекториям, обладающих ускоренным или замедленным движением, при толчках, остановках, при комбинации вращательных и поступательных движений? Этот сложный вопрос можно упростить, представив себе сначала, что должно получиться с точки зрения теории Ритца, а затем уже полученные результаты перевести на язык теории Эйнштейна.
Но, как бы ни было, если соображения, высказанные в настоящей статье справедливы, то теория Эйнштейна заключает в себе хотя и в замаскированном виде, признание зависимости скорости света от скорости источника. Обе теории, следовательно, не конкурируют по отношению к опытным фактам и выбор между ними нужно делать только на основании теоретических соображений.
Имеется Лаборатория и в ней наблюдатель; вне Лаборатории – красный источник свата, неподвижный но отношению к Лаборатории, и зелёный источник света, удаляющийся от Лаборатории с большою скоростью. Мгновенно открывается отверстие в стене Лаборатории, так что через это отверстие проникают одновременно красный и зелёный свет и начинают распространяться по направлению к противоположной стене Лаборатории. Через короткий промежуток времени лучи света достигают глаза наблюдателя, стоящего у этой стены.
Наблюдатель решает вопрос, увидит ля он
а) сперва красный цвет,
б) или с самого начала белый 2).
Я утверждаю:
теория Ритца требует: сперва красный,
теория Эйнштейна требует: сразу белый.
Я спрашиваю г. Орлова:
а) допускает ли он, что теории Ритца и Эйнштейна требуют именно указанные выше два положения или он оспаривает это?
b) если он допускает это, то считает ли он всё-таки правильным своё утверждение (
стр. 172): "… результаты опытов… в согласии с теорией Ритца".Когда открывается отверстие в стене, противоположной от наблюдателя, и оба луча – красный (от неподвижного источника) и зелёный (исходящий из удаляющегося источника) одновременно попадают в лабораторию, то возможны два случая:
1) Наблюдатель увидит сначала красный свет.
2) Наблюдатель с самого начала увидит белый свет.
Разберём второй случай, противоречащий теории Ритца. Можно доказать, что этот случай противоречит также и теории Эйнштейна, и, следовательно, теории относительности вообще. Чтобы сделать это ясным, мы сначала несколько изменим обстановку этого гипотетического опыта и введём в рассуждение то обстоятельство, что каждый луч света вышел из источника в определённый момент.

Рис. 3.
Допустим, что опыт производят два наблюдателя (см. рис. 3): наблюдатель B находится непосредственно позади отверстия и получает оба луча одновременно с открытием отверстия. Наблюдатель A находится около противоположной стены; лучи достигают его спустя малое время. Допустим, что лучи от красного (на рис. E) и от зелёного (на рис. F) источников света попадают в глаз наблюдателя отдельно друг от друга. Наконец предположим, что лучи удаляющегося источника света датированы, т.е. заключают в себе указание на момент выхода их из источника; напр., если зелёный источник света прикрыт прозрачным циферблатом, по которому движется секундная стрелка (возможен какой угодно другой способ вместо часов). Луч, вышедший из удаляющегося источника света в тот момент, когда последний находился в точке F, на расстоянии x от B спустя время X/C достигает B. В этот момент отверстие открывается, и наблюдатель B получает оба луча, которые затем проходят через лабораторию до A, причём длина лаборатории равна Δx.
Если в момент открытия отверстия часы B показывают момент t, то момент, которым отмечен дошедший до B зелёный луч равен t–x/C–vx'/C2, так как x/C – время передачи луча, и
vx'/C2 – время, на которое отстала все процессы в движущейся системе, с точки зрения B. Спустя время Δx/C наблюдатель A получает тот же самый луч! В момент получения наблюдателем A зелёного и красного разность между показанием его часов и тем моментом, которым отмечен зелёный луч достигнет (x+Δx)/C+vx'/C2. Между тем, по теории Эйнштейна эта разность должна равняться (x+Δx)/C+v(x'+Δx')/C2. По теории Эйнштейна наблюдатель в этот момент должен получить более ранний луч, но так как в данном случае этот более ранний луч задержан препятствием, то теория Эйнштейна расстраивается. Наблюдатель A найдёт, что время в системе движущегося источника отстало на величину vx'/C2, а не на величину v(x'+Δx')/C2, как должно быть по теории Эйнштейна! Дело происходит таким образом, как будто в течение времени Δx/C, пока первый луч проходит расстояние от B до A, относительность времени не существовала, и в движущейся системе зелёного источника время двигалось тем же, а не более медленным темпом, нежели в неподвижной системе AB. Так как величину Δx можно предположить как угодно большой, то и отклонения от теории Эйнштейна могут быть как угодно велики.Возвратимся теперь к гипотетическому опыту в той форме, какая приведена проф. Эренфестом.
Посла открытия отверстия наблюдатель с самого начала увидит белый свет, т. е. красный и зелёный лучи достигнут его глаз одновременно. Но мы теперь уже знаем, что это возможно только потому, что по крайней мере, с момента открытия отверстия и до момента получения наблюдателем первого луча относительности времени не существовало.
Этот вывод можно было, также, ожидать a priori, так как, c точки зрения классической механики, разбираемый нами случай не представляется возможными согласовать с теорией относительности.
Итак, приведённый проф. Эренфестом гипотетический опыт в действительности имеет значение "experimentum crusis" между теорий Ритца с одной стороны – и теориями, рассматривающими свет, как возмущение абсолютно неподвижной среды – с другой. Теорию Эйнштейна в данном случае возможно устранить до опыта, так как оба допустимых исхода опыта ей противоречат.
Тезис моей статьи – теория Эйнштейна заключает в себе косвенное признание зависимости скорости света от скорости источника – таким образом, остаётся в силе.
Дата установки: 14.04.2011
[вернуться к содержанию сайта]