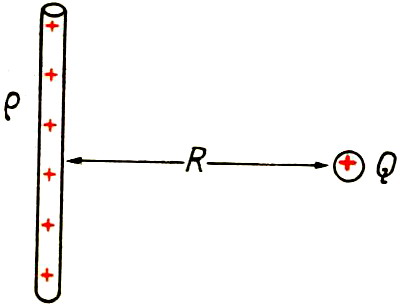
Фиг. 185. Точечный заряд Q на расстоянии R от заряженного проводника с плотностью заряда ρ CGSE(Q)/см.
[
вернуться к содержанию сайта]Теорию относительности Эйнштейна можно получить, распространив принцип относительности Галилея на уравнения теории электричества – уравнения Максвелла. Галилей предположил, что принцип общей симметрии заключается в следующем: законы физики должны быть одинаковыми с точки зрения любого наблюдателя, движущегося с постоянной скоростью, независимо от величины и направления этой скорости. Другими словами, не должно существовать привилегированной системы отсчёта, или, что то же самое, способов определения абсолютной скорости. Этот принцип общей симметрии и называется принципом относительности.

Фиг. 185. Точечный заряд Q на расстоянии R от заряженного проводника с плотностью заряда ρ CGSE(Q)/см.
Однако пока мы не внесём некоторые существенные изменения, законы электричества, несомненно, будут противоречить принципу относительности. “Покоящийся” и движущийся наблюдатели будут получать два разных результата из одного и того же эксперимента. Для иллюстрации рассмотрим простой пример: точечный заряд Q расположен на расстоянии R от проводника, заряженного одноимённым зарядом с плотностью ρ CGSE(Q)/см. На заряд Q действует электростатическая сила F=QE, где E=2ρ/R [см. формулу (7.10)]. Таким образом, сточки зрения покоящегося наблюдателя
F=2Qρ/R. (11.1)
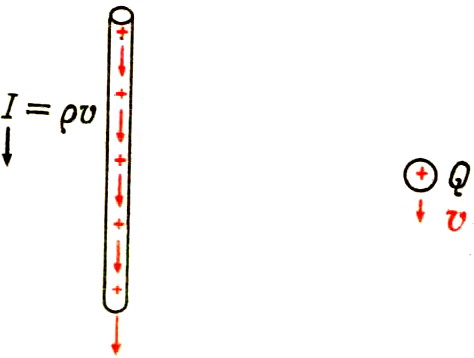
Фиг. 186. Та же картина с точки зрения наблюдателя, движущегося вверх со скоростью v.
Теперь представим себе второго наблюдателя, движущегося параллельно проводнику со скоростью v. Этот наблюдатель обнаружит, что на заряд Q, кроме электростатической силы, действует также магнитная сила. С точки зрения движущегося наблюдателя вдоль проводника течёт электрический ток I=ρv, а заряд Q также движется параллельно проводнику со скоростью v. Из формулы (8.10) можно найти действующую на заряд Q магнитную силу FB= QBv/с, причём напряжённость магнитного поля В, создаваемого прямолинейным током, равна B=2ρv/сR. Таким образом,
FB=(Qv/с)(2ρv/сR)=(2Qρ/R)(v2/с2)
есть магнитная сила, действующая на заряд. Эта магнитная сила притяжения должна складываться с электростатической силой отталкивания. Наблюдатель, движущийся со скоростью v, обнаружит, что результирующая сила, действующая на заряд Q, должна быть равна
F=2Qρ/R–(2Qρ/R)(v2/с2),
или
F=(2Qρ/R)(1–v2/с2). (11.2)
Количественно этот результат меньше результата, полученного покоящимся наблюдателем [см. (11.1)], в 1/[1–(v2/с2)] раз. Итак, из рассмотренного примера ясно, что законы электричества приводят к различным результатам в разных системах отсчёта. Но, согласно принципу относительности Галилея, сила, действующая на заряд Q и его ускорение, не должна зависеть от скорости наблюдателя.
Ясно, что принцип относительности Галилея, справедливый в рамках классической механики, несовместим с уравнениями Максвелла. Чтобы устранить это противоречие, надо пересмотреть либо принцип относительности, либо уравнения Максвелла, либо классическую механику. Рассмотрим три возможных способа устранения противоречия:
1. Принцип относительности пригоден для механики и непригоден для электродинамики. Законы электричества справедливы только для одной привилегированной системы отсчёта. Только в этой системе свет распространяется со скоростью v=c.
2. Принцип относительности выполняется как в механике, так и в электродинамике, но законы электричества сформулированы в гл. 7 и 8 непоследовательно. Эти законы можно последовательно видоизменить с тем, чтобы получить требуемый результат, согласно которому свет всегда распространяется с постоянной скоростью c относительно источника. Это видоизменение уравнений Максвелла называется теорией излучения.
3. Принцип относительности справедлив и в механике и в электродинамике, а видоизменить следует законы и принципы механики. Именно эту возможность и выбрал Эйнштейн. Он видоизменил определения массы, энергии, импульса и свойства пространства и времени. Благодаря этому законы механики наряду с законами электричества стали удовлетворять принципу относительности.
Возможен ещё один вариант объяснения результатов Майкельсона и Морли (второй способ, стр. 269). Надо переформулировать законы электричества, с тем чтобы свет всегда испускался со скоростью с относительно источника. Однако такое объяснение также было отвергнуто на основании астрономических наблюдений. Если бы эта теория излучения была справедлива, то движение двойных звёзд казалось бы нам возмущённым и противоречащим законам Кеплера. Это происходило бы потому, что при движении одной из звёзд в направлении Земли со скоростью v её свет проходил бы весь путь со скоростью (относительно Земли) c+v и попадал бы на Землю раньше, чем свет, испускаемый звездой, движущейся от Земли. Скорость последнего составляла бы с–v, и он попадал бы на Землю позднее.
Мы видим, что всякие попытки объяснить нулевой результат Майкельсона и Морли отвергались дополнительными экспериментами и наблюдениями.
И, наконец, оставлялся возможность (третий способ, стр. 270) была серьёзно исследована Альбертом Эйнштейном в 1905 г. Эйнштейн исследовал вопрос о том, какие изменения надо произвести в классической механике, чтобы совместить уравнения Максвелла с принципом относительности. К счастью, эта задача математически оказалась вполне определённой, имеющей единственное решение. Но для многих физическая интерпретация математических результатов оказалась затруднительной, поскольку казалось, что эти результаты противоречат здравому смыслу.
Один из основных математических результатов теории Эйнштейна гласит: скорость света всегда равна c=3·1010 см/сек независимо от скорости наблюдателя или источника. Таким образом, два наблюдателя, один из которых покоится по отношению к удалённой звезде, а другой очень быстро движется к ней, измеряют одно и то же значение скорости света, идущего от звезды. Этот результат, конечно, мог бы согласоваться с измерениями Майкельсона и Морли, но он кажется противоречащим здравому смыслу. Для получения этого результата пришлось пересмотреть существующие представления о пространстве и времени.
Дата установки: 10.02.2011
[