[вернуться к содержанию сайта]

    γ-Кванты при прохождении через среду испытывают три основных вида взаимодействия (все они электромагнитные): фотоэффект, эффект Комптона и процесс образования электрон-позитронных пар.

    Фотоэффект является главным механизмом поглощения мягких γ-квантов в тяжёлых веществах. В процессе фотоэффекта вся энергия γ-кванта E_γ передаётся одному из электронов атома. При этом небольшая её часть (равная энергии связи электрона в атоме ε_e) идёт на отрыв электрона, а остальная преобразуется в его кинетическую энергию Т_e (и пренебрежимо малую кинетическую энергию атома отдачи Т_ат<<Т_e):

Е_γ =ε_e+Т_e.                        (1)

    Измеряя энергию вылетевшего из атома фотоэлектрона, можно оценить энергию γ-кванта. Фотоэффект на свободном электроне невозможен.

    Эффектом Комптона называется процесс рассеяния γ-кванта на свободном электроне. В процессе рассеяния γ-квант изменяет направление своего движения и теряет часть энергии. Избыток его энергии передаётся комптоновскому электрону. Изучение комптоновских электронов также позволяет определять энергию γ-квантов.

    Если энергия γ-квантов превосходит 2m_eс² ~ 1 Мэв, то в окрестности ядра за счёт энергии γ-кванта становится возможным процесс образования электрон-позитронных пар. Этот процесс невозможен в вакууме.

    При взаимодействии γ-квантов с ядрами последние могут переходить в возбуждённое состояние (§ 4). γ-Кванты с энергией, превышающей несколько мэгаэлектронвольт, могут вырывать из ядра протоны, нейтроны, α-частицы, т. е. вызывать ядерные реакции (подробнее см. § 6).

    Из школьного курса физики вы знаете, что атомное ядро было открыто Резерфордом в 1911 г. в опытах по изучению рассеяния α-частиц на тонких фольгах. Чтобы объяснить отклонение небольшого количества α-частиц на большие углы (вплоть до 180°), Резерфорд предположил, что в центре каждого атома расположено тяжёлое (до 99,98% массы всего атома) положительно заряженное ядро очень малых размеров (~10^–13—10^–12 см). Вокруг ядра на относительно очень больших расстояниях (~10^–18 см) вращаются Z электронов (Z — порядковый номер элемента в периодической таблице Менделеева). Эта модель атома была названа ядерной или планетарной, так как в соответствии с этой моделью строение атома напоминает миниатюрную солнечную систему, в которой роль Солнца выполняет ядро, роль планет — электроны, а роль гравитационного притяжения — кулоновское взаимодействие между разноимённо заряженными ядром и электронами.

    Планетарная модель на первых порах очень понравилась физикам, однако вскоре с ней возникли серьёзные затруднения, так как она не удовлетворяла условию устойчивости.

    В § 12 мы говорили о том, что заряженная частица, движущаяся с ускорением, обязательно должна тратить свою энергию на излучение. Электрон, вращающийся вокруг атомного ядра, имеет центростремительное ускорение, значит, из-за излучения его энергия должна постепенно уменьшаться. Уменьшение энергии будет приводить к уменьшению скорости вращения, т. е. к уменьшению центробежной силы, которая перестанет уравновешивать силу кулоновского притяжения. В результате электрон начнёт по спирали приближаться к ядру и в конце концов упадёт на него. Выходит, что если поверить планетарной модели, то атом надо сравнивать не с Солнцем и планетами, а скорее с Землёй, вокруг которой в пределах атмосферы вращаются искусственные спутники. Из-за сопротивления воздуха спутники постепенно снижают свою скорость и приближаются к Земле по спирали. Таким образом, по планетарной модели получается, что все атомы должны быть неустойчивы. А это, как вы прекрасно знаете, противоречит эксперименту.

    Второе, очень важное возражение против планетарной модели заключается в том, что она допускает испускание атомами лучей света с любой длиной волны, в то время как из опыта следует, что конкретные атомы испускают излучение только строго определённых длин волн.

    Положение казалось совершенно безвыходным. С одной стороны — модель, которая построена на основе твёрдо установленных и неоднократно проверенных законов механики и электродинамики. С другой стороны — эксперимент, в котором нельзя сомневаться. И они противоречат друг другу, да так радикально, что примирить их невозможно!

    Выход был найден в 1913 г. Н. Бором, который не пытался примирить противников, а поверил опыту и видоизменил планетарную модель так, чтобы она согласовалась с ним. Для этого Бору пришлось допустить то, что до него казалось совершенно недопустимым, а именно существование в атоме стационарных орбит электронов с определёнными радиусами. Радиус орбиты r находится из условия

m_evr = nћ,                            (53)

где т_e— масса электрона; v — скорость; п — целое число (1, 2, 3, ...), которое было названо главным квантовым числом; ћ — постоянная Планка, равная ћ=l,05·10^–27 эрг·сек=6,6·10^–16 эв·сек. Величина m_evr называется моментом количества движения электрона; условие (53) означает предположение о квантовании момента количества движения электрона в атоме. Таким образом, согласно Бору, электрон в атоме может иметь только строго определённые состояния вращения (определённую скорость на орбите с данным радиусом).

    По мысли Бора, электрон, находящийся на одной из стационарных орбит, не излучает и не поглощает энергии. Испускание или поглощение энергии атомом происходит только при переходе электрона с одной орбиты на другую и притом вполне определёнными порциями — квантами:

ΔE=hν,                            (54)

где h=2πћ=6,6·10^-27 эрг·сек=4,1·10^-15 эв·сек.

    Теория Нильса Бора получила название квантовой теории атома.

    С точки зрения классической физики предположения Бора (они называются постулатами) равносильны тому, что искусственный спутник Земли при движении в атмосфере не будет тормозиться и что спутник можно запустить не на любую орбиту, а только на орбиты с вполне определёнными радиусами, например равными 100, 200, 300 км и т. д., но не 101, не 102 км и т. п.

    Вы вряд ли бывали на космодроме в Байконуре и, вероятнее всего, пока ещё не участвовали в запуске искусственных спутников Земли, но из газет, журналов, из всего накопленного опыта развития нашей космонавтики вы прекрасно знаете, что мысли, высказанные в предыдущем абзаце, являются бредовыми. Такого не может быть!

    Вот так же до Бора никто не сомневался в том, что такого не должно быть и для электронов в атоме. И только Бор оказался настолько смел и прозорлив, что не побоялся выдвинуть столь необычную, столь “сумасшедшую” (как он сам впоследствии стал называть очень радикальные взгляды) теорию.

    Опираясь на свои постулаты, Бор вычислил радиусы возможных орбит, энергии, которыми на них обладают электроны, и длины волн света, испускаемого или поглощаемого атомом при переходе электрона с одной орбиты на другую. Совпадение расчётных длин волн с экспериментальными оказалось удивительно хорошим (с точностью до 0,001%). На основании расчётов, сделанных по теории Бора, были предсказаны и обнаружены на опыте новые спектральные серии.

    В дальнейшем теория Бора была усовершенствована другими физиками. Круговые орбиты были заменены эллиптическими, движение электронов по ним стали рассчитывать не по классической, а по релятивистской механике и др. Всё это позволило ещё лучше понять наблюдающиеся закономерности в оптических спектрах, в частности объяснить поведение излучающего атома в магнитном поле, природу тонкого, а впоследствии и сверхтонкого расщепления спектральных линий.

    Однако вместе с успехами теории накапливались и возражения против неё. Дело в том, что для получения каждого нового успеха в теорию приходилось вводить всё новые и новые квантовые числа. Вслед за главным квантовым числом п в теорию были введены орбитальное квантовое число l, а затем магнитное (т) и спиновое (s) квантовые числа. Правда, каждое из них вводилось вполне логично — как мера квантования момента количества движения или его проекции. Но каждый раз эти квантовые числа и диапазон возможных значений для них приходилось постулировать.

    Сначала были постулированы возможные значения для квантовых чисел, затем их пришлось ограничить специальными запретами (правила отбора). Потом для объяснения периодической системы Менделеева пришлось постулировать так называемый принцип Паули, который запрещает двум электронам находиться в одном и том же состоянии (иметь одинаковыми все квантовые числа).

    В конце концов в теории накопилось слишком много ниоткуда не следующих постулатов.

    Не обходилось дело и без серьёзных противоречий. Так, например, последнее спиновое квантовое число s в усовершенствованной теории Бора интерпретируется как собственный момент количества движения электрона — спин. Электрон в некотором смысле должен быть уподоблен заряженному вращающемуся волчку (с той существенной разницей, что он может иметь не любое количество состояний вращения, как обычный волчок, а только два).

    Но вращающийся электрический заряд должен обладать магнитными свойствами, которые можно, с одной стороны, рассчитать, а с другой — обнаружить на опыте. Так вот, при сравнении расчёта с экспериментом было обнаружено расхождение: экспериментальное значение магнитного момента электрона оказалось вдвое больше расчётного.

    Итак, несмотря на всю революционность взглядов Бора, в его теории осталась некая непоследовательность, приводящая к затруднениям и расхождениям с экспериментом. Эта непоследовательность объясняется тем, что, выдвинув новое положение о квантовании момента количества движения, Бор развивал его, пользуясь методами обычной механики, автоматически перенеся их на мир микрочастиц. В частности, в теории Бора подразумевалось, что движение электронов в атоме происходит по определённым траекториям подобно тому, как это имеет место в обычной (классической и релятивистской) механике (см. § 14). А между тем опыт доказывает, что для микрочастицы понятие траектории теряет смысл.

    Не менее замечательный успех выпал и на долю другого квантовомеханического уравнения — релятивистского уравнения Дирака. В частности, при помощи этого уравнения удалось разрешить упомянутые в конце § 15 затруднения с введением в квантовую теорию понятия спина и с величиной магнитного момента электрона. Оказалось, что в теории Дирака нет необходимости постулировать спин и магнитный момент электрона, так как их существование является следствием самого уравнения. При этом уравнение предсказывает именно то значение магнитного момента, которое получается из опыта (напомним, что теория Бора давала вдвое меньшее значение).

    Но особенно великолепным достижением Дирака следует считать предсказание позитрона — античастицы по отношению к электрону.

    Анализируя своё уравнение, Дирак пришёл к выводу, что для каждого значения импульса р оно имеет два решения, соответствующие двум разным значениям полной энергии электрона:

E₁ = +(т_e²с⁴ + р²с²)^1/2 и E₂ = –(т_e²с⁴ + р²с²)^1/2                (61)

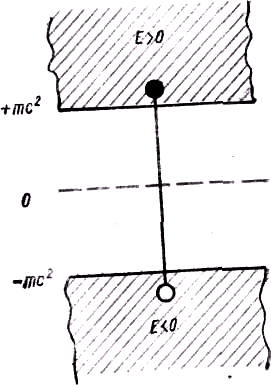
(см. формулу (21) из § 9). Например, при р=0 электрон может иметь энергию E₁ = т_eс² и E₂ = –т_eс², так что E₁–E₂=2т_eс². При p=p₀>0 разность энергий E₁–E₂>2т_eс². Возможные значения энергии электрона можно изобразить схематически в виде двух заштрихованных областей, находящихся на расстоянии 2т_eс² друг от друга (рис. 19). Из анализа следовало, что оба решения совершенно равноправны, т. е. электрон может находиться не только в верхней области рисунка, где E > 0, но и в нижней, где Е<0; он также может переходить из одной области в другую.

Рис. 19

    Конечно, Дирак прекрасно понимал, что результат, который у него получился, выглядит по меньшей мере странно. Ведь частица с отрицательной полной энергией — это частица с отрицательной массой (вы помните, что т=E/с²?). А согласно классической механике (второй закон Ньютона), частица с отрицательной массой должна двигаться против действующей на неё силы (так как векторы ускорения и силы будут иметь разные знаки, т. е. будут направлены в противоположные стороны).

    Представляете, какая бы у нас с вами была интересная жизнь, если бы это предсказание было верным? Вертолёты, самолёты и космические корабли взлетали бы вверх сами собой с ускорением g. Ходить по Земле было бы так же трудно, как сейчас по потолку. Атмосфера и все незакреплённые предметы (например, вода в океанах, озёрах и реках) улетели бы в космическое пространство; да и сама Земля полетела бы прочь от Солнца, как футбольный мяч после сильного удара, и летела бы до тех пор, пока притяжение другой звезды не оттолкнуло бы её в другую сторону...

    Но подарим эту тему для детальной разработки нашим фантастам (кажется, она ещё не была ими использована) и вернёмся к электрону.

    Дирак понимал все эти трудности и поднял руку на своё уравнение, чтобы изгнать из него решение с отрицательной энергией и массой (рис. 20). Вероятно, у него в это время было примерно такое же настроение, как у Тараса Бульбы, когда он встретил своего сына-предателя.— Я тебя породил, я тебя и убью! — Но расправиться с уравнением оказалось не так-то просто, потому что оно было правильное и приводило к правильным следствиям, проверенным на опыте (вспомните спин и магнитный момент электрона). Вывод же относительно существования частиц с отрицательной энергией и массой был тоже одним из следствий этого правильного уравнения. И всё-таки выход был найден!

    Дираку пришлось примириться с существованием отрицательных решений, однако эти решения удалось иначе интерпретировать.

    Давайте вместе с Дираком предположим, что состояния с отрицательной энергией и массой действительно существуют, но поскольку им соответствуют минимальные значения энергии, то они полностью заполнены электронами, так что образуется сплошной ненаблюдаемый фон необычных (с m<<0) электронов. Предположим далее, что мы сообщили (например, с помощью γ-кванта) одному из необычных электронов энергию E>2т_eс², достаточную для перемещения электрона из области E <0 в область E>0 (см. рис. 19). Такая операция разрешается уравнением. Тогда в верхней области появится ещё один обыкновенный (E > 0, m >0) электрон, а из нижней исчезнет один необычный (E <0, m<0) электрон, т. е. там возникнет “дырка” в сплошном фоне. Легко сообразить, что дырка будет обладать свойствами обычной (m>0) частицы с массой, равной массе электрона, и с противоположным ему электрическим зарядом. Действительно, как движется дырка? Обязательно навстречу необычному электрону, так как она может “занять место электрона” только после того, как он сам займёт место дырки. Это так же, как при игре в шашки: когда шашка (необычный электрон) передвигается вперёд на свободную клетку (дырка), то свободная клетка оказывается сзади шашки, т. е. она как бы передвигается ей навстречу. Но это означает, что дырка движется не против силы (как необычный электрон), а по силе, т. е. она ведёт себя как нормальная частица с положительной массой. Совсем просто понять, что масса дырки в точности равна массе электрона и что она имеет противоположный по знаку и равный по величине электрический заряд (+e). В самом деле, если из ненаблюдаемого фона отрицательно заряженных электронов с отрицательными массами извлечь один электрон, то в фоне будет не хватать одного отрицательного электрического заряда и одной отрицательной массы электрона. В результате этого фон перестанет быть ненаблюдаемым и обнаружит себя как частица с положительной массой, равной массе электрона, и единичным положительным электрическим зарядом.

    Так был предсказан позитрон. А в 1932 г. позитрон был обнаружен экспериментально в составе космических лучей. Его след был обнаружен на одной из фотографий, сделанных с помощью камеры Вильсона, помещённой в магнитное поле.

    Открытие позитрона блестяще подтвердило правильность кван-товомеханического уравнения Дирака. Одновременно его можно рассматривать как подтверждение принципа Паули, который был использован в рассуждениях Дирака. Однако и это не все!

    Последующие измерения параметров позитрона показали, что он действительно имеет массу, тождественно равную массе электрона, у него противоположный электрону электрический заряд (+е), тот же спин (1/2) и противоположный магнитный момент, он стабилен (т. е. живет в вакууме бесконечно долго).

    Обратите внимание на следующее важное обстоятельство. Образование отрицательно заряженного электрона и положительно заряженного позитрона происходит под действием электрически нейтрального γ-кванта. Этот результат представляется вполне естественным с точки зрения закона сохранения электрического заряда. Суммарный электрический заряд системы остаётся неизменным.

    Это очень распространённый закон. Другим примером его применения является ионизация нейтрального атома водорода. Если от атома водорода также с помощью γ-кванта, но значительно меньшей энергии, оторвать электрон, то мы получим две различные частицы с разными по знаку, но одинаковыми по величине электрическими зарядами: положительно заряженный протон и отрицательно заряженный электрон. Оба процесса удовлетворяют закону сохранения электрического заряда. (На этом основании Дирак одно время даже отождествлял “дырку” с протоном.) Но процесс первого типа (образование двух частиц за счёт энергии γ-кванта) возможен для электрон-позитронной пары и невозможен для электрон-протонной пары. Значит, дело заключается не только в электрических, но и ещё в каких-то других зарядах, которые равны и противоположны по знаку у электрона и позитрона, но не у электрона и протона. По аналогичной причине не наблюдается совместного образования электрона и μ⁺-мезона, хотя их суммарный электрический заряд также равен нулю.

    Две частицы, имеющие тождественные массы, время жизни и спин, но противоположные электрический заряд, магнитный момент и некоторые другие заряды, о которых мы будем говорить позже (§ 20, п. 4), называются частицей и античастицей по отношению друг к другу. Электрон и позитрон являются примером частицы и античастицы.

    На примере рассуждения с дыркой мы видели, что частицы и античастицы рождаются вместе, парами. Нетрудно убедиться, что погибают они тоже вместе. Обратимся снова к рис. 19 и рассмотрим процесс перехода одного электрона из области Е>0 на свободное место (в дырку) в области Е<0. В этом процессе одновременно исчезает в верхней области электрон, а в нижней дырка, т. е. позитрон. Но зато при этом освобождается энергия

ΔE = E₁–E₂ ≥ 2т_eс²,

которая реализуется в виде энергии излучения двух γ-квантов.

    Описанный процесс превращения электрона и позитрона в два γ-кванта с той же суммарной энергией называется аннигиляцией*.

    Если от схемы перейти к физической реальности, то следует иметь в виду, что аннигиляция может происходить только при встрече электрона с позитроном в одном и том же месте пространства. Можно было бы думать, что из-за малых размеров частиц вероятность такой встречи мала. Однако это неверно потому, что в нашем мире очень велика концентрация электронов. Любое вещество состоит из атомов, а все атомы содержат электроны. Поэтому даже единственный позитрон, попав в плотную среду (не вакуум), неизбежно и быстро встретится с электроном и проаннигилирует с ним.

    Аннигиляция электрон-позитронных пар — отнюдь не редкое явление, так как в нашем мире довольно много позитронов. Выше (§ 12) мы видели, что позитроны образуются при распаде μ⁺-мезонов, которых много в составе космических лучей, а также в пучках частиц, получаемых на ускорителях; позитроны образуются также при β⁺-распаде искусственно радиоактивных ядер. Наконец, позитроны можно получить, практически реализовав ту самую схему рассуждения, с которой мы начали разговор (см. рис. 19), т. е. получая с помощью γ-квантов высокой энергии электрон-позитронные пары. В настоящее время на этом пути в Советском Союзе и в некоторых других странах имеются очень большие достижения: физики научились не только получать позитроны, но и накапливать их и ускорять до высоких энергий. Но об этой интереснейшей, но более практической стороне вопроса мы поговорим в § 36 и 38, а сейчас снова вернёмся к принципиальным вопросам квантовой механики.

    На примере предсказания и открытия позитрона было впервые показано, что природа симметрична относительно существования частиц и античастиц. Впоследствии это положение было сформулировано в общем виде как принцип зарядового сопряжения. Согласно этому принципу, каждой частице соответствует античастица с тождественными массой, спином и временем жизни и противоположными зарядами. При встрече частицы с античастицей они аннигилируют, в результате чего их энергия покоя преобразуется в другую форму энергии. Есть античастицы и у протона и нейтрона. Они называются антипротоном и антинейтроном. В настоящее время обе эти античастицы научились получать в опытах на ускорителях. Наблюдался для них и процесс аннигиляции. Он действительно сопровождается превращением всей энергии покоя нуклона и антинуклона (2m_Nc²) в другую форму энергии. Все дальнейшие подробности о свойствах антинуклонов и других античастиц опять-таки выходят за рамки этой главы. Поэтому мы отсылаем вас к § 38, а сейчас продолжим разговор о достижениях квантовой механики.

* В переводе слово “аннигиляция” означает “уничтожение”, но нужно понимать, что никакого уничтожения материи и энергии в этом процессе не происходит, так как энергия покоя электрона и позитрона превращается в энергию излучения двух γ-квантов. Материальные частицы превращаются в материальное электромагнитное поле.

Дата установки: 01.09.2007
[вернуться к содержанию сайта]

W