[
вернуться к содержанию сайта]Де Ситтер показал, что в случае, если бы скорость света была постоянной относительно источника, отдалённые двойные звёзды показали бы некоторые особенности, которые не наблюдались. Обычно это расценивается как доказательство справедливости второго эйнштейновского постулата специальной теории относительности. Но есть несколько путей лишения этого доказательства законной силы. Один из наиболее многообещающих путей – использование для света риманова пространства – и рассматривается в этой статье.
Значения для визуально двойных, спектрально-двойных и цефеид рассчитаны для случая евклидова пространства и риманова пространства постоянной положительной кривизны (
R=5 световых лет). Принятие риманова пространства позволяет отклонить теорию относительности Эйнштейна и придерживаться обычных представлений о времени и всех представлений об евклидовом пространстве в пределах нескольких световых лет. Космическое пространство остаётся евклидовым для материальных тел, но свет рассматривается как движущийся в римановом пространстве. Таким образом, время, необходимое свету, чтобы дойти до нас от наиболее удалённых звёзд, составляет всего 15 лет.Основная гипотеза1
специальной теории относительности состоит в том, что в свободном пространстве скорость света постоянна относительно наблюдателя, независимо от движения источника или наблюдателя. Это предположение противоречит всему человеческому опыту, и оно может быть включено в теорию только путём отмены обычных представлений о пространстве и времени.Альтернативное предположение, состоящее в том, что скорость света постоянна относительно источника, отстаивалось в "эмиссионной теории" Ритца2
. По-видимому, единственное свидетельство в пользу гипотезы Эйнштейна даёт поведение двойных звёзд3. Если скорость света не зависит от скорости звёздного источника, то наблюдаемое движение звезды по её орбите будет истинным движением, не считая постоянного интервала времени, необходимого свету для путешествия от звезды до Земли. С другой стороны, если скорость звезды и скорость света складываются, то видимая орбита исказится, и видимая звёздная величина будет меняться.Оживлённая дискуссия по этому вопросу имела место в 1913 г. между Де Ситтером3
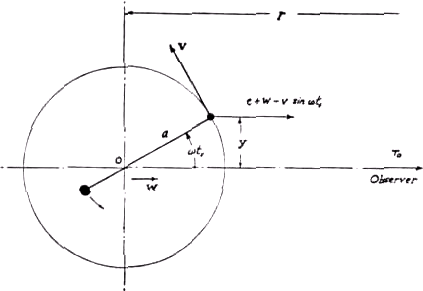
, Фрейндлихом4, Гутником5, и Цурхелленом6. В 1924 были снова выдвинуты аргументы Де Ситтером7, Ля Розой8, Бернхеймером9, и Тиррингом10. Настоящая статья снова открывает вопрос, дабы исследовать возможности, которые игнорировались в более ранних дискуссиях.Рассмотрим двойную звезду (рис. 1) и наблюдателя, который находится в плоскости орбиты на расстоянии
r (r>>a) от центра орбиты. Внешняя звезда светится и имеет постоянную скорость v. Её спутник считается излучающим лишь незначительное количество света. Центр масс двойной движется со скоростью w относительно наблюдателя.
Рис. 1. Круговая орбита двойной звезды.
Допустим, что есть двое часов, одни на звезде, а одни у наблюдателя. Показание первых обозначим
ts, а показание вторых – t. Теория относительности Эйнштейна не используется, так что часы могут быть синхронизированы.Принимая закон сложения скоростей, мы находим, что скорость света, идущего к наблюдателю, равна (
c+w) - v sinωts. Время, необходимое свету, чтобы достичь наблюдателя есть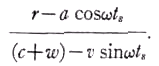
Показания часов наблюдателя в момент, когда он видит звезду в положении, изображённом на рис. 1, есть
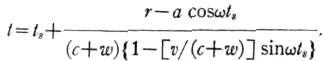 (1)
(1)
Поскольку
v и w очень малы в сравнении со скоростью c (менее 0,1 процента), то уравнение (1) может быть записано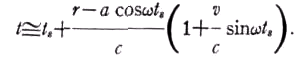
Также, поскольку
a<<r, то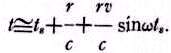
Удобно выразить это уравнение в обозначениях смещения звезды от её центрального положения:
y/a
= sin ωts.Тогда
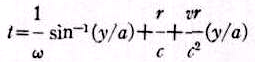
или
θ = sin
–1(y/a) + Г·(y/a), (2)где θ определяет угловое положение звезды на её орбите, исправленное с учётом скорости света:
θ =ω
ts – r/c. (3)Характеристическая константа есть
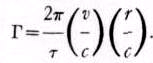 (4)
(4)
Рисунок 2 показывает видимое движение звезды, каким оно видится отдалённому наблюдателю. Если Г=0, то движение истинно синусоидальное, а для Г < 0.1, движение очень мало отступает от синусоидального. Однако, поскольку Г нарастает, то кривая наклоняется, и функция может стать многозначной. Например, при Г=2 одна звезда видна, если угол θ изменяется от 0,69 до 2,45 радиана; но при θ =2,45, наблюдатель внезапно начнёт видеть три звезды в различных точках на той же самой орбите. Это продолжается до значения θ =3,83, при котором звезда видится вернувшейся к её единичному состоянию. Это явление также можно было бы выявить спектрографом. Каждая спектральная линия была бы единственной для 0,69 < θ < 2,45, но проявлялась бы в виде трёх линий в других частях цикла.
Теперь рассмотрим критическое состояние. При увеличении значения Г мы достигнем случая, когда
dθ/d(y/а) = 0, после которого кривая становится многозначной. Из уравнения (2),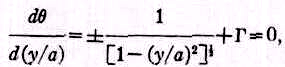
или
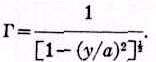 (5)
(5)
Рисунок 2 показывает, что этот нулевой наклон возникнет при
y/a=0, поэтому уравнение (5) даёт для первой критической точки,Г
1=1,00. (6)Для величин Г меньших единицы никакие многократные образы не могут возникнуть.
Таблица I. Визуальные двойные.
|
Название |
Параллакс p (") |
Расстояние (световые годы) |
Период (годы) |
(v/c) |
Г E |
|
δ Equ |
0.060±.006 |
54.3 |
5.70 |
7.82×10-5 |
4.68×10-3 |
|
κ Peg |
0.026±.005 |
125 |
11.3 |
9.77×10-5 |
6.78×10-3 |
|
ε Hya |
0.020±.005 |
163 |
15.3 |
7.47×10-5 |
5.00×10-3 |
|
42 Corn |
0.063±.008 |
51.7 |
25.9 |
4.02×10-5 |
5.05×10-4 |
|
85 Peg |
0.092±.006 |
35.4 |
26.3 |
3.36×10-5 |
2.84×10-4 |
|
Σ 3121 |
0.056±.008 |
58.2 |
34.3 |
3.47×10-5 |
3.70×10-4 |
|
ζ Her |
0.111±.005 |
29.4 |
34.5 |
3.51×10-5 |
1.88×10-4 |
|
α CMi |
0.312±.006 |
10.4 |
39.0 |
3.30×10-5 |
5.55×10-5 |
|
β 416 |
0.169±.016 |
19.3 |
42.2 |
2.55×10-5 |
7.32×10-5 |
|
μ HerBC |
0.111±.006 |
29.4 |
43.2 |
2.70×10-5 |
1.15×10-4 |
|
Krüger 60 |
0.257±.004 |
12.7 |
44.3 |
2.15×10-5 |
3.87×10-5 |
|
ξ Sco |
0.040±.005 |
81.5 |
44.7 |
4.00×10-5 |
4.58×10-4 |
|
Σ 2173 |
0.052±.006 |
62.7 |
46.0 |
4.41×10-5 |
3.78×10-4 |
|
τ Cyg |
0.050±.006 |
65.2 |
47.0 |
3.85×10-5 |
3.36×10-4 |
|
α CMa |
0.371±.004 |
8.78 |
50.0 |
4.07×10-5 |
4.49×10-5 |
|
β 648 |
0.064±.005 |
50.9 |
56.6 |
3.44×10-5 |
1.94×10-4 |
|
ξ UMa |
0.146±.006 |
22.3 |
59.8 |
2.85×10-5 |
6.67×10-5 |
|
99 Her |
0.042±.006 |
77.6 |
63.0 |
3.76×10-5 |
2.91×10-4 |
|
α Cen |
0.758±.010 |
4.29 |
78.8 |
2.94×10-5 |
1.01×10-5 |
|
70 Oph |
0.192±.005 |
17.0 |
87.7 |
2.66×10-5 |
3.24×10-5 |
|
γ CrB |
0.022±.006 |
148 |
87.8 |
3.76×10-5 |
3.98×10-4 |
|
0 Σ 79 |
0.027±.004 |
121 |
88.9 |
2.35×10-5 |
2.01×10-4 |
|
ξ Boo |
0.168±.007 |
19.4 |
153 |
1.87×10-5 |
1.49×10-5 |
|
Σ 2052 |
0.055±.006 |
59.2 |
132 |
1.91×10-5 |
4.64×10-5 |
|
ο 2 EriBC |
0.203±.008 |
16.0 |
248 |
1.36×10-5 |
5.52×10-6 |
|
α Gem |
0.076±.004 |
42.8 |
306 |
3.58×10-5 |
3.14×10-5 |
|
η Cas |
0.182±.005 |
17.9 |
346 |
1.59×10-5 |
5.17×10-6 |
Интересен также временной эффект. Для
w<<c, уравнение (1) преобразуется в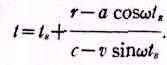
Дифференцирование даёт
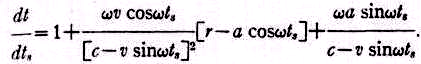
Если
a<< r и v<<c,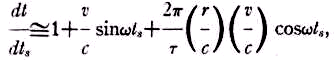
или
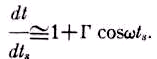 (7)
(7)
Предположим, что звезда испускает к наблюдателю
Qs джоуль/стерадиан в течение интервала времени Δts. Излучение приходит к наблюдателю не в интервале Δts, а в интервале Δt:Δ
t = Δts[1+Гcosωts]. (8)Если бы звезда не перемещалась, средняя интенсивность
11 источника, измеренная наблюдателем была быD
0= Qs/r2Δt = Qs/r2Δts (ватт/м2).Но для движущейся звезды видимая интенсивность
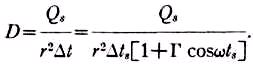
Их отношение есть
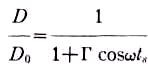 . (9)
. (9)
Если Г = 1, наблюдатель будет регистрировать периодическое изменение яркости в пределах от
D0/2 до бесконечности.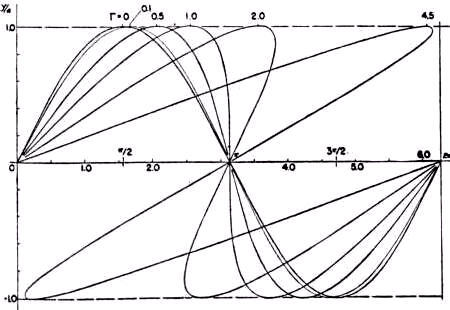
Рис. 2. Видимое поведение двойных, каким оно воспринимается отдалённым наблюдателем. Искажение синусоидальной кривой, созданное различием в скорости света от различных участков орбиты (с учётом сложения скоростей). Эффект становится всё более выраженным при увеличении Г: Г=(2π
/τ) (v/c) (r/c). Критическое условие возникает при Г = 1, выше которого имеются многократные образы звезды.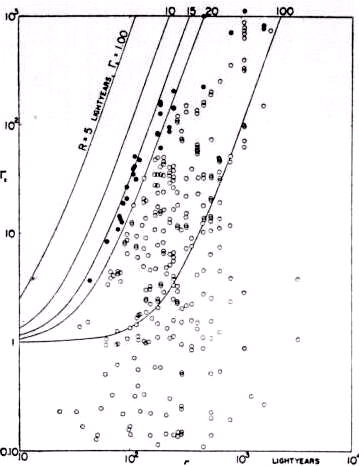
Рис. 3. ГE как функция евклидового расстояния для спектрально двойных. Чёрные точки внесены в Таблицу II. Кривые построены для ГR=1,00 и космических констант 5, 10, 15, 20 и 100 световых лет.
Малочисленность точек ниже 70 световых лет отчасти вызвана ограниченным числом звёзд возле Земли. Малое число точек выше 1000 световых лет – это артефакт, вызванный нехваткой данных о параллаксах удалённых звёзд. Однако в интервале между 70 и 1000 световыми годами точки распределены довольно хорошо [равномерно – С.С.]. Это делает их резкую границу на кривой R = 15 весьма впечатляющей.
Среди сотен переменных звёзд, которые были исследованы, ничего вроде подобного изменения ни разу не наблюдалось. Поэтому нужно заключить, что или теория неправильна или Г всегда много меньше единицы. Возможно, Г могло бы быть сопоставимо с 0,1 даже и без того, чтобы у звезды можно было заметить искажение видимой орбиты или изменение видимой яркости.
Принимая классическую волновую теорию, можно было б ожидать, что видимая частота излучения будет меняться обратно пропорционально временному интервалу уравнения (7), или
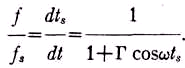 (10)
(10)
Это привело бы к огромному Доплер-эффекту, как было отмечено Цурхелленом.
6 Однако на основании квантовой теории эти сильные изменения не могут ожидаться. Ля Роза8 и Де Ситтер7 находились в бесспорном согласии относительно того, что уравнение (10) можно игнорировать.Предшествующий анализ показывает необычные явления, которые должны возникнуть у двойных достаточно короткого периода, наблюдаемых с достаточно большого расстояния, если принять закон сложения скоростей [для света – С.С.]. Анализ может быть распространён и на общий случай наклонной эллиптической орбиты с излучением света обеими звёздами, но общие выводы остаются теми же.
Сначала рассмотрим визуально двойные. По их поводу Бергманн говорит:12
"Если бы скорость света зависела от его источника, двойные звёзды породили бы необычные явления. ... В некоторых случаях мы должны были б одновременно наблюдать один и тот же компонент двойной звёздной системы в различных положениях, и эти 'звёздные привидения' исчезали бы и вновь возникали в ходе их периодических движений."
Чтобы проверить подобные утверждения, мы рассчитали величины Г для визуально двойных. Величины Г были во всех случаях много ниже критической величины равной единице (раздел. 2), оказываясь обычно порядка 10-5
, как показано в Таблице I. Поэтому мы приходим к выводу, что данные о визуально двойных абсолютно ничего не доказывают в отношении постоянства скорости света. Вопреки заявлениям Бергмана и других, гипотеза Ритца не ведёт ни к каким многократным образам визуально двойных, и при этом она не предсказывает мультиплетных спектральных линий для этих звёзд.Подобный же анализ может быть произведён в отношении спектрально двойных. Данные для 282 звёзд были взяты из Пятого Каталога13
Мора и Неубауэра. Расстояния были рассчитаны по шлезингеровским значениям14 тригонометрического параллакса. Когда тригонометрические величины были недоступны, использовались спектральные данные или динамические параллаксы. Большинство рассчитанных значений Г было выше критической величины, равной единице, в некоторых случаях превышая тысячу.Данные (за исключением 60 звёзд с Г < 0.1) представлены на рис. 3, а список отобранных звёзд дан в Таблице II. Согласно теории (раздел 2), высокие значения Г должны привести к необычным явлениям, которые не наблюдаются. И вывод отсюда, что, либо гипотеза Ритца должна быть отклонена, как настаивают релятивисты, либо должны быть произведены коренные преобразования значений расстояний или скоростей. Эти возможности будут рассмотрены в разделе 6.
Для пульсирующей звезды максимальная скорость
v звёздной поверхности измерена спектроскопически. Очевидно, применим тот же самый критерий Г, что и для двойных звёзд. Если Г> l, то к наблюдателю приходит свет одновременно из нескольких фаз пульсации, что должно привести к мультиплетным спектральным линиям. Ничего подобного не наблюдается.Таблица II. Некоторые спектрально двойные (Г
R вычисленно для R=5 световых лет).|
Номер по ликскому каталогу |
Название |
P ('') |
r (светоые годы) |
τ (дни) |
v (км/с) |
Г E |
Г R |
|
5 |
Σ 12 A |
0.017 (дин) |
192 |
0.842 |
87.96 92.57 |
153 161 |
0.0328 0.0345 |
|
6 |
AO Cas |
0.002 (спек.) |
1628 |
3.523 |
218.5 234.5 |
772 827 |
2.81×10-4 3.01×10-4 |
|
11 |
13 Cet A |
0.052±0.008 |
62.6 |
2.082 |
37 |
8.48 |
0.0478 |
|
14 |
π Cas |
0.018 () |
181 |
1.964 |
117.3 119.0 |
82.5 83.7 |
0.0210 0.0213 |
|
23 |
ζ Phe |
0.013 (дин) |
250 |
1.670 |
125 180 |
143 206 |
0.0140 0.0201 |
|
34 |
X Tri |
0.004 (спек.) |
815 |
0.972 |
110 |
705 |
2.02×10-3 |
|
52 |
CC Cas |
0.017 (спек.) |
192 |
3.369 |
141.6 291.8 |
61.3 126.2 |
0.0132 0.0272 |
|
21 |
β Aur |
0.037±.0004 |
88.0 |
3.960 |
108.9 111.0 |
18.4 18.8 |
0.0390 0.0398 |
|
149 |
RC Ma |
0.039±.0008 |
83.4 |
1.136 |
24.0 |
13.5 |
0.0333 |
|
152 |
B 1945 |
0.029 (спек.) |
112 |
1.933 |
94.6 116.8 |
41.8 51.6 |
0.0435 0.0536 |
|
156 |
α 1 Gem |
0.073±0.003 |
44.6 |
2.928 |
31.88 |
3.72 |
0.0539 |
|
169 |
V Pup |
0.003 (спек.) |
1085 |
1.455 |
199 342 |
1132 1942 |
1.38×10-3 2.37×10-3 |
|
174 |
B 2227 |
0.038±0.010 |
85.7 |
1.563 |
30.28 |
12.7 |
0.0288 |
|
195 |
ο Leo |
0.028±0.007 |
116 |
1.686 |
60 |
31.6 |
0.0296 |
|
229 |
B 3182 |
0.026±0.005 |
125 |
1.271 |
63.2 |
47.5 |
0.0358 |
|
246 |
ζ U Ma A |
0.0400.005 |
81.3 |
1.81 |
42.0 |
14.4 |
0.0383 |
|
304 |
B 4247 |
0.030 (спек.) |
109 |
2.308 |
97.4 108.7 |
35.0 39.1 |
0.0400 0.0446 |
|
345 |
d Ser |
0.014±0.006 |
232 |
1.850 |
90 100 |
86.1 95.6 |
0.0105 0.0117 |
|
368 |
+16° 3758 |
0.041±0.010 |
79.3 |
4.812 |
86.03 86.04 |
10.8 10.8 |
0.0309 0.0309 |
|
432 |
B 5579 |
0.007 (спек.) |
463 |
1.729 |
109.7 |
224 |
3.50×10-3 |
|
452 |
B 5764 |
0.034±0.012 |
95.5 |
2.616 |
74.8 96.0 |
20.9 26.8 |
0.0349 0.0447 |
|
— |
TX Cnc |
0.007 |
463 |
0.386 |
112 217 |
1038 2010 |
0.0163 0.0314 |
Таблица III демонстрирует результаты для типичных цефеид. Данные о скорости для 144 цефеид были заимствованы из статьи Джоя15
. Расстояния были вычислены по формуле Шэпли,16 при условии отсутствия поглощения света в межзвёздном пространстве. Расстояния в основном намного больше расстояний из предыдущих таблиц; что приводит к получению больших значений Г. Поскольку нельзя найти никакого другого объяснения, то цефеиды предоставляют доказательство даже более решающее, чем данные спектрально двойных, – доказательство того, что скорость света не имеет и примеси скорости источника.Долгопериодические переменные, типа ο Кита, были также исследованы. Результаты исследований показали, что, подобно визуальным двойным, эти звёзды не дают никакой информации для выбора между гипотезами Ритца и Эйнштейна.
Таблица III. Цефеиды (Г
R рассчитано для R=5 световых лет).|
Название |
r (световые годы) |
τ (дни) |
v max (км/с) |
Г E |
Г R |
|
SU Cas |
1 015 |
1.95 |
11.0 |
43.7 |
6.4×10-5 |
|
DT Cyg |
790 |
2.50 |
8.5 |
20.5 |
6.3×10-5 |
|
AD Gem |
5 700 |
3.79 |
36.0 |
413 |
3.5×10-6 |
|
Y Aur |
5 200 |
3.86 |
19.5 |
200 |
2.2×10-6 |
|
CG Cas |
20500 |
4.36 |
21.0 |
753 |
1.4×10-7 |
|
FF Aql |
980 |
4.47 |
7.1 |
11.8 |
2.0×10-5 |
|
δ Cep |
460 |
5.37 |
19.7 |
12.9 |
2.0×10-4 |
|
η Aql |
730 |
7.18 |
20.8 |
16.1 |
6.3×10-5 |
|
PZ Aql |
31 000 |
8.76 |
19.5 |
528 |
2.8×10-8 |
|
ζ Gem |
650 |
10.15 |
14.2 |
6.96 |
3.9×10-5 |
|
AP Her |
20 000 |
10.42 |
20.0 |
292 |
5.7×10-8 |
|
RW Cam |
7 400 |
16.41 |
31.0 |
107 |
4.1×10-7 |
|
MZ Cyg |
98 000 |
21.17 |
29.5 |
1044 |
1.7×10-9 |
|
RX Lib |
38 000 |
24.95 |
14.5 |
169 |
4.9×10-9 |
Тот факт, что Г превышает критическую величину для многих цефеид и спектрально двойных, не обязательно доказывает, что скорость света независима от скорости источника. Есть следующие возможности:
(1) Скорость света постоянна относительно наблюдателя (Эйнштейн).
(2) Скорость света постоянна относительно источника (Ритц). Отклонения из раздела 2 считаются реально существующими, но (a) расстояния уменьшаются, (b) скорость света увеличивается на больших расстояниях, или (c) доплеровские смещения не дают истинной скорости.
(3) Понятие скорости не применимо к свету, так что
c не может складываться со скоростью материальных тел (Паладжи).17Если принять гипотезу Ритца, то величина Г должна оставаться значительно меньше единицы. Но Г зависит от
v, r и c, согласно уравнению (4); так что изменением любого из этих трёх параметров можно удовлетворить критерию Г < l.Наиболее многообещающая из этих возможностей – уравнение (2a). Предположим, что свет путешествует в римановом пространстве. Обычное расстояние
r, используемое астрономами, остаётся неизменным в отношении материальных тел; но для света оно заменяется на соответствующее риманово расстояние18 s:s=2R
tаn–1(r/2R), (11)где
R - космическая константа 19 (радиус кривизны) пространства. Скорость света, c=ds/dt, является постоянной относительно источника. Поэтому методика данной статьи по сути сохраняет космическое пространство неизменным, но уменьшает время, требуемое свету для путешествия от звезды до Земли. Мы постулируем18 также, что доплеровское смещение даёт евклидову скорость источника относительно наблюдателя, dr/dt. Скорость света, приходящего от движущегося источника, согласно принципу Ритца, есть c плюс ds/dt источника, соответствующей доплеровской скорости dr/dt. На основании геометрии Эвклида,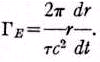 (12)
(12)
Соответствующее Г для риманова пространства есть
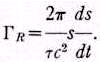 (13)
(13)
Но риманова метрика
18 даётся выражениемds
= dr/[1 + (r/2R)2],В таком случае
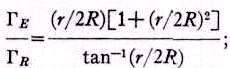 (14)
(14)
И если Г
R имеет критическое значение равное единице, то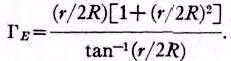
Кривые критического Г
E по r представлены на рис. 3 для нескольких значений R.Таблица IV. Несколько избранных спектрально двойных (Г
R вычислено для R=5 световых лет).|
Номер по ликскому каталогу |
Название |
P ('') |
r (световые годы) |
τ (дни) |
v (км/с) |
Г E |
Г R |
|
436 |
δ Cap |
0.065±.007 |
50.2 |
1.023 |
65.7 |
24.6 |
0.257 |
|
196 |
WU Ma |
0.019±.007 |
171.2 |
0.334 |
134 188 |
524 964 |
0.157 0.289 |
|
273 |
ι Boo B |
0.079±.005 |
41.2 |
0.268 |
115 231 |
136 272 |
2.44 4.88 |
|
— |
VW Cep |
0.053 |
61.4 |
0.278 |
75 230 |
126 386 |
0.747 2.29 |
Предполагая, что свет ведёт себя так, словно космическое пространство является римановым, мы далее рассмотрим космическую константу
R. Эта константа должна быть достаточно большой, чтобы метрика оставалась практически евклидовой для всей солнечной системы; но все же R должно быть достаточно малым, чтобы Г < 1 для всех звёзд.Таблица V. Расстояние и скорость (для
R = 5 световых лет).|
Эвкклидово расстояние r |
r/ 2R |
Риманово расстояние s |
v R/vE |
|
1 световой год |
0.10 |
0.997 светового года |
0.990 |
|
4 |
0.40 |
3.81 |
0.860 |
|
10 |
1.0 |
7.85 |
0.500 |
|
30 |
3.0 |
12.5 |
0.100 |
|
100 |
10.0 |
14.7 |
0.99×10-2 |
|
103 |
100 |
15.6 |
1.0×10-4 |
|
104 |
1000 |
15.7 |
1.0×10-6 |
|
∞ |
∞ |
15.71 |
0 |
Рисунок 3 показывает, что точки, по-видимому, имеют довольно резко очерченную границу на
R = 15 световых лет. Данные для некоторых спектрально двойных, у которых ГR приближается к единице для R = 15 приведены в Таблице II. Эти радиусы кривизны также удовлетворяет критерию Г для визуально двойных, цефеид и долгопериодических переменных.Единственные исключения – несколько звёзд (Таблица IV) с очень короткими периодами. Одна звезда, δ Cap, по-видимому, имеет очень надёжные данные, но эта точка находится скорее возле кривой
R = 5 с рис. 3, чем R= 15. И нельзя найти никакого другого примера подобного типа. Спектральные линии WUM-звёзд так размыты20, что эти звёзды можно не рассматривать, пока не станет доступной дальнейшая информация.Остаётся вопрос изменения блеска11
по уравнению (9), которое требует, чтобы ГR было значительно меньше единицы. Если использовать в качестве критерия ГR=0,1, то уравнение (14) показывает, что кривые с рис. 3 должны быть преобразованы в сторону уменьшения посредством одной логарифмической операции. При этих условиях кривой, которая удовлетворяет крайним точкам, будет кривая R= 5, а не R = 15. Поэтому на основании имеющихся данных мы экспериментально устанавливаем значение R вR
=5 световых лет=4,73×1016 м.Это значение
R достаточно велико, чтобы в солнечной системе нельзя было обнаружить никакого отклонения от евклидова пространства. Среднее расстояние от Плутона до Солнца – 5,91×1012 м или 6,26×10-4 световых лет. Таким образомr
/2R=6,26×10-5и
dr/ds
=l+(6,26×10-5)2,дающее отклонение от евклидовой метрики порядка 10
-7 процента. Даже для самых близких звёзд эффект римановой метрики мал. Например, для α Centauri [альфа Центавра – C.С.], r=4,3 светового года и изменения метрики составляют всего около 18 процентов.Таблица VI. Видимые изменения светимости.
|
Ликский номер |
Название |
r (световые годы) |
Эксцентриситет |
m |
Г R |
Max D/Do |
Δm |
|
Переменные |
|||||||
|
52 |
CC Cas |
192 |
0.102 |
7.3-7.4 |
0.0132 |
1.013 |
0.014 |
|
121 |
β Aur |
88.0 |
0.00 |
2.07-2.16 |
0.0390 |
1.039 |
0.042 |
|
149 |
RC Ma |
83.4 |
0.013 |
5.38-5.98 |
0.0333 |
1.033 |
0.036 |
|
Постоянные звёзды |
|||||||
|
5 |
Σ 12 A |
192 |
0.027 |
6.1 |
0.0328 |
1.033 |
0.036 |
|
11 |
13 Cet A |
62.6 |
0.1 |
5.6 |
0.0478 |
1.048 |
0.052 |
|
14 |
π Cas |
181 |
0.010 |
5.02 |
0.0210 |
1.021 |
0.023 |
|
23 |
ζ Phe |
250 |
0.14 |
4.13 |
0.0140 |
1.014 |
0.015 |
|
152 |
B 1945 |
112 |
0.002 |
5.27 |
0.0435 |
1.044 |
0.047 |
|
156 |
α 1 Gem |
44.6 |
0.002 |
2.85 |
0.0539 |
1.054 |
0.059 |
|
174 |
B 2227 |
85.7 |
0.051 |
5.67 |
0.0288 |
1.029 |
0.031 |
|
195 |
ο Leo |
116 |
<0.02 |
3.76 |
0.0296 |
1.030 |
0.032 |
|
229 |
B 3182 |
125 |
0.00 |
5.12 |
0.0358 |
1.036 |
0.039 |
|
246 |
ζ U Ma A |
81.3 |
0.541 |
2.40 |
0.0383 |
1.038 |
0.042 |
|
304 |
B 4247 |
109 |
0.00 |
5.91 |
0.0400 |
1.040 |
0.043 |
|
368 |
+16° 3758 |
79.3 |
0.073 |
6.46 |
0.0309 |
1.031 |
0.033 |
|
452 |
B 5764 |
95.5 |
0.00 |
4.66 |
0.0349 |
1.035 |
0.038 |
Сравнение евклидовых и римановых значений представлено в Таблице V. То что космическая константа равная 5 даёт значения Г
R, которые значительно ниже критических значений, продемонстрировано в последних колонках Таблиц II и III. Этот вывод отражён также в Таблице VI, которая представляет дополнительные данные по некоторым из критических спектрально двойных Таблицы II. Максимальная величина ГR - приблизительно 0,05, которая не должна дать никакого заметного нарушения орбиты и лишь очень малое изменение видимой звёздной величины.Седьмая колонка Таблицы VI включает в себя величины максимального относительного блеска, вызванного изменением в Δ
t. Из уравнения (9) максимальное отношение получается, когда ωts = π и имеет место(D/D0)max=1/(1–
ГR). (9a)Восьмая колонка показывает соответствующие изменения, которые нужно ожидать в звёздной величине:
Δ
m = 2,500 log (D/D0)max. (15)Для переменных звёзд это отклонение в одну двадцатую звёздной величины или меньше, конечно, не было б обнаружено. Но если экспериментальные данные докажут, что другие звёзды Таблицы VI действительно постоянны по величине точнее чем в 0,05
m, то теория должна быть изменена или же уменьшено значение космической константы ниже уровня R=5.Поскольку нет никакого основания для гипотезы о том, что скорость света ведёт себя подобно обычной скорости, то предшествующее объяснение, по-видимому, предлагает простую и разумную картину мира, которая позволяет сохранить неизменными все наши обычные представления о местном пространстве и времени. Теория относительности Эйнштейна отклоняется.
** Скорость света в свободном пространстве всегда равна с относительно источника, и имеет для наблюдателя величину, которая зависит от относительной скорости источника и наблюдателя. Верным остаётся принцип относительности Галилея, как и в ньютоновской теории тяготения.* Представлено на съезде американского оптического общества, Нью-Йорк, 21 марта, 1953 г.
**Использование преобразований Галилея вместо преобразований Лоренца требует изменения уравнений Максвелла. Этот вопрос будет рассматриваться в другой статье.
1. A. Einstein, Ann. Physik 17, 891 (1905).
2. W. Ritz, Ann. chim. et phys. 13, 145 (1908).
3. W. de Sitter, Physik. Z. 14, 429, 1267 (1913).
4. E. Freundlich, Physik. Z. 14, 835 (1913).
5. P. Gutnick, Astron. Nachr. 195, 265 (1913).
6. W. Zurhellen, Astron. Nachr. 198, 1 (1914).
7. W. de Sitter, Bull. Astron. Inst. Netherlands 2, 121 (1924);
там же c. 163.8. M. La Rosa, Z. Physik 21, 333 (1924); Z. Physik 34, 698 (1925).
9. W. E. Bernheimer, Z. Physik 36, 302 (1926).
10. H. Thirring, Z. Physik 31, 133 (1925).
11. Moon and Spencer, J. Opt. Soc. Am. 36, 666 (1946); Lighting Design (Addison-Wesley Press, Cambridge, Massachusetts, 1948).
12. P. G. Bergmann, Introduction to the Theory of Relativity (Prentice-Hall, Inc., New York, 1942), p. 19.
13. J. H. Moore and F. J. Neubauer, "Fifth catalog of the orbital elements of spectroscopic binary stars," Lick Observatory Bull. 20, No. 521.
14. F. Schlesinger.
General Caеalog of Slellar Parallaxes (Yale University Observatory, 1935); H. N. Russell and C. E. Moore, The Masses of the Stars (University of Chicago Press, Chicago, 1940), Table 53.15. A. H. Joy, Astrophys. J. 86, 363 (1937).
16. H. Shapley, Galaxies (The Blakiston Company, Philadelphia, 1943), p. 62.
17. M. Palágyi, Ausgewählte Werke (J. A. Barth, Leipzig, 1925), Vol. III.
18. P. Moon and D. E. Spencer, "Riemannian space for astronomy" (в печати).
19. E. W. Hobson, The Domain of Natural Science (Cambridge University Press, Cambridge, 1923), p. 144.
20. O. Struve, Stellar Evolution (Princeton University Press, Princeton, 1950), p. 175.
Дата установки: 22.07.2007
[
вернуться к содержанию сайта]