[вернуться к содержанию сайта]
Несмотря на постоянно возобновляемые усилия исследователей, природа атомов и молекулярных сил нам всё ещё пока очень мало известна. В самом деле, большая трудность задачи заключается в том, что в большинстве случаев мы наблюдаем не свойства атомов, но сложные средние явления, зависящие от беспорядочного молекулярного движения и внешних причин. Есть, однако, одно важное исключение из этого правила: спектры простых тел непосредственно дают нам сведения о различных видах колебаний атомов; ибо расположение линий в спектре почти совершенно не зависит ни от температуры, ни от внешних условий, ни даже от действия молекул друг на друга. Очевидно, если бы по колебаниям электрических зарядов атома можно было судить о силах, которые их производят, и о расположении или движении самих зарядов,– то задача была бы решена. Чрезвычайная точность спектральных измерений даёт нам по этому вопросу многочисленные и ценные документы, но написанные, к сожалению, иероглифами, которых мы не умеем разбирать. Но всё-таки, благодаря замечательной простоте некоторых эмпирических законов, связывающих друг с другом длины волн отдельных линий спектра, некоторые результаты в этом направлении были получены. И действительно, из нижеследующего будет видно, что задача для водорода во всяком случае имеет очень простое решение, вполне согласное с общим взглядом на строение атомов, сложившимся под влиянием последних открытий.
Припомним замечательную формулу, найденную Бальмером (Balmer), которая связывает между собой длины волн λ спектральных линий водорода. Её можно написать следующим образом, обозначая через N некоторую постоянную:
![]()
Давая m последовательно значения 3, 4, 5,... ,32, мы получаем точные длины волн всех линий водорода. Если есть ошибка, то, по-видимому, она меньше одной стотысячной.
Пикеринг (Pickering) открыл в спектре некоторых звёзд, в которых преобладает водород, вторую серию линий, которую мы ещё не умеем воспроизвести в лаборатории; эта серия выражается формулой:
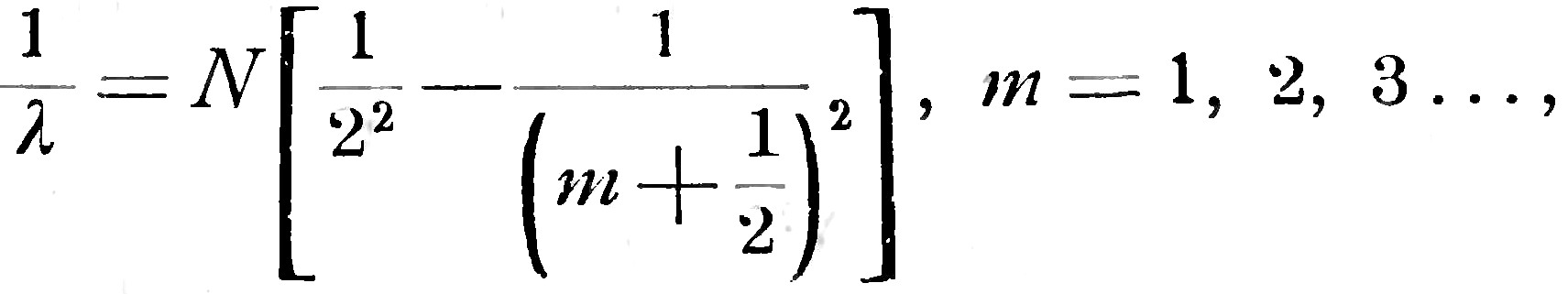
в которой N обозначает ту же постоянную, что и выше.
Согласно Бальмеру (Balmer) и Ридбергу (Rydberg) есть основание думать, что в действительности эти формулы должны содержать каждая два произвольных целых числа m и n; таким образом, спектр водорода выражался бы формулами:
![]() (1)
(1)
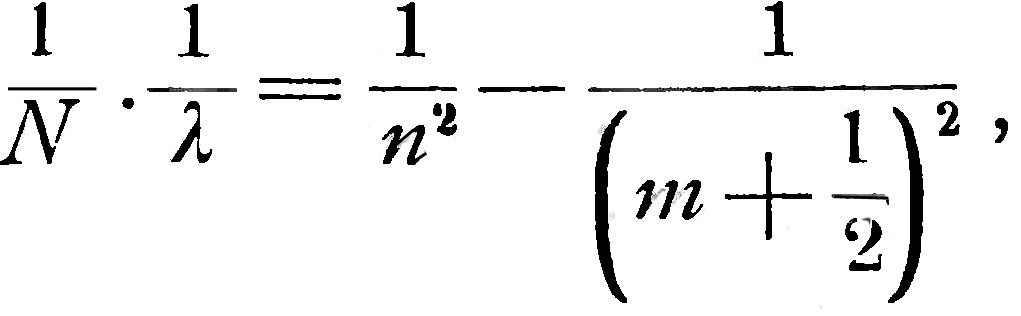 (2)
(2)
где значения n= 3, 4 ... соответствуют инфракрасным линиям. Эта гипотеза совсем недавно получила блестящее подтверждение. По моим указаниям Пашен (Paschen) нашёл, действительно, две инфракрасные линии водорода, которые ему удалось измерить с большой точностью1. Он получил:
λ=18 751,3±1
U.Å 2и
λ=1
2 817,6±1,5 U.Å;формулы же
![]()
дают:
λ=18 751,6 и
12 818,7.Итак, согласие формул с наблюдением не оставляет желать ничего лучшего.
Формулы эти настолько просты, что стремление найти такие механические или электромагнитные системы, колебания которых выражались бы ими, нельзя считать лишёнными смысла. Впрочем, подобные законы были, как известно, найдены Ридбергом, Кайзером (Kayser) и Рунге (Runge) и в других спектрах. И в этих случаях также доказано3, что формулы содержат два произвольных целых числа. По Ридбергу в первом приближении можно написать их так:
![]()
и более точно, как указал автор настоящей статьи:
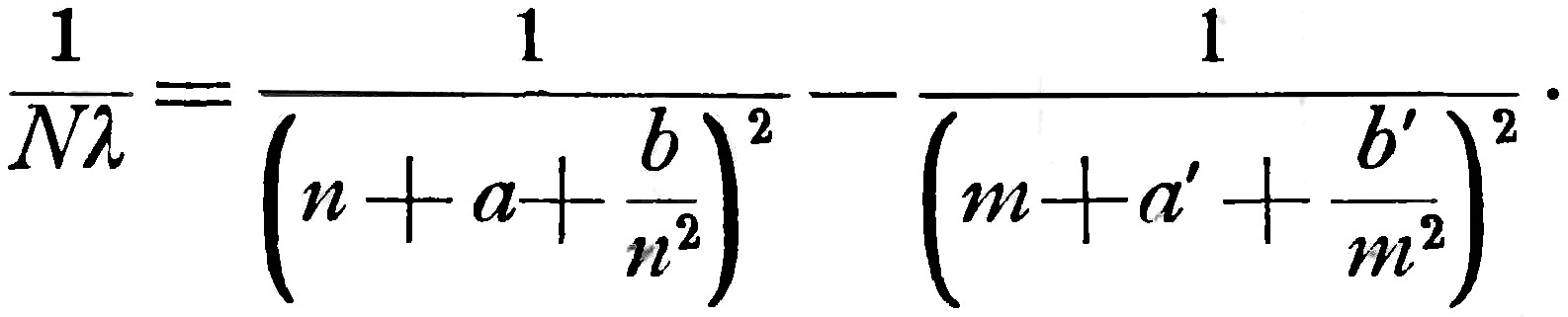 (3)
(3)
Здесь N имеет то же значение, как и в случае водорода, тогда как постоянные a, b, a', b' различны для различных элементов. Выбирая их надлежащим образом и полагая m=1½, n=2, 3 ..., мы из формулы (3) получаем "главную серию" Кайзера и Рунге; для n=2, m=2½, 3½ … мы получаем вторую побочную серию; системам значений n=3, m=2½ ... и т. д. также соответствуют наблюдавшиеся линии. Заменяя a', b' некоторыми новыми постоянными a'', b'', получаем для n=2, m=3, 4, 5 ... первую побочную серию, которая для m=∞ имеет тот же предел, что и вторая. И в этом случае удалось найти инфракрасные линии n=3, m= 3, 4 и т. д. Но, если вместо того, чтобы сочетать, как мы сделали выше, первый член, содержащий a и b, со вторым, содержащим a', b' или a'', b'', мы напишем выражение:
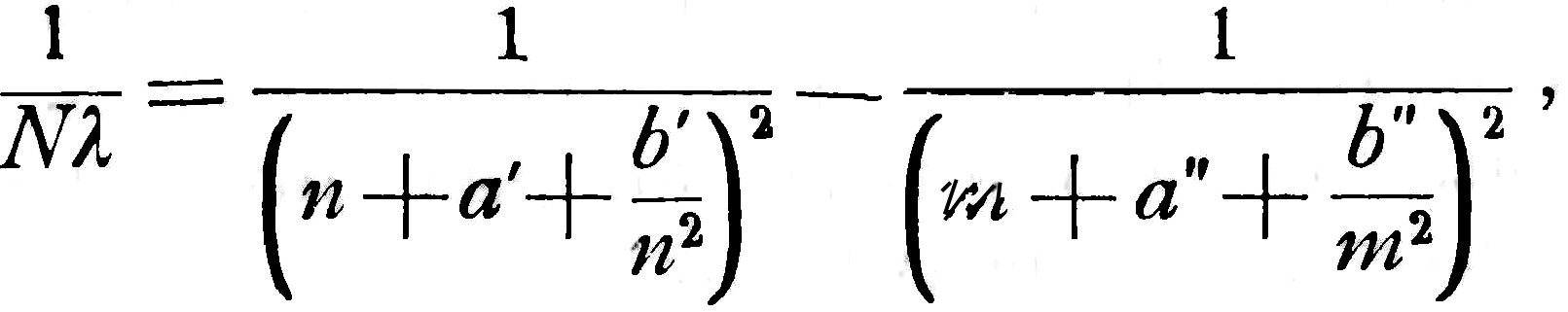 (4)
(4)
в котором сочетаются a', b' в первом члене с a'', b'' во втором то мы получим новые линии, которые действительно наблюдались, по крайней мере, в некоторых спектрах. Этот результат особенно ясно указывает на значение этих формул. Наконец, комбинируя аналогичным образом главную серию саму с собой, мы получаем для лития и натрия:
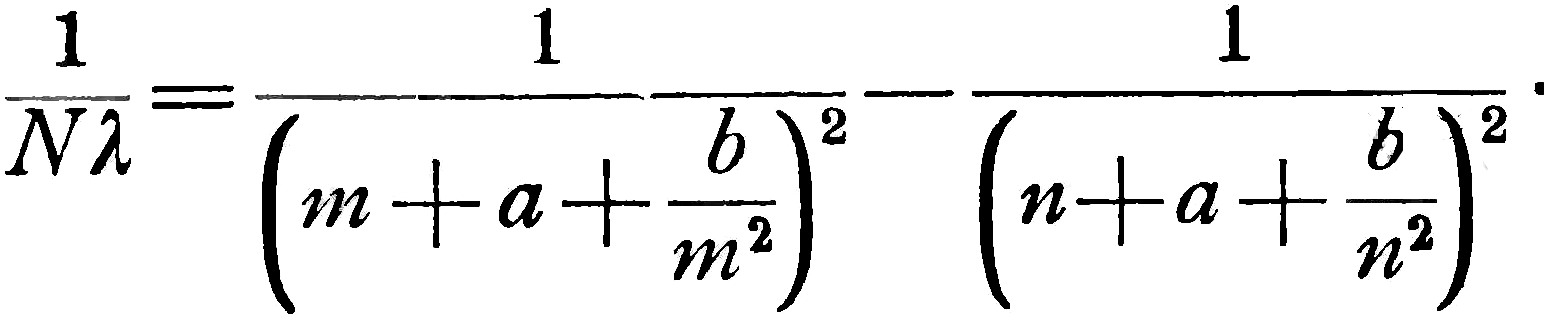 (5)
(5)
Из этих законов следует, что, складывая или вычитая частоты двух наблюдаемых линий или серий, мы получаем частоту новой линии или целой серии линий. Ошибки, которые при этом получаются, бывают того же порядка, что и экспериментальные неточности. Так, например, для гелия мы находим для самой яркой линии системы (4) 1/λ=26244,86; опыт же даёт 26244,78.
Этим я и ограничусь. Итак, мы видим, что:
1. Простые законы получаются всегда для 1/λ, т.е. для частоты.
2. При бесконечном увеличении одного или другого из целых чисел полученные частоты стремятся к определённому пределу.
3. Каждый из двух членов формулы имеет, некоторым образом, самостоятельное существование, и, комбинируя различным образом такие члены, мы получаем линии спектра.
Эти общие выводы вполне ясно оттеняют большую разницу, существующую между упругими, электрическими и другими нам известными колебаниями, с одной стороны, и колебаниями, соответствующими спектральным линиям, с другой. Прежде всего,– и на этом лорд Рэлей (Rayleigh) особенно настаивал,– простые законы колебательных явлений относятся, за малыми исключениями, к квадратам частот, а не просто к частотам. Это происходит оттого, что уравнения движения содержат не только координаты, определяющие состояние систем, но и вторые производные или ускорения. В самом деле, когда дело идёт о колебаниях, время входит только в форме sinν(t–t0),– выражение, вторая производная которого содержит множитель ν2. Следовательно, для определения частоты ν так как sinν(t–t0) исчезает из результата, мы получаем, в конце концов, уравнение относительно ν2 и только в исключительных случаях можно алгебраически извлечь квадратный корень. Дело обстояло бы иначе, как замечает это лорд Рэлей, если бы дифференциальные уравнения были первого порядка. К сожалению, введение ускорений со всех точек зрения представляется безусловно необходимым, так что на первый взгляд наше положение кажется безвыходным.
Однако, следующая простая гипотеза выведет нас из затруднения. Если силы, которые производят колебания, не будут определяться положением или деформаций системы, как это обыкновенно бывает для упругих и других систем, а будут зависеть от скоростей, то в уравнениях движения, кроме этих скоростей, будут содержаться их первые производные, т. е. ускорения; они будут первого порядка по отношению к скоростям.
Магнитная сила удовлетворяет именно этому условно; более того, мы уже не можем сомневаться в существовании мощных магнитных полей внутри атомов. По теории ферромагнетизма П. Вейссa4 (P. Weiss), эти поля, по крайней мере, порядка 107 гауссов (порядок величины молекулярного магнитного поля). Эта теория, как известно, нашла себе замечательное подтверждение в количественном объяснении аномалий удельной теплоты железа, никеля и кобальта. С другой стороны, Гёмфрейз (Humphreys) для объяснения законов перемещения лишь под влиянием давления (явление, открытое им несколько лет тому назад), должен был приписать эти законы взаимному действию молекулярных полей порядка величины 108 гауссов.
Легко показать, что с таким полем возможно бесконечным множеством способов получить колебания корпускулы с частотой, пропорциональной этому полю и порядка величины, соответствующей световым колебаниям. Достаточно, например, подчинить корпускулы условию, чтобы они оставались на определённом элементе поверхности или в данной плоскости: эта корпускула, будучи приведена в движете, будет совершать круговое движете частоты ν, пропорциональной составляющей Hn поля H, перпендикулярной к плоскости. Если к полю Hn прибавляется новое поле H'n, которое само по себе вызвало бы колебание частоты ν', то наложение обоих полей даст частоту ν+ν'. Таким образом, мы действительно получаем линейную зависимость, требуемую законом постоянных разностей и законами, приведёнными выше.
Предположим теперь, что силы, которые производят колебания, соответствующие линейчатым спектрам, или, точнее, спектрам с линиями, расположенными в серии, были бы исключительно магнитные. Эта гипотеза позволит нам объяснить существование предела частот и, в особенности, даст простое истолкование формул (1) и (2) для водорода; более того, она даст нам возможность понять происхождение аномальных и сложных явлений Зеемана (Zeeman). И тогда эта гипотеза станет тем более вероятной, что, несмотря на усилия многочисленных исследователей, до сих пор не было найдено никакого удовлетворительного решения ни той ни другой задачи.
Допустим (это будет наиболее простая гипотеза), что поле производится магнитом, и предположим, ввиду симметрии, что корпускула расположена на продолжении линии, соединяющей полюсы, на расстоянии r1 от первого и r2 от второго полюса, и что она совершает малые колебания в плоскости, перпендикулярной к этой линии. Пусть μ будет магнитный заряд одного из полюсов; тогда частота будет пропорциональна полю в точке, где находится корпускула, т. е.
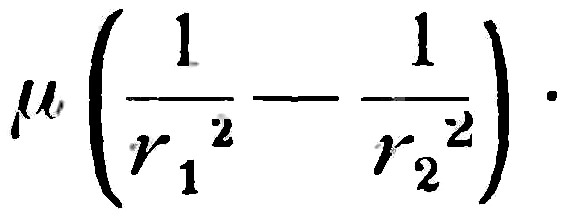
Пусть А будет коэффициент, который зависит только от заряда и от массы корпускулы; мы получим тогда:
частота ![]()
В этом виде мы уже узнаем столь любопытное строение формул (1)–(4).
Теперь, чтобы получить в точности формулы для водорода, достаточно предположить магнит состоящим из произвольного числа m' магнитов, тождественных между собою, каждый длиною а, расположенных в ряд один за другим. Кроме того, пусть магнит будет неизменно связан с элементом поверхности, в котором корпускула должна совершать колебания, посредством некоторого числа частичек таких же размеров, как магнитики, и так же расположенных в ряд, но не обладающих магнитными свойствами. Расстояния r1, r2 будут тогда кратными a; пусть r1=na, r2=ma, тогда частоты будут:
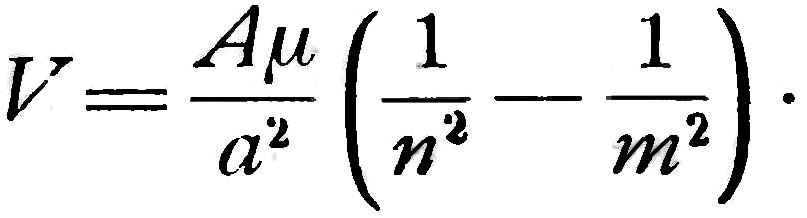
Остаётся только выбрать надлежащим образом постоянные A, μ, a, чтобы получить формулу (1) для водорода.
В общем, необходимо допустить, что при тех условиях, при которых водород даёт серию Бальмера, он способен находиться в различных состояниях, образуя некоторым образом полимеры. Это происходит оттого, что магнитные и немагнитные элементы, природу которых нет надобности точнее определять, могут в большем или меньшем числе образовывать группы наподобие прямолинейных чёток и присоединяться к атому водорода. Или же, чтобы дать конкретный образ, возьмём намагниченный стержень и два медных стержня той же длины и расположим их по прямой друг за другом. В том конце системы, где находится медный стержень, поместим надлежащий электрический заряд и дадим ему небольшой импульс; этот заряд будет колебаться и даст линию Hα. Приложив к концу первого второй намагниченный стержень, тождественный с первым, мы получим линию Hβ, третий стержень даст Hγ и т. д. Не противоречит ли подобное объяснение современным взглядам на строение материи? Нет основания утверждать это. Действительно, в теле вращения, которое вращается вокруг своей оси, легко распределить электричество различными способами так, чтобы это тело было эквивалентно элементарному магниту. Впрочем, вращательные или круговые движения электрических зарядов внутри атомов необходимы для объяснения магнетизма; причём первые более устойчивы. С другой стороны, системы, дающие линейчатые спектры,– и на этом также лорд Рэлей особенно настаивал, должны быть чрезвычайно устойчивы, так как в противном случае линии сделались бы расплывчатыми. Следовательно, если допустить, что химический атом есть собрание различных элементов, то гипотеза неизменной связи между этими элементами станет особенно вероятной. Наконец, из различных способов соединять переменное число элементов наиболее простой, бесспорно, это располагать их в ряд.
Вполне очевидно, что всякая отдельная гипотеза о строении атомов, могущая объяснить большое число линий спектров, покажется на первый взгляд более или менее невероятной. Стоит только над этим подумать, чтобы отдать себе в этом отчёт. Даже водород, кажущийся наиболее простым из элементов, имеет несколько спектров и испускает сотни линий самого разнообразного характера. Поневоле приходится допустить, что это простота очень относительная, и считать себя счастливым, если удастся найти хоть простые геометрические соотношения и известные силы, действующие по простым законам; это удовлетворяет гипотезе, которой мы занимаемся. Впрочем, можно изменить нашу систему различными способами,– например, избегать введения немагнитных элементов и т. д.
Важно, чтобы колебания производились магнитным полем, происходящим от двух полюсов, причём каждый из этих полюсов может занимать внутри атома несколько различных положений, но всегда расположенных на прямых линиях и на одинаковых расстояниях друг от друга.
Обобщение этих гипотез нас приводит к другим формулам таким же, как (2) и (3), причём всегда имеется предел для колебаний. Наблюдение нам дало тот замечательный результат, что множитель N один и тот же для всех тел. Наша теория требует, чтобы не только колеблющаяся корпускула, но и "элементарные магниты" были одни и те же для всех тел. Таким образом, наряду с корпускулами появляется второй новый элемент, входящий в состав всякой материи.
Известно, что в магнитном поле самым сложным образом обыкновенно разлагаются именно те линии, которые принадлежат к сериям. Насчитано пятнадцать и даже девятнадцать составляющих, причём очень часто расстояния между ними относятся, как целые числа. Лоренц (Lorentz) сделал попытку объяснить эти разложения, заменяя простой электрон элементарной теории системами с n степенями свободы, причём нужно столько же систем, сколько существует спектральных линий. Несмотря на чрезвычайную сложность этой гипотезы, она лишь в очень небольшом числе случаев даёт объяснение наблюдавшихся разложений, притом не физическое, а только математическое: закон же рациональных соотношений так и остаётся непонятным. Дело обстоит иначе с нашей гипотезой.– В большинстве случаев, под совместным действием внешнего и гораздо более сильного внутреннего поля, магнитная система будет совершать такие периодические колебательные движения, которые могут быть разложены в ряд Фурье (Fourier). Отсюда получаются для колеблющегося электрона более сложные движения, а вычисления показывают, что колебания можно разложить в сумму синусоидальных членов, соответствующих линиям частоты V0±mω, где V0 обозначает первоначальную частоту, m целое число, а ω период движения атома. Отсюда ясно, что расстояния составляющих находятся, действительно, в рациональных отношениях друг к другу; поляризация этих составляющих совпадает с той, которая получается из опыта. Один электрон, в большинстве случаев, сам по себе даёт бесконечное число составляющих, из которых только некоторые достаточно сильны, чтобы их можно было заметить; их число зависит от быстроты сходимости ряда. Итак, с этой точки зрения для вращательных движений атома явление Зеемана играет роль гармонического анализатора.
Можно ли из всего вышесказанного заключить, что колебания спектров, имеющих серии, действительно обязаны своим происхождением интенсивным магнитным полям? Вполне понятно, что подобное заключение не представляется нам убедительным; на первый взгляд недостаточно знать колебания системы, чтобы составить себе представление о её строении. Чтобы быть убедительной, теория должна давать простое объяснение совокупности всех наблюдений и связывать их с другими областями. Все другие способы объяснения должны казаться для нашей мысли несравненно менее экономными. Для этого и необходимо их всех разрабатывать, и потому я хотел бы в заключение сказать несколько слов об одном из этих способов, единственном, который в настоящее время заслуживает серьёзного внимания.
Как известно, колебания упругих тел, подобно колебаниям серий спектра, существуют в бесконечном числе; их частоты зависят от некоторых целых чисел, которые суть числа узловых линий (хладниевы фигуры) или же узловых поверхностей, характеризующих каждое колебание. Для прямоугольной мембраны мы имеем V2=am2+bn2, где а и b – постоянные, а m и n – целые числа. Но в противоположность спектральным сериям, при бесконечном увеличении чисел m и n то же происходит и с числом V.– При более глубоком анализе это можно объяснить тем, что силы, производящие упругие колебания, уничтожаются на маленьком расстоянии. Мог бы явиться вопрос, не дадут ли другие силы, действующие по закону Ньютона или по другим законам, формул типа (1), (2) и (3). Эта гипотеза была исследована автором этой статьи, а затем Фредгольмом (Fredholm) и Адамаром (Hadamard). Эту гипотезу можно математически выразить уравнениями интегральными, а не дифференциальными. Из этих изысканий следует, что закон квадратов расстояний и бесконечное число других, действительно дают предел для колебаний. К сожалению, аналогия, по-видимому, на этом и кончается, ибо, чтобы на самом деле получить формулы (1) и (2) для водорода, нужно ввести законы невероятной сложности; из простых же интегральных уравнений Фредгольма нельзя их вывести. Впрочем, недостаточно найти для каждой серии спектра соответствующий ей особый закон; нужно, чтобы этот закон не был слишком неправдоподобен и не слишком превосходил бы своей сложностью ту формулу, которую нужно было объяснить.
Тот факт, что уравнение в этой гипотезе содержит квадраты частот, не может ещё способствовать упрощению задачи, а скорее указывает на большое значение замечания Лорда Рэлея, о котором было выше упомянуто. Чтобы иметь исключения из этого правила, нужны сложные логические построения. Наконец, если мы оставим в стороне всякое предубеждение с физической точки зрения и будем просто стараться удовлетворить математическим условиям задачи, то мы будем приведены к системам, в которых только основание колебания даёт заметное излучение; излучение же высших гармонических почти что равно нулю вследствие влияния узловых линий; поэтому их нельзя было бы заметить.
Несмотря на это, все эти гипотезы заслуживают тщательного изучения; хотя они и не применимы к линиям серии, но они могут применяться к другим линиям, о расположении которых мы ничего не знаем, а также и к полосатым спектрам, основные законы которых, данные, как известно Деландром (Deslandres), представляют много важных аналогий с законами известных колебательных систем.
В общем, для объяснения самой простой серии спектров водорода и других тел следует приписать колебания этих линий влиянию мощных магнитных полей магнитных полюсов, распределённых в атоме по простым геометрическим законам. Важно отметить, что энергия этих систем исключительно электромагнитная.
Дата установки: 23.08.2012
[вернуться к содержанию сайта]