[вернуться к содержанию сайта]

В статье показано, что физики допускают математическую ошибку, считая, что любые решения уравнения Даламбера являются функциями запаздывающих потенциалов. Приводится доказательство того, что существуют вырожденные (мгновенно действующие) решения этого уравнения. Требование от уравнений релятивистской ковариантности не спасает их от появления вырожденных решений. Таким образом, физика постулирует предельную скорость распространения взаимодействий, а на деле описывает взаимодействия зарядов через мгновенное взаимодействие. Релятивистские теории оказываются внутренне противоречивыми и их использование в области физики плазмы, астрофизики, создании термоядерного синтеза грозит ошибками и непредсказуемыми результатами.

Эта статья посвящена анализу одной “застарелой” математической ошибке в физике, которой около ста лет. Она послужила основой многих противоречий. Результаты обсуждались на нескольких форумах. Авторы признательны оппонентам (С. Подосенову, В. Морозову, Г. Деревягину, В. Сомову и другим) за критику, “каверзные” вопросы и рекомендации, которые способствовали более точному изложению проблемы.

1. Вырожденные решения

Хорошо известно, что для различных начальных условий решение неоднородного волнового уравнения будет различным. Но мы его дополним следующим важным положением: решения неоднородного волнового уравнения в зависимости от начальных условий могут быть функционально различными. Решения могут иметь либо запаздывающий характер, либо мгновенно действующий характер (вырожденные решения).

Выдвигается положение (не отражённое в учебниках по математической физике), что среди совокупности всех начальных условий существует класс таких начальных условий, при которых решение уравнения Даламбера имеет мгновенно действующий характер.

Доказательство опирается на возможность введения дополнительных условий (таким условием, например, может служить уравнение непрерывности или родственное ему), которые снимают необходимость задания начальных условий, т.е. приводят уравнение Даламбера (уравнение гиперболического типа) к уравнению эллиптического типа.

1. Итак, с помощью уравнения непрерывности (или иного эквивалентного условия) мы сводим уравнение Даламбера к уравнению эллиптического типа и находим его решение.
2. Найденное решение полученного уравнения эллиптического типа удовлетворяет исходному уравнению Даламбера (вырожденное решение).
3. Оно является мгновенно действующим.
4. Из полученного решения мы всегда можем найти начальные условия задачи Коши для уравнения Даламбера.
5. Задание этих начальных условий позволяет найти решение уравнения Даламбера (то же самое вырожденное решение), используя регулярные методы, без введения дополнительных условий (например, без введения уравнения непрерывности). Это решение единственно и является мгновенно действующим (вырожденным), а не запаздывающим.

Итак, начальные условия, при которых имеет место вырожденное решение задачи Коши для уравнения Даламбера, существуют.

Примером может служить решение уравнения Пуассона

,

которое одновременно является решением уравнения Даламбера

при соответствующих начальных условиях.

Ниже это положение будет проиллюстрировано и на других примерах.

Важно отказаться от иллюзии (предрассудка), что решение волнового уравнения всегда является функцией только запаздывающих и опережающих потенциалов, а появление вырожденных (мгновенно действующих) членов в решении волнового уравнения исключено.

Функциональная зависимость решений волнового уравнения от выбранных начальных условий это, прежде всего, математическая задача. Именно математики должны дать её решение. Однако в стандартных учебниках по математической физике внимания этой проблеме практически не уделяется. В результате в электродинамике существует масса проблем, связанных с “вырождением решений” и требующих анализа.

1. “Рождение” заряда

Убеждение, что уравнения Максвелла не способы описывать “рождение” зарядов, достаточно прочно “укоренился” в сознании тех, кто профессионально занимается проблемами электродинамики. С одной стороны, этот факт опирается на известный всем закон сохранения заряда. С другой, потенциалы поля заряда описываются волновым уравнением, и вопрос о возможности или невозможности описания “рождения” ещё не имеет обоснования. Ниже мы рассмотрим этот вопрос и те интересные следствия, которые из анализа проблемы.

Рассмотрим два тонких соосных заряженных цилиндра, вставленных друг в друга, как показано на рис. 1. В силу того, что равномерно распределённые по поверхности заряды имеют противоположный знак и равны по величине, потенциалы вне этих цилиндров (исключая краевые эффекты) наблюдаться не будут.

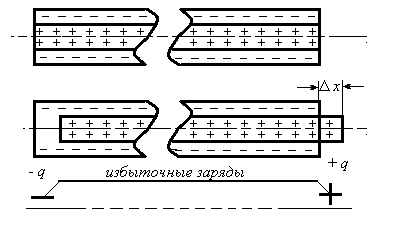
Рис. 1

Теперь сдвинем один цилиндр вдоль общей оси на очень небольшое расстояние D х. Тогда слева на краю системы появится “избыточный” заряд отрицательного знака, а справа – положительный заряд, равный по величине отрицательному. Таким образом, в соответствии с законом сохранения заряда мы “родили” на большом расстоянии друг от друга два разноименных заряда.

Уравнения Максвелла в калибровке Лоренца являются линейными дифференциальными уравнениями. По этой причине мы можем использовать для описания появления потенциалов полей зарядов принцип суперпозиции. Другими словами, мы можем дать раздельное описание “рождения” потенциалов каждого из этих двух зарядов. Ниже мы это сделаем для положительного заряда. Потенциалы отрицательного заряда могут быть описаны аналогичным образом.

Начнём с математической постановки задачи для волнового уравнения. Итак, имеем неоднородное волновое уравнение

            (2.1)

где f – обильность источника (вынуждающая сила).

Под начальными условиями только для уравнения (2.1) для определённости будем считать условия при t = 0:

u (r; 0) = j (r); u_t(r; 0) = y (r).             (2.2)

Все другие условия для текущего времени t (например, неподвижные или подвижные границы и т.д.) мы будем относить либо к граничным условиям, либо к условиям связи.

Что здесь интересного?

1. До момента времени t = 0 вынуждающая сила (обильность источника) f формально “отсутствует” для данной задачи; “не существует”, если хотите.
2. Если эта сила и действовала до этого времени, отголосок её действия и действия других сил, существовавших до начального момента времени (t = 0), отражён (заложен) в начальных условиях (2.2). Начальные условия (2.2) это “фотография следов” того, что уже произошло.

Следовательно, при описанной постановке задачи мы имеем законное право, рассматривать момент времени t = 0 как момент “рождения” вынуждающей силы f.

1. Точечный заряд

Любой заряд имеет конечные размеры. Однако в электродинамике обычно используется идеализация – точечный заряд. К точечному заряду можно прийти, когда радиус заряда пренебрежимо мал по отношению к характерным размерам (расстояниям) в физической задаче. При этом потенциал вне заряда не зависит от радиально симметричного распределения плотности внутри самого заряда, а определяется суммарной величиной заряда q и расстоянием от точки наблюдения до заряда. Если в дальнейшем мы намереваемся использовать точечную идеализацию заряда, исходная модель заряда не играет принципиальной роли.

Итак, пусть рождающийся в момент времени t = 0 заряд представляет собой сферу, на поверхности которой этот заряд распределён равномерно с плотностью s = q / 4p a², где а – радиус сферы.

Потенциал при r = 0 должен быть ограничен. Начальные условия нулевые.

А) Имеем уравнение для потенциала поля заряда:             (3.1)

В силу сферической симметрии

Обозначив u = r f , получим уравнение, которое напоминает уравнение для струны.



Итак, задача сведена к действию точечного источника, находящегося на расстоянии а от начала координат. Чтобы потенциал u не возрастал во времени, необходимо, чтобы конец струны был “закреплен” в начале координат: u(0; t) = 0.

В) Решение для a > r > 0 имеет вид

при ct >> 2a

т.е. потенциал f равен

при ct >> 2a

где

Решение для r > a , когда ct > 2a

при 2a < r < ct - a

Соответственно, потенциал f равен

            (3.2)

при 2a < r < ct - a имеем .

Заметим, что “вычитание” потоков в выражении (1.2) связано с наличием какого-то отражающего “керна” в центре заряда (ср. струна, закреплённая в начале координат). “Керн” обеспечивает отражение потенциала от центра заряда с потерей фазы, равной p . Причина существования керна неизвестна, но он присутствует в любой модели заряда. Именно он ограничивает рост потенциала во времени.

С) Устремив в выражении (2) а к нулю, получим             (3.3)

Это конечный результат – потенциал, возникший при рождении точечного заряда. Никакого математического или физического криминала здесь нет. “Рождение” заряда прошло весьма благополучно (корректно). По форме выражение (3.3) напоминает решение уравнения Пуассона для покоящегося точечного заряда

            (3.4)

Различие между (3.3) и (3.4) только в множителе h (ct - r). Если считать, что заряд родился в незапамятные времена, граница, определяемая h (ct - r), столь далека, что, можно считать её расположенной в бесконечности. На этом основании считается, что выражения (3.3) и (3.4) можно считать равноправными. Физики так и поступают, а это ошибка!

2. Различие решений

Чтобы показать различие решений (3.3) и (3.4), предположим, что мы можем “включать” покоящийся точечный заряд q на малое время d t через равные промежутки времени. Начальным условием каждого последующего “рождения” будут служить потенциалы и их производные по времени, образованные предыдущими “рождениями”, существующие в момент времени нового “рождения”.

Мгновенно действующий потенциал, определяемый выражением (3.4), будет равен нулю, когда заряда нет. Но когда заряд появляется хотя бы на короткое время d t , мгновенно и одновременно во всем пространстве появляется потенциал, определяемый выражением (3.4). Столь же мгновенно он исчезает при исчезновении заряда.

Рассмотрим теперь запаздывающий потенциал, описываемый выражением (3.3). Здесь появление заряда на время d t и его исчезновение сопровождает совсем иная картина изменения потенциала.


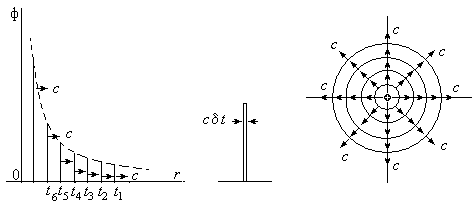
Рис. 2

При существовании заряда в течение времени d t в пространстве возникает потенциал в виде тонкого сферического слоя, который распространяется вдоль радиуса со скоростью света. Величина потенциала по мере удаления этого потенциала от “точки рождения” убывает в пространстве как 1/r. Последовательность “включений” заряда рождает “раздувающиеся” со скоростью света концентрические сферы.

Если величина интервала между “рождениями” стремится по величине к длине d t, то сферы сливаются между собой, образуя непрерывное и независящее от времени распределение потенциала (3.3) внутри сферы радиуса r < ct. Однако “скрытое” или “замаскированное” движение потенциала сохраняется.

Итак, мы выявили принципиальное различие выражений (3.3) и (3.4).

3. Запаздывающий потенциал движущегося заряда

Ещё более значительное различие характера изменения потенциалов проявляется, когда мы рассматриваем равномерно движущийся заряд. Пусть этот заряд движется с постоянной скоростью v вдоль оси х.

            (5.1)

Прямое решение в форме запаздывающих потенциалов (при нулевых начальных условиях) даётся формулой Кирхгофа [1]

            (5.2)

где ; расстояние отсчитывается от точки наблюдения до точки нахождения заряда.

В физической литературе обычно приводится рисунок поверхностей равных потенциалов (см. рис. 3) которые движутся в свободном пространстве со скоростью v вместе с зарядом. Кажется, что эти поверхности “прикованы” к заряду и движутся с ним синхронно.

 


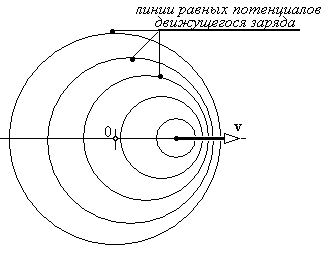
Рис. 3

Будем (как и в предыдущем случае) “включать” движущийся точечный заряд q на малое время через равные промежутки времени. Когда заряд появляется на короткое время d t, он генерирует потенциал. Этот потенциал, как и в случае неподвижного заряда, распространяется со скоростью света от точки появления заряда. Картина процесса приведена на рис. 4.


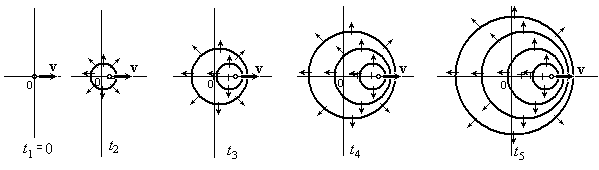
Рис. 4

Вновь образуются “раздувающиеся” сферы, которые теперь уже не являются концентрическими. Очевидно, что распространение потенциала не сопровождается переносом энергии. Причина: потенциал образуется двумя потоками, которые вычитаются друг из друга. Это было показано в первом параграфе.

Оба рисунка (рис. 3 и рис. 4) выглядят практически одинаково. В действительности сферические поверхности (рис. 4) распространяются в стороны со скоростью света от точек своего “рождения”. Линии же равного потенциала “перемещаются” со скоростью v вдоль оси х.

Когда расстояние между точками “рождения” уменьшается, и мы переходим к непрерывному перемещению заряда. Только тогда распространяющиеся сферические поверхности (рис. 4) смыкаются, образуя рельеф, изображённый на рис. 3, который “маскирует” действительную картину процесса.

4. Мгновенно действующий потенциал движущегося заряда

Совершенно иная картина возникает, если мы рассматриваем мгновенно действующий потенциал заряда, удовлетворяющий уравнению Пуассона. Для такого случая, используя своё преобразование, Лоренц получил формулу

            (6.1)

Вид линий равного потенциала для этого случая приведён на рис. 5.

Линии равного потенциала в обоих случаях (рис. 3 и рис. 5) перемещаются синхронно с зарядом с той же скоростью вдоль оси х. Но в характере эквипотенциальных поверхностей, изображённых на этих рисунках, видно принципиальное различие. Пуассоновский потенциал (рис. 5) симметричен в противоположность запаздывающему потенциалу (рис. 3). Помимо этого, когда заряд “рождается”, вокруг него мгновенно во всём пространстве образуется потенциал. Если же заряд “исчезает”, столь же мгновенно исчезает и окружающий его потенциал.


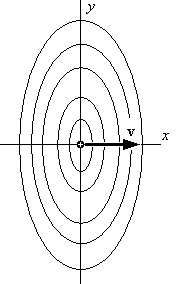
Рис. 5

И, тем не менее, в физике укоренился предрассудок, что потенциалы, изображённые на рис. 3 и рис. 5 одинаковы (!), т.е. представляют одну и ту же картину. Любому здравомыслящему человеку ясно, что утверждение об эквивалентности этих потенциалов не имеет под собой почвы; но только не физикам-релятивистам. Их попытка доказать эквивалентность [2] – умышленная или неосознанная фальсификация.

5. Строгое решение

Мы не будем использовать лёгкий путь Лоренца, а попробуем получить лоренцевские потенциалы прямым решением волнового уравнения. С одной стороны, это послужит иллюстрацией для первого параграфа. С другой стороны, это позволит нам рассматривать и сравнивать решения в одних и тех же пространственных координатах и при одном и том же течении времени. Последнее обстоятельство делает возможным сопоставить решения непосредственно, избегая затрагивать вопросы, связанные со специальной теорией относительности.

Известно, что векторный потенциал равномерно движущегося заряда связан со скалярным потенциалом соотношением . Помимо этого, существует условие для калибровки Лоренца . Нетрудно показать, что эти два выражения дадут уравнение непрерывности для скалярного потенциала

            (7.1).

Им мы и воспользуемся, чтобы преобразовать уравнение (5.1). Используя (7.1) мы можем исключить в уравнении (5.1) производную потенциала по времени.

            (7.2)

Учитывая (7.2), волновое уравнение (5.1) приводится к уравнению эллиптического типа

            (7.3)

Теперь нам нет необходимости задавать начальные условия, поскольку производная по времени от потенциала f в уравнении отсутствует!

Далее делаем замену и обращаем выражение (7.3) в уравнение Пуассона.

            (7.4)

Решением этого уравнения будет потенциал Лоренца.

(7.5)

Выражение (7.5) тождественно выражению (6.1) и является прямым решением волнового уравнения при выполнении условия непрерывности.

1. Выражение (7.5) является решением волнового уравнения (удовлетворяет волновому уравнению).
2. Выражение (7.5) является мгновенно действующим.
3. Выражения (5.2) и (7.5) являются результатами решения одной и той же физической задачи, описываемой одним уравнением: нахождение потенциалов заданного источника, хотя начальные условия для них различные. Эти решения существуют в едином пространстве и являются функциями общего времени. Они не сводимы друг к другу, поскольку соответствуют различным начальным условиям.
4. Заметим также, что преобразование Лоренца, являясь линейным алгебраическим преобразованием координат и времени, не меняет функционального характера полей. Если потенциал неподвижного заряда является мгновенно действующим, то потенциал равномерно движущегося заряда также является мгновенно действующим (но никак не запаздывающим). Требование релятивистской “ковариантности” не спасает уравнения от появления взаимодействий мгновенного характера.

Казалось бы, что вырожденные решения (мгновенно действующие поля и потенциалы) должны отсутствовать в физических теориях. Их отсутствие гарантируется постулатами Специальной теории относительности. Постулат о конечной скорости распространения взаимодействий утверждает, что скорость света является предельной скоростью распространения “всего и вся”.

Но релятивистская физика - “особая” наука. Здесь, как говаривал персонаж А. Райкина: “два пишем, “один” на ум пошло”! Оказывается, что практически всегда взаимодействия заряженных частиц описываются с помощью “релятивистски ковариантных” мгновенно действующих потенциалов.

Что же ошибочно: мгновенное взаимодействие или же тот самый постулат? Ответа вы не дождётесь. Релятивисты, как обычно, объявят логическое противоречие “парадоксом” и будут приводить “умные” объяснения, ссылаясь на “искривления пространства и времени”. Объективно решение этой математической проблемы смогут оценить только математики.

Научная теория не должна содержать логических противоречий и математических ошибок. В противном случае она превращается в эклектику. Мы пишем об этой математической ошибке потому, что взаимодействие заряженных частиц лежит в основе физики плазмы. С ней связаны такие важные направления как астрофизика, термоядерный синтез и другие. На исследования по созданию установок термоядерного синтеза выделяются огромные средства. Экспериментальные установки будут строиться не на “интуиции”, а исходя из теоретических предпосылок.

Если оглянуться во времени, то ещё 50 лет назад физики с оптимизмом утверждали, что проблема термоядерного синтеза будет решена не позднее, чем через 10 – 15 лет. “А воз и ныне там!”. Естественно, деньги на исследования текут, текут…

А что можно ожидать от теории, если она непоследовательна (эклектична) и имеет математические ошибки? В лучшем случае растрата финансовых средств. В худшем – “фейерверк” подобный Чернобыльской катастрофе. В её основе будет та самая математическая ошибка, о которой мы написали выше.

Но если бы это была единственная математическая нелепость. Если внимательно присмотреться, можно обнаружить ещё несколько. Например, известно, что принцип наименьшего действия реализуется с помощью математического вариационного принципа. Для этой цели записывается функционал и отыскивается экстремум этого функционала. Экстремум реализуется на траектории (экстремаль), которая описывается дифференциальным уравнением (уравнение движения).

В отличие от классических теорий релятивистский функционал постоянен и не имеет экстремумов. Все получаемые из него релятивистские уравнения движения неоднозначны и не реализуют принцип наименьшего действия.

Приходится, с сожалением, признать, что фундаментальные основы современной релятивистской физики представляет собой удручающее зрелище. Мы попытались оценить возможные изменения в основах физики, если эти ошибки будут исправлены. В форме популярной статьи это сделано в [3], строгой форме это изложено в [4], [5].

В Интернете легко найти множество статей с критикой СТО, ОТО, квантовых и других теорий. Со временем этот поток критики не уменьшается. Почему же РАН и ведущие специалисты не реагируют на критику?

Причина в философии естествознания. Уже в начале прошлого века началось массированное наступление на материализм, попытки замены материализма позитивизмом. Сейчас о материализме вспоминают изредка. Позитивизм занял прочные позиции в философии естествознания [6]. Используя недозволенные методы давления на оппонентов и студентов (“Не понимаешь СТО? – Ты дурак, и тебе не место в физике”), позитивисты присвоили себе исключительное право на научную ИСТИНУ.

Такое понятие как “гносеологическая ошибка” исчезло из физической лексики. А ведь “гносеологическая ошибка” это ошибка в объяснении явлений, в интерпретации формул и результатов эксперимента. Она возникает, если физик опирается на ошибочное (нематериалистическое) миропонимание (т.е. мировоззрение = философию). Вот по какой причине важна роль философии в физике. Позитивизм оказался весьма агрессивен [6] и породил нездоровый прагматизм (истинно то, что полезно для меня). Понятие “научная истина” приобрело субъективный смысл (истина должна совпадать с мнением научного Авторитета).

Те люди, которые сумели сохранить независимость (суверенность) мышления, постоянно пытаются обратить внимание РАН на состояние физических теорий. Но никто из РАН не способен “перешагнуть” через собственные амбиции, высокомерие и веру в свою “непогрешимость”. К ним обращаться бесполезно. По этой причине остаётся обратиться к общественности через СМИ с вопросами:

• Вам не жаль средств, которые (в условиях мирового кризиса) будут безрассудно растрачиваться на проекты, основанные на сомнительных теориях?
• Вы можете “надавить” на релятивистов, требуя от них отчёта, или же станете с безразличием ждать, когда “грянет гром” Второго Чернобыля?

1. Тихонов А.Н., Самарский Ф.Ф. Уравнения математической физики. ГИТТЛ, М. 1953.
2. Ландау Л.Д., Лифшиц Е.М. Теория поля. ГИФФМЛ, М. 1960.
3. Корнева М.В., Кулигин В.А., Кулигина Г.А. Математическая ошибка, которая исказила физику. http://n-t.ru/tp/ns/mo.htm , ritz-btr.narod.ru, 2008.
4. Корнева М.В., Кулигин В.А., Кулигина Г.А. Анализ классической электродинамики и теории относительности. http://n-t.ru/tp/ns/ak.htm , http://ritz-btr.narod.ru/kuligin-1.html, 2008
5. Кулигин В.А., Кулигина Г.А., Корнева М.В. Ревизия теоретических основ релятивистской электродинамики. http://n-t.ru/tp/ns/rt , 2007.
6. Кулигин В.А. Вавилонская башня вульгарного позитивизма. http://n-t.ru/tp/ns/vb.htm , 2004.

Дата установки: 06.01.2009
[вернуться к содержанию сайта]

W