[вернуться к содержанию сайта]

JOURNAL OF THE OPTICAL SOCIETY OF AMERICA
VOLUME 52, NUMBER 9, SEPTEMBER 1962
Direct First-Order Experiment on the Propagation of Light from a Moving Source
WALLACE KANTOR*
U. S. Navy Electronics Laboratory, San Diego 52, California
(Received December 1, 1961)

INTRODUCTION

    A REVIEW of the kinematic experimental basis of the Einstein special theory of relativity was undertaken by the author. The investigation of these experiments was motivated by the results of an operational analysis of the Einstein theory about which certain doubts were indicated. A critical examination of the kinematic experimental evidence reported in the literature was found to be inconclusive, theoretically incorrect, or in disagreement with the Einstein theory contrary to its popularly considered overwhelming corroboration.¹ No report of an experiment of a direct nature which was above reproach was found. The validity of the Einstein postulate on the propagation of light has therefore always had to be inferred on the basis of indirect kinematic and dynamic experimental results. These were first-order convection effects (Einstein's "addition" theorem), second-order Doppler effects, second-order time dilation but no length-contraction effects, second-order mass effects, and seemingly plausible arguments (not actual experiments) advanced for the de Sitter "effect."

    A direct interferometric light-transit-time experiment was initially conceived by the author some two years ago. It was undertaken in a modified and simpler form in mid-June 1961. The result was observed in early October 1961.

    The two light beams, formed by a beam splitter by reflection and transmission of light from a common, stationary, collimated xenon source, are coherent and traverse the interferometer [Fig. 1(a)] in opposite directions recombining at the beam splitter to produce vertical interference fringes which were seen with the aid of a telescope focused almost for infinity. Two very thin (about 0.005 in.) transparent glass windows were mounted perpendicularly to the plane of a rotating disk at opposite ends of the same diameter [Fig. l(b)]. At one end of the disk diameter perpendicular to that on which the windows were mounted, a small magnet was embedded in the disk. A triggering signal was obtained by means of a small pickup coil mounted just below the disk magnet. This signal was used to produce a very short flash (15 μsec) of light from the xenon source. The light flash occurred when the windows were in a position normal to each longitudinal light path of the interferometer, as shown in Fig. 1(b).

    The windows were approximately four-tenths of the height of the interferometer optics, so that the lower part of the light beams went through the windows while the upper six-tenths passed above them. The optical path length through the windows was not quite the same as the geometrical path length above the windows due to the tiny but finite thickness of the windows. This slight difference produced no noticeable difference in the fringe separations or the fringe pattern seen in the whole field of view through the windows and above them when the disk was stationary. The disk rotation being only counterclockwise, the light beam transmitted by the beam. splitter passed through the windows in opposition to their motion, while the reflected light beam went around the interferometer in the opposite direction and through the windows concurrent with their motion.

Fig. 1. (a) Photograph of the transit time interferometer experiment, (b) Photograph of disk, windows, and compensating mirror system.

    Phenomenologically, the light incident at the face of the moving or stationary window is absorbed and reemitted in the medium of the window with the characteristic medium speed (c/n) relative to the window. Traveling to the opposite face of the window the light is emitted from the window with the characteristic speed c relative to the moving or stationary window. The Einstein postulate on light propagation assumes that the speed of the light emitted from the moving window is independent of the window motion, so that its speed relative to the interferometer optics or the laboratory is also c. The transit time of each light beam around the interferometer passing through and above the windows would therefore be essentially unaltered whether the windows were stationary or in motion, and as a consequence the fringes seen through the windows would remain unaltered relative to the fringes seen above the windows. In fact, apart from an experimentally negligible convection effect with moving windows, the whole fringe system would in no way be changed or displaced, since the conditions of initial interference with stationary windows would be unaltered. A dependence of the speed of the light (emitted from the moving windows) relative to the interferometer would mean that the transit time around the interferometer of the part of light beam passing through concurrently with the window motion would be decreased, while that of the oppositely traveling light beam would be increased. Such a transit time difference would manifest itself as a displacement or shift of the fringes seen in the field of view of the windows relative to fringes seen above the windows; the transit time difference of the light above the windows remains zero and unchanged. The experiment, purely phenomenologically and qualitatively, would yield directly a "yes" or "no" verdict on the validity of the Einstein postulate independently of any indirect theoretical constructs or inferences.

    An unambiguous, easily noted shift of the fringes in the field of view of the moving windows was observed relative to the fringes seen above the windows (Fig. 2). The observation was in qualitative agreement with the effect predicted from the relative dependence of the speed of light on the motion of its source. The convection effects due to the motion of the windows and the air were demonstrated to be experimentally negligible compared to the transit-time effects due to the use of such thin windows and the small refractive index of air.

    The next section describing the apparatus may, at the discretion of the reader, be omitted on a first reading.

APPARATUS

    The optical table seen in Fig. 1(a) consisted in part of two flat steel plates between which a nine-in. layer of very resilient porous rubberized hog's hair was placed. This "sandwich" was supported on a horizontal open box-like frame-work of steel channel beams which were spot welded to the top of a low flat steel table. A zinc alloy (Kirksite) was cast and machined into a flat slab 56 in. long and 26.25 in. wide. It was four in. thick. The slab, weighing about 1400 lb, was placed on top of the "sandwich" producing a static deflection in the rubberized hog's hair of 6 in. The zinc surface then stood about 35 in. above the floor.

    Centered at one end of this arrangement a circular hole 5 in. in diameter was machined beforehand into the zinc slab and the two steel plates. The hog's hair in this hole was removed, and through the hole was mounted, free and clear, a small air-driven 1/4 hp motor, the shaft of which protruded about 3 in. above the zinc surface. The motor mount was kinematically supported by three pointed leveling screws in corresponding conical holes on the surface of the flat steel table below the "sandwich." A flat circular aluminum disk 3/16 in. thick and 10.760 in. in diameter was mounted on the protruding shaft of the motor.

    Each leg of the steel table was provided with a leveling bolt by means of which the zinc surface could be made quite horizontal with the aid of a spirit level. The plane of the disk could then be made parallel to the zinc surface by means of the motor-instrument screw mount. The interferometer, which was fastened to the zinc surface, was by this arrangement isolated from motor and table conducted vibrations. Adjacent to (but not touching) the end of the steel table removed from the motor, a low wooden table was placed on the concrete floor. An optical bench, supporting a light source, an iris and an achromatic collimating lens (f/1.9, focal length 5 in.), was clamped to the wooden table. This may be seen at the left of Fig. 1(a).

    The interferometer shown in Fig. 1(a) and Fig. 1(b) was mounted on the two halves of a flat aluminum ring, 3/16 in. thick, whose inside and outside diameters wen 8¾ in. and 15¾ in., respectively. The positions of the mirror and beam-splitter mounts were carefully scribed on the ring. The necessary screw holes were drilled and tapped and the ring was then cut in half on its transverse diameter. The two halves were then bolted onto the carefully laid out positions at the opposite ends of the zinc surface. The beam splitter was 1 in. square and ¼ in. thick. Three of the mirrors were also 1 in. square and 13/32 in. thick. The fourth mirror was the same thickness and 1 in. high by 3 in. long even though a length of 1 in. would have been satisfactory. All the mirrors were cut from the same piece of BSC-2 glass after its surface was ground and polished to λ/20 for the mercury green line. The beam splitter was made of BSC-2 Schott glass with λ/20 surfaces. The bottom edges of all these optical pieces stood 2¼ in. above and parallel to the zinc surface. The top surface of the motor-driven aluminum disk was 2⅜ in. above the zinc surface. An aluminum reflecting surface was vacuum evaporated on the mirrors. The beam-splitter vacuum evaporated layer yielded 35% transmission and 37% reflection for mercury light (λ=5461 Å) at 45° incidence. No protective coating was deposited on any of the aluminized surfaces.

    An 1/8 in. cylindrical Alnico magnet rod was ground to the same thickness as the disk and was press fitted into a hole in the disk at a radius of 5 in. A corresponding brass plug of equal weight was similarly imbedded at the opposite side of the disk to obtain dynamic balance. On the perpendicular diameter two 1/8-in. cylindrical aluminum posts were press fitted into jig-bored holes at a radius of 5.0675 in. Two more were likewise placed on the same diameter at a radius of 4.5675 in. The posts which protruded above the disk 0.395 in. were then carefully milled halfway so that flat surfaces were presented which were 0.0025 in. displaced behind the diameter on which the post centers were collinear. Thin glass windows 0.005 in. thick, 5/8 in. wide, and 0.395 in. high were ultrasonically cut from microscope cover glass carefully selected under mercury light so that their faces were parallel to about ¼λ. These windows were fixed to the flat post surfaces with Eastman 910 contact cement. The horizontal aperture of the windows was then 3/8 in. The disk and the posts had previously been painted black as were the mounts of the interferometer optics.

    A honeycomb coil, wound on a powdered iron core, was mounted on a semicircular aluminum ring 5 in. in radius. This ring was fastened onto the zinc by screws. The flat surface of the core was in very close proximity (about 0.005 in.) to the magnet in the disk. The coil could also be displaced to and fro along the periphery under the disk on the semicircular ring to which it was fastened by a thumb screw. The arrangement may be seen in Fig. 1(b). The coil was connected to an audio amplifier by a thin shielded wire which went down through the hole in the "sandwich." The output of the amplifier was connected to the 6-V filament winding of a small power transformer. Signals of as much as 400 V could be taken off the high-voltage winding of the transformer, which was used to externally drive a stroboscope (General Radio Company Strobotac type 631-B). A germanium diode was connected across the Strobotac input so that only one side of the positive and negative going signal from the pick-up coil was used. A Hewlett-Packard model 523-B electronic counter recording on 1- or 10-sec intervals was also connected to the Strobotac input so that the average speed of the disk could be measured. The Strobotac was used in turn to drive an intense continuous-spectrum xenon-light source in the form of a General Radio Company Strobolux type 648-A. The 9-in. aperture of the Strobolux was occluded by a reflecting cover except for a 9/16-in. hole at the center. The Strobolux generated light flashes of 15×10^-6 sec duration, 61 times a sec when the disk was rotating at its maximum speed. Under this synchronized stroboscopic light a given window was always seen at the same position. One had the impression that the counterclockwise rotating disk was being moved to and fro by a handle fixed to it when the pick up coil was moved back and forth. Similar but smaller motion could be obtained by varying the bass and treble controls of the amplifier.

    The coil position was fixed so that the vertical plane of the windows was normal to the field of view of the interferometer. The position was not found to be critical for the fringe pattern obtained until the windows were almost out of the field of view which was about 15° from the normal position. When the interferometer was adjusted to produce vertical straight fringes and the windows were in their normal position, the fringes were undistorted in the bottom part of the field occupied by the windows. They were perfectly straight and vertical over the whole field with and without the windows. The fringe system was not affected when the windows were oscillated by displacing the disk by hand back and forth by as much as some 15°.

    Alignment of the interferometer proved to be critical and difficult. Two small thin vertical sandblast-finish aluminum screens were mounted on heavy brass bases. The screens were scribed with fine vertical and horizontal lines for the top, bottom, sides, and center of the field of view. Additional vertical lines were scribed where the edges of the shadow of the window posts would fall in collimated light. The screens were placed normal to and in the field of view by obtaining coincidence of the lines scribed on their brass base with the longitudinal lines scribed on the zinc which were initially used to locate the two halves of the interferometer. The zinc lines were central to the interferometer optics. Adjustment prevailed when the shadows of the window posts and the top edges of the windows coincided and fell in the correct position on the screen when the screen was placed first in front of one window and then in front of the other. The collimated light beam was also directed correctly into the interferometer by inserting both screens near the disk and adjusting the mirror adjacent to the beam splitter [Fig. l(a)] so that each screen was illuminated in its central field area.

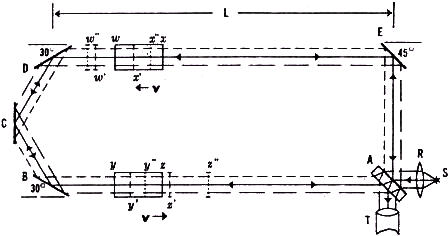
Fig. 3. Interferometer diagram with windows grossly exaggerated.

THEORY AND OBSERVATIONS

    A diagram of the interferometer is given in Fig. 3 in which for purposes of clarity the thickness of the windows is grossly exaggerated, so that they appear as rectangular rods. Expressions for the transit time t_t of the light beam transmitted through A, and the transit time t_r of the light beam reflected from A will now be obtained. Let the moving window faces, moving with speed v, be near the static normal positions denoted by w, x, y, z when the transmitted and reflected light beams leave the beam splitter A. The subsequent dynamic positions, w', x', y', z', w'', x'', y'', z'' have also been indicated in Fig. 3, and it is readily found that

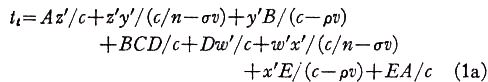
and

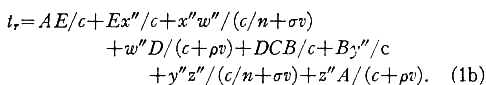
    The factors ρ and σ are carried for complete generality. The Einstein postulate assumes that ρ≡0 and requires that the convection coefficient σ, derived from the Einstein "addition" theorem, by prescribed as 0<σ<l. Classically σ≡1 and ρ = 1 in vacuo, but in a gas such as air ρ would probably be less than unity and could be expected to depend on the gas density. The transit time difference ∆t=t_t -t_r to first order in v/c=β, can be found from Eqs. (1a) and (1b).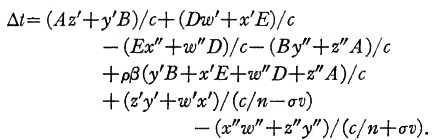

        (2a)

    Denoting the window thickness by l it follows that w'x'=y'z'=l-δs', where δs' represents the distance a window moves during the transit of the transmitted light beam through the window. The transmitted beam moves in opposition to the window motion. Similarly for the reflected light beam w''x''=y''z''=l+δs''. It then follows that

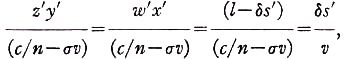        (2b)

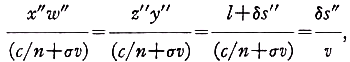        (2c)

and that

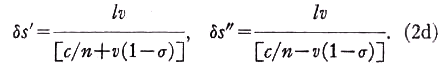
    Referring to Fig. 3 it is readily established that

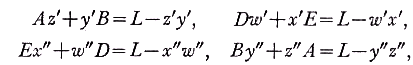
where L=AB=DE. Further

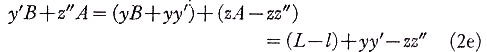
and

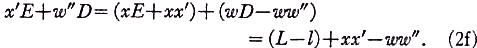
    It is next recognized that

    yy'/v= first two terms of Eq. (1a),

    xx'/v= first six terms of Eq. (1a),

    ww''/v= first three terms of Eq. (1b),

    zz''/v=first seven terms of Eq. (1b).        (2g)

    The terms yy', xx', ww'', zz'' are all found to be of first or higher order, in v/c=β and may therefore be neglected since they only occur in Eq. (2a) multiplied by ρβ. With the aid of Eqs. (2b-g), the expression for the fringe shift in terms of the wavelength, Δ=cΔt/λ, is finally obtained from Eq. (2a);

    Δ=2ρβ (L-l)/λ+4βln/λ-4βln²(1-σ)/λ.         (3a)

    The window centers were located at a radius R of 12.24 cm and the maximum tangential-window center speed was v= 2πR·61≈4690 cm/sec and therefore β≈1.56×10^-7. The window thickness was l≈1.27×10^-2 cm and the refractive index was n≈1.5. According to the Einstein theory ρ≡0 and σ=1-n^-2 so that Eq. (3a) reduces to

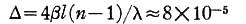            (3b)

for λ=5000 Å. According to Laub, Lorentz, and Zeeman the convection coefficient is given as σ=1-n^-2-λn^-2dn/dλ and Eq. (3a) reduces to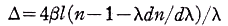

            (3c)

and again, a wholly negligible fringe shift is predicted for this experiment since |dn/dλ| ≈ 10^-5 for glass.

    The expression given by Zeeman² in his experiments on light convection in moving quartz and glass rods about 1 m long is equivalent to Eq. (3c). The convection coefficient σ in Eqs. (3a,b,c) can be shown to be unity in contradiction to the Einstein-"addition" theorem when account is taken of the Einstein-time dilation and length-contraction effects. Relative to an "observer" on the moving window the rest length of the window will be denoted by l₀ and the transit time t₀ of the light through the window is given by t₀=l₀n/c. In Eq. (2d) δs', δs'', and l are laboratory quantities. The contracted laboratory length of the moving window is expressed as l= l₀(1-β²)^1/2. The dilated laboratory transit time of the light through the moving window is expressed as t=t₀(1-β²)^1/2=l₀n(1-β²)^1/2/c=ln/c and it is independent of the concurrence or opposition of the light to the window motion. The laboratory window transit time is also given by Eq. (2d) when divided by v, so that it is to be concluded accordingly that δs'=δs'' which is satisfied if and only if σ≡l since v≠0. Alternatively since

   

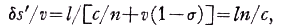
or

   

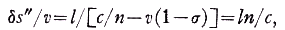
then c/n±v(l-σ)=c/n. This can only be satisfied if σ≡l since v≠0. The only fringe shift to be expected if σ≡l and also ρ≡0 would according to Eq. (3a) be given as

   

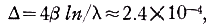
which is experimentally negligible. It is clear that in this experiment in which l≈1.27×10^-2 cm and β≈1.56×10^-7 the Einstein postulate (ρ≡0) predicts no visible fringe shift.

    Classically σ≡l and 0< ρ <l and Eq. (3a) reduces to

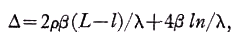            (4a)

where the first term represents a transit time difference effect and the second a convection effect. In this experiment L≈118 cm so that effectively Eq. (4a) reduces to

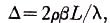            (4b)

whose maximum value for ρ=1 is about 0.74 for λ =5000 Å. The observed maximum, fringe shift with "white" light at 61 rps was Δ≈0.5. The use of "white" light precludes a sure estimate for λ, and it would be erroneous to infer that ρ≈2/3 in air.

    The fringe shift shown in Fig. 2 was obtained when the source iris was wide open and no filter was used. The camera shutter was open for ten seconds using ASA 3000 Polaroid film. The motor speed was 51 rps so that the actual exposure time was about 7.65×10^-3 sec. A fringe shift of almost, but not quite, half of the distance between fringes was seen when the iris was nearly closed and the motor ran at maximum speed. The definition of the two dark bands on either side of the central bright fringe with the small aperture was superior to that with the wide-open aperture, but the fringe pattern was very dim and the shift was ascertained relative to the upper stationary fringe system in the field of view. Attempts to photograph them failed, but to the eye the shift was more readily seen to depend directly on the disk speed β becoming just discernible at 10 rps. The fringe shift also appeared to depend linearly on the disk speed but no reliable measurement of this was readily available.

    The convection effect of the air which is in motion due to the fan-like centrifugal action of the rotating disk and windows can be shown to be negligible. The length of the air column in motion could, be judged to be about 25 cm since at that distance from the center of the disk a just perceptible breeze could be felt on the back of the hand. Notwithstanding this, it will be assumed, as a gross exaggeration, that all the air along the longitudinal dimension of the interferometer is in motion with a speed equal to the maximum tangential speed of the windows. The maximum fringe shift to be expected due to the convection of light by the air, according to the Einstein theory, is calculated from Eq. (3b) to be Δ≈4.4×10^-4 with l≈118 cm, β≈1.56×10^-7, n-l≈3×10^-4, and λ=5000 Å. Classically the same gross approximations lead according to the second term of Eq. (4a) to an expected maximum value of Δ≈1.5. The Einstein (or Fresnel) convection effect for air is thus seen to be quite negligible even under the most favorable assumptions for its occurrence.

    Michelson and Morley, in an experiment on the convection of light by air flowing at 2500 cm/sec (β=8.3×10^-8) through a pipe 3.02 m long observed a fringe shift of Δ≈0.01.³ On the basis of their result air flowing at 4690 cm/sec (the maximum window speed) along a path of 118 cm would be observed to produce a fringe shift of Δ≈0.01×1.56×10^-7×118/8.3×10^-8×302≈0.007. Bearing in mind the exaggerated favorable assumptions involved in deducing this fringe shift, it can readily be appreciated that air convection effects in the present experiment are quite negligible.

    The nonuniform distribution of the air, due to its compression in front of the windows and its rarefaction behind them together with its centrifugal component of motion away from the longitudinal light path, might conceivably have resulted in a dynamic prismatic refractive effect to which the observed fringe shift could be attributed. The shift might also be due in part to a possible dynamic bending and bowing of the windows and their supporting posts even though none could be seen under the stroboscopic light from the source.

    An experimental demonstration that a dynamic prismatic or mechanical deformation effect was not the case was simply achieved. A Mylar film (2.54×10^-3 cm thick) mounted on a heavy brass based frame was introduced normal to the field of view in each light path at the same time. Each film was placed about 30 cm from the mirrors B and D, respectively, so that they were quite close to the disk between the disk and the mirror E and the beam splitter A, respectively.

    Phenomenologically the Mylar film would transmit light through itself with its own characteristic medium speed, and the light upon leaving the Mylar would then travel with the characteristic speed c relative to the Mylar and the interferometer since the Mylar is stationary. The effective length of the interferometer would then depend on the position of the Mylar (in the present case L≈30 cm) and the transit time shift represented by Eq. (4b) would be correspondingly decreased. A shift of the fringes due to a dynamic prismatic refractive or mechanical deformation effect would be unaffected by the presence of the Mylar.

    A fringe shift with the Mylar present was barely discernible at 51 rps and abrupt removal of the Mylar resulted in the expected appearance of a sudden shift of the fringes to ∆≈0.3. The dependence of the magnitude of the fringe shift on the presence of the Mylar indicated that the fringe shift was not due to a dynamic refractive or mechanical deformation effect, since this effect would have persisted independently of the presence of the Mylar.

    The Mylar film effect was carried out at the close of the experiment and due to a crippling lack of time it was not possible to construct a guide upon which the two Mylar films could be moved parallel to themselves along the light path. Such an arrangement would have permitted the very desirable ability to have measured the fringe shift as a function of L.

DISCUSSION

    The transmitted light beam passed through the windows in opposition to their motion, while the reflected beam went through concurrent with their motion. Effects which might tend to displace the fringes due to static temperature and density inhomogeneities in the air and the windows would be canceled, since each light beam suffers the same refractions in transit around the interferometer in opposite directions, so that each beam takes the same time to traverse the interferometer. This was borne out by manually oscillating the disk and observing that the vertical fringe field remained quite steady until the windows were almost out of the field of view.

    The dynamic inhomogeneities in the air due to pressure gradients and turbulence, together with possible bowing and bending of the windows and their supporting posts when the disk was in motion, would likewise not be expected to introduce any optically anisotropic or asymmetrical refractive or prismatic effects to which the observed fringe shift might be attributed. These dynamic deformations and air distributions are also spatially symmetrical for both windows and take place extremely slowly compared with the speed of the light, so that they are essentially similar to static conditions. The magnitude of the fringe shift would have had to remain unaltered when the Mylar film was present if the shift were due to a dynamic refractive prismatic effect. Observation of the fringe field while the motor coasted from full speed to rest showed no change in the fringes under light which was not synchronized by the disk magnet and pickup coil signal. The xenon source was allowed to run at the 60-cycle powerline frequency instead, and the vertical fringes remained fixed and undistorted above and down through the field of view of the windows. The entire fringe field was sometimes but not always observed to distort at certain discrete critical resonant speeds when the motor was driven from rest to full speed, so that complete isolation of the interferometer from motor vibration was not achieved. These resonant speeds were of course avoided during other observations.

    The mirror arrangement BCD was provided so that a light ray passing through the outside edge of one window where the tangential speed was v+δv would then pass through the inner edge of the second window where the tangential speed was v-δv. The rotary motion of the windows was by this arrangement compensated for, so that effectively the motion was translational for the short duration of the light flash. The equally important spatial coincidence of the opposed light beams returning to the beam splitter was also maintained by the BCD mirror system. The significance of this feature of the interferometer should be particularly noted since the sole reason for a fringe shift in the field of view of the windows relative to the fixed fringe field above the windows could only be due to a difference in transit time of the parts of the two opposed light beams passing through the windows, since the convection-effect fringe shift for air and such thin windows was experimentally negligible.

    The moving transparent windows behaved like moving light sources, since they absorbed and emitted the light incident on them, analogously to a moving radio receiver-transmitter. This is established by the effect of the Mylar. Further optical evidence for this is found (despite his erroneous conclusions) in the work of Majorana⁴ on the Doppler effect observed from light reflected from a moving mirror and also from a moving glass-enclosed glowing mercury plasma. Related observations are those of Fabry and Buisson⁵ on the Doppler effect on light diffusely reflected from a moving paper surface. No difference in transit time of the opposed light beams would be expected if the Einstein hypothesis were valid, since the speed of the light would be absolute and independent of the motion of the windows. The Einstein theory would predict that the vertical fringe system would remain everywhere visibly unchanged in the field of view when the disk was rotating identical to the fringe situation with the disk stationary.

    The Einstein theory would further predict that no net change of wavelength would be observed in light which passed normally through a glass plate which was in uniform rectilinear translation relative to the stationary source and terminus of the light. Thus the wavelength λ' noted at the window receding from the fixed light source, or the mirror E, would be given by

   

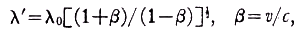
where λ₀ is the source wavelength. This would be absorbed and emitted by the window whose motion relative to the mirror D is that of approach, so that the wavelength λ'' noted at D would be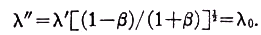

   

    The same result can be found for the oppositely moving light beam. Classically

   

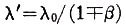
and

   

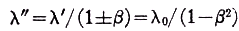
so that to first order in β, λ''=λ₀. Under either theory the conditions for coherent interference are satisfied for first-order effects.

    An unambiguous easily noted shift of the fringes in the field of the windows was observed when the disk was in motion. The effect was quite pronounced since the shift of the fringes took place relative to the stationary fringe field above the windows, as may be seen in Fig. 2. The magnitude of the fringe shift was seen to depend directly on the speed of the disk. When the motor was driven at high speed and the xenon lamp, flashing for 15 μsec, was allowed to run "free" at the 60-cycle line frequency unsynchronized by the disk, the fringe field was identical to the case when the disk was stationary. The switch on the Strobotac was then abruptly turned to the next position whereby the xenon light flashes were synchronized by the disk, and the window part of the fringe system was seen to shift suddenly and quite dramatically relative to the stationary upper part which remained fixed relative to the telescope crosshairs. The shift could be made to go to the left or to the right by appropriately adjusting the plane of the beam splitter, whereby the virtual sources were interchanged. Introducing a number 74 Kodak Wratten filter for the mercury green line in front of the telescope had the effect of making the fringes appear slightly better defined but at great loss of brightness. The shift was nevertheless discernible.

CONCLUSIONS

    The experiment described in this paper demonstrates in a solely qualitative manner a "yes" or "no" result of a direct nature on the transit time of light from a moving light source, since the convection effects are entirely negligible. Qualitative agreement with two of the variables in the classical expression for the expected fringe shift in this experiment has been observed. It must be concluded that the Einstein postulate on light propagation is untenable since according to this postulate no appreciable fringe shift should have been observed in this experiment.

    An impartial repetition of this experiment for quantitative effects at atmospheric and vacuum conditions with monochromatic light (without undue limitation on time, money, and facilities) by physicists whose primary skill lies in experiment rather than theory should, it is hoped, be undertaken in the near future. The Zeeman^{2, 6} work on the convection of light in flowing water and moving quartz and glass rod should also be undertaken.

ACKNOWLEDGMENTS

    The author is immeasurably indebted to Dr. D. A. Wilson of the U. S. Navy Electronics Laboratory for his enthusiastic support of this work. Mr. Franklin L. Davis, model maker, was very helpful by the willing dispatch with which he created much of the apparatus. The Norair Division of the Northrop Corporation generously provided the gratuitous loan of the basic optical table. The U. S. Naval Ordnance Test Station of China Lake, California, also assisted the author materially and financially.

_______________________________________________

* Present address: California Western University, San Diego 6, California.

1 W. Kantor (unpublished).

2 P. Zeeman and A. Snethlage, Proc. Roy. Acad. Amsterdam 22, 512 (1920); P. Zeeman, W. de Groat, A. Snethlage, and G. C. Dibbitz, ibid. 23, 1402 (1922).

3 A. A. Michelson and F. W. Morley, Am. J. Sci. 31, 385 (1886).

4 Q. Majorana, Phys. Rev. 11, 411 (1918); Phil. Mag. 37, 145 (1919).

5 H. Buisson and C. Fabry, J. Phys. 8, 234 (1919).

6 P. Zeeman, Proc. Roy. Acad. Amsterdam, 17, 445 (1914); 18, 398 (1915); 22, 461 (1920).

Дата установки: 27.04.2008
[вернуться к содержанию сайта]

W