[вернуться к содержанию сайта]

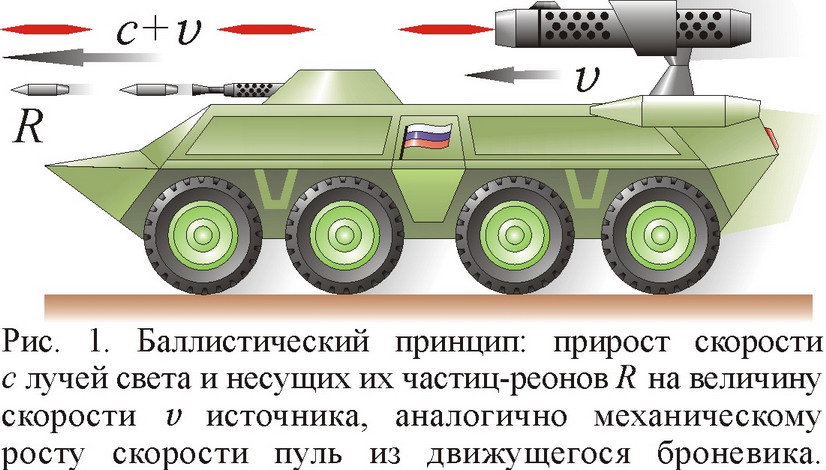
    Люди, впервые услышав о Баллистической Теории Ритца (БТР) и баллистическом принципе сложения скорости света со скоростью его источника (рис. 1), обычно не могут поверить, что учёные вместо этого простого классического правила пользуются в расчётах абсурдным постулатом специальной теории относительности (СТО) о постоянстве скорости света. Поэтому, не допуская мысли, что физики могут ошибаться, многие начинают считать, что повседневный опыт доказывает правоту Эйнштейна. Ведь в наше время высоких технологий и прецизионных приборов, казалось бы, нельзя проморгать зависимость скорости света от движения источника. Так, полагают, что лазерные дальномеры, радиолокационные установки, в основу работы которых положено измерение времени движения электромагнитных сигналов, давали б заметные ошибки, если бы скорость света мало-мальски зависела от движения источника. А между тем такие приборы прекрасно работают и с огромной точностью выдают расстояния до объектов. Потому и считают, что теория относительности оправдывается, а баллистическая теория отвергается наблюдениями. В пример часто ставят глобальную навигационную систему (GPS и её отечественный аналог, ГЛОНАСС), модули для пользования которой сейчас легко встраивают не только в портативные навигаторы, но и в мобильник за умеренную плату. Точная работа этой системы, основанной на методе радиолокации сигналов, посланных с нескольких спутников, и включающей скорость света в качестве константы, якобы стопроцентно опровергает баллистическую теорию. Однако, как покажем далее, эти и другие радиолокационные замеры на поверку не только не противоречат БТР, но как раз подтверждают эту классическую теорию и опровергают СТО.

    Начнём с того, что поправки, вносимые зависимостью скорости света от скорости источника, крайне незначительны, а потому обычно их трудно заметить. В самом деле, метод радиолокации основан на измерении времени T движения электромагнитного сигнала от источника к приёмнику (или туда и обратно при отражении сигнала по принципу эхо, откликнувшегося с запаздыванием после ауканья). Зная скорость света c, по школьной формуле можно легко найти расстояние до объекта L=cT (или L=cT/2, если сигнал идёт туда и обратно, затрачивая двойное время). При этом, вопреки русской пословице, в СТО считают, что вне зависимости от того, как движется аукающий радиоизлучатель, объект всегда откликается одинаково, спустя одинаковое время задержки T. А по БТР, если источник движется к приёмнику и сообщает свою скорость V сигналу, то время задержки снизится, так как скорость света станет c'=c+V, а расстояние найдётся уже по формуле L'=(c+V)T. Разница значений по БТР и СТО составит Δ=L'–L=VT=LV/c. Поскольку скорость света огромна, c=300000 км/с=3·10⁸ м/с, то даже при скорости сверхзвукового самолёта V~300 м/с на дистанции в 10 км погрешность определения расстояния будет Δ=LV/c=0,01 м, то есть всего 1 см, что на такой дальней дистанции совершенно незаметно и на порядки превышает погрешности метода и измерительной техники. Поэтому выявить разницу между БТР и СТО можно, лишь в космосе, на огромных космических расстояниях L и при космических скоростях V.

    Самое интересное, что подобные радиолокационные нестыковки и впрямь были открыты, в том числе у недавно нашумевших аппаратов "Пионер", радиолокационные измерения расстояний до которых сильно расходятся с теоретическими. Да и в авариях космических аппаратов, посланных к Марсу, в том числе отечественных "Фобосов", многие винят ошибки навигации и второй постулат СТО. Впервые подобные нестыковки были обнаружены ещё полвека назад при радиолокации Венеры. Радиолокационные станции систематически обнаруживали расхождения рассчитанных на основе оптических наблюдений положений Венеры и показаний радиолокационных приборов. Ошибки носили систематический характер и на порядки превышали погрешность радиолокационного метода. Из-за того, что отражённый Венерой сигнал приобретал после отражения скорость планеты, сигнал приходил раньше теоретического в моменты приближения, и позже – в моменты удаления планеты. В итоге астрономы устранили эту проблему чисто формально, переместив Венеру на несколько сот километров по орбите в направлении её движения [1]. Важно, что тот же порядок величины имела и ошибка, которую внесла бы зависимость скорости радиосигнала от движения Венеры. Также систематические ошибки возникали и при замерах радиолокационными станциями, расположенными по разные стороны Земли. Расстояния до Венеры, одновременно измеренные радиолокационными станциями СССР и США, систематически различались ввиду того, что одни станции за счёт суточного вращения Земли двигались к Венере, а расположенные на другом конце Земли – удалялись, сообщая свою скорость радиосигналу. Как показал Брайан Уоллес, эти систематические расхождения между данными станций сразу исчезают, если воспользоваться классической формулой сложения скорости света и источника (БТР), отвергнув постулат постоянства скорости света СТО [2]. Однако вскоре данные радиолокационных замеров были изъяты из общего пользования, что привело Уоллеса к мысли, что США осознали ошибочность СТО и справедливость классического правила, намеренно засекретив этот закон с целью его дальнейшего использования в "звёздных войнах".

    И вот здесь мы вплотную подходим к теме GPS, поскольку эта глобальная позиционная система, как известно, была разработана именно военным ведомством США, будучи создана для целей "звёздных войн", и лишь позднее стала доступна гражданским лицам. Работа системы GPS тоже основана на методе радиолокации. Система включает в себя сеть наземных станций слежения и группу искусственных спутников (численностью до 24-х) на нескольких орбитах, плоскости которых развёрнуты под разными углами. GPS-модуль, встроенный в наземное устройство параллельно принимает радиосигналы, посланные несколькими спутниками. В этих сигналах закодирована информация о местоположении каждого спутника (контролируемом станциями слежения), а также время испускания сигнала, задаваемое сверхточными часами. Вычитая это время из реального времени приёма сигнала, GPS-приёмник находит время T движения сигнала и соответственно расстояние L=cT до спутника. Измерив так расстояния L₁, L₂, L₃, L₄ сразу до трёх–четырёх спутников, и располагая их координатами, микроЭВМ из тригонометрии легко рассчитывает положение GPS-приёмника на земной поверхности (рис. 2). Также GPS позволяет, последовательно (с интервалом в секунду) измеряя положение приёмника, находить его скорость, деля путь на время.

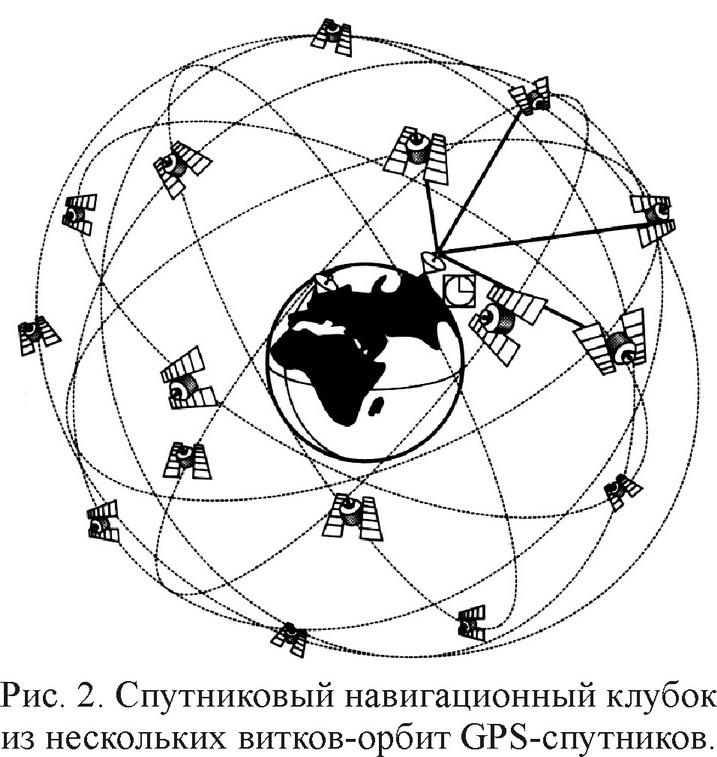
    Итак, казалось бы, формула L=cT работает, поскольку работают GPS-навигаторы, что будто бы отвергает баллистическую теорию. Но в этом случае, равно как и в ряде других опровержений, авторы обычно голословны и не утруждают себя подробным рассмотрением выводов БТР и расчётами по этой теории для сравнения их с наблюдениями. Из-за этого противники теории Ритца постоянно попадают впросак, поскольку при подробном рассмотрении приводимые ими аргументы свидетельствуют как раз в пользу БТР, а не СТО. Так и в данном случае. В самом деле, рассчитаем, какие поправки в расчёт расстояний надо внести в случае зависимости скорости света от скорости источника. Спутники навигационной системы расположены на орбите радиуса R порядка 26000 км, то есть летят на высоте примерно 20000 км над Землёй, имеющей радиус r=6400 км (рис. 3). На такой орбите скорость V спутников составляет около 4 км/с. Поскольку расстояние до Земли L=20000 км, то полагают, что поправка, вносимая БТР, составляет Δ=LV/c≈267 м. Эта величина на порядок больше обычных ошибок GPS-навигаторов (хотя у прежних моделей точность составляла как раз около сотни метров). Поэтому полагают, что БТР противоречит принципу работы GPS. Но это ошибка, нечаянно или намеренно допускаемая теми, кто слабо разобрался в сути БТР.

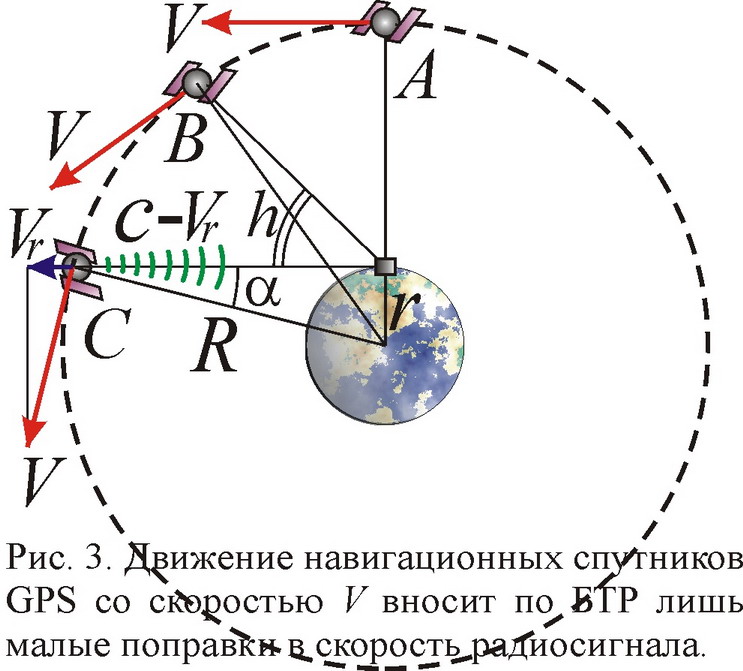
    Ведь скорости источника и света по баллистической теории складываются не арифметически, а векторно, согласно классическому закону сложения скоростей. Таким образом, для скорости распространения радиосигнала вдоль луча зрения существенна только составляющая V_r скорости V источника вдоль этого луча (лучевая скорость спутника). В таком случае скорость радиосигнала, приходящего со спутника, есть c'=c–V_r, а поправка расстояния Δ=LV_r/c. Если спутник удаляется, то V_r>0 и скорость приходящих сигналов снижается по сравнению со световой, а если спутник движется к приёмнику, то V_r<0, а скорость c' приходящих сигналов увеличена. Если же спутник движется поперёк луча зрения, то, как бы высока ни была его скорость V, получим V_r=0 и c'=c. Так вот, поскольку спутник летит по высокой круговой орбите, то его орбитальная скорость, перпендикулярная радиус-вектору R, направлена поперёк луча зрения, так что V_r заметно меньше V. Так, если спутник находится в зените, то V_r=0 и постепенно увеличивается при уменьшении высоты h спутника над горизонтом. Как легко найти, если приёмник расположен в плоскости орбиты спутника, то V_r= V·sinα·cosh, где sinα=r/R≈0,25. Таким образом, даже максимально возможная по БТР ошибка в определении расстояния до спутника будет равна Δ=LV_r/c=67 м. Такая ошибка возникает лишь в предельном случае, если спутник виден возле линии горизонта. На деле же приёмник обычно регистрирует спутники с высотой h не ниже 10–15º над горизонтом. Кроме того, надо учесть, что, так же как спутник не часто виден на горизонте, так же редко и приёмник оказывается в плоскости орбиты спутника. В общем случае приёмник расположен под углом θ к плоскости орбиты спутника, из-за чего лучевая скорость будет ещё меньше V_r=V·sinα·cosh·cosθ (рис. 4). Отсюда Δ=LV_r/c=LV·sinα·cosh·cosθ/c. Поскольку cosh и cosθ никогда не превосходят единицы, а среднее значение модуля косинуса составляет 0,63, то средняя ошибка Δ=27 м. Это значение уже того же порядка, что и ошибка обычных GPS-навигаторов.

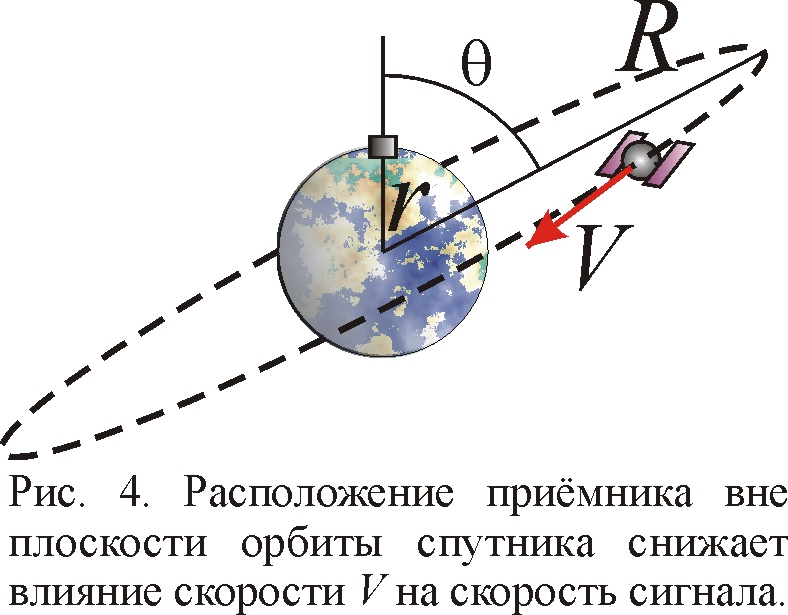
    Но и эта средняя ошибка в 27 м относится лишь к определению расстояния до одного из спутников. Реально же для вычисления координат нужны, как помним, данные хотя бы трёх-четырёх спутников. Если учесть, что все они дают ошибки разного знака, случайно суммируемых в разных направлениях, то их сложение и усреднение ещё в несколько раз уменьшит ошибку определения координат приёмника. Кроме того, полученный результат даёт общую ошибку определения координат, то есть сумму ошибок положения по высоте и по горизонтали. Поэтому ошибка в определении положения на земном шаре будет ещё в полтора раза меньше. В итоге средняя вносимая БТР поправка определения горизонтальных координат составляет всего 5–10 м. Но именно такой порядок ошибки по горизонтали (и чуть больше по вертикали) обычно и заявляют производители навигационных систем GPS и ГЛОНАСС. Реальная же ошибка навигаторов нередко даже превосходит заявленную.

    Вот и выходит, что БТР не только не противоречит работе GPS-навигаторов, но и предсказывает ошибки того же порядка, что и реально выявленные. Поэтому вполне возможно, что эти ошибки вызваны неучтённой зависимостью скорости сигналов от скорости излучивших их спутников и могут быть устранены, если учесть эту зависимость в расчётах (как в случае локации Венеры [2]). Конечно, обычно говорят, что ошибки вызваны иными причинами: распространением радиосигнала в атмосфере и ионосфере, меняющих скорость сигнала (которую не всегда точно известна), техническими погрешностями (неточностью, несинхронностью часов), ошибками в определении координат спутников и т.д. Все эти ошибки, конечно, имеют место, но роль их обычно невелика, а потому их легко выделить и устранить за счёт их специфики. Так, толщина атмосферы и ионосферы ничтожна в сравнении с дистанцией L и составляет порядка 100 км, причём скорость сигнала в атмосфере мало отличается от скорости света. К тому же эта ошибка легко устраняется сравнением времени прихода двух сигналов, переданных на разных частотах и имеющих разные скорости в атмосфере.

    В том, что источник ошибки скрыт в неучтённой зависимости скорости сигнала от скорости спутника, убеждает не только принципиальная неустранимость ошибки, но и то, что ошибка эта явно зависит от высоты h спутника над горизонтом. Так в приполярных областях Земли, где спутники не поднимаются высоко над горизонтом, ошибка определения координат заметно превосходит обычную, что естественно, поскольку при малой высоте cosh≈1. Эта ошибка вряд ли вызвана только большей толщиной атмосферы и ионосферы при скользящем падении радиолуча (как говорилось, эффект этот легко учесть, ведя передачу сигнала на двух частотах). Так же и несколько большая погрешность в определении высоты в сравнении с горизонтальной ошибкой может быть отчасти объяснена с помощью БТР. На практике можно легко проверить, насколько велико влияние скорости спутников на величину ошибки. Для этого достаточно провести обычный тест для GPS-навигаторов: положить навигатор неподвижно на высоком месте и в течение некоторого времени фиксировать выдаваемые им координаты. Эти координаты обычно дают разброс точек в пределах круга с радиусом порядка десяти метров, что сразу демонстрирует типичную ошибку навигационной системы. Если при этом для каждого из замеров знать положения на орбитах сигналящих спутников, то можно легко рассчитать, какие поправки внесло бы влияние их скорости, а также проверить, соответствует ли эта поправка направлению и величине смещения точек от центра. Обнаружение заметной корреляции докажет справедливость БТР.

    Не будучи в силах полностью устранить ошибку, вносимую влиянием скорости, с ней борются различными обходными путями. Один из способов состоит в увеличении числа передающих спутников и параллельно принимаемых каналов. Благодаря этому, если над горизонтом одновременно видны 6–10 спутников, то положение приёмника можно определить гораздо точнее, проводя вычисления по разным группам спутников, комбинируя их по три в разных сочетаниях и для каждой группы определяя положение приёмника, а после находя среднее положение. Поскольку лучевые скорости спутников имеют разную величину и знак, то вносимые скоростями ошибки в среднем гасят друг друга и потому среднее расчётное положение близко к действительному. Радиолучи, словно дротики, случайно отклонившиеся от центра мишени, если усреднить координаты их попаданий, дадут в среднем положение близкое к необходимому. Или просто ЭВМ сразу рассчитывает положение приёмника в виде координат точки с наименьшим квадратичным отклонением от сфер с радиусами L₁, L₂, L₃, … L₁₀ и центрами на спутниках. Этот метод, при котором вдобавок часто в ходе усреднения отбрасываются крайние, явно ошибочные точки, позволяет снизить ошибку в несколько раз.

    Другой метод состоит в измерении не абсолютного, а относительного положения приёмника, если рядом имеется базовая станция с точно известными координатами. Сравнивая координаты, рассчитанные GPS-системой для мобильного приёмника и приёмника на станции, можно по разности этих координат найти точное положение приёмника относительно станции. Поскольку вносимая движением спутников ошибка будет той же, что и для приёмника на близлежащей станции, то такой дифференциальный метод даёт точность определения координат от одного сантиметра до метра. Лишь дифференциальные, а отнюдь не прямые методы GPS-навигации (где существенно влияние скорости спутников), дают такие рекордные точности. Наконец, возможен и такой компенсирующий метод, какой был применён при радиолокации Венеры [1]: в расчётах спутник просто считают смещённым вперёд по орбите на соответствующее расстояние. Благодаря этому то же самое время задержки сигнала получается в предположении, что скорость радиосигнала не зависит от скорости спутника за счёт искусственно завышенного или заниженного расстояния до него. Такой приём может свести ошибку определения координат почти до нуля. Причём это может получиться нечаянно, поскольку координаты спутника определяют с помощью станций слежения опять же на основе радиолокационных данных, а потому ошибка может изначально вноситься в координаты спутника, маскируя влияние его скорости и вызванные ей погрешности. Применяется и ряд других корректирующих программ, в том числе с привлечением дополнительных опорных станций и геостационарных спутников, а так же корректирующие программы расчёта.

    Затронув роль корректирующих программ, стоит заметить, что в некоторые из них, особенно в те, что применяют американские военные, возможно, уже закладывается зависимость скорости света от скорости источника. На эту мысль наводит не только заявление Уоллеса о том, что военное ведомство США знает о справедливости баллистического принципа, но и то, что именно военные первыми разработали спутниковые системы навигации, а значит, должны были тщательно исследовать все источники ошибок. Кроме того, весьма интересно, что у спутниковой системы есть два режима работы: точный и приближённый, с погрешностью порядка 50 метров, который может быть включен правительством США в любое время (например, в военное), дабы ограничить возможности GPS для гражданских лиц. Не исключено, что такая смена режимов производится в действительности не направленным искажением работы системы, а просто переходом с новой на старую версию программы, в которой не учтена зависимость от скорости спутников, то есть не работает соответствующая корректирующая программа. Реальное существование такой программы могли бы подтвердить профессиональные программисты. Таким образом, ограничение доступа к полноценному GPS может оказаться просто видоизменением прежнего засекречивания информации о работе баллистического принципа.

    О том, что американские военные и разработчики давно уже столкнулись фактами, противоречащими теории относительности, говорит хотя бы работы Рональда Рэя Хатча, одного из американских основателей компании по космической навигации, специалиста по GPS и радиолокации. Хатч открыто и аргументировано признался, что результаты GPS, космические радиолокационные наблюдения противоречат специальной и общей теории относительности. Поэтому тем, кто пытается приводить GPS в качестве подтверждения СТО, следовало бы сначала послушать Хатча и его коллег, имеющих прямое отношение к этой тематике. Таким образом, согласно Уоллесу и Хатчу, вполне возможно, что ряд успехов американской космической навигационной системы связан с отказом от СТО и применением БТР. В таком случае отечественной космической промышленности тоже давно пора перевооружиться. Особенно это касается систем космической навигации, системы ГЛОНАСС, спутниковых лазерных систем, которые могут взять на вооружение БТР и баллистический принцип (рис. 5). Впрочем, не исключено, что и в отечественных радиолокационных системах незаметно учтён этот принцип. Например, в физике плазмы уже давно пользуются так называемой баллистической теорией эхо в отношении электромагнитных волн Ван Кампена. Эти незатухающие волны (предсказанные ещё А. Власовым как одно из решений его кинетического уравнения), несутся вместе с потоком частиц плазмы и потому во многом аналогичны световым волнам, переносимым вместе с модулированным потоком частиц-реонов. А ведь плазма – это основная среда космического пространства. Так что учёные уже давно могли перенести баллистические законы на движение световых сигналов в космосе.

    Если баллистический принцип реально подтвердится с помощью методов спутниковой навигации или иным путём, то под совсем другим углом предстанет и деятельность тех, кто на самом высшем уровне покрывал теорию относительности (якобы из научных соображений), а также без веских оснований препятствовал продвижению БТР. Их деятельность оказалась подрывной не только в плане уменьшения обороноспособности страны, но гораздо больше – в плане снижения научного потенциала России. Впрочем, наука ещё может возродиться, если вернётся к основам, к классической физике, включая баллистическую теорию Ритца. Спутниковые навигационные системы лишь ещё раз подтвердили справедливость этой теории. Повторилась космическая история, имевшая место век назад, когда Де Ситтер пытался опровергнуть теорию Ритца на том основании, что двойные звёзды в случае сообщения своей орбитальной скорости испущенному свету показали бы ряд необычных эффектов, в том числе звёздные орбиты оказались бы преимущественно вытянуты в направлении к Земле. И хотя из-за громадности скорости света эти эффекты тоже оказались малозаметными (что повлекло преждевременный отказ от БТР), они всё же были обнаружены. Так, эффект избыточной вытянутости орбит был открыт ещё в начале XX века и назван эффектом Барра [3]. Таким образом, Де Ситтер и другие релятивисты, повторяющие из книги в книгу его опровержение баллистической теории, сами себе роют яму, когда, ссылаясь на пример двойных звёзд, раз за разом расписываются в справедливости БТР и своём незнании реальных астрономических фактов. Так же и все другие выпады релятивистов против БТР (включая анализ ошибок GPS и ГЛОНАСС) неизменно обращаются против самих же релятивистов, оказавшихся побитыми собственным оружием. Перефразируя пословицу из эпиграфа на военный лад, можно выразиться словами Александра Невского: "Кто с мечом к нам придёт – от меча и погибнет!".

С. Семиков

1. Дёмин В.Н., Селезнёв В.П. Мироздание постигая. М.: Молодая Гвардия, 1989.
2. Уоллес Б. Радарные измерения относительной скорости света в космосе // Spectroscopy Letters, 2(12), р. 361, 1969.
3. Семиков С. Ключ к загадкам космоса // Инженер, №3, 2006.

Дата установки: 03.05.2010
[вернуться к содержанию сайта]

W