Прибор Леонардо для решения задачи Альхазена (реконструкция).
[вернуться к содержанию сайта]
8. ОПТИКА У ГРЕКОВ.
Другой заслугой александрийской науки был толчок, данный ею оптическим исследованиям.Оптикой увлекались ещё философы классического периода, которые больше интересовались физиологическими, а не физическими проблемами. Они задавались вопросами: каким образом мы видим, каково соотношение между ощущением и видимым предметом? Дискуссия была, по-видимому, долгая и страстная, но дошедшие до нас документы весьма немногочисленны и толкования их сомнительны. Мы упомянем здесь теории, развитые в классический период и вновь появлявшиеся в ходе позднейшей истории.
По-видимому, именно пифагорейцы первые выдвинули гипотезу об особом флюиде, который испускается глазами и “ощупывает” как бы щупальцами предметы, давая их ощущение. Атомисты же были сторонниками испускания предметами “призраков”, или “образов” (ειδολα, или, как говорили в средние века, “specie”), которые, попадая в глаза, приносят душе ощущение формы и цвета. Эмпедокл попытался примирить обе теории, но по-настоящему это удалось лишь Платону, почему теория эта и связывается с его именем. Согласно Платону, от предметов исходит специальный флюид, который встречается с “мягким светом дня”, “ровно и сильно” бьющим из наших глаз. Если оба флюида подобны друг другу, то, встречаясь, они “крепко связываются” и глаз получает ощущение видимого. Если же “свет очей” (единственное выражение, сохранившееся от теории Платона и бытующее сейчас, но в переносном смысле) встречается с несхожим флюидом, он гаснет и не даёт глазам никаких ощущений.
Аристотель не следовал ни теории пифагорейцев об испускании света глазами, ни теории сторонников Демокрита о его проникновении в глаз извне. Однако трудно понять, какую теорию он сам поддерживал. Некоторые историки охотно истолковывают одно тёмное место в трудах Аристотеля ["De anima" (“О душе”), II, 7] как указание на теорию распространения света, основанную на изменении среды, находящейся между глазом и предметом.
4. АЛЬХАЗЕН. Наиболее ярким в арабской физике был, несомненно, период Ибн Аль-Хайтана, известного на Западе под именем Альхазена. Он жил и работал в Египте одновременно с Аль-Бируни; умер Альхазен в Каире в 1039 г. По всеобщему мнению, это был наиболее крупный физик средневековья. Кроме того, он был астрономом, математиком и комментатором Аристотеля и Галена.
Это последнее обстоятельство имеет для нас особое значение. Галену, жившему между 130 и 201 гг. н. э., принадлежит наряду с прочим заслуга рассмотрения глаза как одного из органов чувств нашего организма, описание его строения и выяснение функции зрительного нерва. В теории зрения Гален в основном придерживался идей Платона, но, с одной стороны, придавал большое значение внешнему флюиду, исходящему из Солнца, а с другой – уточнил, что “свет очей”, вырабатываемый мозгом, идёт по оптическому нерву к сетчатой оболочке, рассеивается в стекловидном теле глаза и вновь собирается на хрусталике, который, по Галену, есть орган восприятия. Короче говоря, с этого времени в механизме зрения начинает играть роль строение органа чувств – глаза.
Альхазен принял без изменения анатомическое описание глаза, данное Галеном, но отбросил как совершенно излишнюю вещь “свет очей”. В своём первом фундаментальном постулате он утверждает:
“Естественный свет и цветовые лучи воздействуют на глаза” 11.
Этот постулат он подкрепляет наблюдением, что глаза испытывают боль при попадании на них солнечного света, прямого или отражённого от зеркала, приводя также другие примеры ослепления. Под естественным светом (lux per se) Альхазен понимает белый солнечный свет, а под цветовыми лучами – свет, отражённый от цветных предметов.
Затем с помощью ряда хорошо поставленных опытов физико-физиологического характера он показывает несостоятельность представления о свете, исходящем из глаз и ощупывающем тела. В главе IV своего труда он описывает анатомическое строение глаза, заимствовав его у Галена, и далее заявляет:
“Зрительный образ получается с помощью лучей, испускаемых видимыми телами и попадающих в глаз” 12.
Здесь речь идёт уже не о световых лучах Евклида, а, так сказать, об обращённых световых лучах, которые идут не от глаза к предмету, а от предмета к глазу. Но не это является главным открытием Альхазена. У Евклида, как и у всех греческих физиков, зрение рассматривалось как глобальное явление; считалось, что ощущение воспринимает разом, в едином процессе образ всего наблюдаемого тела, потому ли, что внешняя “оболочка” тела, отделившись, проникает в зрачок, или же потому, что “свет очей” ощупывает его одновременно со всех сторон. Альхазен же с гениальной интуицией разложил этот глобальный процесс на бесконечное множество элементарных процессов: он полагал, что каждой точке наблюдаемого предмета соответствует некоторая воспринимающая точка глаза. Но чтобы объяснить отсутствие избранных направлений наблюдения предмета, нужно предположить, что из каждой точки предмета выходит бесконечное число лучей и в зрачок тоже попадает бесконечное число лучей. Но как же тогда одной точке предмета может соответствовать лишь одна воспринимающая точка? Альхазен преодолел эту трудность, приняв что из всех лучей, проникающих в глаз, действенным является лишь луч, перпендикулярный всем глазным оболочкам, которые он считал концентрическими. Поэтому на переднюю поверхность хрусталика, который, по Альхазену, и есть орган чувства, действуют те лучи, которые, исходя из любой точки наблюдаемого предмета, проходят через геометрический центр глаза. Таким образом, Альхазен устанавливает точное соответствие между точками предмета и точками восприятия на внешней поверхности хрусталика и приходит к выводу:
“Зрительный образ получается с помощью пирамиды, вершина которой находится в глазу, а основание – на видимом теле” 13.
Насколько это положение отличается от евклидова! Это тот же классический закон перспективы, но физика явления здесь изменена. Поэтому, несмотря на серьёзные недостатки этого положения, оно представляет собой громадный шаг вперёд.
Почему же Альхазен не продолжил световые лучи за центр глаза до сетчатой оболочки, сделав её местом образования изображения? Ему нетрудно было дойти до постановки этой проблемы: он знал нервное строение сетчатки, а оптику, обладающему его проницательностью, должно было казаться странным наличие свойства ощущения у столь прозрачной среды, как хрусталик. Но поставив проблему, он тотчас же вынужден был отказаться от её решения, испуганный её следствиями. Действительно, если лучи пересекаются в центре глаза, то на сетчатке они образуют перевёрнутое изображение. Но видел ли кто-нибудь когда-нибудь мир перевёрнутым?
Альхазен знал по опыту, а не только на основе элементарных геометрических рассуждений, что на сетчатке изображения должны получаться перевёрнутыми. Действительно, несколькими страницами дальше после приведённого отрывка он описывает опыт с “камерой-обскурой”, чтобы доказать, что лучи, исходящие от разных тел, могут пересекаться, не испытывая изменений. Он помещает различные свечи перед стенкой тёмной камеры с отверстием и, глядя на поверхность, наблюдает свет от всех этих свечей.
“...и если накрыть какую-либо свечу, то исчезает также соответствующий свет на рассматриваемой стене, а если снять колпак со свечи, то возвращается и свет. И в этом можно убедиться в любой момент. Значит, если бы лучи света перемешивались в воздухе, то они перемешивались бы и в плоскости отверстия, оставались бы перемешанными после отверстия, и различить их было бы невозможно. Но мы видим, что это не так, значит, лучи света не перемешиваются” 14.
Достаточно первого чтения этого интереснейшего отрывка, чтобы убедиться, что Альхазен многократно и аккуратно ставил опыты с камерой-обскурой. Поэтому он обязательно должен был наблюдать перевёртывание изображения, хотя в приведённой цитате он об этом не упоминает.
Лишь Леонардо да Винчи оказался столь проницательным и храбрым, что из этого опыта отважился сделать вывод о сущности механизма зрения. И действительно, Леонардо описывает весьма подробно камеру-обскуру и, отметив перевёртывание изображения, замечает: “То же происходит и внутри глаза” 15.
Всего шесть слов – и великое открытие!
Но вернёмся к Альхазену, который выдвинул свою теорию зрения и, чувствуя её недостаточность, многократно видоизменял её, приспосабливая для объяснения результатов оптических экспериментов, которые мало-помалу накапливались. Следует заметить, что средневековая геометрическая оптика была значительно сложнее современной, потому что мы получаем изображения на экранах, тогда как в средние века рассматривали изображение в глазу, где имеют место явления физиологической оптики, а не только геометрической.
Во второй книге Альхазена рассматриваются свойства зрения, а третья целиком посвящена оптическим иллюзиям, обманам зрения (deceptiones visus) или галлюцинациям (hallucinationes), как называли их переводчики. Несмотря на имеющиеся здесь интересные наблюдения в области физиологической оптики, эта книга Альхазена оказала дурную услугу физике, ибо вдохновила и усилила то направление мистического характера, которое оставалось сильным ещё во времена Галилея и которое учило не доверять органам чувств, особенно зрительным восприятиям: “Так легко, – говорил ещё Альхазен, – принять светлячок за фонарь!”
Книги IV, V и VI посвящены экспериментальному и геометрическому рассмотрению плоских, сферических, цилиндрических и конических зеркал. В предложении 39 книги V сформулирована знаменитая задача о сферическом зеркале, получившая название задачи Альхазена: при данном положении зеркала, светящейся точки и глаза найти точку зеркала, в которой происходит отражение.
Альхазен решает её, используя пересечение гиперболы с окружностью, сложным и запутанным путём, который трудно проследить даже сейчас. Этой задачей занимались математики на протяжении нескольких последующих веков. Только в 1676 г. Гюйгенс первым указал на простое геометрическое решение, а в 1776 г. Кестнер (1719–1800) дал впервые аналитическую постановку этой задачи, приводящую к уравнению четвёртого порядка.

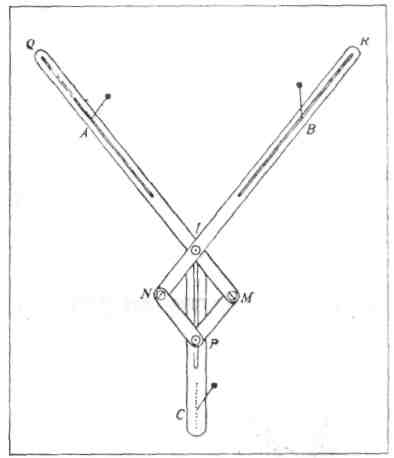
Прибор Леонардо для решения задачи Альхазена (реконструкция).
Леонардо да Винчи после многочисленных попыток, одни из которых кончались ошибочным убеждением в том, что ответ найден, а другие наводили на мысль о неразрешимости задачи, в конце концов пришёл к “конструктивному” решению задачи, т. е. решению с помощью построенного им механического прибора, замечательного тем, что в нём впервые применена пятизвенная шарнирная система. Этот прибор, восстановленный лет тридцать назад, находится сейчас в Институте механики Неаполитанского университета.
Последняя, VII книга оптики Альхазена посвящена полностью преломлению света. Здесь следует отметить усовершенствование прибора Птолемея (см. гл. 1) для экспериментального исследования этого явления и достигаемое таким образом увеличение точности измерения, что тем не менее не позволило Альхазену найти точный закон преломления. Но особенно следует подчеркнуть, что Альхазен ввёл новое понятие, которое привело Декарта к открытию правильного закона преломления (см. гл. 5). Альхазен начал ставить механические опыты по падению тел на площадки; он разлагал скорость брошенного тела на две составляющие – перпендикулярную и параллельную поверхности площадки – и затем применял результаты этих опытов к свету, заключая, что при переходе света из менее плотного тела в более плотное нормальная составляющая его скорости уменьшается.
Важно не то, что на самом деле это не так. Существенно введение нового понятия – разложение скорости света на составляющие, параллельную и перпендикулярную границе раздела двух тел.
5. ТРУДЫ АЛЬХАЗЕНА И ЗАПАДНАЯ НАУКА. Фундаментальный трактат Альхазена, отличающийся новизной, оригинальностью и стройностью построения, был переведён на латинский язык, по всей вероятности, в XII столетии, быть может Герардом Кремонским (ок. 1114–1187), и распространялся в рукописи до первого печатного издания, выпущенного в 1572 г. Риснером (ум. в 1580 г.). Риснер разбил этот трактат на отдельные книги и главы и отредактировал его. В средние века этот трактат был скорее знаменит, чем известен. Автора его называли по преимуществу Auctor perspectivae. Этому названию не следует удивляться. Как бы странно это ни выглядело с точки зрения современной классификации наук, в средние века оптика, учение о перспективе и метеорология представляли собой единую науку. Мы сказали, что этот трактат был скорее знаменит, чем известен, потому что теории зрения, т. е. наиболее оригинальной части трактата, в Средневековье не повезло. Вплоть до конца XVI века и позднее наиболее принятой теорией зрения оставалась туманная теория “образов”, или “видимостей”, которые отрываются от тел и проникают в глаз смотрящего. Сейчас трудно объяснить, почему теория Альхазена не имела успеха. Может быть, его экспериментальный подход слишком отличался от общепринятого философского подхода того времени и поэтому казался трудным. Может быть, авторитет античных философов оставался сильнее авторитета более позднего автора, к тому же ещё иноверца. Может быть, глобальная концепция зрения, которая теперь вызывает улыбку, казалась настолько ясной интуитивно, что это скомпенсировало её серьёзные теоретические недостатки.

Деформация изображения в коническом зеркале. (М. В е t t i n i, Apiaria universae philosophiae mathematicae, 1642.)
По сравнению с трактатом Альхазена был более распространён в средние века трактат по оптике Вителлия, о личности которого мы знаем очень мало. Неизвестно даже его точное имя (Вителлин, Вителион, Вител?). По-видимому, он был выходцем из Польши, долго жил в Италии, учился примерно с 1262 по 1268 г. в Падуе, а затем в Витербо. Между 1270 и 1278 гг. он написал трактат по оптике, в котором, беззастенчиво заимствуя у Евклида, Птолемея и прежде всего у Альхазена, изложил по существу содержание и методы физики арабов.
По сравнению с трактатом Альхазена здесь можно отметить два новых факта: доказательство того, что параболические зеркала имеют единственный фокус (слово focus в современном смысле слова введено Кеплером 16 в 1604 г.), положение, которое было сформулировано, согласно фрагменту рукописи, найденному в 1881 г., ещё греческим автором, возможно, Анфимием из Траллеса (ок. 550 г. н. э.), и тщательное исследование радуги.
Мы уже видели (гл. 1), что столь величественное и грандиозное явление, как радуга, привлекло внимание ещё первых греческих наблюдателей, но только Декарту удалось дать полное его объяснение. Вителий заметил, что радугу нельзя объяснить простым отражением света на водяных каплях, что нужно учесть при этом также преломление солнечных лучей в этих каплях.
17. РОЖДЕНИЕ НАУКИ ОБ ЭЛЕКТРИЧЕСТВЕ. Гильберту мы обязаны зарождением науки об электричестве, остававшейся до 1600 г. практически на уровне знаний Фалеса, когда было известно лишь, что натёртый янтарь – а может быть, ещё некое неведомое вещество, называемое “линкурием”,– притягивает соломинки. Трудно поверить, что такое универсальное свойство приписывалось в течение многих столетий только янтарю. Одна из главных причин, пожалуй, заключается в том, что электризация трением других тел настолько слаба, что эффект ускользает, если нет чувствительных приспособлений, позволяющих специально его выделить. Говоря современным языком, нужно было преодолеть порог явления.
Возможно, это предвидел знаменитый поэт и учёный Джероламо Фракасторо (1483–1553), который в 1550 г. в книге “De sympathia et antipathia rerum” (“О симпатии и антипатии вещей”) описывает прибор, состоящий из стерженька, подвешенного в одной точке наподобие магнитной стрелки. С помощью такого прибора Фракасторо устанавливает, что янтарь притягивает не только соломинки, но и серебро.
Но если Фракасторо не пошёл дальше в своём экспериментальном исследовании, то Гильберт, поняв, какую помощь мог бы ему оказать прибор Фракасторо, тотчас сам изготовил его, назвал его версором и систематически применял в своих исследованиях, описанных в гл. II книги II “О магнитах”.
С помощью этого первого электроскопа Гильберт показал, что притягивает не только натёртый янтарь, но и алмаз, сапфир, карбункул, опал, аметист, берилл, горный хрусталь, стекло, сланцы, сера, сургуч, каменная соль, квасцы. Все эти тела он назвал “электрическими телами”. Абстрактное понятие “электричество” появилось в 1650 г. Гильберт установил также, что каждое из этих тел притягивает не только соломинки и щепочки, но и все “металлы, дерево, листья, камни, комки земли и даже воду и масло” 17.
Гильберт полагал, что другие тела не притягиваются подобно металлам, многим сортам дерева и камня. Он заметил также, что пламя уничтожает свойство притягивания, приобретаемое при трении.
После столь обильной экспериментальной жатвы Гильберт попытался построить теорию притяжения электрических тел. Он отбросил оба объяснения, дававшиеся в XVI веке притяжению янтарём. Одно предполагало, что теплота обладает свойством притягивать и янтарь притягивает именно потому, что нагревается от трения. Но уже Бенедетти показал, что теплота обладает свойством разрежать или конденсировать, а отнюдь не притягивать. Гильберт повторяет рассуждение Бенедетти, добавляя, что если бы теплота обладала свойством притягивать, то притягивали бы все нагретые тела, а не только янтарь. Другая теория была весьма древнего происхождения, так как восходила ещё к Лукрецию. Согласно этой теории, истечения от натёртого янтаря вызывают разрежение воздуха, так что соломинки вталкиваются более плотным воздухом в частичный вакуум, образуемый этими истечениями. Однако, если бы было так, замечает английский учёный, горячие тела и пламя тоже должны были бы притягивать, а наэлектризованное тело должно было бы притягивать пламя находящейся поблизости свечи, но оно не только не притягивает его, а даже теряет свою силу в присутствии пламени.
Критика Гильберта, безусловно, правильна, но выдвигаемая им теория представляется не более правдоподобной, чем отвергаемые. Согласно Гильберту, все тела берут начало только от двух первичных элементов – воды и земли. Те, которые берут начало от воды, обладают свойством притягивать, потому что из воды исходят особые истечения, которые “подобно распростёртым рукам” хватают тело и несут его к источнику истечения. И, проникнув в него и как бы зацепив его, они удерживают это тело, пока не ослабеют и, обессилев, не отпустят жертву. В таком духе рассматриваются и другие случаи. Нельзя сказать, чтобы теория Гильберта была лучше теорий Кардана или Порты.
Подчёркивая различие между магнитным и электрическим притяжением (оно было замечено ещё Карданом, тогда как раньше оба эти явления считались одной природы), Гильберт заметил ещё один важный факт: влажные тела трудно поддаются электризации трением, тогда как на притяжении магнитов влажность не сказывается.
Не останавливаясь на других характерных различиях электрических и магнитных явлений, заметим в заключение, что наука об электричестве, сводившаяся раньше к единственному забавному факту, была благодаря Гильберту обогащена многочисленными новыми явлениями, точными наблюдениями, инструментальной техникой, которая сама по себе есть новый этап в науке. Уильям Гильберт вполне заслуживает титула “отца науки об электричестве”.
21. РАБОТЫ ПО МАГНЕТИЗМУ ПОСЛЕ ГИЛЬБЕРТА. Труд Гильберта (см. гл. 3, § 16 и 17), новый по методу и революционный по содержанию, нашёл в Италии своих первых поклонников и первых критиков. Среди поклонников были такие, как Галилей, а среди критиков – Никола Кабео (1585–1650), который, как и Гильберт, опирался на эксперименты. В 1629 г. Никола Кабео опубликовал в Ферраре свой труд “Philosophia magnetica” (“Магнитная философия”), представляющий интерес не только из-за некоторых имеющихся в нём новых положений, о которых мы скажем ниже, и не из-за иллюстрации магнитных явлений, уже открытых Гильбертом, а потому, что он позволяет понять аргументы, не всегда научного характера, которые побуждали автора противиться главной идее Гильберта – представлению о Земле как о большом магните. Цель книги Кабео была опровергнуть утверждение о количественном совпадении данных о земном магнетизме и о магнетизме шара Гильберта. И если Гильберт, чтобы подтвердить свою теорию, показывает, что кусок железа, помещённый вдоль земного магнитного меридиана, намагничивается, то Кабео как раз пытается обесценить это доказательство, опровергая его с помощью нового, открытого им явления: расположенные по вертикали железные предметы намагничиваются, причём южный полюс оказывается наверху, а северный – внизу.
Если Гильберт не принимает изложенную у Лукреция античную теорию притяжения янтаря, поскольку ему представляется, что истечения из янтаря, отталкивая воздух, должны были бы отталкивать и лёгкие тела, то, согласно Кабео, такое отталкивание действительно существует и в нём можно убедиться на опыте, который и является первым доказательством электрического отталкивания. Кабео натирал кусок янтаря и приближал его к деревянным опилкам. Сначала опилки прилипали к янтарю, выстраивались в линии на его поверхности, слегка колебались, как при лёгком ветре, затем начинали качаться сильнее и в конце концов отскакивали.
Кабео восхищался экспериментальной частью труда Гильберта, но пытался обесценить его теории. Мы говорим “пытался”, потому что, не заменив их другими, более вероятными, он ограничился пережёвыванием устарелых представлений, от которых новое научное мышление уже отказалось.
Это новое мышление проявил Бенедетто Кастелли, когда он в заметке о магнетизме попытался дать теорию строения магнитов, их намагничивания и магнитного притяжения. К сожалению, эта заметка “Discorso” (“Рассуждение”) оставалась неизданной вплоть до 1883 г. В ней Кастелли приводит ряд более или менее известных опытов, из коих особенно интересен опыт по определению формы магнитного поля, проведённый почти так же, как это делается в наши дни: под листом бумаги помещается магнит, а сверху насыпаются магнитные опилки (сейчас применяются простые железные опилки).
Кастелли полагал, что существуют “магнитные тела первого рода”, в которых рассеяны магнитные частицы, т. е. крошечные магнитные иглы, способные ориентироваться под действием внешнего магнита, после чего все они или большая их часть остаются в новом положении. Существуют ещё “магнитные тела второго рода”, в которых беспорядочно рассеянные магнитные частицы обладают склонностью возвращаться в первоначальное положение. Пусть теперь читатель сопоставит эти гипотезы с предположениями, высказываемыми в современных курсах и касающимися строения магнитов по Юингу. Такое сравнение покажет, что различие имеется лишь в словах; из него станет ясно, каким образом Кастелли с помощью своих простых гипотез объясняет строение магнитов, временное и постоянное намагничивание и притяжение магнитов.
Гримальди в своём трактате “De lumine” (“О свете”) также посвятил свыше 30 страниц магнетизму, где он описывает старые и новые эксперименты (среди последних – опыт с намагниченной проволокой, которая в результате многократного сгибания и выпрямления теряет свои магнитные свойства), пытаясь затем объяснить их с помощью гипотезы картезианского типа о единой материальной магнитной жидкости, перетекающей от одного полюса магнита к другому. Каждое ненамагниченное магнитное тело, как, например, железо, содержит неупорядоченную жидкость; магнит упорядочивает её и, таким образом, индуцирует в теле магнитные свойства. Для теории Гримальди, хотя она и получена из картезианских предпосылок, характерно, что она вводит представление о единой жидкости и не строит гипотезы о форме образующих её частиц (см. § 1).
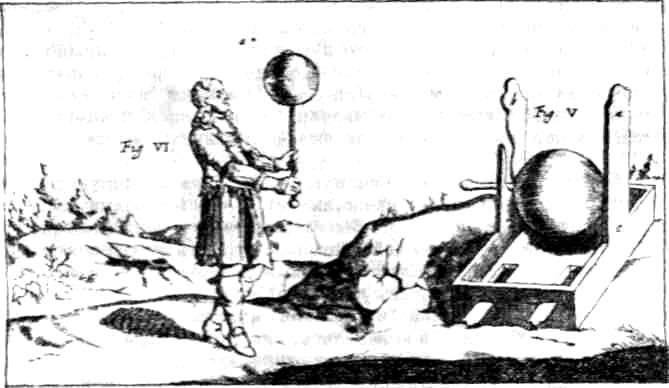
Первая электростатическая машина. Справа – вращающийся шар из серы, слева – наэлектризованная пушинка, висящая над шаром из серы, который тоже наэлектризован.
22. ЭКСПЕРИМЕНТЫ ГЕРИКЕ ПО ЭЛЕКТРИЧЕСТВУ. Введением версора Гильберт дал достаточно чувствительный инструмент для обнаружения электрических явлений, а Отто фон Герике, построив свой вращающийся шар из серы, во много раз усилил эффект.
Герике изготовил шар из плавленой серы “размером с голову ребенка” и продел сквозь него по диаметру железную ось, вокруг которой шар приводился во вращение. К поверхности шара прикладывалась сухая ладонь. Таким образом, речь идёт о первой электростатической машине, основанной на трении. Наэлектризованный серный шар притягивал листочки золота, серебра, бумаги и т. п., которые, как впоследствии заметил уже Кабео, отталкивались, а потом вновь притягивались, если до них сначала дотрагивались каким-нибудь другим телом. Особенно интересным и занимательным был подобный опыт с пушинкой, которая, оттолкнувшись от наэлектризованного шара, после соприкосновения с ним ещё некоторое время оставалась висеть в “сфере действия” шара и по мере перемещения шара могла следовать за ним по всей комнате. Можно было заметить, что эта пушинка, перемещаясь по комнате, сама притягивает все окружающие предметы, а если сил для этого у неё оказывается недостаточно, то приближается к ним сама, особенно если эти предметы имеют какие-нибудь выступы. Если приблизить к пушинке палец, то пушинка забавно мчится к нему, затем поворачивает вновь к шару, от шара снова к пальцу и так продолжается довольно долго. Кроме того, шар передаёт свою способность притяжения нити длиной свыше локтя (67 см), так что теория притяжения через посредство воздуха оказывается несостоятельной. И, наконец, если электризовать серный шар в темноте, то он сверкает подобно сахару, раздробляемому пестиком, причём слышно характерное потрескивание.
Опыты Герике, значение которых очевидно, были повторены Бойлем с тем же результатом. Бойль добавил ещё один эксперимент (подобный эксперимент члены Академии опытов ставили с магнитами и предполагали провести с наэлектризованными телами, но он у них не удался). С помощью пневматической машины Бойль показал, что электрическое и магнитное притяжение проявляется и в пустоте. Тем самым была окончательно разрушена старая теория о действии через воздух. Но что же предлагают физики вместо воздуха? Не что иное, как возврат к старой теории Гильберта о жидкости, истекающей из заряженного тела и “зацепляющей” лёгкие тела. В этом заключается объяснение Бойля. Этим Ньютон объяснил явление “электрического танца”, которое он получил, натерев тканью стеклянный диск, укреплённый в бронзовом кольце и расположенный на расстоянии примерно 8 мм от поверхности стола, на котором были разбросаны кусочки бумаги.
Обычно говорят, что декартово понимание физики механистично. Но понимание Галилея и Ньютона тоже было механистичным, потому что под механицизмом понимаются все иногда противоречащие друг другу теории, которые объясняют все физические теории с помощью системы движений, подобных движению механизма. Нам представляется, что механицизм Декарта отличается от механицизма Галилея-Ньютона двумя существенными чертами. Первое, более очевидное отличие только что отмечалось - это понятие силы. Для Галилея и Ньютона сила - это физическая реальность, не сводимая к свойствам пространства и движения; для Декарта та же сила, как мы видели, - это свойство пространства. Механицизм Декарта противостоит динамизму Ньютона, доведённому до крайнего предела Рожером Босковичем в XVIII и Майклом Фарадеем в XIX веке. Согласно этим динамистам, непосредственно данной является сила; так называемая материя исчезает, а её "почтенные качества", как называл их Оствальд, суть не что иное, как свойства полей сил в пустом пространстве. Но механицизм Декарта противостоит также и атомизму, согласно которому именно атомы создают поля сил, а их скрытые движения объясняют все физические процессы. Очевидно, декартово учение, отождествляющее вещество с протяжённостью, не могло быть атомистическим в традиционном демокритовом смысле слова.
13. СТАТИСТИЧЕСКИЕ ЗАКОНЫ. Мы уже говорили, что утверждение второго начала термодинамики в формулировке Клаузиуса не соответствовало традиционным механическим представлениям. Механика всегда рассматривала процессы природы как обратимые, тогда как второе начало термодинамики считает их необратимыми. Кинетическая теория превращает это несоответствие в противоречие: если теплота сводится к движению отдельных молекул, подчиняющемуся обратимым динамическим законам, то как же можно совместить обратимость отдельных процессов с необратимостью в целом? По-видимому, одной из причин острой борьбы между представителями энергетического направления — Ранкином, Гельмгольцем, Оствальдом, Махом — и сторонниками атомистики, которую “энергетики” считали слишком грубой и наивной, является именно вопрос о противоречии между обратимостью динамических процессов и вторым началом термодинамики. Согласно энергетической школе, противоречие может быть снято, если отказаться от одной из посылок, поэтому они были склонны отказаться от кинетической теории и вернуться к агностической концепции Майера.
Однако это противоречие было преодолено совсем иным путём. Первым пошёл по этому пути Максвелл, поставив перед собой конкретную задачу кинетической теории газов: если молекулы газа находятся в непрерывном движении, то какова скорость определённой молекулы в определённый момент?
Максвелл начинает с замечания, что предположение Бернулли о равенстве скоростей всех молекул принять нельзя. Действительно, если бы даже в какой-либо определённый момент все молекулы газа имели одну и ту же скорость, то такое идеальное состояние тотчас нарушилось бы в результате взаимных соударений молекул. Так, если молекула А налетает на молекулу В перпендикулярно направлению её движения, то легко рассчитать, что молекула В ускоряется, а молекула А замедляется.
Но проследить мысленно или рассчитать судьбу каждой отдельной молекулы из бесчисленного количества молекул, содержащихся в объёме газа, не представляется возможным. Можно, согласно Максвеллу, лишь определить статистическое распределение их скоростей, т. е. ответить не на вопрос о том, какова скорость отдельной определённой молекулы, а на вопрос, сколько молекул имеют определённую скорость в заданный момент. В основу своего расчёта Максвелл положил следующие интуитивные предпосылки: ни одно направление движения не является привилегированным; ни одно значение скорости не является привилегированным или запрещённым (т. е. молекула может принимать все значения скорости от нулевой до максимальной); каждый газ, предоставленный самому себе, приходит в конце концов в стационарное состояние, в котором статистическое распределение скоростей остаётся постоянным во времени. Иными словами, если две молекулы со скоростями а и b сталкиваются и после соударения приобретают скорости р и q, то одновременно две другие молекулы со скоростями р и q сталкиваются и приобретают соответственно скорости а и b, так что число молекул, имеющих скорости а, b, ..., р, q, ..., остаётся постоянным. Исходя из этих гипотез и некоторых других, менее существенных, к которым он прибегает по ходу рассуждений, Максвелл пришёл к известной формуле для распределения скоростей молекул газа. Эта формула вызвала длительную дискуссию, утихшую лишь в последние годы, когда молекулярные насосы позволили произвести её экспериментальную проверку. Не прослеживая всей дискуссии, достаточно подчеркнуть огромное значение введения статистических законов. На место причинных динамических законов становятся статистические законы, позволяющие предвидеть эволюцию природы не с абсолютной достоверностью, а лишь с большой степенью вероятности. Понятие вероятности физического явления, неявно введённое Максвеллом, было применено в 1878 г. Людвигом Больцманом (1844-1906) для преодоления трудностей, связанных со вторым законом термодинамики. В связи с этим находится классический мысленный эксперимент Максвелла (1871 г.): пусть газ разделён на две части диафрагмой с небольшим отверстием, которое может перекрываться задвижкой, и пусть некий “демон”, способный видеть молекулы и стерегущий этот проход, открывает задвижку для молекул, движущихся в одном направлении, и закрывает её для молекул, движущихся в противоположном направлении. Через некоторое время произойдёт сжатие всего газа в одной из половинок объёма, и второе начало термодинамики будет нарушено.

Людвиг Больцман.
Эти трудности были преодолены Больцманом с помощью радикального нововведения: второе начало термодинамики рассматривается не как достоверный закон природы, а лишь как в высшей степени вероятный. Вот известное рассуждение Больцмана, приведённое им для иллюстрации такого понимания. Пусть мы имеем, говорит Больцман, два сосуда, соединенных небольшим отверстием, и пусть сначала в каждом из сосудов имеется по одной молекуле. Вследствие движения молекул может случиться, что одна из молекул пройдёт сквозь отверстие между сосудами и окажется в другом сосуде. При этом произойдёт самопроизвольное сжатие газа вопреки утверждению второго закона термодинамики. Но если бы в каждом из сосудов было первоначально не по одной, а по две молекулы, то ясно, что такое сжатие менее вероятно; ещё менее вероятным оно становится для 4, 8, 16, ... молекул в каждом сосуде. Так вот, второе начало термодинамики утверждает не об абсолютной достоверности, а о высокой степени вероятности. Вероятность отклонения от термодинамического закона была рассчитана, и для иллюстрации полученной величины, несоизмеримой с вероятностями событий, встречающихся в обычной жизни, придумывалось множество примеров. Приведём один из них. Допустим, обезьяна долбит по клавишам пишущей машинки с непрерывной подачей бумаги. Какова вероятность, что она напечатает “Божественную комедию” Данте? Ясно, что рассчитать её нетрудно; полученная при этом вероятность ещё во много раз больше термодинамических вероятностей. Но поскольку мы практически совершенно уверены, что обезьяна никак не сможет написать “Божественную комедию”, тем больше оснований быть уверенными в справедливости термодинамических законов.
Но практическая справедливость закона представляет интерес для инженера, а учёные видят, что второй закон термодинамики из ранга достоверных законов переходит в ранг вероятных. Между достоверностью и вероятностью, пусть даже и очень большой, учёный видит непроходимую пропасть. Таким образом, классическая физика оказалась перед лицом неизбежного дуализма. Имея перед собой какой-либо закон, претендующий на описание явления, физика должна теперь задавать себе вопрос: что это — динамический, причинный закон или же статистический, вероятностный?
Перед лицом такого дуализма физики разделились на два лагеря. Меньшинство хотело преодолеть этот дуализм, отрицая существование достоверных законов и придавая всем законам вероятностный характер. Большинство же стремилось свести все статистические законы к элементарным, динамическим. Статистические законы, говорили они, — это синтез отдельных динамических причинных законов, которые наше сознание не в состоянии проследить в их совокупности. Вероятность, возникающая в статистических законах, это, как говорил Пуанкаре, просто мера нашего незнания. Наука не может опираться на статистические законы, она должна добраться до индивидуальных динамических законов, лежащих в основе статистических, потому что только таким образом наше мышление сможет следовать за причинными связями в природе. Эти физики, очевидно, полностью придерживались строгого детерминизма явлений природы, провозглашённого Лапласом фундаментальным принципом в его известном утверждении:
“Мы должны рассматривать существующее состояние Вселенной как следствие предыдущего состояния и как причину последующего. Ум, который в данный момент знал бы все силы, действующие в природе, и относительное положение всех составляющих её сущностей, если бы он ещё был столь обширным, чтобы ввести в расчёт все эти данные, охватил бы одной и той же формулой движения крупнейших тел Вселенной и легчайших атомов. Ничто не было бы для него недостоверным, и будущее, как и прошедшее, стояло бы перед его глазами” 10.
Этим детерминистским подходом вдохновлялся Бьёркнес, когда в начале XX столетия излагал грандиозную программу исследований, направленных на то, чтобы свести свою метеорологическую статистику к отдельным динамическим законам. Но в то время, когда Бьёркнес составлял эти грандиозные планы, уже стала складываться современная физика, которой предстояло, как мы увидим в гл. 15, революционизировать традиционные схемы.
6. ЭЛЕКТРОДИНАМИКА АМПЕРА. Одновременно с работами Био и Савара, и даже на несколько месяцев раньше, провёл свои теоретические и экспериментальные исследования Ампер. 18 сентября 1820 г. он сообщил Парижской Академии наук о своём открытии пондеромоторных взаимодействий токов, которые он назвал электродинамическими. Точнее говоря, в этом своём первом докладе Ампер назвал эти действия “вольтаическими притяжениями и отталкиваниями”, но потом стал именовать их “притяжениями и отталкиваниями электрических токов”. В 1822 г. он ввёл термин “электродинамический”. Ампер был плодовитым и искусным изобретателем неологизмов. Именно ему мы обязаны такими словами, как электростатический, реофор, соленоид, и многими другими.
Говорят, что, когда Ампер зачитал свой доклад об электродинамических действиях токов, один из его коллег по окончании чтения спросил: “Но что же, собственно, нового в том, что вы нам сказали? Само собой ясно, что если два тока оказывают действие на стрелку, то они оказывают действие также и друг на друга”. Ампер, захваченный врасплох, не знал, что ответить. Но ему на помощь пришёл Араго. Он вынул из кармана два ключа и сказал:
“Вот каждый из них тоже оказывает действие на стрелку, однако же они никак не действуют друг на друга”. Такой случай, по-видимому, действительно был, потому что Ампер в своей большой работе “Mémoire sur la theorie mathétmatique des phénomènes électro-dynamiques uniquement déduite de l'expérierace”1 (“О математической теории электродинамических явлений, однозначно выведенной из опыта”) считает нужным заметить, что из опыта Эрстеда нельзя было логически заключить о взаимодействии двух токов, как из действия двух кусков железа на стрелку нельзя сделать вывода об их взаимодействии. Но рассказывают ещё и о другом случае. Лаплас присутствовал на первой публичной демонстрации опыта Ампера. Публика уже расходилась, и Лаплас у выхода стал ждать ассистента, Даниэля Колладона; увидев его, он хлопнул его по плечу и, пристально глядя на него, спросил: “А не вы ли это, молодой человек, подталкивали провод?”2

Андре Мари Ампер.
Сразу же после открытия Эрстеда физикам показалось вполне естественным объяснить его тем, что при прохождении электрического тока через проводник последний становится магнитом. Такое объяснение было принято Араго, который приступил к опыту, упомянутому в § 4, исходя именно из этого представления. Оно было принято также и Био 3, который упорно придерживался его ещё много лет. Его придерживались также Дэви и Берцелиус. Последний уточнял, что каждое поперечное сечение проводника, по которому проходит ток, становится двойным магнитом с противоположными полюсами. Однако Ампер предложил другое объяснение, которое и является самым гениальным его вкладом в науку: не проводник, по которому течёт ток, становится магнитом, а, наоборот, магнит представляет собой совокупность токов. В самом деле, говорит Ампер, если мы предположим, что в магните присутствует совокупность круговых токов, текущих в плоскостях, точно перпендикулярных его оси, в одном и том же направлении, то ток, идущий параллельно оси магнита, окажется направленным под углом к этим круговым токам, что и вызовет электродинамическое взаимодействие, стремящееся сделать все токи параллельными и направленными в одну сторону. Если прямолинейный проводник закреплён, а магнит подвижен, то отклоняется магнит; если же магнит закреплён, а проводник подвижен, то движется проводник.
Легко понять, что в то время, в 1820 г., гипотеза Ампера казалась исключительно смелой, и не удивительна поэтому та сдержанность, с которой она была встречена. Гипотеза Био и Араго казалась куда более правдоподобной. Но когда в 1821 г. Фарадей установил вращение токов в магнитном поле, Ампер заметил, что такой эффект нельзя объяснить никаким распределением магнитиков в проводнике, через который проходит ток; такое распределения могло вызвать лишь силы притяжения или отталкивания, но никак не вращающую пару сил.
Ампер заботился больше о том, чтобы найти опытное подтверждение своей собственной гипотезы, нежели о критике чужих теорий. Он подумал, что если магнит понимать как систему круговых параллельных токов направленных в одну сторону, то спираль из металлической проволоки по которой проходит ток, должна вести себя как магнит, т. е. должна принимать определённое положение под воздействием магнитного поля Земли и иметь два полюса. Опыт подтвердил предположения относительно поведения такой спирали под действием магнита, но не совсем ясны были результаты опыта, относящиеся к поведению спирали под действием магнитного поля Земли. Тогда Ампер решил взять для выяснения этого вопроса один единственный виток проводника с током; оказалось, что виток ведёт себя точно как магнитный листок.
Таким образом обнаружилось непонятное явление: один-единственный виток ведёт себя как магнитная пластина, а спираль, которую Ампер считал в точности эквивалентной системе магнитных пластинок, вела себя не совсем как магнит. Пытаясь разобраться, в чём тут дело, Ампер с удивлением обнаружил, что в электродинамических явлениях спиральный проводник ведёт себя точно как прямолинейный проводник с теми же концами. Из этого Ампер заключил, что в отношении электродинамических и электромагнитных действий элементы тока можно складывать и разлагать по правилу параллелограмма. Поэтому элемент тока можно разложить на две составляющие, из которых одна направлена параллельно оси, а другая — перпендикулярно. Если суммировать результаты действия разных элементов спирали, то результирующая окажется эквивалентной прямолинейному току, идущему по оси, и системе круговых токов, расположенных перпендикулярно оси и направленных в одну сторону. Поэтому, чтобы спираль, по которой проходит ток, вела себя точно как магнит, нужно скомпенсировать действие прямолинейного тока. Этого Ампер, как известно, добился очень просто, выгнув вдоль оси концы проводника. Но всё же существовало различие между спиралью, по которой проходит ток, и магнитом: полюса спирали находились только на концах, тогда как полюса магнита — во внутренних точках. Чтобы устранить и это последнее различие, Ампер оставил свою первоначальную гипотезу о токах, прямо перпендикулярных оси магнита, и принял, что они расположены в плоскостях, находящихся под разными углами к оси.
Сразу же после своих первых электродинамических опытов Ампер решил вывести формулу для величины силы, возникающей между двумя элементами тока, чтобы из этой формулы можно было найти силу, действующую между двумя частями проводников данной формы и положения. Не имея возможности проводить опыты с элементами тока, Ампер в 1820 г. попытался сначала использовать следующий метод: провести тщательные и многочисленные измерения действия двух конечных токов разной формы и положения, затем принять какую-либо гипотезу о взаимодействии двух элементов тока, вывести из неё взаимодействие двух конечных токов и далее модифицировать эту гипотезу до тех пор, пока теоретические и экспериментальные результаты не окажутся в полном соответствии. Это классический путь, многократно испробованный в подобных исследованиях, однако Ампер вскоре убедился в том, что этот способ в данном случае был бы построен на сплошных догадках и желаемые результаты можно получить более прямым путём.
Установив, что подвижный проводник находится точно в равновесии под действием равных сил, вызываемых неподвижными проводниками, размеры и форму которых можно без нарушения равновесия изменять при соблюдении условий, допустимых опытом, Ампер получил возможность непосредственно рассчитать, каково должно быть взаимодействие двух элементов тока, чтобы равновесие при таких условиях действительно не зависело от формы и размеров неподвижных проводников. Он смог успешно применить этот гораздо более узкий критерий, потому что опытным путём было определено четыре случая равновесия, два из которых ещё и сегодня приводятся курсах физики (равенство абсолютной величины сил, действующих на одинаковые токи, текущие в противоположных направлениях; одинаковое действие на прямолинейный подвижный проводник двух неподвижных проводников, прямого и изогнутого, одинаково удалённых и имеющих концы в одних и тех же точках).
Исходя из этих четырёх экспериментальных постулатов, Ампер путём довольно сложного доказательства вывел первую из формул электродинамического взаимодействия элементов тока, за которой последовали многие другие формулы, выведенные рядом учёных (Грассманн, Вебер, Риман и др.). Все эти формулы применялись для расчёта, и все они подвергались критике. Эти формулы давали величину силы, действующей между двумя элементами тока, в зависимости от сил токов, расстояния между элементами и их взаимного положения.
В ходе теоретических исследований выяснилось, что части одного и того же проводника должны взаимно отталкиваться. Этот факт представлялся Амперу настолько важным, что он счёл возможным положить его в основу электродинамики и поэтому решил найти ему непосредственное экспериментальное подтверждение. Таковое Ампер получил в сентябре 1822 г. с помощью приспособления, упоминаемого ещё в некоторых современных курсах физики. Это сосуд, разделённый перегородкой на два отделения, заполненных ртутью и соединенных подвижным проводником, плавающим в ртути. При прохождении тока по проводнику из одного отделения в другое подвижный проводник смещается.
Из своей формулы взаимодействия элементов тока, рассматривая магнит как систему молекулярных токов, Ампер вывел первый закон Лапласа, а из него способом, описываемым во всех современных учебниках, — закон Био и Савapa. Ампер вывел также закон Кулона для магнитостатического взаимодействия двух магнитов, рассматриваемых как две токовые системы. Другое благоприятное для своей теории обстоятельство Ампер видел в том факте, что незадолго до того выведенная Пуассоном формула для силы действия магнитного элемента на элемент северного или южного флюида совпадает с формулой, получающейся из его теории для очень маленькой замкнутой плоской петли тока. Отсюда сразу же следует, что если замкнутый малый плоский контур тока эквивалентен элементарному магнитику, то, разлагая, как это рекомендуется и сейчас в учебниках, конечный контур на отдельные кольца, можно показать, что замкнутый контур действует точно так же, как элементарные магнитики, которые равномерно распределены по ограниченной этим контуром произвольной поверхности так, что их оси нормальны поверхности. Это знаменитая теорема эквивалентности Ампера.
Ампер понимал, что к тем же проверяемым опытом выводам можно прийти, исходя и из других законов взаимодействия элементарных токов, поэтому особенно подчёркивал другое достоинство своей теории — её способность сводить к единой причине (взаимодействию двух элементов тока) три вида взаимодействий, кажущихся совершенно различными: магнитостатические, электромагнитные и электродинамические. Но главное достоинство своей формулы (единственной, которая, по его мнению, имеет право называться действительно элементарной) он видел в том, что она изгнала из физики “вращательные силы”, сведя все силы природы к взаимодействию частиц вдоль соединяющей их прямой.
Таким образом, в этой большой работе, опубликованной в 1827 г. и охарактеризованной Максвеллом как “совершенная по форме и непревзойдённая по точности”, Амперу удалось восстановить механистическую концепцию, сильно поколебленную опытом Эрстеда. Но как раз работы того же Максвелла позволили установить, что это всего лишь “заплата”.
Вебер положил в основу своей теории электрического тока, рассматриваемого как истинный поток заряженных частиц, электромагнитное действие движущегося заряда; Максвелл также принял эту концепцию. По совету Гельмгольца Роуланд в 1876 г. с помощью классического эксперимента, вызвавшего длительную дискуссию, прекратившуюся практически лишь в 1903 г. благодаря Пуанкаре, доказал, что движущийся по окружности электрический заряд оказывает на магнитную стрелку точно такое же действие, как и круговой ток. Более того, при увеличении скорости заряда растёт и сила, действующая на каждый полюс стрелки, т. е. величина силы зависит от скорости заряда. Между тем для механистической концепции характерно объяснение всех явлений силами, зависящими лишь от расстояния между частицами. Опыт Роуланда не только подтверждал существование “вращательных сил”, но вводил новый элемент, совершенно чуждый механистической концепции и потому сильно её поколебавший.
Однако вернёмся ещё раз к работе Ампера. Оставив в стороне его резкую полемику с Био, полную личных выпадов, мы хотим заметить, что Ампер объясняет, как это он уже делал и в 1821 г., земной магнетизм существованием внутренних токов в земном шаре — это одна из многочисленных и малоудовлетворительных теорий, пытающихся объяснить земной магнетизм.
В 1822 г. Леопольд Нобили подкрепил взгляд Ампера, создав “прибор”, состоящий из
“...сферического шара, обмотанного металлической проволокой в направлении параллелей, которая соединяется концами с цинковым и медным электродами вольтова столба” 4.
Этот прибор в некоторых курсах физики называют “шаром Барлоу”, хотя Барлоу представил его описание в Королевский институт лишь 26 мая 1824 г., т. е. через два года после опубликования статьи Нобили.
5. ПЕРВЫЕ ПРЕДСТАВЛЕНИЯ О СЛОЖНОМ СТРОЕНИИ АТОМОВ. Вторая часть работы Джозефа Джона Томсона, в которой изложен упоминавшийся нами в гл. 11 метод определения отношения заряда электрона к его массе, посвящена рассмотрению строения вещества. Из первых опытов, как мы уже говорили, следовало, что “корпускулы” обладают массой, которая несомненно значительно меньше, нежели масса самого простого атома, однако, по мнению Дж. Дж. Томсона, не меньше десятой или сотой доли массы атома водорода. Томсон считал приемлемой гипотезу Праута, согласно которой различные химические элементы представляют собой различные соединения атомов первоэлемента одной и той же природы. Если заменить атомы водорода из гипотезы Праута “корпускулами”, то теория первоэлемента согласуется как с опытными данными, так и с выдвинутой в то время для объяснения особенностей спектров звёзд гипотезой Нормана Локкайера.
Но как располагаются “корпускулы” в атоме? Дж. Дж. Томсон считал, что можно принять модель Босковича или даже просто модель “некоторого числа взаимоотталкивающихся частиц, сдерживаемых вместе некоторой центральной силой”. К сожалению, экспериментальное изучение такого “коллектива” частиц так стремительно усложняется с ростом числа частиц, что практически становится невозможным. Поэтому целесообразнее прибегнуть к модельным представлениям, чтобы уяснить возможную структуру этих атомов, состоящих из корпускул.
По мнению Дж. Дж. Томсона, самой простой моделью следует считать модель плавающих магнитов 8, предложенную американцем Альфредом Майером. В этой модели магниты самопроизвольно располагаются в состоянии равновесия под действием взаимного отталкивания и силы притяжения большого магнита. Если плавающих магнитов не больше пяти, то они располагаются в вершинах правильного многоугольника; если же их больше, то они располагаются несколькими кольцами. Например, если магнитов шесть, то один помещается в центре, остальные пять его окружают, располагаясь в вершинах правильного многоугольника; если магнитов 29, то один помещается в центре, его окружает первое кольцо из 6 магнитов, второе, большее кольцо из 10 магнитов и третье, еще большее кольцо из 12 магнитов. Если принять эту систему магнитов за модель атома, причём число магнитов будет пропорционально атомному весу, то из неё сразу же следует, что если, скажем, какое-нибудь свойство зависит от числа магнитов в самом меньшем круге, то, поскольку кольцо такого типа может повторяться в нескольких моделях, появляется возможность рационального объяснения периодической системы элементов. Какая соблазнительная перспектива для физики конца прошлого века!
Но, к сожалению, эта модель смогла продержаться лишь несколько месяцев. В самом деле, её достоверность связана с идеей о небольшом числе составляющих атом “корпускул”, порядка нескольких десятков. Но если для представления строения простейшего атома требуется вообразить целое облако из тысяч “корпускул”, то такая модель, очевидно, не давала бы никаких возможностей для экспериментального изучения, а может быть, и для теоретического. Вот почему, когда вскоре после этого Дж. Дж. Томсон и другие установили, что эти “корпускулы” (отныне мы будем называть их современным именем — электроны) обладают массой, во много раз меньшей массы атома водорода, Томсон вынужден был (в 1899 г.) изменить свою модель. Теперь она выглядела так: нейтральный атом содержит большое число электронов, отрицательный заряд которых компенсируется
“чем-то, что делает пространство, в котором рассеяны электроны, способным действовать так, как если бы оно имело положительный электрический заряд, равный сумме отрицательных зарядов электронов” 9.
Эта вторая томсоновская модель атома всё ещё страдает некоторой неясностью, но по сравнению с первой это уже большой шаг вперёд, потому что она признает, что атом состоит не только из электронов, но из электронов и из чего-то, точно ещё не определённого, которое служит как бы центром образования атома.
6. ATOM ТОМСОНА. Вторая модель Дж. Дж. Томсона вскоре получила более чёткий характер благодаря работе лорда Кельвина, чей огромный авторитет, несомненно, сильно помог дальнейшему успеху модели Томсона. В этой работе, появившейся в 1901 г., выдвигается предположение, что поток отрицательного электричества, состоящий из электронов (которые Кельвин, пожалуй, этимологически более правильно называет электрионами по аналогии с термином ионы), свободно пронизывает не только пустое пространство между атомами, но и сами атомы. Кроме того, Кельвин постулирует притяжение между атомом обычной материи и электроном, определяемое следующим законом:
Притяжение атомом внешнего электрона обратно пропорционально квадрату расстояния между их центрами, а притяжение электрона, находящегося внутри самого атома, пропорционально расстоянию между их центрами.
Этот закон, согласно знаменитой теореме Ньютона, равносилен допущению о равномерном распределении положительного электричества в пространстве, занимаемом атомом обычной материи. Из этого следовало, что существует два рода электричества: отрицательное, “зерновидное”, и положительное в виде непрерывного облака, как обычно представляли себе “флюиды”, и в частности эфир.
Обычная незаряженная материя представляет собой совокупность атомов, содержащих столько электронов, сколько необходимо для того, чтобы вне атома нейтрализовать электрические силы. Короче говоря, модель атома Кельвина предполагает, что в атоме имеется равномерное сферическое распределение положительного электричества и определённое число электронов. Но при чтении статьи Кельвина нельзя понять, является ли для него так называемая материя носителем этого электрического заряда или же она отождествляется с ним. Эта же двусмысленность потом будет присуща и последующим моделям атома.
Как бы там ни было, простейшая модель атома представляет собой равномерное сферическое распределение положительного электрического заряда с одним электроном в центре. Что же касается атомов с двумя и более электронами, то здесь возникает проблема устойчивости, которую Кельвин без долгих рассуждений разрешает утверждением, что электроны, вероятно, располагаются по сферическим поверхностям, концентричным границе атома, находящимся внутри него, и, должно быть, вращаются вокруг центра.
Модель Кельвина подымала две важные проблемы. Вращающиеся электроны должны были бы, согласно электромагнитной теории света, вызывать электромагнитные волны и магнитное поле. Как проявляются оба эти явления? Изучением этого занялся Дж. Дж. Томсон и примерно в течение пятнадцати лет оставался верным модели Кельвина, которая была воспринята физиками как развитие модели Дж. Дж. Томсона и поэтому в течение первых двух десятилетий нашего века называлась “атомом Томсона”.
Томсон установил сначала (1903 г.), что вращающиеся электроны должны создавать эллиптически поляризованные световые волны. Что же касается магнитного поля, создаваемого вращающимися зарядами, то, как показывала теория представление об электронах, вращающихся под действием силы, пропорциональной расстоянию, не может объяснить магнитных свойств тел, если только движение происходит без рассеяния энергии. Если допустить, что движение частиц испытывает торможение по какой-то неизвестной причине, то таким образом можно было бы объяснить парамагнетизм. Но происходит ли на самом деле рассеяние энергии? Томсон не высказывается ясно на этот счёт, предчувствуя серьёзные следствия, которые повлекло бы за собой такое утверждение. За год до этого Вильгельм Фохт тоже был вынужден для объяснения пара- и диамагнетизма привлечь довольно сложную гипотезу о вращающихся электронах, тормозимых в их движении постоянными соударениями. В противоположность заключениям Томсона и Фохта Пьер Ланжевен в одной чрезвычайно важной работе 1905 г., на которую всё ещё продолжают опираться книги по теории магнетизма, считает возможным придать гипотезе Ампера точное истолкование с помощью модели вращающихся по замкнутым траекториям электронов. Ланжевен показал также, что эффект Зеемана можно объяснить гипотезой вращающихся электронов, даже не зная закона притяжения, удерживающего электроны на орбите.
Механическая устойчивость атомной структуры была исследована Дж. Дж. Томсоном в его следующей работе в том же 1904 г. Он пришёл к выводу, что электроны должны находиться в быстром вращательном движении, причём скорость их не меньше некоторой определённой предельной величины, а если электронов много (больше восьми), то они располагаются несколькими кольцами (отсюда и связь между структурой атомов и периодической системой элементов) и число электронов в каждом кольце уменьшается с уменьшением радиуса самого кольца. В радиоактивных атомах вследствие излучения скорость электронов постепенно уменьшается; когда она достигает предельной величины, устойчивость нарушается и происходит взрыв атома, в результате которого выбрасываются частицы и устанавливается новая структура атома.
Известно, что атом Томсона не устоял перед критикой и перед опытной проверкой. Но было бы неверно думать, что его исследование было бесполезно. Напротив, оно представляло собой ценное руководство для теоретических и опытных изысканий того времени и выявило основные проблемы, которые предстояло решить при любой модели атома, принимающей электроны его составной частью. Эти проблемы можно свести к трём: связь между числом и распределением электронов и массой атома; природа и распределение положительного электричества, компенсирующего общий отрицательный заряд электронов; природа и распределение массы атома.
Томсон понимал, что главная проблема, перед которой стоит любая модель атома, состоит в нахождении такого пути, который позволил бы по данным опыта как-то судить о числе электронов, содержащихся в атоме. И он нашёл такой путь, предположив, что каждый электрон является центром рассеяния излучения, падающего на атом. Если основываться на этой гипотезе, то четыре явления позволяли получить необходимые оценки: рассеяние рентгеновских лучей, поглощение катодных лучей, дисперсия света и отклонение быстрых заряженных частиц при их прохождении через вещество.
Идя по этому пути, Дж. Дж. Томсон и многие другие исследователи, среди которых самыми известными были Краутер и Баркла, пришли к выводу, что число электронов в атоме должно быть пропорционально атомному весу. Точнее говоря, Краутер, исходя из опытов по рассеянию лучей, пришёл в 1910 г. к выводу, что число электронов должно быть в 2-3 раза больше атомного веса данного элемента; Баркла же по данным о рассеянии рентгеновских лучей в 1911 г. пришёл к выводу, что в лёгких атомах число электронов должно равняться примерно половине их атомного веса. Эти данные взаимно противоречивы, но их объединяет одно: число электронов каким-то образом связывается с массой рассматриваемого атома. Разве уже один этот качественный вывод, который впоследствии побудит других к более тщательным исследованиям, не делает атом Томсона достойным упоминания?
Гораздо труднее получить данные, необходимые для решения второй проблемы, касающейся положительного заряда атома. Здесь вопрос не столь ясен, как в случае с отрицательными зарядами. И все же, по мнению Томсона, имелись два указания на существование положительного заряда в атоме. Испускание α-частиц радиоактивными веществами заставляло предполагать, что они исходили изнутри атома, более того, они представляли собой составную часть атомов в радиоактивных элементах. А разве устойчивые элементы не могли иметь тот же состав?
“По-моему, — писал Томсон в 1913 г., — можно быть уверенным, что и другие атомы, помимо атомов радиоактивных элементов, могут быть тоже разложены и что гелий может быть получен в качестве продукта такого разложения”.
Более того,— и это как раз и есть второе указание на существование положительного заряда в атоме — Томсону показалось, что он наблюдал (каким метким кажется нам замечание Гальвани о том, что часто каждый из нас видит в явлениях то, что хочет увидеть!), как некоторые металлы, бомбардируемые быстрыми катодными лучами, испускали гелий. Однако этот факт был позже опровергнут Марией Кюри.
11. СПЕКТРАЛЬНЫЕ СЕРИИ. С самого начала исследования светового спектра (см. гл. 8) физики заметили, что, несмотря на кажущийся беспорядок, в распределении спектральных линий элементов имеется некоторая закономерность. Первым, кто открыл здесь точное соотношение, был, пожалуй, Джонстон Стони. В 1870 г. он заметил, что частоты линий С, F, h солнечного спектра, соответствующих линиям α, β, δ спектра водорода, относятся между собой как 20:27:32. Установление этого факта сразу же навело его на мысль, что эти три линии, должно быть, имеют своим источником какое-то периодическое явление внутри молекулы водорода. Он утвердился в этом предположении, когда в следующем году в сотрудничестве с Дж. Рейнольдсом установил, что частоты линий спектра поглощения хлористого хромила (CrO2Cl2) находятся при определённых условиях в простых отношениях с частотами гармоник скрипичной струны.
В 1885 г. Иоганн Бальмер (1825-1898) показал, что результаты Стони можно рассматривать как частный случай более общего закона. Он нашёл, что длины волн (или обратные им величины, называемые “волновыми числами”) линий видимого спектра водорода могут быть выражены простой формулой, с помощью которой длины волн различных спектральных линий получаются при приписывании некоторой переменной целых значений от 3 и больше5. Ободрённые успехом Бальмера, Ридберг в 1889 г., а Кайзер и Рунге в 1890 г. также начали исследования спектров. Ридберг нашёл серию линий для таллия и ртути, а проводившиеся в течение нескольких лет работы Кайзера и Рунге, применивших метод фотографирования, составили целую эпоху в этой области. Они исследовали также интенсивность спектральных линий, различие между искровыми и дуговыми спектрами и установили серии линий для многих элементов, в частности для щелочных элементов и щелочноземельных.
В XX веке работы сосредоточились на изучении серий водорода. В 1904 г. Лайман нашёл ещё одну серию водорода в ультрафиолетовой части спектра, в 1909 г. Пашен нашёл серию водорода в инфракрасной части, а в 1922 г. Блэккет установил вторую серию в инфракрасной части спектра 6.
Все эти серии описываются формулами, похожими на формулу для серии Бальмера. В них входит постоянная, называемая в спектроскопии постоянной Ридберга, величина которой определена с большой точностью. Все эти серии установлены чисто экспериментально и обладают одной особенностью: волновые числа спектральных линий получаются каждый раз приписыванием только целых значений некоторой переменной, входящей в формулу. В физике были известны только два случая, когда величины менялись не непрерывно, а лишь по целым числам: это явление интерференции и явления собственных колебаний тел (например, струны).
Благодаря этой особенности математического выражения серий часто случается, что частота линии представляет собой сумму частот двух других линий. Из всей этой группы эмпирических формул Ритц вывел так называемый комбинационный принцип, являющийся основой современной спектроскопии. Этот принцип можно выразить так: для каждого элемента можно найти совокупность чисел, называемых спектральными термами рассматриваемого атома, таких, что частота любой спектральной линии данного элемента равна разности двух спектральных термов этого элемента.
Вплоть до 1913 г. не было никакого намёка на то, каким образом можно было бы теоретически истолковать эти серии, а тем более комбинационный принцип; они оставались лишь эмпирическими формулами, точными, но таинственными. Одно казалось ясным в первом десятилетии нашего века: весь этот комплекс многочисленных неопровержимых экспериментальных фактов должен был определяться структурой элементарных частиц материи. Классическая электродинамика объясняла излучение существованием в излучающей материи электрических зарядов, обычно неподвижных, но под влиянием внешних воздействий могущих совершать колебания вокруг центра равновесия с вполне определёнными частотами с одновременным испусканием излучения. Постепенно осцилляторы (как называют колеблющиеся электрические заряды) теряют свою энергию на излучение и возвращаются в состояние покоя. Таким образом, классическая электромагнитная теория объясняла спектральные линии, которые, однако, согласно этой теории, получались совершенно отличными по положению и по свойствам от того, что давал опыт. Анри Пуанкаре, отмечая эту неудачу классической электродинамики, писал:
“Исследование распределения линий сразу же заставляет вспомнить гармонические соотношения в акустике, но различие всё же огромно; не только волновые числа не являются последовательными целыми кратными одного и того же числа, но мы не находим никаких аналогий с корнями трансцендентных уравнений, к которым приводятся многочисленные проблемы математической физики: задача об упругих колебаниях тела произвольной формы, задача о волнах Герца для осциллятора любой формы, задача Фурье об охлаждении твёрдого тела. Эти законы проще, но они совсем иной природы... Во всём этом ещё не отдают себе достаточно отчёта, и я думаю, что здесь заключается одна из самых важных тайн природы” 7.
10. ПРИНЦИП НЕОПРЕДЕЛЁННОСТИ. Мы уже упоминали о том, что ещё в 1925 г. Гейзенберг придерживался феноменологического подхода. Согласно взглядам этого немецкого учёного, физика должна отказаться от всяких моделей и объяснений. С философской точки зрения эта мысль не нова, в сущности это концепция прагматической философии; она же была положена в основу теории относительности. Но принятая за основу новой квантовой механики и доведённая до крайних логических следствий, она сильно способствовала возрождению прагматических гносеологических теорий, выдвинутых в своё время Махом, Оствальдом, Ваилати, и скоро привлекла на свою сторону многих учёных и философов. Как ранее прагматисты XIX века восставали против атомистики, считая её слишком грубой и наивной, так и теперь новая школа объявила, что причиной кризиса в физике было наивное представление об электроне как о частице, как о “материальной точке” классической механики. Гейзенберг надеялся преодолеть противоречие волна-частица, понимая эти два понятия лишь как некие аналогии и довольствуясь тем, что “совокупность атомных явлений невозможно непосредственно выразить нашим языком”. Нужно отказаться от представления о материальной точке, точно локализованной во времени и пространстве. Физика, лишённая всяких метафизических наслоений, может дать либо точное положение частицы в пространстве при полной неопределённости во времени, либо, наоборот, точное нахождение во времени при полной неопределённости в пространстве.
Точнее говоря, наша физика может в лучшем случае определить, какова вероятность нахождения в определённый момент того, что мы называем частицей, в некотором объёме пространства (не обязательно совпадающего с физическим пространством). Таково неизбежное следствие введения в физику квантовых скачков.
В 1927 г. Гейзенберг, поддержанный Бором и его школой, предложил принять эту неустранимую неопределённость в качестве специфического закона новой квантовой физики. Величину этой неопределённости можно было подсчитать по-разному. Так, Гейзенберг подсчитал предельную точность, с которой можно определить положение и скорость электрона, исходя из перестановочных соотношений квантовой механики. Как показал Бор в 1928 г., волновая механика позволяет ещё более наглядно прийти к этому результату. Ещё более наглядным представляется следующее рассуждение, основывающееся на мысленном эксперименте, предложенном Бором вниманию физиков в том же году и быстро получившем широкую известность.
Предположим, что мы хотим определить положение и количество движения электрона в определённый момент. Самый точный физический метод, который мы можем применить,— это осветить электрон пучком фотонов. Произойдёт столкновение электрона с фотоном, и положение электрона будет определено с точностью до длины волны примененного фотона, как это известно из классической оптики и почти само собой очевидно. Поэтому следует применять фотоны минимальной длины волны, т. е. большой частоты, и, следовательно, обладающие большой энергией hν и большим количеством движения hν/c. Но чем больше количество движения фотона, тем сильнее он изменит количество движения электрона. Чтобы положение электрона было определено точно, частота фотона должна была бы быть бесконечной, но тогда бесконечным было бы также его количество движения, так что и количество движения электрона осталось бы совершенно неопределённым. И наоборот, если мы хотим точно определить количество движения электрона, то, как вытекает из аналогичного рассуждения, неопределённым окажется положение электрона. Если выразить количественно это рассуждение, то получится, что если Δq — неопределённость положения, а Δр — соответствующая неопределённость количества движения, то Δq·Δр≥h.
Если вместо сопряжённых величин р и q взять другие две сопряжённые величины, например энергию и время, то мы придём к аналогичному неравенству. Эти неравенства представляют собой квантовомеханические соотношения неопределённостей.
1. Есть русский перевод в книге: А. М. Ампер, Электродинамика, Л., 1954.
2. Raoul de Piсtet, Étude critique du matérialisme et du spiritualisme par la physique expérimentale, Génève, 1896, p. 101–105. Однако этот случай, о котором многие рассказывают, скорее всего, вымышлен, ибо маловероятно, что Лаплас ждал публичной демонстрации опыта, чтобы узнать об открытии Ампера. Ведь сам Ампер вспоминает о полученных от Лапласа советах, как увеличить эффект в опыте Эрстеда, изогнув проводник так, чтобы оп проходил и над стрелкой и под нею. И потом совершенно неверно, будто первая публичная демонстрация опыта была проведена, как пишет Пикте, в 1823 или 1824 г. с несовершенными приборами, которые не позволили добиться желаемого эффекта, разочаровав публику и огорчив Ампера. Уже в феврале 1821 г. Ампер построил свою “скамью”, использовав при этом многочисленные приспособления, изготовленные знаменитым Пиксием. Этой “скамьёй” воспользовался затем Деламбр, когда 2 апреля 1821 г. повторил перед Парижской Академией наук основные опыты Ампера.
3. В 1820 г. Био утверждал, что когда прямолинейный ток действует на магнитную молекулу, то “природа этого действия та же, что и для намагниченной стрелки, помещённой на периферии проводника в определённом направлении, постоянном по отношению к направлению вольтаического тока*. Био и другие физики, разделявшие его мнение, объясняли электродинамическое действие взаимодействием элементарных магнитов, возникающих под действием тока в каждом проводнике: каждый проводник, по которому проходит ток, превращается в магнитную трубку. Био оставался твёрдым в этом своём убеждении, хотя уже в 1820 г. Гей-Люссак и Вельтер придумали эксперимент, повторенный с тем же результатом Дэви и Эрманом, в котором показано, что два сильно намагниченных трубчатых кольца не проявляют взаимодействия.
4. L. Nоbili, Sul confronto del circuiti elettrici coi circuiti magnetici, Modena, 1822, в кн. Memorie ed osservazioni edite ed inedite del cavaliere Leopoldo Nobili... colla descrizi-one ed analisi de'suoi apparati ed istrumenti, Firenze, 1834, II, p. 23.
5. Если — волновое число линии водородного спектра, то серия Бальмера выражается формулой ν0=R(1/22-1/n2), где R — константа, называемая постоянной Ридберга, равная 109678, а п принимает целые значения 3, 4, 5, ... . Теоретически число линий бесконечно, но из формулы видно, что последующие линии располагаются всё ближе и ближе. Начиная с определённого предела, они становятся уже неразличимыми, потому что их интенсивность уменьшается в направлении к фиолетовой части спектра.
6. Если формулу, приведённую в предыдущем примечании, написать в виде ν0=R(1/m2-1/n2) и принять т=1, а n= 2, 3, 4, ... , то получится серия Лаймана (ультрафиолет). Если положить т=2, а n=3, 4, 5, ... , то получится серия Бальмера. Если принять m=3, а n= 4, 5, 6, ... , то получится серия Пашена (в инфракрасной части спектра). Наконец, если принять m= 4, а n= 5, 6, 7, ... , то получится серия Блэккета.
7. H. Роinсаré, La valeur de la science, Paris, 1908, p. 205.
8. Опыты, проведённые в 1878—1879 гг. Майером, представляются нам интересными. В небольшой сосуд, наполненный до краёв водой, помещались плавающие маленькие пробочные цилиндрики, в каждый из которых была вертикально вставлена намагниченная игла, едва выглядывавшая из пробки. Все обращённые вверх острия игл имели одинаковую полярность. Над этими плавающими магнитами в 60 см от кончиков игл был помещён противоположный полюс вертикально расположенного цилиндрического магнита. Майер разделяет конфигурации, полученные с разным числом иголок, на группы или классы (первичные, вторичные, третичные...) и замечает, что устойчивые конфигурации одного класса образуют ядра (nuclei) последующих. С одним и тем же числом игл можно получить несколько конфигураций, одна из которых более устойчива, чем другие: колебания внешнего магнита, получаемые передвижением его по вертикали, приводят к переходу одной конфигурации в другую. Например, 29 магнитов, кроме конфигурации, указанной в тексте, позволяют получить ещё более устойчивую кофигурацию, состоящую из четырёх колец, которые от центра к периферии насчитывают соответственно 1, 6, 9 и 13 магнитов. Такое поведение плавающих игл, по мнению Майера, может служить моделью структуры молекул, способной объяснить реальное поведение тел, например явления увеличения объёма в некоторых случаях затвердевания, явления аллотропии и изомеризма.
9. J. J. Т h о m s о n, On the Masses of the Ions in Gases at Low Pressures, Phil. Mag., (5), 48, 547 (1899).
10. Théorie analytique des probabilités par M. le Compte Laplace, 2 éd., Paris, 1814, p. 2. (Первое издание вышло в 1812 г. без “Введения”.)
11. Opticae thesaurus Alhazeni arabis libri septem, nunc primum editi… Basileae, 1572, Lib. I, prop. 1, p. 1.
12. Там же, р. 7.
13. Там же, р. 10.
14. Там же, Lib. I, prop. 19, p. 17.
15. Леонардо да Винчи, Ms. D., f. 8 г. Так историки цитируют рукописи Леонардо, хранящиеся во Французском институте, которые Вентури (первым исследовавший их) пометил буквами от А до М. В первый раз они были опубликованы факсимиле, т. е. точно, как в оригинале (как известно, Леонардо писал перевёрнутым шрифтом то ли для сохранения секрета, то ли шутки ради) и во французском переводе Равессоном-Мольеном, “Les manuscrits de Léonard de Vinci”, Paris, 1881–1891 (6 vol.). Комиссия по трудам Леонардо да Винчи (Comissione Vinciana) перепечатала их. Рукопись D – одна из самых упорядоченных и полных; это оригинальный трактат по физиологической оптике, в котором, между прочим, впервые упоминается зависимость расширения зрачка от изменения интенсивности падающего на него света. (Ms. D., i. 5 v.) (f. 8 означает восьмой – лист, буквы r и v – соответственно лицевую и оборотную стороны листа. – Прим. перев.)
16. Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur, 1604.
17. W. Gilberti, De magnete, magneticisque corporibus et de magno magnete tellure physiologia nova, Londini, 1600. р. 68. (Есть русский перевод: В. Гильберт, О магните, магнитных телах и о большом магните – Земле, М., 1956.)
Дата установки: 22.03.2009
Последнее обновление: 30.10.2010
[вернуться к содержанию сайта]