[
вернуться к содержанию сайта]Как было отмечено в предыдущем параграфе, на протяжении многих лет инерция электронов рассматривалась как главное препятствие для работы ламп СВЧ. Такое положение вызвало, естественно, попытки найти метод управления электронами, в котором явления, связанные с временем пролёта электронов, не только не оказывали бы вредного влияния, но, наоборот, служили бы задаче управления электронами. В этом направлении в разных странах, начиная с 1932 г., проводились исследования, которые к 1939 г. привели к разработке клистронов — ламп, действие которых основано на принципе модуляции электронов по скорости.

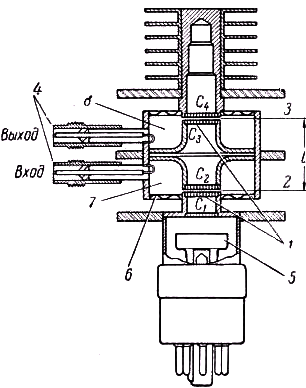
Рис. 428. Двухконтурный клистрон.
1
— сетки резонаторов; 2, 3 — зазоры между сетками резонаторов; 4 — коаксиальные вводы; 5 — электронная пушка; 6 — гибкая диафрагма, 7 — полость I резонатора; 8 — полость II резонатора.1. Модуляция по скорости и группировка электронов.
Воспользуемся при анализе процесса модуляции по скорости рис. 428, изображающим разрез двухконтурного клистрона, описание деталей конструкции которого будет дано немного ниже.Электроны, выходящие из пушки под напряжением U0, попадают в узкий зазор между двумя сетками С1 и С2, где существует синусоидальное высокочастотное напряжение, поданное с помощью коаксиального ввода 4. Пройдя зазор, электроны вступают в пространство дрейфа С2С3, имеющее потенциал U0. Пусть зазор настолько узок, что время пролёта электронов через него много меньше периода колебаний. Тогда можно говорить о моменте прохождения электронов между сетками. В этот момент ВЧ напряжение между сетками равно Uмsin ωt и электроны выходят из зазора со скоростью
![]() (50.1)
(50.1)
если пренебрегать скоростью вылета электронов из катода.
Uмsin ωt называется модулирующим напряжением. Обозначая![]() (50.2)
(50.2)
Формула (50.2) показывает, что поток электронов, имевший при выходе из пушки везде однородную плотность и состоявший из электронов одинаковой скорости, после прохождения через зазор состоит из электронов со скоростями
v0+Δv, где Δv = v0(Uм/U0)sin ωt, хотя остаётся сначала однородным по плотности. Такой поток электронов называется модулированным по скорости. Проследим изменения, происходящие с течением времени в модулированном по скорости потоке. Формула (50.2) показывает, что в течение одного полупериода электроны будут выходить из зазора с увеличенными скоростями, а в течение другого — с уменьшенными. Найдём, как будет изменяться положение электронов, прошедших в разные моменты времени через зазор по отношению к электрону, прошедшему через зазор в момент перехода напряжения от ускоряющего к замедляющему полупериоду. Ранее прошедшие электроны имеют меньшую скорость, и прошедшие позже электроны их догоняют. На некотором расстоянии от зазора плотность электронов в пучке делается резко неоднородной, в нём образуются сгустки и разрежения.Явления образования сгустков можно проследить на пространственно-временной диаграмме (рис. 429), по вертикальной оси которой отложено расстояние от зазора и по горизонтальной оси — время. Электроны, пройдя зазор, движутся равномерно в пространстве с постоянным потенциалом. Значит, график движения каждого электрона — прямая, тангенс угла наклона которой равен его скорости. В зазор электроны входят равномерным потоком
, поэтому на графике прямые начинаются из равноотстоящих точек на оси абсцисс и между двумя последовательными линиями диаграмм следует подразумевать одинаковое число электронов. Соответственно знаку синуса прирост скорости Δv может быть больше или меньше нуля.На рис. 429 принято, что положительному полупериоду на осциллограмме напряжения соответствует положительное Δ
v. Диаграмма отчётливо показывает, что в пучке электронов образуются сгустки и разряжения, причём на каждый период колебаний приходится один сгусток, центром которого служат электроны, прошедшие через зазор без изменения скорости в момент перехода модулирующего поля от торможения к ускорению.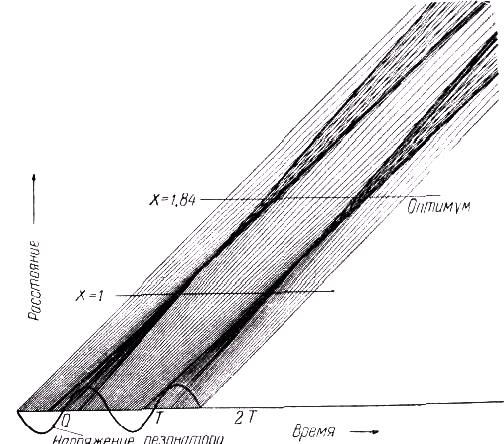
Рис. 429. Пространственно-временная диаграмма движения электронов в пространстве дрейфа.
Из диаграммы нетрудно понять, что расстояние, на котором сгусток достигает максимальной плотности, зависит от отношения
Uм/U0 (глубины модуляции), но существенно, что даже при Uм<<U0, т. е. при слабой модуляции, будет достигнута такая же степень неоднородности пучка, как и при сильной модуляции, но только на большем расстоянии от зазора. Наконец, на рис. 429 видно, что на больших расстояниях сгусток делается двойным (с двумя максимумами плотности). Описанный процесс носит название группировки электронов.Очевидно, что сила тока в пучке, ставшем неоднородным по плотности, уже не является постоянной. За один период колебаний модулирующего напряжения образуется один сгусток и, следовательно, ток группированного пучка будет иметь составляющую частоты, равной частоте модулирующего сигнала.
В реальных клистронах угол пролёта в зазоре между сетками может быть не очень малым, и тогда в формулу (50.2) нужно внести соответствующую поправку. Для этого нужно усреднить ВЧ напряжение
Uмsin ωt за всё время пролёта электрона. Время пролёта всех электронов через зазор можно считать одинаковым, так как Uм<<U0. Это время равноτ=
d/v0,где
d — расстояние между сетками. Для электрона, находящегося и момент t посередине зазора, среднее напряжение равно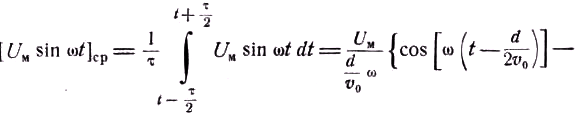
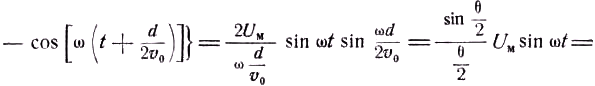
![]() (50.3)
(50.3)
где θ
=ωd/v0=ωτ – угол пролёта электрона в зазоре; ξ=sin(θ/2)/(θ/2) – коэффициент взаимодействия зазора. Таким образом, при учёте времени пролёта в зазоре нужно в формуле (50.2) вместо Uм написать ξUм и она примет вид![]() (50.4)
(50.4)
Величина ξ
=sin(θ/2)/(θ/2) встречалась в теории ВЧ осциллографа (§ 36). Её график был представлен на рис. 301. При уменьшении ширины зазора θ→0 и ξ→1, так что формула (50.4) переходит в формулу (50.2). Но вообще при θ≠0 всегда ξ<1 и при θ=π, 2π, 3π, ... ξ =0. Это понятно, так как при θ = 2π, 4π ... βремя пролёта в зазоре составляет Т, 2Т, ... , и ускорение, испытанное электроном, в точности компенсируется торможением. Очевидно, что модуляция по скорости тем сильнее, чем меньше θ, т. е. чем уже зазор. Рассмотрим электрон, находящийся посередине зазора в момент t0 (время “отбытия”). Этот электрон будет на расстоянии z от места отбытия через время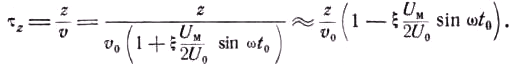 (50.5)
(50.5)
Время “прибытия” в точку
z равно![]() (50.6а)
(50.6а)
где через τz0=z/v0 обозначено время, в течение которого электрон, не изменивший скорости, доходит до точки z. Умножая обе части этого равенства на ω и полагая (z/v0)/T= τ/T=N, получим, что коэффициент при sin ωt0 будет равен
![]() (50.7)
(50.7)
Здесь
N — число периодов, в течение которых электрон, движущийся с неизменной скоростью v0, достигает точки z, a T=2π/ω. Величина X, часто встречающаяся в теории клистрона, носит название параметра группировки. Смысл этого названия будет выяснен ниже. Теперь формула (50.6а) примет вид![]() (50.66)
(50.66)
где θ
z0= ωτz0 = 2πN — пролётный угол электронов, не изменивших скорости между зазором и точкой z.Выделим группу электронов с суммарным зарядом
dq, проходящую через зазор в течение небольшого промежутка времени dt0. Эта группа через сечение z пучка пройдёт в течение промежутка dtz. Очевидно, чтоi0dt0=izdtz, (50.8a)
где
i0 — ток в зазоре, т. е. постоянный ток пучка электронов, а iz — ток в сечении z.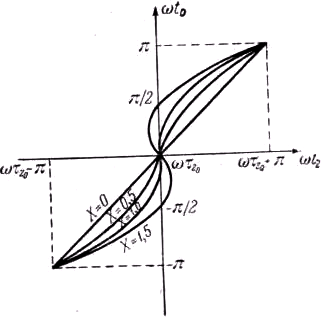
Рис. 430.
Формула (50.8a) остаётся справедливой и в том случае, когда во время пути одни электроны будут обгонять другие и к сечению придут в изменённом порядке. Эго значит, что
dt0 и dtz могут иметь разные знаки. Зависимость “угла времени прибытия” ωtz от “угла времени отбытия” ωt0 для четырёх значений параметра группировки X = 0; 0,5; 1; 1,5 представлена па рис. 430, причём по оси абсцисс отложено ωtz. Эти кривые можно использовать для построения зависимости iz от tz, исходя из соотношения![]() (50.8)
(50.8)
где справа стоит абсолютная величина наклона кривой
t0 = f(tz) там, где t0 — однозначная функция tz и сумма абсолютных величин наклонов там, где эта функция неоднозначна (участки кривых при Х>1). Знак dtz не нужно принимать во внимание, так как отрицательная величина dt0/dtz означает, что электроны приходят к сечению z в изменённом порядке, но все они проходят через z в одном и том же направлении и следовательно при вычислении тока заряды их складываются. Зависимость iz/i0 от ωtz показана на рис. 431, но, прежде чем делать выводы из этого рисунка, рассмотрим аналитическое решение задачи.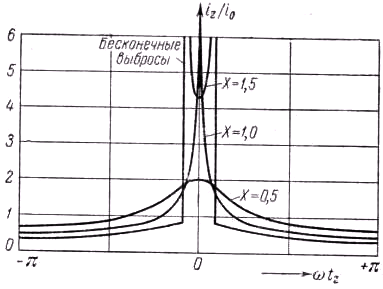
Рис. 4.31.
Из формулы (50.66) следует:
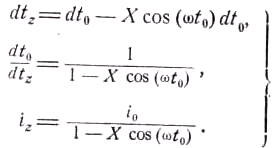 (50.9)
(50.9)
Формулу (50.66) можно представить в виде
ω
tz – ωtz0 = ωtz – θz0 = ωt0–X sin ωt0. (50.6в)Из формул (50.9) и (50.6в) следует, что
iz – периодическая и притом чётная функция tz. Следовательно, её можно представить в виде ряда Фурьеiz/i0=a0+ a1cos(ωtz–θz0)+ a2cos[2(ωtz–θz0)] + ... (50.10)
Коэффициент
an ряда имеет вид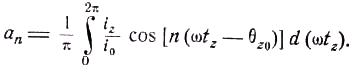
Заменяя
d(ωtz) согласно (50.8) через d(ωt0)i0/iz и воспользовавшись формулой (50.66), получим: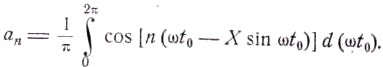 (50.11)
(50.11)
Отсюда следует, что а
0=1. Для п≠0 интеграл (50.11) можно выразить через бесселевы функции первого рода различных порядков:an=2Jn(nX),
и следовательно,
iz = i0[1 + 2J1(X)cos(ωtz–θz0)+2J2(X)cos[2(ωtz–θz0)] + ... ]. (50.12)
Существенно, что наибольшие значения функций Бесселя
J1(X), J2(X), ... — величины одного порядка *). Сначала нас, однако, будет интересовать только первая гармоника тока основной частотыiz1 = 2i0J1(X)cos(ωtz–θz0)= 2i0J1(X)cos(ωtz–2πN) (50.13)
Как известно
J1(X), а значит и амплитуда тока iz1, достигает максимума при Х =1,84. Это оптимальное значение параметра группировки, если, как в усилителе и генераторе, желательно иметь наибольшее значение гармоники основной частогы.Сгруппированный электронный поток достигает наибольшего уплотнения в плоскости, где Х=
1, но в плоскости Х = 1,84 достигает наибольшей величины первая гармоника (частоты ω) электронного тока. Поэтому в этой плоскости должен находиться тот элемент конструкции лампы, через который возбуждается резонансный контур, настроенный на частоту ω. Таким элементом конструкции на рис. 428 являются сетки С3 – С4.Вследствие наличия высших гармоник, имеющих значительные амплитуды, полный ток резко несинусоидален. На рис. 431 показано, как изменяется
iz/i0 в течение одного периода для Х =0,5; 1,0; 1,5. При Х=1 в момент максимума iz/i0 делается бесконечно большим, как это видно из соотношения (50.9), а при Х >1 кривая имеет два бесконечно больших максимума. Так как Х пропорционально z, то при заданных Uм, U0 и ξ картина, соответствующая разным t, будет получаться на разных расстояниях от зазора. На рис. 432 общая картина распределения плотности зарядов или, что то же самое, плотности тока в пространстве, где происходит группировка, представлена на “трёхмерной диаграмме”, где по двум направлениям по-прежнему отложены время и расстояние от зазора, а по вертикальной оси — плотность тока. На диаграмме наиболее острые “пики” тока получаются там, где самые быстрые электроны как раз догоняют самые медленные. Несколько дальше от модулирующих сеток пики раздваиваются, так как быстрые электроны обгоняют медленные и выходят вперёд.В развитой выше теории группировки не было принято во внимание электростатическое взаимодействие электронов, заставляющих сгустки “расплываться”. Поэтому на рис. 431 и получились бесконечно большие пиковые значения плотности тока.
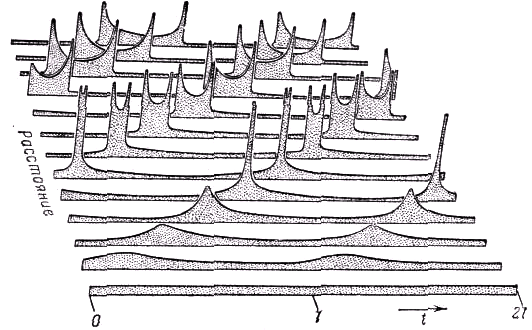
Рис. 432. Трёхмерная диаграмма группировки электронов.
Очевидно, что в СВЧ триоде также имеет место скоростная модуляция, но вследствие малости углов пробега её воздействие на распределение пространственного заряда невелико.
стр. 313
6. Из истории клистрона.
Как почти все крупные изобретения в области электроники, изобретение клистрона связано с именами многих исследователей. Принцип скоростной модуляции, т. е. идею о возможности группирования электронов в ВЧ поле в результате разности их скоростей, впервые отчётливо высказали московский радиофизик А. А. Витт (1932) и французский учёный Клавье (1933 г.)| [Л.6.14]. Но видимо, идея использования скоростной модуляции в то время была близка многим исследователям; в том же 1932 г. Д. А. Рожанский в Ленинграде пытался осуществить прибор со скоростной модуляцией. В 1934 г. был запатентован и в 1935 г. описан О. Гейлем и А. А. Арсеньевой-Гейль проект электронно-лучевого генератора, основанного на использовании группирования электронов. За этим последовал ряд работ в том же направлении, из которых особенно успешной оказалась работа братьев Вариан (1939 г.), прибор которых во всех существенных чертах не отличался от современного двухконтурного клистрона. Работа братьев Вариан была выполнена в Стэнфордском университете (США), и в ней принимали участие Ханзен, один из крупных специалистов в области электродинамики СВЧ и Вебстер, которому принадлежит теория группирования. В СССР также в 1939 г. исследовательской группой, возглавлявшейся Н. Д. Девятковым, были разработаны оригинальные конструкции двухконтурных клистронов.Отражательные клистроны появились в 1940—1941 гг. В СССР первые авторские свидетельства на отражательные клистроны были получены Н. Д. Девятковым и его сотрудниками (1940 г.), а также В. Ф. Коваленко (1940 г.) За рубежом отражательный клистрон был описан впервые, по-видимому, Варнеком (1941 г.) и Сеттоном.
Теория клистрона вследствие его относительной простоты (прямолинейные траектории электронов, взаимодействие с СВЧ полем только в пределах узкой щели) разработана лучше, чем теория других СВЧ ламп (Пирс, Варнек, Я. П. Терлецкий, С. Д. Гвоздовер и др.).
*) Величина максимумов для функций Бесселя первого рода различных порядков даётся таблицей (с точностью до второй значащей цифры):
|
Порядок |
1 |
2 |
3 |
5 |
10 |
20 |
|
Величина максимума |
0,58 |
0,48 |
0,42 |
0,37 |
0,30 |
0,24 |
Дата установки
: 23.03.2008