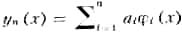
[
вернуться к содержанию сайта]После того как уже много лет назад я имел удовольствие в течение краткого времени видеть Вас и Вашего друга Ритца здесь, в Лейдене, наши пути не пересекались.
Из письма Лоренца Эренфесту от 20 апреля 1912 г. [
1, стр. 214]Большое влияние на моё развитие имело общение с моими близкими друзьями: Г. Герглотцем (ещё с гимназических лет), В. Ритцем и А. Иоффе (в Санкт-Петербурге), а также возможность совместной работы с моей женой – особенно по вопросам, которые требовали абстрактного анализа.
Из письма Эренфеста Лоренцу от 6 мая 1912 г. [
1, стр. 218]... И всё же, если обратиться к личности Эренфеста, нельзя не удивиться, с каким широким кругом крупнейших учёных связывали его узы тесной дружбы (как это было в случае Ритца, Эйнштейна, Бора, Борна), и чувства глубокой взаимной симпатии и уважения.
В.Я. Френкель "Лоренц и Эренфест" [
1, стр. 227]Хотя 1903 год Эренфест в своих письмах и называет "венским", он часто отлучался из родного города. Так, в апреле-мае вместе со своим гёттингенским другом Вальтером Ритцем они направляются в Голландию, в Лейден, где профессором теоретической физики был в то время уже имевший мировую известность Лоренц. Популярность голландского физика основывалась как на его оригинальных работах, так и на ряде монографических курсов физики и математики.
[
9, стр. 30]В годы студенчества Эренфеста Лоренц уже имел общеевропейскую известность; личное их знакомство состоялось весной 1903 г. В апреле этого года Эренфест и его товарищ Вальтер Ритц (швейцарец, обучавшийся в Гёттингене) совершили совместную поездку в Лейден. Надо сказать, что Лейден того времени славился не только Лоренцем, но и Камерлинг-Оннесом, директором криогенной лаборатории, в которой велись захватывающе интересные исследования низкотемпературных свойств твёрдых тел. И вот вместе с Ритцем Эренфест придумал остроумный метод выбора тем для диссертационных работ: они брали учебник физики и обращались к предметному указателю. Один зачитывал собранные там термины, а другой добавлял сакраментальное: "при низких температурах".
В.Я. Френкель "Лоренц и Эренфест" [
1, стр. 228]Летние каникулы 1903 года Эренфест провёл в Италии, пребывание в которой произвело на него неизгладимое впечатление (он запечатлел его в беглых заметках на страничках своих записных книжек). Домой он возвращался через Швейцарию, где, по предварительной договорённости с Ритцем, провёл несколько дней в гостях у своего друга.
[
9, стр. 31]Здесь мы можем только вскользь упомянуть о его [Эренфеста] вкладе в теорию интерференционных явлений, возникающих при рассеянии рентгеновского излучения на многоатомных молекулах; в теорию осмотического давления; в теорию броуновского движения (упрекнув его при этом, возможно с достаточным правом, в чрезмерно большом пристрастии к маленьким парадоксам); об его известной волново-механической теореме о классическом движении центра волнового пакета, о стимулирующем влиянии на возникновение спинорного исчисления (с его математической стороны), наконец, об его вкладе в разъяснение физических основ специальной теории относительности на раннем этапе её развития, особенно в связи с понятием "скорости сигнала", а также и о вступительной речи в Лейдене ("К вопросу о кризисе гипотезы светового эфира"), в которой он пытался воздать должное противоречащей опыту и несостоятельной, но привлекательной по исходным предпосылкам теории своего рано умершего друга В. Ритца, известного открытием комбинационного принципа для спектров.
В. Паули "Пауль Эренфест" [
1, стр. 245]В маленькой квартирке на Kirchweg, 1, которую снимали в Гёттингене Софья Евгеньевна и Татьяна Алексеевна [Афанасьева], стала собираться гёттингенская молодёжь, привлечённая чисто русским гостеприимством и радушием хозяек. Среди молодых людей выделялся Вальтер Ритц (1878-1909), товарищ Эренфеста, впоследствии получивший широкую известность своими работами по спектроскопии ("комбинационный принцип Ритца"). Впрочем, в числе гостей можно было видеть и более старших по возрасту физиков и математиков. Так, здесь бывал и Герман Минковский (1864-1909). Один из студентов Гёттингенского университета тех лет, ученик Ф. Клейна математик Вальтер Литцман в своих воспоминаниях пишет о том, какими привлекательными были вечера в этом доме. Там всегда звучала музыка, а потом гости приглашались к ужину, во время которого "тётя Соня", прекрасно готовившая, дивила всех вкуснейшими блюдами русской кухни.
[
9, стр. 28] РИТЦ Вальтер (22.II 1878-7.VII 1909) – швейцарский физик-теоретик и математик. Р. в Сионе. Окончил Цюрихский ун-т (1900). Работал в Гёттингене, Бонне, Париже, Цюрихе, Тюбингене.
Работы по физике посвящены спектроскопии, теории теплового излучения, электродинамике. В 1908 открыл закон, согласно которому волновое число любой спектральной линии равно разности двух термов из множества термов, присущих данному элементу.
Формулу, описывающую любую спектральную линию элемента, дал в 1890 И. Ридберг. Отсюда и название “принцип Ридберга – Ритца”, или “комбинационный принцип Ридберга – Ритца”. В математике известен “метод Ритца” – метод решения вариационных задач (1908).
[
2, стр. 234]За три месяца до своей смерти Герман Минковский, находясь в Лейпциге, писал председателю Швейцарского совета по делам образования: “...В своё время Луи Коллрос казался мне, да, пожалуй, и другим коллегам, самым одарённым в области математики из всех студентов своего курса, а это немало значит, ибо именно этот немногочисленный курс факультета VI-A дал видных исследователей: Альберта Эйнштейна, Вальтера Ритца и Марселя Гроссмана...
[
3, стр. 123]"Работы Гильберта в этой области принадлежат к его наиболее глубоким и выдающимся достижениям. Они знаменуют больше, чем завершение целого этапа, – писал один из его более поздних учеников, которому также принадлежит важная заслуга в этой области. – Доказательство существования Гильберта не только было существенно упрощено и обобщено усилиями многих математиков, но ему был также придан важный конструктивный характер. Физик Вальтер Ритц создал под влиянием Гильберта из реабилитированного принципа Дирихле мощный метод для численного решения краевых задач, пользуясь дифференциальными уравнениями в частных производных, метод, который уже в наше время превратил вычислительные машины в становящееся всё более эффективным средство численной математики...."
[
4, стр. 92] Комбинационный принцип. Таким образом, излучение атома водорода характеризуется величинами T(n)=R/n2 (n=1, 2, 3, ...), которые называются спектральными термами.
Все излучаемые частоты могут быть представлены как комбинации термов вида ωnl= T(l)–T(n).
Это правило, сформулированное Ритцем (1908), называется комбинационным принципом Ритца.
[
5, стр. 79]Метод Ритца. В качестве пробной функции берётся линейная комбинация функций φ
=α1φ1+α2φ2+...+αnφn, где αi – вариационные параметры. Их значение определяется из условий экстремальности E. После вычисления соответствующих интегралов в формуле (53.8) условия экстремума ∂E/∂αi=0 дают n линейных уравнений для n неизвестных коэффициентов αi. Эту систему алгебраических уравнений не очень трудно решить. Обычно метод Ритца даёт для основного состояния достаточно хорошие результаты.Вариационный метод решения уравнения Шредингера [5, стр. 282]
Ему [Бору] надо было убедиться, что эти [боровские] постулаты всегда работают безотказно. И он взволнованно пережил подтверждение своей правоты, когда встретил последнюю по времени – самую обобщённую формулу Вальтера Ритца.
...Тридцатилетний гёттингенец опубликовал её пять лет назад. Она стала известна под именем комбинационного принципа в спектроскопии. Ритц не разглядел прозрачного смысла этого принципа, как Бальмер не понял своего детища. И тут не было их вины. Старый Бальмер умер в 1898-м – за два года до появления идеи квантов. Молодой Ритц безвременно ушёл из жизни в 1909-м – за два года до появления планетарной модели.
[
6, стр. 121]Последняя по времени создания – самая обобщённая – формула Вальтера Ритца давала такое описание для любых спектральных серий... Формула Ритца недаром называлась комбинационным принципом в спектроскопии: к комбинированию целых чисел сводилось вычисление частот в атомных спектрах... Вальтер Ритц работал в Гёттингене и принадлежал к выдающейся школе спектроскопистов. И сам он обнаружил талант выдающегося исследователя, когда в возрасте тридцати лет опубликовал свой комбинационный принцип (1908).
[
7, стр. 86]Я хотел бы сказать также не только об Эйнштейне-мыслителе, но и о вдохновлявшем меня многолетнем пребывании Эйнштейна в тихом университетском городке в Нью-Джерси. Разве я могу забыть то великодушие, с которым он относился ко мне, тогда ещё новичку в Принстоне, во время наших первых дискуссий о физике? Среди других воспоминаний об этих первых встречах и о более позднем сотрудничестве осталось то глубокое впечатление, которое произвело на меня его восхищение Ньютоном, восхищение проницательностью и научным мужеством Ньютона... Дальнейшие дискуссии с Эйнштейном были посвящены сущности электричества, дальнодействию и известному расхождению между Эйнштейном и Ритцем в вопросе о необратимости излучения.
[
8, стр. 15-16]РИТЦА И ГАЛЁРКИНА МЕТОДЫ, широко распространённые прямые методы решения гл. обр. вариационных задач и краевых задач математич. анализа (см. Краевые задачи, Вариационное исчисление).
М е т о д Р и т ц а применяется большей частью для приближённого решения вариационных задач и тех краевых задач, к-рые сводятся к вариационным. Пусть задан функционал V[y(x)] (или более сложный функционал) и требуется найти такую функцию у(х), принимающую в точках х0 и х1 заданные значения α=у(х0) и β=y(х1), на к-рой функционал V[y(x)] будет достигать экстремума. Значения исследуемого на экстремум функционала V[y(x)] рассматриваются не на всех допустимых в данной задаче функциях у(х), а лишь на всевозможных линейных комбинациях вида
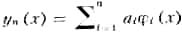
с постоянными коэффициентами аi, составленных из п первых функций некоторой выбранной системы φ1(x
), φ2(x), ..., φn(x), ... (от удачного выбора этой системы функций зависит эффективность применения метода к решению конкретных задач). Необходимым условием выбора системы функций φi(x) является требование, чтобы функции уп(х) удовлетворяли условиям уп(х0)=α и yn(х1)=β для всех значений параметров аi. При таком выборе функций уп(х) функционал V[y(x)] превращается в функцию Ф(а1, а2, ..., аn) коэффициентов аi; последние выбирают так, чтобы эта функция достигала экстремума, т. е. определяют их из системы уравнений∂Ф/∂аi=0 (i = 1, 2, ..., п).
Напр., пусть требуется решить задачу о минимуме интеграла
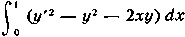
при условии y(0)= y(1)= 0. В качестве функций φi(x) можно взять хi(1-x), тогда
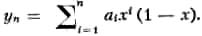
Если п= 2, то y2= х(1-x)(a1+а2х). Для определения коэффициентов a1 и а2 получаем после вычислений два уравнения
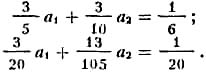
Решением этих уравнений являются числа a1= 71/369 и а2= 7/41. Следовательно, у2(х)=х(1-x)(71/369 +х·7/41). Полученное приближённое решение отличается от точного на величину порядка 0,001.
Найденное этим методом приближённое решение уп(х) вариационной задачи при нек-рых условиях, касающихся в основном полноты системы функций φi(x), стремится к точному решению у(х), когда п→∞.
Метод был предложен в 1908 нем. математиком В. Ритцем (W. Ritz). Теоретич. обоснование метода дано сов. математиком Н. М. Крыловым (1918).
М е т о д Г а л ё р к и н а является широким обобщением метода Ритца и применяется гл. обр. для приближённого решения вариационных и краевых задач, в том числе и тех, к-рые не сводятся к вариационным. Осн. идея метода Галёркина состоит в следующем. Пусть требуется в нек-рой области D найти решение дифференциального уравнения
L[u] = 0 (1)
(L — нек-рый дифференциальный оператор, напр. по двум переменным), удовлетворяющее на границе S области D однородным краевым условиям:
и = 0. (2)
Если функция и является решением уравнения (1) в области D, то функция L[u] тождественно равна нулю в этой области и, следовательно, ортогональна (см. Ортогональность) любой функции в области D. Приближённое решение уравнения (1) ищут в виде
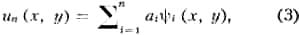
где ψi(х, y) (i = 1, 2, ..., п) — линейно независимые функции, удовлетворяющие краевым условиям (2) и являющиеся первыми п функциями нек-рой системы функций ψ1(х, y
), ψ2(х, y), …, ψn(х, y), ..., полной в данной области. Постоянные коэффициенты аi выбирают так, чтобы функция L[un] была ортогональна в D первым п функциям системы ψi(х, y):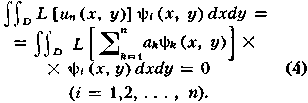
Напр., пусть в области D требуется решить уравнение Пуассона
L[и]= ∂2и/∂x2+∂2и/∂y2-f(х, у)= 0
при условии и=0 на S. Выбирая систему функций ψi(х, y), ищем решение в виде (3). Система уравнений (4) для определения коэффициентов аi имеет вид:
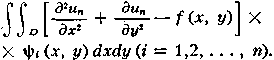
Функции ψi(х, y) можно, в частности, выбирать, пользуясь следующими соображениями. Пусть ω(х, у) — непрерывная функция, имеющая внутри области D непрерывные частные производные второго порядка и такая, что ω(х, у)>0 внутри D, ω(х, у)= 0 на S. Тогда в качестве системы функций ψi(х, y) можно взять систему, составленную из произведений ω(х, у) на различные степени х и у: ψ0= ω, ψ1= ωх, ψ2= ωх2, ψ3= ωхy, …. Напр., если границей области D является окружность S радиуса R с центром в начале координат, то можно положить ω(х, у)= R2- х2- у2.
Метод Галёркина применяется при решении широкого класса задач; более общая его формулировка даётся в терминах функционального анализа для решения уравнений вида Аи-f=0, где А — линейный оператор, определённый на линеале, плотном в нек-ром гильбертовом пространстве Н, и — искомый и f — заданный элементы пространства Н.
Метод получил распространение после исследований Б. Г. Галёркина (1915); ранее (1913) он применялся для решения конкретных задач теории упругости И. Г. Бубновым, в связи с чем иногда именуется методом Бубнова—Галёркина. Теоретич. обоснование метода принадлежит М. В. Келдышу (1942).
Лит.: Галёркин Б. Г., Стержни и пластинки. Ряды в некоторых вопросах упругого равновесия стержней и пластинок, “Вестник инженеров”, 1915, т. 1, № 19, с. 897-908: Михлин С. Г., Вариационные методы в математической физике, 2 изд., М.—Л., 1970; Канторович Л. В. и Крылов В. И., Приближённые методы высшего анализа, 5 изд., Л.—М.. 1962; Ritz W., Neue Methode zur Lösung gewisser Randwertaufgaben, “Gesellschaft der issenschaften zur Göttingen. Math.-physik. Klasse. Nachrichten”, Göttingen, 1908; его же, Über eine neue Methode zur Lösung gewisser Variationsprobleme der mathematischen Physik, “Journal für die reine und angewandte Matheimatik”, 1909, Bd 135.
В. Г. Карманов.
[10, Т. 22, стр. 137]1. Эренфест П. Относительность. Кванты. Статистика. (сборник статей), М.: Наука, 1972.
2. Храмов Ю.А. "Физики": биографический справочник. М.: Наука, 1983.
3. Зелиг К. Альберт Эйнштейн, М.: Атомиздат, 1966.
4. Рид К. Гильберт, М.: Наука, 1977.
5. Матвеев А.Н. Атомная физика. М.: Высш. шк., 1989.
6. Данин Д.С. Нильс Бор, М.: Молодая гвардия, 1978.
7. Данин Д.С. Вероятностный мир, М.: Знание, 1981.
8. Уилер Дж.А. Предвидение Эйнштейна, М.: Мир, 1970.
9. Френкель В.Я. Пауль Эренфест, М.: Атомиздат, 1977.
10. Большая Советская Энциклопедия. (в 30 томах). Изд. 3-е. М., 1975.
Дата установки: 12.11.2007
Последнее обновление: 16.12.2009
[