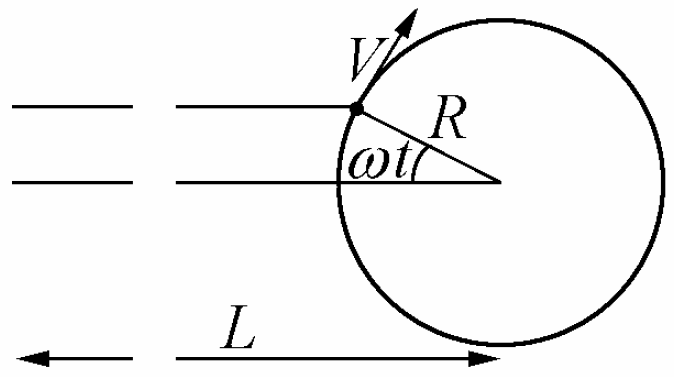
Рис. 4.1.
[вернуться к содержанию сайта]
Яркий пример нарушения галилеевского сложения скоростей – парадокс двойных звёзд. Пусть далеко от Земли имеется двойная звёздная система, в которой звёзды вращаются вокруг общего центра масс с периодом T≈1 год. Это отнюдь не экзотика: большинство звёзд входит в состав кратных систем. Рассмотрим последствия очень естественной, хорошо согласующейся с бытовым здравым смыслом баллистической гипотезы – пусть скорость света складывается со скоростью источника, по Галилею. Выберем систему, видную с ребра, в которой звёзды движутся попеременно к нам или в обратном направлении. С расстояния L свет удаляющейся звезды дойдёт по баллистической гипотезе за время t1=L/(c−V), а когда она же будет приближаться, пройдя половину орбиты, мы увидим сигнал через t2=T/2+L/(c+V). Разность этих времён t2−t1=T/2−2LV/(c2−V2) при достаточном расстоянии L может быть отрицательной – более поздний сигнал придёт раньше из-за большей скорости распространения. Мы увидели бы, как звезда носится по орбите со скоростью, никак не согласующейся с законами Кеплера, особенно если t2−t1 близко к нулю.

Рис. 4.1.
Поучительно рассмотреть не только два момента, а всю динамику видимого движения звезды. Как видно из рис. 4.1, для момента t “баллистическая скорость” cx=c−Vsin(ωt). Время прихода света с расстояния L
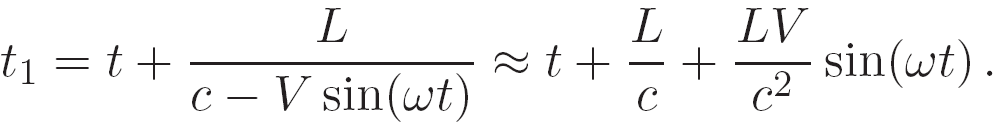
Большое постоянное слагаемое L/c можно отбросить (это просто выбор летоисчисления – начала отсчёта времени наблюдения). Тогда время t1 как функция времени t будет суммой линейной функции и синусоиды. При небольших расстояниях L роль синусоиды невелика, t1≈t, и движение звезды выглядит “нормальным”: её координата y колеблется, как и положено при вращении: y=Rsin(ωt1). Конечно, видим мы зависимость именно от времени наблюдения t1.
С ростом L увеличивается амплитуда синусоиды, и положение меняется. На рис. 4.2 показана зависимость t1(t) для L=1,4c2/ωV. Каждому времени наблюдения отвечает горизонтальная линия, а её пересечения с кривой определяют фазу, в которой видна звезда. Обратим внимание на промежуток 2,9<ωt1<3,3. Здесь есть три пересечения горизонтали с кривой, следовательно, звезда видна в трёх положениях одновременно.
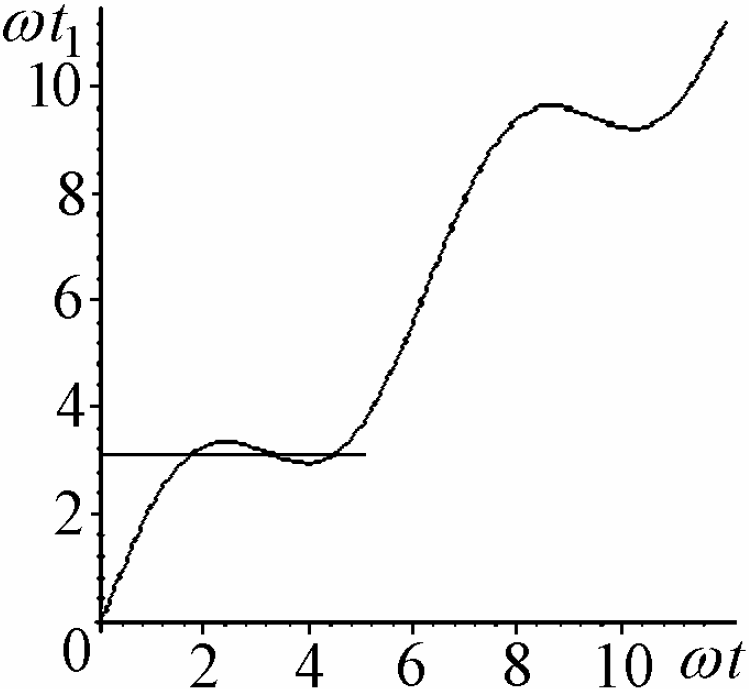
Рис. 4.2.
Попробуем описать, что видит наблюдатель. Самое левое пересечение – это “нормальное” решение, продолжающее более ранний ход событий. Но в момент ωt1≈2,9 “возникает” ещё одна звезда и тут же раздваивается. На рис. 4.3, где показана зависимость вертикальной координаты от времени наблюдения, новое изображение возникает в точке A. Один из фантомов летит навстречу первому изображению, а второй движется в прямом направлении, причём в момент возникновения скорость обоих бесконечна. При ωt1≈3,3 пятящийся фантом аннигилирует с тем, который мы считали нормальным (точка B), и остаётся только одно видимое изображение звезды. Надо полагать, что теперь оно и будет “нормальным”.
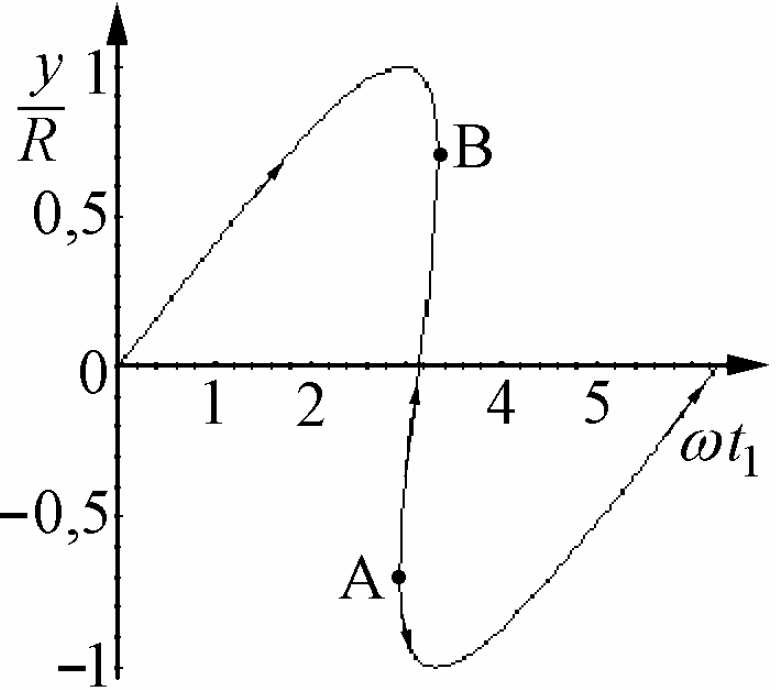
Рис. 4.3.
Заметим, что выбранное расстояние можно записать и как L=cT·(1,4c/2πV). Здесь cT – это примерно световой год. В скобке стоит число довольно значительное – порядка 1,4·3·105/(2π·30)≈2200, столько будет световых лет. Но астрономически это не такое большое расстояние, и с него звёзды отлично можно наблюдать. Точнее, на таких расстояниях звёзды видны хорошо, но телескоп не разделяет детали кратных систем: видна одна яркая точка вместо двух. Тем не менее можно различать отдельные компоненты по их спектрам (так называемые спектрально-двойные звёзды). Свет звезды, движущейся по направлению к Солнечной системе, становится более коротковолновым, а удаляющейся – длинноволновым (эффект Доплера). Легко показать (в качестве упражнения сделайте это сами), что относительное изменение длины волны пропорционально продольной скорости: Δλ/λ=Vsin(ωt)/c. Поэтому наблюдаемый сдвиг спектра зависит от времени наблюдения так же, как поперечная координата (изображённая на рис. 4.3 зависимость), в частности, будут появляться и исчезать “лишние” источники. При большем удалении можно было бы увидеть пять, семь и т.д. изображений одновременно, если бы была правильна баллистическая гипотеза. Таких чудес на небе не нашли. Пришлось признать, что скорость света не зависит от движения источника.
Баллистическая гипотеза неявно заменяет свет потоком песчинок или горошин. Но свет – это электромагнитная волна, вещь совсем другая. Лучи света могут интерферировать (например, гасить друг друга, если направления полей от двух источников противоположны) и дифрагировать (огибать препятствия). Такие явления несвойственны летящим горошинам. Не удивительно, что баллистическая гипотеза не работает. Чем же её заменить? По аналогии с упругими волнами ожидали, что световые волны распространяются в специальной среде (эфире), как звук – в воздухе. Предполагалось, что эфир нужен только для электромагнитных волн, что он не имеет заметной плотности и не оказывает сопротивления движению тел в том смысле, что свободно через них протекает. (Сейчас понятно, что это довольно странный набор свойств). Тогда движение источника и не должно влиять на скорость света, поскольку, оторвавшись от источника, свет шёл бы по эфиру.
Дата установки: 29.07.2013
[вернуться к содержанию сайта]