[
вернуться к содержанию сайта]В последнее время Г. Л. Лоренц
1, Джинс2 и Ритц3 выступили в этом журнале с изложением своих взглядов на эту чрезвычайно важную проблему, что облегчает критическое осмысление её современного состояния. Считая полезной дискуссию учёных, серьёзно занимающихся этой проблемой, даже если она и не приведёт к окончательному результату, я хочу сказать следующее.1. Известные до настоящего времени законы электродинамики проще всего выражаются в форме дифференциальных уравнения Максвелла–Лоренца в частных производных. Уравнения в форме, содержащей функции запаздывающего аргумента, я рассматриваю, в противоположность Ритцу 3
, только как вспомогательные математические формулы. Меня принуждает к этому прежде всего то обстоятельство, что эти уравнения не включают в себя закон сохранения энергии; в том же, что закон этот выполняется строго, сомневаться, по-моему, не следует, пока не будут найдены веские аргументы для отказа от этого путеводного закона. Правильно, конечно, что уравнения Максвелла для пустого пространства сами по себе не говорят ничего о том, что они изображают лишь промежуточную конструкцию; но точно то же самое, как известно, можно сказать и об уравнениях движения Ньютона, равно как и о всякой теории, которая должна быть дополнена другими теориями, чтобы дать единую картину комплекса явлений. Дифференциальные уравнения Максвелла тем и отличаются от уравнений, содержащих функции запаздывающего аргумента, что в каждое мгновение и во всякой неускоренной системе координат они дают выражение для энергии и количества движения рассматриваемой системы. В теории, оперирующей с функциями запаздывающего аргумента, мгновенное состояние системы вообще нельзя описать, не используя для этого предшествующих состояний. Если, например, источник света А испустил световой сигнал в сторону экрана В, но этот сигнал ещё не достиг экрана В, то согласно теориям, оперирующим с запаздывающими силами, световой сигнал представлялся бы только с помощью явлений, происходивших ранее в излучающем теле при испускании света. Тогда энергию и количество движения — если только вообще не отказываться от этих величин — пришлось бы изображать в виде интегралов по времени.Но Ритц как раз и утверждает, что опыт принуждает нас отказаться от дифференциальных уравнений и заставляет ввести запаздывающие потенциалы. Однако, на мой взгляд, его доводы нельзя признать убедительными.
Если мы положим вместе с Ритцем
и
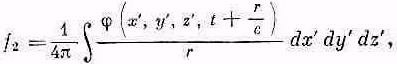
то как
f1, так и f2 будут решениями уравнения(1/c2)∂ 2f/∂t2
–Δf =φ (x, y, z, t),а значит,
иf
3 = a1f1 + a2f2тоже будет решением при условии а
1 + а2 = 1. Однако неверно, что решение f3 является более общим, чем f1 и что, полагая a1 = 1, а2 = 0, мы совершаем переход к частному случаю. Когда полагаютf
(x, у, z, t) = f1,то при этом вычисляют электромагнитное действие в точке х, у,
z из тех движений и конфигураций электрических зарядов, которые существовали до момента времени t. Полагая жеf
(x, у, z, t) = f2используют для определения указанного электромагнитного действия такие движения и конфигурации, которые происходят после момента времени
t.В первом случае электромагнитное поле вычисляют по совокупности процессов испускания, во втором — по совокупности процессов поглощения. Если процесс происходит в замкнутом (конечном) пространстве, его можно описывать как равенством
f=f
1,так и
f=f
2.Если же рассматривается поле, распространяющееся из конечного объёма в бесконечность, то можно, казалось бы, использовать только равенство
f=f
1,потому что при этом не учитываются процессы поглощения. Но здесь мы встречаемся с парадоксом бесконечности. Всегда возможно пользоваться любым из двух равенств, так же как можно мысленно удалять поглощающее тело. Значит, нельзя сделать вывод, что решение
f=f1 является более специальным, чем решение a1f1+ a2f2, где a1+ a2 =1.To обстоятельство, что тело “не получает энергию из бесконечности без того, чтобы какое-нибудь другое тело не потеряло соответствующий квант энергии”, на мой взгляд, также не может служить аргументом. Прежде всего, если придерживаться опыта, можно говорить не о бесконечности, а лишь о пространствах, расположенных вне рассматриваемого объёма. Но, кроме того, из ненаблюдаемости подобного процесса утверждать о необратимости электромагнитных элементарных явлений можно не с большим правом, чем обосновывать необратимость элементарных движений атомов с помощью второго начала термодинамики.
2. Мнению Джинса можно противопоставить утверждение о том, что применять общие результаты статистической механики к полости, заполненной излучением, по-видимому, недопустимо. Однако закон, выведенный Джинсом, можно получить также следующим образом 4.
Ион, осциллирующий около положения равновесия вдоль оси
X, излучает и поглощает, по теории Максвелла, в единицу времени в среднем равные количества излучения только в том случае, когда между средней колебательной энергией Ēν и плотностью энергии излучения ρν при собственной частоте осциллятора ν существует соотношениеĒ
ν=с3ρν/8πν2, (I)где с — скорость света. Если осциллирующий ион может взаимодействовать такжe c мoлeкyлaми газа (или вообще с системой, описываемой молекулярной теорией), то при условии, что в среднем через осциллятор не переносится энергия от газа в пространство с излучением, в соответствии с молекулярной теорией теплоты с необходимостью должно выполняться равенство
Ē
ν=RT/N, (II)где
R — универсальная газовая постоянная, N — число атомов в одном грамм-атоме, Т — абсолютная температура 5.Из этих двух соотношений следует
ρν
= R8πν2T/Nс3, (III)что в точности совпадает с законом, найденным также Джинсом и Г. А. Лоренцом
6.3. По моему мнению, нельзя сомневаться в том, что наши современные теоретические представления с необходимостью приводят к закону, защищаемому Джинсом. Но с не меньшей уверенностью можно утверждать, что формула (III) противоречит опыту. Почему же твёрдые тела испускают видимый свет, начиная лишь с определённой, довольно резко ограниченной температуры? Почему всё вокруг не заполнено ультрафиолетовым излучением, если оно всё же испускается при обычной температуре? Как можно сохранять долгое время в кассетах высокочувствительные фотопластинки, если они постоянно испускают коротковолновое излучение? Относительно дальнейших аргументов я сошлюсь на § 166 уже цитированной книги Планка. Таким образом, мы должны, пожалуй, сказать, что опыт заставляет нас отвергнуть либо соотношение (I), являющееся следствием электромагнитной теории, либо соотношение (II), выводимое из статистической механики, либо, наконец, оба эти соотношения.
4. Зададим вопрос: в каком отношении находится теория излучения Планка к указанной в пункте 2 теории, построенной на общепринятых в настоящее время теоретических основах? Ответ на этот вопрос, по-моему, затруднён тем, что Планк допускает в изложении своей теории некоторую логическую незавершённость. Сейчас я постараюсь коротко разъяснить это.
а) Придерживаясь точки зрения, что необратимость процессов в
природе является только кажущейся и что необратимый процесс заключается в переходе к более вероятному состоянию, необходимо сначала дать определение вероятности W состояния. Единственным таким определением, которое, по-моему, стоит рассматривать, является следующее:Пусть А
1, А2,..., Аl, — все состояния, в которых может находиться замкнутая система при заданной энергии, или, точнее говоря, все состояния, которые мы можем различить в такой системе с помощью некоторых вспомогательных средств. Согласно классической теории, система через некоторое время переходит в какое-то одно из этих состояний (например, Аl) и затем остаётся в нём (термодинамическое равновесие). Согласно же статистической теории, система всё время проходит через нерегулярную последовательность состояний А1,..., Аl 7. Если мы наблюдаем систему очень продолжительное время Θ, то будет существовать некоторая часть τν этого времени, такая, что система в течение τν и только τν находится в состоянии Аν. Отношение τν/Θ будет стремиться к некоторому пределу, который мы и назовём вероятностью W рассматриваемого состояния Аν.Исходя из этого определения, можно показать, что для энтропии
S должно выполняться соотношениеS
= (R/N) ln W+ const,где константа будет одинаковой для всех состояний с равной энергией.
б) Ни Больцман, ни Планк не давали определения
W. Они полагали чисто формально, что W равна числу “комплексий” рассматриваемого состояния.Требуя теперь, чтобы эти комплексии были равновероятными, причём вероятность комплексий определяется аналогично тому, как в пункте “а” — вероятность состояния, мы приходим в точности к определению вероятности состояния, данному в “а”; нужно только ввести в определение логически необязательный элемент — “комплексию”.
Хотя указанное соотношение между
S и W выполняется только в том случае, если вероятность “комплексий” определяется либо указанным, либо же другим эквивалентным способом, ни Больцман, ни Планк не определяли эту вероятность. Однако Больцман всё же признал, что выбранная им молекулярно-теоретическая картина предписывала вполне определённым образом сделанный им выбор “комплексий”, он рассказал об этом в своей работе “О связи...”, опубликованной в 1877 г. в журнале Wiener Sitzungsberichten (стр. 404 и 405) 8. В своей теории излучения Планк также не был свободен в выборе “комплексий”. Он имел бы право записать два соотношенияS =
(R/N) ln Wи
W
= числу комплексий,добавив лишь условие, что комплексии надо выбирать так, чтобы они были равновероятными в созданной им теоретической картине на основе статистического распределения. На этом пути он пришёл бы к формуле, защищаемой Джинсом. Как бы ни радовался каждый физик, что Планк, к счастью, отбросил это требование, всё же не следует забывать, что формула излучения Планка несовместима с теоретическими основами, из которых Планк исходил.
5. Легко видеть, каким образом можно изменить основы теории Планка для того, чтобы формула излучения Планка действительно являлась следствием теоретических основ. Я не буду приводить здесь соответствующие выводы и только сошлюсь на мои статьи по этому вопросу 9
. Результат таков: формула излучения Планка получается, если1) придерживаться выведенного Планком из теории Максвелла соотношения (I), связывающего энергию резонатора и плотность излучения 10
;2) видоизменить статистическую теорию теплоты, введя следующую гипотезу: электрически заряженная система, которая способна, совершая колебания с частотой
ν, превращать энергию излучения в энергию вещества и, наоборот, может находиться в колебательных состояниях не с произвольной энергией, а только с энергией, кратной величине hv; при этом h — постоянная, введённая Планком в его формуле излучения.6. Так как только что предложенная модификация основ теории Планка с необходимостью ведёт к глубочайшим изменениям наших физических теорий, крайне важно отыскивать по возможности простые независимые интерпретации формулы излучения Планка или закона излучения вообще,
предполагая его известным. Ниже приводятся два подхода к этому вопросу, отличающиеся своей простотой.Соотношение
S = (R/N)lnW до сих пор применяли главным образом для того, чтобы, определив сначала на основе более или менее законченной теории величину W, вычислять затем энтропию. Но это соотношение можно использовать также и для обратной задачи — для определения статистической вероятности отдельного состояния Аν некоторой замкнутой системы по найденным из опыта значениям энтропии Sν. Теорию, дающую иные, чем найденные таким способом значения вероятности состояния, следует, очевидно, отвергнуть.В опубликованной ранее работе 11
, в которой я впервые изложил теорию световых квантов, уже применялся этот метод определения статистических свойств теплового излучения в замкнутой полости. Однако, поскольку там я исходил из формулы излучения Вина, справедливой только в пределе малых значений ν/T, проведу здесь аналогичное рассмотрение, которое выявит простой смысл формулы излучения Планка.Возьмём два сообщающихся объёма
V и v, ограниченных диффузно отражающими стенками. Пусть в этих объёмах находится тепловое излучение, частоты которого заключены в интервале dν. Пусть Н и η означают энергии излучения, мгновенно находящегося соответственно в V и v. Тогда через некоторое время с известным приближением будет выполняться пропорция Н0:η0 = V:v. В любой наперёд заданный момент времени энергия η будет отклоняться от η0 в соответствии со статистическим законом, получаемым непосредственно из соотношения между S и W и в дифференциальной форме имеющим видdW =
const e(N/R)S dη.Вводя обозначения Σ и σ для энтропии излучения, находящегося в двух указанных объёмах, и полагая
η = η0 + ε, имеемd
η = dε.и
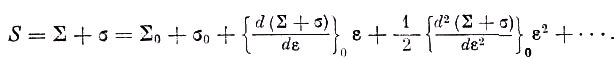
Так как в предположении
V >> v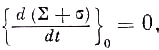
то предыдущее соотношение приобретает вид
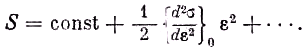
Сохраняя первый неисчезающий член разложения, что приводит к тем меньшей ошибке, чем больше
v по сравнению с кубом длины волны излучения, получаем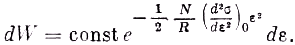
Отсюда для среднего значения
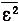квадрата флуктуации энергии излучения, находящегося в объёме v, получаем
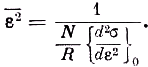
Если формула для плотности излучения известна, то из неё можно вычислить σ
12. Рассматривая формулу излучения Планка как эмпирическую, после простого вычисления получаем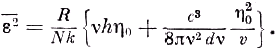
Итак, мы получили легко интерпретируемое выражение для средней величины флуктуаций энергии излучения, находящегося в
v. Покажем теперь, что современная теория излучения несовместима с этим результатом.Согласно современной теории, флуктуации происходят только от того, что бесконечно большое число лучей, составляющих излучение объёма
v, пронизывает пространство и интерферирует между собой, создавая мгновенное значение энергии, то большее, то меньшее суммы энергий отдельных лучей, которая получилась бы в отсутствие интерференции. Таким способом можно было бы точно определить величину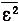 в результате довольно сложного математического рассмотрения. Мы ограничимся здесь простыми рассуждениями на основе анализа размерностей. Потребуем, чтобы выполнялись следующие условия:
1. Величина средней флуктуации зависит только от длины волны λ
, dλ, σ θ v, причём σ означает плотность излучения, отнесённую к длинам волн (σdλ =ρdν).2. Так как энергии излучения в соседних интервалах длин волн и “объёмы”
13 просто складываются, а соответствующие флуктуации взаимно независимы, то величина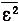 при данных λ и ρ должна быть пропорциональна dλ θ v.
3. Величина
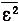имеет размерность квадрата энергии.
Тем самым выражение для
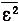получается полностью, с точностью до постоянного числового множителя (порядка 1). Этим способом мы получаем выражение σ2λ4vdλ, κоторое после подстановки введённых выше переменных даёт второй член только что выведенной формулы для 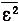. Но только этот второй член мы и получили бы, исходя из формулы Джинса. Тогда можно было бы также приравнять отношение R/Nk постоянной величине порядка единицы, что соответствует определению элементарных квантов, данному Планком 14. Первый же член в выражении для 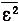, который для окружающего нас видимого излучения по величине намного больше второго, в современной теории не может быть получен.
Полагая вместе с Планком
R/Nk = 1, мы увидели бы, что первый член, если бы он был единственным, даёт такие флуктуации энергии излучения, как будто излучение состоит из движущихся независимо точечных квантов с энергией hν. Это можно показать простым вычислением. Напомним ещё раз, что первый член даёт тем больший вклад в среднюю относительную флуктуацию энергии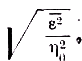
чем меньше энергия η
0, и что величина относительной флуктуации, обусловленной первым членом, не зависит от величины объёма v, в котором находится излучение; я напоминаю это, чтобы показать, как глубоко отличаются фактические статистические свойства излучения от того, что мы должны ожидать от нашей современной теории, основанной на линейных однородных дифференциальных уравнениях.7. Выше мы вычисляли флуктуации распределения энергии, чтобы получить представление о природе теплового излучения. Теперь мы вкратце покажем, как можно прийти к вполне аналогичным результатам, вычисляя флуктуации светового давления (а значит, и количества движения)
.Пусть в полом пространстве, окружённом со всех сторон веществом с абсолютной температурой Т, находится зеркало, свободно движущееся нормально к своей плоскости 15
. Если мы представим себе, что зеркало движется с некоторой скоростью с самого начала, то вследствие этого движения передняя сторона зеркала будет отражать больше излучения, чем задняя сторона; поэтому на переднюю сторону зеркала световое давление будет больше, чем на заднюю. Значит, на зеркало вследствие его движения относительно полости с излучением будет действовать сила, подобная силе трения, которая должна была бы постепенно уменьшать количество движения зеркала, если бы не существовало бы источника движения, в среднем точно компенсирующего потерю количества движения, обусловленную упомянутой силой трения. Следовательно, рассмотренным ранее беспорядочным флуктуациям энергии излучения соответствуют также беспорядочные флуктуации количества движения или действующих на зеркало со стороны излучения сил давления, которые должны привести зеркало в движение, даже если первоначально оно покоилось. Среднюю скорость зеркала можно теперь определить из соотношения между энтропией и вероятностью, а закон упомянутых сил трения — из закона излучения, предполагаемого известным. Вычисляя затем из этих двух результатов влияние флуктуаций давления, можно опять делать выводы относительно структуры излучения или, точнее говоря, относительно элементарных процессов отражения излучения от зеркала.Обозначим через
v скорость зеркала в момент времени t. Под действием упомянутой выше силы трения в следующий промежуток времени τ эта скорость уменьшается на Pvτ/т, где т — масса зеркала, Р — замедляющая сила, соответствующая единичной скорости зеркала. Обозначим, далее, символом Δ то изменение скорости зеркала за время τ, которое соответствует беспорядочным флуктуациям светового давления. Скорость зеркала к моменту времени t + τ будет равнаv –
Pvτ/т+Δ.В качестве условия того, что в течение времени τ скорость
v в среднем не изменяется, мы получаем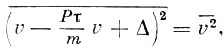
или, опуская бесконечно малые величины и учитывая, что среднее значение
vΔ очевидно, обращается в нуль,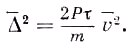
Здесь
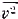можно сразу заменить с помощью уравнения
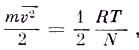
выводимого из соотношения между энтропией и вероятностью. Прежде чем указать значение константы трения Р, мы уточним условия рассматриваемой задачи, сделав предположение, что зеркало идеально отражает излучение в определённом интервале частот (между
ν и ν + dν), но для излучения другой частоты оно абсолютно прозрачно. В результате вычислений, которые я для краткости изложения опускаю, на основе чисто электродинамического исследования мы получаем соотношение, справедливое для любого распределения излучения,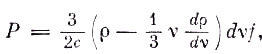
причём ρ снова означает плотность излучения при частоте
ν, f — площадь зеркала. Подставляя найденные значения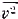 и Р, получаем
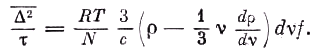
Преобразуя это выражение с помощью формулы излучения Планка, находим
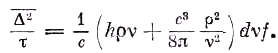
Большое сходство этого соотношения с выведенной в предыдущем разделе формулой для квадрата флуктуаций энергии (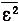) бросается в глаза 16
8. Из обоих последних рассуждений, по-моему, неопровержимо вытекает, что излучение должно иметь другую структуру, чем мы теперь думаем. Хотя наша современная теория, как показывает превосходное согласие
теории и эксперимента в оптике, правильно даёт единственные непосредственно наблюдаемые средние по времени значения, она с необходимостью приводит к законам о свойствах теплового излучения, несовместимым с опытом, как только мы будем основываться на соотношении между энтропией и вероятностью. Отклонение наблюдаемых на опыте значений от теоретических проявляется тем сильнее, чем больше ν и меньше ρ. При малых ρ временные флуктуации энергии излучения в некотором заданном пространстве или флуктуации силы давления излучения на некую плоскость намного больше, чем можно ожидать согласно нашей современной теории.Мы видели, что закон излучения Планка можно понять на основе гипотезы, что энергия осциллятора, обладающего частотой
ν, может существовать только в виде квантов величиной hν. Согласно сказанному выше, недостаточно предполагать, что излучение может испускаться и поглощаться только в виде квантов этой величины и что, следовательно, дело сводится к свойству излучающего или поглощающего вещества; рассуждения в разделах 6 и 7 показывают, что флуктуации пространственного распределения излучения, равно как и флуктуации светового давления, следуют так, как если бы излучение состояло из квантов указанной величины. Правда, всё-таки нельзя утверждать, что квантовая теория является простым следствием закона излучения Планка и что другие интерпретации его невозможны. Но заведомо можно утверждать, что квантовая теория даёт простейшую интерпретацию формулы Планка.Необходимо подчеркнуть, что приведённые выше соображения в основном не потеряли бы своего значения и в том случае, если бы формула Планка оказалась неверной, так как с теорией световых квантов связана лишь та часть формулы Планка, которая достаточно подтверждена опытом (то, что из неё в пределе больших
ν/T получается закон излучения Вина).9. Экспериментальное изучение следствий теории световых квантов является, на мой взгляд, одной из важнейших задач, которые предстоит решить современной экспериментальной физике. Полученные до настоящего времени следствия можно подразделить на три группы.
а) Получаются опорные точки для определения энергии элементарных процессов, связанных с поглощением и, соответственно, испусканием излучения определённой частоты (правило Стокса; скорость катодных лучей, возбуждённых светом или рентгеновскими лучами; катодная люминесценция и т. д.). Сюда относится также интересное применение Штарком теории световых квантов для объяснения своеобразного распределения энергии в спектральной линии, испускаемой каналовыми лучами17
.Ход рассуждений
при этом всегда такой: если некоторый элементарный процесс порождает другой процесс, то энергия последнего не больше, чем первого. Но если один из этих элементарных процессов является поглощением или испусканием света определённой частоты, то энергия его известна (равна hν).Особый интерес представляет изучение исключений из закона Стокса. Для объяснения этих исключений необходимо предполагать, что световой квант испускается только после того, как соответствующий излучающий центр поглотит два кванта. Частота таких событий, а значит и интенсивность излучаемого света длины волны меньшей, чем у возбуждающего света, должна быть в этом случае при слабом облучении пропорциональной квадрату интенсивности возбуждающего света (в соответствии с
законом действующих масс), в то время как по правилу Стокса при слабом облучении следовало бы ожидать пропорциональности первой степени интенсивности возбуждающего света.б) Если при поглощении 18
каждого светового кванта происходит некий элементарный акт, то число таких элементарных актов равно E/hν, где Е — полная энергия и ν — частота поглощённого света.Таким образом, если, например, при ионизации в газе поглощается свет с энергией Е и частотой
ν, то следует ожидать, что при этом будет ионизовано E/Nhν грамм-молекул газа. Это соотношение лишь на первый взгляд предполагает знание N; ведь если написать формулу Планка в виде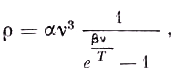
то число ионизованных грамм-молекул будет
E/Rβν.Это соотношение, уже указанное в моей первой работе по этому вопросу
19, оставалось, к сожалению, пока незамеченным.в) Сказанное ниже, в разделе 5, ведёт к модификации кинетической теории теплоёмкости 20
и к определённым связям между оптическими и тепловыми свойствами тел.10. По-видимому, трудно построить теорию, полностью объясняющую световые кванты так, как наша современная молекулярная механика в соединении с теорией Максвелла — Лоренца объясняет формулу излучения Джинса. Тот факт, что речь идёт лишь о модификации
наших современных теорий, а не о полном отказе от них, вытекает уже из того, что закон Джинса в пределе (для малых ν/T), видимо, выполняется. Указание на то, каким образом можно осуществить эту модификацию, даёт чрезвычайно важный, на мой взгляд, анализ размерностей проделанный Джинсом несколько лет назад. Этот анализ — изменённый в нескольких пунктах — я коротко воспроизвожу ниже.Представим себе, что в замкнутом пространстве находятся идеальный газ, излучение и ионы, причём последние благодаря своему заряду обеспечивают обмен энергией между газом и излучением. Следует ожидать, что в теории излучения, связанной с рассмотрением этой системы, играют существенную роль и, значит, входят в искомое выражение для плотности излучения ρ следующие величины:
а) средняя энергия η молекулы (с точностью до неназванного множителя, равного
RT/N),б) скорость света с
,в) элементарный квант электричества ε
,г) частота ν
.По размерности ρ, учитывая только размерности четырёх перечисленных величин, можно теперь просто определить, какой вид должно иметь выражение для ρ. Подставляя вместо
η ηначение RT/N, получаем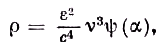
где
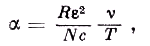
а ψ — неизвестная нам функция. Это соотношение содержит закон смещения Вина, сомневаться в котором, пожалуй, уже вряд ли возможно. Это надо понимать как подтверждение того, что, кроме перечисленных четырёх величин, никакие другие размерные величины в законе излучения роли не играют.
Отсюда мы заключаем, что в выражении для ρ коэффициенты ε2/c4
и (Rε2/Nc) с точностью до безразмерных числовых множителей, которые, естественно, анализ размерностей определить не в состоянии, должны равняться соответствующим коэффициентам в формуле излучения Планка (или Вина). Так как упомянутые неопределённые безразмерные числовые множители вряд ли существенно изменят порядки величин, то можно положить 21:h/c3 =
ε2/c4 и h/k=Rε2/Nc,следовательно,
h
= ε2/c и k=N/R.Именно из второй пары этих уравнений Планк определил величину элементарного кванта материи или электричества. По поводу выражения для
h следует отметить, чтоh
=6·10-27и
ε
2/c = 7·10-30.Здесь не хватает целых трёх порядков. Это, конечно, можно отнести на счёт неизвестных безразмерных множителей.
Самое важное в этом выводе заключается в том, что он сводит квантовую постоянную света
h к элементарному кванту электричества ε. Теперь надо вспомнить, что для электродинамики Максвелла–Лоренца элементарный квант ε является чуждым 22. Для того чтобы сконструировать электрон, необходимо привлечь неэлектродинамические силы; обычно вводится жёсткий остов, который должен препятствовать развалу электрона под влиянием взаимодействия между его электрическими массами. Но, на мой взгляд, из соотношения h = ε2/c вытекает, что та модификация теории, которая даёт как следствие элементарный квант ε, будет также содержать в себе квантовую структуру излучения. Фундаментальное уравнение оптики
необходимо будет заменить таким уравнением, в которое входит в виде коэффициента также универсальная постоянная
ε (вероятно, её квадрат). Искомое уравнение (или система уравнений) должно быть однородным по размерности. При преобразовании Лоренца оно должно переходить в самое себя. Оно не может быть линейным и однородным. Оно должно — по крайней мере, если закон Джинса действительно выполняется в пределе малых ν/T — переходить в пределе больших амплитуд в уравнение D(φ)=0.Мне ещё не удалось найти удовлетворяющую этим условиям систему уравнений, о которой можно было бы сказать, что она пригодна для построения элементарных электрических и световых квантов. Однако многообразие возможностей, по-видимому, не настолько велико, чтобы отпугнуть от этой задачи.
Дополнение
Из раздела 4 читатель легко может получить неправильное впечатление об отношении Планка к его собственной теории теплового излучения. Поэтому я считаю уместным заметить следующее.
В своей книге Планк много раз подчёркивает, что его теорию не следует понимать как нечто законченное и замкнутое. Например, в конце предисловия он говорит буквально следующее: “Мне хочется здесь особо подчеркнуть, что развитая в книге теория не претендует ни в какой мере на законченность, хотя, как мне кажется, она открывает целесообразный путь для изучения процессов излучения энергии с
той же точки зрения, с какой рассматриваются молекулярные движения” 23.Соответствующие противопоставления в моей статье следует понимать не как возражения, в собственном смысле этого слова, против теории Планка, но только как попытку более отчётливо, чем это делалось ранее, осознать и применить принцип связи энтропии и вероятности. Более отчётливое понимание этого принципа было необходимо потому, что без этого последующие рассуждения в статье, которые привели к выводу о молекулярной структуре излучения, оказались бы недостаточно обоснованными. Чтобы моё понимание принципа не выглядело специально придуманным для этого случая, я должен был показать, почему существовавшая формулировка этого принципа не вполне меня удовлетворяла.
Берн, январь 1909 г.
Поступила 23 января 1909 г.
* Zum gegenwärtigen Stand des Strahlungsproblems. Phys. Zs., 1909, 10, 185–193.
H. A. Lorentz. Phys. Zs., 1908, 9, 562. J. H. Jeans. Phys. Zs., 1908, 9, 853. W. R i t z. Phys. Zs., 1908, 9, 903. Ср. A. Einstein. Ann. Phys., 1905, 17, 133 (Статья 7). М. Planck. Ann. Phys., 1900, 1, 99; М. Рlanck. Vorlesungen über die Theorie der Wärmestrahlung, III. Kapitel. (Ссылка на 1-е издание. Существует русский перевод лишь с 5-го переработанного издания.— Ред.). Следует ещё раз подчеркнуть, что это соотношение есть неизбежное следствие статистической теории теплоты. Предпринятая на стр. 178 только что цитированной книги Планка попытка поставить под сомнение общую применимость соотношения (II) покоится, как мне кажется, лишь на пробеле в трудах Больцмана, заполненном с того времени исследованиями Гиббса. То, что последнее утверждение является единственно возможным, непосредственно вытекает из свойств броуновского движения. Ср. также L. Boltzmann. Vorlesungen über Gastheorie. 1. Bd. S. 40. (См, перевод: Л. Больцман. Лекции по теории газов. Ч. I. М. 1953, §6.— Ред.). A. Einstein. Ann. Phys., 1906, 20, 199 (Статья 10) и Ann. Phys., 1907, 22, 569 (Статья 13). Это соотношение получается в том случае, если предположить, что электромагнитная теория излучения даёт, по крайней мере, правильные средние по времени значения. Но, учитывая успехи теории в оптике, едва ли можно сомневаться в этом. A. Einstein. Ann. Phys., 1905, 17, 132 (Статья 7). Ср., например, соотношение (230) в многократно цитированной книге Планка. Разумеется, только в случае, когда они достаточно велики. В указанном выше интерференционном рассмотрении мы получили бы, конечно, (R/Nk)=1. Движения зеркала, о которых здесь говорится, совершенно аналогичны так называемому броуновскому движению. Указанную формулу можно записать в виде (принимая при этом R/Nk=1):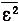=(hρν+c3ρ2/8πν2)vdν.
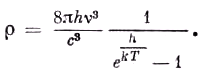Ср. Lеvi-Сivita. Compt. Rend. 1907: “Sur le mouvement etc.”
Из предисловия к 1-му изданию. — Прим, ред.
Дата установки:
10.12.2007
