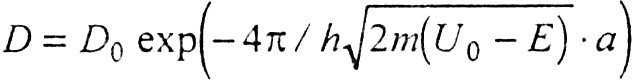 (1)
(1)[вернуться к содержанию сайта]
Существование туннельного эффекта рассматривается в квантовой механике как одно из доказательств волновой природы микрочастиц. Однако, в формуле для расчёта этого эффекта присутствуют параметры только корпускулы и нет ни одного, относящегося к волне. Кроме того, в последние годы экспериментально доказано, что поверхностный потенциальный барьер кристалла, и. следовательно, p-n перехода в кристалле имеют не равномерный, а пик-горочный характер около каждого атома.
Сопоставление этих фактов в статье на примере электрона в p-n переходе приводит к выводу о том, что в данном явлении происходит не туннельный эффект волны, а канавное прохождение корпускул в межатомных расстояниях, где потенциальный барьер имеет значение ниже среднего, а в расчётах среднее принимается за высоту равномерного потенциального барьера.
Существование туннельного эффекта рассматривается в квантовой механике как одно из доказательств волновой природы элементарных микрочастиц. Эффект состоит в том, что, например, электрон, обладающий кинетической энергией своего движения несколько меньшей, чем потенциальный барьер перед ним, имеет некоторую вероятность всё же преодолеть этот барьер.
Из общих соображений кажется очевидным, что с частицей-корпускулой этого произойти не может, и следовательно, электрон в данном случае является волновым образованием, для которого высота барьера не имеет значения.
Для величины туннельного эффекта при прямоугольном сечении потенциального барьера приводится формула [1; 2]:
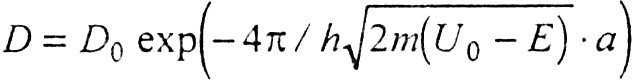 (1)
(1)
где: D – коэффициент прозрачности барьера; D0 – величина порядка единицы; 4π/h – постоянная Планка: m – масса микрочастицы; U0 – высота потенциального барьера; Е – кинетическая энергия микрочастицы; а – ширина барьера.
Однако, если в данном случае электрон является, как принято, волновым образованием, то в формуле (1) должны присутствовать длина волны электрона, "оптические" плотности барьера и среды около него, поглощение волны в этих средах, но никак не масса и кинетическая энергия микрочастицы. Кроме того, для просачивания чистой волны совсем не важна высота барьера, так как главную роль здесь играют соотношения "оптических" плотностей на границах барьера, угол падения волны и поглощение её в обеих средах. Этих параметров в формуле (1) совсем нет.
Почему возникло такое явное несоответствие – в формуле используются параметры только частицы-корпускулы и нет ни одного параметра, характеризующего волну и её прохождение в средах, а утверждается, что в туннельном эффекте только волна может просачиваться сквозь потенциальный барьер? Может быть, это могут делать всё же и корпускулы?
Чтобы определить действительную сущность туннельного эффекта, нужно чётко и точно представить условия, соответствующие реальности, при которых он проявляется.
Высота потенциального барьера в полупроводниковых диодах, в которых используется туннельный эффект, составляет не сотни и не десятки, а всего 0,3–0,6 В, и просачивание частиц сквозь барьер начинается при отпирании этого барьера напряжением всего в 0,1–0,2 В. то есть их энергия при этом всего на 0,2–0,4 эВ ниже потенциального барьера. Кроме того, толщина потенциального барьера для проявления туннельного эффекта должна быть чрезвычайно тонкой, всего в десятки атомных слоёв ~ 10–7 ... 10–6 см.
При объяснении сущности туннельного эффекта в приведённых выше условиях потенциальный барьер почему-то представляли себе в виде стены с ровным, как по линейке, верхом. В таком феноменологическом представлении, конечно, частица-корпускула, имеющая уровень энергии на 0,2–0,4 эВ ниже потенциального барьера, не может его пройти.
В то же время известно, что волны, даже отражаясь от преграды, всё же просачиваются в неё на глубину порядка длины волны. Для справки, у света длина волны l(св)~10-5 см, размеры атомов d(ат)~(3÷5)·10–8 см, а длина волны теплового электрона l(e)~2,5·10-5 см. Следовательно, утверждают, что "при толщине барьера 10–7 ... 10–6 см и длине волны теплового электрона l(e)=2,5·10-5 см, он только в качестве волны может просочиться сквозь потенциальный барьер, что и доказывает волновую природу электрона."
Однако, феноменологическое представление о ровном, как натянутый канат, потенциальном барьере совершенно не соответствует действительности, и что он именно такой ровный, как линейка, ещё никто не доказал.
Дело обстоит как раз наоборот. В последние десятилетия разработан принципиально новый прибор – потенциальнометрический микроскоп. Основная часть его состоит в чрезвычайно острой игле, такой, что её остриё состоит всего из единиц атомов. Проводя этим остриём вдоль поверхности кристаллов на расстояниях, сравнимых с межатомными, измеряют ток, который проходит из кристалла через воздушный промежуток и иглу. Ток зависит от величины потенциала, который создаёт ближайший атом в точке острия иглы. Оказалось, что распределение потенциала у поверхности кристалла совсем не имеет ровного характера, а состоит из пик-горок против каждого атома, по которым можно даже сосчитать количество атомов и измерить расстояния между ними.
Например, иллюстрацией к этому в [3] приведён компьютерный фотоснимок распределения потенциалов атомов на поверхности кристалла кремния. На снимке видно, что каждый атом образует потенциальную пик-горку, высотой 2,5 Å при его собственном примерно таком же размере. Хорошо видна кристаллическая решётка расположения атомов и дислокации отдельных атомов на ней. Ещё раз подчеркнём, что фотоснимок представляет верхнюю часть потенциального барьера поверхности кристалла.
Не подлежит сомнению, что потенциальный барьер "p-n" перехода в полупроводнике будет иметь ещё больший пик-горочный характер, поскольку образуется примесными атомами, которые вкраплены в меньшем количестве среди атомов основного кристалла полупроводника.
Таким образом, экспериментально доказано, что верхняя часть потенциальных барьеров на атомном уровне имеет холмисто-пиковый характер. Величину этих неровностей можно оценить из того, что энергия связи внешних электронов атомов имеет величины от нескольких до десятка электрон-вольт; и уж несколько десятых вольта эти неровности вполне могут быть.
Исследователи же, феноменологически рассматривая до сих пор этот барьер ровным, как линейка, приписывали ему среднее значение, с которым и оперировали, не обращая внимания на его лазейки-канавы, которые находятся ниже среднего значения. Именно по этим потенциальным канавам электроны, даже будучи частицами-корпускулами, и проходят реальный потенциальный барьер, даже имея энергию на 0,2–0,4 эВ меньшую, чем его среднее значение.
Данное рассмотрение согласуется и с тем, что при генерировании СВЧ-частот на туннельных диодах, амплитуда колебаний не превышает ~0,2 В. Таким образом, обсуждаемый эффект просачивания электрона "сквозь" потенциальный барьер следует называть не "туннельным", а канавным, и производится он не волной, а частицей-корпускулой.
[1] Яворский Б.М., Детлаф А.А. Справочник по физике, М., Наука, 1974, с. 733.
[2] Савельев И.В. Курс обшей физики, т. 3, М., Наука, 1982, с. 86.
[3] Независимая газета, прил. Наука № 3 от 17.03.1999 г., с. 4.
Дата установки: 30.06.2013
[вернуться к содержанию сайта]