Рис.
[вернуться к содержанию сайта]
Синхротронное и черенковское излучение отличает острая направленность вдоль скорости V излучающих частиц. Считалось, что эта направленность объясняется лишь специальной теорией относительности (СТО) и противоречит баллистической теории Ритца (БТР) [1]. Но фактически свойства излучений, следующие из теории Ритца и классической оценки V, соответствуют опытам [2–4]. Это относится и к замерам скорости синхротронного излучения в опыте Е. Александрова и на установке SLAC, где скорость излучения c' и электронов V не измерялась напрямую [4, 5]. Согласно теории Ритца, скорость электронов V добавляется к скорости света c относительно них, и расчётная скорость c' = c + V зависит от метода измерения V. При классической оценке V результаты опытов соответствуют теории Ритца [2–5].
Скорость V частиц находят по их импульсу p = m'V = eBR, где R – радиус траектории частицы массы m' и заряда e в магнитном поле B. Для ультрарелятивистских частиц импульс p ≈ mγс, откуда находят γ-фактор. В классической механике m' равно массе покоя m и V = γс [4]. Добавление V к скорости света c сосредотачивает излучение в конусе с осью V и углом образующей θ = arcsin(c/V) ~ 1/γ [2, 3].
Импульс излучения соответствует пролёту электроном отрезка орбиты d ~ Rθ ~ R/γ, с которого излучение поступает в детектор на расстоянии L [6]. Из начала A отрезка d свет дойдёт за время tA = (d + L)/(c + V), из конца B – через время tB = d/V + L/(c + V) после излучения в A. Длительность импульсов ΔT = tB – tA ≈ d/cγ2 ≈ R/cγ3, в согласии с СТО [6], а их спектр формируют гармоники частоты вращения, вплоть до f ~ 1/ΔT ~ γ3c/R, что соответствует опыту [6]. По теории Ритца спектр зависит и от длины пути света L в канале вывода, что находит косвенные подтверждения [2].
Аналогично, в ондуляторе длины d найдём ΔT ≈ d/cγ2, в согласии с опытом и СТО [6]. В ондуляторе с шагом магнитов b частота колебаний электрона f = V/b, а регистрируемая по доплер-эффекту частота излучения f ' = f(1 + V/c) ≈ γ2c/b [3], в согласии с СТО [6]. То есть релятивистская и баллистическая теории приводят к близким угловым θ(γ), временным ΔT(γ) и частотным f '(γ) характеристикам синхротронного (ондуляторного) излучения. Сделать выбор между теориями можно путём прямых замеров скорости частиц из синхротронов пролётным методом [4, 5]. Обычно релятивистскую скорость v оценивают из формул СТО, связывающих импульс p ≈ mγс и скорость частиц v = c(1 – 1/γ2)1/2. А классическая теория даёт сверхсветовое значение V ≈ γс, не противоречащее принципам работы синхротрона [3, 4].
Другой способ измерения V основан на исследовании черенковского излучения частиц: его свойства тоже следуют из теории Ритца. Ещё в 1888 г. О. Хевисайд предсказал, что заряд, летящий в среде, должен излучать. По теории Ритца это излучение приобретает в среде с показателем преломления n лишь часть скорости заряда V [5], так что скорость излучения с' = c/[n – V/(c + V)]. Если V ≥ с', то огибающая волновых фронтов образует конус черенковского излучения, а в рамках СТО излучение генерируется при v ≥ c/n. То есть измерение скорости частиц по порогу v = c/n (СТО) и порогу V = с' (БТР) даёт разные значения. Однако зависимость порогового n от γ в СТО и БТР – сходная. В пороговых счётчиках скорость ультрарелятивистских частиц измеряют по показателю преломления газа n = 1 + δ (где δ << 1), при котором возникает излучение. В СТО v = c/n ≈ c(1 – δ), откуда пороговое значение δ = 1/2γ2. В баллистической теории из условия V = с' порог δ = 1/γ2 с точностью до множителя 1/2 совпадает с релятивистским. Эта разница вызвана неточностью зависимости с'(V) при ультрарелятивистских скоростях (γ >> 1) и даёт простой критерий проверки теории Ритца, где измеренная величина δ << 1 соответствует сверхсветовым скоростям V ≈ сγ ≈ с/δ1/2. То есть и здесь основной критерий проверки теории Ритца – это прямое измерение V пролётным методом [5].

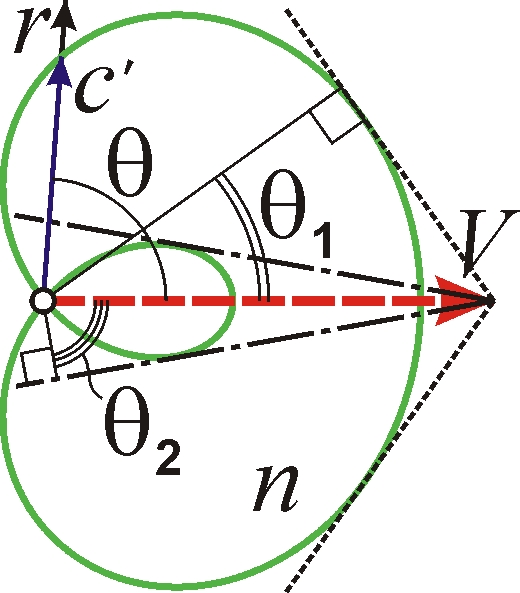
Рис.
Угол θ черенковского излучения в теории Ритца выражается неоднозначно (см. рис.). Если на скорость с' = c/[n – Vr/(c + Vr)] в направлении θ влияет лишь радиальная компонента скорости заряда Vr = Vcosθ, то при V ~ с волновой фронт приобретает форму с'(θ) = c/[n – (c/Vcosθ + 1)–1] отличную от сферы. А при V ≥ с (в СТО отвечает v ≥ 0,71с) волновой фронт – самопересекающийся, с особенностью типа лепестка. Тогда, кроме нормального конуса черенковского излучения (внешней огибающей фронтов, с углом θ1 на рис.), формируется узкий конус – огибающая лепестка (с углом θ2). При n < 1,5 этот аномальный конус образуется при допороговых значениях γ. Условие генерации излучения V = c/[n – V/(c + V)] даёт два решения: V1, 2 = c(–1 ± [1 + 4/(n – 1)]1/2)/2, где V1 отвечает порогу генерации нормального черенковского излучения, а V2 – допороговому (аномальному) излучению, существующему в диапазоне с ≤ V ≤ |V2|.
Допороговую генерацию подтверждают эксперименты [7]. Если конус нормального черенковского излучения сужался при росте n или V, то аномальный – расширялся, в согласии с теорией Ритца. На фотографиях [8] наблюдалось два кольца: одно отвечало нормальному черенковскому эффекту (θ1), а второе, аномально широкое кольцо,– излучению от частиц с v > с [8]. В рамках теории Ритца его генерируют те же частицы: аномальное излучение и формирует 2-е кольцо (θ2).
Итак, свойства синхротронного, ондуляторного и черенковского излучений не противоречат теории Ритца, а её выводы совпадают с СТО. В ряде случаев баллистическое описание точнее релятивистского и объясняет аномалии этих излучений.
1. Newburgh R.G. // American Journal of Physics. 1972. V. 40, №8. P. 1173.
2. Семиков С.А. // Вестник ННГУ. 2014, №1(2). С. 180.
3. Семиков С.А. // Инженер. 2011. №11–12. С. 24.
4. Семиков С.А. // Инженер. 2013. №6–9. С. 18.
5. Семиков С.А. // Вестник ННГУ. 2013, №4(1). С. 56.
6. Михайлин В., Тернов И. Синхротронное излучение.– М.: Знание, 1988. 64 с.
7. Тяпкин А.А. // Краткие сообщения ОИЯИ. 1993, №3[60]-93. C. 26.
8. Водопьянов А.С., Зрелов В.П., Тяпкин А.А. // Письма в ЭЧАЯ. 2000. № 2[99].
см. презентацию в формате PPT
Дата установки: 06.06.2014
[вернуться к содержанию сайта]