[вернуться к содержанию сайта]

Предложена схема прямой экспериментальной лабораторной проверки независимости скорости света от скорости источника, в которой измеряемый эффект первого порядка по v/c.

    Прямое экспериментальное подтверждение в лабораторных условиях независимости скорости света от скорости источника имело бы принципиальное значение.

    Опубликованная в 1956 г. работа А. М. Бонч-Бруевича [^{1, 2}] основывается на астрономических наблюдениях; в ней сравнивается скорость света от разных краёв солнечного диска. Эта работа не представляется нам вполне убедительной.

    С одной стороны, автор исходит априорно из некоторых допущений о скорости света после отражения от зеркала, а с другой, в силу принципиально малой точности метода, результаты наблюдений имеют большой разброс, превышающий в несколько раз ожидаемый по классической теории эффект, и для получения окончательного результата автору пришлось статистически обработать очень большое (1727) число наблюдений, причём наиболее резко выпадающие были вообще отброшены.

    В силу сказанного, нельзя считать, что эта работа даёт прямую экспериментальную проверку независимости скорости света от скорости источника.

    Ниже излагается схема прямой лабораторной проверки постулата о постоянстве скорости света, при применении которой различие эффектов, рассчитанных по постулату и по классической теории, составляет величину порядка v/c (а не v²/c²), что позволяет проверить постулат с неизмеримо большей точностью, чем при любом другом методе.

    Основная идея метода заключается в применении интерферометра с движущимся зеркалом. Как показывает расчёт, скорость движения зеркала в этом опыте может быть порядка одного метра в секунду и даже меньше.

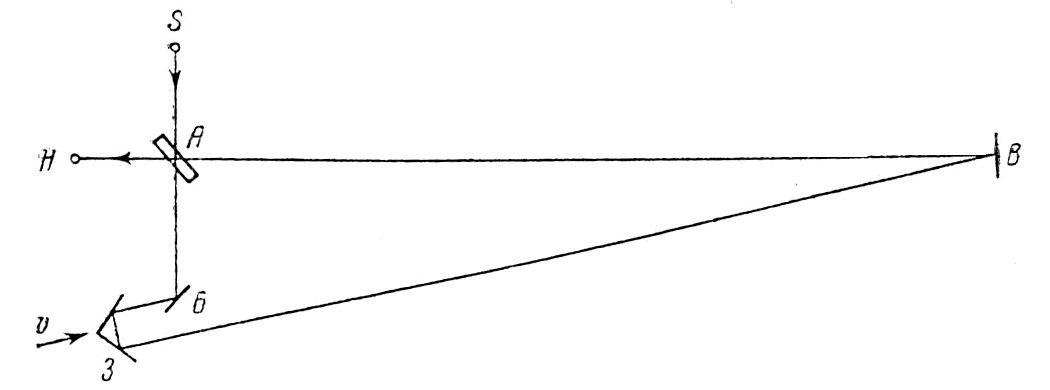
    Один из вариантов схемы опыта изображён на рисунке, где S – источник монохроматического света, А – полупосеребрённая пластинка, Б и В – плоские зеркала, Н —наблюдатель интерференционной картины, З – система двух взаимно-перпендикулярных плоских зеркал, которая может двигаться по направлению стрелки с регулируемой скоростью v.

    Применение системы З создаёт возможность сохранения параллельности падающего и отражённого лучей при перемещении зеркал и сильно уменьшает влияние нарушения строгой параллельности движения; кроме того, этой системой устраняется аберрация света, так как в данном случае аберрация одного зеркала компенсируется аберрацией другого.

    Луч света, исходящий из S в A, разделяется на два луча. Левый луч идёт по пути АБЗВА, а правый – по пути АВЗБА: соединившись в A, оба луча идут к наблюдателю Н. Когда З неподвижны, длина обоих путей одинакова, и наблюдатели видит определённую интерференционную картину.

    Если привести систему зеркал З в движение со скоростью v длина обоих путей становится неодинаковой и, при постоянстве скорости света, произойдёт смещение интерференционных полос. Покажем, что при любой постоянной скорости v смещение полос будет устойчиво.

    Заметим, прежде всего, что частота света ν после отражения от З изменится одинаково для обоих лучей: они возвратятся в А и попадут к Н с одинаковой частотой ν'.

    Обозначим длину АБЗ через, длину ЗВА через l₂. Хотя l₁ и l₂ переменны, их разность L=l₂–l₁ постоянна. На прохождение АБЗ левый луч затрачивает время t₁=(l₁–vt₁)/c, откуда t₁=l₁/(c+v). На прохождение ЗВА тот же луч затрачивает время t₂=(l₂–vt₁)/c=[l₂–vl₁/(c+v)]/c. Полное время левого луча

T_л=t₁+t₂=l₁/(c+v)+[l₂–vl₁/(c+v)]/c.

    Аналогично для правого луча – полное время

T_п=l₂/(c+v)+[l₁–vl₂/(c+v)]/c.

    Разность во времени

ΔT=T_л–T_п=2v(l₂–l₁)/c(c+v)=const

    Следовательно, интерференционная картина устойчива.

    Смещение полос

δ=cΔT/λ'=2vL/λ'(c+v)≈2vL/λc.                        (1)

    Для примера, при L=30 м, v=1 м/сек и λ≈5000 Å смешение составит 0,4 полосы.

    Если бы скорость света зависела от скорости источника, то после отражения от З она была бы равна с+2v, что как раз бы компенсировало разность путей и никакого смещения полос не произошло бы:

T_л=l₁/(c+v)+[l₂–vl₁/(c+v)]/(c+2v)=(l₁+l₂)/(c+2v)=T_п.

    Таким образом, предлагаемый нами опыт может доказать, с большой точностью, независимость скорости света от скорости источника.

    Небольшие погрешности, как то: отклонение движения зеркал от строго параллельного и равномерного, неточность измерения длины L и скорости v, проведение опыта в воздухе, а не в пустоте и т. д., не превышающие, по нашей оценке, нескольких процентов, не смогут исказить результат опыта. Если бы далее оказалось, что действительные погрешности значительно превысят нашу оценку, по какой-либо непредвиденной причине, или если в распоряжении экспериментатора будет интерферометр с небольшой чувствительностью, можно было бы увеличить смещение полос за счёт увеличения L или v.

Поступила в редакцию
15 сентября 1960 г.

[1] А. М. Б о н ч-Б р у е в и ч. ДАН СССР, 109, 481, 1956.

[2] А. М. Б о н ч-Б р у е в и ч, В. А. Молчанов. Оптика и спектроскопия, 1, 113, 1956.

A laboratory experiment is suggested which can be employed to directly verify whether the velocity of light is independent of the velocity of the source. The effect is of the first order in v/c.

Дата установки: 03.02.2012
[вернуться к содержанию сайта]

W