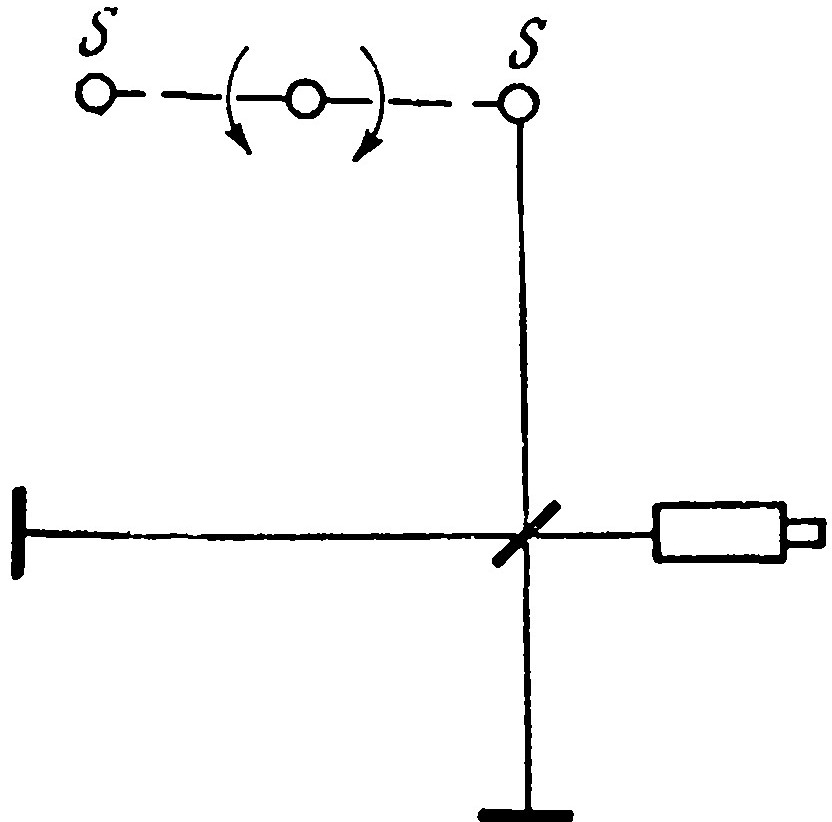
Рис. 1. Схема опыта Майораны
[вернуться к содержанию сайта]
Мы намерены это предположение (принцип относительности) превратить в предпосылку и сделать, кроме того, добавочное допущение ... именно, что свет в пустоте всегда распространяется с определённой скоростью и, не зависящей от состояния движения излучающего тела.
А. ЭЙНШТЕЙН, 1905 г.
За последние годы осуществлён ряд экспериментальных работ, посвящённых подтверждению независимости скорости света от скорости источника. Для полноты обзора из прежних работ можно отметить эксперименты Майораны [1] и Бонч-Бруевича [2].

Рис. 1. Схема опыта Майораны
Опыт Майораны заключался в измерении сдвига интерференционных полос в интерферометре Майкельсона с неравновесными плечами при замене неподвижного источника света движущимся (рис. 1). Если скорость света не зависит от скорости источника, то длина волны λ изменяется и сдвиг полос f составит
f=lv/λc,
где l – разница хода обоих лучей, v – скорость источника, c – скорость света.
В опыте: v=79,77 м/сек, l=232 мм, λ – 0,546 мк, что даёт согласно формуле (1) f=0,113 полосы. Поскольку применялось реверсивное движение источника, то смещение должно было удвоиться и составить 0,226 полосы. Эксперимент показал смещение f=0,238 полосы, совпадающее с ожидаемым с точностью 5%.
Однако, как заметил сам Майорана, результат опыта нельзя считать вполне убедительным доказательством независимости скорости света от скорости источника, так как фактически измерялась скорость света, прошедшего через разделительную пластинку и отразившегося от неё, а не непосредственно от движущегося источника.
В опыте Бонч-Бруевича источниками света служили противоположные края солнечного диска, разница скорости которых, в силу вращения Солнца, составляет около 3,5 км/сек. С помощью системы зеркал солнечный свет пропускался через модулятор, направлялся к отдалённому на расстояние 1 км зеркалу и возвращался обратно. Время прохождения модулированным сигналом двухкилометрового пути определялось с помощью фазометрического устройства для каждого из краёв солнечного диска поочерёдно. Если бы скорость света складывалась со скоростью источника, то разница времён должна была бы составить 75·10–12 сек. Разница между измеренными временами принимала как положительные, так и отрицательные значения и в несколько раз превосходила указанную выше величину, что обусловливалось флуктуациями в атмосфере, дрожанием зеркал и т. п. Статистическая обработка 1727 измерений дала среднюю разницу (1,4±3,5)·10–12 сек, что в пределах погрешности эксперимента подтверждает независимость скорости света от скорости источника.
Данный опыт нельзя считать вполне убедительным, так как в нём, как и в опыте Майораны, не измерялась скорость света непосредственно от движущегося источника.
Из новейших экспериментов следует отметить работу Кантора [3].
Автор исходит из предположения, что свет, падающий на поверхность прозрачного стекла, поглощается и вновь испускается со скоростью c/n, где n – коэффициент преломления. Дойдя до задней поверхности, свет опять поглощается и испускается далее со скоростью c относительно стекла. Точно так же отражающее зеркало является новым источником. Движущуюся стеклянную пластинку, через которую проходит свет, автор рассматривает как движущийся источник света. Схема эксперимента изображена на рис. 2.
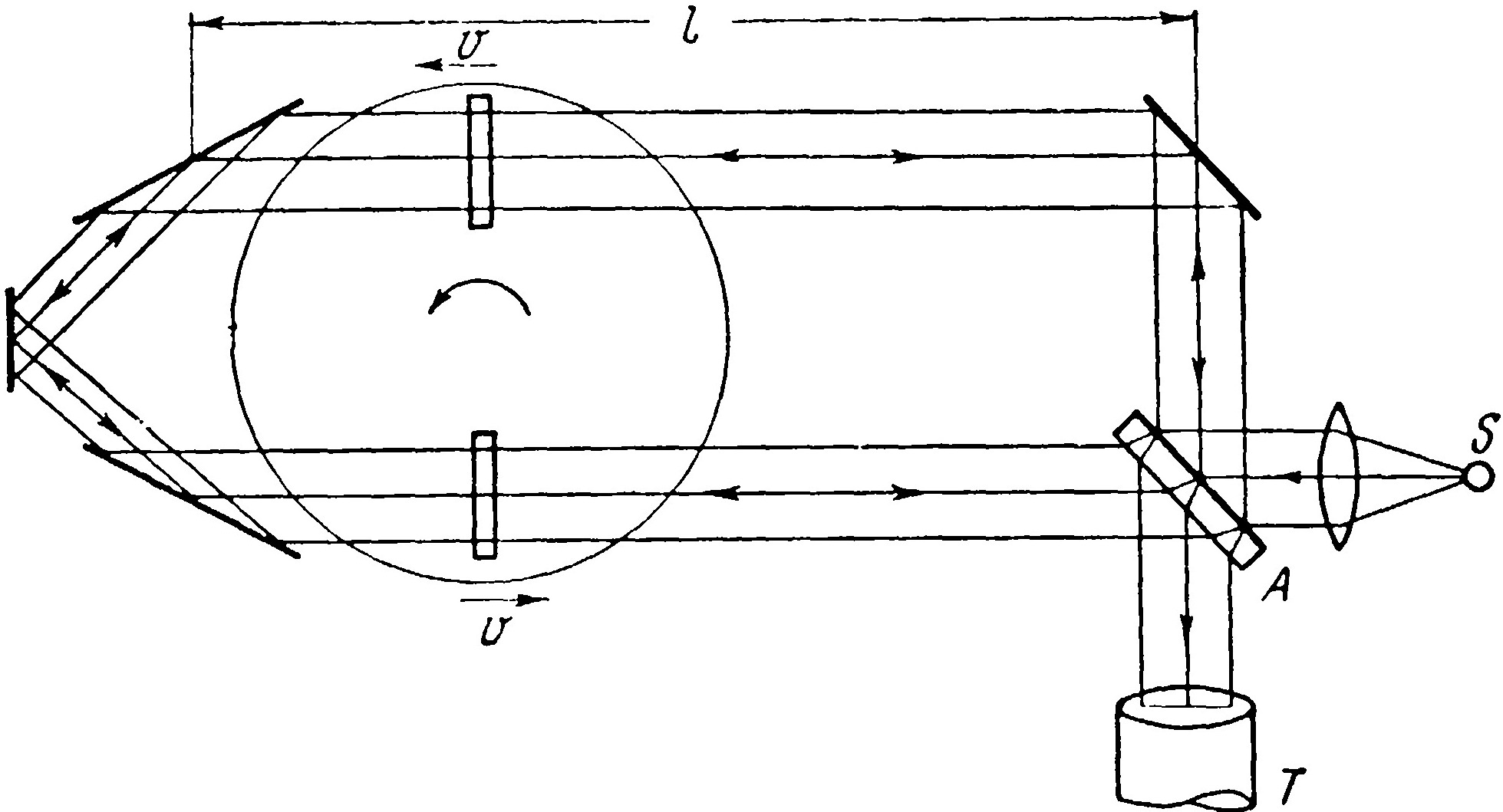
Рис. 2. Схема опыта Кантора
Свет от источника S делится пластиной А на два луча, проходящие интерферометр в противоположных направлениях. Интерференционная картина рассматривается в трубу T. По пути лучи проходят через два стеклянных окошка размером 5/8·0,''395, толщиной 0,''005, расположенных на диске диаметрально на расстоянии 12,24 см от центра. Диск вращается со скоростью 61 об/сек, так что линейная скорость центра окошка 4690 см/сек. Часть световых пучков проходит над окошками и даёт интерференционную картину от неподвижного источника S. Таким образом, в трубу видны одновременно две интерференционные картины – от подвижного и неподвижного источников, что позволяет определить сдвиг полос между ними. Расстояние l=118 см. Наблюдение ведётся в белом свете ксеноновой лампы, вспышки которой синхронизированы с моментами, когда окошки движутся вдоль луча. Если пренебречь, ввиду малой толщины окошек, незначительным влиянием увлечения света в них, то при независимости скорости света от скорости источника обе интерференционные картины (от света, прошедшего через окошки, и света, прошедшего поверх их) должны совпадать и сдвиг полос должен быть равен нулю. Если же скорость света складывается со скоростью источника, то для луча, идущего против часовой стрелки, на отрезке от окошка до следующего неподвижного зеркала она составит c+v, а для луча, идущего по часовой стрелке, c–v. Тогда сдвиг полос должен быть равен
f=2lv/λc=0,74.
Автор наблюдал сдвиг полос – 0,5.
Для проверки на расстоянии 30 см от зеркал помещали неподвижные прозрачные плёнки, уменьшая тем самым l. В этих условиях сдвиг полос уменьшался до 0,3.
Кантор интерпретирует результат своего опыта как качественное доказательство зависимости скорости света от скорости источника и, следовательно, как качественное опровержение специальной теории относительности.
Для количественного доказательства предлагалось провести повторный, более тщательный эксперимент, а также тщательное повторение опытов Физо и Зеемана по увлечению света движущимися средами, результаты которых противоречат опыту Кантора.
Некоторые авторы объявили опыт Кантора неопровержимым доказательством ошибочности теории относительности [4]. Другие стали доказывать совместимость результатов опыта с релятивистской теорией, в особенности с общей теорией относительности [5–8]. И те и другие проявили излишнюю поспешность, не убедившись в действительном существовании самого эффекта.
Тщательное повторение опыта Кантора произвели Бабкок и Бергман [9] (рис. 3). Авторы учли замечания Фокса [10], ставившего под сомнение корректность любого опыта по проверке независимости скорости света от скорости источника, если этот опыт произведён в воздухе или в газовой среде. По мнению Фокса, фотоны, сталкиваясь с молекулами воздуха, поглощаются и вновь испускаются со скоростью c относительно воздуха. Этот эффект проявляется, по его мнению, уже при толщине слоя воздуха в 1 мм1.
Бабкок и Бергман поместили установку в вакуум, усовершенствовав синхронизацию стробоскопа с положением окошек и уточнив измерение скорости последних.
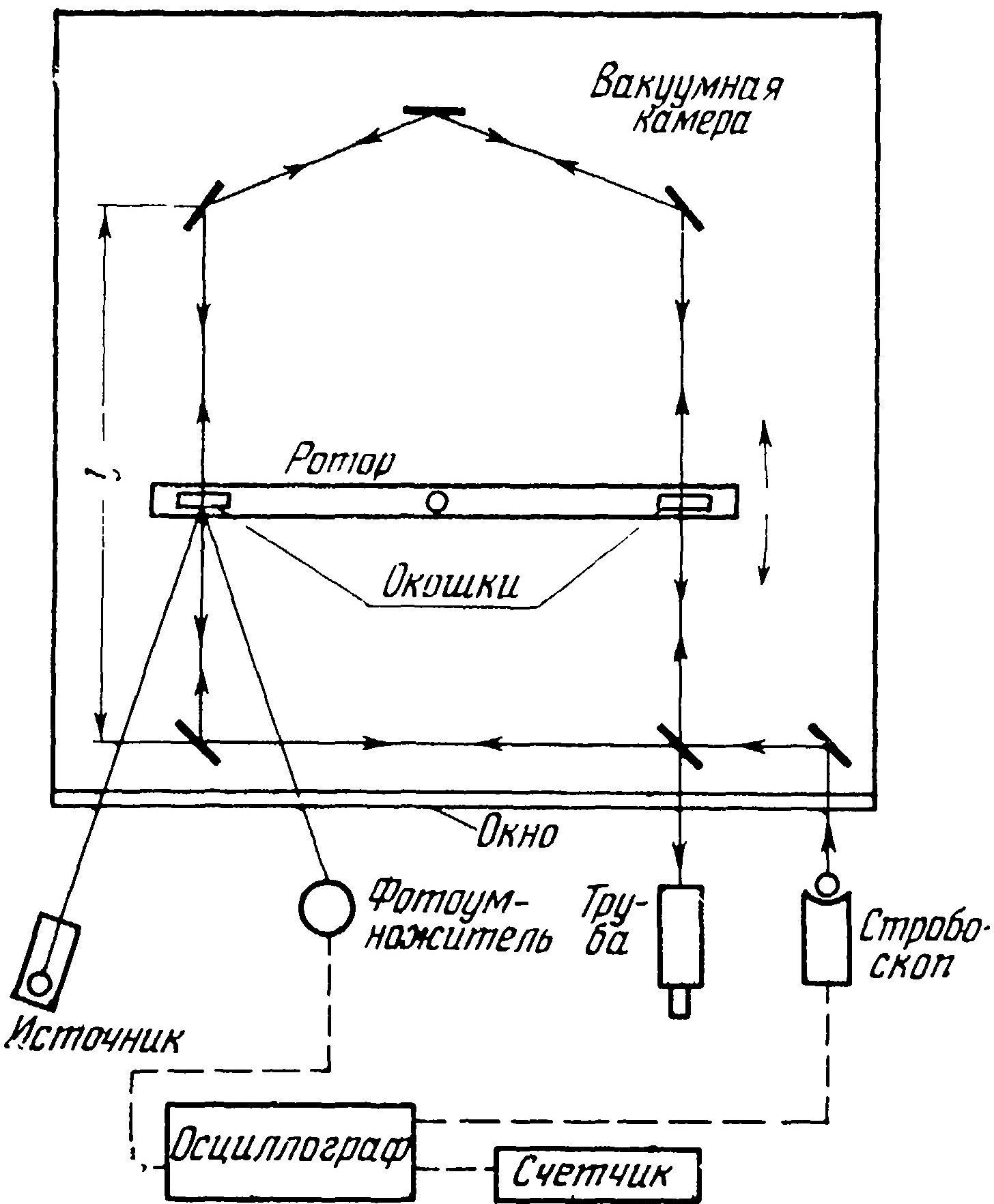
Рис. 3. Схема опыта Бабкока и Бергмана
Но самое существенное то, что они увеличили расстояние l до 276 см и применили реверсивное вращение диска с окошками, так что ожидаемый (по Кантору) сдвиг интерференционных полос увеличился до 2,9.
Результат измерений показал, что смещение полос не превышает 0,02, что хорошо согласуется с принципом независимости скорости света от скорости источника.
Ещё до эксперимента Бабкока и Бергмана Джемс и Стернберг изящным способом показали ошибочность взглядов Кантора [11]. Идея их опыта заключалась в следующем. Отдельные участки окошка, установленного на вращающемся диске, обладают различной скоростью. Следовательно, если, согласно Кантору, скорость света складывается со скоростью окошка, то свет должен стать неоднородным по скорости, фронт волны должен поворачиваться, т. е. луч должен изгибаться на угол
θ=
pωx/c,где ω – угловая скорость, x – расстояние до места наблюдения, а p – коэффициент.
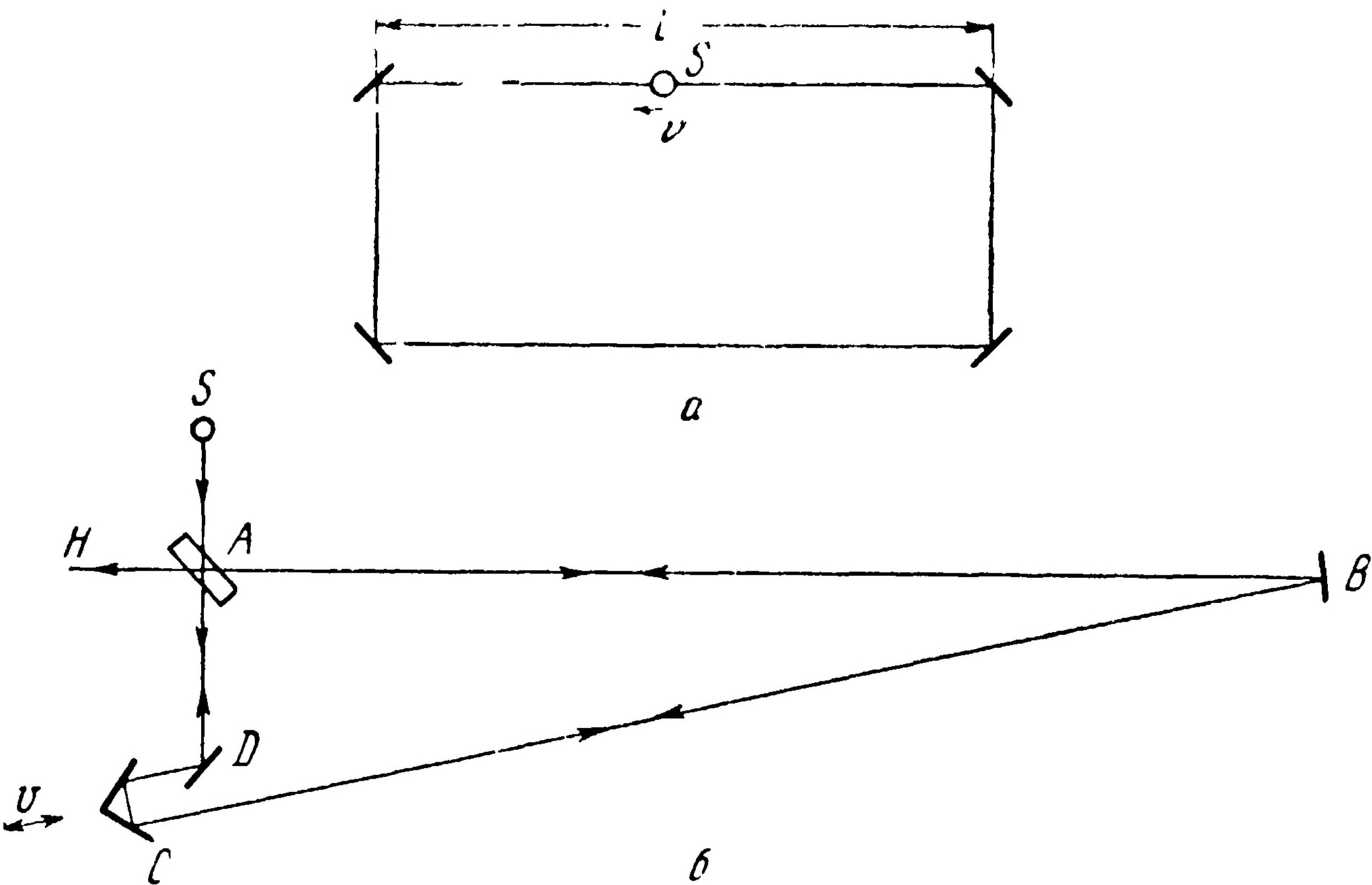
Рис. 4. Схемы опыта, предложенного А. Г. Барановым
а – принципиальная, б – практическая
В опыте Джемса и Стернберга ω=1500 Å (14500 об/мин) и x=20 м. При p=1 угол θ, как полагает Кантор, должен был бы равняться 20''. Телескоп, которым пользовались экспериментаторы, имел разрешение 0,''5; но никакого поворота луча не было обнаружено. Таким образом, p либо меньше 0,025, либо равен нулю.
Из двух последних опытов видно, что скорость света, прошедшего через движущуюся стеклянную пластинку, не изменяется. Уместно будет отметить, что ещё до работы Кантора в СССР был предложен эксперимент для проверки независимости скорости света от скорости источника [12]. Принципиальную идею этого метода можно понять из рис. 4, а. Монохроматический источник S испускает когерентные лучи в противоположных направлениях. Обойдя контур из неподвижных зеркал, лучи возвращаются к S и образуют интерференционную картину. Когда источник S неподвижен, пути обоих лучей одинаковы. Если же источник движется со скоростью v, то левый луч догоняет его, а правый идёт навстречу. Разница путей в этом случае при длине контура L составляет 2Lv/c; отсюда при независимости скорости света от скорости источника сдвиг интерференционных полос должен быть
δ
1=2Lv/λc.Если же скорость света складывается со скоростью источника, то изменение длины пути компенсируется изменением скорости света. Действительно, в этом случае время обхода контура
t=(L+vt)/(c+v)=L/c
не зависит от v и оба луча возвратятся в S одновременно, как и в случае неподвижного источника; сдвиг полос будет равен δ2=0. Наконец, если скорость c+v сохраняется лишь до первого неподвижного зеркала, а после отражения от него вновь равна c, то получится промежуточный сдвиг, а именно
δ
3=(L+L1)v/λc,где L1=L–l.
Следовательно, опыт должен дать однозначный ответ на вопрос о независимости скорости света от скорости источника. Практически предлагалось осуществить эксперимент по схеме, изображённой на рис. 4,б.
Все узлы установки, за исключением системы взаимно-перпендикулярных зеркал С, неподвижны. Система С совершает возвратно-поступательное прямолинейное движение с помощью кривошипного механизма с регулируемым числом оборотов. Стробоскопические вспышки монохроматического источника синхронизируются с моментами времени, когда зеркала проходят через среднюю точку пути, т. е. обладают наиболее равномерной скоростью. Для этой схемы, как и для принципиальной,
δ
1=2Lv/λc, δ2=0, δ3=(L+L1)v/λc,где L=ABC–CDA, L1=AB–AD.
К достоинствам данного метода относятся: положительное (а не нулевое, как в других опытах) смещение интерференционных полос при независимости скорости света от скорости источника; одинаковая скорость всех точек зеркал С в силу их прямолинейного движения; отсутствие на пути лучей стеклянных пластинок, искажающих результат опыта; большая чувствительность.
При L=15 м (длина установки ~ 8 м) и использовании прямого и обратного движения достаточно скорости зеркал 1 м/сек для получения сдвига полос δ1=0,4. К сожалению, до сих пор эксперимент не осуществлён.
Опыт, не связанный с интерференцией, проделали Нильсон и др. [13]. Они измеряли время полета γ-квантов, испускаемых возбуждёнными подвижными и неподвижными ядрами. Пучок α-частиц, разогнанных в циклотроне до 14 Мэв, направлялся на две мишени, расположенные друг за другом с расстоянием между ними 30 см. Одна из мишеней содержала ядра С12, другая – ядра О16. В результате неупругого рассеяния ядра возбуждались в реакциях С12 (α, α') С12* и О16 (α, α') O16*.
Время жизни O16* на возбуждённом уровне (6,13 Мэв) равно 1,2·10–11 сек, и ядро успевает остановиться до испускания γ-кванта. Время жизни С12* на возбуждённом уровне (4,43 Мэв) равно 6,5·10–14 сек, и ядро успевает излучить γ-квант до потери скорости отдачи, приобретённой при столкновении с α-частицей. Измерение эффекта Доплера показало, что средняя скорость ядра С12* в момент излучения равнялась (1,8±0,2)·10–2c, а скорость ядра O16* действительно близка к нулю.
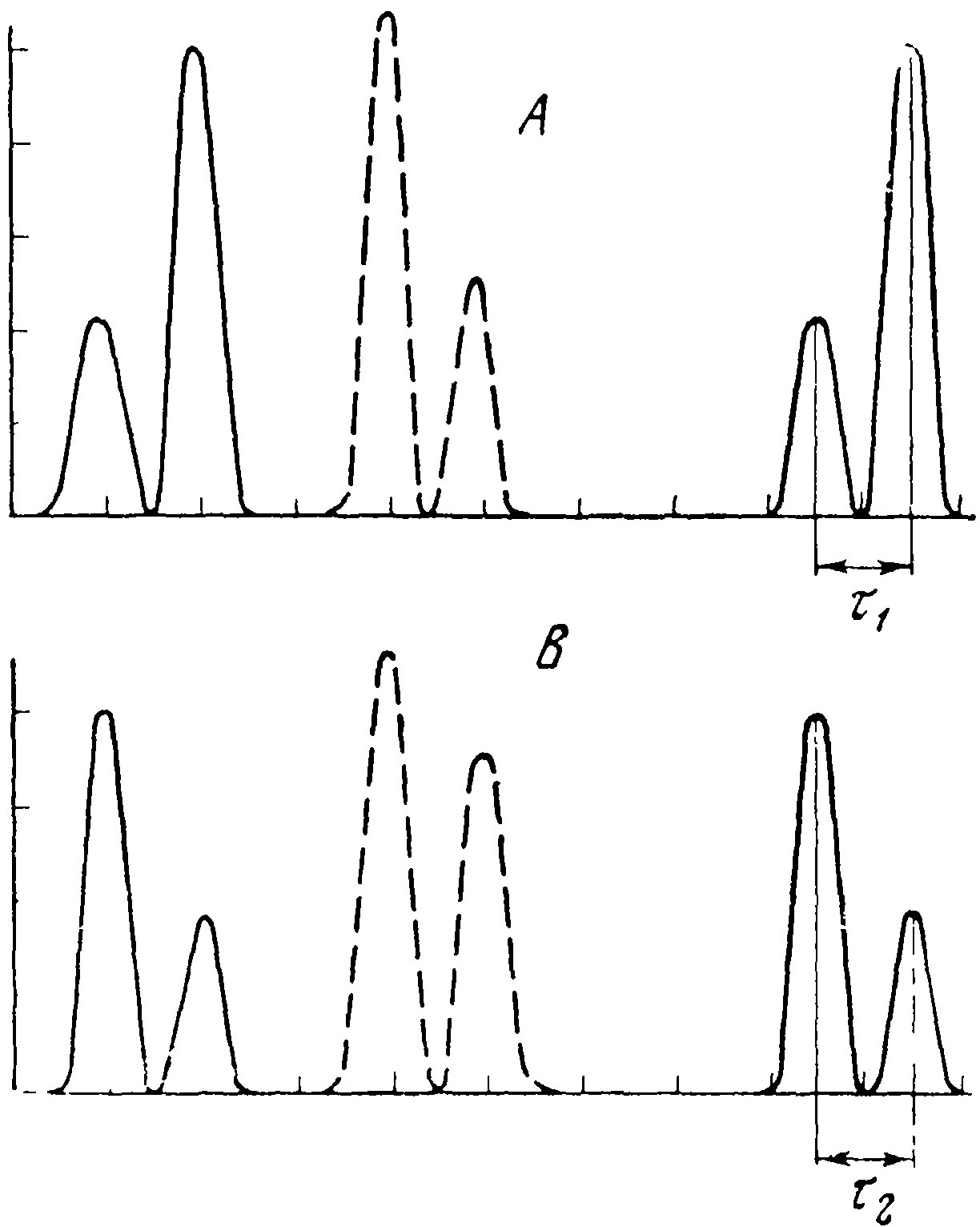
Рис. 5. Спектры времени пролёта γ-квантов в опыте Нильсона
Приёмник располагался на расстоянии 5 м от мишеней вблизи оси пучка α-частиц, и регистрировались промежутки времени между импульсами от обеих мишеней. Другой (контрольный) детектор был установлен на расстоянии 1 м от мишени. На рис. 5 изображены спектры времени пролёта, причём А соответствует спектру для случая, когда впереди установлена мишень с С12, а В, когда мишени поменяли местами. Пунктирные пики соответствуют сигналам, полученным от контрольного детектора, а сплошные (крайние) – от основного. Во избежание совпадения контрольных сигналов с основными первые были сдвинуты с помощью линии задержки. Расстояние между одинаковыми основными пиками соответствует периоду циклотрона и определяет масштаб времени.
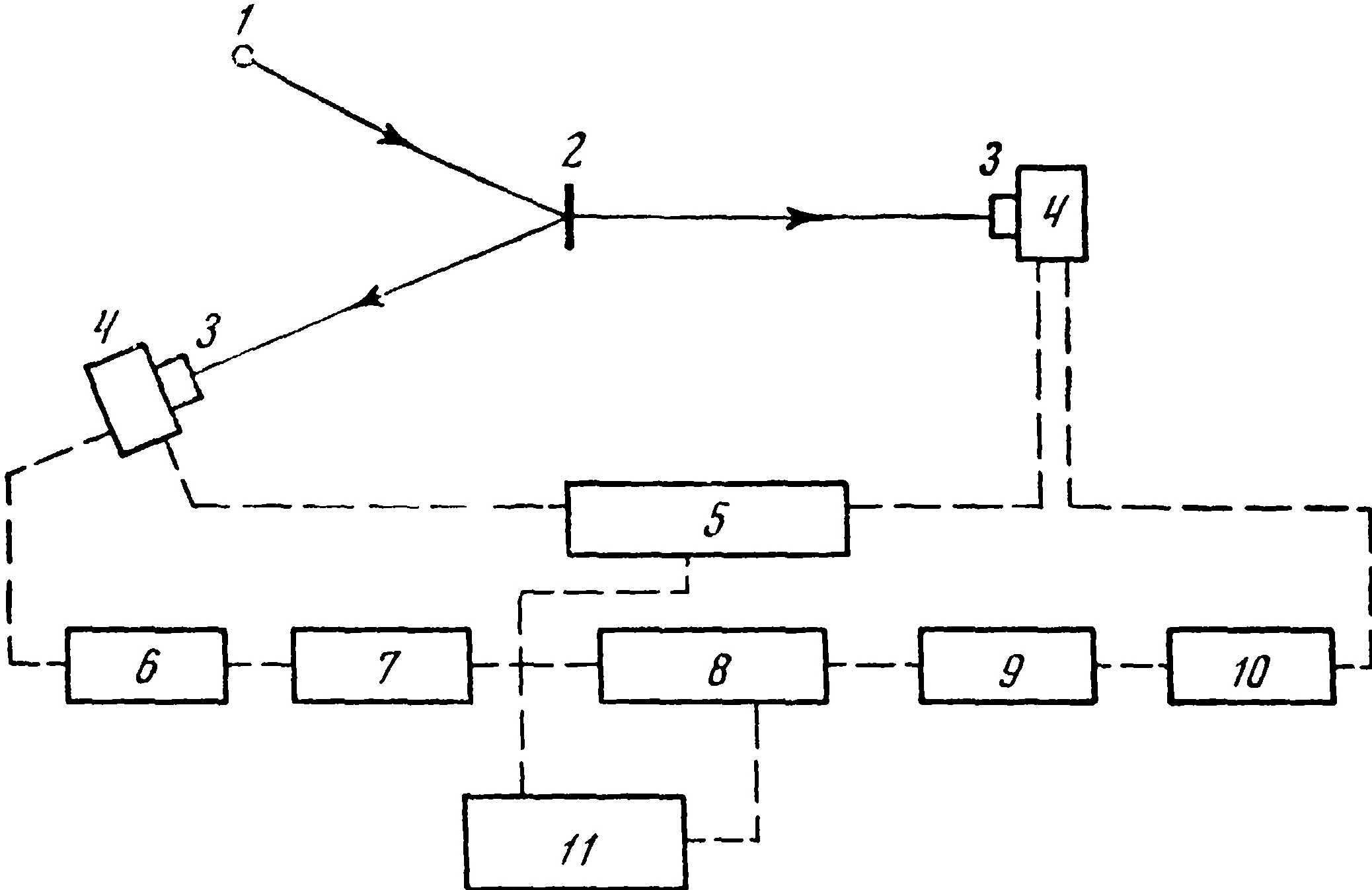
Рис. 6. Схема эксперимента Садэ
Если τ1 – промежуток времени между импульсами для случая A, a τ2 – для случая В, то Δτ=τ1–τ2 должно равняться нулю при независимости скорости света от скорости источника и
Δτ=2·
400·1,8·10–2/c=0,5·10–9 сек,если скорость света складывалась бы со скоростью источника.
Результаты опыта показали, что Δτ=(–0,2±0,2)·10–9 сек, что рассматривается как подтверждение принципа независимости.
Несколько отличен опыт Садэ [14], использовавшего для получения γ-квантов аннигиляцию позитрона с электроном на лету. Схема эксперимента показана на рис. 6.
Источник позитронов (Cu64) расположен в точке 1.
В точке 2 находится мишень из органического вещества (perspex) толщиной 1 мм, в которой происходит аннигиляция. На одинаковом расстоянии (60 см) от мишени расположены два приёмника 3 (кристалл NaJ (T1) размером 1½×1½'') с фотоумножителями 4. Один из приёмников установлен по направлению, составляющему угол 20° с линией полёта позитрона, а другой под углом 135°, так что угол между направлениями обоих приёмников равен 155°. Одноканальные анализаторы пропускают к многоканальному анализатору лишь импульсы от тех γ-квантов, энергия которых находится между 0,511 и 0,65 Мэв, что соответствует энергии аннигиляции в полёте. Сравниваются времена пролёта γ-квантов до обоих приёмников.
Когда центр масс аннигилирующих позитрона и электрона находится в покое, то возникающие γ-кванты разлетаются в противоположных направлениях (180°) с одинаковой скоростью c. Если же центр масс имеет какую-то скорость, то угол между направлениями γ-квантов меньше 180° и по этому углу можно судить о скорости центра масс, т. е. о скорости источника. Углу 155° в рассматриваемом опыте соответствует скорость порядка 0,5 с.
При независимости скорости света от скорости источника время пролёта обоих γ-квантов должно быть одинаково. Если бы скорость света зависела от скорости источника, то к скорости c должна была бы прибавиться проекция скорости источника на направление γ-кванта, и времена пролётов были бы неодинаковы.
Измерения, проведённые при различных расположениях установки, показали совпадение времён с точностью до ±10%.
Хотелось бы отметить следующее. Чтобы совпадение моментов регистрации обоих γ-квантов свидетельствовало о равенстве их скоростей, необходима уверенность в их одновременном испускании, т. е. в их происхождении от одного и того же акта аннигиляции. Однако при большой скорости источника (порядка 0,5c), как предполагается в эксперименте, частоты обоих квантов, одинаковые в системе центра масс аннигилирующих частиц, должны в силу эффекта Доплера сильно отличаться друг от друга в лабораторной системе.
Вследствие пропорциональности энергии квантов частоте (Е=hν) также сильно будут отличаться в лабораторной системе и их энергии. Расчёт показывает, что квант, летящий под углом 20° к линии движения центра масс, обладает энергией порядка 0,9–1,1 Мэв, а квант, летящий под углом 135°,– энергией порядка 0,4 Мэв. На эти энергии и должны быть настроены одноканальные анализаторы.
Поскольку в описанном эксперименте анализаторы были настроены на энергию 0,511–0,65 Мэв, нам остаётся непонятной уверенность автора в происхождении обоих квантов от одного акта аннигиляции.
Кроме описанных выше опытов, были также предложены эксперименты с использованием распада π0 и K-мезонов для получения весьма быстрых источников γ-квантов [15]. Однако пока нет никаких сведений об осуществлении подобных опытов2.
Из настоящего обзора видно, что ни одна из осуществлённых до сих пор экспериментальных проверок, правда немногочисленных, не противоречит принципу независимости скорости света от скорости источника.
За последнее время были проведены также экспериментальные работы по проверке принципа относительности.
Как известно, принцип относительности Галилея был распространён Эйнштейном также на электромагнитные явления после отрицательных результатов по обнаружению “эфирного ветра” в опытах Майкельсона и др. Майкельсон определил, что скорость “эфирного ветра” не превосходит 1/20 скорости Земли по орбите. Описываемые ниже эксперименты показали, что скорость “эфирного ветра” не превышает 1/1000 скорости Земли. Точность этих экспериментов примерно в 50 раз превосходит точность опытов Майкельсона и Морли. Идея этих экспериментов, которую выдвинул Мёллер [17], заключается в следующем.
Если существует “эфирный ветер”, то это должно отразиться на величине эффекта Доплера. Действительно, пусть источник света частоты ν0 движется со скоростью u в лабораторной системе. Тогда воспринимаемая частота в направлении движения
ν=ν
0(1+u/c),где c скорость света.
“Эфирный ветер”, имеющий скорость v в направлении движения источника, изменит скорость света, и она станет равной c+v. Тогда наблюдаемая в лабораторной системе частота будет
ν
1=ν0(1+u/(c+v)),При противоположном направлении “эфирного ветра” эта частота равна
ν
2=ν0(1+u/(c–v)).Отсюда
ν
2–ν1≈2uvν0/c2.В качестве движущихся источников света Мёллер предложил использовать аммиачные мазеры. Скорость молекул аммиачных мазеров порядка 0,6 км/сек, а скорость Земли по орбите 30 км/сек.
Отсюда
ν
2–ν1=2·6·104·30·105·ν0/9·1020=4·10–10ν0.Как известно, стабильность частоты ν0 аммиачных мазеров достигает 10–10 на длительных интервалах и 10–12 на кратковременных.
Установив в противоположном направлении два одинаковых мазера и поворачивая установку, мы должны обнаружить изменение их биения, если имеется “эфирный ветер”. Опыт был осуществлён в 1958 г. [18]. На раме, которую можно было вращать вокруг вертикальной оси, были смонтированы два аммиачных мазера со всем необходимым вспомогательным оборудованием. Направление лучей противоположное. Основная частота мазеров была 23870 мггц. Биение двух мазеров составляло около 20 гц и непрерывно регистрировалось. Примерно через минуту после регистрации биений в положении запад-восток, установка поворачивалась на 180° и биения вновь регистрировались. Серия измерений состояла из 16 поворотов, совершаемых в течение 20 мин; серии повторялись каждый час (более 12 час. подряд), так что направление запад-восток охватывало вследствие вращения Земли все направления плоскости экватора. При каждом повороте на 180° наблюдалось систематическое изменение частоты биения на 1 гц. Это систематическое изменение вызвано земным магнетизмом и местными магнитными полями, от которых установка не была защищена.
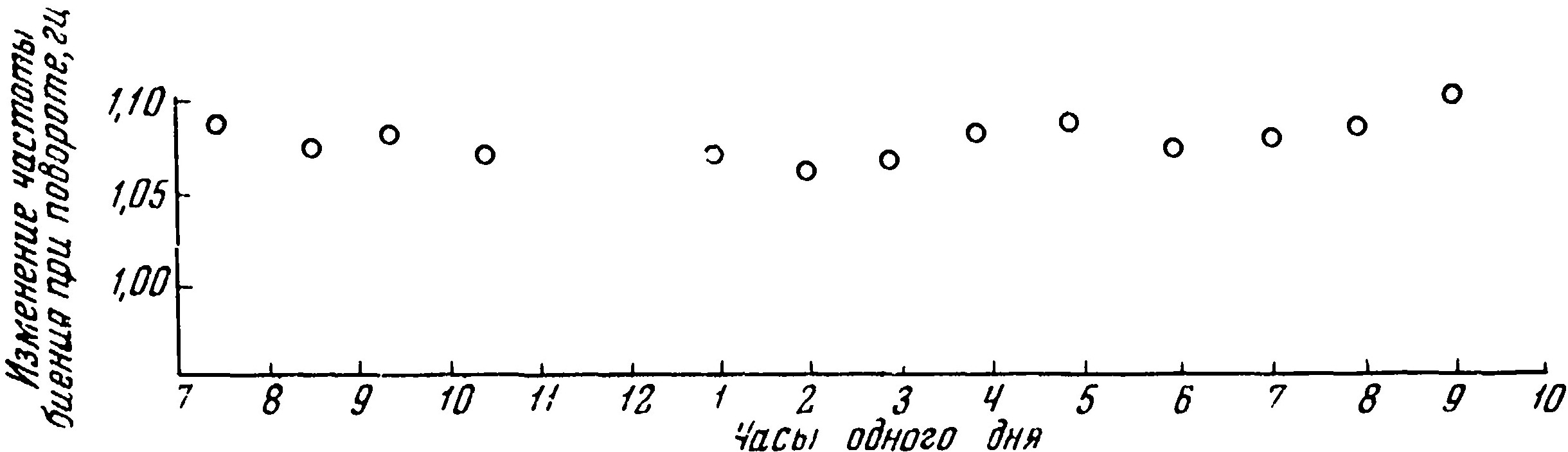
Рис. 7. Изменение частоты биения со временем
Такое предположение подтверждается тем, что это систематическое изменение не зависело от времени дня, т. е. от ориентации Земли, и было большим в будни, чем в субботу, когда помехи от промышленных установок снижались.
Что же касается флуктуаций изменения частоты биений, то они оказались, как видно из рис. 7, меньше ±1/50 гц, в то время как по теории эфира оно должно было быть около 20 гц.
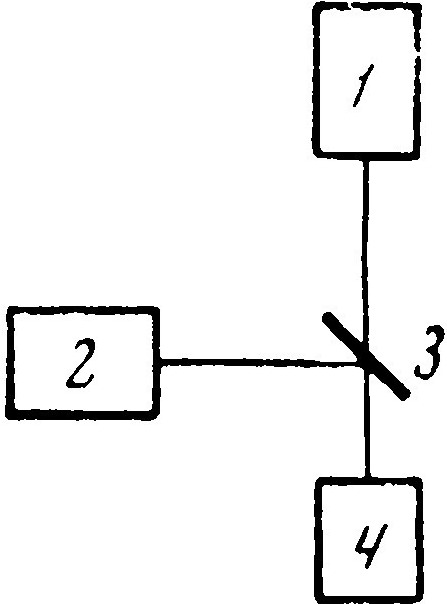
Рис. 8. Схема эксперимента с двумя лазерами
1 – лазер № 1; 2 – лазер № 2; 3 – разделительная пластинка; 4 – фотоумножитель
Таким образом, доказано, что скорость “эфирного ветра”, по крайней мере, в 1000 раз меньше скорости Земли по орбите и не превосходит 30 м/сек.
Опыт был повторен с использованием газовых лазеров на смеси Не–Ne, дающих свет в инфракрасном диапазоне [19].
Как видно из схематического рис. 8, два лазера устанавливались под углом 90°, и разделительная пластинка направляла оба луча на фотоумножитель, воспринимающий их биение. Всё устройство было подвешено на проволоке и совершало крутильные колебания на 90°.
Результат опыта оказался таким же, как и с аммиачными мазерами.
1. Q. M a j о r a n a. Philos. Mag., 1919, 37, 145.
2. А. М. Б о н ч - Б р у е в и ч, В. А. Молчанов. Оптика и спектроскопия, 1956, 1, 113.
3. W. К a n t o r. J. Opt. Soc. America, 1962, 52, 978.
4. P a l a c i o s J u l i o. Rev. Real a, 1963, 57, 237.
5. P. B u r c e v. Phys. Letters, 1963, 5, 44.
6. P. R. W h i 1 e, R. A. A 1 p h e r. J. Opt. Soc. America, 1963, 53, 760.
7. A. B i e r m a n, С. H. v о n K e n s c h i t s k i, D. P a n d r e s. J. Opt. Soc. America, 1963, 53, 1008.
8. V. V у s i n. Phys. Letters, 1964, 8, 36.
9. G. С. В a b с о с k, Т. G. Bergman. J. Opt. Soc. America, 1964, 54, 147.
10. J. G. Fox. Amer. J. Phys., 1962, 30, 297.
11. J. F. J a m e s, R. S. S t e r n b e r g. Nature, 1963, 197, 1192.
12. А. Г. Б а р а н о в. ЖЭТФ, 1961, 40, 860.
13. Т. A l v ä g e r, A. T. N i l l s o n, J. А. К j e l l m a n. Nature, 1963, 197, 1191.
14. D. S a d e h. Phys. Rev. Letters, 1963, 10, 271.
15. W. G. V. R o s s e r. Nature, 1961, 190, 249.
16. T. A. A l v ä g e r, F. T. F а r 1 а у, Т. К j e 11 m a n, T. W a 1 1 i n. Test of the second postulate of special relativity in the Gev Region.– Phys. Letters., 1964, 12 (3), 260–262.
17. G. M ø 1 1 e r. Nuovo Cimento Suppl., 1957, 6, 381.
18. J. P. С a d e r h о 1 m, G. F. В 1 a n d, B. L. H a v e n s, С. H. T o w n e s. Phys. Rev. Letters, 1958, 1, 342.
19. T. S. J a s e j a, A. J a v a n, J. M u r r a y, С. Н. Т о w n e s. Phys. Rev., 1964, 133, 1221.
Дата установки: 10.02.2012
[вернуться к содержанию сайта]